
A Robust Particle Filtering Approach with Spatially-dependent Template
Selection for Medical Ultrasound Tracking Applications
Marco Carletti
1
, Diego Dall’Alba
1
, Marco Cristani
1,2
and Paolo Fiorini
1
1
Department of Computer Science, University of Verona, I-37134, Verona, Italy
2
Istituto di Scienze e Tecnologie della Cognizione (ISTCnr), Consiglio Nazionale delle Ricerche (CNR), Trento, Italy
Keywords:
Medical Image Applications, Ultrasound Tracking, Particle Filtering, Template Selection, Motion Flow.
Abstract:
Tracking moving organs captured by ultrasound imaging techniques is of fundamental importance in many
applications, from image-guided radiotherapy to minimally invasive surgery. Due to operative constraints,
tracking has to be carried out on-line, facing classic computer vision problems that are still unsolved in the
community. One of them is the update of the template, which is necessary to avoid drifting phenomena in
the case of template-based tracking. In this paper, we offer an innovative and robust solution to this problem,
exploiting a simple yet important aspect which often holds in biomedical scenarios: in many cases, the target
(a blood vessel, cyst or localized lesion) exists in a semi-static operative field, where the unique motion is due
to organs that are subjected to quasi-periodic movements. This leads the target to occupy certain areas of the
scene at some times, exhibiting particular visual layouts. Our solution exploits this scenario, and consists into
a template-based particle filtering strategy equipped with a spatially-localized vocabulary, which in practice
suggests the tracker the most suitable template to be used among a set of available ones, depending on the
proposal distribution. Experiments have been performed on the MICCAI CLUST 2015 benchmark, reaching
an accuracy (i.e. mean tracking error) of 1.11 mm and a precision of 1.53 mm. These results widely satisfy the
clinical requirements imposed by image guided surgical procedure and show fostering future developments.
1 INTRODUCTION
Surgical practice is constantly replacing traditional
invasive approaches with minimally invasive surg-
eries (MISs), which provide many benefits for the
patient such as reduced post-operative complications
and faster recovery. These MISs require accurate po-
sitioning of the surgical tools to guarantee the cor-
rect treatment of the diseased area. Although these
procedures could be performed blindly, the introduc-
tion of medical image guidance could improve the
outcome of the procedure even in case of very com-
plex cases. This image guidance is further important
when the target area is moving, for instance due to
breathing motions in abdominal and thoracic areas.
The tracking of respiratory dynamics requires a real
time feedback and error in order of 1 mm to guaran-
tee the expected precision and accuracy of the proce-
dure; moreover, the tracking method should guaran-
tee its processing performance over a long period of
time (in the order of several minutes) compatible with
the duration of the most critical step of the procedure
(De Luca et al., 2013).
Between all the possible image guidance tech-
nologies, ultrasound (US) image provides some inter-
esting characteristics that could not be found in other
medical image modalities (such as computer tomog-
raphy (CT) or magnetic resonance imaging (MRI)):
US is not based on ionizing radiation, the acquisition
device does not require a dedicated room since the
scanner is compact and lightweight and US is able to
acquire images in real time, with very high acquisi-
tion rate up to 100 frames per second. Unfortunately,
all these interesting characteristics come at the cost of
lower contrast and spatial details compared to other
modalities and strong presence of non-Gaussian noise
with complex statistical properties, usually referred
as speckle. According to (Douglas et al., 2001), the
US guided percutaneous procedures are constantly in-
creasing in United States, due to the continuous im-
provement of scanner technology and lower costs.
More than 90% of the total procedures are performed
under US guidance for cancer management, which is
the second most common cause of death in United
States (Siegel et al., 2015).
All the structures in abdominal and pelvic areas
524
Carletti, M., Dall’Alba, D., Cristani, M. and Fiorini, P.
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications.
DOI: 10.5220/0005725505220531
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 524-533
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The figure shows the strong changes in the appearance of different regions of interest, extracted in different temporal
and spatial positions of the image sequence. In (a), the original frame extracted from the US sequence MED-05-1 with the
regions of interest in the highlighted boxes. From (b) to (d) the appearance of the corresponding regions at different instants
of the sequence.
are subjected to breathing motions, that makes re-
ally complex an accurate targeting of pathological ar-
eas for diagnosis and treatment. These regions have
been tracked on US sequences using different ap-
proaches: speckle tracking, optical flow, intensity-
based, feature-based and hybrid methods (see Section
2 for a review).
In all these cases tracking has to face classical
problems which are still of interest in the computer
vision community, like the model drifting (Matthews
et al., 2004; Rattani et al., 2009). This problem holds
in the template-based tracking strategies, where the
object to track is modeled by an exemplar; such ex-
emplar has to be chosen in order to match with the
moving target, and in principle should be able to cope
with changes in appearance, pose, illumination etc.
Unfortunately, a single template does not meet these
requirements, and strategies of template updating are
needed. In general, these strategies modify the ap-
pearance of the target to track, employing mecha-
nisms of soft renewal given by online learning tech-
niques (Matthews et al., 2004; Rattani et al., 2009).
In biomedical applications, online strategies are often
not capable to cope with the dramatic changes that the
object of interest undergoes in the target area (as vis-
ible in Figure 1), resulting in very frequent tracking
failures.
In this paper, we present a tracking approach that
represents a valid solution for the problem of the
model drifting, which is especially suited to scenar-
ios characterized by the following constraints:
• The sensor that captures the target area is static,
that is, the unique motion in the scene is due to
foreground entities; one or more of these moving
entities are the targets to track;
• The moving entities follow quasi periodic trajec-
tories, possibly changing their appearances dras-
tically and where a given appearance could be
statistically associated to a given position in the
tracking area.
These constrains are really common in US guided
surgical procedures, since the most common causes
of physiological deformation and movements are
breathing motions and hearth beat, which are both
highly repetitive (despite the temporal frequency may
change). Even if we release the first constraint, we
can still use an external tracking system to compen-
sate for the movement of the US sensor (Mercier
et al., 2005).
An example of such constraints are reported in
Figure 1, in which liver vessels subjected to breath-
ing motions and deformations are considered. These
requirements are very typical in the case of structures
subjected to respiration motion on US sequences: our
claim is that these phenomena have been never taken
actively into account, and this is a mistake, since on
the contrary they could be exploited as advantages.
The proposed approach consists in a particle filter-
ing framework (Isard and Blake, 1998), in which the
target is tracked by employing an advanced template
matching procedure in the observation step; the nov-
elty lies on the fact that the template is not unique, but
it is chosen among a dictionary of templates, and that
these templates are selected in dependence on the po-
sition in which the target is assumed to be (that is,
checking the position of each particle as it is sam-
pled from the proposal distribution). The dictionary
is built by a semi-automatic training stage, in which
the only supervision required to the user amounts to a
selection of a small set of ground truth positions of the
target(s) (max 30 locations): once the positions have
been defined, a non parametric clustering approach
(affinity propagation (Frey and Dueck, 2007)) operat-
ing on the x,y coordinates and the visual appearance
individuates those zones that more reliably could be
represented by a given template. The approach has
also a single parameter to set, which is the width of
the observation window, plus the duration of the dic-
tionary training stage, which however is usually set
by following medical guidelines (see Section 4 for de-
tail). This promotes our approach for practical use by
medicians. Also, an automatic procedure to rescue
the failure of tracking is proposed exploiting the as-
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications
525

sumption of the localization of the target.
Extensive experiments have been performed on
the MICCAI CLUST 2015 benchmark, showing on
24 video sequences very convincing results; in partic-
ular, on the benchmark data we overcome all the com-
parative baselines, reaching an average accuracy (i.e.
mean tracking error) of 1.11 mm and a precision of
1.53 mm. Moreover, these results widely satisfy the
clinical requirements imposed by common US guided
surgical procedures.
The paper is structured as follows: literature re-
view is presented in Section 2, while in Section 3 the
proposed tracking method is described. In Section 4
the evaluation procedure and results are described and
discussed, and, finally, Section 5 is left for the conclu-
sion and future development of the proposed method.
2 LITERATURE REVIEW
Considering the physical principles behind US image
formation, speckle tracking has been applied to US bi-
dimensional images in (Lubinski et al., 1999), while
the tri-dimensional case has been studied in (Har-
ris et al., 2010) and (Lediju et al., 2010). These
approaches suffer from the technical and hardware
limitations of the actual US scanners and the com-
plex deformation and motion of tissues imaged with
US; therefore, these methods do not obtain perfor-
mance compatible with the challenging clinical con-
ditions. Estimating the optical flow in US image
is a very complex problem due to poor data char-
acteristics. Despite all these limits, a differential
approach called Iterative Conditional Models (ICM)
has been originally introduced in (Geman and Ge-
man, 1984), and later its computational performances
have been improved in (Liu, 2009). Phase Con-
gruency (PC) (Kovesi, 2003) is a processing tech-
nique based on frequency analysis that is robust to
noise, intensity variation and artifacts. As a result
of these properties, PC analysis has been used to
overcome the described US limitations in different
applications in (DallAlba and Fiorini, 2015) (Gau-
tama and Van Hulle, 2002), (Tomasi et al., 2010).
Many block matching (BM) methods have been ap-
plied to US tracking, for instance a multi-scale ap-
proach based on spectral principal component anal-
ysis (PCA) (De Luca et al., 2013) is able to obtain
tracking accuracy in the order of 1 mm. Other multi-
scale and iterative approaches have been presented
in (Bouguet, 2001) and (Farneb
¨
ack, 2003) with com-
parable results.
A similar approach to BM is Template Matching
(TM), where a template is defined at the beginning
of the tracking process and is matched in subsequent
images under the assumption of invariant appearance
of the template. In US images, it is very difficult that
this assumption is satisfied, therefore improved meth-
ods have been proposed in literature based on tem-
plate updating (Matthews et al., 2004; Rattani et al.,
2009) or dictionaries (Mei et al., 2007).
Most of the available TM and BM methods are
based on raw pixel intensity; instead, feature based
methods extract more structured information from US
images. Edge information were among the first fea-
tures used; for instance, in (Guerrero et al., 2007), a
probabilistic edge detector method combined with a
Kalman filter obtains results comparable to the one
of an expert clinician on the segmentation and track-
ing of vessels. Other methods for the same clinical
problem are presented in (Angelova and Mihaylova,
2011) and (Zhang et al., 2010), based respectively on
Multi Model Particle Filter and snake segmentation
supported by a Bayesian filter. Another type of fea-
ture used for US tracking is the salient point extrac-
tion, even if it is not clear how to obtain a stable and
robust extraction in US images. Despite this limit,
salient points have been used for multi-modal image
registration in (Wong and Bishop, 2008) and image
matching in (DallAlba and Fiorini, 2015).
Hybrid methods have been introduced to over-
come the limitations of all the approaches previously
described, by combining two or more of them in a
single framework. A BM method combining PC and
intensity information to define an improved similarity
metric is described in (Cifor et al., 2012). The same
group extends the previous work for the diffeomor-
phic registration of 2D images (Cifor et al., 2013).
In (K
¨
onig et al., 2014), the authors propose a multi-
resolution approach for vessel tracking based on rect-
angular templates for the computation of Normalized
Gradient Field (NGF). In (Somphone et al., 2014),
a sparse demons approach is proposed for the mini-
mization of tracking drift in long US image sequence,
with the goal of minimizing a previously defined en-
ergy function (Thirion, 1998).
At this point, one may ask why other modern
strategies of tracking cannot be taken into account,
as the one of tracking with the support of a detector.
The presence of a detector in a tracking pipeline may
serve to initialize the tracker with a proper template
(Holzer et al., 2015), to create consecutive detections
to be associated in the target-by-detection paradigm
(Avidan, 2007), to help the tracking in the observation
step by suggesting where the object most probably lo-
cates (Breitenstein et al., 2009), or to work indepen-
dently on the tracker in a joint framework, updating
its detection model in an online fashion (Kalal et al.,
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
526

2012). In all the cases, a robust detector has to be
available, which is not a standard assumption in the
case of biomedical applications, where the object of
interest is often poorly distinguishable from the sur-
rounding background and whose appearance changes
radically (as visible in Figure 1).
For this reason, other approaches are often taken
into account, such as the template-based techniques
(previously explained), but also recipes based on B-
splines (Barbosa et al., 2012) or level sets (Dekel
et al., 2013).
3 METHOD
The approach follows the standard pipeline of the par-
ticle filtering procedure (Isard and Blake, 1998), com-
posed by the phases of sampling, dynamics appli-
cation and observation, anticipated by a preliminary
step of initialization. Also, as an extension of the ob-
servation phase, a procedure to resolve the tracking
failure is proposed. The observation and the initial-
ization steps are the ones which embed the novelties
of our approach. In the following, each of these steps
will be explained in the details.
3.1 Initialization
The initialization serves to individuate the first po-
sition where the object to track is located, but most
importantly to build the spatially dependent template
dictionary D before the tracking starts. To reduce the
noise of the images, each frame in the sequences is
preprocessed with a median filter, using a square 3×3
support area.
The idea is to let the human operator select a few
ground truth points in the image sequence (using a
simple interface which can stop/play the streaming to
ease the annotation with a single mouse click for each
object of interest), storing at each selection the x, y
coordinates and the visual appearance of the object
of interest, in terms of an array of grayscale values.
Concerning the appearance modeling, the user selects
a particular fixed dimension d ∈ R
2
+
that individuates
a rectangular patch, so that the point selected by the
user corresponds to the center of the observation win-
dow. The selection of the observation window size
is in practice the only parameter the user has to set
(in addition to the training points) and the values of
all the remaining parameters are dependent on these
numbers, which will be kept fixed during the whole
tracking procedure. After the template selection, the
arrays composed by coordinates and visual appear-
ance of the training locations are given to the affin-
ity propagation clustering approach (Frey and Dueck,
2007), which provides a set of regions in which each
one of them is represented by as a single template, as
visible in Figure 2. In particular, the affinity propaga-
tion builds a similarity matrix S between the training
arrays, where at position i j corresponds the following
similarity measure:
S(i, j) = kp
i
− p
j
k
2
(ssim(T
p
i
, T
p
j
) − 1) (1)
Above, the first factor is the square euclidean distance
between the selected training points p
i
and p
j
, mul-
tiplied by a visual similarity score that is modeled
by the structural similarity measure (ssim) of (Wang
et al., 2004), that compares the templates T
p
i
and T
p
j
centered in p
i
and p
j
. In practice, the probability of
a point to be the centroid of a cluster augments when
the point is far or dissimilar to the others.
The structural similarity exploits the luminance,
contrast and structural components of two n-
dimensional signals and computes a bounded score
which describes the perceived quality (or similarity)
between them. The ssim function is upper bounded
to 1 but is not lower bounded. Despite this fact, we
found that considering as zero the negative results of
ssim does not provide visible side effects in the pro-
posed system. Based on the S matrix, the affinity
propagation algorithm iterates until a partitioning of
the training points is obtained, automatically selecting
also the number of clusters. In the experiments, ap-
proximately 30 training points are required to obtain
complete classification from the clustering method,
ensuring the convergence of the propagation proce-
dure in less than 200 iterations (see the experiments
Section 4). The clustering algorithm returns the dic-
tionary of reference templates. For each cluster, it is
selected the nearest point to the centroid, in an eu-
clidean distance sense, and its appearance is used as
reference.
3.2 Sampling
Given the initial position of the target to track, a set
of np particles is initialized with uniform weight and
spread over the location (see later for the automatic
selection of np). The spread g ∈ R
2
+
is equal to
g = 0.4d, so the 99% of the particles are included
in the region of interest. After the first iteration, the
sampling stage simply accounts for the previous pos-
terior distribution to select those particles that more
probably represent the state of the target. In particu-
lar, the state of the target is represented by its location
l
t
= [u v]
T
in terms of centroid of the bounding box
and appearance. In conclusion, the state of a particle
at time t is:
x
t
= hl
t
, T
l
t
i (2)
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications
527

Figure 2: The template dictionary is obtained from the clustering of the user annotations and the selection of the most
representative template for each cluster. See text for more details. Images (a) and (b) are the original and zoomed frames,
where the user selects the target positions used in the training phase; (c) represents the result of the clustering procedure and
(d) is the vocabulary built with the nearest elements to the centroid of each cluster.
3.3 Dynamics Application
The dynamics of the target is a probabilistic distribu-
tion composed by different elements: h, that is the
story of the target at the previous time frame t − 1;
f, that is the averaged intensity and the mean vector
of the motion flow modeling the global motion in the
observation area, computed over the observation win-
dow; finally, a Gaussian random variable, modeling
the noise of the sensor. In particular, the history com-
ponent is the last speed vector computed as the differ-
ence between the previous two estimated state loca-
tions:
h
t
= l
t−1
− l
t−2
(3)
The motion flow is computed using the algorithm pro-
posed by (Liu, 2009), that performs a conjugate gradi-
ent analysis based on a multiresolution approach. The
method demonstrates a very efficient way to solve the
motion flow problem since, instead of considering the
entire frame, this algorithm performs the computa-
tion only on the observation window of the target. To
reduce the noise influence in the motion estimation,
an entropy analysis is formulated. Let F be the flow
map composed by N speed vectors computed via (Liu,
2009). We introduce the normalized entropy measure
H(F) = −
∑
N
i
F
i
log
2
F
i
log
2
N
(4)
If H(F) is lower than a confidence threshold (in this
case 0.05), the flow component f is discarded, consid-
ering the history twice. The dynamic distribution is
obtained from the combination of the previous com-
ponents, that is
l
t
=
1
2
(f + h) + N (l
t−1
, g
2
), (5)
where the first and second member are respectively
the deterministic and stochastic component.
3.4 Observation
The observation step exploits the dictionary of the
templates, which is built in the initialization step (pre-
viously described in Section 3.1). In practice, af-
ter the application of the dynamics, each sample has
a novel position that is compared against the dictio-
nary created during initialization, selecting the near-
est neighborhood in terms of spatial location. This
indicates the most suitable template to compare the
sample with, where the comparison is carried out us-
ing the ssim measure between the observation window
centered over the hypothesized sample location and
the chosen template. Since the dimensions of the re-
gion of interest of the target is fixed (i.e. it is the only
free parameter of the proposed method), it is possi-
ble to extract a template T
l
t
from the current frame
centered in the target location l
t
. The extracted patch
is then compared with the reference dictionary built
in the initialization stage by the structural similarity
measure, producing the confidence π
t
of the current
state x
t
as:
π
t
= p(x
t
) = ssim(T
l
t
, D(l
t
)) (6)
where D(l
t
) selects from the dictionary the closest ref-
erence template to x
t
. The extraction probability of
a particle depends on its confidence computed at the
time t − 1.
This is a hard selection strategy (at the end, one
sample is associated with only one template), which
has been compared against a soft variation (the sam-
ple is assigned to a mixture of templates, each of them
weighted by a quantity proportional to the distance
w.r.t. the sample) without exhibiting clear advantages.
Therefore, it has been preferred the hard selection op-
tion, which in addition is faster in terms of computa-
tional performance.
3.5 Rescue Procedure
Tracking failures occur when a few frames are lost or
the instantaneous motion of the target is greater than
the observation window size. When the system loses
the target, we notice a unique behaviour in the like-
lihood function estimation that drops to 20% of con-
fidence, as shown in Figure 3. Also, if the target is
lost it is reasonable to assume that it is located in the
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
528

neighborhood of the last valid estimated status of the
tracker.
Following these assumptions, we propose here a
rescue procedure, which is triggered when the likeli-
hood function returns a value L ∈ [0, 1] below a user
defined threshold θ ∈ [0, 1]. The strategy consists
in temporarily disabling the deterministic component
and amplifying the stochastic gain g, which becomes:
g =
2 − L
2.5
d (7)
Due to experimental evidence (on a small subset of se-
quences), we define θ = 0.2. The deactivation of the
deterministic component is necessary because we do
not know what causes the loss of the target. The res-
cue procedure gives robustness to the system, avoid-
ing the manual reinitialization by the user. When
L ≥ θ the spread g returns to its original value as de-
scribed in Section 3.2.
4 EXPERIMENTS
The proposed algorithm needs the tuning of only one
parameter: the dimensions of the observation window
d ∈ N
2
+
. Concerning the number of breathing cycles
nbc ∈ N during which the user selects the training
points, we set it equal to 10 as suggested in (De Luca
et al., 2013). Please note that there are other two pa-
rameters the user could optionally tune: the number of
particles np ∈ N and the gain g ∈ R
2
+
of the stochas-
tic component of each particle filter. We propose an
autotuning procedure to avoid any calibration phase.
Once the user has set the dimensions of the windows,
we compute the other parameters as:
np =
1
4
kdk
2
(8)
g =
1
2.5
d (9)
The equation 8 gives a good compromise between ef-
ficiency and robustness of the system. The gain in
equation 9 is set to include the 99% of the particles
in the observation window assuming normal distribu-
tion.
4.1 Benchmarks
We evaluate our system on the training data from the
MICCAI CLUST 2015 benchmark (only training data
are available at the moment of writing, since test-
ing data will be released after the publication of the
CLUST 2015 results), composed of 24 US sequences,
that we call datasets in the rest of the paper. The
benchmark is subdivided in four categories accord-
ing to the US setup used for the image acquisition:
CIL (2 vids), ETH (12 vids), ICR (4 vids) and MED
(8 vids). Each image sequence has duration between
1 and 10 minutes, with a mean number of frames of
3408±1142. Detailed information about each dataset
are reported in Table 1.
Table 1: Datasets statistics. Im.res indicates the real size
that corresponds to one pixel in the scene.
Dataset Num. Im.rate Im.res. Num.
Name Imgs. (Hz) (mm) Points
CIL-01 1342 18 0.50 2
CIL-02 1075 18 0.50 1
ETH-01-1 3652 25 0.71 2
ETH-01-2 4650 25 0.71 2
ETH-02-1 2620 16 0.40 1
ETH-02-2 4878 16 0.40 1
ETH-03-1 4588 17 0.36 1
ETH-03-2 4191 17 0.36 1
ETH-04-1 5247 15 0.42 2
ETH-04-2 4510 15 0.42 2
ETH-05-1 4615 15 0.40 2
ETH-05-2 3829 15 0.40 2
ICR-01 4858 18 0.41 3
ICR-02 3481 18 0.41 2
ICR-03 3481 18 0.41 3
ICR-04 3481 18 0.41 4
MED-01-1 2455 20 0.41 3
MED-02-1 2458 20 0.41 3
MED-02-2 2443 20 0.41 3
MED-02-3 2436 20 0.41 5
MED-03-1 2442 20 0.41 2
MED-03-2 2450 20 0.41 3
MED-04-1 3304 20 0.41 1
MED-05-1 3304 20 0.41 2
The benchmark provides ground truth measure-
ments that consist in the coordinates of the targets for
a subset of all the frames (approximately 10%). To
compare our system with other approaches we com-
pute three score values, according to the ones used in
the original benchmark: mean tracking error (MTE)
for the accuracy, that is the mean of the absolute posi-
tion error between our measurements and the ground
truth annotations, the standard deviation (STD), that
is calculated as the norm of the square root of position
error variance, and the 95
th
percentile of the position
errors. Lower values indicate better performance.
To better understand the contribution of each part
of the proposed method, we consider the following
cases:
B - Base : the dictionary only contains the first ob-
servation window centered on the target;
R - Rescue : as the previous case, but with the addi-
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications
529
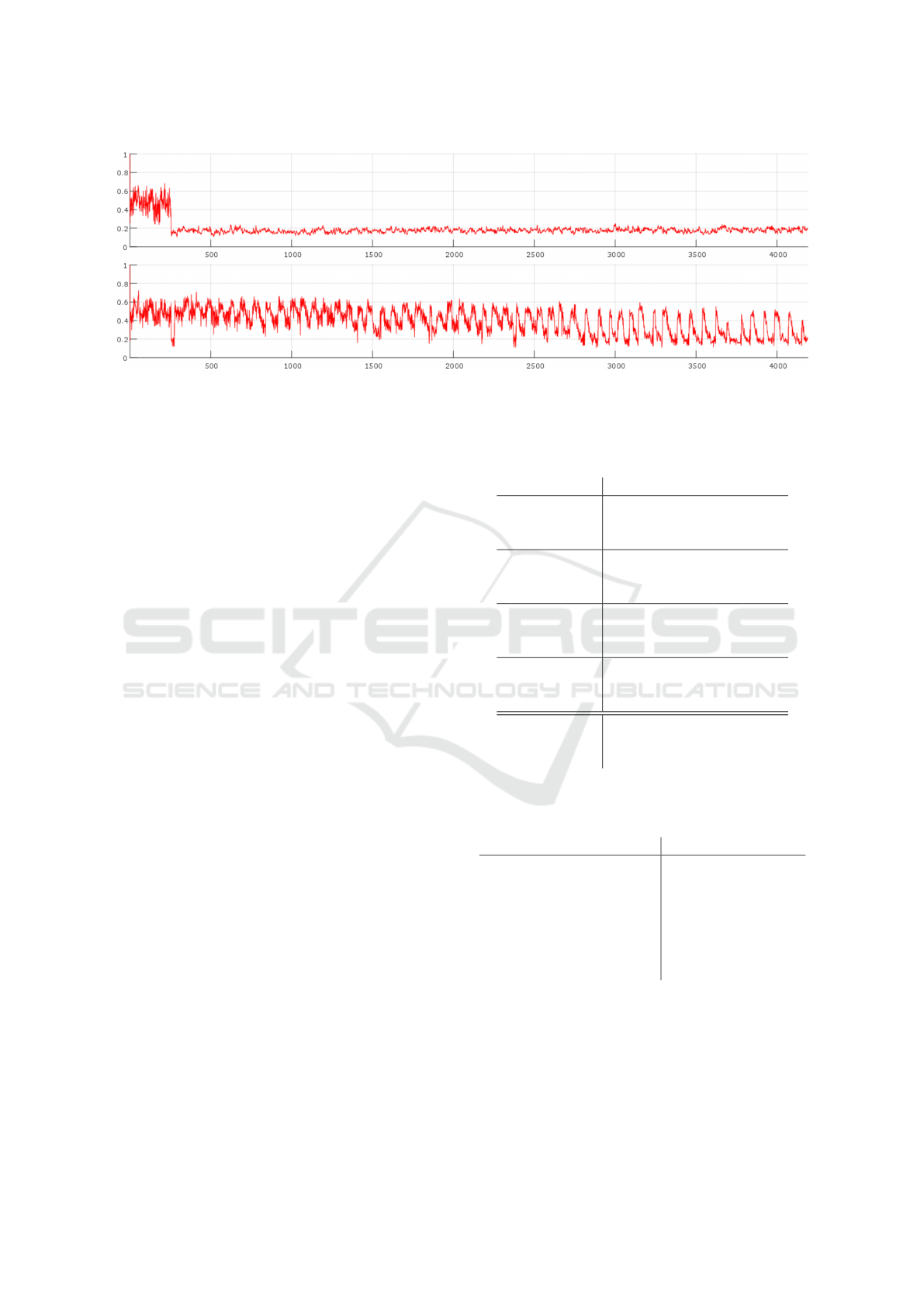
Figure 3: The figure shows the likelihood estimation of the target in the ETH-03-2 dataset before and after the activation of
the rescue procedure (respectively the upper and lower images). After the tracking error at frame 255, the target is lost by the
tracking system. The oscillations in the lower image are due to the breathing of the patient. On the axes, the number of frames
(X) and the normalized confidence (Y).
tion of the rescue procedure;
D - Dictionary : the dictionary is introduced as de-
scribed in Section 3;
RD - Rescue+Dictionary : the combination of the
previous case and the rescue procedure.
The results of each considered case are presented
in Table 2.
The results of the D-case demonstrate the pos-
itive impact of the template dictionary if compared
to the B-case, showing a best accuracy and precision
in almost all the sequences. Concerning the rescue
procedure (R-case), its activation improves the accu-
racy performance by 10% if compared to the B-case.
When both dictionary and rescue procedure are em-
ployed (RD-case), the performance of the method de-
creases the tracking error of 10% if compared the pre-
vious cases. In particular, if compared with the B-
case, the impact of the dictionary and the rescue pro-
cedure improves the overall performance of more than
30%. These final results demonstrate the accuracy of
the method, which is slightly higher than 1 mm. This
is an interesting result if compared to clinical require-
ments (Keall et al., 2006; Shirato et al., 2007) where
high accuracy and robustness are foundamental char-
acteristics. If compared with the CLUST 2014 works,
that are shown in Table 3, our algorithm achieves
competitive results.
The results of the RD-case prove the necessity of
a rescue procedure to give robustness against track-
ing errors. Despite the simplicity of the proposed ap-
proach, the results are very encouraging.
Another interesting comparison is made with the
approach proposed by (De Luca et al., 2013). Using
affine registration, the method achieves an accuracy
of 0.9 mm but requires manual reinitialization when
a frame drop accours. Also, the algorithm is com-
putationally expensive and does not ensure real-time
Table 2: Results of the proposed method on different
datasets. Error in millimiters.
Base R D RD
CIL
MTE 1.71 1.62 1.38 1.28
STD 1.58 1.58 1.13 1.09
95P 2.67 2.50 1.91 1.72
ETH
MTE 2.20 1.58 1.16 1.06
STD 2.37 2.03 1.68 1.69
95P 5.93 5.21 3.16 2.31
ICR
MTE 0.83 0.77 0.75 0.69
STD 1.04 0.98 1.11 1.11
95P 1.59 1.46 1.46 1.26
MED
MTE 1.74 1.92 1.77 1.41
STD 2.40 2.72 2.86 2.22
95P 5.30 5.60 6.80 3.84
Total
MTE 1.62 1.47 1.23 1.11
STD 1.85 1.83 1.70 1.53
95P 3.87 3.69 3.33 2.28
Table 3: CLUST 2014 challenge results of 2D point-
landmark tracking. Results are in millimetres and ranked
according to increasing mean tracking error.
MTE STD 95P
(K
¨
onig et al., 2014) 1.51 1.88 4.06
(Rothl
¨
ubbers et al., 2014) 1.52 1.38 4.08
(Kondo, 2014) 1.83 3.16 4.82
(Benz et al., 2014) 1.84 2.42 5.34
(L
¨
ubke and Grozea, 2014) 1.91 2.47 5.32
(Somphone et al., 2014) 2.00 2.87 5.59
(O’Shea et al., 2014) 2.61 3.78 7.98
processing. A second solution uses a fast BM ap-
proach that achieves lower accuracy (2.18 mm). With
a preliminary training approach, similar to the one
proposed in our work, (De Luca et al., 2013) reaches
an accuracy of 0.84 mm in the first case and 0.97 in
the second one. Our solution overcomes the compu-
tational complexity of the referred solution exploiting
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
530

a fast particle filter approach with an acceptable de-
crease in the results. The proposed method works up
to 15 Hz and the computational complexity for one in-
stance of the system (each instance is a single target)
is proportional to the number of particles, for each
one we calculate the structural similarity, and the size
of the observation window. The complexity is then
O(kdk
4
) but, since the observation windows are usu-
ally small (in the order of 20 × 20 pixels) the high
exponent is not a significant limitation.
Our algorithm runs up to 15 Hz in Matlab R2015a
on a Intel Core i7-2670QM@2.2GHz and achieves a
mean accuracy of 1.11 ± 1.53 mm with a mean 95
th
percentile of 2.28 mm when frame drops occur. The
reference vocabulary gives a significant boost in the
accuracy results, but only with the rescue procedure
the system achieves robustness against outliers.
5 CONCLUSIONS AND FUTURE
WORKS
In this paper a novel approach for tracking in 2D US
image sequences is proposed. The presented tech-
nique consists in a particle filter framework in which
the target is tracked exploiting its semi-periodic dy-
namics and by building a spatially-localized vocab-
ulary with a semi-automatic learning phase. Also,
a rescue procedure is developed to face the problem
of fast movements of the scene or frame drops. Our
method takes advantage from the intrinsic noise ro-
bustness of the CONDENSATION algorithm (Isard
and Blake, 1998), the structural similarity measure
(Wang et al., 2004) that evaluates the similarity be-
tween two images in a perception sense and the fast
optical flow approach proposed by (Liu, 2009). Also,
the proposed approach requires the tuning of only one
parameter, that is the dimensions of the observation
window.
The results confirm our assumptions about the
modeling of the variation of the appearance of the
target by exploiting the periodicity of the dynamics.
Using a single template as reference is a fast solution
but suffers from significant variations of the template.
The vocabulary allows to better describe the appear-
ance model and the space where the target moves,
giving robustness to the system. Unfortunately, the
vocabulary does not manage degenerated cases like
frame drops or fast movements of the scene. The pro-
posed rescue procedure allows to resolve these prob-
lems and gives a significant boost to the overall per-
formance. Results are very promising if compared
with the clinical requirements and the state-of-the-art
solutions.
Future works include a CPU/GPU implementation
to further reduce the lag caused by the computational
complexity. Other optimizations may concern the us-
age of a faster image similarity metrics and optical
flow algorithm, especially for a possible 3D exten-
sion. Also, the median filter used to reduce the noise
should be used only in the neighborhood of the target.
REFERENCES
Angelova, D. and Mihaylova, L. (2011). Contour segmenta-
tion in 2d ultrasound medical images with particle fil-
tering. Machine Vision and Applications, 22(3):551–
561.
Avidan, S. (2007). Ensemble tracking. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
29(2):261–271.
Barbosa, D., Bernard, O., Heyde, B., Dietenbeck, T., Houle,
H., Friboulet, D., and D’hooge, J. (2012). B-spline ex-
plicit active tracking of surfaces (beats): Application
to real-time 3d segmentation and tracking of the left
ventricle in 3d echocardiography. In Ultrasonics Sym-
posium (IUS), 2012 IEEE International, pages 224–
227. IEEE.
Benz, T., Kowarschik, M., and Navab, N. (2014). Kernel-
based tracking in ultrasound sequences of liver. Chal-
lenge on Liver Ultrasound Tracking CLUST 2014,
page 21.
Bouguet, J.-Y. (2001). Pyramidal implementation of the
affine lucas kanade feature tracker description of the
algorithm. Intel Corporation, 5:1–10.
Breitenstein, M. D., Reichlin, F., Leibe, B., Koller-Meier,
E., and Van Gool, L. (2009). Robust tracking-by-
detection using a detector confidence particle filter. In
Computer Vision, 2009 IEEE 12th International Con-
ference on, pages 1515–1522. IEEE.
Cifor, A., Risser, L., Chung, D., Anderson, E. M., Schnabel,
J., et al. (2012). Hybrid feature-based log-demons reg-
istration for tumour tracking in 2-d liver ultrasound
images. In Biomedical Imaging (ISBI), 2012 9th IEEE
International Symposium on, pages 724–727. IEEE.
Cifor, A., Risser, L., Chung, D., Anderson, E. M., Schn-
abel, J., et al. (2013). Hybrid feature-based diffeomor-
phic registration for tumor tracking in 2-d liver ultra-
sound images. Medical Imaging, IEEE Transactions
on, 32(9):1647–1656.
DallAlba, D. and Fiorini, P. (2015). Bipco: ultrasound fea-
ture points based on phase congruency detector and
binary pattern descriptor. International journal of
computer assisted radiology and surgery, 10(6):843–
854.
De Luca, V., Tschannen, M., Sz
´
ekely, G., and Tan-
ner, C. (2013). A learning-based approach for
fast and robust vessel tracking in long ultra-
sound sequences. In Medical Image Computing
and Computer-Assisted Intervention–MICCAI 2013,
pages 518–525. Springer.
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications
531

Dekel, S., Sochen, N., and Avidan, S. (2013). Incremental
Level Set Tracking. Springer.
Douglas, B. R., Charboneau, J. W., and Reading, C. C.
(2001). Ultrasound-guided intervention: Expand-
ing horizons. Radiologic Clinics of North America,
39(3):415 – 428.
Farneb
¨
ack, G. (2003). Two-frame motion estimation based
on polynomial expansion. In Image Analysis, pages
363–370. Springer.
Frey, B. J. and Dueck, D. (2007). Clustering by
passing messages between data points. science,
315(5814):972–976.
Gautama, T. and Van Hulle, M. M. (2002). A phase-based
approach to the estimation of the optical flow field us-
ing spatial filtering. Neural Networks, IEEE Transac-
tions on, 13(5):1127–1136.
Geman, S. and Geman, D. (1984). Stochastic relaxation,
gibbs distributions, and the bayesian restoration of
images. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, (6):721–741.
Guerrero, J., Salcudean, S. E., Mcewen, J., Masri, B., Nico-
laou, S., et al. (2007). Real-time vessel segmenta-
tion and tracking for ultrasound imaging applications.
Medical Imaging, IEEE Transactions on, 26(8):1079–
1090.
Harris, E. J., Miller, N. R., Bamber, J. C., Symonds-Tayler,
J. R. N., and Evans, P. M. (2010). Speckle tracking
in a phantom and feature-based tracking in liver in the
presence of respiratory motion using 4d ultrasound.
Physics in medicine and biology, 55(12):3363.
Holzer, S., Ilic, S., Tan, D., Pollefeys, M., and Navab, N.
(2015). Efficient learning of linear predictors for tem-
plate tracking. International Journal of Computer Vi-
sion, 111(1):12–28.
Isard, M. and Blake, A. (1998). Condensationconditional
density propagation for visual tracking. International
journal of computer vision, 29(1):5–28.
Kalal, Z., Mikolajczyk, K., and Matas, J. (2012). Tracking-
learning-detection. Pattern Analysis and Machine In-
telligence, IEEE Transactions on, 34(7):1409–1422.
Keall, P. J., Mageras, G. S., Balter, J. M., Emery, R. S.,
Forster, K. M., Jiang, S. B., Kapatoes, J. M., Low,
D. A., Murphy, M. J., Murray, B. R., et al. (2006). The
management of respiratory motion in radiation oncol-
ogy report of aapm task group 76a). Medical physics,
33(10):3874–3900.
Kondo, S. (2014). Liver ultrasound tracking using long-
term and short-term template matching. Challenge on
Liver Ultrasound Tracking CLUST 2014, page 13.
K
¨
onig, L., Kipshagen, T., and R
¨
uhaak, J. (2014). A
non-linear image registration scheme for real-time
liver ultrasound tracking using normalized gradient
fields. Challenge on Liver Ultrasound Tracking
CLUST 2014, page 29.
Kovesi, P. (2003). Phase congruency detects corners and
edges. In The australian pattern recognition society
conference: DICTA 2003.
Lediju, M., Byram, B. C., Harris, E. J., Evans, P. M., Bam-
ber, J. C., et al. (2010). 3d liver tracking using a matrix
array: Implications for ultrasonic guidance of imrt.
In Ultrasonics Symposium (IUS), 2010 IEEE, pages
1628–1631. IEEE.
Liu, C. (2009). Beyond pixels: exploring new representa-
tions and applications for motion analysis. PhD the-
sis, Citeseer.
Lubinski, M., Emelianov, S. Y., O’Donnell, M., et al.
(1999). Speckle tracking methods for ultrasonic elas-
ticity imaging using short-time correlation. Ultra-
sonics, Ferroelectrics, and Frequency Control, IEEE
Transactions on, 46(1):82–96.
L
¨
ubke, D. and Grozea, C. (2014). High performance on-
line motion tracking in abdominal ultrasound imag-
ing. Challenge on Liver Ultrasound Tracking CLUST
2014.
Matthews, I., Ishikawa, T., and Baker, S. (2004). The tem-
plate update problem. IEEE Transactions on Pattern
Analysis & Machine Intelligence, (6):810–815.
Mei, X., Zhou, S. K., and Porikli, F. (2007). Probabilistic
visual tracking via robust template matching and in-
cremental subspace update. In Multimedia and Expo,
2007 IEEE International Conference on, pages 1818–
1821. IEEE.
Mercier, L., Langø, T., Lindseth, F., and Collins, L. D.
(2005). A review of calibration techniques for free-
hand 3-d ultrasound systems. Ultrasound in medicine
& biology, 31(2):143–165.
O’Shea, T., Bamber, J., and Harris, E. (2014). Liver fea-
ture motion estimation in long high frame rate 2d ul-
trasound sequences. Challenge on Liver Ultrasound
Tracking CLUST 2014.
Rattani, A., Freni, B., Marcialis, G. L., and Roli, F. (2009).
Template update methods in adaptive biometric sys-
tems: a critical review. In Advances in Biometrics,
pages 847–856. Springer.
Rothl
¨
ubbers, S., Schwaab, J., Jenne, J., and G
¨
unther, M.
(2014). Miccai clust 2014: Bayesian real-time liver
feature ultrasound tracking. Challenge on Liver Ul-
trasound Tracking. MICCAI, pages 45–52.
Shirato, H., Shimizu, S., Kitamura, K., and Onimaru, R.
(2007). Organ motion in image-guided radiotherapy:
lessons from real-time tumor-tracking radiotherapy.
International Journal of Clinical Oncology, 12(1):8–
16.
Siegel, R. L., Miller, K. D., and Jemal, A. (2015). Cancer
statistics, 2015. CA: A Cancer Journal for Clinicians,
65(1):5–29.
Somphone, O., Allaire, S., Mory, B., and Dufour, C. (2014).
Live feature tracking in ultrasound liver sequences
with sparse demons. Challenge on Liver Ultrasound
Tracking CLUST 2014, page 53.
Thirion, J.-P. (1998). Image matching as a diffusion pro-
cess: an analogy with maxwell’s demons. Medical
image analysis, 2(3):243–260.
Tomasi, M., Barranco, F., Vanegas, M., D
´
ıaz, J., and Ros,
E. (2010). Fine grain pipeline architecture for high
performance phase-based optical flow computation.
Journal of Systems Architecture, 56(11):577–587.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.
(2004). Image quality assessment: from error visibil-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
532

ity to structural similarity. Image Processing, IEEE
Transactions on, 13(4):600–612.
Wong, A. and Bishop, W. (2008). Efficient least squares
fusion of mri and ct images using a phase congruency
model. Pattern Recognition Letters, 29(3):173–180.
Zhang, X., G
¨
unther, M., and Bongers, A. (2010). Real-time
organ tracking in ultrasound imaging using active con-
tours and conditional density propagation. In Medi-
cal Imaging and Augmented Reality, pages 286–294.
Springer.
A Robust Particle Filtering Approach with Spatially-dependent Template Selection for Medical Ultrasound Tracking Applications
533
