VAR a New Metric of Cryo-electron Tomography Resolution

Hmida Rojbani

1,2

and Atef Hamouda

University of Strasbourg, 67412, Illkirch Cedex, France

Faculty of Science of Tunis, University Tunis El Manar, 2092 El Manar Tunis, Tunisia

Keywords:

Electron Tomography, Resolution, Metric, 3D Structures, Tilt Angles.

Abstract:

Motivate by reaching a better understanding of the biological cells, scientists use the Transmission Electron

Microscope (TEM) to investigate their inner structures. The cryo-electron tomography (cryo-ET) offers the

possibility to reconstruct 3D structure reconstruction of a cell slice, that by tilting it according different an-

gles. The resolution limits is the biggest challenge in the cryo-ET. The two phases involved in increasing the

resolution are the acquisition phase and the reconstruction phase. In this work, we focus in the last one, as the

biologists treat the acquisition phase within the phase of acquisition itself. The resolution of reconstruction

depends on many factors such as: (1) the noisy and missing information from the collected projections data,

(2) the capacity of processing large data sets, (3) the parametrization of the contrast function of the micro-

scope, (4) errors of the tilt angles used in projections. In this paper, we presented a new method to evaluate

the resolution of a reconstruction algorithm. Then the proposed method is used to show the relation between

errors of the tilt angles used in projection and the degradation of the resolution. The resolution evaluation tests

are made with different reconstruction methods (analytic and algebraic) applied on synthetic and real data.

1 INTRODUCTION

The resolution is a key characteristic of the 3D re-

constructed object, it affects the visual quality of the

object and it can limit the performance of the segmen-

tation method if it fails to attain the highest level pos-

sible. The highest reachable resolution in cryo-ET is

around 5

A, which allows us to locate small objects

as ribosomes, nucleosomes, .... As requirement to

achieve such resolution one must lower the dose of

electrons used on the specimen during the acquisition

and that to minimize the weight of radiation damage

(Egerton et al., 2004). This reduction decreases the

signal to noise ratio and delivers low contrast image.

Moreover, the thickness of the ice used in the ﬁxation

of the sample affects also the ﬁnal resolution of the

reconstructed volume (Stagg et al., 2006). Therefore,

the techniques requested to obtain high-resolution 3D

structures must be reﬁned in order to handle the low

contrast and at the same time very noisy data (Sorzano

et al., 2004).

Mainly, the reconstruction methods that are used

in cryo-ET, they are belongs to two different fam-

ily: (i) the analytic family, where we ﬁnd meth-

ods as ﬁltered back-projection methods, or direct

Fourier inversion methods implemented in Fourier

space (Penczek, 2010); (ii) the algebraic family,

where iterative real-space methods are implemented,

such as ART (Gordon et al., 1970) or SIRT (Gilbert,

1972).

In fact, we will focus in this paper on the resolu-

tion, speciﬁcally how we can judge if this resolution

is a high resolution or not? The rest of the paper will

be structured as follows: in section 2, we discuss the

resolution in the literature, and we present the differ-

ent method of reconstruction found in the literature

in section 3. In section 4, we give our approach for

judging the resolution quality; followed by present-

ing the evaluation of the results in section 5. Finally,

we summarize and give some perspectives.

2 RESOLUTION: DEFINITION

AND METHODS

One of the conversional question in the image-

processing ﬁeld is how we can deﬁne the resolution of

an image. The term ”resolution” in its popular knowl-

edge refers to the pixel count or the dimensions of an

image. Unfortunately,this opinion has no real relation

with the true meaning of the term resolution. Resolu-

tion is simply the ability to tell if a set of pixels rep-

resents distinct object rather than one object (cf. red

156

Rojbani, H. and Hamouda, A.

VAR a New Metric of Cryo-electron Tomography Resolution.

DOI: 10.5220/0005725801540159

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 156-161

ISBN: 978-989-758-175-5

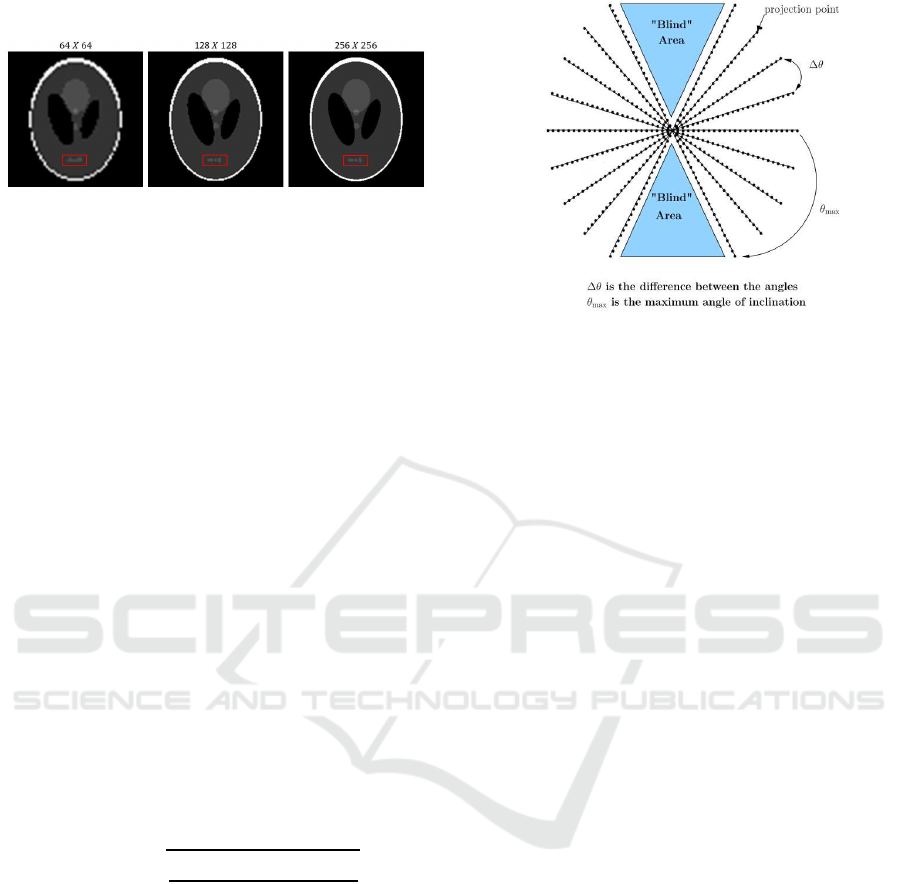
rectangles in Fig. 1).

Figure 1: Effect of pixel resolution.

In electron microscopy, our ﬁeld of interest, res-

olution (A.K.A spatial resolution) refers to the mini-

mum distance between adjacent and in the same time

distinguishable objects in the image; which can be

both detected and interpreted (O’Keefe and Allard,

2004).

Another deﬁnition of spatial resolution is given by

(Midgley and Weyland, 2003), where if the alignment

condition of the projection images is satisﬁed, the res-

olution of the reconstructed object will be depends

from number of projection used in the reconstruction

), maximum angle reached in the tilting operation

(θ

max

) (cf. Fig. 2) and the lateral dimension of the re-

constructed volume (D). The resolution is different

in each axis of the plan. Let us assume that that the

object is in OXYZ space, the axis of tilt is parallel to

the axis OX and the electron beam is parallel to the

OZ axis. Thus, it is possible to deﬁne the spatial res-

olution of the reconstructed volume along three plans

as:

• XY: the resolution is equal to the resolution of the

original 2D projections.

• XZ: the resolution is deﬁned as πD/n

• ZY: the resolution is degraded by a factor e

from

the resolution of XZ. This factor is equal to :

max

+ sinθ

max

cosθ

max

− sinθ

max

cosθ

max

We have another idea to determine the spatial res-

olution; our idea is based on a simulation of our vi-

sual experience with the image. The aim of proposing

this new approach is to verify the truth of argument

that said the uncertainty on the tilt angles due to me-

chanical imprecision of the TEM has no effect on the

ﬁnal reconstructed object resolution (Colliex, 1998).

To test this theory, we used different reconstruction

method that are presented in the next section.

Figure 2: Illustration of sampling data in the Fourier space.

3 RECONSTRUCTION METHODS

In this section, we will discuss the commonly used

methods in cryo-ET reconstruction. In general, there

are two major families of tomographic reconstruction

methods (Frank, 2006). One is the set of analytical

algorithms, based on the direct data inversion. The

other is the set of algebraic (iterative) methods, based

on the inverseproblem, which seeks to reconstruct the

object by iteratively optimizing a criterion deﬁning a

range ﬁdelity between the real projections data and

the reconstructed object.

Analytical methods can use the fast Fourier trans-

form in the calculation of the solution, which can

accelerate the execution time of tomographic recon-

struction. This is a considerable advantage com-

pared to iterative methods. However, an analytical

reconstruction will be effective only if the number of

projection is high and they are uniformly distributed

around the object, which is not the case of cryo-ET.

Moreover, analytical methods are not adapted to the

introduction of additional information on the object

to be used in reconstruction to increase its effective-

ness. For this reason, we will concentrate only on the

algebraic reconstruction.

As mentioned above many algebraic reconstruc-

tions algorithm exist in the literature. In this paper,

we will concentrate in how the model of pixels dis-

tribution in the projection are calculated, not in how

the reconstruction algorithm works. In general, the

problem of tomography represented by the relation

between the projections p

provided by the micro-

scope according to angle θ

and the reconstructed ob-

ject f, as follows:

= W

f, (1)

Thereby, the projection problem is modeled as an

VAR a New Metric of Cryo-electron Tomography Resolution

157

equation system whose matrix W

is sparse. The ma-

trix W

holds the coefﬁcients of the projections ac-

cording to the angle θ

; ∀i ∈ [1 n

]. Here, our target is

which is the best method to ﬁnd W

or which method

provide better resolution with a small number of pro-

jection (n

3.1 Modelisation of the Projection

Matrix W

A reconstruction of good quality requires accurate

modelling of the data acquisition process, or the pro-

jection matrix. Several methods are proposed in the

literature to model this matrix. Standard models such

as ”voxel driven” and ”ray driven” (Joseph, 1982) are

based on direct sampling, which gives modelling er-

rors and artifacts in the reconstructed image. The

model ”voxel driven” (cf. Fig. 3(a)) is based on con-

necting the source to the projection plane by passing a

line through the middle of voxel of interest. However,

the model ”ray driven” (cf. Fig. 3(b)) is based on con-

necting the source to the centre of the cell of interest

on the projection plan by a passing a line through the

image.

To overcome the shortcoming of these two algo-

rithm, (Man and Basu, 2004) proposed another model

called ”distance driven” that modelled the line projec-

tion in the shape of stairs to give a better modelling.

This method’s role is to match the borders of each

voxel and the borders of each cell of the projection

plan on a common line; the difference between these

points deﬁnes the projection coefﬁcients. Measure the

exact intersection area is a difﬁcult task, for this rea-

son, this area will be approximated. For example, to

estimate the projection coefﬁcient p

in Fig. 3(c), we

can use the follow equation (Chen et al., 2015):

∆

n+1

− y

m+1

) f

+ (y

m+2

− x

n+1

) f

m+2

− y

m+1

This is the usual method used in the cryo-ET algebraic

reconstruction.

Recently, Momey et al. (Momey et al., 2011) pro-

posed the use of B-splines as an alternative to the ap-

proach of ”distance driven” (cf. Fig. 3(c)). The B-

Splines are piecewise polynomials, which are charac-

terized by the degree of the constituent polynomials.

The recent work of the sampling theory, (Thevenaz

et al., 2000) (Unser, 2000), have demonstrated their

effectiveness to represent a continuous signal with

good accuracy. One of the most signiﬁcant enhance-

ments provided by the new approach ”spline driven”

proposed by Momey et al. (Momey et al., 2014) is the

reduction of the angular sampling projections with-

out any quality loss. Indeed, this method is based on

(a) ”voxel driven” (Man and Basu, 2004)

(b) ”ray driven” (Man and Basu, 2004)

Figure 3: The various methods to create a projection matrix.

the idea of presenting the objects in the image by B-

splines instead of using classical cubic grid. Even the

lines of projections are modelled by B-splines. This

model improves the calculation of the projection co-

efﬁcients.

In this paper, we want to verify if the using of the

iterative algebraic methods can affect and decrease

the resolution of the reconstruction or not. For this,

we will compare between SIRT (with the ”distance

driven”) and the ﬁltered back-projection (FBP), us-

ing our new metric of resolution. More details of

this approach called Visual Assumption of Resolution

(VAR) is in the next section.

4 VISUAL ASSUMPTION OF

RESOLUTION

The aim of using electron microscopy is reaching an

atomic resolution, which is a hard target to reach in

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

158

the biological imaging case, due to the sensibility na-

ture of biological simples to electron radiation. The

solution was to minimize in one side the electron dose

used in acquisition (providing a low contrast image

with low SNR) and in the other side the number of ex-

posing to this dose (providing a small number of pro-

jection leading to a mediocre reconstruction). In this

work, we will concentrate only on the effect of the

projections number putting in mind that in the syn-

thetic tests we will control everything else to be in the

perfect conditions. The purpose of our metric VAR is

to see how much is the loss of resolution according to

the real objects resolution.

If we analyze visually the reconstructed object we

ﬁnd that the building shape of objects in the image

change dramatically according to number of iteration

of the reconstruction algorithm, the number of pro-

jection (n

) used in reconstruction (cf. Fig. 4). The

changes can be described by perturbation in the bor-

ders of object, which leads to fusion of object if they

are near each other. In addition, there are a slight

change in the spectral of the object. Hence, we have

the idea of using these two modiﬁcation to calculate

the rate of loss in resolution from the real object.

Figure 4: Resolution decrease after reconstruction with

SIRT (100 iteration) and n

= 71.

The VAR metric has two section, the ﬁrst interpret

the space (pixel) diversity between the original and re-

constructed image (noted as VAR

space

) and the second

outline their the spectral (radiometry) variation (noted

as VAR

spectral

To calculate VAR

space

we will count the differ-

ence between the nonzero number of pixel in the orig-

inal image and in the reconstructed image. The found

value will be normalized by the nonzero number of

pixel in the original image. The equation to calculate

VAR

space

as follow:

VAR

space

∑

i=1

−

∑

i=1

∑

i=1

(2)

Where N is the total number of pixel in the image,

= 1 (respectively O

= 1) if the i−th pixel of the re-

constructed (respectively original) image is nonzero,

= 0 (respectively O

= 0) otherwise. VAR

space

will

equal to zero if two image has the same number of

nonzero pixels, otherwise will be greater than zero.

Now, to calculate VAR

spectral

we will count the

difference between the sum of the spectral of all pix-

els between the original image and the reconstructed

image. As the previous calculation, the difference will

be normalized by the sum of the original image. The

equation to calculate VAR

space

as follow:

VAR

spectral

∑

i=1

PxR

−

∑

i=1

PxO

∑

i=1

PxO

(3)

Where PxR

(respectively PxO

) is the spectral of

the i− th pixel of the reconstructed (respectively origi-

nal). The same as the previous, VAR

spectral

will equal

to zero if two image has the same amount of radiome-

tries, otherwise will be greater than zero.

The value of VAR will be the mean between

VAR

space

and VAR

spectral

VAR =

VAR

space

+VAR

spectral

(4)

One can notice that for VAR to be efﬁcient the

tested image must simple structured. The tests and

results of applying VAR in different situations are

shown in the next section.

5 RESULTS

Several experiments were conducted to assess the

efﬁciency of the proposed method on 2D and 3D

data. The experiments involve 62 2D and 25 3D syn-

thetic gray-level images randomly generated at dif-

ferent size N = 128, 256, 512. A sample of 2D the

synthetic images used are shown in the ﬁgure 5.

Figure 5: 2D synthetic images.

We will calculate also the cross-correlation coef-

ﬁcient (equation (5)). It is a criterion to measure the

degree of similarity between the original image and

the reconstructed image. This coefﬁcient is equal to 1

when the reconstructed image coincides exactly with

the original image and zero otherwise.

Corr =

∑

i=1

(PxO

− M(O))(PxR

− M(R))

∑

i=1

(PxO

− M(O))

∑

k=1

(PxR

− M(R))

(5)

where M(.) is the mean of the radiometry of the

image.

VAR a New Metric of Cryo-electron Tomography Resolution

159

The ﬁrst phase of testing was to study the effect of

different number projection (n

) over the resolution

of the reconstruction. For the record, all the algebraic

reconstruction in this section used a ﬁxed number of

iteration equals to 100 iterations. The mean results

are shown in table 1 and table 2.

Table 1: The mean evaluation of 2D and 3D synthetic data

for the FBP.

Size 128 256 512

Corr 0.89 0.93 0.95

VAR 0.67 0.59 0.58

Table 2: The mean evaluation of 2D and 3D synthetic data

for the SIRT with ”distance driven” method.

Size 128 256 512

Corr 0.92 0.95 0.96

VAR 0.52 0.39 0.31

We can see clearly the upper hand of the SIRT

over the FBP. Moreover, we notice in table 1 that even

if the correlation is good, the resolution was poor. For

this reason, we can say that correlation is not a trusted

evaluation measure to prove the performance of a re-

construction. In the followed tests, we calculate only

VAR.

The mean results according to deferent angular er-

ror (AE) applied on tilt angles are given in table 3 for

= 360 and in table 4 for n

= 71, which is the usual

number used in the real case of cryo-ET.

Table 3: The results for 3D synthetic data with n

= 360.

◦

≤ 1

◦

≤ 2

◦

FBP 0.56 0.88 0.92

SIRT 0.15 0.23 0.34

Table 4: The results for 3D synthetic data with n

= 71.

◦

≤ 1

◦

≤ 2

◦

FBP 0.82 0.99 1.32

SIRT 0.24 0.38 0.57

It is clear that if the tilt angles are erroneous, than

the resolution will decrease even if we use all the pos-

sible tilt angles.

6 CONCLUSION

In this paper, we proposed a new metric to calculate

the resolution of the reconstruction object. The pur-

pose of this metric VAR is to verify to performance

of the reconstruction algorithm used and their efﬁ-

ciency to preserve the resolution of the real object.

We showed here, the upper hand of the algebraic iter-

ative methods. In addition, we showed also the effect

of an erroneous tilt angles over the results of the re-

constructed object.

REFERENCES

Chen, J.-L., Li, L., Wang, L.-Y., Cai, A.-L., Xi, X.-Q.,

Zhang, H.-M., Li, J.-X., and Yan, B. (2015). Fast par-

allel algorithm for three-dimensional distance-driven

model in iterative computed tomography reconstruc-

tion. Chinese Physics B, 24(2).

Colliex, C. (1998). The Electron Microscopy. Presses Uni-

versitaires de France.

Egerton, R., Li, P., and Malac, M. (2004). Radiation dam-

age in the TEM and SEM. Micron, 35(6):399–409.

Frank, J. (2006). Electron tomography: methods for three-

dimensional visualization of structures in the cell.

Springer.

Gilbert, P. (1972). Iterative methods for the three-

dimensional reconstruction of an object from projec-

tions. Journal of Theoretical Biology, 36(1):105–117.

Gordon, R., Bender, R., and Herman, G. (1970). Al-

gebraic Reconstruction Techniques (ART) for three-

dimensional electron microscopy and X-ray photog-

raphy. J Theor Biol, 29(3):471–481.

Joseph, P. (1982). An improved algorithm for reprojecting

rays through pixel images. Medical Imaging, IEEE

Transactions on, 1(3):192–196.

Man, B. D. and Basu, S. (2004). Distance-driven projection

and backprojection in three dimensions. Physics in

Medicine and Biology, 49(11):2463.

Midgley, P. and Weyland, M. (2003). 3d electron mi-

croscopy in the physical sciences: the development

of z-contrast and {EFTEM} tomography. Ultrami-

croscopy, 96(34):413 – 431. Proceedings of the In-

ternational Workshop on Strategies and Advances in

Atomic Level Spectroscopy and Analysis.

Momey, F., Denis, L., Mennessier, C., Thiebaut, E., Becker,

J.-M., and Desbat, L. (2011). A new representation

and projection model for tomography, based on sep-

arable b-splines. In Nuclear Science Symposium and

Medical Imaging Conference (NSS/MIC), 2011 IEEE,

pages 2602–2609.

Momey, F., Thiebaut, E., Mennessier, C., Denis, L., and

Becker, J.-M. (2014). Spline driven: high accuracy

projectors for 3D tomographic reconstruction from

few projections. submitted.

O’Keefe, M. and Allard, L. (2004). A standard for

sub-ngstrom metrology of resolution in aberration-

corrected transmission electron microscopes. Mi-

croscopy and Microanalysis, 10:1002–1003.

Penczek, P. (2010). Chapter one - fundamentals of

three-dimensional reconstruction from projections. In

Grant, J., editor, Cryo-EM, Part B: 3-D Reconstruc-

tion, volume 482 of Methods in Enzymology, pages

1–33. Academic Press.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

160

Sorzano, C., de la Fraga, L., Clackdoyle, R., and Carazo, J.

(2004). Normalizing projection images: a study of im-

age normalizing procedures for single particle three-

dimensional electron microscopy. Ultramicroscopy,

101(24):129–138.

Stagg, S., Lander, G., Pulokas, J., Fellmann, D., Cheng, A.,

Quispe, J., Mallick, S., Avila, R., Carragher, B., and

C.S.Potter (2006). Automated cryo-em data acquisi-

tion and analysis of 284742 particles of groel. J Struct

Biol, 155:470–481.

Thevenaz, P., Blu, T., and Unser, M. (2000). Interpolation

revisited [medical images application]. Medical Imag-

ing, IEEE Transactions on, 19(7):739–758.

Unser, M. (2000). Sampling-50 years after shannon. Pro-

ceedings of the IEEE, 88(4):569–587.

VAR a New Metric of Cryo-electron Tomography Resolution

161