
Shape and Reflectance from RGB-D Images
using Time Sequential Illumination
Matis Hudon
1,2
, Adrien Gruson
1
, Paul Kerbiriou
2
, Remi Cozot
1
and Kadi Bouatouch
1
1
IRISA, Rennes 1 University, Rennes, France
2
Technicolor, Rennes, France
Keywords:
Depth Enhancement, Depth Discontinuity, Time Multiplexed Illumination, Image Pairs, Pure Flash Image.
Abstract:
In this paper we propose a method for recovering the shape (geometry) and the diffuse reflectance from an
image (or video) using a hybrid setup consisting of a depth sensor (Kinect), a consumer camera and a partially
controlled illumination (using a flash). The objective is to show how combining RGB-D acquisition with
a sequential illumination is useful for shape and reflectance recovery. A pair of two images are captured:
one non flashed (image under ambient illumination) and a flashed one. A pure flash image is computed by
subtracting the non flashed image from the flashed image. We propose an novel and near real-time algorithm,
based on a local illumination model of our flash and the pure flash image, to enhance geometry (from the noisy
depth map) and recover reflectance information.
1 INTRODUCTION
Low-cost RGB-Depth scanners have recently led to
a little revolution in computer graphics and computer
vision areas with many direct applications in robotics,
motion capture and scene analysis. The main con-
cern of such depth sensors is their low accuracy due
to noise and their inherent quantization (see raw depth
image in Figure 1). The idea of improving depth us-
ing the information contained in the associated RGB
image has been widely explored (Diebel and Thrun,
2005; Richardt et al., 2012; Nehab et al., 2005; Wu
et al., 2014). It relies on building a complete model
of the scene by estimating and ideally extracting sep-
arately materials, 3D shape and illumination. The
depth sensor usually provides a rough estimate of the
scene geometry which is then refined using lighting
and materials (extracted from RGB images) as well
as shape from shading-based algorithms.
On the other hand, stereo photometry methods
have been used for years to extract finer geometry and
materials from images of a scene (Woodham, 1980;
Kim et al., 2010; Debevec, 2012). Unfortunately, the
use of stereo photometry is inappropriate in most of
the shooting scenarios as it requires finer calibration
and a complex lighting setup. Therefore stereo pho-
tometry methods cannot be easily incorporated into a
traditional movie framework.
In our new technique, we explore the possibilities
given by a hybrid setup consisting of a depth sensor
together with a partially controlled illumination. We
target a low-cost and the least intrusive possible setup.
Our idea is to use RGB flashed and non-flashed image
pairs. To obtain such pairs we perform a time sequen-
tial illumination by triggering flash illuminations on
half the frames of the RGB camera and then extract-
ing two sequences of the same scene: one correspond-
ing to the scene with its natural illumination and no
alterations, preserving then the shooting framework,
and another containing flashed images.
With a proper combination of the two images of
an image pair, we create a pure flash image, as if the
unknown ambient illumination had been switched off,
which amounts to take a picture of the scene under the
flash illumination only (DiCarlo et al., 2001). This
provides us with a sequence of images with a con-
trolled and simple illumination, which simplifies the
ill-posed problem of retrieving separately shapes and
albedos from a single image. We use raw depth input
to estimate a rough normal map, and our knowledge
of the flash illumination to reconstruct high quality
normals and albedos for each pixel using a simple it-
erative mean square optimization. The main contribu-
tions of this paper are:
• a new method, to efficiently recover geometry
and albedo from image sequences, using a hybrid
setup combining sequential illumination and con-
sumer depth sensors;
534
Hudon, M., Gruson, A., Kerbiriou, P., Cozot, R. and Bouatouch, K.
Shape and Reflectance from RGB-D Images using Time Sequential Illumination.
DOI: 10.5220/0005726305320541
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 534-543
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Raw depth image Flash contribution image
Refined normals Refined reflectance iter. 0 final iter.
NormalsReflect.
Figure 1: Our method takes as input a flash image registered with a depth map (Kinect). The flash image is computed using
flashed and non flashed image pairs which represent two successive video frames. With these inputs our algorithm use an
optimization process to produce refined normal and reflectance maps.
• robustness to multiple albedo scenes;
• near real-time performance.
2 RELATED WORK
Shape from Shading. (Horn, 1970) Introduced the
shape from shading technique, using intensity pat-
terns across an image, under the assumption of Lam-
bertian reflectance and uniform illumination, to ex-
tract 3D geometry. Later (Horn and Brooks, 1989)
explored variational approches to shape from shad-
ing. (Bruckstein, 1988) derived fine height maps from
scenes illuminated from above, using a shape from
shading method based on a recursive way of deter-
mining equal-height contours. More recently (Pra-
dos and Faugeras, 2005; Fanello et al., 2014) used
controlled light sources near the camera optical cen-
ter and took into account the inverse squared distance
attenuation term of the illumination in a shape from
shading approach.
Depth Upsampling. (Diebel and Thrun, 2005)
used Markov Random Fields to fuse data from a low
resolution depth scanner and a high resolution color
camera. (Richardt et al., 2012) proposed an efficient
and effective depth filtering and upsampling tech-
niques for RGB-D videos, but take no advantage of
shading in their framework. Their heuristic approach
look plausible but may not be metrically accurate.
(Nehab et al., 2005) devised an efficient algorithm for
combining depths and normals while taking advan-
tage of each to create the best geometry possible for
computer graphics purposes. (Wu et al., 2014) pre-
sented a real-time method to solve the inverse ren-
dering problem using an effective parametrization of
the shading equation. Their method allows refining
a depth map captured by consumer depth camera for
lambertian scenes with a time varying uncontrolled
illumination. Recently (Or-El et al., 2015) proposed
a novel method to enhance the depth captured with
low-cost RGB-D scanners without the need to explic-
itly find and integrate surface normals. Their method
gives accurate results and runs in real-time, it achieves
10 fps for 640 × 480 depth profiles. We provide
more details on this technique in the result section
as we compare it to our method. (Newcombe et al.,
2015) presented an impressive SLAM method capa-
ble of reconstructing non-rigid deforming scenes in
real-time, by fusing RGBD scans captured from com-
modity sensors.
Intrinsec Image Decomposition. (Shen et al.,
2008) described the possibility of separating, in a sin-
gle image, shading from reflectance by relying on
the observation that distinct points with the same
intensity-normalized texture configuration generally
have the same reflectance value. (Shen and Yeo,
2011) based on chromaticity to show that the re-
flectance in a natural image is sparse. Using this spar-
sity prior they formulated a regularized least square
minimization problem that can be solved efficiently,
their algorithm successfully extract an intrinsic image
from a single image.
Photometric Stereo was firstly introduced by
(Woodham, 1980). (Higo et al., 2010) pushed the
photometric stereo a little further replacing the lam-
bertian prior by three reflectance properties: mono-
tonicity, visibility and isotropy. This allows to capture
more surfaces including specular ones, but the system
requires many pictures with different directions of il-
lumination. (Tunwattanapong et al., 2013) presented
a way for acquiring geometry and spatially varying
reflectance properties using spherical harmonic illu-
minations. They developed a system comprising a ro-
tating arm capable of reproducing spherical harmonic
illumination. Photometric stereo works very well for
fixed scenes but as it requires at least three observa-
tions of the scene under different and non co-planar
illuminations, it is by nature difficult to use for video.
Several attempts have been made to adapt photomet-
ric stereo to video. Indeed, (Kim et al., 2010) and
(Hern
´
andez et al., 2007) use colored lights to obtain
several images (with different lighting directions) in a
single snapshot. (de Decker et al., 2009) used both
colored lights and time multiplexed images to per-
form photometric stereo (with more than 3 light di-
rections) on video sequences. This method resolves
low frame rate issues inherent in photometric stereo
Shape and Reflectance from RGB-D Images using Time Sequential Illumination
535

applied to video, but suffers from some issues. For
example, the method fails when the spectra of one of
the light sources and the albedo of an object do not
overlap. (Wenger et al., 2005) proposed a method to
acquire live-action performance of an actor, allowing
lighting and reflectance to be designed and modified
in post-production. They obtained excellent results
but need a highly controlled environment and a syn-
chronization device between lights and cameras. (De-
bevec, 2012) presented a variety of facial scanning
and reflectance measurements works achieved with
light stage system. They obtained results that are very
impressive but cannot be incorporated in many tradi-
tional shooting scenarios as they require a complex
lighting and synchronization setup.
Image Pairs. After the report of (Xiao et al.,
2001), that showed that, using active light sources,
it is possible to measure object information indepen-
dently of the passive illuminant. (DiCarlo et al., 2001)
had the idea of combining two images, one with am-
bient unknown illumination and the other with an ad-
ditional controlled and known illumination, to obtain
an image without ambient illumination and then es-
timate the spectral power distribution of the ambient
illumination. More recently (Petschnigg et al., 2004)
used pairs of flashed and non flashed images for vari-
ous applications in digital photography, including de-
noising, detail transfer, white balancing and red-eye
removal.
3 GENERAL IDEA
Under the assumption of Lambertian scene a pho-
tometric stereo-baed method uses three observations
(three images) of the same scene, under different il-
luminations, to compute surface normals and diffuse
reflectances (albedo). Now imagine a single albedo
scene illuminated by a single known light source. It is
possible to estimate a rough normal map with a low-
cost RGB-D sensor, and so for each point in the scene
it is easy to compute the diffuse reflectance from the
shading equation and the rough normal map. As the
measured normals are not perfectly estimated the dif-
fuse reflectance computed for each point is different
rather than similar (errors on normal estimation af-
fect the diffuse reflectance estimation), but the scene
is supposed to be a single albedo scene, which means
that all the diffuse reflectances have to be equal. If
we suppose that the errors on normal estimation are
equally distributed over the range of possible nor-
mal directions, a single albedo of the scene can be
estimated by averaging all the obtained diffuse re-
flectances. We now have an estimate of the scene dif-
fuse reflectance together with a knowledge of the only
light source within the scene. The normal map esti-
mate can then be improved using the shading equa-
tion. Those new computed normals can be used as
input for a novel per-point estimation of diffuse re-
flectance. This process can be repeated until conver-
gence.
For natural scenes, we relax the assumption of sin-
gle albedo to consider multiple albedos by assuming
that the reflectance of these scenes is sparse (Shen
and Yeo, 2011). Using chromaticity, we can cluster
points in the scene so that each cluster contains points
of nearly the same diffuse reflectance. As for illumi-
nation, we use pairs of flashed and non flashed images
to extract pure flash images (DiCarlo et al., 2001).
Light Source Modeling. We assume that the
flash LED light source is small, consequently the light
source will be characterized by its intensity I
s
:
I
s
(ω
i
) = L
s
· ∆S ·|N(S) · ω
i
| (1)
where ∆S is the surface area of the flash light source,
L
s
its emitted luminance, N(S) its normal and ω
i
its
emission direction. With this assumption, we can eas-
ily compute the reflected luminance L of an point P as
seen through a pixel in direction ω
c
as:
L(P,ω
c
) = f r(P,ω
i
→ω
c
) · I
s
(ω
i
) ·
|N(P).ω
i
|
k
P − S
k
2
(2)
where f r is the bidirectional reflectance distribution
function (BRDF) of the surface, ω
i
the emission di-
rection of the light source, N(P) the surface normal
at P and
k
P − S
k
the distance between the flash light
source and P.
Scene Illumination. Let p be a pixel of coordi-
nates (u, v) on the camera sensor (centered coordi-
nates). This pixel can be projected onto the scene as
a 3D point P(u,v) expressed in the camera coordinate
system by using the camera parameters:
P(u,v) =
u.D(u, v)/ f
x
v.D(u,v)/ f
y
−D(u, v)
(3)
where ( f
x
, f
y
) are the camera focals and D(u,v) is the
depth value given by the depth sensor expressed in
the rgb camera coordinate system. For a Lambertian
surface, the luminance of a point P can be expressed
as:
L(P(u,v), ω
c
) = k
d
(u,v) · I
s
(ω
i
) ·
|N(u,v).ω
i
|
d
2
(4)
where d =
k
P − S
k
. The diffuse reflectances k
d
(for
each color component RGB) and the surface normals
N are stored into two different 2D buffers. From now
on, we will use p = (u,v) and L(P(u, v),ω
c
) = L(p)
for each RGB component c.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
536

Ambiant
Image
Flashed
Image
Raw Depth
Map
-
Chroma.
Clustering
(Sec. 4.1)
Computes
Normals
(Sec. 4.2)
Normal Map
Filtering
(Sec. 4.3)
Reflectance
Estimation
(Sec. 4.4)
Reflectance
Filtering
(Sec. 4.4)
Normal
Refinement
(Sec. 4.5)
Conv?
Frame t
Frame t+1
1
2 3
4
Refinement
process
Refined reflectance
Refined normals
Yes
No
N
f
K
d
K
d
N
i
N
0
I
C
Kinect
Pure Flash
Image
I
f
K
d
N
final
30 Hz
Camera 60 Hz
30 Hz
Figure 2: Our framework picture. Green boxes represent the different processings of our algorithm. Orange boxes represent
the values given by the sensors at different times. Red box is the result of our algorithm.
380 430 480 530 580 630 680 730 780
Wavelength
Relative radiant power
0
20
40
60
80
100
Unknown Ambient
Unknown Ambient + Flash
Flash
Numerical Difference
Figure 3: Blue: Spectrum of a white Lambertian point un-
der the unknown ambient illumination. Red: Spectrum of a
white Lambertian point under unknown ambient illumina-
tion and flash illumination (total spectrum). Green: Spec-
trum of a white Lambertian point under pure flash illumi-
nation. Purple: difference between the total spectrum and
the ambient spectrum, this difference spectrum completely
matches the pure flash spectrum.
Pure Flash Image from Image Pairs. Our goal is
to create a pure flash image from a pair of two images:
a flashed and non-flashed one (also called ambient im-
age). As we record our images with a time sequential
illumination we use the same aperture and exposure
time for the two images. The flashed image can be
recovered by subtracting the ambient image from the
flashed one, provided that the images are linear and
do not contain any underexposed and saturated pix-
els. As shown in Figure 3, to validate this substraction
(to compute the pure flash image) we have captured
a white Lambertian point under several illuminations
with a spectrometer and subtracted the spectrum of
the ambient illumination from the total spectrum (ob-
tained after trigging the flash). This results in a spec-
trum that matches the spectrum obtained with a pure
flash illumination. To make sure that the combination
of the two images of a pair provides a pure flash im-
age, three caveats should be considered: (1) the two
images must be taken with the same camera param-
eters (exposure time, aperture, focal length), (2) the
images have to be linear, (3) the pixels color should
not be saturated nor underexposed in the two images.
Moreover, as a luminous power decreases with the in-
verse squared distance, objects too far away might not
receive enough light energy from the flash illumina-
tion. This restraints the scenario setup to scenes not
too far from the camera.
4 OUR APPROACH
Our approach is summarized in Figure 2. First, our
hybrid setup (a camera, a Kinect and a Flash) is com-
pletely calibrated to register the Kinect depth image
to the RGB camera. The illumination of the scene
is known (pure flash image) thanks to our time se-
quential illumination. Moreover, as we also know the
extrinsic and intrinsics parameters of our setup, we
can project the depth map (provided by the Kinect)
onto a 3D point map in the camera coordinate sys-
tem. Before refining the normal and the reflectance
maps, we compute a rough normal map from the raw
depth map provided by the Kinect (Section 4.2). Then
we use the pure flash image to cluster (K-means clus-
tering) the 3D points seen through the pixels camera,
each cluster containing points of nearly the same dif-
fuse reflectance (Section 4.1). Then we start our iter-
ative refinement process consisting of 4 steps. In the
first step (Section 4.3), we filter the normal map, the
weights being depended on luminance to preserve ge-
ometry details and coherence. The second step (Sec-
tion 4.4) performs an estimation of a reflectance map
from the pure flashed image and the filtered normal
map. In third step (Section 4.4), a filter is applied to
the reflectance map with weights depending on chro-
Shape and Reflectance from RGB-D Images using Time Sequential Illumination
537

maticity. During the last step (Section 4.5), the nor-
mal map is refined thanks to a shading least square
minimization that allows to fit our model to the pure
flash image. Finally, we repeat those steps until con-
vergence, say when both the normal and reflectance
maps do not vary anymore. Now, we will detail the
differents steps in the following subsections. For con-
venience purpose, as the images and the depths are
registered, from now on, a point is either a pixel p of
an image captured by the camera or the 3D point P
seen through p.
4.1 Chromaticity Assumption
As in (DiCarlo et al., 2001), we suppose that the chro-
maticity of the scene is sparse. This assumption al-
lows us to perform a color segmentation of the scene
based on quadratic chromaticity distance. The seg-
mentation consists in applying a K-means clustering
to the input image so that each pixel is assigned a clus-
ter of a given chromaticity (Figure 4). Each pixel is
projected onto a 3D point with a diffuse reflectance.
Each cluster is supposed to contain pixels of nearly
the same diffuse reflectance. We initialize the K-
means centers (10 in our current implementation) by
spreading them in the chromaticity gamut. More ro-
bust clustering techniques are left for future work.
Chromaticity Clusters false color
Figure 4: The chromaticity image is used to cluster surfaces
with similar diffuse reflectances. We can observe that the
t-shirt, the background and the skin are classified into dif-
ferent clusters.
4.2 Computing Normal Map from
Quantified Depth Data
Let us use the raw depth map (captured by the Kinect)
to compute N(p), the normal associated with a pixel
p. To compute this normal, we need to express the
depth changes (δ
x
(u,v), δ
y
(u,v)) as follows:
δ
x
(u,v) = D(u + 1,v) − D (u − 1,v) (5)
δ
y
(u,v) = D(u,v + 1) − D (u,v − 1) (6)
The normal, associated with the pixel p, can be
estimated as:
T
x
(p) =
2 ·
D(p)
f
x
0 −δ
x
(p)
T
(7)
T
y
(p) =
0 2 ·
D(p)
f
y
−δ
y
(p)
T
(8)
N(p) = T
x
(p) × T
y
(p) (9)
where T
x
(p) and T
y
(p) are respectively the tangents to
the surface according to the X and Y axes respectively.
Note that, as the Kinect depth map is quantized, it
represents a piece-wise constant approximation of the
real depth map (see Figure 1). Due to this quanti-
zation artifact, most of the normals, computed from
this depth map, will be oriented toward the camera,
which is a poor initial guess for our normal map re-
finement algorithm. This quantization artifact makes
the normal map noisy. Consequently, to overcome
the quantization artifact and other possible artifacts,
an important part of our algorithm consists in filtering
the normal map. This filtering is detailed in the next
subsection.
4.3 Normal Map Filtering
To remove noise in the normal map, we apply a bilat-
eral filter to the normals N (computed from the depth
map) to get filtered normals N
f
:
N
f
(p) =
1
W
n
(p)
∑
s∈Ω(p)
Ψ
N
(s, p)N(s) (10)
where W
n
(p) is a normalization factor, Ω(p) a neigh-
borhood of the pixel p and Ψ
N
the weighting function.
The expression of the weighting function depends on
the luminance L of the pixels of the pure flash image
and on the normals:
Ψ
N
(s, p) = exp
−
(L(p)
−
L(s))
2
2σ
2
l
−
k
N(p)
−
N(s)
k
2
2σ
2
n
!
where σ
l
and σ
n
are weighting parameters related to
luminance and normal respectively. Numerical values
used in our experiments are given in the results sec-
tion. The reason of adding the luminance information
in the weighting function is to preserve geometry de-
tails, as the luminance value changes locally with the
normal orientation.
4.4 Reflectance Estimation and
Filtering
Let us consider the case of Lambertian surfaces. The
RGB pixel values of p captured by the camera can be
estimated as follows:
I(p) =
I
s
(ω
i
)
d
2
· k
d
(p) · |N(p).ω
i
| (11)
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
538

I
s
, d, ω
i
are known as the source illumination is con-
trolled, k
d
(p) is the diffuse reflectance of a Lam-
bertian surface. k
d
is commonly expressed for each
{r,g,b} component. Refining the normal map re-
quires an estimation of those diffuse reflectances.
Once the first rough estimation of the normals has
been performed, Equation 2 is used to estimate the
reflectance map:
k
d
(p) =
d
2
I
s
(ω
i
)
·
I(p)
|N(p).ω
i
|
, (12)
where I(p) is the {r, g,b} value of a pixel of the
pure flash image and I
s
the intensity of the flash light
source. The reflectance map is rough as it is computed
from a rough depth map. However, the pure flash im-
age can help improve the reflectance map, provided
that the two following assumptions are satisfied:
1. if two points have the same normal, the difference
between their pixel values is only due to albedo
change,
2. the distribution of reflectance over the image is
sparse to ensure a reliable segmentation (Sec-
tion 4.1).
According to the two above assumptions, any
albedo change is due to chromaticity change (DiCarlo
et al., 2001), in other words any chromaticity change
entails an albedo change. Consequently, the impact of
normal aberration, on the reflectance map, can be re-
duced by averaging the diffuse reflectances of points
lying in a neighborhood. This averaging operation is
performed using another bilateral filter:
k
f
d
(p) =
1
W
d
(p)
∑
s∈Ω(p)
Ψ
d
(s, p)k
d
(s) (13)
where W
d
(p) is the normalization factor, Ψ
d
being the
weighting function which depends on chromaticity
similarities. Indeed, if two points are not assigned the
same chromaticity cluster (Section 4.1), their weights
are set to zero. The condition that two pixels p and s
belong to the same cluster is:
C(s, p) = (C(s) = C(p)) and (|m(s) − m(p)| < t
m
)
where C(p) is the cluster id associated with pixel p,
m(p) is the maximum of the r,g,b values of the pixel
p and t
m
a threshold value that we set to 0.5. The
second term is added to make the distinction between
black and white points. Finally, the expression of the
weight used in Equation 13 is given by:
Ψ
d
(s, p) =
(
exp
−
k
m(s)−m(p)
k
2
2σ
2
m
if C(s, p)
0 otherwise
where σ
m
is a weighting parameter. Numerical val-
ues used in our experiments are given in the results
section. To avoid that black, white and grey pixels
mingle during the filtering process, we use a weight
which depends on the maximum m of the r,g,b val-
ues of each pixel.
4.5 Normal Map Refinement
Once the reflectance map filtered, the next step con-
sists in refining the normal map. Our refinement relies
on the lambertian model and a least-square error like
algorithm for the three channels of each pixel. Equa-
tion 4 can be written as:
I(p) =
I
s
(ω
i
) · k
d
(p)
d
2
· (N
x
ω
x
+ N
y
ω
y
+ N
z
ω
z
) (14)
Let us assume that the right k
d
reflectances are avail-
able, the goal is to find the three components of nor-
mal N that minimize ξ over the set of the three rgb
components:
ξ(p) =
∑
c
(S (p,c) − (N
x
ω
x
+ N
y
ω
y
+ N
z
ω
z
))
2
S (p,c) =
I(p,c) · d
2
k
d
(p, c) · I
s
(ω
i
)
where k
d
(p, c) and I(p,c) are respectively the diffuse
reflectance and the value of pixel p for the color chan-
nel c. We want to find the minimum error with respect
to (N
x
,N
y
,N
z
), which is reached when:
∂ξ
∂N
x
(p) = 0 → N
x
=
∑
c
(S (p,c) − N
z
ω
z
− N
y
ω
y
)
3 · ω
2
x
∂ξ
∂N
y
(p) = 0 → N
y
=
∑
c
(S (p,c) − N
x
ω
x
− N
z
ω
z
)
3 · ω
2
y
∂ξ
∂N
z
(p) = 0 → N
z
=
∑
c
(S (p,c) − N
x
ω
x
− N
y
ω
y
)
3 · ω
2
z
In the minimization process, each normal N =
N
x
N
y
N
z
T
is initialized with the rough normal
map computed from he Kinect depth data, then each
component of the normals is computed through an it-
erative scheme until convergence.
4.6 Global Convergence
The plots on Figure 5 illustrate the convergence of
the Normal Map and the diffuse reflectance map when
applying our iterative algorithm. We computed the
mean distance between the normal map (respectively
the diffuse reflectance map) evaluated at the current
iteration and the normal map (respectively the diffuse
reflectance map) evaluated at the preceding iteration.
Shape and Reflectance from RGB-D Images using Time Sequential Illumination
539

Diffuse Coefficients
Normals
70
0.12
0.10
0.08
0.06
0.04
0.02
60
50
40
30
20
10
Mean distance
Mean distance
1
19
5
10
15
1
19
5
10
15
Number of Iterations
Number of Iterations
Figure 5: Plots representing the convergence of Normals
and Diffuse Reflectances for each iteration.
Figure 5 demonstrates that only a few iterations
are necessary to reach a steady state. Indeed, only
4 − 5 iterations are necessary to reach a high quality
Normal and reflectance maps.
5 RESULTS
Our experimental setup consists of: a Kinect depth
sensor (depth res. 640 × 480, frame rate 30 fps), a
Ueye Industrial Camera (res. 1280 × 960, frame rate
60 fps with a global shutter) and a flash LED light.
An electronic board is used to synchronize the camera
with the flash. This allows to sequentially acquire an
image pair: flashed and non flashed. So, we are able
to generate an image pair at 30 fps. The Kinect is not
synchronized due to its own limitations. The depth
image is upsampled to match the camera resolution.
We have implemented our technique in C++ and
used CUDA 6.5 to speedup all the steps of our al-
gorithm. The details of the algorithm timings are
summarized in Table 1. All the timings in this ta-
ble have been measured on an a Xeon ES 2640 CPU
2.50GHz×2 (32GB Ram) and an Nvidia Geforce
GTX 580. Note that the image registration step is
not included into our timings. Indeed, its perfor-
mance depends on the setup and the chosen technique.
For example, in (Or-El et al., 2015), this operation
takes 31.1 ms per frame on an Nvidia Titan GPU.
The algorithm parameters were set to: σ
m
= 0.002,
σ
l
= 0.0004 and σ
n
= 0.02 , these values were car-
ried throughout all experiments. For the two filtering
operations (normal and reflectance maps), we use a
kernel of 20 pixels size except for the Burger scene
(Figure 6) for which we use a kernel of 10 pixels size.
This is due to the fact that the image of this scene is
twice smaller than that of the other test scenes (Fig-
ure 1 and 8).
Our method is compared to (Or-El et al., 2015).
To this end, we used the Matlab code provided by
the authors. Their method aims at enhancing a depth
map by fusing intensity and depth information to cre-
Table 1: Timings of each step of our algorithm. Bold tim-
ings are obtained using the performance improvement de-
scribed in the next subsection. To compute the total time,
we need to multiply the refinement iteration time by the
number of iterations needed to converge to the desired re-
sults. In practice, only 5 iterations are required, which cor-
responds to 5.84 fps or 0.23 fps on a GTX 580 using or not
using the performance improvement. Note that the ”Image
Alignment” step timing is taken from (Or-El et al., 2015).
Operations Time (ms)
Init.
Image Alignment
∗
31.1
Chroma Clustering 7.34
3D Points Estim. 0.24
Refine iter.
Normal Filtering 495.55 (0.43)
Dot Calculation 0.70
Reflectance Estim. 0.26
Reflectance Filtering 345.74 (17.39)
Normal Refinement 7.72
Total Refinement Iteration 849.97 (26.5)
Total Time (5 iterations) 4288.53 (171.18)
ate detailed range profiles. For this purpose, they
use a lighting model that can handle natural illumi-
nation. This model is integrated in a shape-from-
shading technique to improve the reconstruction of
objects. Note that, unlike our method, their approach
refines the depths rather than the normals.
Figure 6 shows a comparison between our method
and the one of (Or-El et al., 2015) for a synthetic
Burger scene. The input depth map is perturbed
by adding a gaussian white noise. To use our al-
gorithm, we rendered the scene using a small light
source that simulates the flash. Our method produces
results with an error smaller than the one obtained
with the method of (Or-El et al., 2015). This is par-
ticularly visible on the tomatoes where fine details are
well recovered. However, there is more noise on the
bread due to clustering issues (Figure 7).
The scene (Figure 8), is a real scene with rela-
tively slow arm movements. Unlike the method of
(Or-El et al., 2015) no mask is used to select the main
object. The input depth map is noisy as it is directly
provided by the Kinect sensor. This noise is different
from the synthetic one used in Figure 6. Compared
to (Or-El et al., 2015), our method provides results
that have less artifacts and fine geometry details are
correctly recovered. The main issue of (Or-El et al.,
2015) method is the use of a bilateral filter which
is applied to filter a lot of data due to the high level
of noise in the raw depth map. Our two filtering
operations are performed using bilateral filters. But,
as we use them at each iteration, a smaller kernel
size is needed, which reduces the artifacts inherent
in large kernel bilateral filters. Furthermore, at each
iteration we compute new normals (Normal Refine-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
540
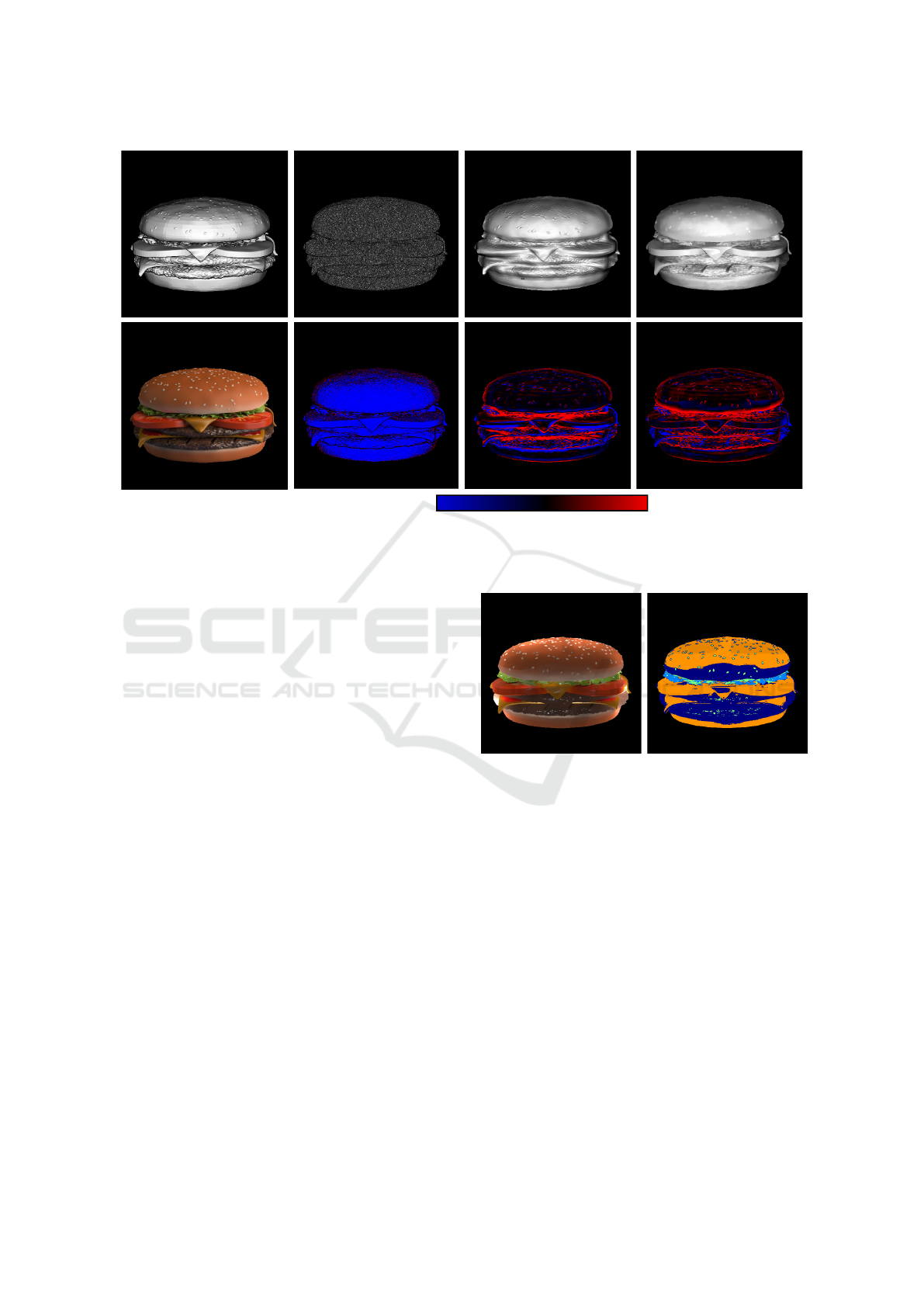
Reference Noisy depth map Or-El et al. 2015 Our method
RGB image
RMSE: 0.668 RMSE: 0.285 RMSE: 0.275
Negative
Positive
Noisy depth map Or-El et al. 2015 Our method
Figure 6: The original burger scene used in (Or-El et al., 2015). Top row show the dot product image (dot product between
the normal and the view direction) using the normals of: the reference solution, the noisy map used as input, (Or-El et al.,
2015) and our method. Bottom row show the RGB image and the false color error on the normal dot product. For better
visualisation the error was multiplied by 3.
ment operation) and new reflectances (Reflectance
Estimation operation). Consequently, artifacts due
to successive bilateral filtering operations are avoided.
Performance Improvement. One of the bottle-
neck of our algorithm is the two filtering operations
(Normal Filtering and Reflectance Filtering) which
take 495.553 ms and 345.74 ms respectively. These
two operations use non separable filters, which are
time consuming. However, to reduce the computing
time, those filters can be approximated by separable
filters with weights carefully computed. The error
due to those approximations are hardly visible. The
computing times needed by the separable version of
these two filters are 0.49 ms (1005× faster) and 17.39
ms (20× faster). All the timings are summarized in
Table 1. Except for the Burger scene, due to the
reduced image size, this optimization has been used
for all the scenes (Figures 1 and 8). Better and more
robust optimization is left for future work.
Application. One direct application of our algo-
rithm is the relighting of a captured scene. Indeed,
our algorithm provides the reflectance and the normal
maps of a scene that we relight with artificial light
sources (Figure 9). In this scene, the movement of the
arms is fast. This explains the artifacts on the arms
due to motion blur.
Clusters false color
Reflectance refined
Figure 7: On the left: the refined reflectance map after con-
vergence of our algorithm. On the right: false color image
to show how the chromaticity-based clustering performs.
We can observe that the tomatoes and the bread lie in the
same cluster. However, due to the local nature of the filter-
ing, these two material have not been merged.
6 CONCLUSIONS
We showed that even with a consumer camera and a
Kinect (capturing noisy depth data) it is possible to re-
cover finer geometry and precise diffuse reflectances
from an image or a video thanks to the use of se-
quential illumination provided by a flash. A pair of
two images are captured: one non flashed image (im-
age under ambient illumination) and a flashed one. A
pure flash image is computed by substracting the non
flashed image from the flashed image. We proposed
an efficient iterative algorithm to recover shapes and
Shape and Reflectance from RGB-D Images using Time Sequential Illumination
541

Raw data Or-El et al. 2015 Our method
Our method
Figure 8: T-Shirt scene captured by our setup. From left to right: The raw data display using the dot product, (Or-El et al.,
2015) using the dot product, our method with the dot product and the reflectance map.
Pure flash image Religthing 1 Relighting 2
Figure 9: The normal and reflectance maps refined by our
algorithm can be used for relighting a scene. Images Re-
lighting 1 & 2 are obtained with different artificial light
source positions. Moreover, sequential lighting makes our
technique capable of capturing video sequences. However,
fast and large movements in the video could create artifacts
due to motion blur.
reflectances from the pure flash image. The fact of
knowing the illumination (flash light source) makes
the extraction of normals and reflectances easier and
more efficient. Indeed, as the position and the pho-
tometry of the flash light source is known, we used a
local illumination model to express the normal and the
diffuse reflectance for each pixel. From the computed
normals we used the illumination equations to deter-
mine the reflectances. In turn, these reflectances are
fed to a process that determines new normals. This
process is repeated until convergence. We showed
that only a few iterations are needed to converge to
the desired results.
REFERENCES
Bruckstein, A. M. (1988). On shape from shading.
Computer Vision, Graphics, and Image Processing,
44(2):139–154.
de Decker, B., Kautz, J., Mertens, T., and Bekaert, P. (2009).
Capturing multiple illumination conditions using time
and color multiplexing. In 2009 IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition (CVPR 2009), 20-25 June 2009, Miami,
Florida, USA, pages 2536–2543.
Debevec, P. (2012). The light stages and their applications
to photoreal digital actors. SIGGRAPH Asia Technical
Briefs.
DiCarlo, J. M., Xiao, F., and Wandell, B. A. (2001). Illu-
minating illumination. In Color and Imaging Confer-
ence, volume 2001, pages 27–34. Society for Imaging
Science and Technology.
Diebel, J. and Thrun, S. (2005). An application of markov
random fields to range sensing. In Advances in neural
information processing systems, pages 291–298.
Fanello, S. R., Keskin, C., Izadi, S., Kohli, P., Kim, D.,
Sweeney, D., Criminisi, A., Shotton, J., Kang, S. B.,
and Paek, T. (2014). Learning to be a depth camera
for close-range human capture and interaction. ACM
Transactions on Graphics (TOG), 33(4):86.
Hern
´
andez, C., Vogiatzis, G., Brostow, G. J., Stenger, B.,
and Cipolla, R. (2007). Non-rigid photometric stereo
with colored lights. In ICCV.
Higo, T., Matsushita, Y., and Ikeuchi, K. (2010). Consen-
sus photometric stereo. In Computer Vision and Pat-
tern Recognition (CVPR), 2010 IEEE Conference on,
pages 1157–1164. IEEE.
Horn, B. K. (1970). Shape from shading: A method for
obtaining the shape of a smooth opaque object from
one view.
Horn, B. K. and Brooks, M. J. (1989). Shape from shading.
MIT press.
Kim, H., Wilburn, B., and Ben-Ezra, M. (2010). Photomet-
ric stereo for dynamic surface orientations. In Com-
puter Vision - ECCV 2010, 11th European Confer-
ence on Computer Vision, Heraklion, Crete, Greece,
September 5-11, 2010, Proceedings, Part I, pages 59–
72.
Nehab, D., Rusinkiewicz, S., Davis, J., and Ramamoorthi,
R. (2005). Efficiently combining positions and nor-
mals for precise 3d geometry. ACM transactions on
graphics (TOG), 24(3):536–543.
Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). Dy-
namicfusion: Reconstruction and tracking of non-
rigid scenes in real-time. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion, pages 343–352.
Or-El, R., Rosman, G., Wetzler, A., Kimmel, R., and Bruck-
stein, A. M. (2015). Rgbd-fusion: Real-time high pre-
cision depth recovery. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recog-
nition, pages 5407–5416.
Petschnigg, G., Szeliski, R., Agrawala, M., Cohen, M.,
Hoppe, H., and Toyama, K. (2004). Digital photogra-
phy with flash and no-flash image pairs. ACM trans-
actions on graphics (TOG), 23(3):664–672.
Prados, E. and Faugeras, O. (2005). Shape from shading: a
well-posed problem? In Computer Vision and Pattern
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
542

Recognition, 2005. CVPR 2005. IEEE Computer So-
ciety Conference on, volume 2, pages 870–877. IEEE.
Richardt, C., Stoll, C., Dodgson, N. A., Seidel, H.-P., and
Theobalt, C. (2012). Coherent spatiotemporal filter-
ing, upsampling and rendering of rgbz videos. In
Computer Graphics Forum, volume 31, pages 247–
256. Wiley Online Library.
Shen, L., Tan, P., and Lin, S. (2008). Intrinsic image de-
composition with non-local texture cues. In Computer
Vision and Pattern Recognition, 2008. CVPR 2008.
IEEE Conference on, pages 1–7. IEEE.
Shen, L. and Yeo, C. (2011). Intrinsic images decomposi-
tion using a local and global sparse representation of
reflectance. In Computer Vision and Pattern Recogni-
tion (CVPR), 2011 IEEE Conference on, pages 697–
704. IEEE.
Tunwattanapong, B., Fyffe, G., Graham, P., Busch, J., Yu,
X., Ghosh, A., and Debevec, P. (2013). Acquiring
reflectance and shape from continuous spherical har-
monic illumination. ACM Transactions on graphics
(TOG), 32(4):109.
Wenger, A., Gardner, A., Tchou, C., Unger, J., Hawkins,
T., and Debevec, P. (2005). Performance relighting
and reflectance transformation with time-multiplexed
illumination. 24(3):756–764.
Woodham, R. J. (1980). Photometric method for determin-
ing surface orientation from multiple images. Optical
Engineering, 19(1):191139–191139–.
Wu, C., Zollh
¨
ofer, M., Nießner, M., Stamminger, M., Izadi,
S., and Theobalt, C. (2014). Real-time shading-based
refinement for consumer depth cameras. Proc. SIG-
GRAPH Asia.
Xiao, F., DiCarlo, J. M., Catrysse, P. B., and Wandell,
B. A. (2001). Image analysis using modulated light
sources. In Photonics West 2001-Electronic Imag-
ing, pages 22–30. International Society for Optics and
Photonics.
Shape and Reflectance from RGB-D Images using Time Sequential Illumination
543
