
Half-precision Floating-point Ray Traversal
Matias Koskela, Timo Viitanen, Pekka J
¨
a
¨
askel
¨
ainen and Jarmo Takala
Department of Pervasive Computing, Tampere University of Technology, Korkeakoulunkatu 1, 33720, Tampere, Finland
Keywords:
Ray Tracing, Bounding Volume Hierarchy, Half-precision Floating-point Numbers.
Abstract:
Ray tracing is a memory-intensive application. This paper presents a new ray traversal algorithm for bounding
volume hierarchies. The algorithm reduces the required memory bandwidth and energy usage, but requires
extra computations. This is achieved with a new kind of utilization of half-precision floating-point numbers,
which are used to store axis aligned bounding boxes in a hierarchical manner. In the traversal the ray origin is
moved to the edges of the intersected nodes. Additionally, in order to retain high accuracy for the intersection
tests the moved ray origin is converted to the child’s hierarchical coordinates, instead of converting the child’s
bound coordinates into world coordinates. This means that both storage and the ray intersection tests with
axis aligned bounding boxes can be done in half-precision. The algorithm has better results with wider vector
instructions. The measurements show that on a Mali-T628 GPU the algorithm increases frame rate by 3% and
decreases power consumption by 9% when wide vector instructions are used.
1 INTRODUCTION
Ray tracing has been a commonly used method to ren-
der off-line images. Due to active research in the field,
there are now multiple frameworks which can achieve
real-time frame rates on high-end hardware. How-
ever, significant progress must be made in the field
before ray tracing is fast enough for consumer appli-
cations on mobile hardware.
The basic operation in ray tracing is ray casting,
which finds the closest intersection of a ray with the
set of scene primitives. In order to reach high perfor-
mance in large scenes with many primitives, ray trac-
ers organize the scene using special acceleration data
structures. The most popular of these structures is the
Bounding Volume Hierarchy (BVH). In BVH, primi-
tives are stored in the leaves of the tree, and each node
contains the Axis Aligned Bounding Boxes (AABB)
of its children. During ray casting, entire subtrees are
then rapidly eliminated by finding that the ray does
not intersect a high-level AABB, without making sep-
arate checks against each leaf primitive in the subtree.
Ray tracing is an expensive operation both in
terms of computation and memory traffic. In recent
years, performance has been improved by leaps and
bounds due to the increased parallel resources avail-
able in modern computing systems. Therefore, the
memory system is often a bottleneck since the scene
hierarchy may be more than tens of megabytes in
size and is accessed in an almost unpredictable order.
There is a large body of research on reducing memory
traffic by representing the AABBs in BVHs in a more
compact or approximate manner. For instance, in a
Shared-Plane Bounding Volume Hierarchy (SPBVH)
(Ernst and Woop, 2011), a tree node infers some of the
AABB coordinates from the parent AABB. In prac-
tice this halves the memory footprint of the nodes.
BVH compression techniques are of high inter-
est for mobile systems due to their limited memory
bandwidth and low power requirement. Several CPU
and GPU vendors have introduced architectural sup-
port for a half-precision (16-bit) floating-point for-
mat (IEEE, 2008), which poses an interesting op-
portunity for the compression. Furthermore, cur-
rent desktop hardware only supports half-floats as a
storage format, but this is changing in the near fu-
ture, as the next-generation of NVidia’s GPUs is also
scheduled to have half-precision computing support
(Huang, 2015).
In this paper, a novel hierarchical half-precision
BVH traversal scheme which computes AABB inter-
section tests natively in half-precision format is pro-
posed. This removes the format conversion overheads
which slowed down prior work (Koskela et al., 2015),
which exploited half-precision only as a storage for-
mat. In the measurements using wide vector instruc-
tions the proposed method improves frame rate by an
average of 3% and energy efficiency by 9%.
Koskela, M., Viitanen, T., Jääskeläinen, P. and Takala, J.
Half-precision Floating-point Ray Traversal.
DOI: 10.5220/0005728001690176
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 171-178
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
171

2 BACKGROUND
Ray tracing is well suited for many ways of paral-
lel computations. Threads can be used, for exam-
ple, to trace multiple rays in parallel. On the other
hand, there are at least two ways in which ray traver-
sal can use vector instructions. First, multiple rays can
be traced together in parallel, which is called packet
tracing. Second, multiple ray-AABB tests can be cal-
culated in parallel. In order to use wider vectors,
BVHs with a greater branching factor than two can be
used, which is called Multi Bounding Volume Hierar-
chy (MBVH) (Ernst and Greiner, 2008). Usually MB-
VHs are labelled based on their branching factor in a
way that MBVH4 means that the tree has a branch-
ing factor of 4 and MBVH8 means that the tree has a
branching factor of 8, et cetera. The two ways of us-
ing vector instructions can be combined. In that case
multiple rays are traced in parallel and all of them test
intersections with multiple AABBs.
There have been many proposed algorithms and
data structures to reduce the amount of data needed
for the ray tracing traversal step. These algorithms
can be divided into two categories.
First, some of the child AABB bounds can be in-
ferred from the parent AABB. Because in the BVH
the AABBs are tightly bound to their child geome-
try, all of the parent bounds are used by at least one
of the children. Some examples of this are Bounding
Interval Hierarchy (BIH), which stores only two co-
ordinate values and one axis in each node (W
¨
achter
and Keller, 2006) and the SPBVH (Ernst and Woop,
2011). Nevertheless, these ideas are not as good with
MBVHs since there are more children, which means
that fewer values for each child can be inferred.
3 RELATED WORK
Another approach is to compress data to reduced pre-
cision data types, at the cost of decompression during
traversal and reduced data quality. Low quality data
causes extra work at traversal, as the ray-AABB inter-
section tests might give false positive hits. Moreover,
algorithms must be carefully designed to avoid false
negatives in intersection tests, which would cause vis-
ible gaps in the scene geometry.
One way to compress the data is to use reduced
precision integer formats (Mahovsky and Wyvill,
2006). Most of the hardware commonly used today
is capable of doing calculations in different integer
precisions. Using integers, the scene is divided into
equally sized quantization steps. This is beneficial if
the details of the geometry are equally divided around
the whole scene.
To avoid too big quantization steps, the data type
can be used hierarchically. In this representation the
value range of the data type is scaled to the parent
node’s AABB bounds, so that the smallest possible
value of the data type corresponds to the parent’s
lower bound and the greatest possible value to the
upper bound. In a deep tree, even with two integer
bits, this kind of hierarchical encoding can achieve
more accuracy per coordinate than single-precision
floating-point format. This is possible because on
every lower level of the tree the quantization steps
get smaller in world coordinates. However, this extra
precision is not useful since the triangles are usually
stored in single-precision format.
The previous work on half-precision floating-
point BVHs (Koskela et al., 2015) only considers the
use of half-precision floating-point numbers as a stor-
age format. This reduces BVH inner node mem-
ory bandwidth and space usage by half, which cor-
responds to an average of 16% reduction in cache
misses and 7% reduction in memory space usage with
MBVH4. Their work evaluates both the BVH with
world coordinate half-precision floating-point num-
bers and the hierarchical representation similar to the
work on integers (Mahovsky and Wyvill, 2006). The
world coordinate half-precision traversal performance
is reduced by the extra traversal caused by the false
positives and the overhead of format conversion when
AABBs are loaded from memory. The hierarchical
half-precision BVH avoids most of the false positives,
at the cost of extra computational overhead.
Instead of converting the hierarchical AABB
bound coordinates into world coordinates, the ray
origin can be converted into hierarchical coordinates
(Keely, 2014). This allows intersection tests to be
computed in a low-precision format, which reduces
the required bit counts significantly. Moreover, this
is beneficial since fewer coordinates need to be con-
verted to different coordinate base (there are six val-
ues in the AABB bounds and only three values in the
ray origin). To avoid overflows in the hierarchical co-
ordinates, the ray origin has to be moved to the edge
of the coordinate range on every traversal step.
4 PROPOSED ALGORITHM
This paper follows the compression category by us-
ing half-precision floating-point numbers. The traver-
sal algorithm used in this paper is based on a simi-
lar idea as the (Keely, 2014) algorithm. The differ-
ence is that instead of adding custom integer hard-
ware to the GPU, the proposed algorithm uses ex-
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
172
00 int nodeIndex = indexStack.pop();
01 half3 rayOrigin = rayOriginStack.pop();
02 half scaleSofar = scaleStack.pop();
03 half disSoFar = distanceStack.pop();
04
05 if(nodeIndex is inner node index){
06 // vectorised ray-AABB slab hit tests
07 // for every ray in the packet against
09 // every child node’s AABB in parallel
10 foreach hitNode that is hit by any ray
11 in the packet and is closer than
12 closest found triangle{
13
14 indexStack.push(hitNode.index);
15
16 // Move ray origin to edge of hitNode
17 half hitDis = max(hitDistance, 0.0);
18 half3 newRayOrigin = rayOrigin +
19 0.99 * hitDis * rayDirection;
20
21 // Convert to deeper hierarchical coords
22 half3 axisRanges = hitNode.upperBound
23 - hitNode.lowerBound;
24 half range = max(axisRanges.x,
25 axisRanges.y, axisRanges.z);
26 float3 mover = 0.5 *
27 (float3)(hitNode.lowerBound +
28 hitNode.upperBound - range);
29 newRayOrigin = (half3)(VAL_RANGE *
30 (((float3)newRayOrigin - mover) /
31 (float)range) + VAL_MIN);
32 rayOriginStack.push(newRayOrigin);
33
34 // Update distance values
35 half newScale = scaleSoFar *
36 (range / VAL_RANGE);
37 distanceStack.push(disSoFar + hitDis *
38 scaleSoFar);
39 scaleStack.push(newScale);
40 }
41 }else{ // Node is leaf node
42 // ray-Triangle tests
43 }
Figure 1: The proposed algorithm in pseudo code. This
consists the inner loop of the BVH traversal.
isting half-precision floating-point hardware, there-
fore, available power savings are more modest. This
kind of hardware is currently found especially in mo-
bile platforms. In addition, this paper describes how
the hierarchical half-precision format, which was de-
signed so that values are converted to world coordi-
nates prior to intersection testing, is modified so that
it better fits calculations in hierarchical coordinates.
On high level the proposed traversal has two new
stages. First, the ray origin is moved to the edges
of the intersected nodes. Second, in order to retain
high accuracy for the intersection tests the moved ray
origin is converted to the child’s hierarchical coordi-
nates, instead of converting the child’s bound coor-
O
0
O &O
B
O
Bb
A
B
Ba
Bb
Ba
Figure 2: Ray origin movement through the hierarchy. The
initial origin is O
0
and because the ray intersects the node B
the origin is moved to O
B
. In the node B, the ray intersects
both nodes Ba and Bb, so the origin is moved to their edges
in corresponding branches of the tree traversal.
dinates into world coordinates. The main point of
these modifications is to keep the values within the
range of the half-precision format. This way the ray-
AABB tests can be done with native half-precision
calculations and the AABBs can be stored in half-
precision. Some hardware floating-point units can
compute twice as many half-precision values with
same latency as single-precision values (Hariharakr-
ishnan et al., 2013). The pseudo code of the proposed
algorithm can be found in Figure 1.
On lines 00 – 01 the algorithm loads the index
of the current node and the current ray origin. The
ray origin is already in the same relative coordinate
base as the child nodes’ AABB bounds, which means
that the ray-AABB test can be performed for every
child AABB with vector instructions without any ex-
tra preparations. In the measurements an unmodified
version of the slab method (Smits, 1998) was used for
ray-AABB hit tests in half-precision.
When using the half-precision floating-point for-
mat, as small a number as 65520 is rounded up to in-
finity. In order to prevent values from being rounded
up to infinity, the hierarchical storage format was
modified to use the interval from VAL_MIN (-16384)
to VAL_MAX (16384), which is one fourth of the maxi-
mum non-infinite half-precision interval.
4.1 Ray Origin Movement
The code after line 10 is executed only for those chil-
dren which are actually intersected. This part could
also be done for all of the children with vector instruc-
tions, but in the authors’ experiments with MBVH4, a
ray hits almost only one AABB in a inner node on av-
erage. In this case vectorizing the lines after 10 to all
of the child AABBs would cause almost three of the
four pieces of data to be trash values. This requires
many registers for the trash values. For these reasons
there was an improvement when the loop was used
to go through the intersected children. Furthermore,
if the hardware supports instruction level parallelism,
i.e., calculating vector and scalar instructions at the
same time, it might be possible to optimize the inner
loop so that in the single ray case at least some parts of
Half-precision Floating-point Ray Traversal
173

(a) Shiny Bunny with one point light (69K trian-
gles).
(b) Normals of Dragon, in other words, just ray
casting (871K triangles).
(c) Sibenik with reflecting floor and two point
lights (75K triangles).
(d) Fairy with one point light (174K triangles).
(e) Sponza with reflecting stone and metal materi-
als and with two point lights (278K triangles).
(f) Conference with all materials reflecting and
with two point lights (331K triangles).
Figure 3: The test scenes used in the measurements.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
174

the ray-AABB tests and coordinate conversions could
be calculated simultaneously.
The index of every intersected child is stored in
the stack on line 14. Next, the ray origin is moved to
the edge of the intersected child AABB on the lines
17 – 19, which can also be seen visualized in Fig-
ure 2. The distance to the child AABBs intersection
is clamped from the lower end to zero, because neg-
ative distances mean that the ray origin is inside the
child AABB. In this case the ray origin is not moved,
but it is still converted to the child’s hierarchical coor-
dinates. The distance is shortened with an epsilon of
0.01, because if the child AABB is planar, i.e., the size
is 0 on some axis, moving the ray origin inside of it
causes false negatives. This was one working epsilon
value found by testing different values. Since the al-
gorithm avoids infinities by using one fourth of the to-
tal half-precision range, the value of the epsilon is not
important. If the BVH tree is unbalanced and contains
child AABBs which are extremely small compared to
their parents, the epsilon value starts to have an effect.
4.2 Coordinate Conversion
The coordinate conversion to the new ray origin is
shown on lines 22 – 32. This conversion changes
the coordinates into a deeper level of hierarchi-
cal coordinates. The idea of the conversion is
first to convert the new ray origin values so that
the coordinates of the intersected child nodes lower
bounds are represented by 0.0 and the coordinates
of the upper bounds are represented by 1.0. Then
this value is multiplied with the total used range
VAL_RANGE = VAL_MAX - VAL_MIN, which makes it
a value from 0 to 32768. Then the interval is moved
with VAL_MIN to be from -16384 to 16384, which was
the desired interval.
A slightly different algorithm than in the previous
work was used, because usually the whole range of
the data type is used on every axis. This means that
going deeper into the hierarchy scales different axes
at different rates. Without correction, this would bend
the rays. More importantly, correcting the direction
would require more computations and one more stack
to store the corrected ray directions. The issue was
solved by scaling all of the axes with just one value
range. The largest range of all of the axes was used
for the scaling. An example is provided in Figure 4.
In the previous work the variable mover was just
set to VAL_MIN, but since in this work only one range
was used on all of the axes, a more complicated mover
was needed. The idea is to move the interval of
the child node into the center of the half-precision
total range. If conventional VAL_MIN was used as
VAL_MIN VAL_MAX
VAL_MAX
VAL_MIN
0
0
A
B
-P P
Figure 4: In contrast to conventional hierarchical BVH stor-
age the proposed approach scales every axis on the largest
range. In the previous work x-axis value VAL MAX would
have been in location P and value VAL MIN in -P. This re-
duces the need for ray direction correction but loses preci-
sion.
mover, the value interval would have started from the
VAL_MIN and the algorithm would have suffered from
the poor precision of the floating-point format with
values far from zero. In Figure 4, this would have
meant that the bounding box had been on the left side
of the dashed square, not in the center.
Single-precision data types were used for the co-
ordinate conversion, since half-precision was causing
errors for small triangles. This part was vectorized
only for the rays in the packet, not for the child nodes.
The child nodes were handled by looping through the
actually intersected ones. This means that even with
the wider data type these lines do not require wider
vector units and the performance impact was only the
type conversions and the extra register space require-
ment. This impact was so small compared to memory
bandwidth savings that it was unmeasurable.
4.3 Maintaining the Traversed Distance
Finally in the lines 35 – 39 the distance that has been
traversed is maintained. This distance in world co-
ordinates is required because the traversal can termi-
nate as soon as it has found a triangle intersection
and all of the AABBs in the stack are further away
than it. In the lines 02 – 03 the distance values are
popped from the stacks. The world coordinate dis-
tance from the current moved ray origin to the found
AABB can be calculated by multiplying the distance
to the AABB, which is in the hierarchical coordinates,
with the value popped from the scale stack. The value
popped from the distance stack is the distance before
intersecting current node. The sum of the distance be-
fore intersecting current node and the scaled distance
to the intersected AABB equals the total world coor-
dinate traversal distance to the AABB. This value is
needed on line 10 to determine if the AABB is further
than closest found triangle.
Half-precision Floating-point Ray Traversal
175
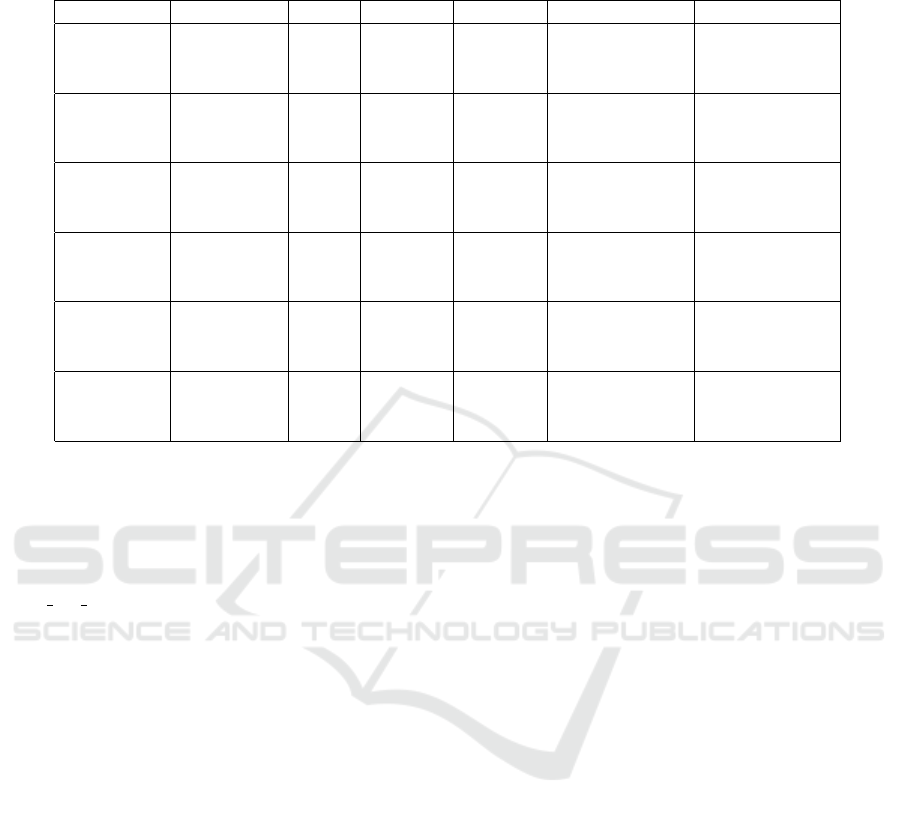
Table 1: Frame rates [frames per second] (more is better). The values are compared to single-precision and all results that
improve on it are bolded. Other measured algorithms were the proposed algorithm and storing the values in half-precision
and converting them to single-precision before computation.
Model Algorithm BVH MBVH4 MBVH8 MBVH4 2 rays MBVH4 4 rays
Bunny
single 2.22 2.13 1.67 1.74 1.38
half storage -5.9% -3.2% 0% -4.0% -2.9%
proposed -30% -23% -11% -19% 0%
Dragon
single 2.80 2.60 1.93 2.17 1.66
half storage -3.6% -3.8% 2.0% 3.7% 0%
proposed -19% -12% -1.0% -8.8% 3.0%
Sibenik
single 0.933 0.934 0.685 0.804 0.716
half storage -4.4% 0.4% 0.3% -4.3% -4.2%
proposed -13% -4.6% -6.9% -5.5% 8.5%
Fairy
single 1.43 1.43 1.04 1.28 1.03
half storage -2.8% -0.7% 2.9% -2.3% -1.9%
proposed -26% -18% -10% -19% 1.0%
Sponza
single 0.445 0.448 0.327 0.372 0.298
half storage -4.0% 0.2% 2.1% -4.6% -3.7%
proposed -23% -15% -5.2% -12% 12%
Conference
single 0.613 0.614 0.500 0.529 0.463
half storage -8.2% -6.2% -3.4% -9.1% -10%
proposed -27% -21% -13% -20% -9.7%
5 TEST SETUP
For the measurements a ray tracer was implemented
using OpenCL. OpenCL was chosen because it has
the cl khr fp16 extension, which provides support for
native half-precision calculations. The tests were run
on the ODROID XU3 board’s Mali-T628 GPU be-
cause it supports most of the features of this exten-
sion. The board also has built-in sensors for power
readings, which were used for the measurements.
During the measurements, the software traced
rays for as long as it took for the variations in the
frame rates to settle. Then, 10 frames of frame rate
and power usage was recorded. The reported num-
bers are averages of these numbers. The frame rate
did not improve after the first frames, which indicates
that the scenes were so massive that they overfilled
the small caches of the Mali.
The images of different test setups can be seen in
Figure 3. The ray tracer used Whitted style ray tracing
(Whitted, 1979). In the scenes with reflections, two
bounces were allowed. In the scenes with lighting, ev-
ery regular ray sent one shadow ray to each point light
if the result was not already known from the normal of
the surface. Explicit vector instructions were used to
test all child nodes simultaneously in BVH, MBVH4
and MBVH8. MBVH16 measurements were not in-
cluded, because it was already hard to fill all branches
of the tree in a MBVH8. Therefore, MBVH16 mea-
surements would not have been representative.
To achieve wider vector instructions packet trac-
ing was also used, yet it is not good for perfor-
mance with incoherent secondary rays (Wald et al.,
2008). Because the packet size is the same with all
of the compared methods, all of them should have
the same performance drawback. With packet trac-
ing MBVH4 was used, since the implemented Surface
Area Heuristic (SAH) (MacDonald and Booth, 1990)
tree builder was best suited for building MBVH4
trees. The rays were assigned to packets based on
their screen space coordinates. With 4 rays testing hits
against 4 AABBs ray-AABB tests were done with 16
elements wide vector instructions, which is the widest
vector width supported by the OpenCL framework.
6 RESULTS
The measured frames per second can be found in Ta-
ble 1 and the measured power usage can be found in
Table 2. Both of the measurements show similar re-
sults. The wider the vector instruction used in the cal-
culations, the better the proposed algorithm is.
With narrow vector instructions such as BVH with
one ray (which stores only two elements in a vector)
the proposed algorithm performs much worse than
regular single-precision traversal. This is because the
little benefit from the smaller AABB memory foot-
print is hidden by the use of extra stacks and the com-
putation overhead from the coordinate conversions.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
176

Table 2: Power readings [W] from GPU and memory, which is shared with the CPU (less is better). The values are compared
to single-precision by dividing the values with the corresponding frame rate. This means that the results are comparable in
terms of actual work performed by the ray tracer. All results that improve on single-precision are bolded. Other measured
algorithms were the proposed algorithm and storing the values in half-precision and converting them to single-precision before
computation.
Model Algorithm BVH MBVH4 MBVH8 MBVH4 2 rays MBVH4 4 rays
Bunny
single 1.22 1.26 1.44 1.46 1.61
half storage 8.9% 4.7% -5.9% 4.8% 10.8%
proposed 46% 27% 4.6% 26% -0.6%
Dragon
single 0.98 1.12 1.41 1.40 1.58
half storage 4.6% -3.3% -10% -6.4% 5.2%
proposed 47% 18% -7.3% 7.1% -8.0%
Sibenik
single 1.32 1.35 1.51 1.62 1.80
half storage 9.0% -0.1% 1.6% 3.5% 10%
proposed 24% 9.5% -0.3% 7.0% -12%
Fairy
single 1.32 1.32 1.53 1.65 1.81
half storage -0.2% -2.1% -4.5% 0.5% 3.7%
proposed 36% 23% 4.0% 20% -11%
Sponza
single 1.32 1.29 1.58 1.72 2.01
half storage 2.8% 3.6% -3.3% 5.3% -0.1%
proposed 44% 29% 5.1% 17% -17%
Conference
single 1.05 1.13 1.35 1.39 1.65
half storage 19% 0.3% -3.8% 5.4% 10%
proposed 58% 30% 8.1% 21% -5.9%
2 4 8 16
0
20
40
Vector width (element count)
Avg. difference (%)
MBV H
packet
Figure 5: The average difference of the proposed algorithm
for regular single-precision traversal (less is better). Cir-
cles and solid lines are power usage. Squares and dashed
lines are computation time. This shows a clear trend that
the wider the vector instructions used the better the perfor-
mance is with the proposed algorithm.
In addition to actual coordinate calculations, the data
for the conversion needs to be parsed from the stored
BVH. Each AABB bound coordinate for every child
node was stored in one vector, which makes the ray-
AABB intersection test faster. However, the proposed
algorithm needs to fetch one value for every inter-
sected child node from all of the six bound vectors.
With 16-element-wide vector instructions, the
proposed algorithm starts to outperform its counter-
part single-precision algorithm. These wide instruc-
tions were only run with the packet tracing, but the
Figure 5 shows a similar trend without packets. This
means that if a ray tracer successfully utilizes wide
vector instructions and the targeted hardware has sup-
port for native half-precision computations the pro-
posed algorithm should be faster. Of course the limit
of 16 elements might be lower or higher on other plat-
forms depending on the vector computation hardware
and the structure of the whole memory hierarchy.
The proposed algorithm’s worse performance in
the Conference scene is likely explained by the poor
precision in the edges of the scene on the first lev-
els of the BVH. Poor precision leads to many extra
rays continuing traversal to the branches where the
computationally heavy parts like the curtains and the
chairs are stored. This only adds extra work to BVH
traversal for finding out that a ray is not actually inter-
secting any primitives in an area of the scene. In the
similar test set-up of the Sponza scene the curtains are
located closer to the origin of the scene where there is
more precision. Furthermore, computationally expen-
sive parts have reflections in the Conference scene,
which makes both the incoming rays and the outgo-
ing rays heavier to compute than in single-precision.
Comparing the half-precision storage and single-
precision methods shows they perform at a similar
level. There is no clear pattern visible for which
results half-precision storage outperforms single-
precision. In contrast, the proposed method is bet-
ter when using widest vectors and also has far greater
differences compared to single-precision. This is be-
Half-precision Floating-point Ray Traversal
177

cause the SAH tree construction has to make very
different trees with far fewer quantization points pro-
vided by the non-hierarchical format. On the other
hand, the proposed algorithm has even more precision
in the lower levels of the tree than single-precision so
it builds similar trees.
7 CONCLUSIONS
This paper describes a new kind of ray traversal
for BVHs, which utilizes half-precision floating-point
computations. The traversal is done by moving the
ray origin to the edge of the intersected child AABB
and then converting the coordinates of the ray origin
into the hierarchical coordinates of the child AABB.
This way the traversal stays in a more suitable range
for the lower precision format. In addition, the hier-
archical half-precision coordinates can provide even
more accuracy than single-precision world coordi-
nates. This is possible since on every lower level the
quantization step in world coordinates gets smaller.
The proposed algorithm works better than single-
precision with wider vector instructions. This means
that if a ray tracing application is fastest with wide
vector instructions then changing to the proposed
traversal should make it even faster. This requires
that the hardware is capable of calculating twice the
amount of half-precision values with same latency as
single-precision calculations, which is quite common
with the hardware that supports native half-precision
calculations.
In the future, the authors are interested in extend-
ing the use of half-precision floating-point numbers to
the rest of the ray tracing algorithm. Another potential
future work is to optimize the proposed algorithm for
possible desktop GPUs with support for native half-
precision calculations.
ACKNOWLEDGEMENTS
The authors would like to thank their funding sources:
TUT graduate school, Academy of Finland (funding
decision 253087), Finnish Funding Agency for Tech-
nology and Innovation (project ”Parallel Acceleration
2”, funding decision 40081/14) and ARTEMIS JU un-
der grant agreement no 621439 (ALMARVI). In ad-
dition, the authors would like to thank Anat Gryn-
berg and Greg Ward for Conference, Frank Meinl for
Sponza, Utah 3D Animation Repository for Fairy,
Marko Daprovic for Sibenik and Stanford 3D Scan-
ning Repository for Bunny and Dragon models. The
authors are also very grateful for the anonymous re-
viewer comments.
REFERENCES
Ernst, M. and Greiner, G. (2008). Multi bounding volume
hierarchies. In Proceedings of the IEEE Symposium
on Interactive Ray Tracing, pages 35–40.
Ernst, M. and Woop, S. (2011). Ray tracing with shared-
plane bounding volume hierarchies. Journal of
Graphics, GPU, and Game Tools, 15(3):141–151.
Hariharakrishnan, K., Barbier, A., and Hedley, F. (2013).
OpenCL on Mali FAQs. ARM.
Huang, J.-H. (2015). Leaps in visual computing. In
Opening Keynote of GPU Techonology Confer-
ence Available at: http://on-demand.gputechconf.
com/gtc/2015/presentation/S5715-Keynote-Jen-
Hsun-Huang.pdf (Referenced: 9/18/2015).
IEEE (2008). Standard for floating-point arithmetic. Std
754-2008.
Keely, S. (2014). Reduced precision for hardware ray trac-
ing in GPUs. In Proceedings of the High Performance
Graphics Conference, pages 29–40.
Koskela, M., Viitanen, T., J
¨
a
¨
askelainen, P., Takala, J., and
Cameron, K. (2015). Using half-precision floating-
point numbers for storing bounding volume hierar-
chies. In Proceedings of the 32nd Computer Graphics
International Conference.
MacDonald, J. and Booth, K. (1990). Heuristics for ray
tracing using space subdivision. The Visual Computer,
6(3):153–166.
Mahovsky, J. and Wyvill, B. (2006). Memory-conserving
bounding volume hierarchies with coherent raytrac-
ing. Computer Graphics Forum, 25(2):173–182.
Smits, B. (1998). Efficiency issues for ray tracing. Journal
of Graphics Tools, 3(2):1–14.
W
¨
achter, C. and Keller, A. (2006). Instant ray tracing: The
bounding interval hierarchy. In EuroGraphics Sympo-
sium on Rendering Techniques, pages 139–149.
Wald, I., Benthin, C., and Boulos, S. (2008). Getting rid
of packets – efficient SIMD single-ray traversal using
multi-branching BVHs. In Proceedings of the IEEE
Symposium on Interactive Ray Tracing, pages 49–57.
Whitted, T. (1979). An improved illumination model for
shaded display. ACM SIGGRAPH Computer Graph-
ics, 13:343–349.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
178
