Design and Analysis of a New Device
for Low-Order Wavefront Aberrations Measurement
Zhou Qiong
1
, Liu Wenguang
1
, Wang Gang
2
, Yan Baozhu
1
, Xi Fengjie
1
and Jiang Zongfu
1
1
College of Opto-electronic Science and Engineering, National University of Defense Technology,
Changsha, Hunan, China
2
Science and Technology on Solid-State Laser Laboratory, Beijing, China
zhouqiong0416@gmail.com
Keywords: Low-Order Aberration, Wavefront Slope, Thermally Induced Distortions.
Abstract: For a high energy laser, thermally induced wavefront distortions include a large proportion of low-order
aberrations with large peak-valley (PV) value.In this paper we design a Low-Order Wavefront Aberration
Detector which can detect the large peak-valley value of low-order phase aberrations. Different from Shack–
Hartmann Wavefront Sensor, this device includes one sepcial diaphragm, six sets of optical focusing system
and six displacement detectors. The length of Low-Order Wavefront Aberration Detector can be controlled
within 200mm. the minimum low-order aberration coefficient of LOWAD is less than 0.5λ which is
determined by the inherent aberration distribution of optical focusing system. And we can choose reasonable
position sensitve detector or four-quadrant photo-detector to detect relatiove displacement of each focal point,
and thus the measurement sensitivity of LOWAD is less than 0.1λ and the measurement capability is more
than 80λ. The new wavefront measurement device can be used to direct measure low-order aberrations for
laser beam with large transverse area and do not need beam contracting system, and the size and cost is greatly
below Shack–Hartmann Wavefront Sensor.
1 INTRODUCTION
Thermally induced wavefront distortions is one of the
main technical challenges in the development of high
power solid laser and the wavefront distortion caused
by thermal effect of solid or gas seriously reduces the
beam quality in far field (Redmond et al., 2007;
McNaught et al., 2009). Shack – Hartmann
Wavefront Sensor (SHWS) is an important device in
a AO system, and is widely used to measure
wavefront distortions.The wavefront of object beam
is divided by an array of transmissive lenses, and the
focus spot position of each beam can be detected by
CCD camera with multiple pixels(Liujing et al.,
2011). The wavefront slope is calculated with
displace of each focus spots, then the distortions can
be reconstructed by implementing zonal methods or
modal methods (Southwell, 1980; Tyson, 2011).
SHWS can be used for real-time wavefront correction
and the spatial resliution is very high, but it is very
expensive and complex. And usually it is designed to
detect the small phaseshift mainly contains higher-
order aberrations. However, for a high energy solid
state laser, thermally induced wavefront distortions
include a large proportion of low-order aberrations
with large peak-valley (PV) value, mainly constituted
of defocus and astigmatism.
In this paper we design a wavefront measurement
device which can detect the large peak-valley value
of low-order phase aberrations the the abbreviation
LOWAD (Low-Order Wavefront Aberration
Detector) is used in our discussion. This measurement
principle of this device still depends on wavefront
slope measurements but only need measurements of
6 spots, and the mathematical algorithm involved to
wavefront reconstrution is easier than zonal or modal
estimation. The new wavefront measurement device
can be used to direct measure low-order aberrations
for laser beam with large transverse area and the size
and weight is greatly less than that of Shack –
Hartmann Wavefront Sensor.
2 PRINCIPLE
In Cartesian coordinates the wavefront distortions
only constituted by defocusing and astigmatism can
be written as (Born and Wolf, 1999)
22
01 2 3 4 5
(, )Wxy a ax ay ax axy ay=+ + + + +
(1)
Then the x-slope measurement S
x
and y-slope
measurement S
y
in Catesian coordinates are
(Hernández-Gómez et al., 2014)
134
24 5
(, )
2
(, )
2
x
y
Wxy
Saaxay
x
Wxy
Saaxay
y
∂
==++
∂
∂
==++
∂
(2)
Then the a
1
~a
5
can be obtained from following matrix
equations
1
3
4
1 2
1 2
1 2
i
j
k
x
ii
xjj
kk
x
S
xy
a
Sx
y
a
a
xy
S
=
(3)
And
2
4
5
1 2
1 2
1 2
i
j
k
y
ii
yjj
kk
y
S
xy
a
Sxya
a
xy
S
=
(4)
Where, x and y are the coordinates of focusing points,
the indexs i,j,k are signed as radom three different
point, respectively. In Eq. (1) there are 5 unknown
parameters a
1
~a
5
which are completely discribe the
spherical curvature and the astigmatic curvature.
Based on the Zernike circle polynomials
()cos
m
n
Z
rm
θ
that are orthogonal and normalized (Born and Wolf,
1999), the relationship between a
1
~a
5
and Zernike
circle polynomials coefficients can be obtain by
00
1, 1 1 1,1 2
222
000
2,0 3 5 2, 2 3 5 2,0
;;
22
(); ();
43 26 43
AaAa
A
aaA aaA
ρρ
ρρρ
−
−
==
=+ =−=
(5)
Where, A
-1,-1
and A
1,1
are tilt abberation
coefficients, A
2,0
is defocus abberation coefficient,
A
2,-2
and A
2,2
are astigmatism abberation coefficients,
ρ
0
is the normalization radius. So for calculating the
defocus aberrations coefficient and astigmatism
aberrations coefficients, we need at least 3 sets of the
x- and y- slopes measurements. In this case LOWAD
is designed to detect displaces of six focus for
measuring beam, which means there are six sets of x-
and y- slopes measurements. From Eq. (3) and Eq.
(4), we notice that there are 20 different sets of values
for a
1
, a
2
, a
3
, and a
5
. The final value is taken as the
average of the 20 values. We have 40 results for a
4
,
two in each combination of three points, so we take
the average of these 40 values. Once the values of
a
1
~a
5
are calaculated, the Zernike abberation
coefficients of wavefront distortions can be obtained
by Eq. (5).
3 DESIGN AND ANALYSIS
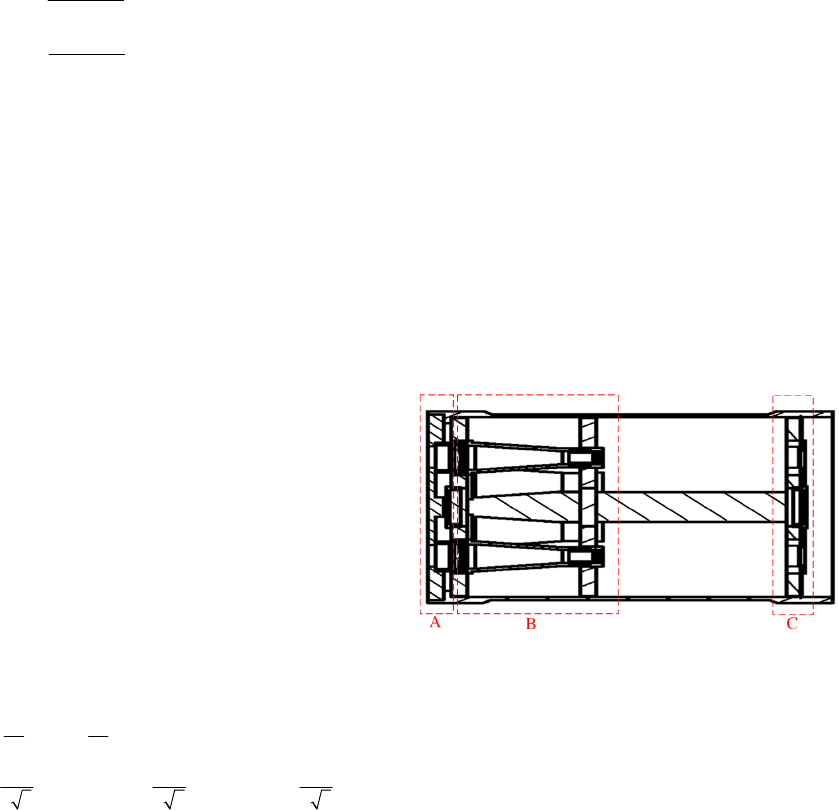
The LOWAD mainly include three parts: one sepcial
diaphragm (Part A), six sets of optical focusing
system (Part B) and six displacement detectors. The
design schematic in cross section view is shown in
Figure 1. Measuring beam is divided to 6 sub-beams
by the sepcial diaphragm, each sub-beam is focused
by focusing optical system, then the displacement of
focal spots can be detected by displacement detectors.
The x- and y- slopes of focal spot can be calculated
by using the focal length of focusing system and the
dispalcement of each focal spot (Tyson, 2011).
Figure 1: Structure diagram of LOWAD.
The distribution of sepcial diaphragm is shown in
Figure 2. In our case, the diameter of incient light
D=150mm, the diameter of each separated circular
area d=25mm, and the distance of ench adjacent
points is ρ
0
=50mm. This diaphragm can separate the
incient light into six sub- lights, and each sub-light
contains the phase information of confirmatory
portion of incident light. As the same as SHWS, we
must focus each sub- lights and measure the relative
displacement of focal points, respectively.
In order to reduce the size of this device and
increase the measurement accuracy, as shown in
Figure 3, we use the focusing optical system rather
than convex lens. The whole focusing system include
2 parts: the first part contains one convex lens (L1)

Table 1: Optical element parameters of focusing optical
system (unit: mm).
Type
Element
Radius of
Curvature
Distance to
next element
L1
Incident surface 69.11 6
Exit surface -28.62 0.727
L2
Incident surface -27.33 2
Exit surface -144.08 77.5
L3
Incident surface -7.798 2
Exit surface
inf
150.7
Figure 2: Distribution of the special diaphragm.
and one concave lens (L2), and the second part is one
convexlens lens (L3). The eauivalent focal length of
focuing system can achieve about 5 times of the
length of whole focuing system. In other words the
f/D of this system can increase 5 times compared with
the focusing lens which has the same size, which
means the optical aberration and chromatic aberration
of focusing system can be controlled in reasonable
range.
Figure 3: Schematic of optical focusing system.
For detecting the wavefront aberrations of
measuring beam accurately, we have optimize the
optical parameters to decrease the aberration of
focusing optical system. The optimized optical
element parameters are listed in Table 1. The actual
focusing distance of this system is about 150mm, but
the equivalent focal length can be more than 1000mm.
The inherent aberration distribution of system is
calculated and shown in Figure 4. The simulation
results is obtained in an ideal optical system without
Figure 4: Simulation inherent wavefront distribution of
optical focusing system (units: λ).
off-axis condition. The PV value of wavefront is
0.2117λ and the RMS value is 0.0599λ. The main
aberration is defocusing and spherical aberrations,
and the Zernike aberration coefficients are 0.011λ and
0.054λ. The results determine the minimum low-
order aberration coefficient of LOWAD.
For our detector the measurement accuracy is
determined by the accuracy of displacement detectors.
Normally for an incient beam with large value low–
order aberrations (the PV value is almost greater than
20λ), the acceptable measurement accuracy of
aberration is 0.1λ, which means the sensitivity of
position detector must be less than 2um. Considering
that the largest PV value of defocusing aberration
which can be measured is about 80λ, the effective size
of detection surface of position detector used in
LOWAD must greater than 2.5mm. Above all, while
based on the requirement of measurement sensitivity
and capability, PSD (position sensitve detector) and
four-quadrant photo-detector can be choosed to using
in LOWAD, which are commercial products and are
much cheaper than CCD camera.
4 CONCLUSIONS
In this paper we designen and discussed a new
detector to reconsruct the thermally induced
wavefront distortions with large peak-valley value
depends on x- and y- slope measurements. The Low-
Order Wavefront Aberration Detector is constituted
of one sepcial diaphragm, six sets of optical focusing
system and six displacement detectors. The actual
focusing distance of this system is about 150mm,
which means the length of Low-Order Wavefront
Aberration Detector can be controlled within 200mm.
The inherent aberration distribution of system is
anaysed. The main aberration is defocusing and
spherical aberrations, and the minimum low-order
aberration coefficient of LOWAD is less than 0.5λ.
And by choosing reasonable PSD and four-quadrant
photo-detector, the measurement sensitivity of
LOWAD is less than 0.1λ and the measurement
capability is more than 80λ. To sum up, the LOWAD
can be used in direct measurement of low-order
aberrations for laser beam with large transverse area
and do not need beam contracting system.
ACKNOWLEDGEMENTS
This work was supported by National Natural Science
Foundation of China (NSFC, No.11504423 and
No.61379065) and Science and Technology on Solid-
State Laser Laboratory Foudation (No.
9140C040101140C04016).
REFERENCES
S. Redmond, S. McNaught, J. Zamel, et al, 2007. 15 kW
near-diffraction-limited single-frequency Nd:YAG
laser, CLEO.
Stuart J. McNaught, Charles P. Asman, Hagop Injeyan, et
al, 2009. 100-kW Coherently combined Nd: YAG
MOPA laser array. Frontiers in Optics 2009/Laser
Science XXV.
Xu Liujing, Yang Ping, Liang Xinbo, et al, 2011.
Application of Hartmann-Shack wavefront detector in
testing distorted wavefront of conduction cooled end-
pumped slab. Chin. J. Lasers.
W. H. Southwell, 1980. Wavefront estimation from
wavefront slope measurement. J. Opt. Soc. Am.
Robert K. Tyson, 2011. Principles of adaptive optics, CRC
Press. Boca Raton & London & New York, 3
rd
edition.
Max Born and Emil Wolf, 1999. Principles of Optics:
Electromagnetic Theory of Propagation, Interferencr
and Difftaction of light, Cambridge University Press.
Cambridge, 7
th
edition.
Geovanni Hernández-Gómez, et al, 2014. Hartmann tests to
measure the sphexical and cylidrical curvatures and the
axis orientation of astigmatic lenses or optical surfaces,
Applied Optics.
Zhou Qiong, Liu Wenguang, Jiang Zongfu,2015. A New
Method to Measure Low-Order Aberrations Based
onWavefront Slope. Proc. of SPIE/Optical Sensors
2015
