Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

Carlotta Schatten and Lars Schmidt-Thieme

Information Systems and Machine Learning Lab,

University of Hildesheim, Universit

atsplatz 1, 31141, Hildesheim, Germany

Keywords:

Performance Prediction, Kalman Filter, Matrix Factorization, Student Simulator, Sequencing, Progress

Modeling.

Abstract:

One new usage of Learning Analytics in Intelligent Tutoring Systems (ITS) is sequencing based on perfor-

mance prediction, which informs sequencers whether a student mastered or not a speciﬁc set of skills. Matrix

Factorization (MF) performance prediction is particularly appealing because it does not require tagging in-

volved skills in tasks. However, MF’s difﬁcult interpretability does not allow to show the student’s state evolu-

tion, i.e. his/her progress over time. In this paper we present a novel progress modeling technique integrating

the most famous control theory state modeler, the Kalman Filter, and Matrix Factorization. Our method, the

Skill Deﬁciency aware Kalman State Estimation for Matrix Factorization, (1) updates at each interaction the

student’s state outperforming the baseline both in prediction error and in computational requirements allowing

faster online interactions; (2) models the individualized progress of the students over time that could be later

used to develop novel sequencing policies. Our results are tested on data of a commercial ITS where other

state of the art methods were not applicable.

1 INTRODUCTION

In Intelligent Tutoring Systems (ITS), adaptive se-

quencers can take past student performance into ac-

count to select the next task or feedback which best

ﬁts the student’s learning needs. One way to approach

the problem is based on assessing the student skills

and matching them to the required skills and difﬁcul-

ties of the available tasks. In this paper we want to

go a step forward with respect to domain independent

performance prediction. From an approach informing

only on the current/next state of the user, we move

to progress modeling, where the students’ state has to

evolve in a meaningful, plausible and therefore inter-

pretable way over time. In this scenario three prob-

lems arise:

1. Tagging tasks with required skills necessitates ex-

perts and thus is a time-consuming, costly, and,

especially for ﬁne-grained skill levels, also poten-

tially subjective.

2. Progress modeling requires the interpretability of

performance prediction’s models that should in-

struct with the student’s inferred state efﬁcient se-

quencing policies.

3. Student progress modeling updates need to occur

online so that each event can be used as reﬁnement

of the prediction.

Problem (1) involves common performance predic-

tion methods and their extensions: Bayesian Knowl-

edge Tracing (BKT) (Corbett and Anderson, 1994)

and Performance Factors Analysis (PFA)(Pavlik

et al., 2009). Therefore, other algorithms like Ma-

trix Factorization (MF) were proposed, which are do-

main agnostic and do not require the authoring ef-

fort of skills’ tagging (Schatten et al., 2015). By us-

ing MF and a simple policy inspired by Vygotsky’s

concept of Zone of Proximal Development (Vygot-

sky, 1978), the so-called Vygotsky Policy Sequencer

(VPS) obtained comparable results with state of the

art rule based sequencers without using rich experts’

knowledge (Schatten and Schmidt-Thieme, 2014). As

pointed out by Manouselis et al. (2011), too high re-

quirements for intelligent components dramatically

affect their integration. Therefore, domain indepen-

dence is particularly appealing because it allows the

integration of adaptive components in large ITS that

do not possess the skills involved in the tasks and can-

not invest the effort of tagging all their contents.

If MF is able to solve Problem (1), it unfortunately

suffers from Problem (2), i.e. it is able to predict

next performances without domain information, but

the parameters of the model cannot be used to in-

terpret the current state of the user and therefore its

progress over time. Moreover, MF online update suf-

Schatten, C. and Schmidt-Thieme, L.

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters.

In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 31-42

ISBN: 978-989-758-179-3

fers of Problem (3). When MF is used for Item Rec-

ommendation, its main application, the time affects

the users differently than in ITS, since voting movies

in different permuted orders will not affect the user’s

ratings. For this reason it is possible to model user

evolution and item characteristics in aggregated time

slices, where more subsequent ratings are considered

as generated from the same static model. On the con-

trary, in ITS after each exercise the students learn

something according to their learning rate. If a stu-

dent sees exercises in order or in reverse order of dif-

ﬁculty there will be not only a change in the scores

obtained, but also in the acquired knowledge. In order

to be able to use the latest model for each decision, an

online updating model is required. Ideally this should

happen in ITS at event level to reﬂect, in the future,

also the inﬂuence of feedbacks and hints.

To overcome these three problems, we developed do-

main independent progress modeling by integrating

the MF algorithms with Kalman Filters, one of the

most famous state modeling techniques of control the-

ory. This is achieved by exploiting equations of a stu-

dent simulator, which mimics the learning process of

a student.

As a result, the model:

• has reduced computational requirements,

• remains domain independent,

• has a reduced prediction error,

• is less sensitive to the lack of user data,

• and is made interpretable.

The presented paper is organized as follows. We ﬁrst

introduce the state of the art about students’ perfor-

mance prediction done with MF (Sec. 2). Then, in

Sec. 3 the algorithms of MF and its online update are

explained. After the Kalman Filters are presented to

the reader in Sec. 4, we combine the latter with MF

and the equations of a student simulator to obtain a

student progress modeler. Finally, in the Experiment

Section (Sec. 5), we analyze the novel algorithm un-

der different perspectives, which involves prediction

error and progress modeling.

2 STATE OF THE ART

MF has many applications like, for instance, dimen-

sionality reduction, clustering and also classiﬁcation

(Cichocki et al., 2009), but its most famous appli-

cation is for Recommender Systems (Koren et al.,

2009), where the algorithm recommends items to a

user by predicting the ratings (s)he would give to

them. Recently the algorithm was extended to time

modeling. In papers predicting movie ratings or doing

item recommendations, such as Xiong et al. (2010)

and Li et al. (2011) the time is modeled with time

slices, so that the user’s model needs to be updated at

each time slice. Because of that, no forecasting can

be done for time slices after the current and last one,

for which data are available. More similar to our ap-

proach is the online method proposed in Rendle and

Schmidt-Thieme (2008) that we explain in detail in

Section 3.2. There, for each new sample available

the model of the user is accordingly updated. Un-

fortunately, the algorithm requires for each update the

entire student’s history. Therefore, computational re-

quirements for systems that work in real time perfor-

mances, such as ITS, becomes too restrictive. As re-

ported by Schatten et al. (2015) 6 seconds were re-

quired for an update, whereas real time performances

should stay under the 0.1 seconds threshold (Nielsen,

1994).

As we explained in the introduction, when the afore-

mentioned algorithms are applied in a new domain

other problems arise. The ﬁrst time that MF was

applied to ITS, Thai-Nghe et al. (2011, 2010, 2012)

associated users with students, items with tasks, and

ratings to the probability of a correct answer at ﬁrst

attempt. Alternatively, as in Schatten et al. (2014a)

and Voss et al. (2015), ratings could be associated to

the percentage of correctly answered questions. Also

other Machine Learning techniques have been used

to model the students’ state. Bayesian Knowledge

Tracing (BKT) is built on a given prior knowledge of

the students and a data set of binary students’ perfor-

mances. It is assumed that there is a hidden state rep-

resenting the knowledge of a student and an observed

state given by the recorded performances. The model

learned is composed by slip, guess, learning and not

learning probability, which are then used to compute

the predicted performances (Corbett and Anderson,

1994). In the BKT extensions difﬁculty, multiple skill

levels and personalization are taken into account sep-

arately (Wang and Heffernan, 2012; Pardos and Hef-

fernan, 2010, 2011; D Baker et al., 2008), whereas

in our framework those aspects are considered at the

same time. MF most famous advantage in comparison

to BKT is the reduced authoring effort, since experts

are not requested to insert the required skills to solve

a task or use a hint. However, MF computed param-

eters cannot be associated to the student’s knowledge

as BKT modeled skills (Pardos and Heffernan, 2011).

In this paper we want to develop a progress modeling

algorithm based on MF online-updating performance

prediction that can work with fast performances to

schedule the recommendation of tasks, hints and feed-

backs. Usual approaches for sequencing are Rein-

forcement Learning techniques, which are applicable

in ITS with strong restrictions (Schatten et al., 2014b),

CSEDU 2016 - 8th International Conference on Computer Supported Education

0.1

0.95 0.1

1 0.5

0.35

0.87 0.2

0.1

0.95 0.1

1 0.5

0.35

0.87 0.2

0.1

0.12

0.3

0.95

0.83

0.85

0.79

0.85

0.2

Students

Contents

Students

Contents

Figure 1: Table of scores given for each student on tasks (or

interacting with generic tasks) (left), completed table by the

MF algorithm with predicted scores (right).

since the collection of an exploratory corpus implies

frustrating users with either too easy and too difﬁ-

cult tasks or random hints and feedbacks. Therefore,

we started from the implementation of Schatten et al.

(2015), where MF was used successfully combined

with a simple policy to schedule tasks with particular

attention to the computational requirements deﬁned

in Schatten et al. (2014c). An additional reason for

choosing Schatten et al. (2015) is the possible exten-

sion to multi-modal data analysis as presented in Jan-

ning et al. (2014a) and Janning et al. (2014b), or hint

sequencing as suggested by Schatten et al. (2014b).

3 ONLINE MATRIX

FACTORIZATION

We deﬁne our problem as a tuple (S,C, ˆy,τ) where,

given a set S of students, s

∈

{

1,...S

}

is the i–th stu-

dent modeled as a vector ϕ

∈ S := R

, where K is the

number of skills involved and S is the student’s space.

C is a set of tasks, where c

∈

{

1,...C

}

is the j–th

task, deﬁned with a vector ψ

∈ C := R

represent-

ing the K skills required to solve a task deﬁned in the

tasks’ space C. In this context we want to ﬁnd a suit-

able prediction function able to compute the predicted

performance ˆy(ϕ

,ψ

) of a student s

on a task c

con-

sidering all his past interactions. In order to do so we

need also to ﬁnd τ : S × C → S a function deﬁning the

follow-up state ϕ

t+1

of a student s

after interacting

with task c

. We explain hereafter how this is done

with pure MF techniques.

3.1 Static Matrix Factorization

Generally, in Recommender Systems MF predicts

which are the future user ratings on a speciﬁc item

based on its previous ratings and the previous rat-

ings of other users (Koren et al., 2009). The concept

has been extended to student performance prediction,

where a student’s next performance, or score is pre-

dicted. The matrix Y ∈ R

×n

can be seen as a table

of n

total tasks and n

students used to train the sys-

tem, where for some tasks and students performance

measures are given. MF decomposes the matrix Y in

two other ones Ψ ∈ R

×K

and Φ ∈ R

×K

, so that

Y ≈

Y = ΨΦ

. Ψ and Φ are matrices of latent fea-

tures, where each task c

, and each student s

, is rep-

resented, i.e. modeled, with a vector of K latent fea-

tures (ψ and ϕ respectively). Although these latent

features cannot be mapped to an exact meaning as

done in BKT technology, in Thai-Nghe et al. (2010)

those values were associated with the skills involved

in the tasks and the skills of the students. The latent

features learned with stochastic gradient descent from

the given performances allow computing the missing

elements of Y for each student i in each task j of a

dataset D (Fig. 1) without manually tagging the skills

of the domain. For this reason this approach has been

called domain independent in Schatten and Schmidt-

Thieme (2014). The optimization function of MF is

represented by:

min

,ϕ

∑

i, j∈D

i j

− ˆy

i j

)

+ λ(

) (1)

where one wants to minimize the regularized Root

Mean Squared Error (RMSE) on the set of known

scores. The prediction function is represented by:

ˆy

i j

∑

k=0

, (2)

3.2 Online Update

Input: History

, λ,Ψ, β, K, iter

Max

Output: ϕ

Ψ ∼ N(0,σ

)

iter

Max

= History

.length ∗ iter

Max

;

for iter = 1 to iter

Max

Select j randomly from History

;

err = y −



∑

k=0



;

for k = 1 to K do

∂err

∂ϕ

+ = β



err ∗ ψ

− λϕ



;

update ϕ

;

end

Algorithm 1: UpMF Rendle et al (2008), where β is the

learning rate, λ is the regularization parameter, Ψ are the

tasks’ latent features, iter

Max

is the number of algorithm’s

iterations, History

are all the tasks IDs j the student i

interacted with with performance y.

One of the criticized problems of MF is that it does

not deal with time, i.e. the latent features are constant

after the ﬁrst training. In order to keep the model

up to date, Schatten et al. (2015) implemented, in a

large commercial ITS, the online update proposed in

Rendle and Schmidt-Thieme (2008). The update, that

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

we will call hereafter UpMF, consists in solving again

the minimization problem of Eq. (1) optimizing only

ϕ with stochastic gradient descent algorithm. This

means the student’s model is learned at each interac-

tion from scratch. Schatten et al. (2015) coherently

with Rendle and Schmidt-Thieme (2008) noticed that

after approximately 20 interactions the model up-

date’s error for UpMF was degenerating. Schatten

et al. (2015) overcame the problem by retraining the

model each night, assuming students would see ap-

proximately 10 tasks per day. This was of course

imposing strong requirements on the machine where

the application ran since the training is more demand-

ing computationally in comparison to the prediction

phase. According to the pseudo-code Alg. 1 reported,

there are two main limitations of this algorithm. The

ﬁrst one is the dependency between the history length

and the number of algorithm’s iterations required to

converge to a solution. The more student’s interac-

tions are available, the more iterations are needed by

UpMF to converge (see Alg. 1). As a consequence the

time required to update the model increases over time.

To keep the update time constant one should select

meaningful samples out of the given history. Unfor-

tunately, we are not aware of previous work analyzing

this aspect in detail. The second issue is related to the

invariance to the samples sequence, i.e. when a sam-

ple is selected out of the ones available old and new

ones are considered equally. This means that the se-

quence has no inﬂuence in the model computation.

4 KALMAN STATE ESTIMATION

FOR MF (KSEMF)

In this Section we present a novel update method that

overcomes the main issues of the current state of the

art. Kalman Filters are one of the most used state es-

timation algorithms in operations research (Kalman,

1960) and therefore constitute a valid approach to our

progress modeling problem. First of all the sequen-

tiality of the measurements plays a major role. Then,

for their recursive structure they do not require the

load of the entire student’s history to compute the

update, so that the update time is constant. Finally,

thanks to our approach, we maintain the domain in-

dependence of the baseline.

4.1 Kalman Filter Theory

The state x at time t is modeled as a linear combina-

tion of the state at time t − 1 and a control input u at

time t − 1 with additive Gaussian noise w (Eq. (3)),

where A and B are matrices of coefﬁcients multiply-

ing the state and control variables respectively.

t+1

= Ax

+ Bu

+ w

(3)

In Eq. 4 the measurements of the environment are

predicted adding the current state estimation multi-

plied by a coefﬁcient matrix H to Gaussian noise v.

t+1

= Hx

+ v

(4)

Instead of learning from scratch the student’s param-

eters after each interaction, the Kalman Filter updates

its estimation at each time step with predict (Eq. (5))

and correct (Eq. (6)) phases integrating in its predic-

tion the novel available information. Kalman Filters

predict the current state ˆx

−

and the error covariance

matrix P

−

by means of Eq. (5), where Q is the state

noise covariance matrix derived from the Gaussian

noise variance w of the state variables.

ˆx

−

t+1

= Aˆx

+ Bu

−

t+1

= AP

+ Q (5)

Then, with a new measurement y

, state estimation

ˆx

and error covariance matrix P

are corrected with

Eqs. 6, where K

is the so-called Kalman Gain and

R the measurement noise covariance matrix derived

from the variance of the measurement noise v

= P

−

t+1



−

t+1

+ R



−1

ˆx

t+1

= ˆx

−

t+1

+ K



− H ˆx

−

t+1



= (I − K

H) P

−

(6)

R, Q and P

are all diagonal matrices whose values

are treated as hyperparameters, e.g. Q = diag(0.01)

means that all Q values on the diagonal are assigned

to 0.01. We want to use this approach to model the

evolution over time of the MF’s latent features and

consequently show the students’ progress over time.

4.2 Kalman State Estimation for Matrix

Factorization (KSEMF)

In this Section we present our novel method for

progress modeling: the Kalman State Estimation for

Matrix Factorization (KSEMF). In order to integrate

the Kalman Filter and MF we ﬁrst need to identify

the state and the control of the system. As aforemen-

tioned, at each time step ϕ

of student s

, i.e. the stu-

dent’s MF latent features, needs to be updated to ϕ

t+1

with a function τ. Under this interpretation, ϕ

should

be the evolving state. The control over the system are

the tasks’ latent features ψ

presented to the student,

whereas the score y

represents the measurement and

its prediction ˆy

at time t (Eq. (7)). Since this algo-

rithm is modeling the state and the interaction with the

CSEDU 2016 - 8th International Conference on Computer Supported Education

environment explicitly, a working Kalman Filter does

not only show that the approach is valid for perfor-

mance prediction, but also that (1) the students’ latent

features can be interpreted as the students’ state and

that (2) the tasks’ latent features can be interpreted as

the tasks’ characteristics.













t+1

= A













+ B













+ w

ˆy

t+1

= H













+ v

(7)

In order to integrate the prediction function of MF

(Eq. (2)) we formalized the relationship between state

and predicted measurement ˆy

as in (8), having then

H = ψ

ˆy













t−1













t−1

+ v

t−1

(8)

Still missing is Eq. (3), i.e. the function τ mapping

the state ϕ

with the state at time t + 1.

4.3 Skill Deﬁciency aware

KSEMF(KSEMF SD)

In order to make KSEMF aware of the student’s

skills deﬁciency, we will model the update function τ,

which represents the learning from one task interac-

tion, in a speciﬁc way. We started from the simulated

student developed in Schatten and Schmidt-Thieme

(2014) that was able to simulate a learning process

with continuous knowledge and score representation

and tasks with multiple difﬁculty levels. Neverthe-

less, we do not exclude the possibility to use also

other equations to model the relationship between ϕ

and ϕ

t+1

. The simulator models a learning process

deﬁned by the Zone of Proximal Development (ZPD)

(Vygotsky, 1978), i.e. a student can learn from a task

only if it is of the correct difﬁculty level. This is de-

ﬁned in the simulated environment as the difference

i, j

between the skills of the student ϕ

and those re-

quired to solve the task ψ

. As a consequence α

i, j

represents the skill deﬁciency of the student.

˜y(ϕ

,ψ

) =max(1 −

||α

i, j

||ϕ

,0)

τ(ϕ

,ψ

)

= ˜y(ϕ

,ψ

)α

i, j

=max(ψ

− ϕ

,0) (9)

In Eq. (9) ˜y represents the simulated score of the

student and the skills are positively deﬁnite. There-

fore ϕ

> ϕ

i2k

means student i is more knowledge-

able than student i2 and ψ

> ψ

j2k

means task j is

more difﬁcult than task j2. Finally ψ

< ϕ

means

a task j is too easy for student i and (s)he cannot

learn from it (Schatten and Schmidt-Thieme, 2014).

To develop the Skill Deﬁciency aware Kalman State

Estimation for Matrix Factorization (KSEMF SD) we

interpreted the simulator modeled skills ψ

and ϕ

for all i, j, and k as the from MF computed latent fea-

tures. We then reformulated the equations modeling

the process, Eq. (9), to ﬁt Eq. (3) and work also with

negative latent features. Therefore, we slightly modi-

ﬁed Eq. (9) to Eq. (10). These changes allowed also

negative latent features, but kept the ZPD properties

of the simulator, i.e. a student cannot learn from too

easy tasks and learns from a task proportionally to his

knowledge and the skills required to solve the task.

The equations were changed as shown in Eq. 10.

˜y(ϕ

,ψ

) = max(1 −

||α

i, j

||ϕ

,0)

τ(ϕ

,ψ

)

= ˜y(ϕ

,ψ

)γδ(α

i, j

> 0)ψ

i, j

= ψ

max(1 − ϕ

/ψ

,0), (10)

where γ is a weight and δ is a Kronecker δ that is equal

to 1 when its condition α

i, j

> 0 is veriﬁed and 0 else-

where. α

i, j

> 0 for max(ψ

− ϕ

,0) when ψ

> 0

and for min(ψ

− ϕ

,0) for ψ

< 0. Under the in-

terpretation ϕ

i,k

= 0 means student i does not possess

skill k and



i,k



> 0 now means having some ability

in skill k. The mathematical properties of the equa-

tions did not change much from the previous version

and are:

1. The simulated performance ˜y of a student on a

task decreases proportionally to his skill deﬁcien-

cies w.r.t. the required skills.

2. The student will improve all the required skills of

a task proportionally to his simulated performance

˜y, his learning rate γ up to the skill level a task

requires.

3. As a consequence it is not possible to learn from

a content more than γ times the required skills.

4. A further property of this model is that tasks re-

quiring twice the skills level a student has, i.e.



≥ 2

, are beyond the reach of a student.

Given Eq. (10) we obtained

(t)

= ϕ

(t−1)

+ (˜y(ϕ

,ψ

)γδ(



))ψ

i.e.

A = diag(1)

and

B = diag(˜y(ϕ

,ψ

)δ(



)γ). (11)

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

5 EXPERIMENT SECTION

In this Section we analyze different aspects of the al-

gorithm. First, we describe the dataset used for the

experiments; then, we analyze the hyperparameters’

selection and the model initialization. Afterwards, we

discuss the ability of the algorithm to model the stu-

dent progress. This is done from different perspec-

tives, which involve the personalization of the state

and the update rate. sensitiveness of the algorithm to

the lack of data.

5.1 Dataset Characteristics

To test the presented algorithm and model the

progress of the students we use the dataset collected

with an ITS with 20 topics about maths for children

aged from 6 to 14, who can practice with over 2000

tasks at school or at home.

An example of questions proposed to the students can

be found in Fig. 2. From these questions proposed

in sets, that we call interactions or tasks, we do not

know which ones precisely were answered correctly

since the ITS aggregates the information in a single

score. For these multiple-skills interactions we do not

possess the skills involved, therefore, in this context,

we cannot use classic BKT and PFA approaches. The

score, as in Schatten and Schmidt-Thieme (2014), is

represented in a continuous interval which goes from

0 to 1. The topics and new skills to be acquired are

introduced following the curriculum of the country.

The tasks are presented with a rule-based sequencer,

which increases the difﬁculty of the tasks once the

student completed and passed all the tasks of the dif-

ﬁculty level. If the tasks are not passed the student

gets a regression exercise or can try again to solve the

task.

Figure 2: Two questions of the commercial ITS.

Of the large dataset of the commercial ITS we se-

lected two subsets described in Tab. 1 in order to

minimize the noise due to the lack of data and monitor

Table 1: Dataset Statistics.

Train

Test

Number of Tasks 2035 2035

Number of Students 24288 713

Total Student-Task 751109 102038

Interactions, N

the progress of the error and latent features over time.

Consequently, we selected only the students i with at

least N

> 10 interactions, where one interaction cor-

respond to a student solving a set of 10 questions ag-

gregated in a single score. The available students are

then divided in two groups. The group of those with

10 < N

< 100 is used to initialize the latent features

of all algorithms (D

Train

, Tab. 1), whereas the others

with N

> 100 are used to test online updates UpMF

and KSEMF

SD (D

Test

Tab. 1).

5.2 Hyperparameters’ Selection

All the model hyperparameters of MF, UpMF and

KSEMF SD were selected with a full Grid Search,

i.e. the inﬂuence on the model error of different

combinations of hyperparameters is analyzed in a

brute force manner. First MF ones were evaluated

considering the RSME obtained with a further split of

Train

. 66% of D

Train

was used to train the MF model

and its 34% was used to test the model with the

different hyperparameters. UpMF and KSEMF SD

best hyperparameters are then selected in the ranges

presented in Tab. 2 according to the performances in

Test

in particular we used the value Total RMSE

computed as in Alg. 2 to evaluate the performances

of the algorithm.

Input: D

Train

, D

Test

, Q, R, P

Use D

Train

and Eq. (1) to obtain Φ

(t=0)

and Ψ;

for each s

interactions in D

test

N do

A = diag(1), H = ψ

;

Compute B using Eq. (11);

ˆy=Predict, Eq. (5);

Correct, Eq. (6);

Err+ = (y − ˆy)

;

end

Total RMSE=

Err/N;

Algorithm 2: Experiments’ Framework.

UpMF and MF hyperparameters are λ, β, iter

Max

and

K. In addition to these, KSEMF SD possesses four

more hyperparameters: Q, R, γ, and P

. The empirical

approach is to model Q, R, and P

as diagonal matri-

ces and test their diagonal values with a logarithmic

scale. The selected hyperparameters are reported in

Tab. 3.

CSEDU 2016 - 8th International Conference on Computer Supported Education

Table 2: Hyperarameters rages tested for UpMF and

KSEMF SD.

Parameters Range Step

Learning Rate β 0.01-0.1 0.01

Latent Features K 2-120 20

Regularization λ 0.01-0.1 0.01

0.001-0.01 0.001

Number of Iterations 10-200 10

Iter

Max

State Noise Cov. Q 0.00001-1 logarithmic

Error Noise Cov. P

0.00001-1 logarithmic

Measurement Noise 0.00001-1 logarithmic

Cov. R

Weight γ 0.00001-1 logarithmic

Table 3: Selected hyperarameters UpMF and KSEMF SD.

Parameters UpMF KSEMF SD

Learning Rate β 0.01 0.01

Latent Features K 102 62

Regularization λ 0.01 0.01

Number of Iterations 100 25

Iter

Max

State Noise Cov. Q - 0.00001

Error Noise Cov. P

- 1

Measurement Noise - 0.001

Cov. R

Weight γ - 0.001

In the future more efﬁcient approaches to hyperpa-

rameters’ selection could be used as the ones sug-

gested by Wistuba et al. (2015) and Schilling et al.

(2015).

5.3 State Variables Initialization

The next question to answer was how to initialize

the latent features of UpMF and KSEMF SD. Since

both algorithms are fully personalized they both suf-

fers from the so called cold-start problem, which oc-

curs when no information is available about the stu-

dents or the tasks. Therefore, a random initialization

of the latent features would lead to very bad perfor-

mances (Voss et al., 2015). Usual approach to solve

the problem is to train a model with the classic MF

algorithm and use the computed tasks’ latent features

to initialize KSEMF SD and UpMF. These are then

kept constant while applying Alg. 2 or Alg. 1. Since

Train

and D

Test

have no overlapping students, the

Test

students’ cold-start problem is solved by includ-

ing in D

Train

data of their ﬁrst interactions with the

ITS, so that their latent features can be learned in a

full training. The samples necessary to avoid the cold

start problem, both for students and tasks, are gen-

0 50 100 150 200

0.15

0.2

0.25

0.3

0.35

Interactions

Total_RMSE

UpMF

KSEMF_SD

KSEMF_SD Cold

UpMF Cold

Figure 3: D

Test

Total RMSE behavior over time: Models

marked with ”Cold” label are initialized with only 1 inter-

action in D

Train

whereas the others with 10.

erally 10. This amount was empirically deﬁned by

Pil

aszy and Tikk (2009). Since these 10 interactions

are not always available, we show also results when

just one interaction is included in D

Train

. The by MF

computed students’ and tasks’ latent features are then

used to initialize respectively Φ

(t=0)

and Ψ of UpMF

and KSEMF SD. The MF results shown in all the sub-

sequent ﬁgures are the ones of the MF used to initial-

ize KSEMF SD, so that it is possible to see the lift

obtained by the KSEMF SD update.

In Fig. 3 we can see how the Total RMSE, computed

as in Alg. 2, evolves over time. Models marked with

the ”Cold” label are initialized with only 1 sample

whereas the others are initialized with 10. MF Cold

behaved like a random predictor with an error around

0.5 and is not shown in Fig. 3. As it is possible to

see, the 10 samples substantially improved the error.

Nevertheless, we believe this is still not an optimal

initialization for KSEMF SD, since for the ﬁrst inter-

actions KSEMF SD is outperformed by UpMF and

MF with 10 samples initialization. KSEMF SD, ini-

tialized with 10 samples, has a similar behavior as MF

because it inherits the error of MF tasks’ latent fea-

tures whereas KSEMF SD error amelioration is due

to the better students’ latent features modeling.

If these 10 interactions are not available, KSEMF SD

Cold converges faster to smaller errors than UpMF

Cold. In Voss et al. (2015) it was discussed how the

cold start problem limits the usage of MF in small ITS

or for short experiments with new students. There-

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

0 20 40 60 80 100 120 140

0.22

0.225

0.23

0.235

0.24

0.245

0.25

0.255

# Latent Features

RMSE

Sensitiveness of RMSE to number of Latent Features

KSEMF_SD

UpMF

Figure 4: RMSE sensitiveness analysis to latent features.

fore, a faster converging error is an appealing prop-

erty, that could further reduce the requirements of MF.

Despite a better performance in the ﬁrst interactions

UpMF error increases over time. The problem was

reported also by Schatten et al. (2015), who, to avoid

this issue, retrained the model each night. This is

however a quite demanding computational require-

ment and, as we will see in Sec. 5.5, can affect the

progress modeling approach we want to use. More-

over, UpMF requires the entire history of one stu-

dent as input parameter for Alg. 1 that in case of DB

implementation will not only slow down the perfor-

mances but also increase the complexity of the sys-

tem. KSEMF SD does not require demanding DB ac-

cesses to extract the entire student’s history since it

uses only information of the current time step to pre-

dict the next one.

Finally, in this experiment we also provide the ﬁrst

proof that KSEMF SD is able to predict the student

performances, meaning that it is possible to interpret

the student’s latent features as their state.

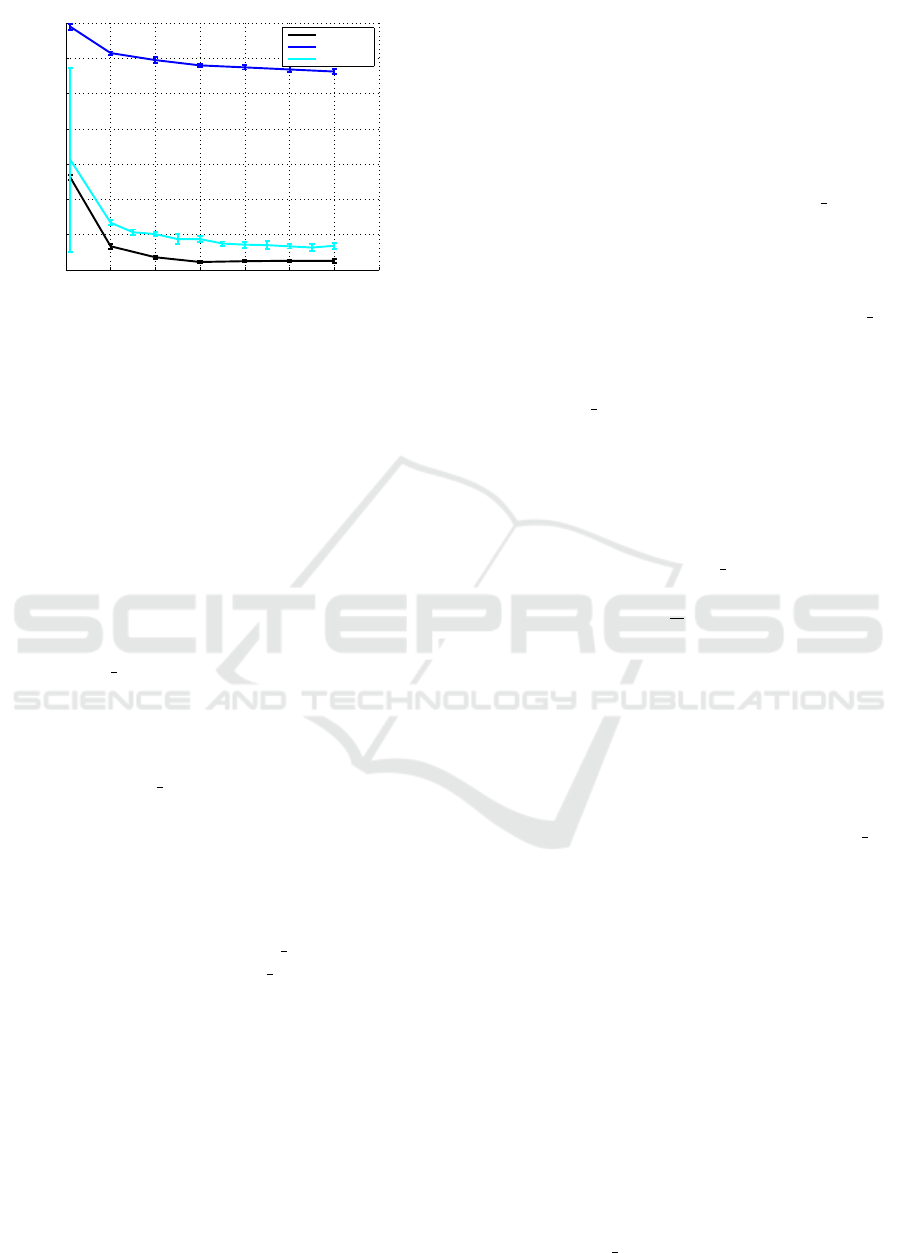
5.4 RMSE Evaluation

In this Section we evaluate the overall algorithm per-

formances by computing the Total RMSE, as in Alg.

2. For MF, UpMF and KSEMF SD we analyze the

sensitiveness to the number of latent features. More-

over, we repeated the experiment ﬁve times to be able

to exclude the variance inﬂuence due to the random

initialization of the MF. As shown in Fig. 4 the algo-

rithm is able to outperform our reference baselines in

all tried latent features conﬁgurations.

5.5 Modeling Student Progress

In order to use the developed algorithm to model stu-

dent progress, it is important to be able to use the

performance predictor as model for the user state and

take decisions accordingly. One of the claimed dis-

advantages of MF approaches in comparison to BKT

and PFA is that the amount of knowledge of the stu-

dent cannot be extracted directly from the latent fea-

tures computed by the algorithms. For this reason

Schatten and Schmidt-Thieme (2014) proposed a se-

quencer which uses only the information coming from

the predicted score. In Fig. 5 it is shown (a) how the

latent features evolve according to KSEMF SD algo-

rithm in a scenario with 62 latent features and (b) how

the latent features evolve according to UpMF algo-

rithm in a scenario with 102 latent features. Fig. 5 (f)

shows the actual score of the student (blue) and the

predicted performance of the student by KSEMF SD

(green) and MF (red). In all displayed examples it

is not possible to understand what is the overall state

evolution of the student. However, the predicting abil-

ity of KSEMF SD let us suppose that the latent fea-

ture have indeed a state meaning for the algorithm

and consequently an evolution according to the stu-

dent’s performance should be monitored. Therefore,

to monitor a meaningful trend, we aggregated the fea-

tures computing the norm 1 normalized for the num-

ber of latent features as in Eq. (12) and depicted the

results in Fig. 5 (c) for KSEMF SD and (d) for UpMF.

kn =

∑

k=0

(12)

Under the interpretation that ϕ

i,k

= 0 means student

i does not possess skill k, whereas



i,k



> 0 means

having some ability in skill k, variable kn could be

understood as the personalized knowledge evolution

or the learning curve of the user. Although UpMF

latent features are learned from scratch after each in-

teraction one can notice in the ﬁgures an evolution

trend, which is as plausible as the one of KSEMF SD.

This also conﬁrms that the latent features in MF ap-

proaches represents the state of the user and their

value could be used to retrieve the students knowledge

amount. We believe this works because the tasks’

latent feature are kept constant. Therefore, in order

to keep track of the current state of the students one

cannot do a full retrain of the UpMF model, as done

by Schatten et al. (2015), since this would reset the

values of the tasks’ latent features, that allow recon-

structing at each interaction the state of the student by

means of the student’s history.

5.6 Personalization

One important aspect of progress modeling is per-

sonalization. MF creates an individualized model

as well for tasks as for students. In order to do so

also for KSEMF SD, each student has his/her own

CSEDU 2016 - 8th International Conference on Computer Supported Education

0 50 100 150 200

−2

(a) State Evolution KSEMF

0 50 100 150 200

−0.5

0.5

(b) State Evolution UpMF

0 50 100 150 200

0.5

0 50 100 150 200

0.05

0.1

(d) Knowledge Evolution UpMF

0 50 100 150 200

0.1

0.2

(e) RMSE Error

0 50 100 150 200

0.5

(f) Score

Figure 5: x-Axis: Number of tasks seen by the student

or interactions. y-Axis: (a) state evolution according to

KSEMF SD with K=62. (b) state evolution according to

UpMF with K=102. (c) and (d): knowledge evolution

for KSEMF SD and UpMF computed as in Eq. (12). (e)

Total RMSE of KSEMF SD (blue), MF (green) and UpMF

(black). (f) Actual performance of the student (blue), pre-

dicted performance by KSEMF SD (green), MF (red).

KSEMF SD equations updating according to his/her

modeled state and performances. Since the simula-

tor equations are based on the state variable, in this

context, also the B matrix is personalized and change

at each interaction. Therefore, the update equations

of KSEMF SD model personalization in two differ-

ent ways. The B matrix represents the inﬂuence of

the student on the update, i.e. what is his/her learn-

ing rate and its skills’ deﬁciency. The control u, i.e.

the tasks’ latent features ψ, represents the inﬂuence

of the task on the knowledge acquisition of the stu-

dent. Hereafter, we will see how the state as well as

the update evolve over time in a personalized way.

0 50 100 150 200

−5

(a) State Evolution Student 1

0 50 100 150 200

(b)Knowledge Evolution Student 1

0 50 100 150 200

0.2

0.4

0 50 100 150 200

−5

(d) State Evolution Student 2

0 50 100 150 200

(e) Knowledge Evolution Student 2

0 50 100 150 200

0.2

0.4

(f) Error Student 2

Figure 6: x-Axis: Number of tasks seen by the student or

interactions. y-Axis:(a) and (d): KSEMF SD state evolu-

tion of two different students, K=62. (b) and (e): kn of

KSEMF SD latent features computed as in Eq. 12. (c)

and (f): Total RMSE of KSEMF SD (blue), MF (green)

and UpMF (black) of two different students.

5.6.1 Personalized State Evolution

See Fig. 6 (b) and (d) to see the personalized latent

features’ trends of KSEMF SD. In Fig. 4 (c) and (f)

and in Fig. 5 (e) we can see the Total RMSEs of the

models for three speciﬁc students. These are overall

coherent with the results presented in Fig. 3. This

information could be used in several ways, e.g. by

later establishing the mapping between the computed

kn trend and the actual knowledge acquisition of the

users, we could design novel policies for sequencing

tasks, feedbacks and hints. In addition, the relation-

ship between kn and the model error should be further

analyzed. This will allow also to monitor the perfor-

mances of the performance predictor over time.

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

0 50 100 150 200

−5

(a) State Evolution KSEMF

0 50 100 150 200

−0.5

0.5

(b) State Evolution UpMF

0 50 100 150 200

0.5

0 50 100 150 200

0.05

0.1

(d) Knowledge Evolution UpMF

0 50 100 150 200

0.5

(e) RMSE Error

0 50 100 150 200

0.5

(f) Update

Figure 7: x-Axis: Number of tasks seen by the student or

interactions. y-Axis: (a) how the state evolves according to

KSEMF SD with K=62. (b) shows how the state evolves

according to UpMF algorithm with K=102. (c) and (d)

show the knowledge evolution, computed as in Eq. (12).

(e) RMSE of KSEMF SD (blue), RMSE of MF (green)

and UpMF (black). (f) Actual Performance of the stu-

dent (blue), predicted performance of the student by the

KSEMF SD (green), predicted performance by MF (red)

and ˜y (turquoise).

5.6.2 Personalized Update Evolution

In this Section we discuss the plausibility of the per-

sonalized update trend derived through Eqs. (10). For

simplicity we considered ˜y, which represents the up-

date of the state, since it is later multiplied with con-

stant γ to obtain B (See Eq. 3). In Fig. 7 (f) we show,

for a student, how ˜y evolves over time. An almost con-

stant update is plausible, since it mimics the learning

rate of the student, which is related to his/her learning

ability. However, its adaptive computation through

the state is of advantage, since it allows the model to

faster adjust to the students’ states changes. In Fig. 8

0 50 100 150 200

0.08

0.1

0.12

0.14

0.16

0.18

0.2

0.22

0.24

0.26

Mean Update

Interactions

Update

Figure 8: Mean Update Over Time Update behavior at

each interaction on average for all students.

we see that the average update for all students evolves

over time converging only in the last interactions to a

constant value. This is explicable with the previously

seen behavior of KSEMF SD in the ﬁrst interactions

(see Fig. 3) and should be seen as another indicator

that the initialization of the algorithm is not optimal.

Although we were not interested in keeping the sim-

ulation properties of the simulator from which we

derived our equations, we brieﬂy discuss why ˆy is

smaller than the actual performance. Since the vari-

ables of ϕ and ψ are not clipped between 0 and 1 as in

Schatten and Schmidt-Thieme (2014)



i, j



is con-

sequently bigger on average and ˜y smaller than the

actual performance. In conclusion, given the amelio-

rated results of KSEMF SD over UpMF, reported in

both Fig. 3 and Fig. 4, we overall showed that the de-

signed equations for KSEMF SD are suitable to up-

date the students’ latent features.

6 CONCLUSIONS

In this paper we presented KSEMF SD a novel

method for student progress modeling based on online

updating MF performance prediction and skills’ deﬁ-

ciency aware Kalman Filters. We go a step forward

with respect to domain independent performance pre-

diction with progress modeling; showing how to rep-

resent the evolution of the students over time in a

plausible way. This is done by assigning a speciﬁc

interpretation to latent features which represents the

state of the student and the characteristics of a task.

In future work, we believe to be able to map the rela-

tionship between the computed kn and the real knowl-

edge evolution. This will hopefully deliver an effort-

less analysis tool to teachers and developers.

The developed algorithm also showed appealing

properties in comparison to another domain indepen-

CSEDU 2016 - 8th International Conference on Computer Supported Education

dent progress modeler. First, the computational re-

quirements are reduced because the entire student’s

history is not necessary to compute the updated la-

tent features. Then, the algorithm remains domain in-

dependent because the tagged skills of the tasks are

not necessary to deliver a score prediction. Finally,

KSEMF SD reduced the prediction error and is less

sensitive to the lack of that. In future work we believe

to further be able to reduce the error by developing a

better initialization of the students’ latent features.

ACKNOWLEDGEMENT

This research has been co-funded by the Sev-

enth Framework Programme of the European Com-

mission, through project iTalk2Learn (#318051).

www.iTalk2Learn.eu.

REFERENCES

Cichocki, A., Zdunek, R., Phan, A. H., and Amari, S.-i.

(2009). Nonnegative matrix and tensor factorizations:

applications to exploratory multi-way data analysis

and blind source separation. Wiley. com.

Corbett, A. and Anderson, J. (1994). Knowledge tracing:

Modeling the acquisition of procedural knowledge.

UMAI.

D Baker, R. S., Corbett, A. T., and Aleven, V. (2008). More

accurate student modeling through contextual estima-

tion of slip and guess probabilities in bayesian knowl-

edge tracing. In ITS, pages 406–415. Springer.

Janning, R., Schatten, C., and Lars, S.-T. (2014a). Fea-

ture analysis for affect recognition supporting task se-

quencing. In ECTEL.

Janning, R., Schatten, C., and Schmidt-Thieme, L. (2014b).

Multimodal affect recognition for adaptive intelligent

tutoring systems. In FFMI EDM.

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Journal of Fluids Engineer-

ing, 82(1):35–45.

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factor-

ization techniques for recommender systems. Com-

puter, 42(8):30–37.

Li, B., Zhu, X., Li, R., Zhang, C., Xue, X., and Wu,

X. (2011). Cross-domain collaborative ﬁltering over

time. In Proceedings of the Twenty-Second inter-

national joint conference on Artiﬁcial Intelligence-

Volume Volume Three, pages 2293–2298. AAAI Press.

Manouselis, N., Drachsler, H., Vuorikari, R., Hummel, H.,

and Koper, R. (2011). Recommender systems in tech-

nology enhanced learning. In Recommender systems

handbook, pages 387–415. Springer.

Nielsen, J. (1994). Usability engineering. Elsevier.

Pardos, Z. A. and Heffernan, N. T. (2010). Modeling indi-

vidualization in a bayesian networks implementation

of knowledge tracing. In UMAP. Springer.

Pardos, Z. A. and Heffernan, N. T. (2011). Kt-idem: intro-

ducing item difﬁculty to the knowledge tracing model.

In UMAP, pages 243–254. Springer.

Pavlik, P., Cen, H., and Koedinger, K. (2009). Performance

factors analysis-a new alternative to knowledge trac-

ing. In AIED.

Pil

aszy, I. and Tikk, D. (2009). Recommending new

movies: Even a few ratings are more valuable than

metadata. In RecSys.

Rendle, S. and Schmidt-Thieme, L. (2008). Online-

updating regularized kernel matrix factorization mod-

els for large-scale recommender systems. In Proceed-

ings of the 2008 ACM conference on Recommender

systems, pages 251–258. ACM.

Schatten, C., Janning, R., and Schmidt-Thieme, L. (2014a).

Vygotsky based sequencing without domain informa-

tion: A matrix factorization approach. In Computer

Supported Education, pages 35–51. Springer.

Schatten, C., Janning, R., and Schmidt-Thieme, L. (2015).

Integration and evaluation of a machine learning se-

quencer in large commercial its. In AAAI2015.

Springer.

Schatten, C., Mavrikis, M., Janning, R., and Schmidt-

Thieme, L. (2014b). Matrix factorization feasibility

for sequencing and adaptive support in its. In EDM.

Schatten, C. and Schmidt-Thieme, L. (2014). Adaptive

content sequencing without domain information. In

CSEDU.

Schatten, C., Wistuba, M., Schmidt-Thieme, L., and

Gutirrez-Santos, S. (2014c). Minimal invasive inte-

gration of learning analytics services in its. In ICALT.

Schilling, N., Wistuba, M., Drumond, L., and Schmidt-

Thieme, L. (2015). Joint model choice and hyperpa-

rameter optimization with factorized multilayer per-

ceptrons. In Tools with Artiﬁcial Intelligence (ICTAI),

2015 IEEE 27th International Conference on, pages

72–79. IEEE.

Thai-Nghe, N., Drumond, L., Horvath, T., Krohn-

Grimberghe, A., Nanopoulos, A., and Schmidt-

Thieme, L. (2011). Factorization techniques for pre-

dicting student performance. Educational Recom-

mender Systems and Technologies: Practices and

Challenges. IGI Global.

Thai-Nghe, N., Drumond, L., Horvath, T., and Schmidt-

Thieme, L. (2012). Using factorization machines for

student modeling. In UMAP Workshops.

Thai-Nghe, N., Drumond, L., Krohn-Grimberghe, A., and

Schmidt-Thieme, L. (2010). Recommender system

for predicting student performance. Procedia Com-

puter Science, 1(2):2811–2819.

Voss, L., Schatten, C., and Schmidt-Thieme, L. (2015). A

transfer learning approach for applying matrix factor-

ization to small its datasets. In EDM2015.

Vygotsky, L. L. S. (1978). Mind in society: The develop-

ment of higher psychological processes. HUP.

Wang, Y. and Heffernan, N. T. (2012). The student skill

model. In ITS2012.

Student Progress Modeling with Skills Deﬁciency Aware Kalman Filters

Wistuba, M., Schilling, N., and Schmidt-Thieme, L. (2015).

Sequential model-free hyperparameter tuning. In

Data Mining (ICDM), 2015 IEEE International Con-

ference on, pages 1033–1038. IEEE.

Xiong, L., Chen, X., Huang, T.-K., Schneider, J. G., and

Carbonell, J. G. (2010). Temporal collaborative ﬁlter-

ing with bayesian probabilistic tensor factorization. In

SDM, volume 10, pages 211–222. SIAM.

CSEDU 2016 - 8th International Conference on Computer Supported Education