A Method to Improve the Precision of Interferometric

Phase-recognization under Open-loop PZT Drive

Liangen Yang, Xuanze Wang, Bingkang Liu, Zhongsheng Zhai and Tao He

School of Mechanical Engineering, Hubei University of Technology, Nanhu, Wuhan, China

Keywords: Phase Recognization, Four Steps Algorithm, Ellipse Fitting, Lagrange Interpolation, Open-loop PZT Drive.

Abstract: For the monochromatic light interferometry under open-loop PZT drive, a high precision method for phase

recognization that satisfies the four steps phase-shift algorithm is proposed. The total idea of the phase

recognization method is as follows. Firstly, two pixels with suitable phase-difference are selected from the

interference field and the interference equations of the two pixels' gray values are established in one driven

cycle of PZT. Secondly, the parameters of interference equations can be obtained by using ellipse fitting

algorithm. Thirdly, the point-to-point step length of PZT drive and sequence phases can be determined

through reverse calculation of sequence phases. Finally, in order to calculate initial phase of every pixels

four interference grayscale images that meet the four steps phase-shift algorithm are designed and calculated

through Lagrange parabolic interpolation. The experimental results have shown that this method decreases

the requirement for hardware, environment and needs less interference grayscale images than traditional

methods. The method can meet the high precision demands of surface topography measurement and has

high processing speed.

1 INTRODUCTION

In the interference measurement of surface

topography by monochromatic light or quasi

monochromatic light, the calculation accuracy of

interferometric phase determines directly the

accuracy of the measurement results. Therefore, the

phase information should be accurately extracted

before unwrapping operation for the interferometric

phase. At present, there are many ways to extract

interferometric phase. For example, three-step

method (Wyant et al., 1984), four-step method

(Wyant, 1982）, five-step method (Hariharan et al.,

1987), FFT algorithm (Wang and Da, 2012), wavelet

transform (Cui et al., 2012), phase retrieval method

used for wavelength-scanning (Liu et al., 2014) or

wavelength-tuning Interferometer (Kato and

Yamaguchi, 2000) and so on. The essence of these

algorithms is to obtain the initial phases of

interference sequence of every pixel by eliminating

the influence of amplitude and offset parameters.

The difference among three-step method, four-step

method and five-step method is the anti-noise-

interference ability. The FFT algorithm requires the

interference sequence for a complete cycle and

always needs a large amount of data processing. As

a result, it has low efficiency. Futhermore, these

methods require PZT be closed-loop controlled,

which increases the difficulty and cost of driver

element (Deng, 2014). Because tiny vibration during

measurement process will lead to the driving step

length change and has a great influence on the final

measurement results, the measurement system has

also very high requirements for measuring

environment.

An algorithm for calculating the interference

phase through arbitrary driving step lengths was

presented (Hao et al., 2009). The requirement of the

approach is as follows. Firstly, find out the

maximum and the minimum gray values of a point

in the interference field from the sequence

interference grayscale images. Then the sequence

phases are calculated. Finally, the sequence phases

of every point in the interference field are computed.

The method doesn't require controlling the driving

step length of PZT, but it costs more time on image

acquisition and needs more interference images than

other methods. When the number of interference

images is small, the real maximum and minimum of

gray values cannot be found out. As a result, this

method cannot be used.

Yang, L., Wang, X., Liu, B., Zhai, Z. and He, T.

A Method to Improve the Precision of Interferometric Phase-recognization under Open-loop PZT Drive.

DOI: 10.5220/0005737701230129

In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 125-131

ISBN: 978-989-758-174-8

Copyright

c

125

This paper has two core problems need to be

solved. The first is how to obtain the initial phase

information of every pixel in the interference field

based on sequence grayscale images under the open-

loop drive conditions of PZT. The second is to

ensure phase information has high recognition

precision and recognition precision is not effected by

environment.

Based on four-step method, this paper proposed a

high accuracy phase recognition method that doesn't

require PZT to be equal driving step length. The

main idea is to acquire exactly the interference

sequence phases or step lengths of PZT by ellipse

fitting algorithm according to gray correlation

information of every pixel in the interference field

based on the interference equations. By extracting

sequence phases of interference grayscale images

and Lagrange parabolic interpolation algorithm (Liu

et al,2010), four interference grayscale images with

phase difference π/2 which meet requirement for

calculation of four-step phase-shift method are

calculated and constructed. Finally, through

interference grayscale images, phase information of

every pixel in the interference field can be obtained

by using four-step method.

2 CALCULATION METHOD OF

PZT DRIVING STEP LENGTH

In theory, gray values g

i

of every pixel in the

interference field satisfies the expression:

CAg

ii



 )cos(

0



(1)

Where i is the No. of driving sequence points

i=1,…, N. θ

i

is the driving sequence phases. A, C, θ

0

are the amplitude, offset and initial phase of every

pixel.

The relation between θ

i

and driving displace-

ment Δ

i

satisfies equation (2):







/4

ii





(2)

Therefore, the driving step length of PZT is

proportional to the interferometric phase. The key to

determine the driving step length is obtain driving

phase of every point in interference sequence θ

i

. The

calculation of θ

i

depends on the calculation of A and

C when the gray values are known. In this section

we discuss how to calculate A and C.

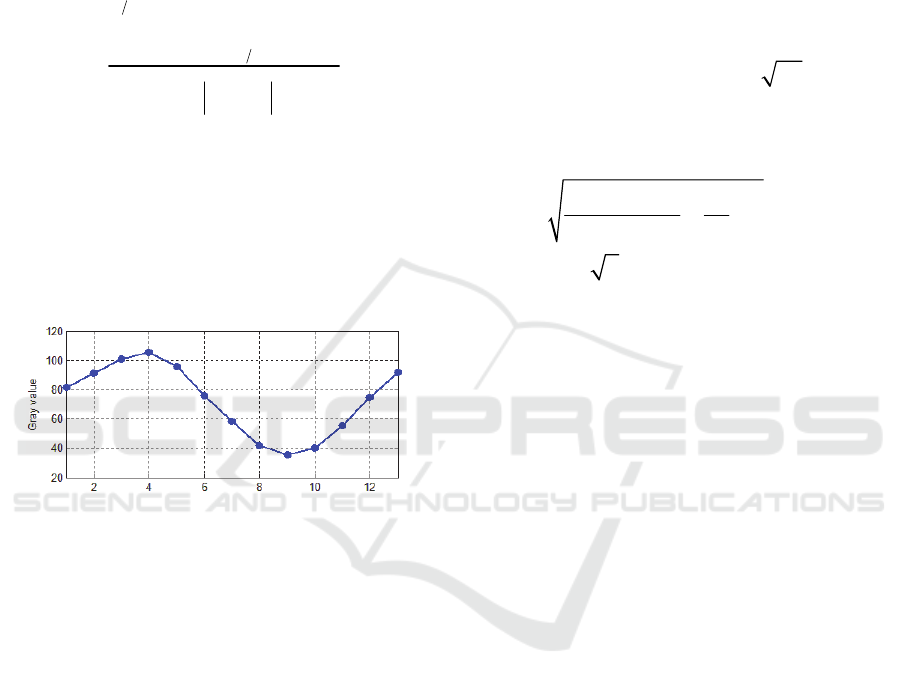
13 sequence phases of a pixel is shown in Fig.1.

The figure shows clearly that the driving step

lengths don't satisfy the equal step lengths condition,

because the sequence gray curve should be an

approximate the trigonometric function curve if the

driving step lengths are equal. This means the gray

values with large random noise.

2.1 Establishment of Interference

Equations

By taking it into account that every point in the

interference field has the same driving step length or

sequence phases at any time of PZT drive and by

choosing two points arbitrarily, sequence gray

values equations can be established as follows:

Figure 1: Sequence gray values of single pixel.

2

0

2

1

22

11

0

111

)cos(









CAg

ii



(3)

If g

1i

, g

2i

are respectively the transverse and

longitudinal coordinates, the theoretical trajectory of

sequence points should be an ellipse. The centers of

the ellipse are respectively C

1

, C

2

. The parameters of

the ellipse are determined by alternating amplitude

A

1

, A

2

and initial phase difference (θ

20

-θ

10

) between

two pixels. The trajectory is a positive ellipse when

the phase difference is π/2.

Parameters C

1

, C

2

, A

1

, A

2

and (θ

20

-θ

10

) can be

obtained through ellipse fitting. The fitting accuracy

of the parameters is mainly affected by the noise of

pixel gray values and the oval shape.

2.2 Method to Improve the Fitting

Precision of the Interference

Equations

Because the fitting accuracy of ellipse parameters is

influenced by the noise of gray values of pixels and

shape of the ellipse, the pixel points used for fitting

should be selected properly and de-noise processing

for the gray values of pixel points should be

conducted.

The gray values of interference sequence satisfy

orthogonal relation and fitted ellipse has highest

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

126

accuracy when the phase difference between two

pixels is π/2. Therefore, the phase difference

between two pixels used for ellipse fitting should

meet requirement of π/2 as far as possible. The

adopted scheme is as follows.

Firstly, the sequence gray values of every pixel

should be calculated as follows in specified area

(where has high SNR):

 



2

121

1

N

mn mn

iiN

mn

N

mn

i

gi gi

s

gi













(4)

Where s

mn

is in [-1,1]. In order to get two points

whose phase difference is π/2, the maximum and the

minimum in absolute values of s

mn

are selected as

the fitted objects. It can be proved in theory that the

phase difference between two pixel points is close to

π/2, which is conducive to enhancing the accuracy of

ellipse fitting.

Figure 2: Neighborhood average sequence gray values.

Secondly, for the two selected pixel points, de-

noise processing can be conducted by neighborhood

average operation for gray values in order to

eliminate the random noise.

The sequence gray average values of

neighborhood 100 points of a pixel is shown in

Fig.2. Compared to Fig.1, the random noise of

sequence gray values has been greatly suppressed by

observing the variation trend of every point's slope

on the curve or the degree of curve smoothing. Fig.2

has shown that the open-loop PZT drive has

disadvantage of unequal linear step lengths.

2.3 Solving Method of Ellipse Fitting

The ellipse fitting is mainly to obtain the regression

coefficients by linear regression of elliptic equation

in a rectangular coordinate system. Then the

parameters of interference equations can be

calculated according to the relation between the

regression coefficients and these parameters.

The elliptic rectangular coordinate equation of

interference equations is shown as below:

0

21

2

21

2

1

2

 ddgcgbggagg

iiiii

i

(5)

Where the parameters a, b, c, d, e can be

obtained by regression calculation based on the

linear least squares fitting. Through the relation

between the parameter equation and coordinate

equation, equation (6) can be derived:

1

20 10

2

12

2

1

21

cos ( / 4 )

(2)/(4 )

()/2

(2)

/sin

44

/

ab

Cacd ba

CcaC

Cac d

c

Ae

AA b

 









 



 



 



















(6)

Where the symbol of phase difference φ is

determined by the rotation direction of sequence

gray values in the ellipse. The symbol is negative

when the direction is counterclockwise, otherwise it

is positive. Vector cross product is adopted as a

method for judging symbol. The judgment equation

is as follows:

)0,,(

)0,,(),,(

222112

221111

cgcg

cgcgddd

zyx









(7)

If d

z

>0, the symbol is negative, otherwise it is

positive.

13 sequence gray values of two pixels after de-

noise processing and zero mean and ellipse fitting

result are shown respectively in Fig.3 (a) and (b).

Because the ellipse fitting accuracy of the data

points in integral period is higher than that of non-

integral period in the same conditions. Therefore, 13

points are used for ellipse fitting.

2.4 Inverse Calculation of Driving

Phases and Step Lengths

According to the result of ellipse fitting, the phase

calculation of two sequence gray values under

certain conditions may be started after getting the

parameters of equation (6). The conditions

mentioned above are as below: (a) the head and tail

points are not used in calculation. (b) Inverse

calculation of phases can be conducted when both

A Method to Improve the Precision of Interferometric Phase-recognization under Open-loop PZT Drive

127

the difference between gray values of the current

point and the front point

1ii

g



and the difference

between gray values of the current point and back

point

1ii

g





are positive or negative. Otherwise

calculation is not conducted.

(a)

(b)

Figure 3: (a) Sequence gray values of two pixels after de-

noise processing and zero mean; (b) ellipse fitting for

sequence gray values of two pixels.

The calculation equations are as follows:

1

11

1101

1

11 2

2202

2

cos

i

ii

i

ii

gC

A

g

C

A





































(8)

Where the symbol of phase is determined by the

differential symbol of current point. If

1

0

ii

gg





,

the symbol of phase is negative, otherwise is positive.

The sequence phases and synthetic phases of

sequence gray values are calculated in Table 1.

Besides the head and tail points, the points that

don't participate in inverse calculation include the

4th, 9th points on the dashed line and the 6th, 12th

points on the solid line in Fig.3.

Based on the fitting phase φ= 1.4543, the method

for calculating the synthetic phases of the 11 points

is as follows: if the phases of two corresponding

points in two sequences both exist, the synthetic

phase

12

()/2

iii









. If the phase only exist

in sequence 1,

1ii





. If the phase only exist in

sequence 2,

2ii









. By rounding with 2π, the

calculated phase is between (-π，π). The synthetic

phases are shown as the final row in Table 1.

10 actual point by point driving phases are

obtained by unwrapping and differential processing

for the 11 synthetic phases. The actual driving step

lengths of PZT can be got by equation (2). Fig.4

shows that actual step lengths of every point are

different from equal step lengths in theory.

3 CONSTRUCTION OF FOUR

INTERFERENCE GRAYSCALE

IMAGES

The four interference grayscale images with phase

difference 90 º can be constructed based on the

actual driving phases and step lengths. After ellipse

fitting, the calculation of actual phase is effective

from the 2th interference image of sampling

sequence. Therefore, the 2th interference grayscale

image is taken as an initial phase grayscale image g

0

and the rest 3 interference grayscale images with

phase difference π/2 are constructed. The

construction method is as follows.

Firstly, unwrapping calculation for the sequence

synthetic phases in Table 1 is conducted and the

starting point is offset to zero by a simple

calculation. The unwrapped phases before and after

Table 1: Sequence phases and synthetic phases.

Sequence

number

2 3 4 5 6 7 8 9 10 11 12

Sequence

phases 1 (rad)

1.032 0.717 X 0.892 1.442 1.892 2.387 X -2.445 -1.968 -1.472

Sequence

phases 2 (rad)

0.688 0.970 1.594 2.151 X -2.578 -2.170 -1.707 -1.198 -0.753 X

Synthetic

phases (rad)

-0.899 -0.601 0.139 0.795 1.442 2.071 2.523 3.122 -2.549 -2.087 -1.472

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

128

shift are shown in Fig. 5.

Then three points whose phases close to π/2, π

and 3π/2 are selected and the differences ε

1

, ε

2

and ε

3

between the three points and its target point are

calculated respectively.

(a)

(b)

Figure 4: (a) The real driving phases of PZT; (b) the real

driving step length of PZT.

Figure 5: The results of synthetic phases after unwrapping

operation.

For example, the three points in Fig. 5 whose

phases close to π/2, π and 3π/2 are the 4th, 6th and

9th point. Radian deviations which take the three

points as the center respectively are (-0.5324,

0.1231, 0.7698), (-0.8010, -0.1711, 0.2806) and (-

0.6912, -0.0789, 0.3828).

Finally, by using Lagrange parabolic

interpolation algorithm the grayscale images of

target phase are reconstructed. For example, the

equation to reconstruct the grayscale image of π/2 is

as shown in equation (9):

/2 12 23 34

gkgkgkg





(9)

Where g

2

, g

3

and g

4

represent respectively gray

values of the 2rd, 3th and 4th grayscale image.

The reconstruction coefficients k

1

, k

2

and k

3

can

be calculated by equation (10):













)])(/[(

2313213

3212312

3121321



k

(10)

The g

π

and g

3π/2

can be got by the same way. The

theoretical calculating data shows that the

truncation errors of gray values of the three

reconstructed grayscale images, which caused by

Lagrange interpolation, are less than 0.21%, 0.24%

and 0.13% respectively.

4 EXPERIMENTAL RESULTS

Taking a square wave specimen with multiple

grooves as measured surface, multi-wavelength

interference grayscales images are sampled and

phases of every sequence interference grayscale

image is extracted by above methods. Four grayscale

image after sequence interference grayscale images

which wavelength is 530nm are reconstructed and

with phase difference π/2 are shown in Figure 6.

At last, phase of every point is calculated from

the reconstructed grayscale images. The equations

for calculation are as follows:

)(tan

0

2/2/3

1

0







gg







(11)

The calculation results of phases of a row in the

interference grayscale image are shown in Fig.7. The

trend of obtained phases reflects the topography

change of square wave specimen with multiple

grooves well. Phases are extracted sequentially from

the sequence interference grayscale images

of 550nm and 640nm wavelength in the same

way. For two-wavelength measurement, if the

difference of wavelength is small, the measuring

range will enlarge quickly, but the measuring

accuracy will be very low (Houairi and Cassaing,

2009). So the phase differences between two near

wavelength (530nm, 550nm) are applied to recognize

the measurement result in a large scale. The phase

differences of two far wavelengths (550nm, 640nm)

are used to reduce the error of measurement result. At

last the phase of single wavelength (550nm) is used to

calculate final measurement result and the relative

heights of every point in the interference grayscale

image, namely the surface topography information,

are got (Warnasooriya and. Kim, 2007).

According to above method, the roughness Ra of

the square wave specimen with multiple

grooves is 0.4390μm by calculation. Based on the

highest national roughness standard of China, Ra of

the square wave specimen with multiple grooves is

calibrated by China National Institute Metrology is

0.44μm. The expand uncertainty of calibration

results is U

95

=5%. Therefore the relative

A Method to Improve the Precision of Interferometric Phase-recognization under Open-loop PZT Drive

129

measurement error δ of the above method is 0.23%.

(a)

(b)

(c)

(d)

Figure 6: Reconstructed four interference grayscale

images with π/2 phase-difference. (a)0º; (b)π/2; (c)π;

(d)3π/2.

Figure 7: The phase results of a row of interference

grayscale image.

5 CONCLUSIONS

The method requires only 12-14 sequence

interference grayscale images to complete the whole

operation and the amount of processing data is

smaller than that of the random driving step lengths

algorithm. It does not require strictly equal driving

step lengths and simplifies control for PZT in

traditional four step method. Through the incidence

relation between sequence gray values of two pixels,

the solution of driving step lengths is transformed to

ellipse fitting problem in the mathematics. The

actual driving step lengths and driving phases under

open-loop PZT drive are obtained accurately, which

provides conditions for constructing the four

sequence interference grayscale images with high

precision. The method has a guiding significance to

related technologies of phase recognition. The

relative error of reconstruction of gray values can be

controlled within 0.5% easily by using the Lagrange

parabolic interpolation algorithm. Therefore, the

PZT in the method is open-loop drive. This method

has good resistance to local environmental vibration

disturbance and the influence of nonlinear driving

error of PZT is small. The method reduces the

difficulty and cost of driving and close-loop control,

and lays a foundation for multi-wavelength

switching measurement.

ACKNOWLEDGEMENTS

The paper is supported by Natural Science

Foundation of China (No. 51275157, 51175154) and

Open Fund of State key Laboratory of Precision

Measuring Technology and Instruments of Tianjin

University ( No. PIL1209).

REFERENCES

James C. Wyant ， Chris L. Koliopoulos ， Bharat

Bhushan, Orrin E. George.( 1984) An optical

profilometer for surface characterization of magnetic

media. ASLE Trans.7, 101-113.

Wyant J C. (1982) Interferometric optical metrology:

basic systems and principles. Laser Focus 5,65-71.

Hariharan P., Oreb B., Eiju T. (1987) Digital phase-

shifting interferometry: a simple error-compensating

phase calculations algorithm. Applied Optics 26,

2540-2505.

Wang Chenxing, Da Feipeng. (2012) A Novel Windowed

Fourier Transform for Phase Retrieval in 3D Shape

Measurement. Acta Optica Sinica 32/6,0612005.

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

130

Cui Shilin, Tian Fei, Li Dehua. (2012) Phase Retrieval

Method with Continuous Wavelet Transform Based on

Exponent Spacing Scales. Acta Optica Sinica 32/7,

0712001.

Liu Jian, Tian Ailing, Liu Bingcai, Wang, Hongjun. (2014)

A Phase Extraction Algorithm in Wavelength Tuning

Interferometry. Acta Optica Sinica 34/3, 0312001.

Jun-Ichi KATO, Ichirou YAMAGUCHI. (2000) Phase-

Shifting Fringe Analysis for Laser Diode Wavelength-

Scanning Interferometer. Optical Review 7/2, 158-

163.

Linjuan Deng, Yunxia Fu, Xiaoyu Cai, Xiao Yu; Li,

Yuan; Lei, Li Hua; Zhao, Dong. (2014) Study on

Phase Shifting Algorithm and System of White Light

Interference. Advanced Materials Research 889-

890,749-754.

Qun Hao, Qiudong Zhu, Yao Hu. (2009) Random phase-

shifting interferometry without accurately controlling

or calibrating the phase shifts. Optics Letters 34/8,

1288-1290.

Liu Dong, Yang Yongying, Tian Chao, Luo, Yongjie;

Zhuo, Yongmo. (2010) Study on Phase Retrieval from

Single Close Fringe Pattern with High Precision.

Chinese J. Lasers 37/2, 531-536.

Kamel Houairi, Frederic Cassaing. (2009) Two-

wavelength interferometry: extended range and

accurate optical path difference analytical eatimator.

J.Opt. Soc. Am. A 26/12, 2503-2511.

N. Warnasooriya, M. K. Kim. （2007）LED-based multi-

wavelength phase imaging interference microscopy.

Opt. Express 15/15, 9239-9247.

A Method to Improve the Precision of Interferometric Phase-recognization under Open-loop PZT Drive

131