Artificial Student Agents and Course Mastery Tracking
Linda DuHadway and Thomas C. Henderson
School of Computing, University of Utah, 50 S. Central Campus Dr, Salt Lake City UT 84112, U.S.A.
Keywords:
Course Transformation, Artificial Student Agents, Bayesian Network, Kalman Filter.
Abstract:
In an effort to meet the changing landscape of education many departments and universities are offering more
online courses – a move that is likely to impact every department in some way (Rover et al., 2013). This
will require more instructors create online courses, and we describe here how agents and dynamic Bayesian
networks can be used to inform this process. Other innovations in instructional strategies are also widely im-
pacting educators (Cutler et al., 2012) including peer instruction, flipped classrooms, problem-based learning,
just-in-time teaching, and a variety of active learning strategies. Implementing any of these strategies requires
changes to existing courses. We propose ENABLE, a graph-based methodology, to transform a standard lin-
ear in-class delivery approach to an on-line, active course delivery system (DuHadway and Henderson, 2015).
The overall objectives are: (1) to create a set of methods to analyze the content and structure of existing
learning materials that have been used in a synchronous, linearly structured course and provide insight into
the nature and relations of the course material and provide alternative ways to organize them, (2) to provide a
Bayesian framework to assist in the discovery of causal relations between course learning items and student
performance, and (3) to develop some simple artificial student agents and corresponding behavior models to
probe the methods’ efficacy and accuracy. In this paper, we focus on our efforts on the third point.
1 INTRODUCTION
As the demand for online and hybrid courses in-
creases (Allen and Seaman, 2013) teachers that are
experienced and talented at designing and present-
ing synchronous, face-to-face courses are being asked
to adapt their material and presentation to an asyn-
chronous, online format. To many this is an unfa-
miliar approach and the process of making the tran-
sition is unclear. Since there is already an investment
in existing material and methods it is not desirable to
abandon them entirely. At the same time, this new
approach provides opportunities for new methods and
material to be of benefit. We describe how AI tools
can greatly enhance this undertaking.
Sometimes an educator is so familiar with the cur-
rent course organization that it becomes a stumbling
block for visualizing alternative options. When an-
ticipating change, it is valuable to see how existing
learning materials can be organized and used in new
ways. The purpose of ENABLE is to provide assis-
tance in making informed changes. Educators making
this transition benefit from a deeper analysis of the
contents and structure of the course material provided
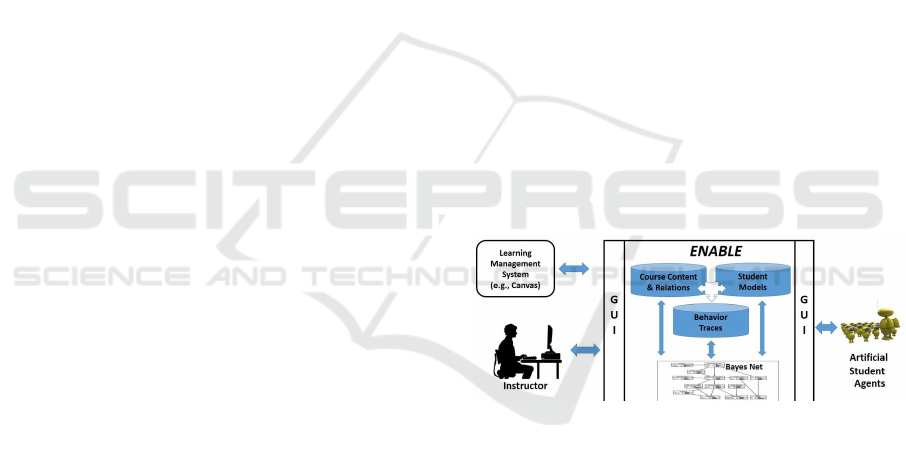
by a set of AI-based methods (see Figure 1).
This set of methods is called ENABLE, which is
Figure 1: The ENABLE Course Transformation System.
not an acronym, but rather a name that reflects the
purpose to enable the implementation of quality ed-
ucational strategies. With ENABLE, educators are
able to see the relations of the existing learning items
using a visual, non-linear presentation, to predict the
impact of the organization of learning items, and to
discover poorly organized or presented material. As
an example, consider the data from a sample CS0
course, Foundations of Computer Science, taught at
Utah State University. The information about the
learning items for this course was gathered from Can-
vas (a standard learning management system) and a
graph was produced representing the current organi-
zation of the course; see Figure 2 (upper). This shows
all the learning items for the course laid out in order
across the days of the semester. The middle figure
DuHadway, L. and Henderson, T.
Artificial Student Agents and Course Mastery Tracking.
DOI: 10.5220/0005738703850391
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 385-391
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
385

shows the relations discovered in the course learning
items using temporal and natural language analysis.
The lower figure shows the final on-line course layout
developed by the instructor using ENABLE.
Figure 2: CS0, Foundations of Computer Science Original
Course Organization (upper). CS0, Initial Course Graph
Relations (middle). CS0, Transformed Course Organization
(lower).
For later reference, we now provide some tech-
nical notation of the course material provided by EN-
ABLE. A course map is a graph, M = (N ,E), where
N is the set of learning item, topic and unit nodes,
and E is the set of precedes, topically precedes, pre-
requisite, occurs in and is in edges (relations). Then
the class map is C = (L,R ), where L ⊂ N is the
set of learning item nodes and R ⊂ E is the set of
prerequisite edges. A path of length k is any legal
sequence P = {n
1
,n
2
,... ,n
k+1
}, where n
i
∈ L and
¬∃i, j ∋ n
j
prerequisite n
i
and i < j. Let P
S
be the
set of nodes in the path P. Then a traversal of C is a
sequence of paths T = (P
1
,P
2
,... ,P
q
) ∋ ∀i P
i
is a path
and ∀ijP
S
i
∩ P
S
j
=
/
0.
2 ARTIFICIAL STUDENT
AGENTS
An automated agent is a process that exists in some
environment and is capable of flexible autonomous
action within that environment in order to meet its
design objectives. Such agents are used in many ap-
plications covering a wide range of systems that vary
from small email delivery systems to large, complex,
mission critical systems such as air traffic control
(Jennings and Wooldridge, 1998). Agents are defined
by the way they perceive their environment and how
they act on that environment. Perceiving the environ-
ment is done through sensors. Sensors range from
cameras and infrared range finders to keystrokes and
data. Acting on the environment is accomplished with
actuators that might be mechanical devices operated
with motors or output displayed to a screen (Russell
and Norvig, 2009). Both the way an agent perceives
its world and how it acts on its environment are very
different based on the purpose of the agent. This pro-
motes the use of agents in a broad range of activities.
The research presented here focuses on their use in
educational applications. Automated agents are used
in a variety of educational applications. Intelligent tu-
toring systems have been in development and use for
decades. An intelligent tutoring system is a system
in which a computer simulates a tutor (Chou et al.,
2003). (Sleeman and Brown, 1982) describes the ma-
jor intelligent tutoring systems that were implemented
early on. These covered a range of subject areas in-
cluding arithmetic, informal gaming, electronics, and
medicine. Later many intelligent tutoring systems
incorporated the use of automated agents (Capuano
et al., 2000; Antonio et al., 2005; Giraffa and Viccari,
1998; Hospers et al., 2003; Moundridou and Virvou,
2002).
User modeling is exhibited by a wide range of sys-
tems. Specifically, student models have been created
and used in educational systems. Most of the work
involving student agents has been done in the field
of intelligent tutoring systems. These learner models
developed in the research laboratory are now used in
advanced commercial learning environments. These
intelligent learning systems have successfully inte-
grated learner models and have achieved widespread
usage (Desmarais and Baker, 2006). The study of stu-
dent modeling and their potential usage continues to
be an active area of research. For more on these top-
ics, see (Anthony and Raney, 2012; Baker et al., 2008;
Brusilovsky et al., 2005; Carmona et al., 2008; Conati
et al., 2002; Garcia et al., 2007; Gardner and Belland,
2012; Gordillo et al., 2013; Kobsa, 2007; Li et al.,
2011; Pardos and Heernan, 2010; Soliman and Guetl,
2013; Vomlel, 2004).
One of the differences between face-to-face
courses and online courses is the possibility of indi-
vidual students moving through the learning items in
different orders. In a classroom setting it is not likely
that students could be working on different learning
items. However, in an online course each student
could be on a different learning item at any given
time. This introduces an entirely different component
to a course. Is it possible to allow students to choose
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
386

for themselves what order to complete the learning
items? Can such flexibility be supported by the EN-
ABLE system? Is it important to establish some lim-
itations to the ordering? Can those limitations be en-
forced? To explore these questions, student agents
were created. These agents are able to traverse the
class map in a variety of orders. This represents a
student moving through learning items in different or-
ders. The agents are limited only by prerequisite re-
lations; a learning item cannot be attempted until the
agent has visited all the prerequisite learning items.
Each automated agent has a set of characteristics and
implements decision making. Each agent can perform
multiple and varied traversals through the course map.
These traversals are quantified by two values, the final
overall score and a rating for topic cohesion. The final
overall score is a percentage computed from the indi-
vidual scores and weights of the learning items. The
topic cohesion is a value that indicates how topically
related the order of the traversal is. A high number for
topic cohesion means the traversal ordered the learn-
ing items closely by topic. A lower number indicates
there was more topic deviation between the learning
items during the traversal. Topic deviation is when
there are no common topics between adjacent learn-
ing items.
In an effort to more closely replicate real stu-
dents, each agent has four characteristics: Intelli-
gence, Work Ethic, Background and Distractability.
These characteristics impact how often an agent de-
cides to not complete a learning item, how well they
do on a learning item, and how they choose which
learning item to do next. The characteristics are ab-
breviated as I, W, B, and D. Each of these character-
istics can have a value of 1, 2, or 3, where the value 1
represents the least favorable and 3 the most favorable
value for each characteristic. An agent first decides
which learning item to consider next. The ones that
are allowed are any learning item which has no re-
maining prerequisites, but there is a bias about work-
ing on learning items in the same unit. This bias is
based on the agent values for Background and Dis-
tractability. The assumptions are that students with
greater background are more comfortable moving be-
tween multiple units and the higher the agent’s Dis-
tractability the more likely they are to move from unit
to unit. Low distractability is the desired trait; a value
of 3 inicates low distractability and a value of 1 in-
dicates high destractability. The number of units to
consider is determined using the following formula:
U = B+ (β− D)
where B is the agent’s rating for Background and D
their rating of Distractability, and β is an appropri-
ate constant determined from actual classroom expe-
rience. The agent randomly selects one item from the
consideration list. This becomes the current item un-
der consideration.
Once an agent selects the current item for consid-
eration, it will determine whether it will work on the
item or not. When an agent decides not to do a learn-
ing item, it receives a zero score for that item. In the
real data the zeros are significant. Although they have
low probability they have considerable impact on the
final score. The decision of whether to do a graded
learning item or not is made based on the characteris-
tics of work and Distractability. The assumptions are
that those who rate high on work are more likely to
complete a learning item while those with high Dis-
tractability are more likely to skip them. The percent-
age of how often a student agent will choose not to
work on a graded learning item is computed from ex-
isting classroom score data. The percentage of ze-
ros is determined for each assignment group and three
groups of students. Assignment groups are identified
during the course analysis phase and a group num-
ber is associated with each learning item. The groups
of students used in this analysis are determined us-
ing percentiles and the final course score. The high
student group are those with a final score between 90-
94 percentiles, inclusive. The middle group are those
students with a final score between 45-54 percentiles,
inclusive. The low student group are the students with
a final score between 5-9 percentiles, inclusive. For
each group of students and each assignment group the
percentage of zeros is computed with the following
formula:
P = N
z
/N
where P is the percentage of zeros, N
z
is the number
of zero scores, and N is the total number of scores.
Each percentage is evenly split between Work and
Distractability.
To determine whether a student agent works on
an ungraded learning item, work, Distractability, and
Background are considered. As with graded learn-
ing items the assumptions are that those with a high
Work Ethic rating are more likely to complete a learn-
ing item while those with high Distractability are less
likely to complete an item. In addition, Background
is considered for ungraded items. The assumption is
that those with more background are less likely to en-
gage with the supplemental material. The following
formula computes a percentage of how often an agent
chooses not to work on an ungraded learning item:
P = α
0
(2−Wα
1
+ Bα
2
− Dα
3
)
where W is the agent’s value of Work Ethic, B is the
agent’s value of Background, D is the agent’s value
of Distractability, and α
i
are coefficients determined
from analysis of previous classes.
Artificial Student Agents and Course Mastery Tracking
387
Each learning item has a different maximum num-
ber of points possible, and the distribution of scores
from the existing course varies significantly from item
to item. There were assignments that resulted in a nice
Gaussian score distribution and others that had a more
uniform distribution. To accommodate such variation
in the possible scores the first formula for determining
the score computes a percentile:
P = max(I,W)γ
1
+ (B+ D)γ
2
− γ
3
where I is the agent’s value of Intelligence, W is the
agent’s value of Work Ethic, B is the agent’s value
of Background, D is the agent’s value of Distractabil-
ity, and γ
i
is determined according to previous classes.
The score associated with this percentile is computed
using the following process. First remove all zero
scores. Zero scores have already been accounted for
when the agent determined whether to complete a
learning item or not. To include them here as well
would give greater weight to zeros than is justified by
the data. The remaining scores are then sorted in as-
cending order. Using this sorted list of scores the rank
is determined using the following formula:
R = P(N + 1)
where P is the desired percentile and N is the total
number of scores. If R is an integer, the P
th
percentile
is the score with rank R. When R is not an integer, the
P
th
percentile is computed by interpolation. Define R
I
as the integer portion of R. Define R
f
as the fractional
portion of R. Find the scores with Rank R
I
and with
Rank R
I
+1. Interpolate by multiplying the difference
between the scores by R
f
and add the result to the
lower score, and then round this result to the nearest
integer.
An exam grade computation depends on the value
of all four agent characteristics. The greatest weight
is on Intelligence. The assumption is that intelligence
will be the most likely indicator of success on an
exam. The next greatest weight is on the value of
Work Ethic. The assumption is that hard work on pre-
vious learning items will result in a better exam score.
A smaller weight is put on Background and Dis-
tractability. The assumption is that increased back-
ground and better focus will help with satisfactory
completion of the exam. The following formula is
used to compute the percentile for this exam:
P = η
0
+ Iη
1
+Wη
2
+ (B+ D)η
3
where I is the agent’s value of Intelligence, W is the
agent’s value of Work ethic, B is the agent’s value of
Background, D is the agent’s value of Distractability,
and η
i
is determined from previous courses.
ENABLE determines an individual weight for
each learning item:
W
i
= W
G
j
(
P
i
P
G
j
)
where W
G
j
is the weight of the assignment group, P
i
is the points possible for this learning item, and P
G
j
is the points possible for the entire assignment group.
The final score can then be computed using the fol-
lowing formula:
F =
N
∑
i=1
(W
i
S
i
)
where W
i
is the weight of the learning item, S
i
is the
score for the learning item, and N is the number of
learning items.
At this point the agents have been created and
their decision-making has been encoded. The system
can now use the agents to generate data. Each agent
has the four characteristics described earlier: Intelli-
gence, Work, Background, and Distractability. Each
of those characteristics can have three values: most
favorable, medium and least favorable. There are a to-
tal of 81 unique character combinations. Seven agents
were created with the characteristics shown in Table
1. Now we have each agent traverse the course a cer-
Table 1: Seven Agent Types.
Type Agents
Background 3 2 1 3 3 3 1
Intelligence 3 2 1 1 2 3 3
Work Ethic 3 2 1 3 2 1 3
Distractability 3 2 1 2 3 1 1
tain number of times. For each run, a trace is pro-
duced that identifies the order the agent traversed the
learning items. A score is kept of each learning item.
At the completion of the run a final score is calcu-
lated. At the end of a series of runs, the mean, max,
min, and standard deviation of the final scores is com-
puted. Table 2 shows the cumulative results from a
1000 run experiment with a variety of agents. These
Table 2: Agent Grades Produced over 1000 Trials.
B I W D Mean Max Min Var
3 3 3 3 97.98 100 91.24 1.88
2 2 2 2 87.43 95.24 74.54 11.77
1 1 1 1 43.83 74.94 17.58 61.47
3 1 3 2 89.25 96.83 74.10 9.73
3 2 2 3 91.98 98.39 80.48 7.40
3 3 1 1 69.34 88.78 36.64 90.44
1 3 3 1 82.13 95.94 57.22 48.44
artificial student agents can be used when analyzing
certain types of student modeling methods for better
understanding the mastery of the learning items.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
388

3 KALMAN FILTER TRACKING
OF MASTERY OF MATERIAL
Given a course map and a method to accurately assess
a student’s mastery level of a specific learning item
(e.g., assign grades to graded learning items), we now
describe a technical approach to model and track stu-
dent mastery of the learning items during a traversal
of the course map. That is, at each step in the traversal
a mastery level can be determined for each learning
item for the particular student.
Let M = (N ,E) be a course map with nodes N
and edges E. Let C = (L,R ) be the corresponding
class map for M , where L is the set of learning items
and R is the set of relations on L. Construct a vector,
x, where x
i
represents the mastery level of the student
for learning item L
i
; we have x
i
is in the range [0,1],
where x
i
= 0 means no mastery and x
i
= 1 means full
mastery.
Furthermore, let x
t
represent the mastery state at
step t. If the student knows nothing at all at the
start, then x
0
= 0; however, if the student has some
backgroundknowledgeconcerning a learning item L
i
,
then x
0
i
can be set to the appropriate amount.
We assume that the prerequisite relation entails
some amount of causal relation between the mastery
of the respective learning items. I.e., if A prerequisite
B, then the probability that the student masters learn-
ing item B depends on the mastery of learning item A.
We further propose as a starting point a linear function
to describe the dynamic learning process (also called
the transition model):
x
t+1
= Ax
t
+ Bu
t
+ ε
where the matrix A describes the relation between
learning item mastery and the matrix B describes the
impact of the control variable, u
t
, at time t. The con-
trol variable describes what learning items the student
works on at time t as well as the amount of work,
while the first term in the transition model (i.e., Ax
t
)
characterizes the learning impact of the mastery of the
previous learning items.
The transition model also includes a characteriza-
tion of the noise of the learning process by means of
the random variable ε ∼ N (0,σ
pi
), where σ
pi
is the
variance in the learning process for each individual
learning item, L
i
. The covariance matrix for the full
vector, x, is called R.
It is also necessary to have a model of the obser-
vation process. Mastery will be measured by means
of graded learning items, and the measurement model
is:
z
t
= Cx
t
+ δ
where C is a k × n matrix providing observations of
the graded learning items. Furthermore, δ ∼ N (0,σ
z
)
where σ
z
characterizes the noise in the measurement
(testing) method. For the full z vector this is given by
the covariance matrix Q.
Given these transition and measurement models,
it is appropriate to use a Kalman Filter (Thrun et al.,
2005) to track the mastery level during a traversal.
Given such a model, then control vectors can be se-
lected to maximize mastery of the learning items
while minimizing needless repetition and effort.
In order to exploit this dynamic Bayesian network
approach, it is necessary to specify the matrices A,B,
and C; the covariance matrices can be set based on
actual class data or based on data generated by the
artificial agents previously described. As a first cut at
a learning material mastery model, let:
x =
1 0 ... 0
a
21
a
22
0 ...
...
a
n1
a
n2
... a
nn
x
1
x
2
...
x
n
+
1 0 ... 0
0 1 ... 0
...
0 0 ... 1
u
1
u
2
...
u
n
where we assume u
t
has one element set to 1 (or some
amount of effort between 0 and 1) meaning that only
one learning item is worked on at a time. For A, a
i, j
=
0 for j > i; for j ≤ i, a
i, j
is set to 0 if ¬(x
i
prerequisite
x
j
); otherwise, a
i, j
=
1
n
ij
, where n
ij
is one plus the
number of learning items that are prerequisites for x
j
.
Consider the simple class map, C , shown in Fig-
ure 3.
Figure 3: Class Map for Simple 5-Learning Item Class;
Learning Items 3 and 5 are Graded.
Then
A =
1 0 0 0 0
0 1 0 0 0
1
3
1
3
1
3
0 0
1
4
1
4
1
4
1
4
0
1
5
1
5
1
5
1
5
1
5
Artificial Student Agents and Course Mastery Tracking
389

1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.5
1
1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.5
1
Sample Number
1 1.5 2 2.5 3 3.5 4 4.5 5
Mastery Level [Actual (B), Estimate (R) Observed (G)
0
0.5
1
1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.5
1
1 1.5 2 2.5 3 3.5 4 4.5 5
0
0.5
1
Figure 4: Mastery Estimates for Five Learning Item Traver-
sal.
and
x
0
=
0
0
0
0
0
Then a simple traversal such as [1,2, 3, 4,5] yields the
mastery level estimates shown in Figure 4.
4 CONCLUSIONS AND FUTURE
WORK
We have developed ENABLE, a course transforma-
tion system, that helps an instructor develop bet-
ter organized on-line versions of standard classroom
courses, and it has been tested on 3 introductory com-
puter science courses at Utah State University. Tech-
nical contributions include:
• course content analysis and transformation using
natural language processing and graph transfor-
mation methods to produce a course map (see
(DuHadway and Henderson, 2015)),
• artificial student agents to traverse the course map
(this paper),
• a learning item mastery model with associated
Kalman Filter mastery tracking (this paper).
This is an innovative and novel application of agent
and AI methods to computing education problems.
In the future, we intend to study the exploitation
of ENABLE in actual on-line versions of computer
science courses in order to validate the approach by
using it with human instructors and students; in the
present work, we have developed new algorithms and
showed their correctness and in simulation experi-
ments based on data from actual classes. Future work
will be undertaken both from the instructor’s perspec-
tive; e.g., using the system to detect content or struc-
tural weaknesses in the course, as well as the student’s
perspective; e.g., projected grades on future items as
well as advice on what to do to improve mastery of
the learning material – this would be accomplished
through the control vector in the Kalman Filter ap-
proach.
Another direction of interest is to extend this sim-
ple linear mastery model to a more realistic nonlinear
model using the Extended Kalman Filter, and use it
to learn the weights in the A matrix, as well as possi-
bly the I, W, B, and D values for individual students.
These issues would first be developedtechnically, and
then studied in the context of actual on-line versions
of these (or other) courses.
REFERENCES
Allen, I. and Seaman, J. (2013). Cahngin Course: Ten Years
of Tracking Online Education in the United States.
Sloan Consortium, Newburyport, MA.
Anthony, A. and Raney, M. (2012). Bayesian Network
Analysis of Computer Science Grade Distributions.
In Proceedings of the 43rd ACM Technical Sympo-
sium on Computer Science Education, pages 649–654,
Raleigh, NC.
Antonio, A. D., Ramirez, J., Imbert, R., and Mendez, G.
(2005). Intelligent Virtual Environmets for Training:
an Agent-based Approach. In Multi-Agent Systems
and Applications IV, Berlin, Germany. Springer.
Baker, R., Corbett, A., and Aleven, V. (2008). More
Accurate Student Modeling through Contextual Es-
timation of Slip and Guess Probabilities in Bayesian
Knowledge Tracing. In Proceedings of the 9th Inter-
national Conference on Intelligent Tutoring Systems,
pages 406–415, Berlin, Germany. Springer Verlag.
Brusilovsky, P., Sosnovsky, S., and Shcherbinina, O.
(2005). User Modeling in a Distributed E-Learning
Architecture. In User Modeling 2005. Lecture Notes
in Artificial Intelligence, (Proceedings of 10th Inter-
national User Modeling Conference, pages 24–29.
Springer Verlag.
Capuano, N., Marsella, M., and Salerno, S. (2000). ABITS:
An Agent Based Intelligent Tutoring System for Dis-
tance Learning. In Proceedings of the International
Workshop on adaptive and Intelligent WE-Based Ed-
ucation Systems. ITS.
Carmona, C., Castillo, G., and Mil’an, E. (2008). Design-
ing a Dynamic Bayesian Network for Modeling Stu-
dents’ Learning Styles. In Proceedings of the Inter-
national Conference on Advanced Learning Technolo-
gies, pages 346–350, Santander, Cantabria, Spain.
IEEE.
Chou, C.-Y., Chan, T.-W., and Lin, C.-J. (2003). Redefin-
ing the Learning Companion: the Past, Present, and
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
390

Future of Educational Agents. Computer and Educa-
tion, 40(3):255–269.
Conati, C., Gertner, A., and Vanlehn, K. (2002). Using
Bayesian Networks to Manage Uncertainty in Student
Modeling. User Modeling and User-Adapted Interac-
tion, 12(4):371–417.
Cutler, S., Borrego, M., Henderson, M., and Froyd, J.
(2012). A Comparison of Electrical, Computer and
Chemical Engineering Faculty Progressions through
the Innovation-Decision Process. In Proceedings of
the Frontiers of Education Conference, Seattle, WA.
IEEE.
Desmarais, M. and Baker, R. (2006). A Review of Re-
cent Advances in Learner and Skill Modeling in In-
telligent Learning Environments. User Modeling and
User-Adapted Interation, 22(1-2):9–38.
DuHadway, L. and Henderson, T. (2015). Informing
Change: Course Content Analysis and Organization.
In Proceedings of the Frontiers of Education Confer-
ence, El Paso, TX. IEEE.
Garcia, P., Garcno, P., and Campo, M. (2007). Evaluating
Bayesian Networks’ Precision for Detecting Students’
Learning Styles. Computers & Education, 49(3):794–
808.
Gardner, J. and Belland, B. R. (2012). A Conceptual Frame-
work for Organizing Active Learning Experiences in
Biology Instruction. Journal of Science Education
and Technology, 21(4):465–475.
Giraffa, L. and Viccari, R. (1998). The Use of Agents Tech-
niques on Intelligent Tutoring Systems. In Proceed-
ings of International Conference of the Chilean Soci-
ety of Computer Science. IEEE.
Gordillo, A., Barra, E., Gallego, D., , and Quemada, J.
(2013). An Online E-Learning Authoring Tool to Cre-
ate Interactive Multidevice Learning Objects Using
E- Infrastructure Resources. In Proceedings of the
IEEE Conference on Frontiers in Education Confer-
ence, pages 1914–1920. IEEE.
Hospers, M., Kroezen, E., Nijholt, A., op den Akker, R.,
and Heylen, D. (2003). An Agent-based Intelligent Tu-
toring System for Nurse Education. Springer, Berlin,
Germany.
Jennings, N. and Wooldridge, M. (1998). Applications of
Intelligent Agents. In Agent Technology, Berlin, Ger-
many. Springer.
Kobsa, A. (2007). Generic User Modeling Systems. In The
Adaptive Web, pages 136–154, NY, NY. Springer.
Li, N., Cohen, W., Koedinger, K. R., and Matsuda, N.
(2011). A Machine Learning Approach for Auto-
matic Student Model Discovery. In Pechenizkiy, M.,
Calders, T., Conati, C., Ventura, S., Romero, C., and
Stamper, J., editors, Educational Data Mining, pages
31–40.
Moundridou, M. and Virvou, M. (2002). Evaluating the Per-
sona Effect of an Interface Agent in a Tutoring Sys-
tem. Journal of Computer Assisted Learning, 18:253–
261.
Pardos, Z. and Heernan, N. (2010). Modeling Individ-
ualization in a Bayesian Networks Implementation
of Knowledge Tracing. In Bra, P. D., Kobsa, A.,
and Chin, D., editors, Proceedings of the 18th Inter-
national Conference on User Modeling, Adaptation
and Personalization., pages 255–266, Big Island, HI.
ACM.
Rover, D., Astatke, Y., Bakshi, S., and Vahid, F. (2013).
An Online Revolution in Learning and Teaching. In
Proceedings of the Frontiers of Education Conference,
Oklahoma City, OK. IEEE.
Russell, S. and Norvig, P. (2009). Artificial Intelligence: A
Modern Approach. Prentice Hall, Upper Saddle River,
NJ.
Sleeman, D. and Brown, J. (1982). Intelligent Tutoring Sys-
tems. Academic Press, London, UK.
Soliman, M. and Guetl, C. (2013). Implementing Intel-
ligent Pedagogical Agents in Virtual Worlds: Tu-
toring Natural Science Experiments in OpenWonder-
land. In Global Engineering Education Conference
(EDUCON), pages 782–789. IEEE.
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
Robotics. MIT Press, Cambridge, MA.
Vomlel, J. (2004). Bayesian Networks in Educational Test-
ing. International Journal of Uncertainty, Fuzziness
and Knowledge-Based Systems, 12:83–100.
Artificial Student Agents and Course Mastery Tracking
391
