
A Two-stage Stochastic Programming Approach for the
Traveling Salesman Problem
Pablo Adasme
1
, Rafael Andrade
2
, Janny Leung
3
and Abdel Lisser
4
1
Departamento de Ingenier´ıa El´ectrica, Universidad de Santiago de Chile, Avenida Ecuador 3519, Santiago, Chile
2
Departamento de Estat´ıstica e Matem´atica Aplicada, Universidade Federal do Cear´a, Campus do Pici, BL 910,
CEP 60.455-760, Fortaleza, Cear´a, Brazil
3
Department of Systems Engineering & Engineering Management, Chinese University of Hong Kong, Shatin,
Hong Kong, China
4
Laboratoire de Recherche en Informatique, Universit´e de Paris-Sud 11, Bˆat. 650 Ada Lovelace, Paris, France
Keywords:
Two-stage Stochastic Programming, Traveling Salesman Problem, Compact Formulations, Iterative Algorith-
mic Approach.
Abstract:
In the context of combinatorial optimization, recently some efforts have been made by extending classical
optimization problems under the two-stage stochastic programming framework. In this paper, we introduce
the two-stage stochastic traveling salesman problem (STSP). Let G = (V, E
D
∪E
S
) be a non directed complete
graph with set of nodes V and set of weighted edges E
D
∪ E
S
where E
D
∩ E
S
=
/
0. The edges in E
D
and E
S
have deterministic and uncertain weights, respectively. Let K = {1,2, ·· · ,|K|} be a given set of scenarios
referred to the uncertain weights of the edges in E
S
. The STSP consists in determining Hamiltonian cycles
of G, one for each scenario s ∈ K, sharing the same deterministic edges while minimizing the sum of the
deterministic weights plus the expected weight over all scenarios associated with the uncertain edges. We
propose two compact models and a formulation with an exponential number of constraints which are adapted
from the classic TSP. One of the compact models allows to solve instances with up to 40 nodes and 5 scenarios
to optimality. Finally, we propose an iterative procedure that allows to compute optimal solutions and tight
lower bounds within very small CPU time.
1 INTRODUCTION
Stochastic programming is an optimization frame-
work which allows to deal with the uncertainty of the
input parameters of a mathematical program (Shapiro
et al., 2009). Thus, it is commonly assumed that
probability distributions take values within a discrete
and finite space which allows to consider sets of sce-
narios for the input parameters. A well known sce-
nario based approach is the “recourse model” or “two-
stage stochastic programming approach” (Gaivoron-
ski et al., 2011; Shapiro et al., 2009). In the con-
text of combinatorial optimization, recently some ef-
forts have been made by extending classical combi-
natorial optimization problems (e.g., Knapsack prob-
lems (Gaivoronski et al., 2011), the maximum weight
matching problem (Escoffier et al., 2010), maximal
and minimal spanning tree problems (Flaxman et al.,
2006; Escoffier et al., 2010), the stochastic maxi-
mum weight forest problem (Adasme et al., 2013;
Adasme et al., 2015)) under the two-stage stochas-
tic programming framework. In this paper, we in-
troduce the two-stage stochastic traveling salesman
problem (STSP) which can be described as follows.
Let G = (V, E
D
∪E
S
) be a non directed complete graph
with a set of nodes V and a set of weighted edges
E
D
∪ E
S
where E
D
∩ E
S
=
/
0. The edges in E
D
and
E
S
have deterministic and uncertain weights, respec-
tively. Let K = {1, 2, ··· , |K|} be a given set of sce-
narios referred to the uncertain weights of the edges
in E
S
. The STSP problem consists in determining
Hamiltonian cycles of G, one for each scenario s ∈ K,
sharing the same deterministic edges while minimiz-
ing the sum of the deterministic weights plus the ex-
pected weight over all scenarios associated with the
uncertain edges. For |K| = 1, the problem reduces
to the classic traveling salesman problem. We pro-
pose two compact polynomial models and a formula-
tion with an exponential number of constraints. These
models are based on the classic TSP (Miller et al.,
1960; Gavish and Graves, 1978; Letchford et al.,
2013). Stochastic programming variants of the travel-
Adasme, P., Andrade, R., Leung, J. and Lisser, A.
A Two-stage Stochastic Programming Approach for the Traveling Salesman Problem.
DOI: 10.5220/0005738801630169
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 163-169
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
163

ing salesman problem have been previously studied,
see for instance (Maggioni et al., 2014; Bertazzi and
Maggioni, 2014). In particular, the two-stage stochas-
tic problem we present in this paper can be seen as a
particular case of the stochastic capacitated traveling
salesmen location problem with recourse (Bertazzi
and Maggioni, 2014). As far as we know, this spe-
cial case has never been studied before in the liter-
ature. Notice that all the applications of the classic
traveling salesman problem can be extended to the
models we present in this paper. We compare numer-
ically the exponential model versus the two compact
polynomial formulations for randomly generated in-
stances. For this purpose, we solve the exponential
model by generating all cycle elimination constraints
at once and also by using a simple iterative algorith-
mic approach which consists of adding violated cycle
elimination constraints within each iteration until no
cycle is found in the current solution. Finally, we use
the iterative algorithm in order to compute tight lower
bounds in significantly short CPU time.
The remaining of the paper is organized as fol-
lows. In section 2, we present the two-stage stochastic
formulations of the problem. Then, in section 3, we
present the iterativealgorithm to solve the exponential
formulation alternatively. Subsequently, in section 4
we conduct numerical results in order to compare all
the proposed models and the algorithmic approach.
Finally, in section 5 we give the main conclusions of
the paper.
2 TWO-STAGE STOCHASTIC
FORMULATIONS
In this section, we propose three stochastic formu-
lations for the STSP that we adapt from the classic
TSP (Miller et al., 1960; Gavish and Graves, 1978;
Letchford et al., 2013). The first one is an exponen-
tial model that contains an exponential numberof sub-
tour elimination constraints (SECs). The second one
is adapted from (Miller et al., 1960), and the third one
corresponds to an extension of the single flow com-
modity model proposed in (Gavish and Graves, 1978).
Consider the non directed complete graph G and the
set of discrete scenarios K as defined in section 1. An
exponential model for the STSP can be written
STSP
1
:
min
{x,y}
(
∑
(i, j)∈E
D
c
ij
x
ij
+
|K|
∑
s=1
p
s
∑
(i, j)∈E
S
δ
s
ij
y
s
ij
)
(1)
subject to :
∑
j:(i, j)∈ E
D
x
ij
+
∑
j:(i, j)∈ E
S
y
s
ij
= 1, ∀i ∈ V, s ∈ K (2)
∑
i:(i, j)∈E
D
x
ij
+
∑
i:(i, j)∈E
S
y
s
ij
= 1, ∀ j ∈ V, s ∈ K (3)
∑
(i, j)∈E(S)∩E
D
x
ij
+
∑
(i, j)∈E(S)∩E
S
y
s
ij
≤ |S| − 1,
S ⊂ V, s ∈ K (4)
x
ij
∈ {0, 1}, ∀(i, j) ∈ E
D
, (5)
y
s
ij
∈ {0, 1}, ∀(i, j) ∈ E
S
, s ∈ K (6)
In (1), we minimize the sum of the deterministic
edge weights plus the expected cost of uncertain edge
weights obtained over all scenarios. The parame-
ter p
s
, ∀s ∈ K, represents the probability for scenario
s ∈ K where
∑
s∈K
p
s
= 1. Constraints (2)-(3) ensure
that the salesman arrives at and departs from each
node exactly once for each scenario s ∈ K. Con-
straints (4) are sub-tour elimination constraints for
each S ⊂ V, s ∈ K. Finally, (5)-(6) are the domain con-
straints for the binary decision variables x
ij
, ∀(i, j) ∈
E
D
and y
s
ij
, ∀(i, j) ∈ E
S
, s ∈ K. The variable x
ij
= 1 if
the deterministic edge (i, j) ∈ E
D
is selected in each
Hamiltonian cycle, ∀s ∈ K, otherwise x
ij
= 0. Simi-
larly, the variable y
s
ij
= 1 if the edge (i, j) ∈ E
S
is se-
lected in the Hamiltonian cycle associated to the sce-
nario s ∈ K, and y
s
ij
= 0 otherwise.
Now let A
D
and A
S
represent the sets of arcs ob-
tained from E
D
and E
S
, respectively where an edge
(i, j) is replaced by two arcs (i, j), ( j, i) of same cost
in each corresponding set. A polynomial compact for-
mulation based on (Miller et al., 1960) is
STSP
2
:
min
{x,y,u}
(
∑
(i, j)∈A
D
c
ij
x
ij
+
|K|
∑
s=1
p
s
∑
(i, j)∈A
S
δ
s
ij
y
s
ij
)
subject to:
∑
j:(i, j)∈ A
D
x
ij
+
∑
j:(i, j)∈ A
S
y
s
ij
= 1, ∀i ∈ V, s ∈ K
∑
i:(i, j)∈A
D
x
ij
+
∑
i:(i, j)∈A
S
y
s
ij
= 1, ∀ j ∈ V, s ∈ K
u
s
1
= 1, ∀s ∈ K (7)
2 ≤ u
s
i
≤ |V|, ∀i ∈ |V|, (i 6= 1), ∀s ∈ K (8)
u
s
i
− u
s
j
+ 1 ≤
(|V| − 1)(1− x
ij:(i, j)∈A
D
− y
s
ij:(i, j)∈A
S
),
∀i, j ∈ V, (i, j 6= 1), s ∈ K (9)
x
ij
∈ {0, 1}, ∀(i, j) ∈ A
D
, (10)
y
s
ij
∈ {0, 1}, ∀(i, j) ∈ A
S
, s ∈ K (11)
u
s
i
∈ R
+
, ∀i ∈ V, s ∈ K (12)
where the constraints (9) ensure that, if the salesman
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
164

travels from i to j, then the nodes i and j are arranged
sequentially for each s ∈ K. These constraints to-
gether with (7) and with the bounds (8) ensure that
each node is in a unique position. Finally, (10)-(12)
are the domain constraints for the decision variables.
A third formulation can be obtained by extending
the classic single commodity flow formulation for the
TSP (Gavish and Graves, 1978). For this purpose,
we assume that the salesman carries |V| − 1 units of
a commodity when he leaves node 1, and delivers 1
unit of this commodity to each node. Using the sets
A
D
and A
S
, we can define additional continuous vari-
ables g
ij
, ∀(i, j) ∈ A
D
and w
s
ij
, ∀(i, j) ∈ A
S
, s ∈ K, rep-
resenting the amount of the commodity (if any) routed
directly from node i to node j, for all s ∈ K. The new
formulation is
STSP
3
:
min
{x,y,g,w}
(
∑
(i, j)∈A
D
c
ij
x
ij
+
|K|
∑
s=1
p
s
∑
(i, j)∈A
S
δ
s
ij
y
s
ij
)
subject to:
∑
j:(i, j)∈ A
D
x
ij
+
∑
j:(i, j)∈ A
S
y
s
ij
= 1, ∀i ∈ V, s ∈ K
∑
i:(i, j)∈A
D
x
ij
+
∑
i:(i, j)∈A
S
y
s
ij
= 1, ∀ j ∈ V, s ∈ K
∑
j:( j,i)∈ A
D
g
ji
+
∑
j:( j,i)∈ A
S
w
s
ji
−
∑
j>1:(i, j)∈A
D
g
ij
−
∑
j>1:(i, j)∈A
S
w
s
ij
= 1
∀i ∈ { 2, . . . , |V|}, s ∈ K (13)
0 ≤ g
ij
≤ (|V| − 1)x
ij
, ∀(i, j) ∈ A
D
(14)
0 ≤ w
s
ij
≤ (|V| − 1)y
s
ij
, ∀(i, j) ∈ A
S
, s ∈ K (15)
x
ij
∈ {0, 1}, ∀(i, j) ∈ A
D
, (16)
y
s
ij
∈ {0, 1}, ∀(i, j) ∈ A
S
, s ∈ K (17)
The constraints (13) ensure that one unit of the com-
modity is delivered to each node, ∀s ∈ K. The bounds
(14)-(15) ensure that the commodity can flow only
along arcs in the solution.
In the next section, we propose an iterative algo-
rithmic procedure that allows to obtain optimal solu-
tions and lower bounds for the STSP while using the
exponential formulation.
3 ITERATIVE PROCEDURE FOR
GENERATING SECS
The procedure to generate SECs is quite general and
it can be adapted straightforwardly using Algorithms
4.1 and 4.2 from (Adasme et al., 2015) to the STSP.
The idea is as follows. If we remove constraints (4)
from STSP
1
and solve the resulting integer linear pro-
gramming problem, then the underlying optimal so-
lution induces a graph G
s
for each s ∈ K that may
contain a cycle with at least three or up to |V| − 1
nodes. In this case, it can be detected by a depth-first
search procedure (Cormen et al., 2009). We refer the
reader to the Algorithm 4.1 in (Adasme et al., 2015)
for a deeper understanding on how we obtain cycles
for each G
s
, s ∈ K. In particular, if the cardinality of
a subset of nodes found with Algorithm 4.1 inducing
a cycle equals |V|, we do not generate the SEC, oth-
erwise Hamiltonian cycles would be infeasible for the
problem. The Algorithm 4.1 is used iteratively by the
Algorithm 1: Iterative procedure to compute lower
bounds for STSP
1
.
Data: A problem instance of STSP
1
.
Result: A lower bound with solution (x, y) for
STSP
1
with objective function value z
b
.
Step 0
: Set ν = 1;
Let STSP
1
ν
be the problem obtained from STSP
1
by
removing the constraints (4) at iteration ν;
Solve the LP relaxation of problem STSP
1
ν
and let
(x
ν
, y
ν
) be its optimal solution of value z
ν
at
iteration ν;
Let z
0
= inf;
Step 1
: while |z
ν−1
− z
ν
| > ε do
foreach s ∈ K do
Construct the graph G
s
= (V, E
d
∪ E
s
) for
scenario s with the rounded solution
( ˜x
ν
, ˜y
ν
) obtained from (x
ν
, y
ν
);
C
s
= searchCycles(G
s
,V);
foreach cycle ∈ C
s
do
Add the corresponding constraint (4) to
STSP
1
ν
;
Set ν = ν + 1;
Solve the LP relaxation of problem STSP
1
ν
and
let (x
ν
, y
ν
) be its optimal solution of value z
ν
at
iteration ν;
return the solution (x
ν
, y
ν
, z
ν
);
Algorithm 4.2 in (Adasme et al., 2015) that we adapt
to solve problem STSP
1
. First, we remove constraints
(4) from STSP
1
and solve the resulting integer opti-
mization problem. Consider the underlying optimal
solution undirected graph G
s
= (V, E
d
∪ E
s
) where V
is the set of nodes and E
d
∪ E
s
is the set of edges such
that E
d
⊆ E
D
and E
s
⊆ E
S
for a given scenario s. If G
s
contains a cycle with three or up to |V|−1 nodes, then
the Algorithm 4.1 detects it. A subset of nodes induc-
ing a cycle defines a new constraint (4) which cuts off
this cycle from the solution space. Problem STSP
1
is
re-optimized taking into account the new added con-
straints. This iterative process goes on until the under-
lying current optimal solution of STSP
1
has no more
A Two-stage Stochastic Programming Approach for the Traveling Salesman Problem
165

cycles. Since the number of cycles is finite, so is the
number of constraints (4) that can be added to prob-
lem STSP
1
. Notice that each subset of nodes contain-
ing at least three or up to |V| − 1 nodes generates one
cycle elimination constraint for a particular scenario.
Also notice that the number of SECs of type (4) that
can be added to problem STSP
1
is at most O(|K|2
|V|
).
Consequently, Algorithm 4.2 adapted to solve STSP
1
,
converges to the optimal solution of the problem in
at most O(|K|2
|V|
) outer iterations. The proof can be
directly deduced from Theorem 2 in (Adasme et al.,
2015). The aforementioned procedure can also be
used to compute lower bounds for STSP
1
. This proce-
dure is depicted in Algorithm 1 and it is described as
follows. First, we remove constraints (4) from STSP
1
and solve the resulting linear programming (LP) re-
laxation of STSP
1
at step 1. Next, we enter into a
while loop searching cycles in the current rounded LP
solution for each s ∈ K. If G
s
contains a cycle with
three or more nodes up to |V| − 1, then the Algorithm
4.1 referred to as “searchCycles(G
s
,V)” in (Adasme
et al., 2015) detects it. A subset of nodes inducing
a cycle defines a new constraint (4). The LP relax-
ation of problem STSP
1
is re-optimized taking into
account the new added constraints. This iterative pro-
cess goes on until the difference between the current
optimal objective function value z
ν
and the previous
one z
ν−1
is less than a small positive value ε.
4 NUMERICAL RESULTS
In this section, we present preliminary numerical re-
sults. A Matlab (R2012a) program is developed using
CPLEX 12.6 to solve STSP
1
, STSP
2
, STSP
3
and their
corresponding LP relaxations. The numerical exper-
iments have been carried out on an Intel(R) 64 bits
core (TM) with 3.4 Ghz and 8G of RAM. CPLEX
solver is used with default options. We generate the
input data as follows. The edges in E
D
and E
S
are
chosen randomly with 50% of probability. The values
of p
s
, ∀s ∈ K are drawn randomly from the interval
[0;1] such that
∑
s∈K
p
s
= 1. Without loss of general-
ity, we assume that the set of scenarios K is finite and
known. Deterministic and uncertain edge costs are
randomly drawn from the interval [0;5]. We set the
parameter ε = 10
−8
in Algorithm 1. Finally, we men-
tion that we solve STSP
1
with up to 15 nodes while
generating all cycle elimination constraints. In par-
ticular, for the instances 1-25, we set the maximum
CPU time to solve the linear models with CPLEX to
at most 2 hours. Except for the last instance where we
set the maximum CPU time to 12 hours. The legend
of Table 1 is as follows. Column 1 shows the instance
number. Columns 2-3 present the number of nodes
|V| and the number of scenarios |K| of each instance,
respectively. Columns 4-8, 9-13 and 14-18 present
the optimal solution of STSP
1
, STSP
2
, STSP
3
, the
number of branch and bound nodes used by CPLEX,
the CPU time in seconds to solve the mixed integer
programs and their corresponding LP relaxations to-
gether with their CPU time in seconds, respectively.
Finally, in columns 19-21, we present gaps we com-
pute as
h
Opt−LP
Opt
i
∗ 100 for STSP
1
, STSP
2
and STSP
3
,
respectively.
From Table 1, we observe that the optimal objec-
tive function values for STSP
1
and STSP
2
are exactly
the same and slightly larger for STSP
3
. We also see
that the CPU times are significantly lower for STSP
2
.
Regarding the number of branch and bound nodes,
we observe that CPLEX requires less nodes for solv-
ing STSP
1
than STSP
2
and STSP
3
, and less nodes for
solving STSP
2
than for STSP
3
. Finally, the LP relax-
ations of STSP
2
can be solved faster than for STSP
1
and STSP
3
. However, we see that the gaps of the LP
relaxations are tighter for the exponential model. Fi-
nally, we observe that all the instances (e.g. 1-24,26)
are solved to optimality with the exception of instance
number 25. In particular, all these optimal solutions
are obtained with STSP
2
that shows a significantly
better performance. Finally, we mention that we can-
not solve, with the exponential model, instances with
more than 15 nodes due to the large number of sub-
tour elimination constraints involved. The instances
in Table 2 are the same as in Table 1. In Table 2,
the legend is as follows. In column 1, we show the
instance number. In columns 2-5, we show the op-
timal solution obtained with the adapted version of
Algorithm 4.2 (Adasme et al., 2015), its CPU time in
seconds, the number of cycles found with this algo-
rithm and the number of iterations, respectively. In
columns 6-10, we present the lower bound obtained
with Algorithm 1, its CPU time in seconds, the num-
ber of cycles found with it, the number of iterations,
and the optimal solution found with STSP
1
while us-
ing all the cycle elimination constraints found with
Algorithm 1, respectively. For the latter, we do not
report the CPU time required by CPLEX. However,
we mention that for most of the instances (e.g. 1-21)
these CPU times are less than 2 seconds. For the in-
stances 22-26, we limit CPLEX to a maximum CPU
time of 1 hour. In particular, for the instance num-
ber 25 we cannot find a feasible solution in 1 hour.
Finally, in columns 11-12, we provide gaps that we
compute by
h
Opt
It
−Opt
R
It
Opt
It
i
∗ 100 and
Opt
It
−Opt
F
It
Opt
It
∗ 100,
respectively. From Table 2, we observe that Algo-
rithm 4.2 can find the optimal solutions for all the
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
166
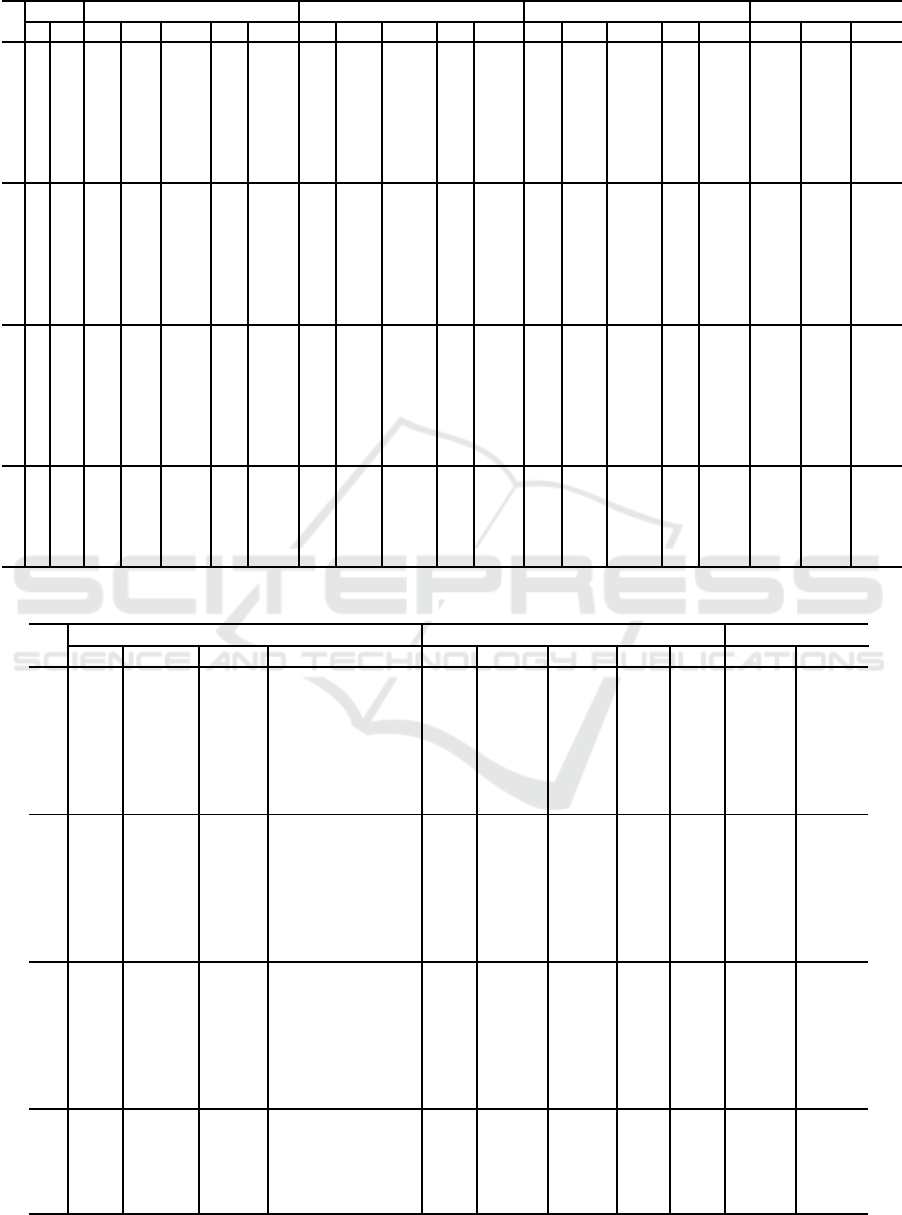
Table 1: Numerical results obtained with the Mixed integer linear models.
#
Inst. Dim. STSP
1
STSP
2
STSP
3
Gaps
|V| |K| Opt B&Bn Time (s) LP Time (s) Opt B&Bn Time (s) LP Time (s) Opt B&Bn Time (s) LP Time (s) Gap
1
% Gap
2
% Gap
3
%
1 4 5 7.50 0 0.27 7.50 0.14 7.50 0 0.14 6.81 0.13 7.50 0 0.14 6.81 0.13 0 9.12 9.12
2
6 5 10.98 0 0.16 10.98 0.14 10.98 28 0.16 9.28 0.14 10.98 0 0.14 10.61 0.13 0 15.49 3.38
3
8 5 7.66 0 0.38 7.65 0.20 7.66 0 0.19 6.90 0.14 7.66 0 0.25 7.32 0.14 0.08 9.90 4.46
4
10 5 12.22 9 1.39 11.16 0.36 12.22 47 0.25 9.42 0.16 12.38 95 0.48 9.89 0.16 8.67 22.93 20.09
5
12 5 10.60 7 6.10 10.30 1.33 10.60 33 0.42 8.09 0.14 10.60 23 0.75 9.01 0.14 2.88 23.69 15.08
6
14 5 12.40 74 47.33 11.29 7.04 12.40 153 0.62 10.28 0.17 12.89 412 3.35 10.45 0.17 8.89 17.10 18.95
7
15 5 9.79 36 87.10 8.65 16.57 9.79 974 1.98 7.43 0.14 10.49 1298 11.72 7.60 0.16 11.69 24.05 27.51
8 4 10 10.16 0 0.27 10.16 0.16 10.16 0 0.16 9.74 0.16 10.16 0 0.16 9.74 0.16 0 4.11 4.11
9
6 10 12.02 7 0.30 11.28 0.14 12.02 31 0.27 10.15 0.28 12.60 34 0.33 10.33 0.12 6.15 15.57 17.95
10
8 10 12.39 15 1.70 11.43 0.20 12.39 136 0.34 9.32 0.16 12.46 97 0.56 10.30 0.16 7.74 24.72 17.36
11
10 10 11.47 27 3.62 11.04 0.50 11.47 596 1.31 10.39 0.17 12.19 508533 828.00 10.66 0.39 3.74 9.41 12.54
12
12 10 11.63 7 12.65 11.51 2.29 11.63 50 0.59 8.64 0.17 11.63 125 1.90 9.88 0.19 0.99 25.73 15.07
13
14 10 13.61 224 214.91 11.90 11.57 13.61 25584 81.73 10.85 0.16 17.57 656991 7200.51 11.42 0.42 12.62 20.32 34.99
14
15 10 12.32 171 439.33 10.62 29.20 12.32 8720 30.97 9.56 0.20 14.00 96228 1377.95 9.79 0.33 13.80 22.42 30.05
15 4 25 10.35 0 0.41 10.35 0.20 10.35 0 0.20 10.15 0.14 10.35 0 0.20 10.15 0.16 0 1.99 1.99
16
6 25 8.64 0 0.36 8.64 0.19 8.64 7 0.23 6.70 0.16 8.64 0 0.20 6.96 0.14 0 22.48 19.51
17
8 25 10.13 0 0.47 10.13 0.44 10.13 15 0.30 9.10 0.17 10.13 0 0.19 9.96 0.17 0 10.17 1.70
18
10 25 12.32 40 10.64 11.48 0.95 12.32 460 2.39 11.25 0.22 13.13 1884 22.00 11.44 0.23 6.79 8.65 12.85
19
12 25 16.70 151 135.99 15.06 5.20 16.70 2473 20.26 13.82 0.22 16.89 1237 42.28 14.11 0.30 9.82 17.27 16.48
20
14 25 13.77 126 1163.72 12.91 29.80 13.77 944 14.17 11.46 0.28 14.13 566 35.79 11.83 0.37 6.27 16.81 16.26
21
15 25 10.30 80 3469.84 8.69 81.57 10.30 614 12.48 7.20 0.95 10.30 413 69.05 7.67 0.98 15.61 30.10 25.55
22 20 5 - - - - - 12.63 34329 139.25 10.47 0.31 13.79 198011 2824.50 11.08 0.39 - 17.06 19.65
23
25 5 - - - - - 12.89 50541 443.95 9.97 0.30 12.98 147422 6962.65 10.11 0.64 - 22.64 22.13
24
30 5 - - - - - 16.76 380096 3254.34 14.67 0.41 27.77 121894 7200.36 15.17 1.11 - 12.48 45.39
25
35 5 - - - - - 13.07 314434 7231.83 10.59 0.56 22.81 55442 7200.55 10.76 1.31 - 19.01 52.80
26
40 5 - - - - - 13.05 625722 29773.38 10.76 0.72 19.88 213290 39599.72 10.96 3.40 - 17.58 44.90
Table 2: Numerical results obtained with the iterative algorithmic procedures.
#
Algorithms 4.1 and 4.2 adapted from (Adasme et al., 2015) Algorithm 1 Gaps
Opt
It
Time (s) #Cycles #Iter Opt
R
It
Time (s) #Cycles #Iter Opt
F
It
Gap
R
% Gap
F
%
1 7.50 0.48 10 2 7.50 0.42 10 2 7.50 0 0
2
10.98 0.28 15 2 10.98 0.30 15 2 10.98 0 0
3
7.66 0.31 20 2 7.65 0.58 97 3 7.66 0.08 0
4
12.22 1.11 43 6 11.16 0.59 94 3 11.64 8.67 4.80
5
10.60 0.52 36 3 10.30 0.61 150 3 10.52 2.88 0.76
6
12.40 1.58 75 6 11.20 0.72 261 3 11.77 9.64 5.03
7
9.79 1.34 53 5 8.54 0.70 233 3 9.69 12.81 0.96
8 10.16 0.34 20 2 10.16 0.33 20 2 10.16 0 0
9
12.02 0.92 64 5 11.28 0.61 133 3 11.88 6.15 1.12
10
12.39 1.72 78 7 11.43 0.80 280 4 11.89 7.74 4.01
11
11.47 2.65 129 8 11.04 1.30 502 6 11.43 3.74 0.39
12
11.63 0.69 60 2 11.51 0.98 439 4 11.63 0.99 0
13
13.61 10.73 227 17 11.88 1.19 655 4 12.96 12.71 4.82
14
12.32 10.65 188 17 10.62 1.72 886 5 11.69 13.86 5.14
15 10.35 0.39 50 2 10.35 0.33 50 2 10.35 0 0
16
8.64 0.33 75 2 8.64 0.36 75 2 8.64 0 0
17
10.13 0.38 100 2 10.13 0.36 100 2 10.13 0 0
18
12.32 3.28 210 5 11.48 1.33 1054 4 12.13 6.79 1.54
19
16.70 17.29 535 14 15.06 1.64 1530 4 16.27 9.86 2.57
20
13.77 12.04 460 11 12.88 1.75 1361 4 13.47 6.49 2.16
21
10.30 11.26 268 5 8.67 3.17 2285 4 10.22 15.81 0.82
22 12.63 57.99 329 41 11.27 1.64 583 5 12.01 10.79 4.89
23
12.89 1706.91 409 43 10.84 2.96 985 5 12.13 15.96 5.90
24
16.76 438.17 325 34 15.64 1.84 599 3 16.29 6.65 2.77
25
12.93 36135.64 799 84 11.23 1.61 488 2 - 13.18 -
26
13.05 56379.58 959 81 11.60 3.38 817 3 12.58 11.16 3.64
A Two-stage Stochastic Programming Approach for the Traveling Salesman Problem
167

2 4 6 8 10 12 14 16
5
10
15
a) Number of scenarios
Optimal Solutions
and lower bounds
2 4 6 8 10 12 14 16
0
200
400
600
b) Number of scenarios
CPU time (s)
2 4 6 8 10 12 14 16
−1000
0
1000
2000
3000
c) Number of scenarios
Number of cycles
and iterations
2 4 6 8 10 12 14 16
0
10
20
30
40
d) Number of scenarios
Gaps (%)
Opt(STSP
2
)
LP(ST SP
2
)
Opt
R
It
Opt
F
It
ST SP
2
LP(ST SP
2
)
Opt
F
It
Cycles
Iter.
LP(ST SP
2
)
Gap
R
Gap
F
Figure 1: Numerical results for STSP
2
varying the number of scenarios using |V| = 16.
instances. In particular, the optimal solution of in-
stance 25 is also found, although at a higher CPU time
when compared to STSP
2
. The number of cycles and
iterations are not so large, e.g., less than 1000 and
100, respectively, for the largest instance. Notice that
the total number of cycles for most of the instances
is huge. However, the number of cycles required by
Algorithm 4.2 to find the optimal solution is signifi-
cantly small. In general, we see that the Algorithm 1
can find tight lower bounds in very short CPU time,
i.e., in less than 4 seconds for all the instances. In this
case, the number of cycles are slightly larger when
compared to Algorithm 4.2. On the opposite, we see
that Algorithm 1 requires less iterations. Finally, we
observe that solving STSP
1
with all the cycle elimi-
nation constraints found with Algorithm 1 allows to
compute tight bounds when compared to the optimal
solution of the problem and optimal solutions in many
cases (e.g. instances 1-3, 8, 12, 15-17). More pre-
cisely, these bounds are computed with gaps which
are lower than 6% for most of the instances.
In order to give more insight with respect to
the performances obtained with the compact model
STSP
2
and with Algorithm 1, in Figure 1, we solve
several instances for fixed |V| = 16 while varying
the number of scenarios from 2 to 16. More pre-
cisely, in Figure 1a, we show the optimal solution
of STSP
2
we denote by Opt(STSP
2
), its LP relax-
ation LP(STSP
2
), the lower bound Opt
R
It
obtained
with Algorithm 1 and the lower bound Opt
F
It
obtained
with STSP
2
while using all the cycle elimination con-
straints found with Algorithm 1. In Figure 1b, we
present the CPU time in seconds for STSP
2
, for its
LP relaxation LP(STSP
2
), and for Opt
F
It
. In the lat-
ter, we include the CPU time required to solve Al-
gorithm 1 and the time required to solve STSP
2
with
CPLEX. In Figure 1c, we show the number of cycles
and iterations required by Algorithm 1. Finally, in
Figure 1d, we present gaps as defined for Tables 1
and 2. From Figure 1a, we mainly observe that the
lower bounds Opt
F
It
remain tight when incrementing
the number of scenarios. In general, we see that the
bounds LP(STSP
2
), Opt
R
It
and Opt
F
It
do not seem to
be affected by the increase in the number of scenarios.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
168

Finally, we observe that the bounds Opt
F
It
are tighter
than Opt
R
It
, and Opt
R
It
are tighter than LP(STSP
2
).
From Figure 1b, we confirm that the Algorithm 1
can find these lower bounds in very short CPU time.
Similarly, the LP relaxation of STSP
2
is obtained very
fast. In Figure 1c, we observe that the number of iter-
ations are very low and that the number of cycles used
to find the lower bounds Opt
F
It
slightly grows with the
number of scenarios. Finally, in Figure 1d, we con-
firm with the gaps, the quality and order of the bounds
presented in Figure 1a.
5 CONCLUSIONS
In the context of combinatorial optimization, recently
some efforts have been made by extending classical
optimization problems under the two-stage stochastic
programming framework (Gaivoronski et al., 2011;
Flaxman et al., 2006; Escoffier et al., 2010; Adasme
et al., 2013; Adasme et al., 2015). In this paper, we
introduce a deterministic two-stage stochastic travel-
ing salesman problem and propose two compact mod-
els and a formulation with an exponential number of
constraints that we adapt from the classic TSP. Subse-
quently, we adapt the iterative algorithmic procedure
proposed in (Adasme et al., 2015) and compute opti-
mal solutions and tight lower bounds for the stochas-
tic traveling salesman problem. Our preliminary nu-
merical results indicate that one of the compact mod-
els allows to solve instances with up to 40 nodes and 5
scenarios to optimality. Finally, the lower bounds are
obtained within a small CPU time for all the tested
instances.
REFERENCES
Adasme, P., Andrade, R., Letournel, M., and Lisser, A.
(2013). A polynomial formulation for the stochastic
maximum weight forest problem. ENDM, 41:29–36.
Adasme, P., Andrade, R., Letournel, M., and Lisser, A.
(2015). Stochastic maximum weight forest problem.
Networks, 65(4):289–305.
Bertazzi, L. and Maggioni, F. (2014). Solution approaches
for the stochastic capacitated traveling salesmen lo-
cation problem with recourse. J Optim Theory Appl,
166(1):321–342.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to algorithms. MIT Press and
McGraw-Hill, Cumberland, RI, USA.
Escoffier, B., Gourves, L., Monnot, J., and Spanjaard, O.
(2010). Two-stage stochastic matching and spanning
tree problems: Polynomial instances and approxima-
tion. Eur J Oper Res, 205:19–30.
Flaxman, A. D., Frieze, A., and Krivelevich, M. (2006). On
the random 2-stage minimum spanning tree. Random
Struct Algor, 28:24–36.
Gaivoronski, A., Lisser, A., Lopez, R., and Xu, H. (2011).
Knapsack problem with probability constraints. J
Global Optim, 49:397–413.
Gavish, B. and Graves, S. C. (1978). The travelling sales-
man problem and related problems. Operations Re-
search Centre, Massachusetts Institute of Technology.
Letchford, A. N., Nasiri, S. D., and Theis, D. O. (2013).
Compact formulations of the steiner traveling sales-
man problem and related problems. European Journal
of Operational Research, 228:83–92.
Maggioni, F., Perboli, G., and Tadei, R. (2014). The multi-
path traveling salesman problem with stochastic travel
costs: a city logistics computational study. Trans-
portation Research Procedia, 1(3):528–536.
Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). In-
teger programming formulations and travelling sales-
man problems. J. Assoc. Comput. Mach., 7:326–329.
Shapiro, A., Dentcheva, D., and Ruszczynski, A. (2009).
Lectures on stochastic programming: Modeling and
theory. MOS-SIAM Series on Optimization, Philadel-
phia.
A Two-stage Stochastic Programming Approach for the Traveling Salesman Problem
169
