
Performance Analysis of Photonically Generated Microwave Signal
using a Dual-parallel Dual-drive Mach-Zehnder Modulator in
Dispersive Media
Amitesh Kumar, Vishnu Priye and Kowshik Moyya
Department of Electronics Engineering, Indian School of Mines Dhanbad, 826004, India
Keywords: Microwave Photonics, Modulator, Optoelectronics and Dispersion.
Abstract: Dispersion is one of the potential limiting parameter for generation of microwave signal using photonic
methods. In this paper, we analyse theoretically, the influence of fiber dispersion parameter on the
photonically generated microwave/millimeter wave signal using dual-parallel dual-drive LiNbO
Mach-
Zender modulators. Intensity at the output of photodetector having, eight and sixteen times frequency of
microwave drive signal and harmonic suppression versus modulation index (β) and filter attenuation is
discussed and it has been found that dispersion plays a major role on generation and transmission of
microwave signal in optical domain.
1 INTRODUCTION
Microwave Photonics (MWP) systems are emerging
as a new aspect for generation and transmission of
microwave and millimeter wave signal in optical
domain for applications such as broad-band wireless
communication system, modern instrumentation, bio-
medical, radar, warfare systems, and recently for THz
Technology. There are various advantages of
photonic generation of the microwave signal like high
band-width, large tunability and immune to
electromagnetic interference over conventional
technique in electrical domain (Yao, 2009; Seeds and
Williams, 2006). The low frequency modulated
double-sideband (DSB) optical signal suffers less
from the chromatic dispersion of the fiber than that of
the high frequency modulated signal when
transmitted through standard single mode fiber
(SSMF) (Schmuck, 1995; Gliese et al., 1996; Smith
et al., 1997) and high frequency signal generated by
DSB technique is limited by the bandwidth of the
optical sources like laser diode or the external
modulator and the fiber chromatic dispersion
(Hofstetter et al., 1995). To overcome these
limitations, a photonic generation method that uses
narrow bandwidth optical components to generate
high frequency electrical signals is one of the
promising solutions now a day. Electrical signal
generation based on optical heterodyning can be
achieved by using either two stable lasers or one laser
with external optical modulator. The electrical signal
generation by beating two free running lasers may
meet system application specifications but is of poor
quality (spectral response). Optical injection locking
and optical phase-locked loop (OPLL) (Yao, 2010)
have been proposed to improve the signal quality.
Methods using a laser with external optical
modulator, such as optical intensity modulator or
optical phase modulator (O'reilly et al,. 1992; Qi et
al., 2005) have shown great potential for producing
high purity, high-frequency microwave/millimeter-
wave signals. Frequency octupled millimeter-wave
signal is proposed using dual-parallel Mach-Zehnder
(DPMZD) and a wavelength fixed optical notch filter
(Zhang and Pan, 2012). Recently a microwave signal
generation using dual-parallel dual-drive Mach-
Zehnder modulator having frequency, sixteen times
of microwave drive signal is proposed (Kumar and
Priye, 2014).
One of the most limiting factor in microwave
photonics systems are dispersion that deteriorate the
performance of generated microwave signal. The
dispersion analysis of reported work (Kumar and
Priye, 2014) is proposed and demonstrated for beat
frequency of 4
th
and 8
th
order optical sidebands,
obtained at the output of respective photo detectors.
266
Kumar, A., Priye, V. and Moyya, K.
Performance Analysis of Photonically Generated Microwave Signal using a Dual-parallel Dual-drive Mach-Zehnder Modulator in Dispersive Media.
DOI: 10.5220/0005741702640269
In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 266-271
ISBN: 978-989-758-174-8
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 PROPOSED MODEL AND
ANALYSIS
In this proposed approach, shown in Figure 1, light
wave emitted from a tunable laser source (TLS) is
launched into to a DPMZM which is driven by two
amplified RF signal with phase difference of /.
The bias voltage of the two arms of upper and lower
dual-drive
MZM are at 0 V and phase
difference between the RF signal of two arms of each
modulator is i.e., MZM is biased at maximum
transmission point (MATP) to suppress all the odd-
order optical sidebands. The output of DPMZD is
passed through fibre Bragg grating (FBG)
wavelength fixed notch filter which is tuned to
attenuate optical carrier of frequency
with
attenuation factor α in dB and splitted into two paths.
From the Figure 1, the splitted signal is launched into
the upper and lower photo detectors (PD
1
& PD
2
)
through optical amplifier (EDFA) and optical fiber of
length 25 km. If the intensity of optical carrier and
modulation index is small only the 4
th
and 8
th
order
sidebands will be significant at the input of PD
1
and
at the input of PD
2,
8
th
and 16
th
order sideband will be
significant after rejection of 4
th
order sidebands
through optical band reject filter, considering high
optical carrier intensity and significant modulation
index. A beat signal with eight and sixteen times the
frequency of the electrical drive signal is generated at
photo detectors, PD
1
and PD
2
respectively. The power
of suppressed sidebands at the output of DPMZM is
transferred into the even-order sidebands (4
th
, 8
th
and
16
th
), improving the signal generation efficiency.
The output electric field from the dual-drive
LiNbO
Mach-Zehnder modulator is given as (Dai et
al. 2013)
E
(
t
)
=
1
2
E
exp
(
j
ω
t
)
exp
j
π
V
(
t
)
V
π
+
V
V
π
+
exp
j
π
V
(
t
)
V
π
+
V
V
π
(1)
Where E
0
and
are, the electric field & angular
frequency of the input optical carrier respectively,
is switching voltage,
is switching bias
voltage,
and
are the DC bias voltage
between two arms, and
(
)
&
(
)
are the RF
modulating electrical signal voltage.
(
)
and
(
)
can be expressed as two sinusoidal functions;
(
)
=
(
)
and
(
)
=
(
+
)
,
where
and
are the amplitude of the two RF
signals,
is the frequency of modulating RF
signal, and is the phase difference between two RF
signals.
The optical field at the output of the DPMZM can
be expressed as
E
(
t
)
=
√
2
E
J
(
β
)
cos
(
ω
t
)
+
∑
√
2
E
J
(
∞
β
)
[
cos
(
ω
t
−
4n
ω
t
)
+
cos
(
ω
t + 4nω
t
)
]
+
∑
√
2 E
J
(
∞
β)
[
cos
(
ω
t − 8nω
t
)
+
cos
(
ω
t + 8nω
t
)
]
+
∑
√
2
E
J
(
∞
β
)
[
cos
(
ω
t
−
16n
ω
t
)
+
cos
(
ω
t
+
16n
ω
t
)
]
(2)
Where J
, J
and J
are the Bessel function of
the first kind and of order 4n, 8n and 16n
respectively, and is the phase modulation index
(PMI). For 0<<2, the Bessel functions J
(β)
and J
(β) for ≥2 are much smaller than J
(β)
and J
(
β
)
. Therefore, it is reasonable to ignore the
optical sidebands with order higher than 16 in our
analysis, so only the carrier, ±4
th
, ±8
th
and ±16
th
order sidebands are left.
Figure 1: Schematic of the proposed microwave signal
generation system. (LD: laser diode; RF: radio frequency;
PC: polarization controller; MZM: Mach-Zehnder
Modulator; EG: electrical gain; PS: phase shift 90
0
; OF:
Optical band reject filter; PD: photo detector; BPF: band
pass filter).
The Figure 2, illustrates the optical spectra at the
output of DPMZM, since the two sidebands
originated from the same optical and microwave
sources, an excellent phase correlation is maintained.
Beating the two sidebands at a PD, a high-spectral-
purity signal, eight times as well as sixteen times
frequency of microwave drive electrical signals is
obtained.
Performance Analysis of Photonically Generated Microwave Signal using a Dual-parallel Dual-drive Mach-Zehnder Modulator in
Dispersive Media
267

Figure 2: The spectrum of the modulated optical signal at
the output of DPMZM using OptiSystem software (Kumar
and Priye 2014).
2.1 Performance Analysis in Dispersive
Media
It is known that in a wide-band electrical
heterodyning system purity of generated signal is
main concern. The generated electrical signal at the
PD, V
out
can be expressed as
(
)
=
(
)
cos
(
8
)
(3)
(
)
=
(
)
cos
(
16
)
(4)
Where R is a constant that is related to the
responsivity of the photodetector (PD). Since the two
optical sidebands originate from the same optical
source, the frequency stability and phase noise of the
generated signal are mainly determined by the
electrical drive signal. Equation (3) and (4) also
shows that the amplitude of the generated electrical
signal can be maximized by optimizing the value
and
respectively.
Assuming that, all unwanted odd-order and even
order optical sidebands generated by the modulation
of the DPMZM due to microwave drive radio
frequency signal, completely suppressed by using a
suitable dc-bias voltage and the attenuation of the
optical notch filter at its notch wavelength is α dB.
From equation (2), the optical signal at the output of
the FBG optical notch filter can be written as
E
(
t
)
=
√
2
E
kJ
(
β
)
cos
(
ω
t
)
+
∑
√
2
E
J
(
∞
β
)
[
cos
(
ω
t
−
4n
ω
t
)
+
cos
(
ω
t + 4nω
t
)
]
+
∑
√
2 E
J
(
∞
β)
[
cos
(
ω
t − 8nω
t
)
+
cos
(
ω
t + 8nω
t
)
]
+
∑
√
2
E
J
(
∞
β
)
[
cos
(
ω
t
−
16n
ω
t
)
+
cos
(
ω
t
+
16n
ω
t
)
]
(5)
Where k is the optical field attenuation factor,
which is related as α =−20log
k.
Generally, for a commercially available MZM,
the maximum available phase modulation index β
is 2. When 0≤≤2, Bessel function
,
&
for ≥1 are all monotonically increasing with
respect to β and monotonically decreasing with
respect to the order of Bessel function n, and
(
2
)
=
0.033996,
(
2
)
=0.00002218 and
(
2
)
=
4.5060 − 014. Hence, it is reasonable to ignore the
optical sideband with a Bessel coefficient higher than
(
β
)
for significant amplitude of optical carrier and
microwave drive (RF) signal in our discussion.
Therefore, equation (5) can be further simplified as
E
(
t
)
=
√
2
E
kJ
(
β
)
cos
(
ω
t
)
+
√
2
E
J
(
β
)
[
cos
(
ω
t
−
4
ω
t
)
+
cos
(
ω
t
+
4
ω
t
)
]
+
√
2 E
J
(
β
)
[
cos
(
ω
t − 8ω
t
)
+ cos
(
ω
t + 8ω
t
)
]
+
√
2
E
J
(
β
)
[
cos
(
ω
t
−
16
ω
t
)
+
cos
(
ω
t
+
16
ω
t
)
]
(6)
-16 -8 -4 0 4 8 16
Figure 3: Illustration of the electrical spectrum at the output
of a PD.
Equation (6) shows that the optical signal consists
of an attenuated optical carrier and six optical
sidebands. The spectrum of this optical signal is
illustrated as shown in Figure 3. The arrow direction
shows that initial phase with respect to the phase of
optical carrier before transmission.
When the optical signal shown in Figure 3 is
transmitted over a single-mode fiber, the chromatic
dispersion of the fiber will cause an extra phase shift
to each optical sideband compare to the optical
carrier. By expanding the propagation constant ()
of the fiber for each optical sideband to a Taylor series
around the angular frequency of the optical carrier
(Okamoto 2000), i.e.
(
±
4
)
=
(
)
+
(
)
(
±
4
)
+
1
2
²
(
)
(
±
4
)
+
⋯
(7)
(
±
8
)
=
(
)
+
(
)
(
±
8
)
+
1
2
(
)
(
±
8
)
+
⋯
(8)
(
±
16
)
=
(
)
+
(
)
(
±
16
)
+
1
2
(
)
(
±
16
)
+
⋯
(9)
8
th
order sideband
4
th
order sideband
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
268
Where
(
0
)
and
(
0
) are the first and second-
order derivative of the propagation constant
(
)
at
angular frequency ω
0
, respectively. The effect of
higher order dispersion is neglected for the single-
mode fiber at 1552nm band (Marshall, Crosignani
and Yariv 2000) and
(
) can be expressed by the
chromatic dispersion parameter D as
(
0
)
=
−
2
0
2
(10)
Where c is the speed of light in vacuum and
is
the frequency of the optical carrier.
The electric field at the end of the transmission
over single-mode fiber of length L can be obtained by
adding the transmission phase delay β
(
ω
±
4nω
)
L , β
(
ω
± 8nω
)
L and β
(
ω
± 16nω
)
L
to the corresponding optical sideband shown in (6).
Electrical harmonic will be generated by applying this
optical signal to a photodiode. The power intensities
(Qi et al. 2005) of the 8
th
and 16
th
order electrical
harmonic I
8
and I
16
respectively are proportional to
the coefficient of optical sidebands.
∝
2
J
(
β
)
+
2k
J
(
β
)
J
(
β
)
cos
64
π
cDL
f
f
(11)
∝
2
J
(
β
)
+
2k
J
(
β
)
J
(
β
)
cos
256
π
cDL
f
f
(12)
(a)
(b)
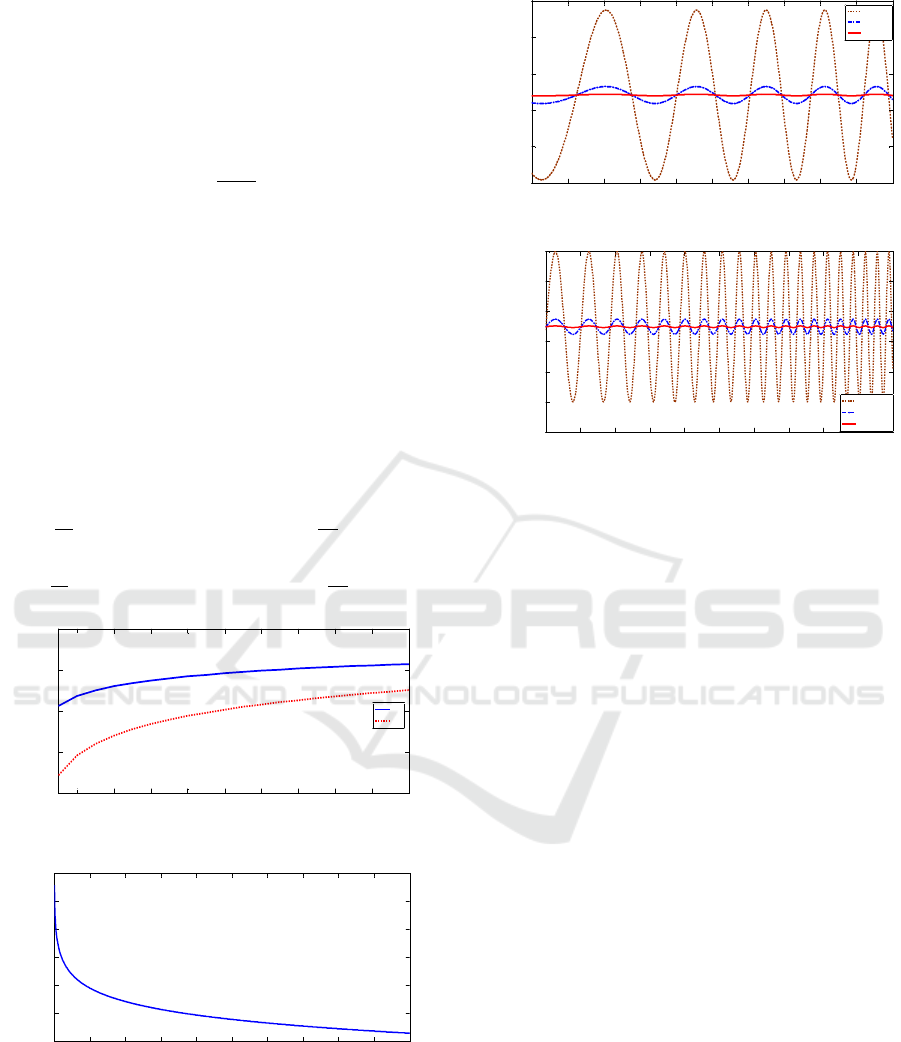
Figure 4: Power intensity and harmonic suppression versus
modulation index (a) Power intensity I
8
& I
16
, eighth and
sixteenth order harmonics. (b) Harmonics suppressions
I
8
/I
16
. (Frequency of the electrical drive.f
=7 GHz.).
(a)
(b)
Figure 5: Power variation versus frequency of the electrical
drive signal. (a) Power variation of I
8
, (b) Power variation
of I
16
. (Modulation index β=0.6).
For a distribution system that operate at 1552.52
nm with a transmission distance of 25 km over a
standared single mode fiber with D= 17 ps/
(nm.km), the power intensity I
8
,I
16
and harmonics
suppression of I
8
/ I
16
verses the modulation index
(0≤≤2) are plotted in Figure 4.
From figure 4(a) the power intensity of 8
th
and 16
th
order harmonics are monotonically increases for 0≤
≤2 and Figure 4(b) show that the harmonic
suppression I
8
/I
16
is monotonically decreases for 0≤
≤2, which is independent of the attenuation of
optical notch filter.
Figure 5(a) and 5(b) shows the power variation of
the generated electrical signals I
8
and I
16
respectively,
which is due to the combined effect of the limited
attenuation of the optical carrier and the chromatic
dispersion of the fiber when tuning the frequency of
the electrical drive signal from 2 to 7 GHz. It is clearly
seen that when ≥40, this power variation is
smaller. This means the amplitude of the eight and
sixteen times of microwave drive signals are stable
over the tuning band when is a constant and is
greater than equal to 40 dB.
2.2 Analysis for Higher Order
Dispersion
By expanding the propagation constant () of the
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-600
-400
-200
0
200
Modulation index
P o w e r in te n s ity [d B m ]
I8
I16
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
100
200
300
400
500
600
700
Harmonic suppression I8/I16 [dB]
Modulation index
2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7
-88.391
-88.39
-88.389
-88.388
-88.387
-88.386
Frequency [GHz]
Pow er variation of I8 [dB]
alpha=40
alpha=60
alpha=80
2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7
-300.9222
-300.9222
-300.9222
-300.9222
-300.9222
-300.9222
-300.9222
Frequency [GHz]
Power variation of I16 [dB]
alpha=40
alpha=60
alpha=80
Performance Analysis of Photonically Generated Microwave Signal using a Dual-parallel Dual-drive Mach-Zehnder Modulator in
Dispersive Media
269
fiber for each optical sideband to a Taylor series
around the angular frequency of the optical carrier up
to 5
th
order dispersion (Okamoto 2000), i.e.,
(
±
2
)
=
(
)
+
(
ω
0
)
(
±
2
n
ω
RF
)
+
(
ω
0
)
(
±
2
n
ω
RF
)
2
+
1
6
β
³
(
)
(
±
2
)
+
β
⁴
(
)
(
±
2
)
+
β
⁵
(
)
(
±
2
)
(13)
The third order dispersion parameter is given by
³
(
)
=
=
(
)
+
2
=
(
)
[
+
2
]
(14)
Where D is Group Velocity Dispersion (GVD) and
D₁ is the Dispersion Slope.
The fourth order dispersion parameter is given by
(Keiser 2008)
⁴
(
)
=
=
(
)
[
+
6
+
6
]
=
(
)
[
₂
+
6
₁
+
6
]
(15)
The fifth order dispersion parameter is given by
(Keiser 2008)
(
)
=
=
(
)
[
+
12
+
3
6
+
24
]
=
(
)
[
₃
+
12
₂
+
36
₁
+
24
]
(16)
The electric field at the end of the transmission
over single-mode fiber of length L can be obtained by
adding the transmission phase delay β
(
ω
±
4nω
)
L , β
(
ω
± 8nω
)
L and β
(
ω
± 16nω
)
L
to the corresponding optical sideband shown in (6).
Electrical harmonic will be generated by applying this
optical signal to a photodiode. The power intensities
(Qi et al., 2005) of the 8
th
and 16
th
order electrical
harmonic I
8
and I
16
respectively for higher order
dispersion are proportional to the coefficient of
optical sidebands
∝
J
(
β
)
+
2k
J
(
β
)
J
(
β
)
cos
(
)
(
8
ω
RF
)
+
(
)
(
8
ω
RF
)
(17)
∝
J
(
β
)
+
2k
J
(
β
)
J
(
β
)
cos
(
0
)
(
16
ω
RF
)
+
(
0
)
(
16
ω
RF
)
(18)
3 RESULTS AND DISCUSSION
In our calculation, we used the electrical drive signal
frequency nearly equal to 7 GHz, optical carrier of
193.1 THz, modulation index () range of 0-2 for the
MZM and assumed the initial phase of the electrical
drive signal for the MZM equal to zero. Referring to
ITU’s G.655 fiber (ITU-T 2009); Fiber chromatic
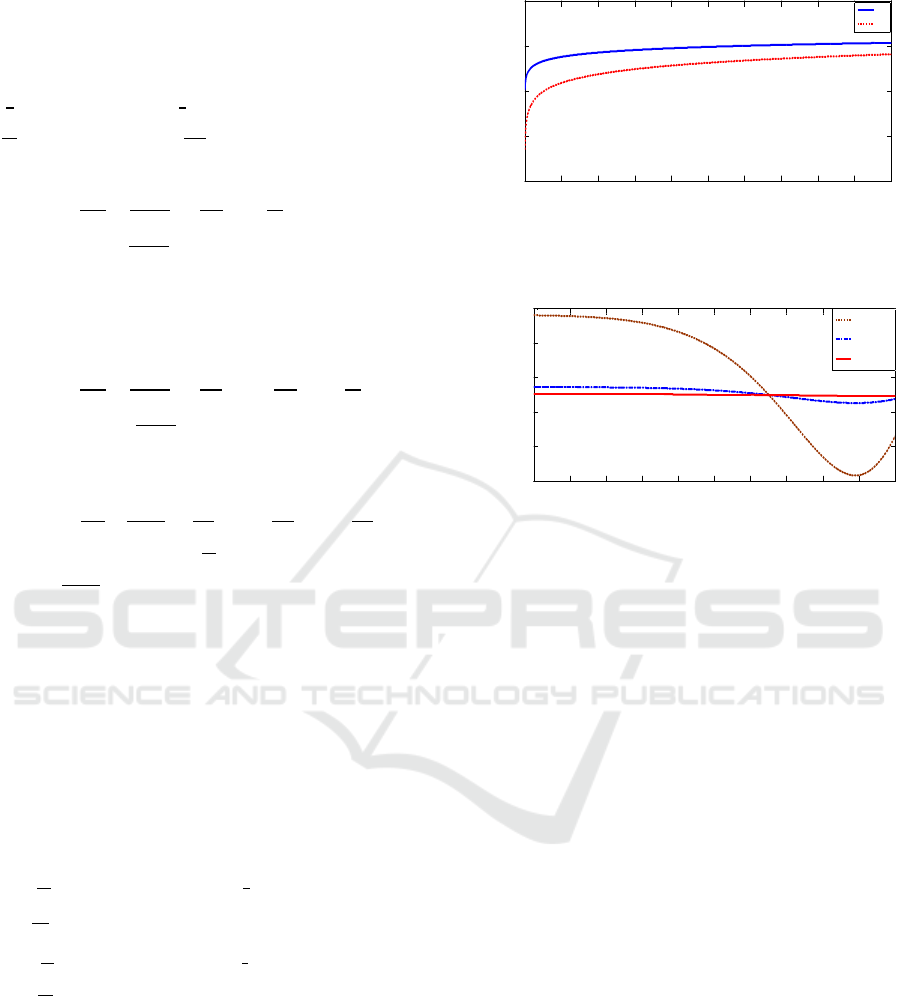
Figure 6: Power intensity I
8
& I
16
, eighth and sixteenth order
harmonics.
Figure 7: Power variation (I
8
) versus frequency of the
electrical drive signal.
dispersion, D = 0.5ps/km-nm, Dispersion curvature,
D
1
= 0.085ps/km-nm², Dispersion curvature, D
2
=
2.3776x10
-4
ps/km-nm
3
,
Electrical field attenuation
factor, =100 dB, Gain of EDFA= 100 and Electric
field strength, E
0
= 10V/m.
4 CONCLUSIONS
In this paper, the detail theoretical analysis of
influence of fiber dispersion on photonically
generated microwave/millimeter wave using dual-
parallel dual-drive LiNbO
Mach-Zender modulators
is investigated. Performance analysis of eighth and
sixteen orders harmonics generated from microwave
drive signal (RF) on SSMF and ITU’s G.655 fiber of
length 25 km are calculated theoretically and it is
observed that dispersion parameters have significant
impact on microwave/millimeter wave signal
generation using photonic technique. The impact
decreases as the order of dispersion term increases.
REFERENCES
Yao, J., 2009. Microwave photonics. Lightwave
Technology, Journal of,27(3), pp.314-335.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-1500
-1000
-500
0
500
Modulation index
P o w e r i n te n s it y [ d B m ]
I8
I16
2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7
x 10
9
-82.195
-82.194
-82.193
-82.192
-82.191
-82.19
Frequency [GHz]
P o w e r v a r i a t i o n o f I 8 [ d B ]
alpha=40
alpha=60
alpha=80
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
270

Seeds, A.J. and Williams, K.J., 2006. Microwave
photonics. Lightwave Technology, Journal of, 24(12),
pp.4628-4641.
Schmuck, H., 1995. Comparison of optical millimetre-wave
system concepts with regard to chromatic
dispersion. Electronics Letters, 31(21), pp.1848-1849.
Gliese, U., Norskov, S. and Nielsen, T.N., 1996. Chromatic
dispersion in fiber-optic microwave and millimeter-
wave links. Microwave Theory and Techniques, IEEE
Transactions on, 44(10), pp.1716-1724.
Smith, G.H., Novak, D. and Ahmed, Z., 1997. Overcoming
chromatic-dispersion effects in fiber-wireless systems
incorporating external modulators. Microwave Theory
and Techniques, IEEE Transactions on,45(8), pp.1410-
1415.
Hofstetter, R., Schmuck, H. and Heidemann, R., 1995.
Dispersion effects in optical millimeter-wave systems
using self-heterodyne method for transport and
generation. Microwave Theory and Techniques, IEEE
Transactions on,43(9), pp.2263-2269.
Yao, J., 2010. Microwave photonics: Photonic generation
of microwave and millimeter-wave
signals. International Journal Of Microwave And
Optical Technology, 5(1), pp.16-21.
O'reilly, J.J., Lane, P.M., Heidemann, R. and Hofstetter, R.,
1992. Optical generation of very narrow linewidth
millimetre wave signals. Electronics Letters, 28(25),
pp.2309-2311.
Qi, G., Yao, J., Seregelyi, J., Paquet, S. and Bélisle, C.,
2005. Generation and distribution of a wide-band
continuously tunable millimeter-wave signal with an
optical external modulation technique. Microwave
Theory and Techniques, IEEE Transactions on, 53(10),
pp.3090-3097.
Zhang, Y. and Pan, S., 2012, September. Experimental
demonstration of frequency-octupled millimeter-wave
signal generation based on a dual-parallel Mach-
Zehnder modulator. In Microwave Workshop Series on
Millimeter Wave Wireless Technology and
Applications (IMWS), 2012 IEEE MTT-S
International (pp. 1-4). IEEE.
Kumar, A. and Priye, V., 2014, December. Photonic
Generation of Microwave Signal Using a Dual-Parallel
Dual-Drive Mach-Zehnder Modulator. In International
Conference on Fibre Optics and Photonics (pp. S5A-
66). Optical Society of America.
Dai, B., Gao, Z., Wang, X., Chen, H., Kataoka, N. and
Wada, N., 2013. Generation of versatile waveforms
from CW light using a dual-drive Mach-Zehnder
modulator and employing chromatic
dispersion. Lightwave Technology, Journal of, 31(1),
pp.145-151.
Okamoto, K., 2000. Fundamentals of optical waveguides.
Academic press, pp 72-72.
Marshall, W.K., Crosignani, B. and Yariv, A., 2000. Laser
phase noise to intensity noise conversion by lowest-
order group-velocity dispersion in optical fiber: exact
theory. Optics letters, 25(3), pp.165-167.
Keiser, G., 2008. Optical fiber communications. Mcgraw-
Hill, Singapore.
ITU-T, R., 2009. G. 655. Characteristics of Non Zero
dispersion shifted single mode optical fiber cable, p.13.
Performance Analysis of Photonically Generated Microwave Signal using a Dual-parallel Dual-drive Mach-Zehnder Modulator in
Dispersive Media
271
