Testing of Micro-optics using Digital Holographic Interferometric

Microscopy

Varun Kumar and Chandra Shakher

Laser Applications and Holography Laboratory, Instrument Design Development Centre,

Indian Institute of Technology Delhi, Hauz Khas, New Delhi 110016, India

Keywords: Digital Holographic Interferometric Microscopy, Phase Map, Micro-lens Array, Micro-optics.

Abstract: Digital holographic interferometric microscopy (DHIM) is used as metrological tool for the testing of

micro-optics. The paper presents the measurement of sag height (h), radius of curvature (ROC), and shape

of micro-lens. The advantage of using the DHIM is that the distortions due to aberrations in the optical

system are avoided by the interferometric comparison of reconstructed phase with and without the object.

1 INTRODUCTION

Micro - optical component such as microlenses and

micro lens array have numerous engineering and

industrial applications for collimation of laser diode,

imaging for sensor system (CCD/CMOS, document

copier machines etc.), for making beam

homogeneous for high power laser, a critical

component in Shack-Hartmann sensor, fiber

coupling and optical switching in communication

technology (Sinzinger 1999, Anderson 1997,

Cormick et al,1999, Hou et al. 2015). Also micro-

optical components have become an alternative to

bulk optics for applications where miniaturization,

reduction of alignment and packaging cost are

necessary (SUSS MicroOptics SA catalog 2007).

The compliance with high-quality standards in the

manufacturing of micro-optical components is a

precondition to be compatible on worldwide

markets. Therefore, high demands are put on quality

assurance. For quality assurance of these lenses, an

economical measurement technique is needed. For

cost and time reason, technique should be fast,

simple, and robust with high resolution. The

technique should provide non contact, non-invasive

and full field information about the shape of micro-

optical component under test. The interferometric

techniques are noncontact type, non invasive and

provide full field information about the shape of the

optical components. The conventional

interferometric technique such as Mach-Zehnder

interferometry, Twyman- Green interferometry and

white light interferometry are available for testing of

micro-optics (Reichelt et al., 2005; Weible et al.,

2004; Wahaba and Kries, 2009). However,

interferometric techniques needs more experimental

efforts for phase measurement (such as phase

shifting techniques) and are thus time consuming

(Reichelt et al., 2005; Weible et al., 2004; Wahaba

and Kries, 2009; Zhang and Yamaguchi, 1998).

White light interferometry is not suited to measure

entire lens profile and yields accurate information

only for vertex of micro-lens (Weible et al., 2004).

Digital holography (DH) overcomes the above

discussed problems. Digital holographic microscopy

(DHM) allows to extract both the amplitude and

phase information of a wavefront transmitted

through the transparent object (micro-lenses array)

from a single digitally recorded hologram by use of

numerical methods (Charrière et al.,2006; Schnar

and Juptner, 1994; Cuche et al. 1999; Cuche et al.

1999, p. 291-293; Schnar, 2005). Due to numerical

reconstruction, the complex object wavefront at

different distances can be reconstructed. Digital

holography provides axial resolution in nanometers

while lateral resolution is limited by diffraction and

the size of the sensor (Cuche et al. 1999; Cuche et al.

1999, p. 291-293).

In this paper, Mach-Zehnder based digital

holographic interferometric system (DHIM) is used

for the testing of refractive micro lens. The

advantage of using the DHIM is that the distortions

due to aberrations in the optical system are avoided

by the interferometric comparison of reconstructed

phase with and without the micro lens array (Anand

142

Kumar, V. and Shakher, C.

Testing of Micro-optics using Digital Holographic Interferometric Microscopy.

DOI: 10.5220/0005742901400145

In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 142-147

ISBN: 978-989-758-174-8

et al., 2011, p. 547). In the experiment, first a digital

hologram is recorded in the absence of micro-lens

array which is used as a reference hologram. Second

hologram is recorded in the presence of micro-lens

array. The presence of transparent micro-lens array

will induce a phase change in the transmitted laser

light. Complex amplitude of object wavefront in

presence and absence of micro-lens array is

reconstructed by using Fresnel reconstruction

method (Schnar and Juptner, 2005). From the

reconstructed complex amplitude, one can evaluate

the phase of object wave in presence and absence of

micro-lens array. Phase difference between the two

states of object wave will provide the information

about optical path length change occurring between

two states. By knowing the value of the refractive

index of micro-lens array material and air, the

surface profile of micro-lens array is calculated.

From the experimentally calculated value of sag

height (h) and diameter of micro-lens (D), the radius

of curvature of micro-lens is calculated.

2 EXPERIMENTAL SET UP AND

THEORY

Figure 1 shows the schematic of experimental set up

of digital holographic microscope. The Experimental

set up is based on Mach- Zehnder interferometer. A

5 mW He-Ne laser (Make – Melles Griot, λ=632.8

nm) is used as a light source. Light from the laser

source is divided into two beams using a beam

splitter BS1. One of the beams acts as a reference

beam and the other acts as an object beam. Light in

the two arms of the interferometers are expanded

and collimated by assembly of spatial filter (SF)

[Make – Newport Corp.] and collimating lens (CL).

Light in the one arm is passed through the object

under test (micro-lenses array). In the experiment,

round shape and plano – convex micro lens array

supplied by THORLABS with micro lens sag height

(h=0.87 μm), diameter (D=146 μm) and radius of

curvature (ROC=3.063 mm) was used. The object

under test was mounted on 2D translation stage in

the object arm of the Mach-Zehnder interferometer

and a microscope objective (20 X, NA=0.40) was

used to increase the lateral resolution of the digital

holographic microscopic system. A similar

microscope objective (20X, NA=0.40) was also used

in the reference arm of the interferometer to match

the curvature in the object and reference wavefront.

A minute angle is introduced in the reference beam

to make the off axis holographic system. The

microscope objectives in both arms and beam

splitter are adjusted in such a way that the

interference fringes are straight; this avoids the need

to perform any digital correction due to spherical

aberration introduced by microscope objectives

(Anand et al., 2011, p. 547). ND filters are used in

the reference arm and object arm to adjust the

intensity for recording good contrast fringes in the

hologram. All the optical components (mirrors,

lenses, beam splitters, ND filters) used in the

experiments are supplied by M/S Melles Griot

(Netherland).

Figure 1: Mach-Zehnder interferometer based Digital

Holographic Microscope for testing of micro lens array.

The object beam interferes with the reference

beam at the hologram plane (CCD Plane). The

hologram with intensity (Schnar and Juptner, 2005)

),( ROORORYXH +++=

(1)

is recorded by CCD sensor (Make – Lumenera

Corporation, Model – Infinity3-1M). In equation 1,

R is the reference wavefront and O is the object

wavefront, and * denote the complex conjugate. The

pixel size on CCD sensor is 6.45μm ×6.45μm. Total

numbers of pixels are 1392×1040 and the sensor

chip dimension is 2/3". Dynamic range of the CCD

sensor is 8-bit. Computer with 64 bit Intel (R) Core

(TM) i5 microprocessor and CPU clock rate of 3.2

GHz was used to process the data. The digital

hologram is stored in computer for further

processing. In order to reconstruct the digital

hologram, a digital reference wave R

is used to

reconstruct the digital transmitted wavefront O(m

,n), and is given by (Schnar and Juptner, 2005).

RORORRORRRHRO

DDDDD

+++==

(2)

At right hand side of equation (2), first two terms

are dc term and correspond to the zero order

diffraction and the third term is the twin image. The

fourth term is the real image. To avoid the overlap

between these three components (dc term, twin

image and real image) during reconstruction, the

Testing of Micro-optics using Digital Holographic Interferometric Microscopy

143

hologram is recorded in off – axis geometry. For this

purpose, angle of reference beam (θ) with normal to

CCD plane is adjusted such that θ is sufficiently

large enough to ensure separation between real and

twin images in reconstruction plane. However, the

angle θ should not small enough so that spatial

frequency of micro interference pattern does not

exceed than the resolving power of CCD sensor

(Schnar and Juptner, 2005, p. R92).

2.1 Hologram Reconstruction

In digital holography reconstruction of object

wavefront is done by numerical methods by

simulating the diffraction of reference wave at the

microstructure of recorded digital hologram using

scalar diffraction theory. The most commonly used

numerical reconstruction methods are Fresnel

reconstruction method, convolution method, and

phase shifting method. The diffraction of

reconstructing wave at the digital hologram is

described by the Fresnel-Kirchhoff integral (Schnar

and Juptner, 2005, p. R90; Wagner et al., 1999). (X

), (X, Y), and (X

, Y

) are the Cartesian co-ordinate

system of the object, hologram and image planes

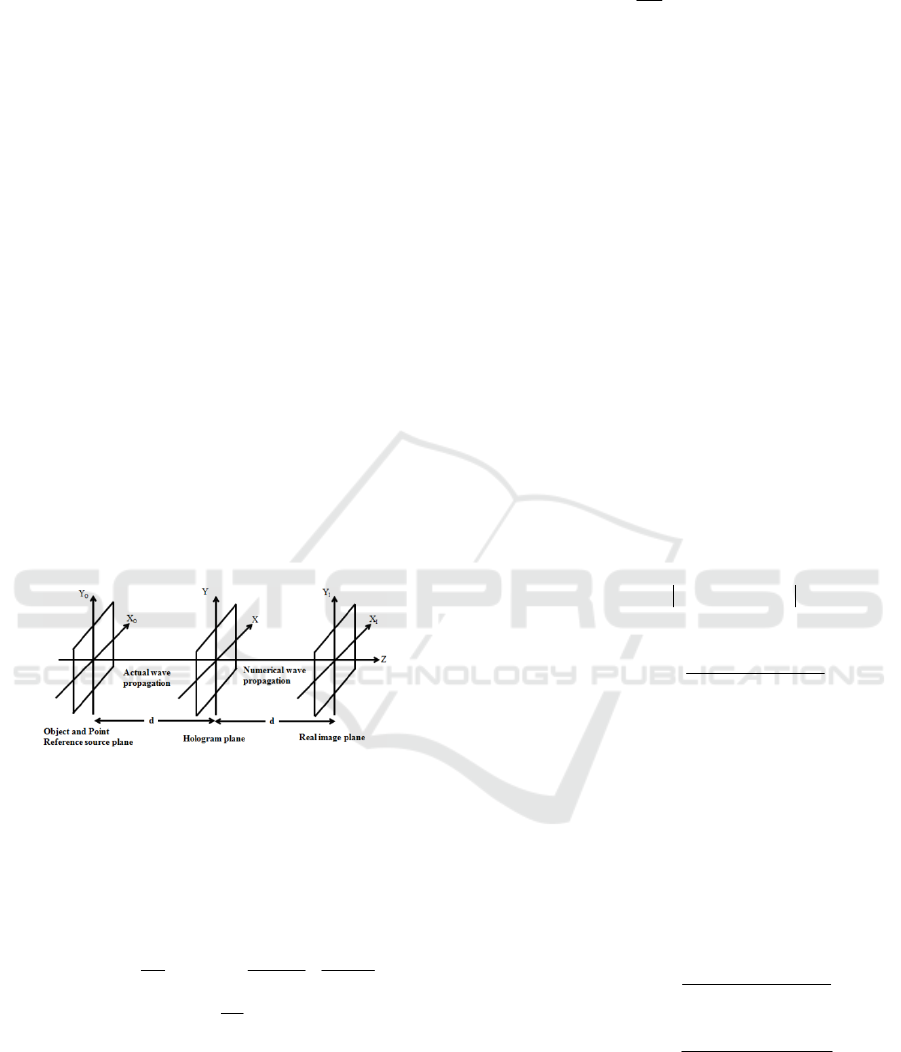
respectively (see Fig. 2).

Figure 2: Cartesian co-ordinate system used in the Fresnel

Reconstruction method.

The digital form of complex amplitude of

diffracted wave in the reconstruction (image) plane

using the Fresnel-Kirchoff diffraction integral with

the Fresnel approximation is given by (Kumar et al.,

2015, p. 1258)

)]}(exp[),(),({

)](exp[),(

2222

YqXp

iqpHqpRFFT

YnXmO

Δ+Δ−×

−=ΔΔ

λπ

(3)

where m, n and p, q are the integers (m, p = 0, 1,

2, 3,..........M-1; and n, q = 0, 1, 2, 3,..........N-1). M ×

N are the number of pixels in the CCD sensor.

and

Y are the pixel size of CCD sensor. H (p, q) is

the recorded digital hologram, λ is the wavelength,

and d is the reconstruction distance respectively.

If we assume that reference wave is a plane wave

of wavelength λ, R

can be expressed as:

()

⎥

⎦

⎤

⎢

⎣

⎡

Δ+Δ= yqkxpkiR

yxD

exp

(4)

Where k

and k

are the components of wave vector.

To remove the dc term and -1 order term, the

recorded raw digital hologram H (p, q) is filtered in

Fourier domain (Takeda et al., 1989; Cuche et al.

2000). For this purpose, first we perform the Fourier

transform on H (p, q), and the Fourier spectrum of H

(p, q) gives the zero order term (dc term), +1 order

and -1 order. Now to remove the dc term and -1

order term, rectangular band pass filter is applied on

the +1 order term. The inverse Fourier transform of

the selected spectrum (+1 order) provide the

complex amplitude containing information about the

object wavefront O (m

X, n

Y, Z=0). Complex

amplitude O (m

X, n

Y, d) at a distance d parallel to

CCD plane is computed from the filtered spectrum

by using equation (3).

Numerical reconstruction of recorded digital

hologram H (p, q) yields the complex amplitude of

object wavefront. Once the complex amplitude of

object wavefront is calculated, the intensity and

phase of the object can be calculated. The intensity

of object wavefront is calculated as (Schnar and

Juptner, 2005, p. R89)

),(),(

IIII

YnXmOYnXmI ΔΔ=ΔΔ

(5)

The phase is calculated as

)],(Re[

)],(Im[

arctan),(

YnXmO

YnXm

ΔΔ

=ΔΔ

(6)

where, the operators Re and Im denote real and

imaginary part of a complex function.

The phase of the two states of object (initial and

final) are evaluated individually from complex

amplitude of object wave front in two states

),(

1 II

YnXmO ΔΔ

and

),(

YnXmO ΔΔ

Interferometric comparison i.e. phase difference

provide information about change between two

states. The phase of initial state and final states can

be written as

)],(Re[

)],(Im[

arctan),(

YnXmO

YnXm

ΔΔ

=ΔΔ

(6a)

)],(Re[

)],(Im[

arctan),(

YnXmO

YnXm

ΔΔ

=ΔΔ

(6b)

The phase takes values between –π and π, the

principal value of arctan function. The interference

phase, which is phase difference between the phase

in presence of object (micro-lens array) and absence

of micro lens array, is calculated by modulo 2π

subtraction (Schnar and Juptner, 2002, p. R94)

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

144

()

()() () ()

()() ()()

⎩

⎨

⎧

<+−

≥−

=Δ

nmnmifnmnm

,,2,,

,,,,

1212

φφπφφ

φφφφ

(7)

The modulo 2π phase difference map of micro

lenslet array and ambient air is unwrapped using

Goldstein phase unwrapping method to remove the 2

π phase discontinuity (Goldstein, 1988).

3 EXPERIMENT RESULTS AND

DISCUSSION

Initially the experiment was carried out on USAF

resolution test chart. Figure 3(a) shows the recorded

hologram of the USAF Resolution test target.

(a) (b)

(c)

Figure 3: (a) Hologram of USAF resolution chart (b)

Fourier spectrum of hologram (c) Intensity image.

A Fourier spectrum of the hologram gives the

virtual image, real image and dc term (zero order

diffraction). Figure 3 (b) shows the Fourier spectrum

of the recorded digital hologram of USAF resolution

test chart. A band pass rectangular filter is applied to

remove the dc term and twin image. Inverse Fourier

transform gives complex amplitude of object

wavefront at CCD plane. Complex amplitude of

object wavefront in reconstruction plane is

calculated by solving equation (3). The intensity

image of the USAF resolution test chart is evaluated

using equation (5) and is shown in Figure 3(c). From

the intensity image of resolution test target, it is

clear that we are able to resolve the small details of

element of 7

group and it corresponds to 228.1

lines pair/mm (i.e width of one line is 2.19 μm in

USAF resolution test target). For resolving one line,

the width of one line (2.19 μm) should be covered

by at least two pixels. The achieved resolution

(1.095 μm) from the holographic set up agrees with

the predicted resolution limit of the microscope

objective (20X, NA=0.40). The resolution limit of

microscope objective is given by Abbe criterion

(0.61λ/NA = 0.965 μm).

3.1 Results of Testing of Micro-lens

Array

First, we record a digital hologram of ambient air (in

absence of micro-lens array) as a reference

hologram. Now, micro-lenses array is mounted on

2D translational stage and inserted in the object arm

of the Mach–Zehnder interferometer. In presence of

micro-lenses array second digital hologram is

recorded. Phases in the two individual states of

object (ambient air and presence of micro-lenses

array) are numerically reconstructed from equation

(6a) and (6b) respectively. Fig.4 (a) shows the

modulo 2π phase difference map of micro-lenses and

ambient air. The modulo 2π phase difference map of

micro- lenses and ambient air is unwrapped using

Goldstein phase unwrapping method to remove the 2

(a)

(b)

(c)

Figure 4: (a) Modulo 2π phase difference, (b) 2D

unwrapped phase difference map of Micro-lens array and

ambient air, and (c) 3D unwrapped phase difference map

of Micro-lens array and ambient air.

Testing of Micro-optics using Digital Holographic Interferometric Microscopy

145

π phase discontinuity. Fig. 4(b) shows the 2D

unwrapped phase difference map of micro-lens and

ambient air. Fig. 4(c) shows the 3D unwrapped

phase difference map of micro-lenses and ambient

air.

Now the optical path length difference (

n × h)

can be connected to experimentally calculated

unwrapped phase difference through the equation

hn ×Δ=Δ

(8)

where

n is the refractive index change (n-n

), n is

refractive index of micro-lens material and n

is the

refractive index of ambient air, and h is the distance

travelled by laser light (λ=632.8 nm) through the

micro-lens array.

Micro-lenses array is made up of fused silica.

Consider, the refractive index of micro lenses array

material is homogeneous. The refractive index of the

fused silica is n = 1.457 at wavelength 632.8 nm.

Refractive index of air n

=1. The height distribution

of the micro-lenses can be evaluated from equation

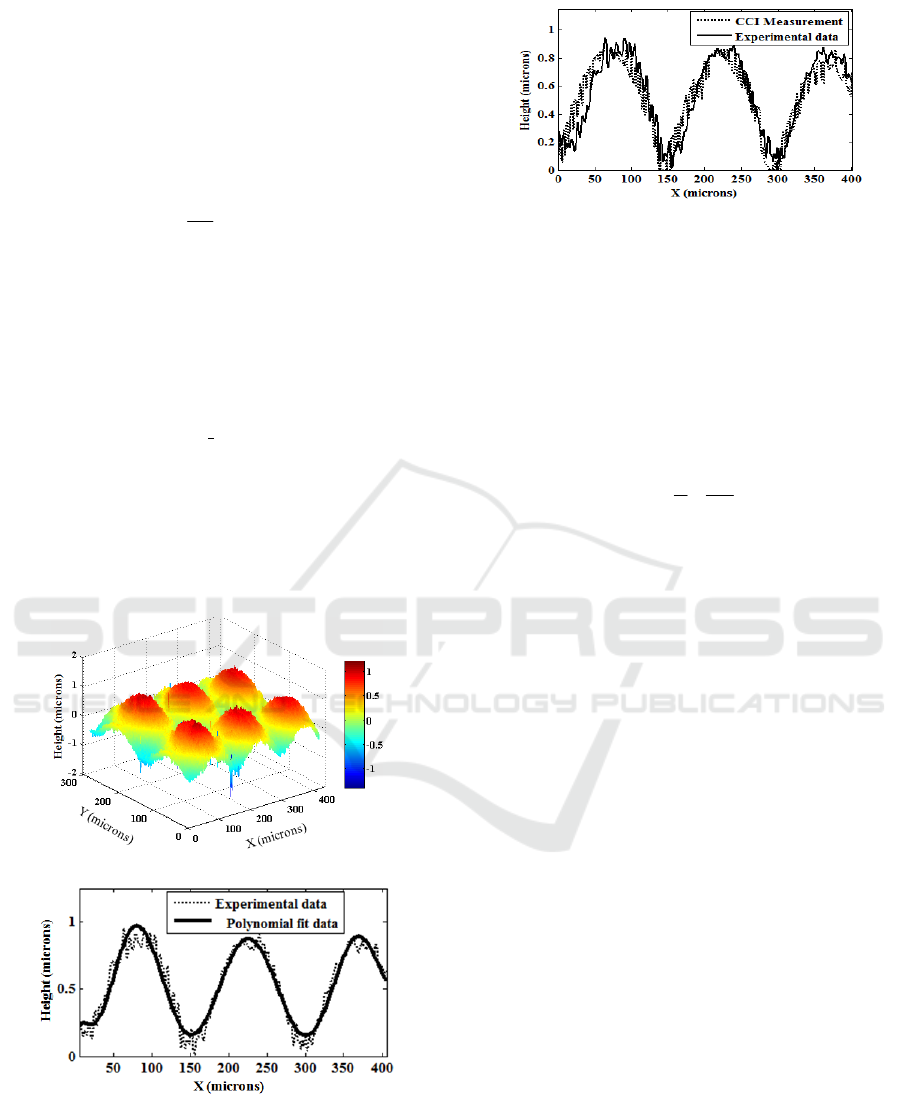
(8). Fig. 5(a) shows the 3D height map of the micro-

lenses array. Fig. 5(b) shows the height profile of

micro-lenses along the line AB as marked in Fig.

4(b).

(a)

(b)

Figure 5: (a) 3D height map of micro-lens Array (b)

Height profile of micro-lenses along the line AB as

marked in Fig. 4(b).

Figure 6: Comparison of height profiles of micro-lenses

array obtained by digital holographic interferometric

microscopy (DHIM) and Coherence Correlation

Interferometer.

The diameter of micro-lens in the micro-lenses

array is D=146 μm and experimentally evaluated

maximal height (sag) of micro-lens of micro-lens

array is h = 0.81 μm. From these values, the radius

of curvature (ROC) is computed according to

equation (Kühn et al., 2007).

ROC

(9)

The computed value of radius of curvature of the

micro-lens array is 3289.91 μm. The sag height of

micro-lens agrees well within the experimental limit

as provided in the specification by the manufacturer

(0.87 μm).

Height profile of micro-lenses measured by

DHIM is compared with commercially available

Coherence Correlation Interferometer

(Manufacturer: Taylor Hobson Ltd. UK, Axial

resolution 0.1 A

). Fig.6 shows the comparison of

height profiles of micro-lenses array obtained by

DHIM and Coherence Correlation Interferometer

(CCI). Root mean square error (RSME) between the

measurement done by DHIM and CCI is 0.12 %.

4 CONCLUSIONS

In this paper Mach- Zehnder based off- axis digital

holographic interferometric microscope (DHIM) is

applied to test the micro-lens array. In the

experiment, round shape and plano – convex micro

lens array supplied by THORLABS with micro lens

sag height (h=0.87 μm) and radius of curvature

(ROC=3.063 mm) was used. The measured value of

sag height (h=0.81 μm) and radius of curvature

(ROC=3.289 mm) of micro-lens array by using

DHIM and data supplied by manufacturer deviate by

0.6 μm (h=6.89 %) and ROC =7.4% respectively.

PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology

146

ACKNOWLEDGEMENTS

The financial assistance received from the Defence

Research and Development Organization (DRDO),

Ministry of Defence, Government of India, under the

project entitled ‘Testing of micro optics using digital

holographic interferometry’ is highly acknowledged.

REFERENCES

Sinzinger, S., and Jahns, J., (1999). Micro-optics. New

York: Wiley.

Anderson, R. H. (1997) Close-up imaging of documents

and displays with lens arrays, Appled Optics, 18 (4),

p. 477- 484.

Cormick, F. B. Mc., Tooley, F. A. P. , Cloonan, T. J.,

Sasian, J. M., Hinton, H. S., Merserau, K. O., and

Feldblum, A. Y. (1999) Optical interconnections using

microlens arrays. Optical and Quantum Electroics. 24

(4). p. S465-S477.

Hou, T., Zheng, C., Bai, S., Ma, Q., Bridges, D., Hu, A.,

and Duley, W. W. (2015) Fabrication,

characterization, and applications of microlenses.

Applied Optics. 54(24), p. 7366-7377.

www.suss-microoptics.com

Reichelt, S. and Zappe, H. (2005) Combined Twyman–

Green and Mach–Zehnder interferometer for

microlens testing. Applied Optics. 44(27), p. 5786-

5792.

Weible, K. J., Volkel, R., Eisner, M., Hoffmann, S.,

Scharf, T., and Herzig, H. P. (2004) Metrology of

refractive microlens arrays in Optical Micro- and

Nanometrology in Manufacturing Technology, Proc.

SPIE. 5458, p. 43–51.

Wahba, H. H., and Kreis, T. (2009) Characterization of

graded index optical fibers by digital holographic

interferometry. Applied Optics. 48 (8), p. 1573-1582.

Zhang, T., and Yamaguchi, I. (1998) Three-dimensional

microscopy with phase-shifting digital holography.

Optics Letter. 23(15), p. 1221-1223.

Charrière, F., Kühn, J., Colomb, T., Cuche, F. M., E.,

Emery, Y., Weible, K., Marquet, P., and Depeursinge,

C., (2006) Characterization of microlenses by digital

holographic microscopy. Applied Optics. 45(5), p.

829-835.

Schnars, U., and Jüptner, W., (1994) Direct recording of

holograms by a CCD target and numerical

reconstruction. Applied Optics. 33(2), p. 179–181.

Cuche, E., Marquet, P., and Depeursinge, C., (1999)

Simultaneous amplitude and quantitative phase-

contrast microscopy by numerical reconstruction of

Fresnel off-axis holograms. Applied optics. 38(34), p.

6994–7001.

Cuche, E., Bevilacqua, F. and Depeursinge, C., (1999)

Digital holography for quantitative phase-contrast

imaging. Optics Letter. 24(5), p. 291-293.

Schnars, U., and Jueptner, W. (2005) Digital Holography:

Digital Hologram Recording, Numerical

Reconstruction and Related Techniques. Berlin,

Germany: Springer-Verlag.

Anand, A., Chhaniwal, V. K., and Javidi, B., (2011),

Imaging embryonic stem cell dynamics using

quantitative 3-d digital holographic microscopy. IEEE

Photonics Journal. 3(3), p. 546-554.

Schnars, U. and Juptner, W. P. O. (2002) Digital

recording and numerical reconstruction of holograms.

Measurement Science and Technology. 13, p. R85–

R101.

Wagner, C., Seebacher, S., Osten, W., and Juptner, W.,

(1999) Digital recording and numerical reconstruction

of lensless Fourier holograms in optical metrology.

Appied Optics, 38(22), p. 4812– 4820.

Kumar, V., and Shakher, C, (2015) Study of heat

dissipation process from heat sink using lensless

Fourier transform digital holographic interferometry,

Applied Optics. 54 (6), p. 1257-1266.

Takeda,M., (1989) Spatial-carrier fringe-pattern analysis

and its applications to precision interferometry and

profilometry : an overview. Proc. SPIE. 1121. p. 73-

88.

Cuche, E., Marquet, P., and Depeursinge, C., (2000)

Spatial filtering for zero-order and twin-image

elimination in digital off-axis holography. Applied

Optics. 39(23), p. 4070-4075.

Goldstein, R. M., Zebker, H. A., and Werner, C., (1988)

Satellite radar interferometry: two-dimensional phase

unwrapping. Radio Science. 23(4), p. 713–720.

Kühn, J., Charrière, F., Colomb, T., Cuche, E., Emery, Y.,

and Depeursinge, C., (2007) Digital holographic

microscopy for nanometric quality control of micro-

optical components. Proc. of SPIE, 6475.

Testing of Micro-optics using Digital Holographic Interferometric Microscopy

147