
Model-driven Approach for Verifying Conformity of Models in the
Presence of Constraints
César Cuevas Cuesta, Patricia López Martínez and José M. Drake
Group of Software Engineering and Real-Time, University of Cantabria, Santander, Spain
Keywords: MDSE, Meta-model, OCL Constraint, Model Transformation, HOT, Verification.
Abstract: This paper presents a model-driven approach for the systematic development of tools for checking the
conformity of models when the domain formalization does not only consist of a meta-model but also on a set
of constraints enhancing it. The strategy is built on top of the idea of representing the result of the verification
as a model which gathers all the constraint violations found in the model, formulating them in a way that
allows their later detailed manifestation, automatic correction or any other potential processing. With that
aim, a meta-model for supporting those models describing constraints violations has been designed. The
verification is applied by means of an M2M transformation that takes as input the model to verify and
generates a model conforming to the designed meta-model. This methodology constitutes the way to
accomplish the final objective: designing a strategy for the development of a generic tool for verification,
regardless any particular meta-model or constraints set. This is performed through the duality of a model
transformation as a processing program but also as a processed artefact (model), by means of the Higher Order
Transformation (HOT) technique.
1 INTRODUCTION
When a domain formalization does not only consist of
a meta-model but also on a set of constraints defined
for it, the models conformity encompasses the basic
compliance to the meta-model as well as the
satisfaction of every constraint. This work focuses on
this second aspect, proposing to perform the
satisfaction verification by means of a completely
model-driven strategy, whose core idea is to apply an
M2M transformation to the model to verify. Hence,
the result of that verification is a new model, idea that
is in complete agreement with the MDE principle
(Schmidt, 2006) (Bézivin, 2005). The structure of
such output model is formalized by a meta-model
defined as part of the methodology. The approach,
although being dependent on the domain
formalization (meta-model and its associated
constraints), is able to support the systematic
development of specific verification tools, each one
suitable for a specific domain formalization.
The actual objective of this work is to design a
strategy for the development of a generic tool for
verification, suitable for any constraints set or even for
any meta-model. The functional foundation for
designing such a generic tool is that it will be based on
a tool generator for the on-the-fly creation of the
required specific tool.
Fig. 1 shows an overview of the proposed strategy,
which provides three assets that are applicable in any
application domain:
The ConstraintViolationDescription (CVD)
meta-model, which formalizes the structure of the
models obtained as result of the verification.
The ConstraintCharacterization (CC) meta-
model, defining mappings between constraints and
the way their violations must be formulated.
The tool generator that produces the specific
verification tools.
Figure 1: Proposed strategy overview.
Using this strategy within a specific domain im-
Cuesta, C., Martínez, P. and Drake, J.
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints.
DOI: 10.5220/0005744504550466
In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 455-466
ISBN: 978-989-758-168-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
455

plies that its formalization includes the definition of
constraints enhancing the domain meta-model, using
OCL clauses. Although OCL distinguishes several
types of constraints (invariants, pre- and post-
conditions, derivation rules, etc.), only invariants are
considered in this work. Thus, in the remainder of the
paper invariant and constraint will be used
indistinctly. In addition, the domain expert must
characterize every constraint, decorating its OCL
implementation with description data, including the
way in which its violations must be described. This is
achieved through a model compliant to the second
meta-model (CC) defined by the strategy. Last, when
the final user attempts to check a model, the
automatically generated tool is used.
Our output models do not only record which
constraints have been violated but also encapsulate the
data needed for describing those violations detected in
the checked model. With this purpose, a preliminary
and extensible meta-model for describing constraint
violations has been designed (CVD). Despite the
extensibility feature, its design aims to achieve a high
level of generality.
The rest of the paper is organized as follows.
Section 2 is devoted to related work that can be found
in the MDSE literature while Section 3 briefly
presents the need for specifying constraints for meta-
models. Section 4 describes the proposed approach for
the systematic development of verification tools,
ranging from the model-based representation of a
verification result to the meta-model supporting these
output models describing constraint violations. This
section also explains the way in which an M2M
strategy can support the approach. Section 5 exposes
the final goal of the work: a strategy for the
development of a generic tool for model verification.
Section 6 addresses the tool implementation using the
ATLAS Transformation Language (ATL). Section 7
presents an application example on top of the MAST2
meta-model. Section 8 ends giving some conclusions.
2 RELATED WORK
The widespread use of Eclipse/EMF (Steinberg et al.,
2009) as modelling platform demands to start this
section with Eclipse OCL. It is an implementation of
the OMG OCL 2.3 specification for use in conjunction
with EMF, allowing specification of constraints in
OCL and verification of models using conventional
EMF tooling. Eclipse OCL is completely trustworthy
for the detection of constraint violations, presenting in
an error dialog box the diagnostic messages created
during the process. However, it presents
expressiveness limitations since it only reports the
name of the violated constraint and the model element
where the violation has been located. Although the
constraint name could roughly indicate the essence of
the problem, in some scenarios another model
checking strategy providing a more verbose and
elaborated description of the problems including, for
example, severity information could be necessary.
Moreover, it could be desirable that the result of the
checking can participate as input in a number of
model-driven processes, depending on the specific
needs that every domain application might present.
Our proposal targets these requirements.
Addresing the verification issue through an M2M
transformation approach is not new. To the best of our
knowledge, it has already been outlined in (Bézivin
and Jouault, 2006) and applied in later works, like
(Diguet, 2009) and (Elaasar et al., 2011).
In Bézivin’s seminal work, applying M2M
transformation on the model to verify gives as result a
so called diagnostic model, compliant to a proposed
meta-model, called Problems. It is an extremely
simple meta-model, with a single class that defines
three attributes, namely severity, location and
description. The present work extends that core idea,
developing a much more ambitious strategy built on
top of a more complete target meta-model (CVD). In
addition, the authors only outline a pattern for
implementing manually the transformation
corresponding to each domain formalization. In
Diguet’s work, the author proposes a diagnosis meta-
model called VERIF and use ATL to implement an
M2M transformation for checking syntactic
correctness constraints on input MARTE models
(formal/2011-06-02: UML Profile for MARTE:
Modeling and Analysis of Real-time Embedded
Systems, v1.1. 2011) as a preleminary step in its main
transformation MARTE to AADL (Feiler et al., 2006).
However, although being more elaborated than the
Problems meta-model of Bezivin, the VERIF meta-
model is still quite simple and, again, the work only
focuses on a specific transformation for a specific
case, although it can be taken as a template. Our
proposal goes beyond these works by aiming at
providing a generic solution independen of the domain
formalization. This genericity is also claimed by the
third work aforementioned, which addresses the
detection of modeling problems through QVTr
transformations from input models (conforming to
any MOF-based meta-model) to result models
(conforming to the pResults meta-model) where
problem occurrences are reported in a structured and
concise manner.
A relatively close work, although following a dif-
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
456

ferent approach is (Oriol and Teniente 2014). The
authors propose a method for efficiently checking
OCL constraints by means of SQL. The core idea
consists in reducing the problem to check the
emptiness of SQL queries. Given an OCL constraint,
it is possible to build an SQL query that returns all
instances that violate it. Hence, the OCL constraint is
satisfied if and only if its corresponding SQL query
returns the empty set. Such queries are computed in an
incremental way by a relational DBMS.
An inspiring work for the design of the CVD meta-
model is (Miliauskaite and Nemuraite, 2005). In this
work, an exhaustive constraints taxonomy is proposed
in order to achieve well-formedness and good quality
of conceptual models. Our CVD meta-model is
slightly different oriented. It does not aim at revealing
types of constraints but at providing suitable
modelling of the data needed for describing
constraints violations, envisioning their later
manifestation or automatic treatment.
It should be remarked that the problem we
address, i.e. the verification of invariants satisfaction,
does not deal with the validation of the domain
formalization (meta-model + constraints) itself. In
this sense, when considering a set of invariants
specified on a domain meta-model, we suppose that
set to be perfectly valid, satisfying the typical
correctness properties: syntactic correctness, no
meta-model over-restriction or under-restriction,
consistency, independence, satisfiability, no
subsumption, no redundancy, etc. See (Delmas et al.,
2013) for a clear distinction between verification of
model instances vs. validation of domain
formalization design. In fact, there exists an important
amount of published research on the topic of
validation, like (Anastasakis et al., 2007; Cabot et al.,
2007; Pérez et al., 2012). However, this dimension is
out of the scope of our work.
3 LAX META-MODELS &
CONSTRAINTS DEFINITION
It is very difficult, almost impossible except for very
simple cases, that a meta-model formulation describes
every semantic detail of the target conceptual domain.
In such an ideal situation, every model instance of the
meta-model would correspond to a valid scenario
within the domain. However, meta-models are usually
formulated by only reflecting the big picture of the
modelled domain, not covering every detail. It leads to
laxities in the meta-models. Under this circumstance,
there can be models that, although compliant to the
lax-formulated meta-model, represent non-valid sce-
narios according to the semantics of the domain.
In addition to the practical impossibility of
describing every semantic detail of the domain, is
quite common to find meta-models formulated with a
degree of accuracy regarding the domain lower than
what could have been reached. This is due to several
reasons, as for example:
Preserving as Simple as Possible the Meta-
model Structure, in order to ease future
extensions and maintenance. If a meta-model is
designed to cover the semantics of the target
domain very deeply, a very complex internal
structure would be required, featured by a large
number of primitive types instead of the usual
ones (int, real, boolean, char, string, etc.) as well
as a very extend hierarchy of class inheritance,
aiming at specializing at maximum the possible
associations and their multiplicities.
Using a Single Meta-model to define models
that, since they participate in different processes,
must satisfy different sets of rules or constraints
depending on the concrete process. For instance,
when different tools in an environment enforce
specific constraints on the models, it may be better
to use a single meta-model according to the core
nature of the described system, enhanced with the
corresponding sets of constraints, instead of
defining a specialized meta-model for each tool.
As an example, Fig. 2 shows an overview of the
MAST environment for the analysis and design of
real-time systems, in which the verification methods
proposed in this work have been applied.
The environment is based on a meta-model, called
MAST-2 (Cuevas et al., 2012), used to describe the
timing behaviour of systems with real-time
requirements to fulfil. Currently, the meta-model
contains 126 classes and is lax-formulated. However,
a set of OCL-formulated constraints ensures that the
models used to describe the targeted real-time systems
correspond to valid scenarios. If the meta-model
would have been defined in order to strictly cover the
target domain, it would require a much more complex
structure with possibly a double number of modelling
classes.
In addition, the MAST environment is equipped
with several analysis and design tools that operate on
the models conforming to the MAST-2 meta-model.
Some of these tools, like the Simulation Tool shown in
Fig. 2, work on models that are simply required to
comply to MAST-2 and to meet its intrinsic
constraints. Other tools, like the Offset-Based
Schedulability Analysis Tool, can only work on
models that satisfy certain additional constraints.
Under a strategy of strict meta-modelling, the environ-
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints
457
ment would have to manage tens of meta-models (very
similar ones, but different), one for each available
analysis tool, as well as the corresponding
transformations between them. In contrast, using a lax
meta-model only requires to specify an appropriate list
of constraints for each environment tool.
Figure 2: The MAST-2 environment.
4 M2M-BASED MODEL
VERIFICATION
4.1 Verification Result in Model Form
The result of a verifying constraints satisfaction by a
model can adopt several different forms. As depicted
in Fig. 3, this work adopts the approach of
representing it as another model whose elements
correspond to violations of constraints occurred in the
verified model. This output model constitutes the base
for a possible manifestation of those violations,
allowing its management by tools in an MDE
environment. The information provided regarding the
detected violations can be as rich as set in a
hypothetical meta-model that the output model must
conform to.
The next subsection presents a meta-model for
these models, output of the verification process. It
defines the data required for describing, at higher or
lower level of detail, the detected violations and it
aims to cover the entire spectrum of constraints
violations that may appear in MDSE models.
4.2 The CVD Meta-model
The CVD (Constraint Violation Description) meta-
model constitutes an initial proposal of meta-model
for the models through which the result of verifying
other models is formulated. It provides a class
hierarchy oriented to the modelling of the data needed
for the description of constraints violations, the more
detail the more depth in the hierarchy.
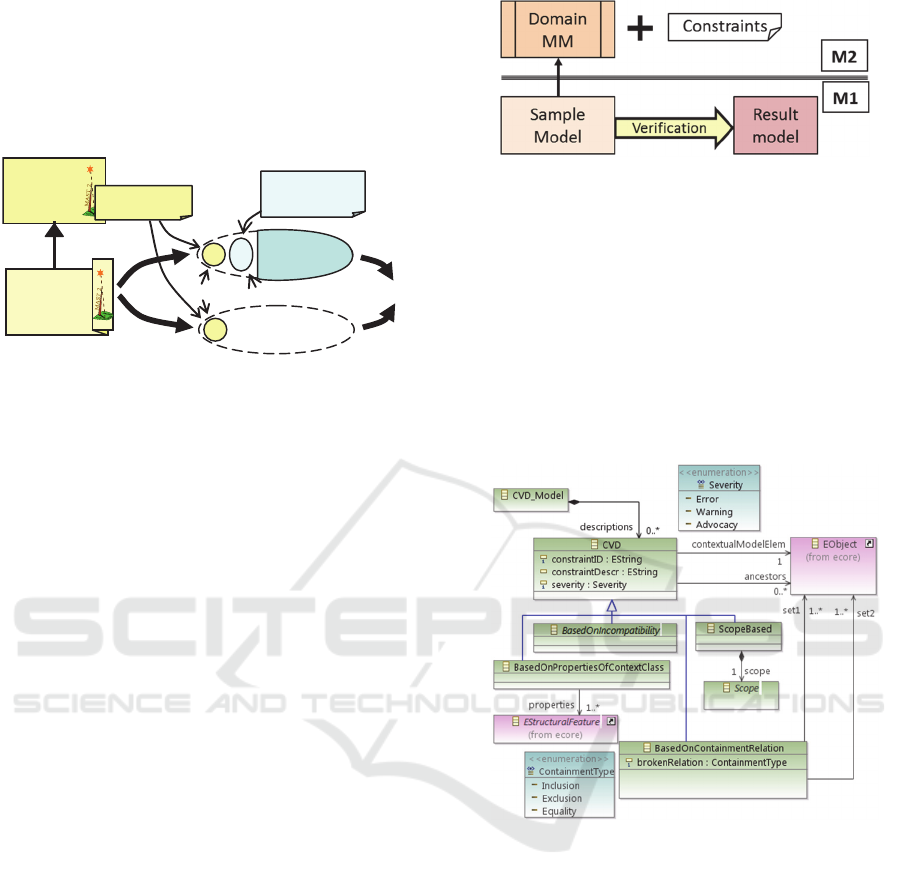
Figure 3: Model representation of verification result.
The CVD meta-model presents a conventional
structure, with a main container class (
CVD_Model
)
and a root class (
CVD
) from which the rest of the meta-
model classes inherit. Thus, a model compliant to
CVD has a single
CVD_Model
instance, which contains
through its
descriptions
association the rest of
model elements, instances of
CVD
or of any of its
subclasses. Fig. 4 shows both the
CVD_Model
and the
CVD
classes along with the top subclasses of the latter.
They are briefly exposed below:
Figure 4: CVD meta-model overview.
CVD
: This class models violations generically,
since it only has attributes for the constraint
identifier along with an optional textual
description and the severity assigned to the risen
problem. It also references the model element
where the violation has been located
(
contextualModelElem
) along with those others
that constitute the path from it towards the main
container of the model (
ancestors
).
Actually, this is sufficient for formulating as a
model the set of violations detected in another
model, since the described information is suitable
for any constraint, regardless its nature, semantics
or OCL formulation.
BasedOnPropertiesOfContextClass
: This class
extends
CVD
by including references to properties
Result
Mast2
S
y
stem model
Mast2
Metamodel
General Mast2
consistenc
y
rules
Offset-based
schedulability
consistency rules
Simulation
tool
Offset-based
schedulability
analysis
General verification
S
p
ecific verification
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
458
of the context class. Hence, it is suitable for
constraints specified on properties of its context
class.
BasedOnIncompatibility
: This class extends
CVD
by including references to model elements
(either two single ones, a single one and a set of
them or two sets, cases corresponding to the
subclasses
BoI_BetweenTwoModelElems
,
BoI_BetweenOneAndSet
and
BoI_BetweenTwoSets
, not shown in Fig. 4) which
can be reached from the contextual model element
through association chains. Hence, it is suitable
for constraints based on setting incompatibilities
between subclasses of two classes (typically
abstract) that are connected to the context class
through association chains.
BasedOnContainmentRelation
: This class
extends
CVD
by including references to two sets of
model elements, instances of the same class. It is
suitable for constraints based on setting a
containment relation between the populations
corresponding to endpoints of two association
chains starting from the context class.
ScopeBased
: This class extends
CVD
by indicating
a scope, i.e. a population of model elements. It is
suitable for constraints whose satisfaction
depends not only on the state of a model element
but also on its siblings within the scope in which
the first one is immersed.
Due to space reasons, the CVD meta-model is not
presented in its entirety. Its complete specification
and Ecore formulation can be found in
http://www.istr.unican.es/members/cesarcuevas/phd/
constraintsVerification.html.
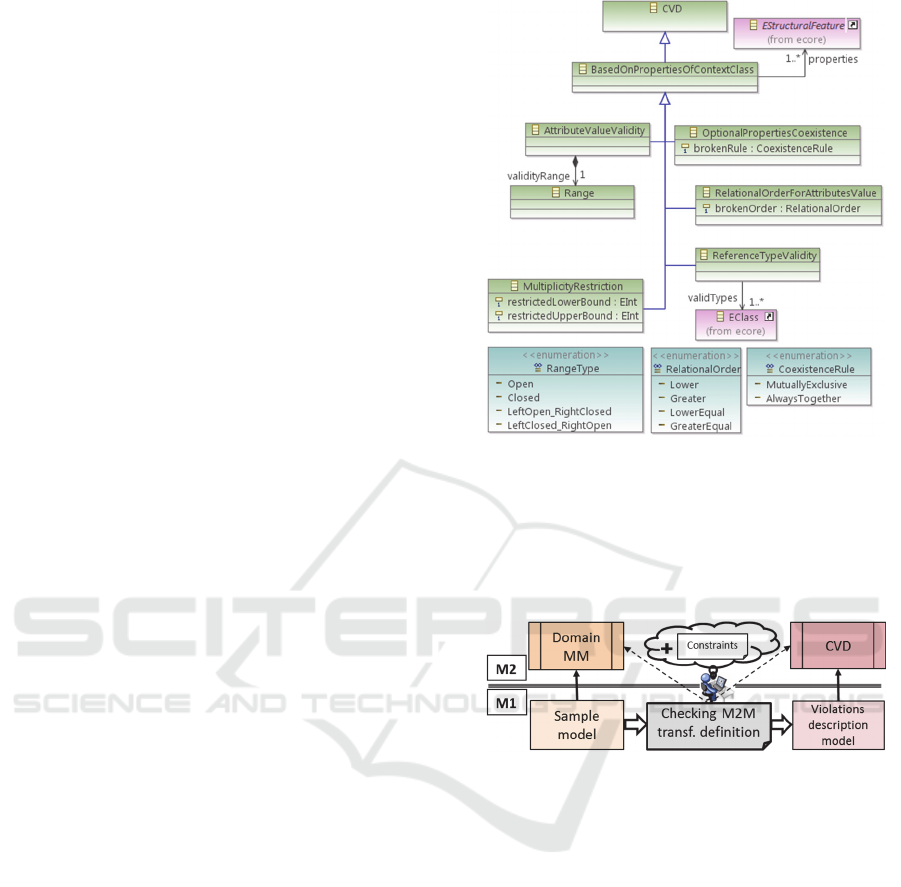
Nevertheless, in order to depict the class hierarchy
more in depth, Fig. 5 shows the subclasses of
BasedOnPropertiesOfContextClass
. The CVD
meta-model offers options for modelling violations of
constraints related to restrict the multiplicity of a
property, the validity range for the value of an
attribute or the valid types for a reference; or related
to impose rules about the coexistence of optional
properties or about the order that the numeric values
of a set of attributes must hold.
4.3 Overview as M2M Transformation
Representing the result of a model verification by
means of another model leads in a natural way to
contemplate the process as an M2M transformation,
defined between the meta-model of the model to be
verified and the meta-model that the result model must
conform to (in this case, the CVD meta-model).
Figure 5: BasedOnPropertiesOfContextClass
subclasses.
Thus, as depicted in Fig. 6, this checking M2M
transformation, when applied on a given model
(Sample model), generates as result the corresponding
model describing the constraints violations, if any.
Figure 6: Checking M2M transformation in action.
Like in any other M2M transformation, visibility
over the source and target meta-models (DomainMM
and CVD, respectively) is required (dotted arrows).
However, in this M2M strategy, the source meta-
model is constraints-naked, i.e. it is not required
neither including nor attaching the constraints to it. It
is enough that the developer knows them in order to
incorporate them to the checking transformation.
4.4 Extension of the Approach
So far, a methodology has been designed using a
strategy based on M2M transformations. This M2M-
based solution solves the addressed conformity
verification problem but without sidestepping the fact
that the strategy implies the development of a different
verification tool (implementation of a different
checking transformation) for every pair domain meta-
model + set of constraints. Fig. 7 shows this drawback.
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints
459
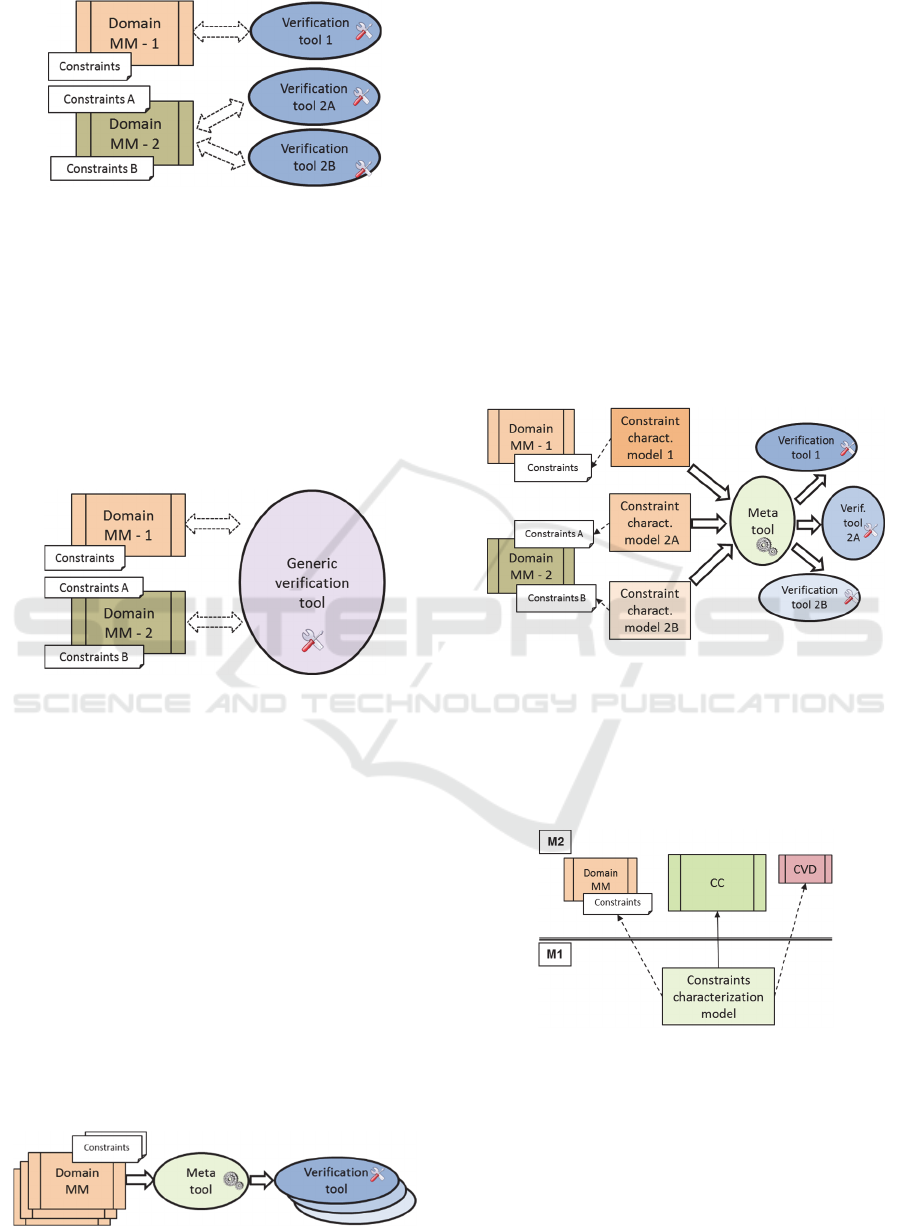
Figure 7: Specific verification tools.
Therefore, once that methodology for the
systematic (but manual) development of specific tools
for model verification has been set, it seems logic to
envision a step forward, a generic tool that could be
applied for the verification of models regardless their
meta-models and corresponding constraints, as shown
in Fig. 8. Thus, the design of a strategy that enables
the development of such a generic verification tool has
been accomplished. It is based on code generation, as
explained in the next section.
Figure 8: Generic verification tool.
5 GENERIC TOOL FOR MODEL
VERIFICATION
5.1 Foundation: Meta-tool for
Automating Tools Generation
Trying to abstract the infinite number of domain meta-
models that the Domain-Specific Language (DSL)
approach promotes, does not seem a suitable option
for creating a generic tool for verification. Hence, our
solution has been the development of a meta-tool for
the on-the-fly construction of the specific verification
tool corresponding to each case. Such a strategy, (Fig.
9), leads to the area of code generation, in this case the
code of a checking M2M transformation.
Figure 9: Meta-tool for generation of tools.
To perform this task, the meta-tool receives as
input the constraints along with the mapping between
each constraint and a CVD class, i.e. the way selected
to model their violations. More specifically, not only
information about what type of violation description
assigned to a constraint is required, but also
information relative to which domain meta-model
elements (typically attributes, associations or
association chains) are assigned to the properties of
the CVD instance. All of this information related to a
constraint (its own data – name, OCL expression and
context class – as well as mapping data) constitutes the
constraint characterization.
Thus, as shown in Fig. 10, our meta-tool for the
generation of ad-hoc verification tools accepts as input
the models encapsulating the set of characterizations
of the specified constraints.
Figure 10: Input models for the meta-tool.
In order to formalize the structure of these
characterization models, a meta-model has been
designed. It is called the ConstraintsCharacterization
(CC) meta-model and its role in the developed
scenario is shown in Fig. 11.
Figure 11: CC meta-model role.
The CC meta-model is exposed in the next
subsection. Later, in subsection 5.3, the design and
operational mode of the created meta-tool is analysed.
Since its purpose is the on-the-fly generation of every
specific tool for verification, the field of generation of
M2M transformations is naturally reached.
The elegance of the model-driven paradigm allows
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
460
the reutilization of the same transformation-based
infrastructure. This technique is known as Higher
Order Transformation (HOT) (Tisi et al., 2009), i.e. a
transformation that operates on transformations – in
this work, a transformation that generates a
transformation –. To achieve this objective, the
concept of M2M transformation needs to be extended
with that of transformation model, so that an M2M
transformation is represented by a model compliant to
the meta-model of the used model transformation
language (MTL).
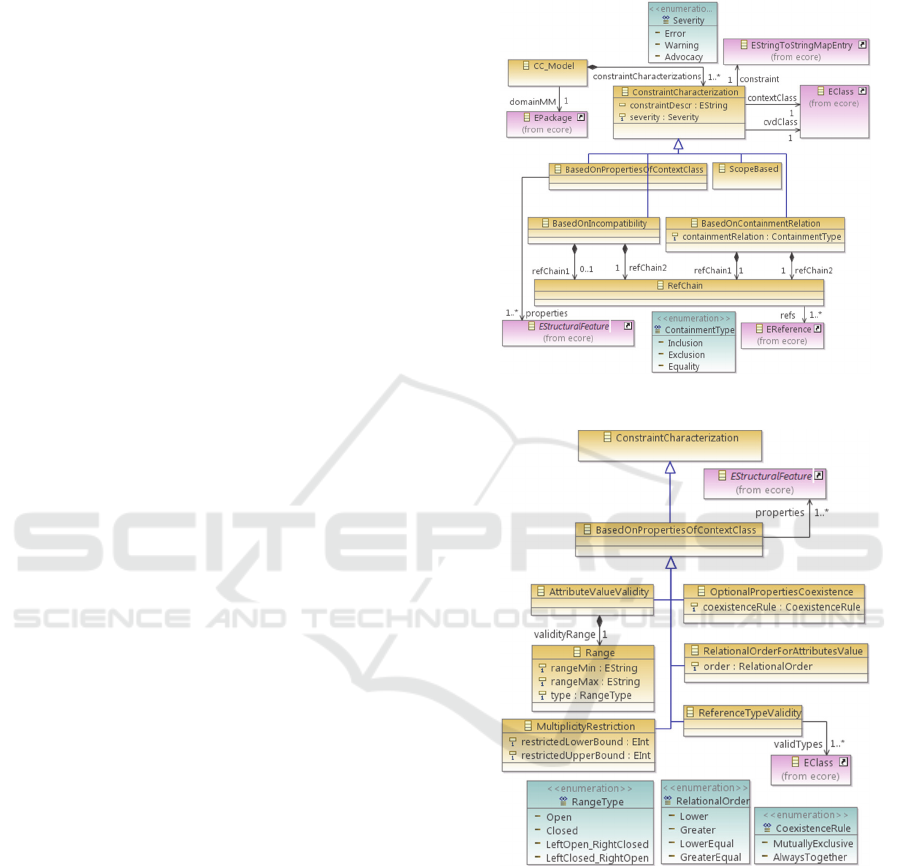
5.2 The CC Meta-model
The CC meta-model supports the models through
which the constraints specified on a domain meta-
model are characterized, in order to feed the meta-tool.
This meta-model presents a structure closely aligned
to the one of the CVD meta-model, even maintaining
name parity between counterpart classes wherever
possible. As CVD, it has a main container class
(
CC_Model
) and a root class (
CC
) from which the rest
of the meta-model classes inherit. A model compliant
to CC has a single
CC_Model
instance, which contains
through its
constraintCharacterizations
association the rest of model elements, instances of
CC
or of any of its subclasses. This main container
instance also references the domain meta-model (an
EPackage
instance in Ecore) enhanced with the set of
constraints to be characterized.
Fig. 12 shows the main container and root classes
of the meta-model along with the top-subclasses of the
latter. Briefly said, each of them is appropriate to
characterize constraints whose violations will be
described by the corresponding CVD counterpart
class. The mapping could also be established to a
superclass of the counterpart one, although this option
will lead to a loss of description information available
in the characterization. However, what is prohibited is
to establish a mapping to a subclass of the CVD
counterpart. In this case, a problem about inexistent
required information would arise when trying to
encode the generation of a violation description
instance during the automatic creation of the checking
M2M transformation.
Due to space reasons, the CC meta-model is not
presented in its entirety. Its complete specification
and Ecore formulation can be found in
http://www.istr.unican.es/members/cesarcuevas/phd/
constraintsVerification.html.
Nevertheless, in order to depict the class hierarchy
more in depth, Fig. 13 shows the subclasses of the
BasedOnPropertiesOfContextClass
. The meta-
model offers options for characterizing constraints
whose violations will be described by instances of the
CVD counterpart classes, hence showing the
alignment between both meta-models.
Figure 12: CC meta-model overview.
Figure 13: BasedOnPropertiesOfContextClass
subclasses.
5.3 HOT as the Core of the Meta-tool
In an M2M working context in which it is possible to
represent a transformation as a model – transformation
model–, a HOT can be defined as an M2M
transformation such that its input and/or output
models are themselves M2M transformations
(transformation models) (Bézivin et al., 2006). Hence,
HOTs take 0..n transformation models as input, produ-
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints
461
ce 0..n as output or both.
The HOT developed in this work responds to the
synthesis pattern (Tisi, Jouault et al. 2009). It can be
defined as the pattern corresponding to HOTs that
generate a transformation (model) from models that
do not represent transformations.
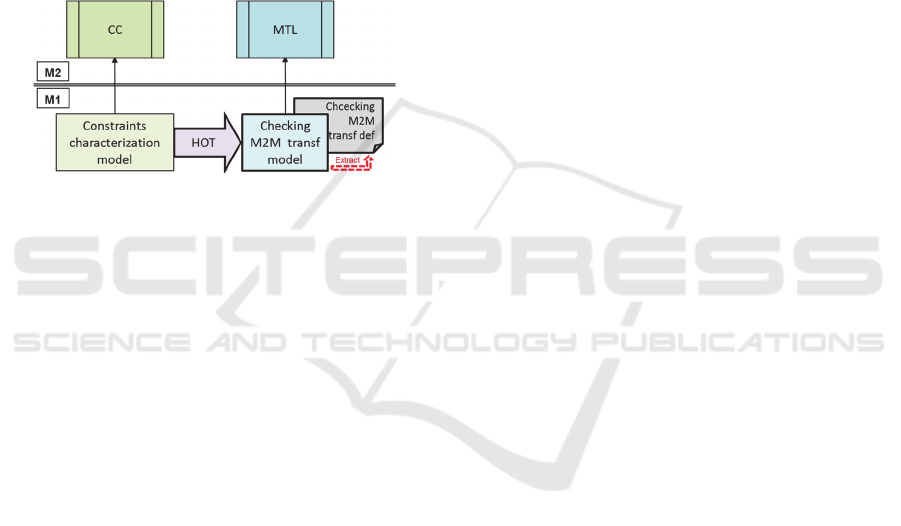
Here, as shown in Fig. 14, there is a single input
model for the HOT to accept, the constraints
characterization one, producing as output a model
compliant to the meta-model of the used MTL. This
output model is the checking M2M transformation
corresponding to the input constraints
characterization, specific to the domain meta-model +
constraints pair along with the mapping decisions
regarding how to model their possible violations.
Figure 14: HOT generates checking M2M transformation.
The final step is the serialization (extraction) of the
produced model in order to obtain the checking M2M
transformation encoded in the textual concrete syntax
of the MTL at hand.
6 ATL IMPLEMENTATION
The widespread ATL is the MTL chosen in this work
for implementing M2M transformations: the HOT and
consequently every generated M2M checking
transformation. ATL is the de facto standard for M2M
purposes, belonging to the AMMA platform (Bézivin
et al., 2005), a complete modelling infrastructure very
well integrated with Eclipse/EMF. ATL is very
suitable for developing HOTs because, although not
all M2M transformation frameworks provide a meta-
model formalizing the abstract syntax of the
transformation language, AMMA/ATL indeed does.
In addition, the meta-model incorporates the whole
OCL meta-model in order to write expressions for
filtering and manipulating models. Another interesting
feature is that the serialization of an ATL model to its
textual representation is also very well supported
through the technical projectors of AMMA.
The ATL code for the HOT at the heart of the
presented methodology as well as the ATL code of a
sample M2M checking transformation (the one
corresponding to the MAST-2 meta-model) can be
found at http://www.istr.unican.es/members/
cesarcuevas/phd/constraintsVerification.html. For
the M2M checking transformations, an
implementation style based on helpers and on called
rules has been selected. One of the main advantages of
this choice is that the resultant ATL code has a very
regular structure, following a uniform pattern easy to
automate. This structure is also properly documented
http://www.istr.unican.es/members/cesarcuevas/phd/
constraintsVerification.html.
7 USE CASE EXAMPLE
In order to illustrate the presented methodology, let’s
consider an example based on the MAST-2 meta-
model. Subsection 7.1 reflects the lax nature of this
meta-model formulation by exposing a selection of its
laxities. Subsection 7.2 addresses the CC model
corresponding to the characterization of the MAST-2
integrity constraints, from which the M2M checking
transformation specific for MAST-2 is generated. In
particular, it is shown the submodel corresponding to
the constraints selected in 7.1. Subsection 7.3
introduces a very tiny MAST-2 model which violates
those constraints. Finally, subsection 7.4 shows the
resultant CVD model produced when applying the
MAST-2 checking transformation to the sample
incoherent model.
7.1 The MAST-2 Lax Meta-model
The MAST-2 meta-model has a non-trivial size (126
classes) and it is lax-formulated, i.e. it presents
several tens of laxities of different nature. Hence, a
set of integrity constraints has been specified for it.
The complete documentation for these
laxities/constraints is accessible at
http://www.istr.unican.es/members/cesarcuevas/phd/
artifactsMAST2.html. Below, there is a reduced but
representative sample of such identified laxities,
along with the corresponding preventing constraints.
As shown in Fig. 15, the
Regular_Processor
class defines two integer-like attributes for describing
the managed interrupt priorities, namely
Max_Interrupt_Priority
and
Min_Interrupt_Priority
. Any compliant model
could present the incoherency of assigning a value for
the minimum greater than the maximum. Thus, an
integrity constraint (named “i_1_3_a”) has been
specified to prevent such an error. Its OCL
formulation is straightforward:
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
462

contextRegular_Processor
invi_1_3_a:
Max_Interrupt_Priority>=
Min_Interrupt_Priority
Figure 15: The Regular_Processor class formulation.
Fig. 15 also shows that the
Regular_Processor
class defines two references of
Timer
type, namely
Timer_List
and
System_Timer
. The first one
represents the set of timing objects associated with a
processor, if any, while the second one specifies the
main one. Hence, it must be part of the timer list, but
any MAST-2 compliant model could present the
incoherency of having processors specifying a system
timer among those ones in the model not listed by its
timer list. Thus, an integrity constraint (“i_3_1_a”)
has been specified to prevent such an incoherency. Its
OCL formulation is also pretty straightforward:
contextRegular_Processor
invi_3_1_a:
ifnotSystem_Timer.
oclIsUndefined()then
Timer_List‐>includes(System_Timer)
else
true
endif
Figure 16: Compatibility between policy and parameters.
Finally, Fig. 16 shows that both the
Scheduler
and
Schedulable_Resource
classes have their
Policy
and
Scheduling_Parameters
references
defined in terms of the abstract classes
Scheduling_Policy
and
Scheduling_Parameters
.
This allows the assignment of any concrete type
of policy or parameters, but an inconsistency may
arise when associating a scheduler and a schedulable
resource, since the corresponding policy and
scheduling parameters objects may be incompatible
(the compatibilities are shown by green lines in the
figure).
Consequently, a preventing constraint (i_3_4_a)
has been defined, setting the appropriate
correspondences. Its OCL code appears below:
contextSchedulable_Resource
invi_3_4_a:
self.Scheduling_Parameters.
oclIsKindOf(Priority_Based_Params)
and
self.Scheduler.Policy.
oclIsTypeOf(Fixed_Priority_Policy)
or
self.Scheduling_Parameters.
oclIsKindOf(Priority_Based_Params)
and
self.Scheduler.Policy.
oclIsTypeOf(FP_Packet_Based_Policy)
or
self.Scheduling_Parameters.
oclIsKindOf(Interrupt_Based_Params)
and
self.Scheduler.Policy.
oclIsTypeOf(Fixed_Priority_Policy)
or
self.Scheduling_Parameters.
oclIsKindOf(EDF_Based_Params)
and
self.Scheduler.Policy.
oclIsTypeOf(EDF_Policy
7.2 CC Model
For the generation of the checking M2M
transformation applicable to MAST-2 models, it is
necessary to feed the meta-tool with a CC model that
encapsulates the characterization of the MAST-2 set
of integrity constraints. The subset of that model for
the three sample constraints considered above is
depicted in Fig. 17.
The first constraint (“i_1_3_a”) is characterized
through an instance of the CC class
RelationalOrderForAttributes‐Value
,
referencing the constraint at hand along with its
context class as well as the CVD class selected for
describing any possible violation. The severity to
be associated and other specific information
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints
463
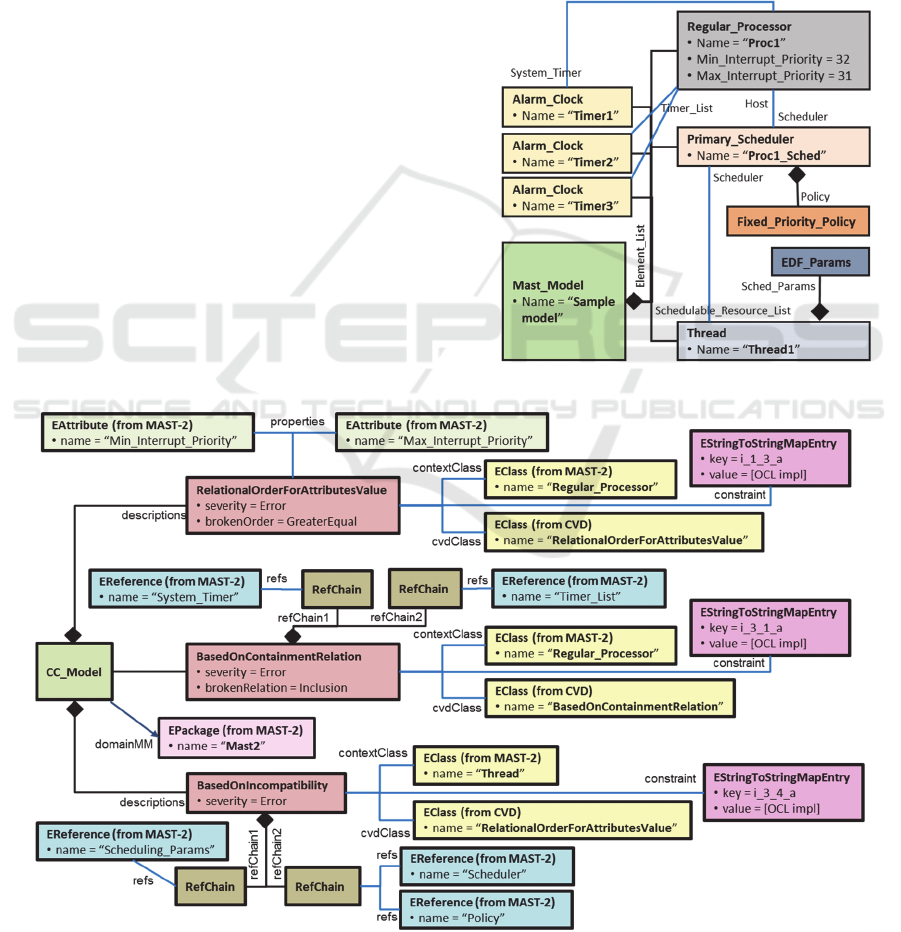
required by the concrete characterization class are
also formulated. In this case, it applies for the
attributes involved in the constraint and the
relational order to be respected. The second
constraint (“i_3_1_a”) is characterized through an
instance of the CC class
BasedOnContainmentRelation
.
The second constraint (“i_3_1_a”) is
characterized through an instance of the CC class
BasedOnContainmentRelation
.
The third constraint (“i_3_4_a”) is characterized
through an instance of the CC class
BasedOnIncompatibility
. The constraint
characterization specifies association chains
indicating how to reach the potentially
incompatible model elements from the contextual
one.
It is worth remarking that, when applying the
strategy, the CC model must be formulated only once,
just like the domain meta-model itself, to generate the
corresponding M2M checking transformation, which
will be later used with any model compliant with the
domain meta-model.
7.3 MAST-2 Sample Model
The MAST-2 sample model for illustration purpose is
partially shown in Fig. 18. It violates the three
constraints presented above.
The model consists of a mono-processor platform
with fixed-priority scheduling policy. The platform is
modelled by the processor Proc1 with its hosted
scheduler (Proc1_Sched) along with its scheduling
policy object. The platform submodel also
encompasses the timers associated to the processor. A
schedulable resource (Thread1), which is part of the
reactive section of the model (not depicted), along
with its scheduling parameters object, and scheduled
by the only existing scheduler, completes this partial
visualization of the model. Its constraints violations
can be seen at a glance.
Figure 18: A sample MAST-2 model (partially shown).
Figure 17: Subset of the CC model for the MAST-2 constraints.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
464

7.4 CVD Model
When applying the checking M2M transformation for
MAST-2 (obtained from the CC model partially
presented in section 7.2) to this MAST-2 sample
model, a CVD model is produced as result, shown in
Fig 19. As it can be observed, each constraint
violation has produced a corresponding description
object:
For the interrupt priorities inconsistency, i.e., the
violation of the i_1_3_a constraint, an instance of
the CVD class
RelationalOrderForAttributesValue
is
generated. As expected, it formulates the ID of the
violated constraint, the severity assigned to the
risen problem and the contextual model element
where the violation is located, as well as the
properties involved in the constraint (the
attributes
Max_Interrupt_Priority
and
Min_Interrupt_Priority
) and the relational
order that has been broken (max ≥ min).
For the timers inconsistency, i.e., the violation of
the i_3_1_a constraint, an instance of the CVD
class
BasedOnContainmentRelation
is
generated.
For the violation of the i_3_4_a constraint, an
instance of the CVD class
BoI_BetweenTwoModelElems
(subclass of
BasedOnIncompatibility,
not exposed in
section 4.3) is generated. This subclass basically
describes the violation of an incompatibility-
based constraint, and in addition to the basic
features (
constraintID
and
severity
attributes
along with the
contextualModelElem
reference),
it points out the two incompatible model elements
(
modelElem1
,
modelElem2
), in this case the
EDF_Params
and
Fixed_Priority_Policy
instances.
8 CONCLUSIONS
This paper has exposed part of the work accomplished
by our research group in order to develop a complete
model-driven strategy and infrastructure for the
development of real-time (RT) applications. The asset
at the core of this effort is the MAST-2 meta-model
for modelling RT systems. As a lax meta-model, a set
of constraints has been specified for it and in addition,
the different analysis and design tools of the overall
MAST environment require specific conditions for the
models to be processed. This paper focuses on the
development of a mechanism for checking invariants
satisfaction that can be invoked by these tools to
alleviate their implementation, since they do not
require implementing a preliminary verification step
The approach for the development of such verification
mechanism is based on the representation of the
verification result as a model generated by means of
an M2M transformation. In order to be a generic
verification tool, regardless the domain meta-model or
particular set of constraints, a HOT has been
implemented for the on-the-fly generation of the
required specific checking transformation. The
developed meta-models needed to support this model-
driven approach have been presented.
Figure 19: Resultant CVD model.
Model-driven Approach for Verifying Conformity of Models in the Presence of Constraints
465

ACKNOWLEDGEMENTS
This work has been partially funded by the Spanish
Government and FEDER funds, with references
TIN2011-28567-C03-02 (HI-PARTES) and
TIN2014-56158-C4-2-P (M2C2).
REFERENCES
formal/2011-06-02: UML Profile for MARTE: Modeling
and Analysis of Real-time Embedded Systems, v1.1.
2011.
Anastasakis, K., Bordbar, B., Georg, G. and Ray, I., 2007.
UML2Alloy: A Challenging Model Transformation.
Model Driven Engineering Languages and Systems.
Springer, pp. 436-450.
Bézivin, J., 2005. On the unification power of models.
Software and Systems Modeling, 4(2), pp. 171-188.
Bézivin, J., Büttner, F., Gogolla, M., Jouault, F., Kurtev, I.
and Lindow, A., 2006. Model transformations?
Transformation models! Model Driven Engineering
Languages and Systems, pp. 440-453.
Bézivin, J. and Jouault, F., 2006. Using ATL for checking
models. Electronic Notes in Theoretical Computer
Science, 152, pp. 69-81.
Bézivin, J., Jouault, F. and Touzet, D., 2005. An
introduction to the ATLAS Model Management
Architecture. Research Report LINA,(05-01), .
Cabot, J., Clarisó, R. and Riera, D., 2007. UMLtoCSP: a
tool for the formal verification of UML/OCL models
using constraint programming, Proceedings of the
twenty-second IEEE/ACM international conference on
Automated software engineering 2007, ACM, pp. 547-
548.
Cuevas, C., Drake, J. M., López Martínez, P., Gutiérrez
García, J. J., González Harbour, M., Medina, J. L. and
Palencia, J. C., 2012. MAST 2 Metamodel.
Delmas, R., Pires, A.F. and Polacsek, T., 2013. A
Verification and Validation process for Model Driven
Engineering, Progress in Flight dynamics, guidance,
navigation, control, fault detection, and avionics 2013,
EDP Sciences, pp. 455-468.
Diguet, J.L., 2009. Checking syntactic constraints on
models using ATL model transformations. Model
Transformation with ATL, pp. 140.
Elaasar, M., Briand, L. and LABICHE, Y., 2011. Domain-
Specific Model Verification with QVT. Modelling
Foundations and Applications. Springer, pp. 282-298.
Feiler, P. H., Gluch, D. P. and Hudak, J. J., 2006. The
architecture analysis & design language (AADL): An
introduction. The architecture analysis & design
language (AADL): An introduction, .
Miliauskaite, E. and Nemuraite, L., 2005. Taxonomy of
integrity constraints in conceptual models, IADIS
Virtual Multi Conference on Computer Science and
Information Systems 2005.
Oriol, X. and Teniente, E., 2014. Incremental Checking of
OCL Constraints through SQL Queries, CEUR
Workshop Proceedings 2014, pp. 23-32.
Pérez, C. A. G., Buettner, F., Clarisó, R. and Cabot, J.,
2012. EMFtoCSP: A Tool for the Lightweight
Verification of EMF Models, Formal Methods in
Software Engineering: Rigorous and Agile Approaches
(FormSERA) 2012.
Schmidt, D. C., 2006. Guest editor's introduction: Model-
Driven Engineering. Computer, 39(2), pp. 25-31.
Steinberg, D., Budinsky, F., Paternostro, M. and Merks, E.,
2009. EMF: Eclipse Modeling Framework. 2nd edn.
Addison-Wesley Longman, Amsterdam, 2nd revised
edition (rev). edition.
Tisi, M., Jouault, F., Fraternali, P., Ceri, S. and Bézivin, J.,
2009. On the Use of Higher-Order Model
Transformations, Model Driven Architecture-
Foundations and Applications 2009, Springer, pp. 18-
33.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
466
