
An Intelligent Speckle Reduction Algorithm for Optical Coherence
Tomography Images
Saba Adabi
1,2
, Silvia Conforto
2
, Anne Clayton
1
, Adrian G. Podoleanu
3
, Ali Hojjat
4
and Mohammad R. N. Avanaki
1
1
Wayne State University, Department of Biomedical Engineering, 818W Hancock St, Detroit, U.S.A.
2
Roma Tre University, Department of Applied Electronics, Via V. Volterra 62, Rome, Italy
3
University of Kent, Applied Optics Group, CT2 7PD, Canterbury, U.K.
4
University of Kent, School of Physical Sciences, CT2 7NH, Canterbury, U.K.
Keywords: Optical Coherence Tomography, Multi-Layer Perceptron (MLP), Speckle Noise Reduction, Artificial Neural
Network (ANN).
Abstract: Optical Coherence Tomography (OCT) offers three dimensional images of tissue microstructures. Although
OCT imaging offers a promising high resolution method, due to the low coherent light source used in the
configuration of OCT, OCT images suffers from an artefact called, speckle. Speckle deteriorates the image
quality and effects image analysis algorithm such as segmentation and pattern recognition. We present a novel
and intelligent speckle reduction algorithm to reduce speckle based on an ensemble framework of Multi-Layer
Perceptron (MLP) neural networks. We tested the algorithm on images of retina obtained from a spectrometer-
based Fourier-domain OCT system operating at 890 nm, and observed considerable improvement in the
signal-to-noise ratio and contrast of the images.
1 INTRODUCTION
Optical coherence tomography (OCT) is an advanced
high resolution, non-invasive imaging modality
which can be used to deliver three-dimensional (3D)
images from microstructures within a tissue. As with
other imaging modalities that employ coherent
detection, OCT images are confounded by speckle
(Podoleanu, 2014) (Goodman, 2007). In an optical
imaging system, speckle imposes a grainy texture on
images and decreases their signal-to-noise ratio
(SNR) and their contrast-to-noise ratio (CNR).
Consequently, speckle reduces the performance of
image segmentation and pattern recognition
algorithms that are used to extract, analyse, and
recognize diagnostically relevant features.
Development of successful speckle noise reduction
algorithms for OCT is particularly challenging. The
reason is that OCT speckle also carries structural
information about the imaged object. A number of
speckle reduction methods for OCT images have been
developed using hardware modifications such as
frequency compounding, shifting the focal plane of
the probe beam, and angular compounding (Shankar,
1986) (Avanaki et al., 2013b). Besides the hardware
modifications, a number of image processing
algorithms have been reported such as adaptive
digital filters, filters based on interval type II fuzzy
algorithm, wavelet transformation with various
configurations, or the use of median, averaging,
Kuwahara filters and their combinations (Goodman,
2007) (Ozcan et al., 2007). We previously introduced
an artificial neural network based (ANN) method for
speckle reduction (Avanaki et al., 2008, Avanaki et
al., 2013a). In that study, we modelled the speckle
using a Rayleigh distribution with a single noise
parameter, sigma, for the entire image. This
parameter is estimated by the ANN. The algorithm
was tested successfully on OCT images of Drosophila
larvae, however we think it has the potential to have
better efficiency. In this paper, we present a new
scheme, in which the image is segmented into several
sections. We also use a new ensemble framework
which is a combination of networks. The noise
parameter is then estimated using the MLP neural
networks for different segments. Using these steps
and a numerical method, the segments, and
consequently the image is denoised. Further
40
Adabi, S., Conforto, S., Clayton, A., Podoleanu, A., Hojjat, A. and Avanaki, M.
An Intelligent Speckle Reduction Algorithm for Optical Coherence Tomography Images.
DOI: 10.5220/0005744700380043
In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2016), pages 40-45
ISBN: 978-989-758-174-8
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
processing was performed to eliminate the blocking
artefact.
2 METHODOLOGY
2.1 OCT Image Acquisition
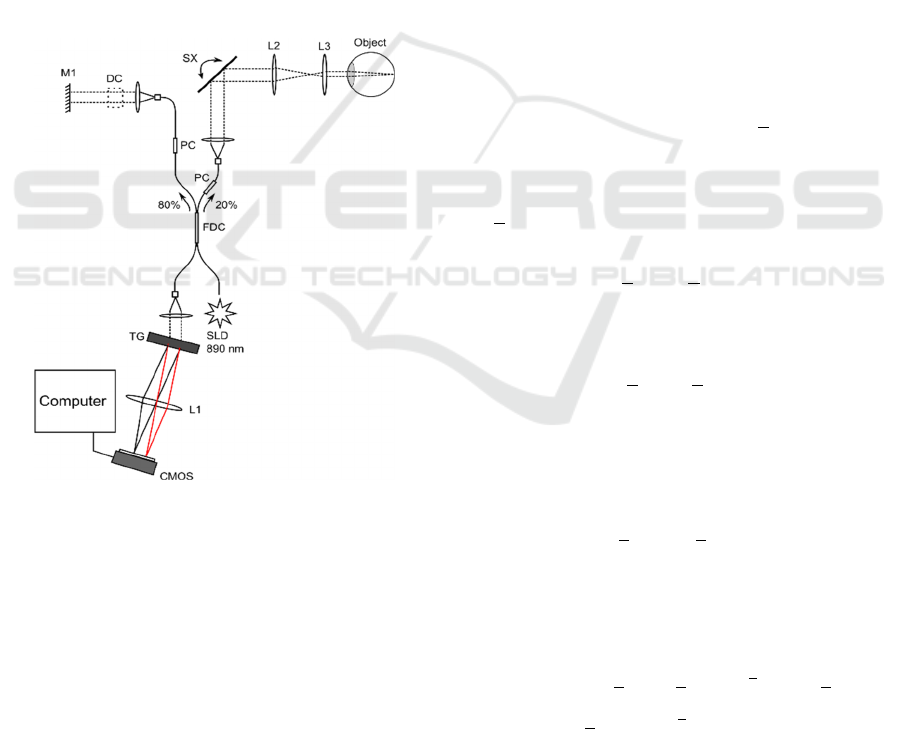
The spectrometer-based Fourier-domain OCT system
used to generate the retinal images is schematically
presented in figure 1. Light from a low coherence
source (two spectrally-shifted super-luminescent
diodes (SLDs), with a central wavelength λ
0
= 890 nm
and linewidth Δλ = 150 nm – Superlum Broadlighter
D890) is directed to the two interferometer's arms via
a fiber-based directional coupler (FDC). The object
arm comprises a galvo-scanning mirror (SX) and an
f-2f-f lens arrangement specifically devised for
retinal imaging.
Figure 1: Spectrometer-based Fourier-domain optical
coherence tomography system. SLD: super-luminescent
diode with a central wavelength λ0 = 890 nm and linewidth
Δλ = 150 nm, L1-L3: Achromatic Lenses, CMOS: Linear
pixel array (line camera), SX: galvo-scanning mirror, TG:
diffraction grating, M1: flat mirror, PC: polarization
controller, FDC: 80/20 fused fiber directional coupler, DC:
dispersion compensating element.
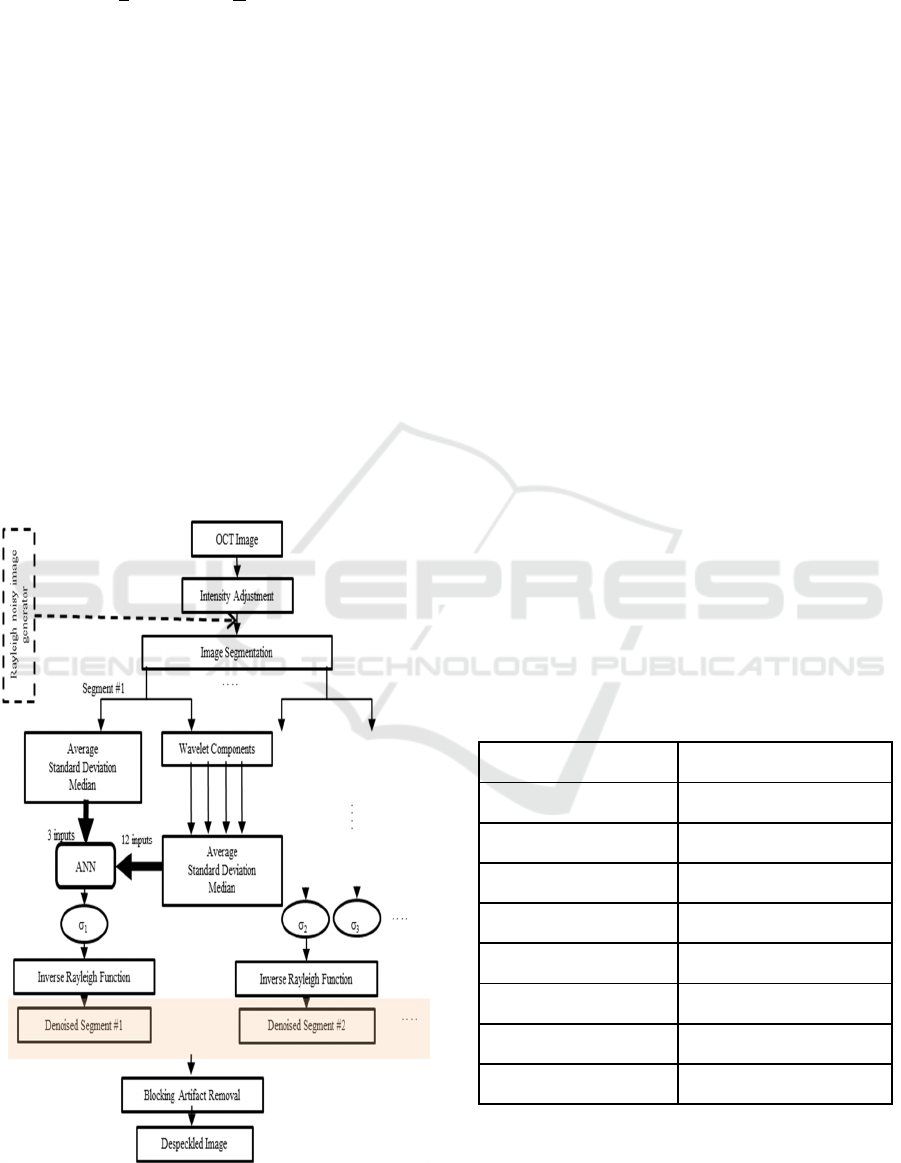
2.2 Speckle Reduction Algorithm
The algorithm we propose is composed of two phases.
The first phase is the training phase. Using a Rayleigh
noisy image generator in MATLAB, 10×10 pixels
images were generated with sigma values (the single
noise parameter employed in the Rayleigh function)
ranging from 0 to 255 in steps of 0.05. For each sigma
value, this procedure was repeated 100 times to
generate numerous noisy images for training.
Three features - average, standard deviation, and
median - were calculated from each segment and its
wavelet sub-bands for training. Wavelet sub-band
images were used to calculate the frequency domain
statistical knowledge of the image. The neural
network used is a combination of several MLP neural
networks. The flow chart of algorithm is given in
figure.2. Three MLP networks and a combiner, which
is responsible for the averaging process, are the main
components of this framework. Each of the MLP
networks is composed of 15 neurons in its input layer,
10 neurons in its hidden layer and one output neuron
to estimate the sigma parameter. The combiner is
responsible for averaging with L neurons in input
layer, L neurons in hidden layer and one output
neuron which can estimate the sigma parameter in an
ensemble fashion (in this paper, L = 3). To show the
advantage of ensemble method over individual neural
networks, let us consider a number of trained MLP
neural networks L with outputs
(where x is an
input vector). These estimate the sigma values using
the i
th
MLP neural network with an error of e
i
with
respect to the desired value of the sigma parameter,
. In this situation, the following equation can be
written as:
(1)
Thus the sum of squared error for the network y
i
can be calculated using eq. (2):
(2)
where [.] denotes the expectation (average or
mean value). Thus the average error for the MLP
networks acting individually can be calculated by eq.
(3).
1
1
(3)
By averaging the outputs
, the committee
prediction is obtained. This estimate will have an
error equal to (eq. (4)):
∑
∑
(4)
Thus, using the Cauchy’s inequality which is
shown in eq. (5), one can show that E
COM
≤ E
AV.
An Intelligent Speckle Reduction Algorithm for Optical Coherence Tomography Images
41
1
1
(5)
The neural network delivered the highest
reliability in the estimation of the sigma value when
a Daubechies 4 (db4) mother function was used.
There are a total of 12 inputs to the neural network.
The transfer function, performance function, learning
function, network size, and number of hidden layers,
were chosen experimentally such that optimum
network reliability is achieved. Such reliability is
defined as the percentage ratio of the difference
between the expected sigma value and the estimated
sigma over the expected sigma value. The averaged
reliability of the sigma estimator network measured
over 20 runs was 99.3 percent that was greater than
our previous ANN that had a reliability of 98.8
percent. The second phase is the testing phase. As
shown in the de-speckling flowchart in figure 2, the
OCT image is initially divided into several segments
based on the homogeneity. Similar to the training
stage, the same pre-processing was applied to each
image, and then the statistical features were extracted
Figure 2: Schematic diagram of the despeckling algorithm.
The blocks in the dotted box are used in the training phase.
from each segment in the image and used as input for
the neural network. The Rayleigh noise parameter
was then estimated for each segment using the trained
network (Avanaki and Hojjatoleslami, 2009). The
estimated sigma is then used along with a numerical
method to solve the inverse Rayleigh function
numerically for each segment. Putting together the
noise model segments, we can generate a noise model
image. The noise model image was deducted from the
original image with a scale factor which was obtained
experimentally. To remove the blocking artifact,
following the method given in (Fitzpatrick, 1975),
some statistical features were extracted from the
original image, based upon which of the despeckled
segments are then stitched together.
3 RESULTS AND DISCUSSION
B-scan OCT images of eye (in-vivo) were used to test
the algorithm. The OCT images before and after de-
speckling algorithm are shown in figure 3. The
number of segments in each image affects the
despeckling efficiency. To improve edge sharpness
and have more effective blocking artifact removal, we
segment our images into eight sub images. The
estimated sigma values for the segments within the
images are given in table 1, table 2 and table 3
corresponded to figure. 3, figure.4, figure.5
respectively.
Table 1: The estimated sigma values for figure. 3, The
number of segments are 8 (4 segments in each row).
Segment # Sigma
1 112
2 56
3 21
4 41
5 131
6 145
7 162
8 143
To evaluate the improvement of the images after
de-speckling, we calculated the signal-to-noise ratio
and the contrast-to-noise ratio (CNR) as defined in
eq. (6) and eq.(7) respectively (Shankar, 1986).
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
42

⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
2
2
10
)(max
log10
b
I
SNR
σ
(6)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
∑
=
R
r
br
br
R
CNR
1
22
)(1
σσ
μμ
(7)
where max(I
2
) represents the maximum of
squared intensity pixel values in a homogeneous
region of interest in the linear magnitude image,
where
b
μ
and
2
b
σ
and CNR represents the mean,
variance of the same background noise region, and
r
μ
and
2
r
σ
represents the mean and variance of the R
region of interest (Shankar, 1986).
Table 2: The estimated sigma values for figure. 4, The
number of segments are 8 (4 segments in each row).
Segment # Sigma
1 98
2 64
3 51
4 45
5 68
6 20
7 39
8 81
Table 3: The estimated sigma values for figure. 5, The
number of segments are 8 (4 segments in each row).
Segment # Sigma
1 75
2 64
3 56
4 68
5 28
6 30
7 27
8 19
In-line with other published work (Shankar,
1986), we used 5 regions (R=5) in the calculation of
CNR. The results of these calculations on three test
images are given in Table 2. We compared the
performance of the proposed method in this article
with some other existing methods (see figure 3, figure
4 ad figure 5). We observed a blurring artifact in the
averaged image, as well as in the median filtered
image that was not observed in the denoised image
using our proposed method. It was also perceived that
the median filtered image is more pronounced in
terms of image contrast. The quantitative assessments
of the despeckled image showed in figure.3, figure.4
and figure.5 demonstrated that the proposed method
can provide an extra enhancement.
Figure 3: Comparative presentation of six despeckling
methods on an original OCT test images acquired from the
retina (optic nerve region) of a volunteer (AP), white male,
provided by Adrian Podoleanu’s lab. (a) Original B-scan
image of optic nerve, lateral size ~ 1-1.2 mm, (b) the B-scan
image after average filtering (window size: 3), (c) the B-
scan image after median filtering (window size: 3), (d), the
B-scan image after wiener filtering (window size: 3), (e) the
B-scan image after Kuwahara filtering (window size: 5), (f)
the B-scan image after SNN filtering (window size: 3), (g)
the B-scan image after using the proposed method.
(g)
(a)
(b)
(c)
(d)
(e)
(f)
An Intelligent Speckle Reduction Algorithm for Optical Coherence Tomography Images
43

of around 8 dB and 0.6 in terms of SNR and CNR
respectively compared to their counterparts in
averaging and median filtering Moreover, the
proposed method surpassed both Symmetric Nearest
Neighbourhood and Winner noise reduction filters by
increment of around 3dB in terms of SNR. However
in case of CNR a difference of 0.2 is observed.
Kuwahara filtered image has a SNR of 4dB and CNR
of 0.1 less than filtered image using proposed method
is depicted in figure.6. It should be noted that this fast
real-time effective algorithm could be enhanced by
utilizing a more accurate estimation of sigma
employing an improved version of ANN and using a
Figure 4: Comparative presentation of six despeckling
methods on an original OCT test images acquired from the
retina (optic nerve region) of a volunteer (AB-fovea), white
male (a) Original B-scan image of optic nerve,(b) the B-
scan image after average filtering (window size: 3), (c) the
B-scan image after median filtering (window size: 3), (d)
the B-scan image after wiener filtering (window size: 3), (e)
the B-scan image after Kuwahara filtering (window size: 5),
(f) the B-scan image after SNN filtering (window size: 3),
(g) the B-scan image after using the proposed method.
more precise valuation of noise model
mathematically. Moreover a possible improvement
can be achieved referring to image segments. A future
study planned to cover those issues.
Figure 5: Comparative presentation of six despeckling
methods on an original OCT test images acquired from the
retina (optic nerve region) of a volunteer (AB-fovea), white
male (a) Original B-scan image of optic nerve, (b) the B-
scan image after average filtering (window size: 3), (c) the
B-scan image after median filtering (window size: 3), (d)
the B-scan image after wiener filtering (window size: 3), (e)
the B-scan image after Kuwahara filtering (window size: 5),
(f) the B-scan image after SNN filtering (window size: 3),
(g) the B-scan image after using the proposed method. The
vertical axis is z-axis.
Table 4: Numerical assessment of the proposed denoising
algorithm using SNR and CNR metrics.
SNR CNR
Original Despeckled Original Despeckled
(I1) 9.2 26 2.5 4
(I2) 12.1 31 3 5.9
(I3) 11.5 24 1.9 3.2
(a) (b)
(c)
(d)
(e)
(f)
(g)
(a)
(b)
(c) (d)
(e)
(f)
(g)
PHOTOPTICS 2016 - 4th International Conference on Photonics, Optics and Laser Technology
44
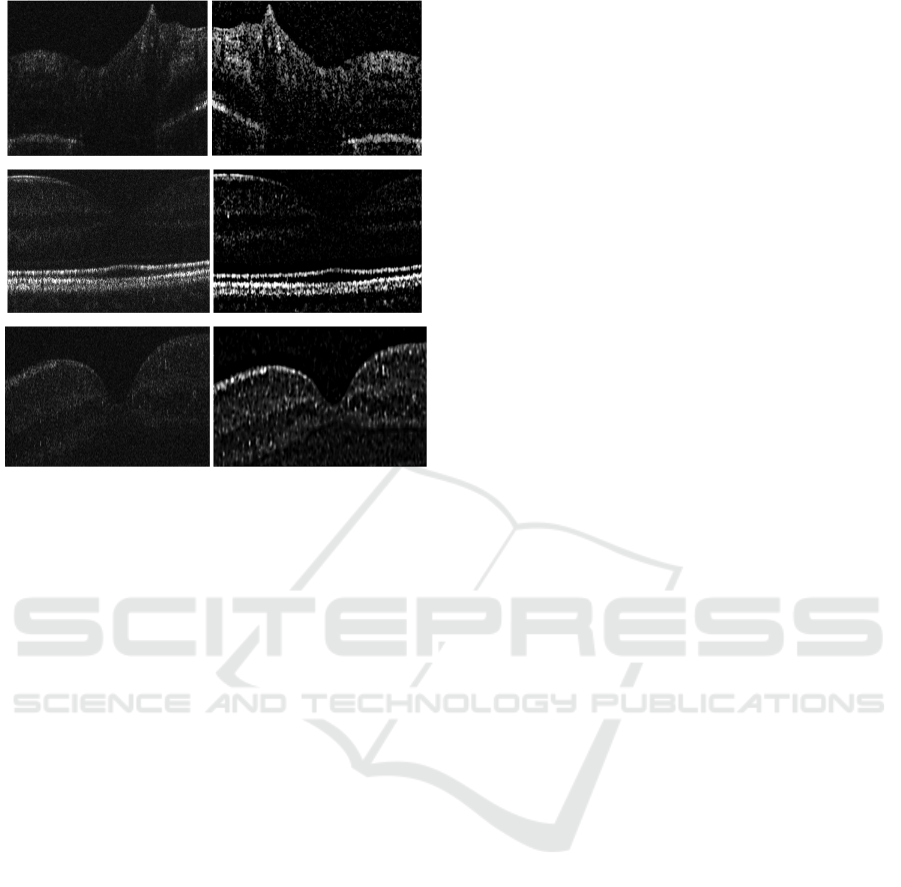
Figure 6: Comparative presentation of three original OCT
test images (I1), (I2), (I3) and of their denoised images.
4 CONCLUSIONS
In this paper, a speckle reduction algorithm was
presented based on the approximation that speckle
noise has a Rayleigh distribution with a noise
parameter, sigma. A new ensemble framework as a
combination of several Multi-Layer Perceptron
(MLP) neural networks was designed to estimate
sigma in the speckle noise model. The sigma
estimator kernel worked with more than 99.3%
reliability on average. The estimated sigma values
were then used in the de-speckling algorithm to
reduce the speckle in the OCT images. The algorithm
was successful in reducing speckle of B-scan images
of human eye. The algorithm reduced the speckle
while preserved the details of the regions. Two well-
established no-reference quality metrics including
SNR and CNR were used for quantitative evaluation,
and demonstrated higher quality images when the
new algorithm was utilized. The proposed algorithm
is also compared with some other bilateral digital
filters and demonstrated a satisfying evaluation.
Respectively, due to the generality of proposed ANN
algorithm, it can be used as a signal processing
method in other image modalities such as
photoacoustic imaging system (Nasiriavanaki et al.,
2014).
REFERENCES
Avanaki, M., Laissue, P. P., Eom, T. J., Podoleanu, A. G.
& Hojjatoleslami, A. 2013a. Speckle reduction using an
artificial neural network algorithm. Applied optics, 52,
5050-5057.
Avanki, M. R., Cernat, R., Tadrous, P. J., Tatla, T.,
Podoleanu, A. G. & Hojjatoleslami S. A. 2013b. Spatial
compounding algorithm for speckle reduction of
dynamic focus OCT images. Photonics Technology
Letters, IEEE, 25, 1439-1442.
Avanaki, M. R. & Hojjatoleslami, A. 2009. Speckle
reduction with attenuation compensation for skin OCT
images enhancement. Proceeding of Medical Image
Understanding and Analysis (MIUA), Kingston
University, London, 14-15.
Avanaki, M. R., Laissue, P. P., Podoleanu, A. G. & Hojat,
A. Denoising based on noise parameter estimation in
speckled OCT images using neural network. 1st
Canterbury Workshop and School in Optical Coherence
Tomography and Adaptive Optics, 2008. International
Society for Optics and Photonics, 71390E-71390E-9.
Fitzpatrick, T. B. 1975. Soleil et peau. J Med Esthet, 2, 33-
34.
Goodman, J. W. 2007. Speckle phenomena in optics: theory
and applications, Roberts and Company Publishers.
Nasiriavanaki, M.R.N, Xia, J., Wan, H., Bauer, A. Q.,
Culver, J. P. & Wang, L. V. 2014. High-resolution
photoacoustic tomography of resting-state functional
connectivity in the mouse brain. Proceedings of the
National Academy of Sciences, 111, 21-26.
Ozcan, A., Bilenca, A., Desjardins, A. E., Bouma, B. E. &
Tearney, G. J. 2007. Speckle reduction in optical
coherence tomography images using digital filtering.
JOSA A, 24, 1901-1910.
Podoleanu, A. G. 2014. Optical coherence tomography. The
British journal of radiology.
Shankar, P. M. 1986. Speckle reduction in ultrasound B-
scans using weighted averaging in spatial
compounding. IEEE transactions on ultrasonics,
ferroelectrics, and frequency control, 33, 754-758.
(I1)
(I2)
(I3)
An Intelligent Speckle Reduction Algorithm for Optical Coherence Tomography Images
45
