MathAuthor: Authoring Interactive Math Exercises for the Web

Edgar Seemann

Furtwangen University, Villingen-Schwenningen, Germany

Keywords:

Mathematics, Teaching, Exercises, Online Courses.

Abstract:

The creation of online exercise sheets or interactive lecture notes for math courses still poses many challenges

for teachers. Authoring tools of e-learning systems typically do not directly support the rendering of mathe-

matic equations. Teachers are therefore required to ﬁnd and install additional plugins. Visual elements such as

plots, drawings or diagrams have to be created using external tools. Exercise questions and student responses

are mostly restricted to simple multiple-choice or ﬁxed answer questions, since common e-learning systems

are not able to process mathematic expressions.

With MathAuthor we propose an authoring environment tailored to the speciﬁc needs of math educators. Math-

Author allows teachers to quickly create interactive exercises with various types of mathematic responses (e.g.

functions, solution sets etc.). Its web-based editing functionality allows a real-time preview of all created

content elements including equations and interactive input ﬁelds. MathAuthor also proposes a language for

describing mathematic plots and 3D drawings, allowing teachers to easily embed graphics (e.g. function

curves or vector geometry drawings). MathAuthor can provide immediate feedback to student responses. This

feedback is generated purely in Javascript, thus requiring no special server component. As a consequence, it

is easy to integrate the resulting exercise sheets into existing websites and e-learning systems.

1 INTRODUCTION

In math education formative assessment tools play an

important role. On the one hand, they allow teachers

to evaluate and guide the student’s learning progress.

On the other hand, they are crucial for students to

get feedback on their own achievements and deﬁcien-

cies. This feedback is also fundamental to support

self-learning. Web-based interactive exercise sheets

represent an easy way to provide such a feedback to

large numbers of students.

Unfortunately, the task of creating interactive ex-

ercise sheets is often daunting and cumbersome to

teachers. Authoring tools of e-learning systems re-

quire teachers to ﬁnd and install appropriate plugins.

Mathematic expressions and equations are only sup-

ported when those plugins have been enabled by an

administrator.

Many exercise types beneﬁt from or rely on vi-

sualizations and supporting pictures or plots. In or-

der to create these visualizations teachers have to use

external tools and import the resulting ﬁgures. This

process is time-consuming and makes it difﬁcult for

teachers to apply future changes or modiﬁcations.

Moreover, many of the external tools used by teachers

have not been developed speciﬁcally for mathematic

drawings. Thus, it is often hard to ensure correct

alignment and accurate proportions of all depicted ob-

jects. This is particularly true for 3D drawings.

Finally, adding interactivity and providing stu-

dents with meaningful feedback to their responses is

challenging. Not every math teacher is a program-

mer and thus interactive elements are limited by the

capabilities of the used e-learning or content manage-

ment system (e.g. Moodle). While e-learning sys-

tems allow teachers to create forms with input ﬁelds,

they typically do not support mathematic expressions

(in particular vectors, matrices, sets, complex num-

bers etc.). They are also not able to handle equivalent

mathematic representations, e.g 0.6 =

or x

+ x =

x(x + 1). Some teachers try to resolve this problem

by adding multiple solution alternatives to their ex-

ercises. But for many cases the number of possible

representations is too large, e.g. when dealing with

functions.

In fact, many teachers shy away from creating

their own exercises due to the challenges described

above. They rather choose to provide students with

links to various websites containing online exercises.

For students this poses a number of difﬁculties. Web-

sites may differ greatly in terms of user interface and

navigation. There is also no common standard for en-

Seemann, E.

MathAuthor: Authoring Interactive Math Exercises for the Web.

In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 231-237

ISBN: 978-989-758-179-3

231

tering mathematic expressions.

Ideally, teachers should adapt exercise problems

to the speciﬁc needs of their students. If we want

to enable and encourage teachers to create their own

content, content creation has to be easy and fast. In

this paper we propose MathAuthor an authoring sys-

tem for interactive math exercises. It allows teachers

quickly create assignment problems containing math-

ematic expressions. Interactive elements provide im-

mediate and automatic feedback to the students’ so-

lution propositions. Without any external tools teach-

ers can deﬁne supporting visualizations like plots and

3D drawings. During content creation a real-time pre-

view of the complete content is rendered in a second

preview pane. In this preview authors can even check

the functionality of interactive elements while editing.

Thus, MathAuthor avoids unnecessary and repeated

switches between editing and viewing modes.

The remainder of the paper is organized as fol-

lows. Section 2 discusses existing approaches to math

authoring. Section 3 describes the proposed authoring

environment in detail and compares it to other author-

ing systems. Finally, section 4 covers some of the in-

teresting implementation aspects and design choices

of the software implementation.

2 RELATED WORK

For authoring mathematic content TeX (Knuth, 1986)

and LaTeX are still the de-facto standard in the com-

munity. In fact, many exercises found online are

downloadable PDF ﬁles produced with LaTeX. While

LaTeX is a versatile authoring tool, it does not offer

any capabilities to add interactive input elements or

student feedback.

Web-based HTML documents allow for interac-

tivity through the Javascript programming language.

Javascript programs may alter the document structure

and content or react to user inputs. Unfortunately,

not everyone is a programmer and implementing in-

teractive elements can be difﬁcult, particularly, if the

computer should process and understand mathematic

expressions. Moreover, the W3C standard descrip-

tion for math elements is MathML (Ausbrooks et al.,

2014), which is currently not supported by all major

web browsers. So while online documents provide a

lot more ﬂexibility for authors, they are quite difﬁcult

for teachers to create.

2.1 HTML Conversion Tools

A simple way to create online exercise sheets for

mathematics is to use an HTML converter. Mi-

crosoft Word can e.g. export existing documents to

the HTML format. The same is true for LaTeX docu-

ments which may be converted with “Pandoc” (Mac-

Farlane, 2014) or the “LaTex2html” tool. In both

cases, formulas and equations are exported as images.

These HTML converters create static pages. Interac-

tive content cannot be produced this way.

Open Mathematical Documents (OMDoc)

(Kohlhase, 2006) and OpenMath (Kohlhase, 2003)

are open standards for creating and describing

mathematic objects and documents. They are markup

languages, which may be converted to HTML.

OpenMath is e.g. used in the intelligent tutoring

system ActiveMath (Melis and Siekmann, 2004).

We, the authors of MathAuthor, believe that OMDoc

and OpenMath are much too complex and too

verbose for writing simple documents. In contrast, T.

Leathrum (Leathrum, 2010) proposes a much more

accessible approach to math authoring. It is based

a LaTex-XHTML hybrid document format, which

allows authors to specify mathematic documents in

a compact way. The main drawback of all these

approaches, however, is the missing interactivity.

2.2 e-Learning Systems with Plugins

e-Learning systems are an obvious choice for author-

ing educational content. Their support for mathe-

matic expressions, however, is limited and teachers

are required to ﬁnd and install additional plugins. The

setup process for these plugins can be difﬁcult and

require advanced knowledge in software administra-

tion. Popular plugins include simple ﬁlters like Math-

Jax (http://mathjax.org), which produces high quality

equation renderings and can e.g. be used in Moodle

or Wikipedia. These plugins typically do not provide

a live preview for mathematics. Mathematic expres-

sions are only rendered after saving a document. Au-

thors therefore have to switch repeatedly between the

editing and viewing mode when an expression was

not entered correctly.

Other plugins extend existing WYSIWYG doc-

ument editors e.g. TinyMCE (http://tinymce.com)

with math capabilities. Possible choices include

Dragmath (http://dragmath.bham.ac.uk), Wiris ed-

itor (http://wiris.com), which both produce ren-

dering results which are not up to par with

with LaTeX or MathJax renderings. MathSlate

(http://dthies.github.io/tinymce4-mathslate) is an edi-

tor extension that requires two plugins. It builds upon

MathJax and allows authors to create equations us-

ing a comfortable math editor. Unfortunately, this

math editor opens a separate popup window and in-

serts only a text representation of the equation in the

CSEDU 2016 - 8th International Conference on Computer Supported Education

232

document preview.

While these plugins allow authors to write mathe-

matic expressions, they do not extend e-learning sys-

tems to support interactive input ﬁelds with mathe-

matic input.

2.3 Interactive Mathematics Software

Specialized mathematic software packages may also

provide authoring tools for interactive exercises.

Maple Clickable Math (MapleSoft, 2014) is a great

tool for creating interactive mathematic exercises.

Unfortunately it can only be used as a desktop soft-

ware. The Wolfram Language (Hastings et al., 2015)

and its associated web services are arguably the most

complete and versatile tools for authoring mathematic

content. This commercial software package also sup-

ports plotting of functions and interactive mathematic

elements. As the software seems to be aimed at de-

velopers, authors need a considerable technical ex-

pertise. Numbas (Perfect, 2015) an e-assessment sys-

tem from the University of Newcastle allows teachers

to setup interactive math exercises. It has a custom

web-based editor and an excellent documentation for

authors. Currently, it does not support the creation

of plots and graphics. Finally, iMathAS (Platz et al.,

2014; Lippman, 2016) is a sophisticated assessment

tool with many features. However, it is rather com-

plex to setup and is designed to work completely sep-

arately from existing e-learning systems e.g. Moodle.

3 MathAuthor AUTHORING

ENVIRONMENT

The goal of this work is to provide teachers with an

easy and fast authoring tool for interactive exercises.

We therefore designed the user interface to be as sim-

ple as possible. Menus and the number of necessary

mouse clicks are kept to minimum. The proposed ed-

itor (see Figure 1) consists of a two pane layout, with

the exercise source code on the left and the rendered

real-time preview on the right. This real-time preview

is fully interactive and authors may check the func-

tionality of created interactive elements while editing.

After ﬁnishing the document, the resulting interactive

exercise sheet can be embedded in any webpage or e-

learning-system. By default MathAuthor applies only

minimal visual styling, i.e. CSS rules. It is possi-

ble to override all styles with CSS rules of an existing

web-site or content-management system. This way,

the exercise headings, fonts, colors etc. seemlessly

blend into other content.

Figure 1: Minimalistic two pane layout of the MathAuthor

editor. Right pane shows the fully interactive real-time pre-

view with example responses. The design can be adapted

via CSS.

Interactive exercises consist of structured text with

equations on the one hand, as well as graphics and in-

teractive elements on the other hand. In the following

we describe, how authors can create these document

parts in the proposed system.

3.1 Text and Equations

Describing structured text with pure markup lan-

guages such as HTML, MathML etc. has proven

not to be optimal for authors. The markup syntax is

rather verbose and requires a lot of additional char-

acters for style and structure information. Wiki sys-

tems have tried to remedy this situation by introduc-

ing the Wiki markup language (Foundation, 2008). In

recent years Markdown has become increasingly pop-

ular and is now standardized under the name Com-

monMark (MacFarlane, 2015). We have adopted

this CommonMark standard, giving authors a ﬂexi-

ble, short and easy to learn syntax for structuring their

documents. The example below shows some a basic

structuring elements. A more elaborate overview of

all syntax elements can be found in the CommonMark

speciﬁcation (http://spec.commonmark.org).

# A h e a d i n g o r s e c t i o n

## A s u b h e a d i n g o r s u b s e c t i o n

∗ l i s t i t e m 1

∗ l i s t i t e m 2

−−−

1 . f i r s t numbered l i s t i t e m

2 . s eco n d numbered l i s t i t e m

For the rare cases when authors have special re-

quirements, which cannot be fulﬁlled with Common-

Mark, authors are allowed to insert additional stan-

dard HTML tags.

MathAuthor: Authoring Interactive Math Exercises for the Web

233

For adding mathematics, authors can use the La-

TeX syntax. Firstly, this syntax is much shorter and

easier to type as MathML. Secondly, it is already

well-known by most mathematicians. We have op-

timized the rendering process such that after each key

press MathAuthor re-renders the preview in real-time.

This real-time preview is crucial for the productiv-

ity of authors. In fact, the live rendering is much

faster than most existing software solutions for La-

teX, which tend to be rather slow. Consequently ex-

isting software solutions mostly do not offer a real-

time preview at all. In order to achieve this rendering

speed we have evaluated various rendering Common-

Mark and LaTeX engines. In our user tests the popu-

lar MathJaX library proved to be too slow for longer

documents. We therefore integrated KaTeX, a LaTeX

renderer from the Khan Academy, in our optimized

parser and rendering stack.

3.2 Interactive Input Elements

Interactive input elements is really what distinguishes

online exercises from paper-based exercise sheets.

They allow students to enter their responses in the fa-

miliar Matlab syntax and receive feedback on their re-

sults. MathAuthor enables authors to create these in-

teractive elements with special tags that augment the

basic CommonMark elements. An input ﬁeld for the

solution of a problem in vector geometry could, e.g.,

look as follows:

< f i e l d >

{

” t e x t ” : ” $\ v ec {p}=$ ” ,

” t y p e ” : ” v e c t o r ” ,

” s o l u t i o n ” : ” [ 4 / 3 ; 0 ; 8 / 3 ] ”

}

</ f i e l d >

Where the solution [4/3; 0; 8/3] is a 3-D vec-

tor in Matlab syntax.

Input elements are fully interactive in editing

mode, allowing authors to quickly check their func-

tionality. All validation and interactive feedback is

handled automatically and is generated in real-time

via Javascript. For this we have implemented a

Javascript math library, which validates a wide range

of math expressions including numbers, number sets,

intervals, vectors, matrices, functions. More details

will be described in Section 4.3. Note that, students

therefore do not have to enter the exact solution text,

but e.g. a numerically equivalent rounded representa-

tion. In the example above a student could e.g. pro-

vide the solution [1.33; 0; 2.66].

Figure 2 shows the rendering of the above exam-

ple with real-time feedback:

Figure 2: Example exercise displaying the feedback to a

student response.

3.3 Plots and Figures

Allowing authors to create and integrate plots and

drawings into their document is essential for some

types of math exercises. A common practice is to cre-

ate these pictures with external tools. Typically, these

tools export graphics ﬁles e.g. PNG or SVG, which

are then manually embedded. As a consequence, the

author has to switch between different tools when cre-

ating content or applying modiﬁcations. Addition-

ally, the information underlying the image data is not

stored within a single main document. Instead, the

author has to keep track of multiple source ﬁles (the

document itself and all image ﬁles). In practice, many

authors forget to store the raw data of their images

(e.g. the Matlab .ﬁg, Photoshop .psd ﬁle). Thus, au-

thors have to recreate the image from scratch when

changes are necessary.

MathAuthor integrates mathematical drawing ca-

pabilities directly into the editor. In order to plot

mathematical functions or curves we adopt a syntax

similar to section 3.2. The curves f

(x) = x

and

(x) = x

− 2x + 1 can, e.g., be displayed as follows:

{

” f 1 ” : ”x ˆ 2 ” ,

” f 2 ” : ”xˆ3 −2∗ x +1” ,

” x r a n g e ” : [ −5 ,5 ] ,

” y r a n g e ” : [ −2 ,1 0]

}

</ p l o t >

Again, plots are rendered in real-time and an ap-

propriate coloring theme is applied. The values for the

x− and y−ranges are optional. The resulting graph is

interactive as well, allowing students to zoom in/out

or translate the curves in x- and y-direction.

Other types of drawings for applications in geom-

etry, vector algebra etc. have different requirements.

Graphics programs are often not well suited for these

kinds of mathematic ﬁgures. Specifying the exact di-

mensions, proportions and alignment of elements is

often tedious and requires navigating menus or popup

windows. MathAuthor implements simple drawing

CSEDU 2016 - 8th International Conference on Computer Supported Education

234

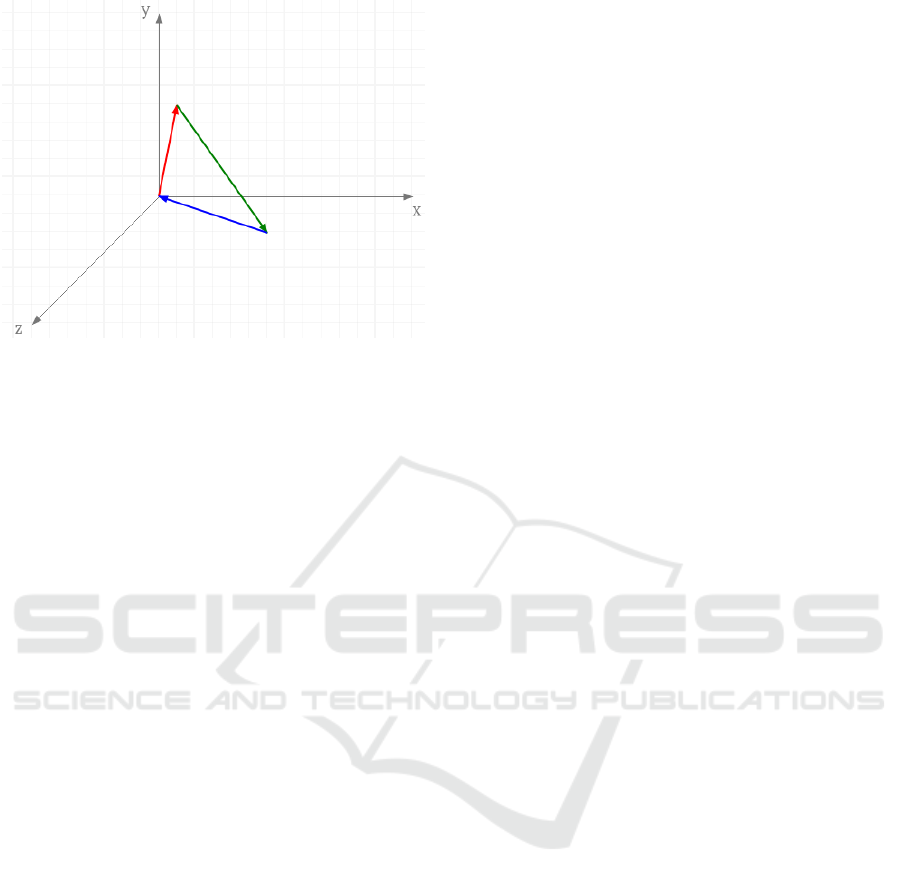
Figure 3: A 3D drawing created within MathAuthor.

engine for these ﬁgures. It allows to create geomet-

ric shapes in both 2D and 3D. The following example

draws a 3D coordinate system with a triangle consist-

ing of 3 vector arrows as depicted in Figure 3.

Axes ( ” 3 d ” ) ;

a=Arrow ( [ 0 , 0 , 0 ] , [ 2 , 4 , 3 ] , ” r e d ” ) ;

b=Arrow ( a . end , [ 8 , 4 , 1 0 ] , ” g r e e n ” ) ;

c=Arrow ( b . end , a . s t a r t , ” b l u e ” ) ;

</ c an va s >

Geometric shapes are created by specifying their

name and their properties. An arrow, e.g. has a start-

ing point, an end point and a color. The drawing

engine is implemented in pure Javascript and allows

authors to use any Javascript programming construct.

In fact, the example above associates the arrows with

variables a, b, c. This allows authors, e.g., to neatly

align elements by refering to the properties of another

shape. Authors may also use more advanced con-

structs such as loops to create sophisticated drawings

or fractals.

4 IMPLEMENTATION

MathAuthor is written in Javascript and runs com-

pletely within a browser. Authors can either install

an instance of the MathAuthor editor on their own

webserver or use a hosted instance. The resulting

HTML exercise sheets are self-sufﬁcient and do not

require a server backend. All computations are done

via Javascript on the client side. The advantage of this

approach is that, exercise sheets may be copied to any

web server or e-learning system.

In the following we will brieﬂy discuss some im-

plementation details of the proposed authoring envi-

ronment.

4.1 Parsing and Rendering

During editing MathAuthor’s interactive exercise

sheets are rendered from the exercise’s source code

after each key press event. We have optimized the

source code parser to allow this to happen in real-

time. The parser is implemented using a stacked

parser concept. In the ﬁrst run, the parser just looks

for special tags such as math expressions, ﬁelds, plots

or drawings. Before the second run, these special

tags are cached in memory and replaced with short

placeholders. In the second run, the parser processes

the CommonMark elements and translates them to

HTML. Finally, all special tags are rendered and in-

serted into the ﬁnal document. Separating the pars-

ing process into two independent runs makes the

parsers both easier to implement and faster. Ren-

dering high quality mathematic equations is particu-

larly time-consuming. We have adopted the KaTeX

(http://khan.github.io/KaTeX) for this part of the ren-

dering stack.

4.2 Input Fields

As described in previous sections input ﬁelds are

speciﬁed using a special tag <field>. The content

of this tag is represented by a JSON object containing

all the necessary data, i.e. text label, solution and an

optional type. JSON, the Javascript Object Notation,

represents a compact way for deﬁning structured data.

In our case, we use simple key value pairs. In order

to ease the input of this JSON data, we provide a key-

board shortcut, which enters a complete JSON snip-

pet along with default values for an input ﬁeld. The

ﬁeld’s data is parsed and converted to HTML using a

Javascript template engine.

Once the ﬁeld has been rendered, we register an

event handler, which calls a Javascript function in

case the content of the input ﬁeld changes or a key has

been pressed. This is all done automatically without

requiring authors to do any programming. The event

handler calls the necessary routines for input valida-

tion.

4.3 Input Validation

During input validation student responses are checked

and compared against a provided reference solution.

This is accomplished by a custom math library which

also runs completely in Javascript.

Our math library has subroutines for all exercise

types allowing it to validate numbers, number sets,

vectors, matrices and functions. Numbers are com-

pared by their numerical value. It therefore does not

MathAuthor: Authoring Interactive Math Exercises for the Web

235

matter if a student enters 2/5 or 0.4. We also account

for rounding issues by allowing students to round any

value to two decimal places. Values in number sets

can be entered in any order. Our library automat-

ically sorts all values and compares them numeri-

cally. Vectors and matrices may be checked by loop-

ing through their elements. Validating symbolic func-

tions requires the most complex routines. Computer

algebra systems have techniques to compare different

function representations. However, it is hard to im-

plement such a functionality in Javascript. More over,

even these sophisticated comparison techniques may

not resolve any possible equivalent representation.

We therefore chose to compare functions by densely

sampling their function values. If two function repre-

sentations are equivalent they obviously have to have

the same sampling values.

The validation procedure for functions ﬁrst parses

the function with a recursive expression parser. This

allows us to evaluate the function using Javascript.

The student response xˆ2+4x+3, e.g., gets converted

to the Javascript expression Math.pow(x,2)+4*x+3.

Note that, due to rounding problems or deﬁnition gaps

not all sample values may match exactly. We there-

fore implemented a fuzzy matching technique, which

allows for the relative values of a limited number in-

dividual samples to differ.

4.4 Plots

Plots are implemented similarly to input ﬁelds. A

keyboard shortcut allows to insert a snippet for a spe-

cial <plot> tag. The tag’s content is parsed and

rendered to HTML. For rendering we adopted the

open source JSX Graph library (http://jsxgraph.uni-

bayreuth.de). Again, event handlers are registered to

allow interactive zooming as well as horizontal and

vertical translation.

4.5 Figures

In MathAuthor ﬁgures are created programmatically

to allow authors to quickly specify exact dimen-

sions, proportions and alignment.We created a new

Javascript library optimized for drawing geometric

shapes and objects in 2D and 3D. Each shape is imple-

mented as a Javascript class, i.e. a prototyped func-

tion. This allows authors to easily access and reuse

object properties such as starting points, end points or

sizes. All data within the special <canvas> tag is in

fact valid Javascript source code. The rendering is ac-

complished by simply executing this source code in

the browsers Javascript engine. Authors are therefore

free to use any Javascript command or control struc-

ture such as loops.

5 CONCLUSION AND

DISCUSSION

MathAuthor follows a unique approach to the cre-

ation of exercises for the web. It allows teachers to

author fully interactive content without sophisticated

programming skills in a matter of minutes. Authors

need nothing more than a web browser and the result-

ing exercises run completely without a server back-

end.

MathAuthor combines and integrates popular ex-

isting solutions for content creation on the web, e.g.

CommonMark, KaTeX or JSX Graph. It also provides

novel libraries and techniques for validating mathe-

matic expressions and drawing graphics. This way,

authors do not have to switch between different soft-

ware tools and all exercise data is stored in a single

document.

Unlike WYSIWYG editors, MathAuthor, with its

two pane editor, is more similar to a basic program-

ming tool. Certainly, this will not appeal to all teach-

ers or authors at the ﬁrst glance. However, content

creation is much faster, since it avoids the often te-

dious navigation in menus and popup windows. This

is particularly true for drawings or plots.

MathAuthor provides a high-quality real-time pre-

view of the complete document. A feature which

is often absent from other editors, where previews

are commonly restricted to the text or equation parts

alone.

REFERENCES

Ausbrooks, R., Buswell, S., Carlisle, D., and

Chavchanidze, G. (2014). Mathematical markup

language (mathml) version 3.0 2nd edition.

http://www.w3.org/TR/MathML3.

Foundation, W. (2008). Wiki markup language.

https://en.wikipedia.org/wiki/Wiki markup.

Hastings, C., Mischo, K., and Morrison, M. (2015). Hands-

on Start to Wolfram Mathematica and Programming

with the Wolfram Language. Wolfram Media Inc.

ISBN: 9781579550776.

Knuth, D. E. (1986). Computers & Typesetting, Volume B:

TeX: The Program. Addison-Wesley.

Kohlhase, M. (2003). Toward openmath version 2. In Math-

ematics on the semantic web.

Kohlhase, M. (2006). An open markup format for mathe-

matical documents. In Lecture Notes in Artiﬁcial In-

telligence. Springer-Verlag.

CSEDU 2016 - 8th International Conference on Computer Supported Education

236

Leathrum, T. (2010). Math authoring for the web made

easier. In Convergence (Mathematical Association of

America).

Lippman, D. (2016). MyOpenMath. myopenmath.com.

MacFarlane, J. (2014). Pandoc user’s guide.

https://github.com/jgm/pandoc.

MacFarlane, J. (2015). The commonmark speciﬁcation ver-

sion 0.22. http://spec.commonmark.org.

MapleSoft (2014). E-Book: Clickable Calculus Study

Guide.

Melis, E. and Siekmann, J. (2004). Activemath: An intel-

ligent tutoring system for mathematics. In Interna-

tional Conference on Artiﬁcial Intelligence and Soft

Computing.

Perfect, C. (2015). A demonstration of numbas, an e-

assessment system for mathematical disciplines. In

Internationl Conference on Compupter Assisted As-

sessment.

Platz, M., Niehaus, E., Dahn, I., and Dreyer, U. (2014).

IMathAS and automated Assessment of mathematical

Proof.

MathAuthor: Authoring Interactive Math Exercises for the Web

237