A Content-based Watermarking Scheme based on Clifford

Fourier Transform

Maroua Affes

1, 2

, Malek Sellami Meziou

, Yassine Lehiani

, Marius Preda

and Faouzi Ghorbel

CRISTAL, National School of Computer Sciences, Mannouba campus, Mannouba, Tunisia

ARTEMIS, Institute TELECOM/TELECOM SudParis, 9, Charles Fourier, Evry, France

Keywords: Image Watermarking, Clifford Fourier Transform, Harris Detector, JPEG Compression, Robustness.

Abstract: In this paper, we propose a new watermarking method based on Harris interest points and Fourier Clifford

Transform. We employed Harris detector to select robust interest points and to generate some non-overlapped

circular interest regions. Each region was transformed into Clifford Fourier domain and the watermark was

embedded into the Clifford transform coefficients magnitude. Experimental results show the robustness of the

proposed method against JPEG compression.

1 INTRODUCTION

Due to the open environment of the internet,

download and distribution of digital media have

facilitated the wide use and sharing of digital

multimedia content. However, these advantages

come with challenging problems for copyright

protection of digital property. In order to protect and

preserve digital content, many regulatory measures,

such as copyright protection, are provided. In this

context, watermarking is one of the most prominent

protection techniques. Often, watermarking methods

are categorized by casting/processing domain, the

watermark signal type, and hiding position. In any

case, good visual fidelity and robustness of the

watermark against common image processing and

geometric attacks are essential. Many watermarking

approaches have been proposed in the literature. A

survey of watermarking techniques can be found in

(Potdar et al., 2005). In general, watermarking

methods can be classified into two generations

(Xiaojun and Ji, 2007), (Potdaret al.,2005): traditional

watermarking schemes and host-content based

methods.

The first generation can be divided into three kinds:

• Template-based watermarking methods: the

template is a repeated structure and it embeds

into the image to estimate the geometric

distortions and to extract the watermark after

reversing the geometric transformation.

• Invariance domain based watermarking

methods which embed the watermark in a

geometrically invariant domain, such as the

Fourier-Mellin domain or log- polar domain.

These methods provide rotation, scaling and

translation (RST) invariance.

• Moment-based watermarking methods which

modify the geometric invariants of the image

including ordinary moments, such as Zernike

moments.

The second generation is based on host contents (Bas

et al., 2002). For example, Kutter, Bhattacharjee and

Ebrahimi (1999) claimed that the watermark

information can be associated with the image content.

The basic idea is to use interest points as Harris

corners or Scale-Invariant Feature Transform (SIFT),

etc, to determine the interest areas. Same areas may

be identified in embedding and extraction processes

even after geometric distortions. Lee , Kim and Lee

HK. (2006) extracted the image feature points by

using SIFT and generated a number of circular patch,

the mark is embedded into each patch additively in

spatial domain. This method can resist general

geometric attacks, but their experimental results show

that the watermark similarities are lower than 0.7.

Lei-da, Bao-long and Lei (2008) proposed a RST

invariant image watermarking scheme using Harris

feature points. They extracted Harris feature points to

generate circular regions. Then these regions was

rotation normalized. This method is robust against

374

Affes, M., Meziou, M., Lehiani, Y., Preda, M. and Ghorbel, F.

A Content-based Watermarking Scheme based on Clifford Fourier Transform.

DOI: 10.5220/0005748403720378

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 374-380

ISBN: 978-989-758-175-5

RST attacks, but it needs inverse normalization,

which introduces error to weaken the robustness

against common signal operation.

In this paper, we propose a content-based

watermarking scheme that uses a Harris feature point

detector. The watermark is embedded into frequency

domain of interest regions. We will give in section 2

an overview of some frequency watermarking

methods. In section 3, Clifford Fourier Transform

will be recalled and we will describe the embedding

and the extraction process of the watermarking

algorithm. Experimental results will be presented in

section 4. We will eventually conclude and give some

possible perspectives for future work.

2 FREQUENCY

WATERMARKING METHODS

The watermark can be embedded directly on pixels or

in the image frequency transform coefficients. The

most used transforms are Discrete Fourier Transform

(DFT), Discrete Wavelet Transform (DWT) and the

well-known Discrete Cosine Transform (DCT).

DCT-based watermarking techniques use the

middle-frequency coefficients because the

modification of low frequencies affects the visual

quality of the image and the modification of high

frequencies causes local distortion along the edges

(Neeta et al., 2010).

The watermarking in DCT domain was first

introduced by Koch and Zhao (1994) by modifying

the magnitude of the middle-frequency coefficients.

This method shows good robustness to JPEG

compression. The image is divided into blocks of size

8x8. After that, some blocs are selected by a specific

function and they are transformed to DCT domain.

Before the embedding process, for each block, a

condition tests two selected mi-frequency

coefficients to study the validation of bloc to embed

the watermark bit. The criterion for valid blocks is

specified by the relationships between the two

selected coefficients. This criterion is used in the

extraction process to know if the block contains a bit

of watermark or not. This method is based on

modifying the magnitude of the selected coefficients.

To create the watermarked image, for each block, it is

required to perform the inverse DCT. The extraction

process is very simple and it is a blind procedure. It

has the same steps of the embedding process. To

estimate the inserted bit, it suffices to read the sign of

the difference between the modules of the two

selected mi-frequency. Using these constraints, the

experimental results indicate that the watermark can,

with sufficient noise margins, survive common

processing, such as lossy compression.

Discrete wavelet transform find a great popularity

in watermarking technique. It supports multi-

channels and gives excellent spatial localization. In

general, the DWT watermarking scheme consists first

in partitioning the cover image into high and low

frequency quadrants. The low frequency quadrant is

again split too into more parts of high and low

frequencies and this process is repeated until the

signal has been entirely decomposed. For the first

decomposition the DWT gives four resolution levels:

LL1, LH1, HL1, and HH1. It is well known that the

maximum energy is located in LL sub-band. So, the

mark is embedded in some selected coefficients from

HL, LH and HH via additive modification. In the

detection process, the same steps as the embedding

process are repeated. Typically, it consists of a

process of correlation estimation (Vaishali and

Sachin, 2011). DWT watermarking method is robust

against JPEG compression, cropping, median

filtering, adding noise and scaling. Unfortunately, this

approach has some disadvantages. Computing DWT

is more time consuming than computing DCT. Also,

it embeds the watermark in an additive way. So, to

detect the watermark, it is necessary to correlate the

watermarked image coefficients with the initial

watermark. Therefore, the image itself must be

treated as noise, which makes the detection extremely

difficult (Potdar et al., 2005), (Seema et al., 2012).

The DFT domain is also used in watermarking

technique because it offers robustness against

geometric distortions like cropping translation,

rotation, scaling, etc. DFT based watermark

embedding techniques can be divided into two kinds.

In the first one, the watermark is directly embedded

by modifying the DFT amplitude and phase

coefficients. In the second case, a template is used to

estimate the transformation and resynchronize the

image. For example, O'Runaidh, Dowling and Boland

(1996) proposed a DFT watermarking algorithm

modifying the DFT phase information. Its

experimental results show that this technique is robust

against image contrast operation and rotation. In

(O'Runaidh and Pun, 1998) authors proposed another

DFT watermarking technique using log-polar

coordinates system. Results show that this scheme is

robust against RST attacks. This technique is

basically used for greyscale images watermarking. To

extend the method, a marginal treatment proposes to

perform watermarking for each colour canal

independently. On other side, a lot of interest to find

another Fourier transform applicable directly on

A Content-based Watermarking Scheme based on Clifford Fourier Transform

375

colour images was reported. As example, the Clifford

Fourier Transform has been proposed in 2010 as a

rigorous solution to overcome the limits of the

classical Fourier transform.

3 PROPOSED WATERMARKING

SCHEME

In this section, we will first remind the principles of

Clifford Fourier transform, which will be used later

for our robust watermarking algorithm against JPEG

compression.

The classical Fourier transform have been used in

many fields such as harmonic analysis and group

theory to process 1D signal and greyscale images. On

colour images, three Fourier transforms are applied

on each channel. To avoid this marginal processing,

several authors have proposed to embed the colour

space in more pertinent geometric spaces such as

quaternions. Sangwine and Ell (2000) defined the

Quaternion Fourier Transform (QFT). They

considered only two Fourier transforms: for the

luminance and chrominance. In the exponential of

Fourier coefficients, they replaced the complex i by

the quaternion. Recently, Batard, Berthier and Saint-

Jean (2010) defined another Fourier Transform,

called Clifford Fourier transform (CFT), which is

mathematically more rigorous. This one clarifies

relations between the Fourier transform and the action

of the translation group through an action spinor

group.

The CFT generalizes the Color QFT (Batard et al.,

2010) because it is based on group representations

theory and Clifford algebras. A pixel of a colour

image can be extended in ℝ

4,0

algebra (vectors of

ℝ

4,0

) as follows:

4321

0)()()()( eexbexvexrxf +++=

(1)

Where x = (x

, x

) and r, v and b are respectively

the red, green and blue channels pixel with

coordinates (x

, x

The CFT is parameterized by a unit vector B whose

expression is as follows :

dxeexfee

BIxuBxuBIxu

Bxu

)(

><−><−><><





(2)

where I

is the scalar pseudo of ℝ

4,0

and B is its

unit bi-vector. Within the Clifford algebras, a vector

can be decomposed in a parallel part and an

orthogonal part depending on the choice of the bi-

vector B. Being f an image and B a bi-vector, this

decomposition is

ffBBfBffBBf

⊥

−−

+=∧+==

).(

(3)

where

).(

−

= BBff

(resp.

)(

−

⊥

∧= BBff

) is the

parallel (resp. the orthogonal) projection of f on a bi-

vector B. The above equation can be rewritten as

follows by this decomposition (Batard et al., 2010):

)()()( ufufu

BB ⊥



(4)

where

() () ()

ux ux

ux B

ue fxe dxfxe dx

<> <>

−

−< >





and

() () ()

ux ux

IB IB

ux IB

BB B

ue fxe dxfxe dx

<> <>

−

−< >

⊥⊥ ⊥





We will use decomposition in our proposed

schema in order to define the criteria of validity for

CFT coefficients to embed the mark.

In order to synchronize the embedded regions and

the extracted regions, we used the local Harris

features. They provide a potential solution for

watermarking to improve the robustness (Papakostas

et al., 2011). Also, we chose to embed the watermark

in the frequency domain which assures its invisibility

and its robustness more than in spatial domain. We

used also the CFT to avoid the marginal treatment of

colour image which can cause sometimes a false

detection of the watermark. CFT is applied on

windows of 8x8 around the keypoint. The detailed

embedding steps are illustrated in Figure 1. We first

transform the colour image to greyscale in order to

detect the interest points with Harris detector. We

construct the circular locally regions. To avoid

overlap between regions (Figure 2a), the Euclidean

distance d between the interest points must be upper

than the double of patch radius (Figure 2b).

To choose the embedding plane, we set up a small

experiment and embed the mark W in three

Figure 1: Embedding processes.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

376

a) b)

Figure 2: Generation of interest regions (a) overlappe

regions, (b) no overlapped regions with Euclidean distance

= 20.

different locations: the parallel part



of CFT, in the

orthogonal part

⊥



of CFT and in both of them. The

results are presented in the following table. To

evaluate the three insertion methods, we use the

PSNR (Peak Signal Noise Ratio) to measure the

imperceptibility of the mark. We note that best results

are obtained in the first case.

Table 1: PSNR variation depending on the embedding

plane.

Image

references

\method



⊥



and

⊥



189003 52,67dB 49,67 dB 48,09 dB

295087 53,14 dB 48,92 dB 47,52 dB

42049 53,37 dB 49,46 dB 48,04 dB

299086 52,89 dB 49,13 dB 48,09 dB

We generate a binary random watermark W = {w

i = 0…N}. To know the size of the mark, we construct

a bitmap, denoted ξ, which contains "1" if the region

B(i) of



is valid i.e. the region can contain a bit of

the mark. The validity of



is computed as

following:

(1) for each region, CFT is applied.

(2) then, two mi-frequency coefficients are

selected. To know the possible location of these two

coefficients, we study the distribution of coefficients

with bases magnitudes values. In this case, we

calculate the average of magnitudes of frequency

coefficients for multiple windows of 8x8 around the

keypoint detected with Harris detector for 30 images.

Figure 3 shows the distribution of the amplitudes for

both DCT and CFT. We can observe that the lower

values of CFT coefficients are shifted to the mi-

frequency coefficients when compared with DCT.

This observation made us choose the support of

potential coefficients where to embed the mark as

illustrated in Figure 4.

a) b)

c) d)

Figure 3: The magnitude of frequency coefficients for DCT

(a) and for CFT (b). Image (c) (resp. Image (d)) represents

the magnitude of frequency coefficients of DCT (resp.

CFT) with the elimination of the DC component.

Figure 4: Possible locations for embedding in 8x8 region

(shadowed area).

(3) let’s denote |Q(k

)| and |Q(k

)|, the two mi-

frequency coefficients selected from the shadowed

area in Figure 4. We apply the following criteria to

choose the coefficients to be permuted:

if |Q(k

)| > |Q(k

)|+p, ξ(i) ← 1 then the

region B(i) is valid

else ξ(i) ← 0.

where p is a marginal noise, in the experiment p

= 0.5. The size of the watermark equals to the number

of "1" on bitmap ξ.

(4) error correcting codes are incorporated in

watermarking system to overcome the corruption of

the watermark in the communication channels. In our

method, we use the Hamming code as an error

detection system to correct bit error. The watermark

is divided into some words, each word contains 4 bits.

The Hamming code is then applied to each word to

generate (7-4) single bit error correcting code. The

use of error-correction codes ensures a better quality

signal at the receiver and a higher recovery increases

the possibility of the perfect match in embedding

process (MacWilliams and Sloane, 1977).

A Content-based Watermarking Scheme based on Clifford Fourier Transform

377

(5) once the robust circular non-overlapping

region and the watermark are generated, we start to

embed the watermark. Similarly with the Zhao

algorithm (Koch and Zhao, 1994), we embed one bit

of the watermark in each region. However, we

integrate it in the CFT domain. So, for each valid

region B(i) (i.e. ξ(i) =1 ) the following steps are

applied:

• CFT is applied

• If W(i) =1

permute |Q(k

)| and |Q(k

)|:

|Q’(k

)| = |Q(k

)| and

|Q’(k

)|=|Q(k

)|;

• If W(i) =0

|Q’(k

)| = |Q(k

)| and

|Q’(k

)|= |Q(k

)|;

• Inverse CFT is applied

The watermarked image f

is then obtained

by combining the watermarked regions.

The extraction process has the same steps as

in embedding process. With Harris detection and

the map ξ, we can specify which regions are

watermarked. The detailed extraction steps are

described in Figure 5. So, for each region if ξ(i)=

1 then W' is computed as follow:

W’ = 1, |Q’(k

)| > |Q’(k

0, |Q’(k

)| < |Q’(k

(5)

Figure 5: Extraction processes.

4 EXPERIMENTAL RESULTS

Several experiments were performed in order to test

the effectiveness of the proposed watermarking

method. The visual perceptibility and robustness

against compression attacks were tested. Experiments

have been conducted on various colour images from

the data base of BSD300 (Berkeley Segmentation

Dataset 300) as illustrated in Figure 6.

Figure 6: Samples from Berkeley Segmentation Dataset

300.

4.1 Visual perceptibility

The watermarked images were assessed for visual

distortion using PSNR. Images in Figure 7 show no

visible degradation. For Lena image, the PSNR value

is 51.07 dB, for Lion 48.90 dB (ref 108085 in the

BSD300). Similar observations were noted for other

test images. These PSNR values are all greater than

30.00 dB which is the empirical value for the image

without any perceivable degradation (Hsieh and

Tesng, 2004).

c) d)

Figure 7: (a) Original and (b) watermarked images at a

PSNR value of 51.07 dB for Lena image and (c) original

and (d) watermarked image at a PSNR of 48.90 dB for Lion

image.

4.2 Robustness to JPEG

Compression Attack

The first frequency watermarking method was

developed by Koch and Zhao (1994). A modified

version of this method was used as a reference to

evaluate the robustness of our method against

compression attacks. The original Zhao method is

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

378

applicable on greyscale images and based on DCT

domain. We extend it to be applicable on colour

image. In fact, we decomposed the RGB image and

we applied Zhao method on the red component. An

error correction Hamming codes is also used.

To evaluate the robustness of the proposed

algorithm, we calculated the Normalized Hamming

Similarity NHS:

WWHD

NSH

)',(

1−=

(6)

where W (resp. W’) is the inserted watermark (resp.

the extracted watermark) and N is its size

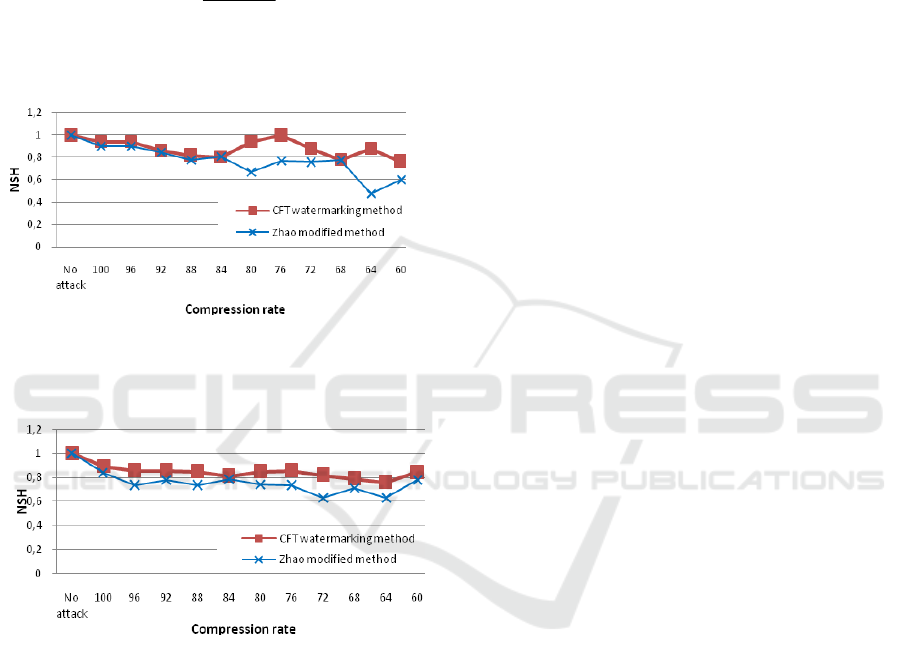
Figure 8: The variation of the NSH depending on the

compression rate for the image “Lena” to CFT

watermarking method and Zhao modified method.

Figure 9: The variation of the NSH depending on the

compression rate the image of ref “295087” to CFT

watermarking method and Zhao modified method.

For all tests, we chose |Q(k

=3,l

=1)| and

|Q(k

=1,l

=5)| as two mi-frequency coefficients of

CFT. They have been modified to carry one bit

watermark in each region.

As shown in Figures 8 and 9, our scheme

performs better than the modified Zhao method under

JPEG compression attack. For example, the NSH for

image Lena with quality factor 80% using ECC is

0.94 and 0.61 for Zhao’s method and it is 0,765 with

quality factor 60% using ECC instead of 0.6 for

Zhao’s method.

5 CONCLUSION

In this paper, we introduced a new method for

invisible watermarking based on CFT. The key idea

of the proposed algorithm is the combination of

generation of the Harris interest regions and colour

image watermarking technique. We first used Harris

detector to generate circular patch for watermark

embedding. Then, we transformed these patches to

CFT domain and we selected two mi-frequency

coefficients. After that, we inserted the watermark on

these selected coefficients by a substitution way. The

capacity of the proposed scheme is flexible, since we

can manipulate the number of feature points as we

want. The experimental results showed that the

proposed scheme preserves not only the high

perceptual quality, but also the robustness against

JPEG compression comparing with Zhao’s method.

Future work will be focused on the geometrics

attacks.

REFERENCES

Bas P., Chassery J. M. and Macq B., 2002. Toward a

content-based watermarking scheme. Traitement du

signal 2002_volume 19 n°1 2002. p.11-17.

Batard T., Berthier M. and Saint-Jean C., 2010. Clifford

Fourier Transform for Color Image Processing. In E.

Bayro-Corrochano & G. Scheuermann, editeurs,

Geometric Algebra Computing in Engineering and

Computer Science, chapitre 8, pages 135–161. Springer

Verlag, 2010.

Hestenes D. and Sobczyk G., 1987. Clifford Algebra to

Geometric Calculus. A Unified Language for

Mathematics and Physics (Fundamental Theories of

Physics). Broché – 31 août 1987.

Hsieh M. S. and Tseng D. C., 2004. Perceptual digital

watermarking for image authentication. Electronic

commerce Research. Volume 4, Issue 1-2 , p.157-170.

Koch E. and Zhao J., 1994. Embedding robust labels into

images for copyright protection. Technical report,

Fraunhofer Institut For Computer Graphics,

Darmstadh, Germany. p.242-251.

Kutter M., Bhattacharjee S. K and Ebrahimi T., 1999.

Toward second generation watermarking schemes. In

Proceedings of IEEE International Conference Image

Processing, vol. 1, Kobe, Japan. p.320-324

Lee H. Y., Kim H. S. and Lee H. K., 2006. Robust image

watermarking using local invariant features. In Optical

Engineering, 2006. p.037002-037002-11

Lei-da L., Bao-long G. and Lei G., 2008. Rotation, scaling

and translation invariant image watermarking using

feature points. In The Journal of China Universities of

Posts and Telecommunications, 2008. p.82-87.

A Content-based Watermarking Scheme based on Clifford Fourier Transform

379

MacWilliams F. J. and Sloane N. J., 1977. Theory of Error

Correcting Codes. 8, North-Holland, Amsterdam,

Netherlands, 1977.

Neeta D., Archana R. and Manthalkar R., 2010. Review of

Robust Video Watermarking algorithms. In

International Journal of Computer Science and

Information Security. p. 237-246.

O’Ruanaidh J., Dowling W. J. and Boland F. M., 1996.

Phase watermarking of digital images. In Proc. IEEE

Int. Conf. Image Processing. p. 239-242.

O’Ruanaidh J. and Pun T., 1998. Rotation, scale, and

translation invariant digital image watermarking. In

Signal Processing. p.303-317.

Papakostas G. A., Tsougenis E.D., Koulouriotis D.E. and

Tourassis, V. D., 2011. On the robustness of Harris

detector in image watermarking attacks. In Optics

Communications. p.4394-4407.

Potdar, V. M., Song Han and Chang, E., 2005. A survey of

digital image watermarking techniques. Industrial

Informatics, 2005. INDIN '05. 2005 3rd IEEE

International Conference. p.709-716.

Sangwine S. J., and Ell T. A., 2000. The discrete Fourier

transform of a colour image. In J. M. Blackledge & M.

J. Turner, editeurs, Image Processing II : Mathematical

Methods, Algorithms and Applications, (Proceedings

of Second IMA Conference on Image Processing, De

Montfort University, Leicester, UK, September 1998),

pages 430–441. Horwood Publishing for Institute of

Mathematics and its Applications, 2000.

Seema M., Hitesh G. and Saurabh M., 2012. Survey of

Digital Image Watermarking Techniques to achieve

Robustness. In International Journal of Computer

Applications, 2012 by IJCA Volume 45-No 13. p.1-8.

Vaishali J. S. and Sachin R. G., 2011. Literature Review of

Wavelet Based Digital Image Watermarking

Techniques. In International Journal of Computer

Applications. p.28-35.

Xiaojun Q. and Ji Q., 2007, A robust content-based digital

image Watermarking scheme. Signal Processing

Volume 87, Issue 6, June 2007, P.1264–1280.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

380