SysML Models and Model Transformation for Security
Florian Lugou, Letitia W. Li, Ludovic Apvrille and Rab
´
ea Ameur-Boulifa
LTCI, CNRS, T
´
el
´
ecom ParisTech, Universit
´
e Paris-Saclay, Campus SophiaTech, 450 route des Chappes, 06410, Sophia
Antipolis, France
Keywords:
SysML-Sec, Security, Model-driven Engineering, Model Transformation, ProVerif, TTool.
Abstract:
The security flaws of embedded systems have become very valuable targets for cyber criminals. SysML-Sec
has been introduced to target the security of these systems during their development stages. However, assessing
resistance to attacks during these stages requires efficiently capturing the system’s behavior and formally
proving security properties from those behaviors. This paper thus proposes (i) novel SysML block and state
machine diagrams enhanced to better capture security features, and (ii) a model-to-Proverif transformation.
ProVerif is a toolkit first released for the formal analysis of security protocol, but it can be used more generally
to assess confidentiality and authenticity properties. This paper demonstrates the soundness of our approach
using a complex asymmetric key distribution protocol.
1 INTRODUCTION
The growing proportion of connected embedded sys-
tems and cyber-physical systems offer more opportu-
nities for attack to cyber criminals. To cite only a few
examples of past attacks on such connected systems,
we can mention ADSL routers (Assolini, 2012), mo-
bile&smart phones (Maslennikov, 2010), avionic or
automotive systems (Hoppe et al., 2011), and smart
objects e.g. the recent vulnerability disclosed on the
Fitbit (Apvrille, 2015). Security flaws have even been
disclosed on medical appliances, such as on the Hos-
pira Symbiq drug pump (ICS-CERT, 2015). Such at-
tacks also target industrial systems whose sensors are
increasingly commonly connected with vulnerable in-
formation systems, as demonstrated by the Stuxnet,
Flame, and Duqu (Maynor, 2006) attacks. The de-
pendability of such systems are targeted with varying
objectives, e.g., terrorist acts and ransomware.
System complexity in terms of code size, distri-
bution, and heterogeneity among others is a major
risk factor. One solution to better consider the risk
of these systems is to take all of their constraints
into account, including security, during their devel-
opment cycle. We previously introduced the SysML-
Sec environment to handle the design of such com-
plex systems, in terms of safety, performance, and
security (Apvrille and Roudier, 2015). SysML-Sec
addresses system development starting from require-
ments and possible attacks, taking into account soft-
ware/hardware partitioning. After the partitioning
stage, SysML-Sec also supports the design of soft-
ware components, again with safety and security in
mind. TTool is the free/open-source support tool of
SysML-Sec (Apvrille, 2003).
TTool relies on UPPAAL for safety proofs, and
on ProVerif to perform security proofs from SysML-
Sec block diagrams. However, SysML-Sec has sev-
eral strong limitations both in terms of modeling
(i.e., modeling security features), and in terms of
proofs (limitations in the models-to-proverif transfor-
mations). The paper addresses several of these lim-
itations, with new modeling and transformation ap-
proaches. In particular, we have fully formalized and
implemented the model transformation.
The next section gives the related work in terms of
modeling and proof environment for security. Section
3 presents SysML-Sec. Section 4 focuses on the mod-
eling extensions as well as on the models-to-proverif
transformations. Section 5 presents the updated ver-
sion of TTool and the validation features. Lastly, sec-
tion 6 concludes the paper.
2 RELATED WORK
Assessing security properties when designing soft-
ware components mostly relies on formal approaches.
For example, (Toussaint, 1993) proposes verifying
cryptographic protocols with a probabilistic analysis
approach. Protocols are represented as trees whose
Lugou, F., Li, L., Apvrille, L. and Ameur-Boulifa, R.
SysML Models and Model Transformation for Security.
DOI: 10.5220/0005748703310338
In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 331-338
ISBN: 978-989-758-168-7
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
331

nodes capture knowledge while edges are assigned
transition probabilities. Although these trees could in-
clude malicious agents in order to model attacks and
threats, security properties are nonetheless not explic-
itly represented. Moreover, for threat analysis, attacks
should be explicitly expressed and manually solved.
(Trcek and Blazic, 1995) defines a formal basic set
of security services for accomplishing security goals.
In this approach, security property analysis strongly
relies on the designer’s experience. Moreover, threat
assessment is not easily feasible.
In more recent efforts, temporal logic languages
have been used for expressing security properties.
(Drouineaud et al., 2004) introduces a first order Lin-
ear Temporal Logic (LTL) into the Isabelle/HOL the-
orem prover, thus making it possible to model both
a system and its security properties, but unfortu-
nately leading to non-easily reusable specific mod-
els. (Ma
˜
na and Pujol, 2008) mixes formal and in-
formal security properties, but the overall verification
process is not completely automated, again requiring
specific skills. Analogously, the Software Architec-
ture Modeling (SAM) framework (Ali et al., 2009)
aims to bridge the gap between informal security re-
quirements and their formal representation and ver-
ification. SAM uses formal and informal security
techniques to accomplish defined goals and mitigate
flaws. Thus, liveness and deadlock-freedom prop-
erties can be verified on LTL models relying on the
Symbolic Model Verifier (SMV). Even if SAM relies
on a well established toolkit - SMV - and considers
a threat model, the ”security properties to proof” pro-
cess is not yet automated.
UMLsec (J
¨
urjens, 2007) is a modeling framework
aimed at defining security properties of software com-
ponents and of their composition within a UML
framework. It also features a rather complete frame-
work addressing various stages of model-driven se-
cure software engineering from the specification of
security requirements to tests, including logic-based
formal verification regarding the composition of soft-
ware components.
More recently, (Shen et al., 2014) developed an ex-
panded UML model extending the sequence diagrams
of UML for security protocol verification. Their
approach also included translating the model into
ProVerif for verification of confidentiality and cor-
respondance. However, our work includes state dia-
grams for the capability to model a broader range of
protocol. Basic sequence diagrams may model only
a single execution, while state diagrams may model
protocol containing if statements and loops. Further-
more, our process includes verification of weak and
strong authenticity.
With regard to our previous publications, we pro-
pose a way to better model situations (e.g., loops) and
their models-to-proverif transformation, taking into
account the capabilities and limitations of ProVerif.
We thus manage to limit cases where the proof of
security properties would fail, without impacting the
safety proof capabilities of SysML-Sec diagrams.
3 CONTEXT
3.1 SysML-Sec
SysML-Sec connects goal-oriented descriptions of se-
curity requirements and attacks (left section of Figure
1), and the fine-grained representation of assets based
on the software / hardware partitioning (right upper
section of Figure 1). SysML-Sec also supports phases
of the V-cycle after the partitioning stage (lower right
of Figure 1), and notably the design of the software-
partitioned functions. The design stage includes the
definition of security mechanisms, and the refinement
of security requirements in security properties to be
proved in the design: we address this stage in the pa-
per. Verification takes place at different engineering
phases. Simulation is mostly used at the partition-
ing stage in order to evaluate the impact of security
mechanisms in terms of performance. Formal veri-
fication intends to prove the resilience of the system
under design to threats. Testing serves a similar pur-
pose, but on the deployed implementation resulting
from the design models (Apvrille and Roudier, 2015).
A SysML-Sec design is composed of SysML
block and state machine diagrams.
SysML-Sec blocks can define a set of methods
corresponding to cryptographic algorithms, such as
encrypt(), to be able to describe security mechanisms
built upon these algorithms, e.g., cryptographic proto-
cols. Blocks can also pre-share values, a feature com-
monly needed to set up cryptographic protocols.
The formal proof of SysML-Sec designs relies
on UPPAAL (Bengtsson and Yi., 2004) and ProVerif
(Blanchet, 2009) respectively for the proof of safety
and security properties.
ProVerif is a toolkit that relies on Horn clauses
resolution for the automated analysis of security prop-
erties over cryptographic protocols, under the Dolev-
Yao model. ProVerif takes in input as a set of Horn
Clauses, or a specification in pi-calculus together with
a set of queries. ProVerif then outputs whether each
query is satisfied or not. In the latter case, ProVerif
tries to identify a trace explaining how it came to the
conclusion that a query is not satisfied.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
332

System Design
SW/HW Partitioning
Requirements
Requirements
Architectural view
Architectural view
Mapping view
Mapping view
Simulation
Formal analysis
Functional view
Functional view
Simulation
Formal analysis
Structural view
Structural view
Behavioral view
Behavioral view
Deployment view
Deployment view
Simulation
Formal analysis
Test
Attacks
Attacks
Simulation
Formal analysis
Contribution
Of this paper
Figure 1: Overall SysML-Sec Methodology.
Safety proofs take into account all design el-
ements besides ones specifically defined for secu-
rity purposes: security-oriented pragmas and crypto-
graphic methods that have no impact on safety prop-
erties (liveness, reachability). Similarly, the proof of
security properties abstracts away irrelevant or non
supported system details. For example, the security
proof does not require temporal information, so tem-
poral operators (after clause) are not taken into ac-
count. Other modeling elements, like loops, are ig-
nored by the translation process.
3.2 Missing Features in SysML-Sec
Design Diagrams
In the years since we first proposed a translation from
a SysML-Sec model to ProVerif, we gathered valu-
able feedback from devoted testers. Among easily
corrected corner cases or usability bugs, some robust-
ness issues indicated more fundamental problems.
These issues were often related to a mismatch be-
tween the semantics of features in SysML-Sec and
their counterparts in ProVerif. We present some of the
most important issues that motivated us to completely
rework the translation process:
Loops. Often, users take advantage of the verification
feature embedded in TTool in order to assess the se-
curity of a system that provides a service. For some
systems, modeling their state machines using loops
seems natural. Unfortunately, ProVerif tries to flatten
the given specification as a first step. Using a straight-
forward translation as it was implemented, verifica-
tion on a design containing loops would not terminate.
We address this significant drawback in this paper.
Private Channels. As in ProVerif, SysML-Sec en-
ables the user to model two types of channels: private
and public. While their semantics should be the same
for ProVerif, their behaviors with respect to reacha-
bility queries differ. ProVerif considers that a mes-
sage sent should always be received. On private chan-
nels, only explicitly specified entities can read the
sent message, while on public channels, the message
can also be read by the attacker. When assessing the
reachability of an event, ProVerif tries to reconstruct
a trace and stop at the exact moment when the event
is triggered. Therefore, if the event occurs just after
a message was sent on a private channel, the message
would not yet be read. ProVerif would thus consider
the trace invalid, returning a cannot be proved result.
As we wished, in our context, to provide the ability
to prove reachability properties, modifying the private
channel representation was also an important issue we
addressed in our work.
4 EXTENDED DIAGRAMS
4.1 Design Diagrams in Depth
In TTool, the user first builds the block diagram and
associated state diagrams as a graphical model. The
block diagram describes the architecture and compo-
nents of the system, and state diagrams associated
with blocks describe their behavior.
We present an example from the European FP7
EVITA project, which defines security architec-
ture for automotive communication systems (Kelling
et al., 2009). In this architecture, safety critical ECUs
(Electronic Control Units) are interconnected with
CAN or Flexray buses. Automotive systems are likely
to be attacked either for economic reasons (activating
optional features for free), or for criminal purposes.
The interconnection of automotive systems to infor-
mation systems (roads signs, tolls, etc.) and Internet
offers new ways to conduct attacks on those systems.
To avoid attacks and their propagation on the
ECUs, session keys are regularly distributed among
groups of related ECUs. Figure 2 presents the block
diagram of an asymmetric key distribution protocol
with entities ECU1 and ECU2. An extract of their
SysML Models and Model Transformation for Security
333

Figure 2: Block Diagram for Asymmetric Key protocol.
Figure 3: State Diagrams for ECU1 and ECU2.
state diagrams describing their communication proto-
col is shown in Figure 3. ECU1 processes the key
and sends it on a public channel, and ECU2 recieves
the message, verifies the key, and uses it to send mes-
sages. The locks show verification results to be de-
scribed in section 5.
The graphical model is translated for verification
in ProVerif, UPPAAL, etc. A detailed formal descrip-
tion is provided in subsection 4.1.2.
4.1.1 Extending SysML-Sec with Pragmas
Not all model parameters and queries are stated
graphically within the block and state diagram. For
example, we needed the capability to declare two at-
tributes equal at the start of a session. We extended
SysML with pragmas, i.e. formal text notes regard-
ing the attributes of the system. Pragmas are classi-
fied into Model Pragma or Property Pragma. Model
Pragmas provide more security-oriented semantics to
attributes of blocks, while Property Pragmas describe
security properties of block attributes or state ma-
chines. The pragmas are described in Table 1.
4.1.2 Formalization of SysML-Sec Diagrams
In an attempt to provide a reliable mathematical base
for the proofs performed by ProVerif on a SysML-
Sec design diagram, we decided to formally express
the transformations performed on the model as it is
described in TTool. This formalization will provide
understanding on both how we managed to link a gen-
eral purpose SysML diagram to a ProVerif specifica-
tion that relies on Horn clauses, and where sources of
incompleteness may come from. This formalization
is also a first step in building a mathematical proof of
equivalence for a future work.
A first transformation translates timer-related ca-
pabilities into a set of blocks and signals. The latter
are inherently taken into account in our formalization.
Formally, let us denote D the set of SysML-Sec
diagrams; d ∈ D ::= (B,M
p
,P
p
), where B is a set of
blocks, M
p
is a set of model pragmas and P
p
is a set
of property pragmas.
We define a block b ∈ B ::=
(A,M ,Σ,ss,E, S,O,T , L), where A is a set of
attributes, M a set of methods, Σ a set of signals, ss
a start state, E a set of end states, S a set of states,
O a set of operations, T a set of transitions and L a
labeling function that associates attributes, methods,
signals and states to their qualified name. Attributes,
methods and signals can be mapped to their matching
graphical elements in the block view, while states,
operations and transitions correspond to the state
machine of the considered block.
To each attribute a ∈ A is associated a type: a set
of concrete values that the attribute may take. We call
valuation a mapping that returns a value for each at-
tribute a ∈ A. We suppose that we are able to con-
struct patterns over A. A pattern denoted p is com-
posed of applications of methods or simple operators
(=, and, +, etc.) to elements of A.The set of patterns
over A is denoted P . We slightly extend the labeling
function L to accept well-formed patterns as input.
The operations set O is defined to be a disjoint
union of sets of elementary operations:
O = O
rdm
] O
out
] O
in
where O
rdm
is a set of randoms operations and O
out
and O
in
a set of out and in actions respectively. We
encode by ν.a the randoms operations, by ¯mhpi the
out actions and by mhai the in actions with m ∈ Σ,
p ∈ P and a ∈ A.
Finally, we define a transition t ∈ T as a tuple
(i,o,g,R) where:
• i ∈ {ss} ∪ S ∪ O is the incoming node.
• o ∈ E ∪ S ∪ O is the outgoing node.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
334

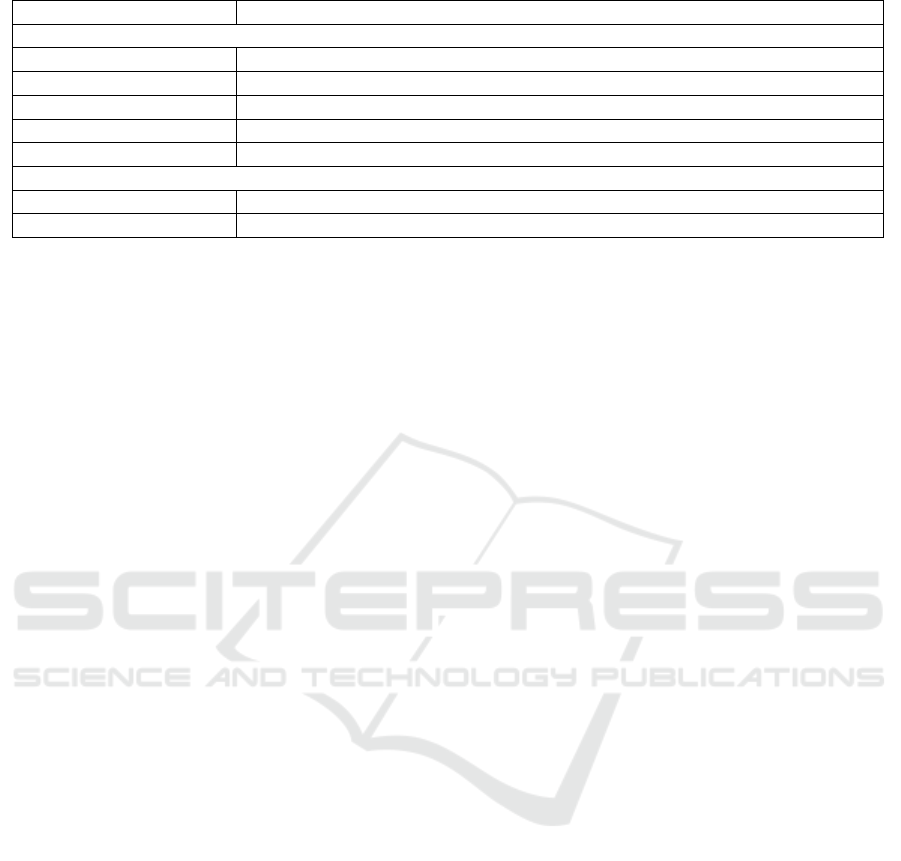
Table 1: Pragma Descriptions.
Pragma Description
Model Pragma
PrivatePublicKeys Two attributes of a block are set as Private Key and Public Key, respectively
InitialSessionKnowledge Listed attributes have the same value at the start of a session
InitialSystemKnowledge Listed attributes have the same value when the system starts
SecrecyAssumption Listed attributes are assumed secret. ProVerif verifies this afterwards
Constant Declares a string as a possible constant value
Property Pragma
Confidentiality/Secret Query the confidentiality of attributes listed
Authenticity Query the weak and strong authenticity of the two attributes at given states
• g ∈ G is a guard, which is a pattern whose valu-
ation is a boolean value. An empty guard is de-
noted true: a pattern that is always evaluated to
true.
• R = (A × P )
i∈N
is a finite family of actions (pairs
attribute and pattern), indexed over N. Each tran-
sition can indeed be labeled with a set of actions
corresponding to assignments of attributes.
We only deal with well formed blocks so as to map
with the intuitive semantic of SysML diagrams. For
instance, no transition can reach the start state (ss) or
come from an end state, and multiple transitions can
only join or split at a state and not at an operation.
As we wish to use the ProVerif backend to per-
form a security proof on a SysML-Sec diagram, such
a diagram must first be translated in order to match an
equivalent representation that ProVerif can handle.
4.2 Semantics of ProVerif
ProVerif works with two different semantics: Horn
clauses and pi-calculus. When translating from
SysML-Sec to ProVerif, we generate a pi-calculus
specification. The generation takes advantage of the
Horn clauses semantic to model concepts, such as
loops in the state machine diagram, that are not di-
rectly supported by ProVerif.
To enable a more thorough understanding of the
proof provided by TTool, one should first familiarize
oneself with the ProVerif proof engine. We thus try
to briefly present ProVerif in this section and refer in-
terested readers to the manuals and white papers for a
better understanding.
Pi-calculus enables description of protocols in term of
processes executing in parallel and exchanging mes-
sages over channels. Processes can split to create con-
currently executing processes, and replicate to model
multiple executions (called sessions) of a given pro-
tocol. Cryptographic primitives, such as symmetric
and asymmetric encryption or hash, can be modeled
through functions that are either constructors, which
create new values, or destructors, which reduce the
number of applied constructors in an expression .
Starting from this specification, reachability, cor-
respondence and confidentiality properties can be
queried and ProVerif will present a result to the user
that is either true if the property is verified, false if
a trace that falsifies the property has been found, or
cannot be proved if ProVerif failed in asserting or re-
futing the queried property. Such failures in prov-
ing properties over an unbounded number of sessions
and unbounded message space are unfortunately un-
avoidable since this problem is undecidable (Durgin
et al., 2004). Thus, sound approximations are made
by ProVerif when translating the pi-calculus specifi-
cation into Horn clauses.
4.3 SysML-Sec to ProVerif Translation
Some components of the SysML-Sec diagram can be
mapped to their ProVerif counterparts quite straight-
forwardly since we borrow the attacker model and
the channel semantic from ProVerif. However, for
other components, like loops on the state machine dia-
gram or private channels, we had to carefully consider
ProVerif reasoning in order to avoid as much as possi-
ble cases where the proof would fail. In the following
sections, we will present the entire translation process
and provide more details about non-obvious features
or situations.
4.3.1 Partitions of a SysML-Sec Diagram
Since a SysML-Sec state machine diagram may con-
tain loops, we need either to unroll these loops up to
a certain limit, or to reuse the part of the translated
specification that could be executed multiple times.
Both of these choices have been considered in static
analysis works and are strategically important, since
allowing jumps in the specification often incurs a loss
in terms of completeness, while flattening the graph
by limiting the number of repetitions affects the cor-
rectness of the proof.
SysML Models and Model Transformation for Security
335

In order to maintain the soundness guaranteed
by ProVerif, we chose not to limit the loops. As
such, the first step in translating a SysML-Sec Dia-
gram composed of well-formed blocks to a ProVerif
specification is to determine the initial state of ev-
ery basic block in every block. A basic block
(s,E, S,O, T ) is a sub-part of a block that can be con-
sidered atomic with only one entry point. From a
block b = (A,M ,Σ,ss,E,S ,O, T , L) ∈ B one can
construct a set of basic blocks (denoted by BB(b))
which forms a partition of the states, operations and
transitions sets.
We define Init
BB
(b) as the set of initial states of
basic blocks. This set is a collection of all states that
have at least two different incoming transitions.
Init
BB
(b) = {ss} ∪ {s|s ∈ S ∧ ∃(i,s,g,R) ∈ T ,
∃(i
0
,s,g
0
,R
0
) ∈ T .(i,s,g,R) 6= (i
0
,s,g
0
,R
0
)}
We give the construction function of basic blocks
from traversal of a SysML-Sec Diagram. This func-
tion denoted by → is specified in terms of a set of
inference rules. The construction rules of each basic
block begins from its initial state.
s ∈ Init
BB
(b)
(s,
/
0,
/
0,
/
0,
/
0)
i ∈ {s} ∪ S ∪ O (i,o,g,R) ∈ T r T
(s,E,S,O,T ) → (s,E,S, O, T ∪ {(i,o,g,R)})
n ∈ E r E ∃(i, n, g,R) ∈ T
(s,E,S,O, T ) → (s,E ∪ {n}, S, O,T )
n ∈ S r S n /∈ Init
BB
(b) ∃(i,n,g,R) ∈ T
(s,E,S,O, T ) → (s,E,S ∪ {n},O,T )
n ∈ O r O ∃(i,n,g,R) ∈ T
(s,E,S,O, T ) → (s,E,S, O ∪ {n},T )
A basic block is built by adding recursively all
transitions and nodes – which are not initial states –
that are in a path starting from an initial state.
4.3.2 Translating Basic Blocks
The translation function of each basic block
(s,E, S,O, T ) ∈ BB(b) is given by the function J., .K :
state, set of transitions → pi-calculus code, unfolding
the set of transitions into a ProVerif specification. We
build the code by concatenating the generated instruc-
tions. For this we use the concatenation operator ⊕.
The translation rules are defined formally in Table 2;
they are listed in the order they should be applied. Let
us briefly explain the translation rules from Table 2.
Rule (a) deals with multiple outgoing transitions, it
should be applied when there are more than one out-
going transitions (|I| > 1). (b) translates guards and
(c) translates actions. (d) and (e) deal with states and
( f ), (g) and (h) with operations. Finally, (i) stops
the translation algorithm. Note that (e) also stops the
translation since it deals with transition linking this
basic block to an other (more details are given in Sec-
tion 4.3.3).
When a state is followed by multiple outgoing
transitions, it can use any of them as long as the
boolean condition that guards the transition is veri-
fied. From a security point of view, any trace of at-
tacks using one of these transitions is valid. This is
conceptually equivalent to letting the attacker choose
which transition to take in case of nondeterministic
transitions. We model this in rule (a) by creating
values corresponding to each transition, making them
public, and waiting for a value corresponding to the
attacker’s choice.
4.3.3 Pragmas and Basic Block Linking
Rule (e) shows how control is passed from one basic
block to the next. ProVerif supports simple process
calls by flattening them, and as a result, does not ter-
minate for diagrams containing loops. Thus, instead
of directly calling basic blocks, we generate tokens
of the form tok(call L(n
0
),arg) and make them avail-
able to the attacker. One such token allows the at-
tacker to execute the basic block whose initial state is
n
0
∈ Init
BB
(b), with the values of the attributes of the
block being passed as argument (arg =
[
a∈A
{L(a)}).
This token should only be used once, and only
in the right session, so we add to the token a ses-
sion identifier to guarantee that the token is forged
and used in the same session, and use a nonce mech-
anism to prevent its reuse. Unfortunately, due to
ProVerif approximations – which are unavoidable –
using nonce affects the ability of ProVerif to prove
properties (mostly strong authenticity) in the presence
of loops.
5 VALIDATION IN TTool
ProVerif results are passed back to TTool as a text
file containing results. Reachable state queries are
performed for all states, while authenticity and con-
fidentiality queries are performed only for attributes
listed in pragmas. Relevant results from the model
from subsection 4.1 are presented either as a list of
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
336

Table 2: Basic block translation rules.
Jn,TK=

















































M
i∈I
”new choice
i
; out choice
i
”
M
”in choice”
M
i∈I

”if choice=choice
i
then” ⊕ Jn
i
,T
0
∪ {t
i
}K

if T=T
0
] T
00
|T
00
={t
i
∈T|t
i
=(n,n
i
,g
i
,R
i
)} (a)
”if L(g) then” ⊕ Jn
0
,T r t ∪ {(n,n
0
,true,R)}K if ∃ t = (n,n
0
,g,R) ∈ T |g 6= true (b)
”let L(a) = L(p) in” ⊕ Jn
0
,T r t ∪ {(n,n
0
,true,R
0
)}K if ∃ t = (n,n
0
,true,R) ∈ T|R = (a, p) :: R
0
(c)
”event enteringState (L(n
0
))” ⊕ Jn
0
,T r tK if ∃ t = (n,n
0
,true,
/
0) ∈ T |n
0
∈S r Init
BB
(b) (d)
”out (chctrl, tok(call L(n
0
),arg)) · ” if ∃ t = (n,n
0
,true,
/
0) ∈ T |n
0
∈ Init
BB
(b) (e)
with arg =
[
a∈A
{L(a)}
”new L(a)” ⊕ Jν.a,T r tK if ∃ t = (n,ν.a,true,
/
0) ∈ T ( f )
”out(L(m),L(p))” ⊕ J ¯mhpi, T r tK if ∃ t = (n, ¯mhpi, true,
/
0) ∈ T (g)
”in(L(m),L(a))” ⊕Jmhai,T r tK if ∃ t = (n,mhpi,true,
/
0) ∈ T (h)
” · ” Otherwise (i)
e.g. Reachable States, Non Reachable States, Confi-
dential Data, Satisfied Authenticity . . . .
For user convenience, the text results are also con-
veyed on the block and state diagrams, as previously
shown in Figure 2 and 3.
After a ProVerif verification, the state diagram dis-
plays the reachability of states, with red locks sig-
nifying unreachable states, and green ones signify-
ing reachable ones. The block diagram displays the
Authenticity and Confidentiality verification results,
shown on pragma as a colored split lock, the bottom
left half referring to Strong Authenticity, and the top
right half referring to Weak Authenticity. A lock half
colored green refers to satisfied authenticity, red to
non-satisfied, and grey refers to that which cannot be
proved. Attributes proven confidential are displayed
with a green lock and those proven non-confidential
are displayed with a red lock.
From the asymmetric key distribution described in
section 4.1, we exemplify the capabilities and limi-
tations of our translation to ProVerif. The ProVerif
verification in Figure 2 shows that confidentiality was
verified for the keys mvksk and idk1sk in both ECU1
and ECU2. Both Strong and Weak Authenticity were
proven for the two authenticity queries shown.
In the state diagrams shown in Figure 3, we con-
firm that states critical to the protocol are reachable,
and that the protocol is capable of completion. States
such as UnexpectedMsg6, which would be reachable
only due to unexpected behavior, are confirmed to be
unreachable.
Next, we demonstrate that we are capable of per-
forming security verification on state diagrams con-
taining loops. Within ECU2, we add a transition from
the last state ProtocolRunEnded back to the first state
WaitingForMsg0 to form a loop. No other modifica-
tions are made to the block or state diagrams. ECU2
is now ready to pair with any willing entity and should
use a different key for each session.
The Confidentiality properties remain identical,
but the authenticity properties have changed as shown
in Figure 4. Strong Authenticity is no longer ver-
ified with the loop because an attacker that would
have intercepted the whole exchange between ECU1
and ECU2 would be able to replay it to ECU2. This
could be corrected by using nonce instead of times-
tamps, which are considered constant. Our case study
presents an example validation and the changes due
to loops.
Figure 4: Asymmetric Key Distribution Protocol with Loop
Authenticity Result.
6 CONCLUSIONS
SysML-Sec targets the full development cycle of a
safe and secure embedded system. It is supported by
a user-friendly toolkit explicitly supporting safety and
security engineering, and offering formal verification
at the push of a button. Yet, previous contributions for
the proof of security properties had strong limitations
both in terms of modeling and proof capabilities. The
paper thus proposes a fully novel approach based on
new modeling elements (pragmas) and a new model-
to-proverif transformation. The paper formalizes both
the modeling elements and the transformation. In par-
ticular, this paper shows that our approach now sup-
ports loops and private channels, and its integration
into TTool.
SysML Models and Model Transformation for Security
337

Nonetheless, translating SysML-Sec diagrams to
ProVerif still includes limitations. They depend either
on ProVerif limitations or on the new translation pro-
cess. We present them here as a warning to potential
users and as leads for potential future work.
Loops. Even though our current translation of loops
enables proof of most properties — proof of strong
authentication would sometimes fail — and gives
sound results for others, the introduction of nonces
for chaining basic blocks may in some cases cause
ProVerif to produce a cannot be proved result. We
made this compromise since loops were likely to re-
duce the completeness of the proof. A possible im-
provement would be to enable the user to manually
provide hints to help ProVerif in its proof for diagrams
containing loops.
Arithmetic. When translating the SysML-Sec dia-
gram to ProVerif we discard any arithmetic-related
operation that is performed in actions or guards. In
fact, ProVerif has no representation for arithmetic, re-
garding operations or even types like numbers. Tak-
ing these operations into account would require us to
deeply modify the ProVerif proof engine, such as in-
terfacing it with a theory solver for instance. This is
not part of our work in the foreseeable future.
Time. Even though timers are taken into account
by our current translation, SysML after clauses are
not yet handled. However, features were added to
ProVerif in order to enable modeling of phases which
could possibly be used to translate these clauses to
some extent.
Other future work include a mathematical proof of
equivalence and a design-to-executable code process
preserving security properties.
REFERENCES
Ali, Y., El-Kassas, S., and Mahmoud, M. (2009). A rig-
orous methodology for security architecture modeling
and verification. In Proceedings of the 42nd Hawaii
International Conference on System Sciences, volume
978-0-7695-3450-3/09. IEEE.
Apvrille, A. (2015). Geek usages for your fitbit flex tracker
hack.lu, luxemburg, october 2015. Slides at fra-
madrive.org/index.php/s/Wk6nxAKMpVTdQl4.
Apvrille, L. (2003). TTool. ttool.telecom-paristech.fr.
Apvrille, L. and Roudier, Y. (2015). SysML-Sec: A model
driven approach for designing safe and secure sys-
tems. In 3rd International Conference on Model-
Driven Engineering and Software Development, Spe-
cial session on Security and Privacy in Model Based
Engineering, France. SCITEPRESS Digital Library.
Assolini, F. (2012). The Tale of One Thousand and One
DSL Modems, kaspersky lab.
Bengtsson, J. and Yi., W. (2004). Timed automata: Seman-
tics, algorithms and tools. In Lecture Notes on Con-
currency and Petri Nets, pages 87–124. W. Reisig and
G. Rozenberg (eds.), LNCS 3098, Springer-Verlag.
Blanchet, B. (2009). Automatic Verification of Correspon-
dences for Security Protocols. Journal of Computer
Security, 17(4):363–434.
Drouineaud, M., Bortin, M., Torrini, P., and Sohr, K.
(2004). A first step towards formal verification of se-
curity policy properties for rbac. In QSIC’04, pages
60–67, Washington, DC, USA.
Durgin, N., Lincoln, P., Mitchell, J., and Scedrov, A. (2004).
Multiset rewriting and the complexity of bounded se-
curity protocols. J. Comput. Secur., 12(2):247–311.
Hoppe, T., Kiltz, S., and Dittmann, J. (2011). Security
Threats to Automotive CAN Networks - Practical Ex-
amples and Selected Short-Term Countermeasures.
Rel. Eng. & Sys. Safety, 96(1):11–25.
ICS-CERT (2015). Hospira lifecare pca infusion sys-
tem vulnerabilities, advisory (icsa-15-125-01b).
https://ics-cert.us-cert.gov/advisories/ICSA-15-125-
01B.
J
¨
urjens, J. (2007). Developing secure embedded systems:
Pitfalls and how to avoid them. In 29th International
Conference on Software Engineering (ICSE 2007),
pages 182–183. ACM.
Kelling, E., Friedewald, M., Leimbach, T., Menzel, M.,
S
¨
ager, P., Seudi
´
e, H., and Weyl, B. (2009). Specifica-
tion and Evaluation of e-Security Relevant Use cases.
Technical Report Deliverable D2.1, EVITA Project.
Ma
˜
na, A. and Pujol, G. (2008). Towards formal specifi-
cation of abstract security properties. In The Third In-
ternational Conference on Availability, Reliability and
Security, volume 0-7695-3102-4/08. IEEE.
Maslennikov, D. (2010). Russian cybercriminals on the
move: profiting from mobile malware. In The 20th
Virus Bulletin Internation Conference, pages 84–89,
Vancouver, Canada.
Maynor, D. (2006). Scada security and terrorism:
We’re not crying wolf! In Invited presentation
at BlackHat BH 2006. Presentation available at:
https://www.blackhat.com/presentations/bh-federal-
06/BH-Fed-06-Maynor-Graham-up.pdf, USA.
Shen, G., Li, X., Feng, R., Xu, G., Hu, J., and Feng, Z.
(2014). An extended uml method for the verifica-
tion of security protocols. In Engineering of Com-
plex Computer Systems (ICECCS), 2014 19th Inter-
national Conference on, pages 19–28.
Toussaint, M. J. (1993). A New Method for Analyzing the
Security of Cryptographic Protocols. In Journal on
Selected Areas in Communications, volume 11, No. 5.
IEEE.
Trcek, D. and Blazic, B. J. (1995). Formal language for
security services base modelling and analysis. In El-
sevier Science Journal, Computer Communications,
volume Vol. 18, No. 12. Elsevier Science.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
338