Machine Learning based Number Plate Detection and Recognition

Zuhaib Ahmed Shaikh, Umair Ali Khan, Muhammad Awais Rajput and Abdul Wahid Memon

Department of Computer Systems Engineering, Quaid-e-Awam University of Engineering,

Science & Technology Nawabshah, Pakistan

Keywords:

Number Plate, Support Vector Machine, Deformable Part Model.

Abstract:

Automatic Number Plate Detection and Recognition (ANPDR) has become of signiﬁcant interest with the

substantial increase in the number of vehicles all over the world. ANPDR is particularly important for auto-

matic toll collection, trafﬁc law enforcement, parking lot access control, and gate entry control, etc. Due to the

known efﬁcacy of image processing in this context, a number of ANPDR solutions have been proposed. How-

ever, these solutions are either limited in operations or work only under speciﬁc conditions and environments.

In this paper, we propose a robust and computationally-efﬁcient ANPDR system which uses Deformable Part

Models (DPM) for extracting number plate features from training images, Structural Support Vector Machine

(SSVM) for training a number plate detector with the extracted DPM features, several image enhancement

operations on the extracted number plate, and Optical Character Recognition (OCR) for extracting the num-

bers from the plate. The results presented in this paper, obtained by long-term experiments performed under

different conditions, demonstrate the efﬁciency of our system. They also show that our proposed system

outperforms other ANPDR techniques not only in accuracy, but also in execution time.

1 INTRODUCTION

The signiﬁcant increase in number of vehicles has

invoked the need of automatic surveillance system.

Speciﬁcally, for automatic number plate detection and

recognition system, image processing based solution

is more accurate due to the following reasons: (i) im-

ages contain a lot of information which can be uti-

lized from different perspectives, (ii) the availability

of high-resolution, high dynamic range and speedy

cameras has made it possible to capture a scene and

analyze it under different lighting conditions, (iii) im-

age processing based solutions for trafﬁc surveillance

are cost-effective, small-sized, portable and robust.

An image processing based ANPDR system is

likely to avoid the need of larger, expensive and heavy

sensors such that the required information can be ex-

tracted from a single image. However, such a sys-

tem also faces some dedicated challenges such as: (i)

computational efﬁciency, (ii) robustness with multi-

scaled and skewed images, (iii) robustness with dis-

torted images, and (iv) acceptable accuracy under dif-

ferent lighting conditions.

Integrating image processing with machine learn-

ing techniques results in an adaptive and more accu-

rate system. Instead of ﬁnding speciﬁc features in

images in order to locate the number plate, training

a number plate detector with pre-extracted features

results in a robust and computationally-efﬁcient sys-

tem. Such system can be efﬁciently implemented on

an embedded platform to achieve mobility and com-

patibility for several tasks.

In this paper, We propose a robust and

computationally-efﬁcient ANPDR system. In of-

ﬂine processing (performed once), we train a number

plate detector using Deformable Part Models (DPM)

(Felzenszwalb et al., 2010)(Felzenszwalb et al., 2008)

and SSVM which can then be applied online for

extracting number plates from the captured images.

The extracted plates are further enhanced using sev-

eral image processing operations and then input to an

OCR module for recognition. Our proposed method

requires a small number of training samples (25-30

images) without requiring any negative samples. Ad-

ditionally, the proposed technique can be used to train

any classiﬁer for detecting and extracting any object

of interest in the images.

The rest of the paper is organized as follows. In

section 2, we discuss the existing ANPDR techniques

along with their pros and cons. Section 3 gives a the-

oretical background of deformable part models. Sec-

tion 4 provides a brief overview of SVM and SSVM.

Section 5 describes the overall methodology along

with several image enhancement operations. Section

Shaikh, Z., Khan, U., Rajput, M. and Memon, A.

Machine Learning based Number Plate Detection and Recognition.

DOI: 10.5220/0005750203270333

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 327-333

ISBN: 978-989-758-173-1

327

6 provides some experimental results and comparison

with the existing techniques. Section 7 concludes the

paper.

2 RELATED WORK

Relevant literature demonstrates a number of ANPDR

techniques. In (Hongliang and Changping, 2004), au-

thors propose a number plate extraction method that

is based on edge detection and analysis as well as

morphological operations. In (Le and Li, 2006), au-

thors propose another hybrid method that detects edge

lines in the edge map and computes a weight based

edge density map. Regions with the densest edges

are selected as candidates and further reﬁned. An-

other edge-based method (Qiu et al., 2009) ﬁnds the

region of interest through various steps and then an-

alyzes the region of interest by the inner and outer

shape features of number plate. A common drawback

of all these edge-based methods is that they result in

high false rate in presence of rich features and similar

shape in images. The technique proposed in (Zhou

et al., 2012) extracts Scale-invariant Feature Trans-

form (SIFT) features of each character in the num-

ber plate and generates a respective principle visual

word unsupervised clustering. The geometrical infor-

mation contained in each visual world is used to ﬁl-

ter false feature matches. However, this method does

not deliver an acceptable accuracy for low-resolution

and distorted images which is an inherent limitation

of SIFT features.

Another technique proposed in (Baggio, 2012) ap-

plies a number of operations on image such as Sobel

ﬁlter, threshold operation, close morphologic opera-

tion, mask on one ﬁlled area, detection of potential

plates, and linear SVM training. After detection, the

number pate is fed to an OCR based on a three-layer

neural network to extract the characters of detected

number plate. This method is not robust for differ-

ent scaling images, especially those with tilted plates.

In (Prates et al., 2013), the authors use Histogram of

Orientated Gradients (HOG) for number plate detec-

tion. This approach builds a pyramid of images that

is scanned using a sliding window approach. HOG

features are extracted for the regions of interest and

provided to a linear SVM classiﬁer. This approach

can ﬂexibly work with images with different scal-

ing. However, the linear SVM is prone to discarding

prior data distribution information within classes due

to major focus on margin maximization.

3 DEFORMABLE PART MODELS

In contrast to HOG features (Dalal and Triggs, 2005)

discussed in the previous section, Deformable Part

Models (DPM) are more effective because they use

spatial-part ﬁlters for sub-objects which result in sig-

niﬁcant improvement in detection accuracy.

DPM models are basically derived from HOG fea-

tures. HOG method is based on evaluating well-

normalized local histograms of image gradient orien-

tations in a dense grid. In order to extract the HOG

features, the image window is divided into small spa-

tial regions (cells) and a local 1-D histogram of gra-

dient directions or edge orientations is computed for

each cell. The combined histogram entries form the

representation. For better performance, a measure

of local histogram energy is accumulated over larger

spatial regions (blocks). The results are then used

to normalize all cells in the block (Dalal and Triggs,

2005).

DPM models use a star-structured part-based

model deﬁned by a root ﬁlter plus a set of part ﬁlters

and deformation models (Felzenszwalb et al., 2010).

Each part model speciﬁes a spatial model and a part

ﬁlter. The spatial model deﬁnes a set of allowed

placements for a part relative to a detection window

and a deformation cost for each placement. The score

of a detection window is the score of the root ﬁlter

on the window plus the sum over parts, the maximum

over placements of that part, and the part ﬁlter score

on the resulting sub-window minus the deformation

cost. Both root and part ﬁlters are scored by com-

puting the dot product between a set of weights and

HOG features within a window (Felzenszwalb et al.,

2008). Figure 1 shows the construction of a feature

pyramid for a number plate. The pyramid is obtained

by extracting HOG features of each level of a standard

image pyramid. The root ﬁlter is placed near the bot-

tom of the pyramid and the the part ﬁlters are placed

near the top of the pyramid. The features extracted

this way from all the training samples are then input

to a SSVM training algorithm to construct a number

plate detector.

4 TRAINING NUMBER PLATE

DETECTOR

For training a number plate detector from the ex-

tracted features, we need margin based parameter

learning that has recently become popular in image

processing. It can be performed with Support Vec-

tor Machine (SVM) which is one of the most pop-

ular machine learning techniques used for classiﬁca-

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

328

Figure 1: Feature pyramid for a number plate.

tion and regression analysis. SVM discovers the opti-

mal boundary between two classes in the vector space

on probabilistic distribution of training by ﬁnding hy-

perplanes. The extracted features of number plates

x ∈ X are used for training with classes Y ∈

{

−1, +1

}

where +1 and −1 represents presence and absence

of number plate, respectively. The hyperplanes are

found with w

x+b, where w

is optimal or minimum

weight from vector of weights for each feature that re-

sembles with a class y ∈ Y and b is a constant called

bias constant (Cortes and Vapnik, 1995).

The traditional linear SVM is a binary classiﬁer

which can make only simple predictions (e.g., yes or

no). In contrast, Structured SVM (SSVM) (Nowozin

and Lampert, 2011)(Wendel et al., 2011) is a more

generalized form of SVM which not only inherits the

appealing features of linear SVM (e.g., convex train-

ing, learning non-linear rules, etc), but also results

in much higher prediction accuracy than linear SVM

(Joachims et al., 2009b). Although SSVM is specially

designed for parsing and more complex predictions in

the form of labeled trees (e.g, natural language pro-

cessing), its higher prediction accuracy and the capa-

bility of learning complex outputs (Joachims et al.,

2009a) are the appealing features to use it for training

a number plate detector.

In SSVM, a weight vector w

is associated to each

class y. During the training, a score is computed for a

given feature and its class label by the following rule,

f (x, y) = w

φ(x) (1)

where φ(x) represents the vector of the extracted fea-

tures from x . SSVM uses the following prediction

rule to map x to the class having highest score.

h(x) = argmax

y∈Y

f (x, y) (2)

The value of y giving the maximum score deﬁnes

the predicted class. SSVM search in the parame-

ter space of f (x, y) is directed to ﬁnd the weights

w = (w

, ..., w

) that satisfy the following inequality.

f (x

, y

) > max f (x

, y

incorrect

) (3)

This leads to the formulation of a parameter vector for

which f (x, y) always produces the highest score to the

correct output. SSVM optimization problem can now

be expressed as follows,

minh(w) =

||w||

R(w) (4)

where

R(w) =

∑

i=1

max

(c(i,Y ) + f (x

,Y |w) − f (x

, y

|w))

(5)

In equation 5, x

represents the i

training sample, y

denotes the correct label for the i

training sample,

and c(i,Y ) is the cost of predicting that the i

training

sample has a label of Y . For the correct label of i

sample, cost becomes zero. R(w) deﬁnes the degree

of error in predicting the label of the i

sample us-

ing parameters w. It is zero when the correct label is

predicted and becomes large for wrong outputs. That

is, the objective function (equation 4) is minimizing

a balance between making the weights small and ﬁt-

ting the training data. The degree of ﬁtting the data is

controlled by D > 0.

5 OVERALL ANPDR SYSTEM

The overall ANPDR system proposed in this paper is

shown in Figure 2.

The various component of the overall system are

as follows.

5.1 Ofﬂine Processing

The ofﬂine processing involves collecting the image

dataset for training, extracting the DPM features from

Machine Learning based Number Plate Detection and Recognition

329

Figure 2: The proposed ANPDR System.

the Regions of Interest (ROI), and training a number

plate detector using SSVM. We obtain images of ve-

hicles having number plates from different locations.

For the training purpose, we use only 25-30 images

with VGA resolution. For extracting DPM features,

the ROIs are marked manually by drawing rectangles

around the number plates and extracting their coor-

dinates which represent the positive training samples.

The negative samples include the entire image other

than the ROI. Figure 3 shows some images from our

dataset.

Figure 3: Example images from our dataset.

After preparing the image dataset, we extract the

DPM features from the ROIs as described in section

3. The extracted feature vectors are then input to the

SSVM for training the number plate detector. Figure

4 shows the construction of the number plate detector.

5.2 Online Processing

In online processing, the trained number plate detec-

tor is applied to the images captured from a camera.

The detector searches for the number plates in the suc-

cessive images and, if found, returns the plate’s coor-

Figure 4: Construction of the number plate detector.

dinates. Figure 5 shows the number plate detection

with the detector trained with SSVM.

Figure 5: Number plate detection with SSVM detector.

After locating the number plate, it is cropped from the

image and the following enhancement techniques are

applied on the extracted image.

5.2.1 Bilateral Gaussian Filtering

A bilateral Gaussian ﬁlter is applied on the cropped

image to remove noise from the image. The ﬁlter-

ing radius is set to 5. Whereas, the sigma-color and

sigma-space is set to 80 from different experimental

results.

5.2.2 Adaptive Thresholding

The ﬁltered image is converted into gray scale and an

adaptive threshold is applied to binarize the image for

handling different lighting conditions. A new inten-

sity value for each pixel is computed by taking the

weighted sum of the neighboring pixels in radius r.

The weights are a Gaussian window which performs

better for textual images.

5.2.3 De-skewing

The extracted number plate may have some skew-

ness which affects the recognition accuracy of the

OCR. Therefore, the skew angle of the binary image

is calculated using probabilistic Hough transform. We

form some dense horizontal lines along the adjacent

pixels and calculate their mean angle d

using equa-

tion 6,

∑

i=1

arctan

−1

(

−y

−x

)

(6)

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

330

where x

and y

represent the end points of the n

lines. We then create a rotation matrix according to

the computed skewness and multiply it with the cen-

ter of the binary image if d

< −2.50 or d

> +2.50.

Figure 6 shows the formation of dense horizontal lines

to compute skewness.

(a) Extracted

plate

(b) Finding

skewness

Figure 6: Computing skewness from dense horizontal lines.

5.2.4 Extracting the Numbers Region

The de-skewed image still contains unnecessary parts

which create muddle during OCR. For removing these

parts and extracting the characters region, contour op-

eration is applied and a bounding box around each

character in the plate is computed. We ﬁnd the region

of interest containing only characters from the coordi-

nates of the bounding boxes of ﬁrst and last character.

All other bounding boxes having area less than a cer-

tain threshold are discarded. The region of interest is

cropped and inverted using a binary threshold to in-

crease accuracy of the OCR operation. Subsequently,

we use an open-source engine Tesseract (Tesseract-

OCR, ) for optical character recognition and extract-

ing the numbers from the image. Figure 7 shows the

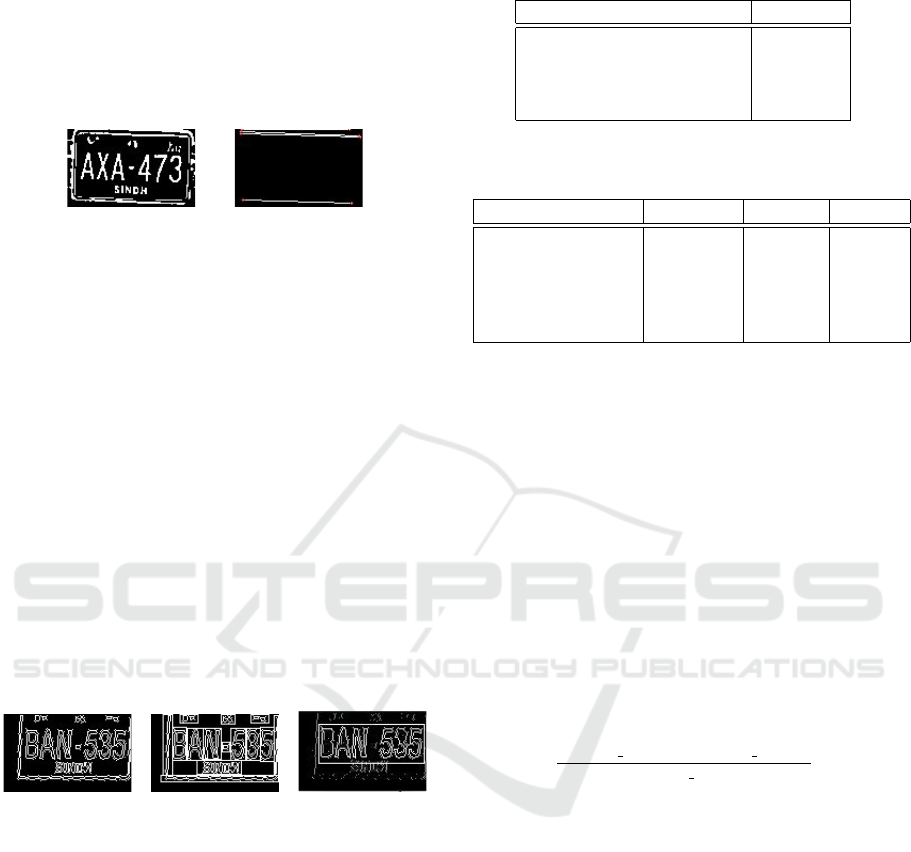
selection of ROI from the bounding boxes.

(a) Extracted

plate

(b) Bounding

boxes

terest

Figure 7: Extracting the ROI from bounding boxes.

6 EXPERIMENTAL RESULTS

AND EVALUATION

We train the number plate detector with only 25-30

images, each annotated with rectangles that bound

each number plate in the image. We then create an im-

age pyramid of 6 levels for each image and the DPM

model is applied over each pyramid level in a slid-

ing window fashion. We use a sliding window of size

100×60 pixels, however, it can be changed according

to the number plate dimensions for a particular region.

The extracted feature vector is then sent to SSVM for

training. We control the degree of ﬁtting the data by

Table 1: Evaluation of the proposed ANPDR system.

Evaluation parameter value

Detection accuracy 96.03%

Recognition accuracy 78.00%

False positive rate 03.97%

Detection+Extraction time 02.80 sec

Table 2: Comparison of the proposed ANPDR with existing

ANPDR techniques.

Technique Accuracy FPR Time

Hybrid 71.40% 28.64% 38.86 s

Vertical edge 70.50% 29.50% 01.40 s

Edge statistics 74.10% 25.94% 07.09 s

Visual words 95.50% 04.50% 07.17 s

Proposed ANPDR 96.03% 03.97% 02.80 s

setting D = 6. In general, a bigger D encourages to

ﬁt the training data better, however, a too large value

might lead to over-ﬁtting. The training continues until

R(w) in equation 4 is less than a certain threshold ε. In

order to solve the SSVM optimization problem more

accurately, we set ε to a smaller value, i.e., ε = 0.001.

The trained detector is then tested for a number of

different scenarios. Figure 8 shows all the stages of

number plate detection and recognition. Note that

our number plate detector can efﬁciently detect multi-

scaled and skewed number plates. In Figure 8b, the

detector is able to detect the distant number plate

which is seen through the windscreen of a car. We

calculate the False Positive Rate (FPR) and the overall

accuracy of our detector by the following equations.

FPR =

no. f alse positive + no. f alse negative

no. test cases

× 100

(7a)

Accuracy = 100 − FPR (7b)

The detection accuracy, false positive rate, recogni-

tion accuracy, and the overall execution time of our

detector are given in Table 1. The experiments were

performed on a PC with 2.5 GHz CPU and 6 GB

RAM.

We also compare the performance of our AN-

PDR system with some existing ANPDR techniques

such as (i) a hybrid method (Le and Li, 2006) com-

prising line detection in the edge map, obtaining an

weight based edge density map, and reﬁning the dens-

est edges, (ii) a vertical edge detection based method

(Qiu et al., 2009), (iii) a method based on the edge

statistics and morphology (Zhou et al., 2012), and (iv)

a method using the visual bag-of-words model (Zhou

et al., 2012). For the sake of fair comparison, we use a

common image dataset (Caltech Cars Dataset, ) with

the same machine conﬁguration. Table 2 shows our

comparison results.

Machine Learning based Number Plate Detection and Recognition

331

(a) Multi-scaled, skewed plates detection

(b) A difﬁcult case of detecting occluded and distant number plate

Figure 8: Testing the detector for different cases.

From Table 2, it is evident that our proposed AN-

PDR system not only outperforms other techniques

with respect to accuracy, but also execution time.

7 CONCLUSION

In this paper, we have proposed an automatic num-

ber plate detection and recognition technique using

deformable part models for extracting the number

plate features and structural support vector machine

for training a number plate detector. The number

plate extracted from the scenes captured by a cam-

era are further enhanced for improving the accuracy

of optical character recognition. The trained detector

can efﬁciently detect multi-scaled and skewed num-

ber plates under varying light conditions. The results

presented in this paper show that our proposed AN-

PDR technique delivers a higher accuracy with much

less execution time as compared to other ANPDR

techniques. Additionally, the proposed technique can

be easily implemented for ANPDR in any region with

small changes in the training parameters.

In future, we aim to migrate our ANPDR system on an

embedded platform with Compute Uniﬁed Device Ar-

chitecture (CUDA) capability for increased portabil-

ity and faster processing by parallel computing. Addi-

tionally, we aim to further improve the accuracy and

detection time by deﬁning a region of interest spe-

ciﬁc to the scene. Our future research is also focused

on improving and optimizing the image enhancement

part of the ANPDR for delivering higher accuracy un-

der extremely low light conditions.

REFERENCES

Baggio, D. L. (2012). Mastering OpenCV with practical

computer vision projects. Packt Publishing Ltd.

Caltech Cars Dataset. http://www.vision.caltech.edu/Image

Datasets/cars markus/cars markus.tar. [Accessed:

30 December, 2015].

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine learning, 20(3):273–297.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion, volume 1, pages 886–893.

Felzenszwalb, P., McAllester, D., and Ramanan, D. (2008).

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

332

A discriminatively trained, multiscale, deformable

part model. In IEEE Conference on Computer Vision

and Pattern Recognition, pages 1–8.

Felzenszwalb, P. F., Girshick, R. B., McAllester, D., and

Ramanan, D. (2010). Object detection with discrim-

inatively trained part-based models. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

32(9):1627–1645.

Hongliang, B. and Changping, L. (2004). A hybrid license

plate extraction method based on edge statistics and

morphology. In Proceedings of the 17th International

Conference on Pattern Recognition, volume 2, pages

831–834.

Joachims, T., Finley, T., and Yu, C.-N. J. (2009a). Cutting-

plane training of structural svms. Machine Learning,

77(1):27–59.

Joachims, T., Hofmann, T., Yue, Y., and Yu, C.-N. (2009b).

Predicting structured objects with support vector ma-

chines. Communications of the ACM, 52(11):97–104.

Le, W. and Li, S. (2006). A hybrid license plate extrac-

tion method for complex scenes. In 18th International

Conference on Pattern Recognition, volume 2, pages

324–327.

Nowozin, S. and Lampert, C. H. (2011). Structured learn-

ing and prediction in computer vision. Foundations

and Trends in Computer Graphics and Vision, 6(3–

4):185–365.

Prates, R., C

amara-Ch

avez, G., Schwartz, W. R., and

Menotti, D. (2013). Brazilian license plate detection

using histogram of oriented gradients and sliding win-

dows. International Journal of Computer Science and

Information Technology, 5(6):39–52.

Qiu, Y., Sun, M., and Zhou, W. (2009). License plate ex-

traction based on vertical edge detection and mathe-

matical morphology. In International Conference on

Computational Intelligence and Software Engineer-

ing, pages 1–5.

Tesseract-OCR. https://code.google.com/p/tesseract-ocr/.

[Accessed: 30 December, 2015].

Wendel, A., Sternig, S., and Godec, M. (2011). Structured

learning and prediction in computer vision. In 16th

Computer Vision Winter Workshop, pages 1–7.

Zhou, W., Li, H., Lu, Y., and Tian, Q. (2012). Princi-

pal visual word discovery for automatic license plate

detection. IEEE Transactions on Image Processing,

21(9):4269–4279.

Machine Learning based Number Plate Detection and Recognition

333