Approaching a Target using a Protection Feature based on Received

Signal Strength Indicator

Kazuyuki Ishii and Naoshi Sato

Information Security, Institute of Information Security,

2-14-1 Turuya-cho, Kanagawa-ku, Yokohama, Kanagawa, 221-0835, Japan

Keywords:

Search, RSSI, Approach and Departure, Protection Step Number, Wireless Device.

Abstract:

The received signal strength indicator (RSSI) which can be obtained during wireless communication, depend-

ing on communication distance, and is used to estimate the distance between a sender and receiver. We focus

on the RSSI to determine whether a mobile node is approaching or departing from a target node (TN). To

determine approach or departure, we implement the protection step number (PSN) as a protection feature that

determines approach or departure when RSSI varies N times of the PSN in a row. N is designed accord-

ing to RSSI deviation, and the value is computed statistically. In this paper, we demonstrate a method for

approaching a TN based on RSSI with and without the proposed PSN.

1 INTRODUCTION

1.1 Background and Motivation

Recently, interest in ad-hoc communication, which

can enable communication between wireless devices,

has been increasing. Wireless devices utilize a non

directional antenna to communicate in any direction

in ad-hoc communication. It can be useful during a

natural disaster as an emergency request from a dis-

aster victim can be received via ad-hoc communica-

tion(Toh, 2001)(Mase and Sakata, 2007). However, it

is difﬁcult for rescue teams to approach disaster vic-

tims if there is a lack of location information rela-

tive to the disaster victims. Thus, we focus on the

received signal strength indicator (RSSI), which can

be obtained during wireless communication. In the-

ory, RSSI is an ordinal scale(Stevens, 1946) that is

inversely proportional to the square of communica-

tion distance in theory(Friis, 1946). Therefore, the

magnitude relationship of the RSSI value represents

distance. The varying strength of the RSSI value

can determine whether one is getting closer o further

away from a disaster victim. Therefore, we study how

wireless devices that receive an emergency request

(mobile node, MN) approach a disaster victim’s re-

questing wireless device (target node, TN).

1.2 Problem Statement

We consider the following problems.

• It is difﬁcult to determine approach or depar-

ture, i.e., moving toward or away from the TN,

respectively, by comparing between RSSI value

because they can change signiﬁcantly in the

same environment due to seasonal and weather

changes(Rappaport et al., 1996).

• It is difﬁcult to estimate the direction of arrival

(DoA) because wireless devices employ non-

directional antennas(Carr, 1993).

For these reasons, it is difﬁcult for the MN to ap-

proach the TN when the distance between the MN and

TN and the direction of the TN’s signal are unknown.

1.3 Objective

When moving to a TN using varying RSSI strengths

depending on measurement points, a protection fea-

ture is implemented to determine approach/departure

(approach/departure determination). We propose the

protection step number (PSN) as a protection feature

to prevent erroneous determination and reduce the

probability of moving in the wrong direction. This

number is designed statistically in consideration of

the current environment. To study an MN moving to

a TN based on RSSI, we assume that the MN and TN

170

Ishii, K. and Sato, N.

Approaching a Target using a Protection Feature based on Received Signal Strength Indicator.

DOI: 10.5220/0005750701700177

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 170-177

ISBN: 978-989-758-171-7

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

can communicate directly. In this study, we evalu-

ate an MN approaching a TN using the PSN through

computer simulation.

The reminder of this paper is organized as follows.

Section 2 discusses related work. Section 3 describes

the proposed method, including an overview, details,

and a description of our computer simulation model.

Approach/departure determination and the PSN are

also discussed in the Section 3. Section 4 presents

various simulation results, including a comparison be-

tween the proposed method and unused it. Section

5 discusses the results of computer simulations, and

conclusions are given in Section 6.

2 RELATED WORK

In order to approach a TN, the following three ele-

ments are considered.

(a) Estimation of distance based on RSSI. Many

studies of positioning techniques using wireless de-

vices have been conducted. In these studies, dis-

tance is estimated by trilateration(

Capkun et al., 2002;

Niculescu and Nath, 2001; Priyantha et al., 2001;

Niculescu and Nath, 2003), which estimates the dis-

tance of an objective node while measuring the dis-

tance from more than three anchor nodes. Trilat-

eration is prone to error in distance estimation due

to error in the measured RSSI value. The trilatera-

tion method requires more than three anchor nodes

,whereas the proposed method uses only two nodes

to approach the TN. (b) Estimation of DoA based on

RSSI. Transmitter hunting is an activity in which par-

ticipants use radio-direction-ﬁnding techniques to lo-

cate one or more radio transmitters hidden within a

designated search area(Harker, 2008). Note that gen-

eral wireless devices supporting ad-hoc communica-

tion use non directional antennas. The hardware used

in transmitter hunting differs from that used in ad-hoc

communication. (c) Movement based on RSSI. We

review studies about using mobile robots for search

and rescue. Such mobile robots approach a TN us-

ing sensor nodes. The mobile robot moves randomly

from P

and stops at one of P

, P

or P

that is

closer to the TN than P

. The movement tracking and

points P

· · · P

are deﬁned by the initial distance d

to the TN, and the moving distance is (1/2)d. The

mobile robot moves to this node by heuristic move-

ment following RSSI-based distance estimation, and

which is repeated(Li et al., 2012). In the literature(Li

et al., 2012), the stopping of movement and change in

moving direction are determined by the difference in

RSSI-based distance estimation, however, no protec-

tion feature is used.

As described above, the related work is described

from three perspectives. These studies use trilatera-

tion for distance estimation, directional antennas to

determine radio direction, and heuristic movementac-

cording to RSSI-based distance estimation. There-

fore, these methods differsfrom the proposed method,

which employs the protection feature.

3 PROPOSAL METHOD

3.1 Overview

Since RSSI values vary with the environment, the

calibration of RSSI propagation model(Mao et al.,

2007) or ﬁltering to remove unwanted components

(noise)(Pathirana et al., 2005) and the communica-

tion distance is required. This study employ an ap-

proaching method that uses approach/departuredeter-

mination based on varying RSSI values from wireless

devices with non directional antennas. The proposed

method does not use calibration or ﬁltering to mea-

sure RSSI or estimate communication distance. It is

difﬁcult to determine approach/departure depending

using RSSI strength. The PSN as a protection feature

is implemented for approach/departuredetermination.

When the protection feature is used and the departure

is determined N times in a row, the moving direction

changes. Approach/departure are determined by de-

creasing and increasing RSSI values, respectively, N

times of the PSN in a row, while the MN moves in

a straight line from a to c. Then, the moving direc-

tion is changed at b

′

when determining approach us-

ing approach/departure determination. An overview

is shown in Fig. 1. With this method, incorrect ap-

proach/departure determination is prevented and the

probability of determining an incorrect moving direc-

tion is reduced. We evaluate an MN approachinga TN

using the PSN according to approach/departuredeter-

mination through computer simulation. The notations

used in this paper are described in Table 1.

3.2 Assumption

The MN assumes a general wireless node that imple-

ments IEEE 802.11b and supports ad-hoc communi-

cation. It is assumed that a non directional antenna

is employed by the MN. In addition, the MN has the

following capabilities.

• RSSI measurement

• Moving distance measurement

• Moving direction control

Approaching a Target using a Protection Feature based on Received Signal Strength Indicator

171

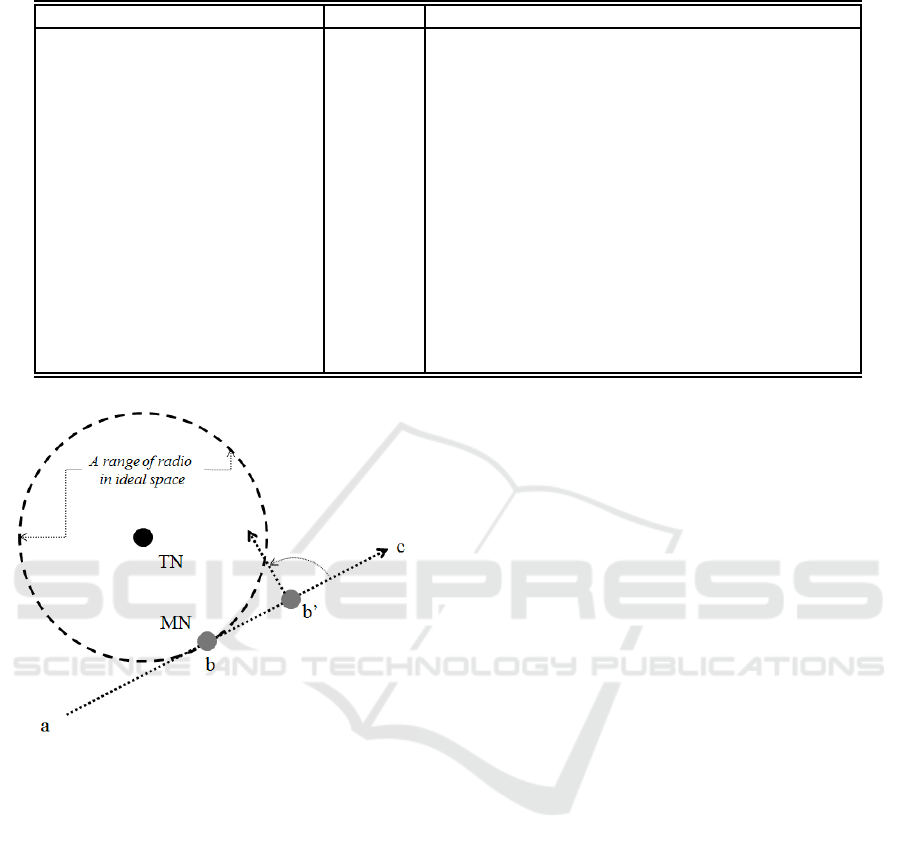
Table 1: Notations.

Name Notation Description

Mobile Node MN Node approaching TN

Target Node TN Node approached by MN

Step width sw Distance of one step

Maximum number of step times limax Maximum number of step times in one trial

RSSI P

RSSI at i (i = 0,1, 2, 3,···)

SRSSI SP

Smoothed RSSI at i

Reference value Ref

rssi

Value to compare with P

Moving direction control amount mangle Amount of change in the moving direction

Protection Step Number PSN Protection feature to determine

Threshold limen Distance from TN to end the approach

Decreasing counter Counter

Increment when P

is decreased compared to Ref

rssi

(Counter

= 0,1,2,3, · · ·)

Increasing counter Counter

Increment when P

is increased compared to Ref

rssi

(Counter

= 0,1,2,3, · · ·)

Signiﬁcance level α Value for signiﬁcance test

Figure 1: Overview of approach/departure determination.

The TN has the same functions and sends a beacon

signal to the MN periodically.

3.3 Details

Here, we describe the TN based on RSSI using ap-

proach/departure determination. The approach proce-

dure for the MN is described below. Fig. 2 shows a

ﬂowchart that describes the approach process.

1. [i+ +] Update i.

2. [MeasureRSSI(P

)] The MN measures RSSI (P

)

at i from the TN.

3. [Set Re ference RSSI] When starting the approach,

becomes the reference value (Ref

rssi

4. [Define Protectionstepnumber] PSN (N) is set.

5. [Target Detection] Check whether the MN is

within limen. If the MN is within limen, the sim-

ulation ends.

6. [CompareRSSI] Compare P

to Ref

rssi

> Ref

rssi

(Approach) →



Counter

= 0

Counter

+ +

< Ref

rssi

(Departure) →



Counter

+ +

Counter

= 0

= Ref

rssi

(Unknown) →



Counter

= 0

Counter

= 0

7. [U pdateRef

rssi

] Compare each counter with N

of the PSN. When Count

≥ N or Count

≥ N,

Ref

rssi

is updated and both counters are reset as

follows.



Counter

= 0

Counter

= 0

Then, Re f

rssi

is selected as the minimum P

be-

tween the current location (t + N − 1) and the

location starting the counting (t) of Count

Count

. In order to prevent from occurring ap-

proach determination frequently, the minimum

RSSI is selected.

Ref

rssi

= min{P

t+1

,...., P

t+N+1

} (1)

8. [Changedirection] Execute the change in moving

direction. The moving direction control amount

(mangle) is 0 when Count

< N or Count

< N.

mangle is π/2 when Count

≥ N. mangle is 0

when Count

≥ N because the MN is approach-

ing the TN. The MN moves in a counterclockwise

direction.

9. [Move] Move sw as a single step. One direction is

selected when the approach process begins.

10. Repeat 1).

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

172

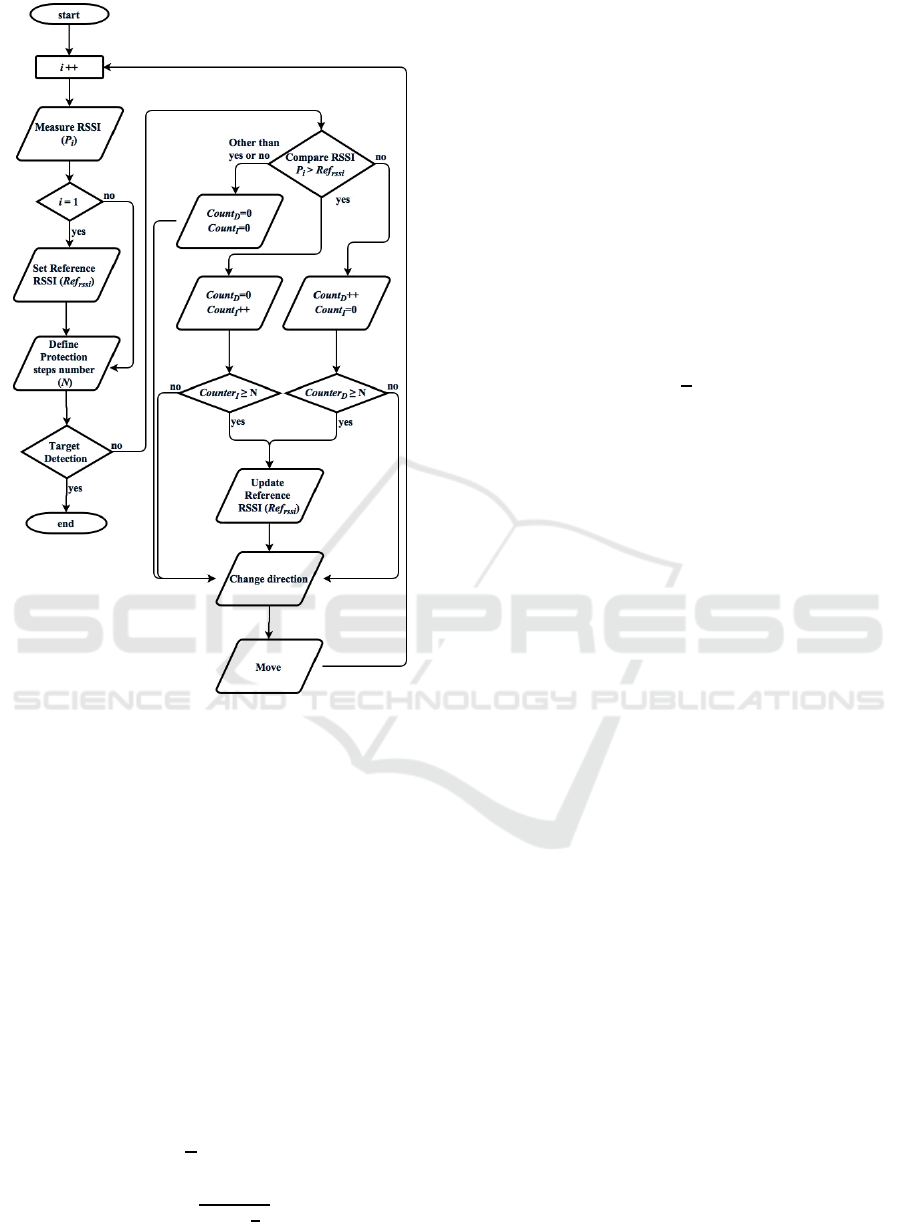
Figure 2: Flowchart of approach in processing for MN.

3.3.1 PSN in Approach/Departure

Determination

The purpose of approach/departure determination is

to determine whether the MN moving toward or away

from the TN according to the measured RSSI at each

step. The MN compares P

and Ref

rssi

to determine

the magnitude relation.

The MN moves a single step and the probability

of determining the MN is approaching or departing is

1/2 when comparing RSSI to Ref

rssi

. We assume that

the MN determines approach or departure N times se-

quentially and the PSN is N. The formula to calculate

probability is



1/2



, and the signiﬁcance level (α)

is used, which is the probability of rejecting the null

hypothesis. Thus, N is the minimum integer value.





< α

N >

log

(α)

log

(

)

(2)

Note that α is set to 0.05 and then N becomes 5.

Due to varying RSSI values caused by environ-

mental conditions, we assume that the deviation of

RSSI is used for the PSN. This deviation is obtained

as the mean deviation while the MN moves. The

mean deviation (MD

) at i is obtained from P

and

the smoothed RSSI (SP

) at i. Then MD

is changed

to SD

because the mean deviation is nearly equal to

1.25× standarddeviation(Jacobson, 1988), SD

[dB]

can be obtained by MD

in mW which is converted

from dBm.

[dB] = |P

[dBm] − SP

[dBm]| (3)

[dB] = 10log

(0.8× MD

[mW]) (4)

is obtained by the nth RSSI from P

i−n+1

to P

mW which is converted from dBm.

[mw] =

∑

t=i−n+1

[mW] (5)

[dBm] = 10log

(SP

[mw]) (6)

where n is the number of samples and i ≥ n − 1 is

satisﬁed. When i is less than n − 1, SP

= P

. In this

paper, the number of samples, n, is 3.

Here, we consider two PSNs. One is a ﬁxed value,

which is calculated statistically, and the other is based

on the deviation of RSSI, which can be obtained while

the MN moves. Thus, the PSN is an integer value

selected as the maximum value of the two PSNs at i.

Note that the PSN is deﬁned as N1 as follows.

N1 ← max{SD

,5} (7)

We determine the approach to the TN when P

in-

creases from Re f

rssi

N1 times in a row, and we deter-

mine departure from the TN when P

decreases from

Ref

rssi

N1 times in a row. It is expected that N1 pre-

vent incorrect determination from the varied P

, i.e.,

the measured RSSI value.

3.3.2 Moving Direction Control

The moving direction control controls the moving di-

rection according to the approach/departure determi-

nation. To increase the possibility of encountering the

TN, the movement trajectory of the MN is a spiral box

search, i.e., mangle is 0 or π/2 in a counterclockwise

direction.

4 RESULT

Here, we evaluate the performance of the proposed

method through computer simulation based on the

PSN (Eq.(7)). First, we compare the incorrect ap-

proach determination rate using the PSN (P

com-

pared to Ref

rssi

), not using the PSN (P

compared to

Approaching a Target using a Protection Feature based on Received Signal Strength Indicator

173

i−1

) and using the PSN (SP

compared to Ref

rssi

) to

evaluate the PSN of N1. For approaching using the

PSN with SP

, Ref

rssi

is selected as the minimum SP

rather than P

in Eq.(1). We then show the erroneous

decision rate of approaching, the average MN moving

distance, and the ratio between the average MN mov-

ing distance and the direct distance between the start

point and the target relative to the start point.

4.1 Computer Simulation

The proposed model is evaluated by computer simula-

tion which deals with the plane on which MN and TN

are allocated and move. In addition, RSSI, which can

be obtained during wireless communication, is simu-

lated. RSSI is measured at i and is denoted by P

4.1.1 Plane of Approach

The plane of approach is a two-dimensional lattice in

the x − y plane. The distance between the lattices is

0.5 [m]. The MN and TN are positioned on this x− y

plane, and it is assumed that there are no obstacles

between these nodes.

4.1.2 MN

The MN moves at a constant speed to adjacent lattice

points on the left, right, top or bottom of the x − y

plane. At each lattice point the MN determines P

from the TN.

4.1.3 TN

The TN is located on at the origin (0, 0) at x− y plane

and does not move.

4.1.4 Radio Propagation Model

The TN transmits signals such as a beacon sig-

nal, and the MN measures P

. The radio propaga-

tion model uses a generic model, i.e., the variations

in RSSI follow a log-normal distribution(Rappaport

et al., 1996)(Fall and Varadhan, ).

[dBm] ∼ N (

[dBm],σ

) (8)

[dBm] = P

[dBm] − 10· γ· log





(9)

Here, P

[dBm] is RSSI measured at i and

[dBm]

is the average RSSI at i. σ

is the variance, i.e., the

varied measurements of RSSI, and N (

[dBm],σ

)

indicates a log-normal distribution of

and σ

. P

[dBm] is RSSI at reference distance d

[m], and d

[m] is 1 [m]. Thus, P

using a free space model(Friis,

1946) (frequency: 2.4 [GHz], transmitting power: 10

[mW](Porcino and Hirt, 2003), antenna gain: 1) as -

30.05 [dBm]. d [m] is communication distance, and

γ is the path loss exponent. It is assumed that d and

γ are unknown parameters in the MN and TN. The

parameters used in Eq.(8) are listed in Table 2.

Table 2: RSSI parameters.

Variance 3

, 6

, 9

, 12

[dB]

RSSI -30.05 [dBm]

at reference distance

Reference distance 1 [m]

γ Path loss exponent 2

Table 3: Simulation parameters.

Parameter Using PSN Unused PSN

sw 0.5 [m] 0.5 [m]

limax 5000 [times] 5000 [times]

limen 5 [m] 5 [m]

N1 max(SD

,5) Not used

mangle 0 or π/2 0 or π/2

4.1.5 Threshold to Terminate Approaching

It is assumed that the TN can be conﬁrmed visually

when the MN approaches it within a certain threshold.

When the MN approaches the TN within the thresh-

old, the approach is terminated.

4.2 Simulation Setup

The proposed method was evaluated using Visual

C++ 2013. In this simulation, an MN and a TN were

positioned on the plane of approaching. The MN

started from the following start points respectively:

in x− y plane, {x,y}={100,100}, {90,90}, {80,80},

{70, 70}, {60, 60}, {50,50}, {40, 40}, {30,30},

{20, 20}. This is a range that the MN can receive the

signal from the TN in roughly maximum -100 [dBm].

The TN is allocated at the origin (0, 0) at x − y

plane and the TN is ﬁxed.

Table 3 used in the simulation. The simulation

was performed 100 times for each starting point.

4.3 Results with and without PSN

The simulation was performed with and without the

PSN (Section 4). Figure 3 shows the erroneous de-

cision rate of approach with using the PSN (P

com-

pared to Re f

rssi

per σ

in Eq.(8)), and Fig. 4 shows

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

174

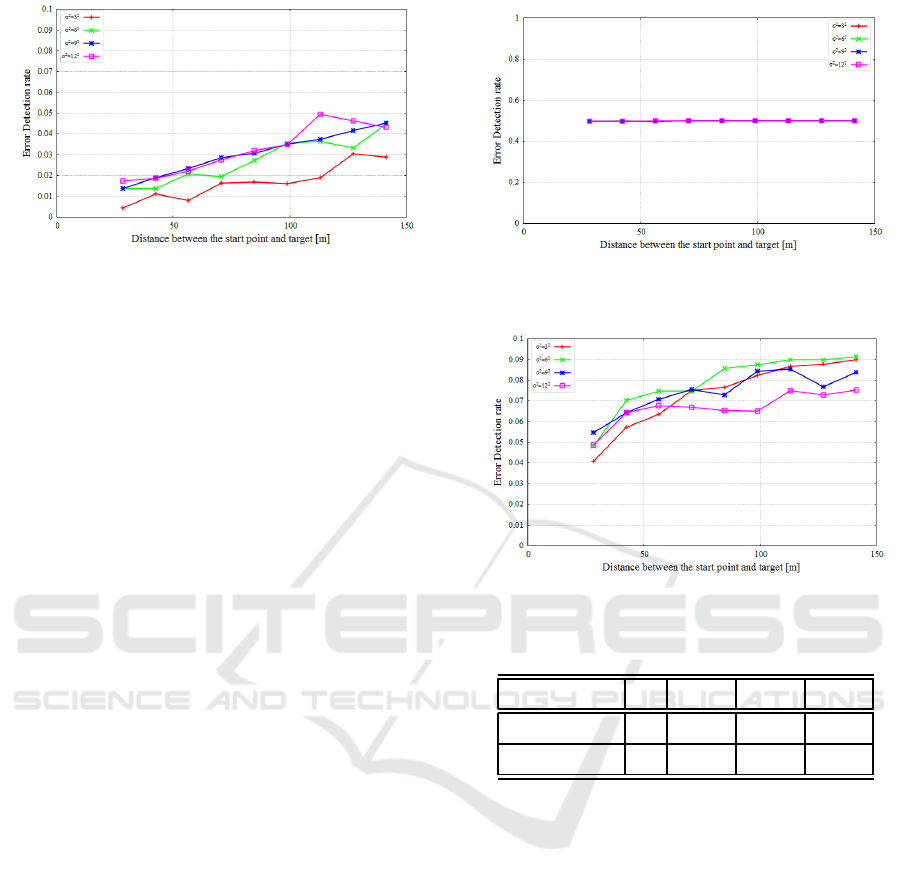
Figure 3: Erroneous decision rate of approach with the PSN

with P

compared to Ref

rssi

the erroneous decision rate of approach without the

PSN (P

compared to P

i−1

per σ

in Eq.(8)). Figure

5 shows the erroneous decision rate of approach us-

ing PSN (SP

compared to Ref

rssi

per σ

in Eq.(8)).

In these ﬁgures, the horizontal axis is the distance be-

tween the start point and the target [m] and the vertical

axis is the error determination rate. As can be seen,

the erroneous decision rate of approach using the PSN

with P

is less than 0.05. This result was expected

because the PSN was set to the maximum value in

this simulation, i.e., either SD

of the deviation or α

of signiﬁcance level is 0.05. The erroneous decision

rate of approach without the PSN was approximately

0.5, and the erroneous decision rate of approach with

the PSN with SP

was approximately 0.05 to 0.1. Ap-

proaching without the PSN is whether the approach or

departure was determined by compared to P

i−1

mea-

sured at a previous step. For approaching using the

PSN with SP

rather than P

, the erroneous decision

rate increases. Next, the approach failure rate with

and without the PSN were compared. The results per

in Eq.(8) are shown in Table 4. If the MN could

not enter limen within limax, the attempt was con-

sidered a failure. The failure rate was computed as

(failed attempts/total attempts) per σ

. All attempts

with the PSN were successful, and the failed attempts

occurred without the PSN.

This result indicates that the PSN of N1 prevented

incorrect determination for an MN when the determi-

nation is based on RSSI. Hereafter, approach with the

PSN using P

is considered and is referred to as ”ap-

proach with the PSN”.

In the next section, we evaluate the approach with

the PSN.

4.4 Average Moving Distance

The average MN moving distance is shown per σ

Eq.(8) in Fig. 6. In the ﬁgure, the horizontal axis is

the distance between the start point and the target [m]

and the vertical axis is error average moving distance

Figure 4: Erroneous decision rate of approach without the

PSN with P

compared to P

i−1

Figure 5: Erroneous decision rate of approach with the PSN

with SP

compared to Ref

rssi

Table 4: Failure rate of approach with and without the PSN.

Using PSN 0 0 0 0

Unused PSN 7 24.67 39.78 47.89

Unit: [%]

[m]. As the start point becomes closer to the TN, the

moving distance decreases, and we can conﬁrm that

the moving distances has a proportionate relationship

to the distance between the start point and the target.

In the next section, the relationship between mov-

ing distance and the distance between the start point

and the target is described.

4.5 Ratio between Moving Distance and

Distance between Start Point and

Target

The ratio of average moving distance to the distance

between the start point and the target is shown per σ

in Eq.(8) in Fig. 7. In the ﬁgure, the horizontal axis is

the distance between the start point and the target [m]

and the vertical axis is the ratio between the moving

distance and the distance between the start point and

Approaching a Target using a Protection Feature based on Received Signal Strength Indicator

175

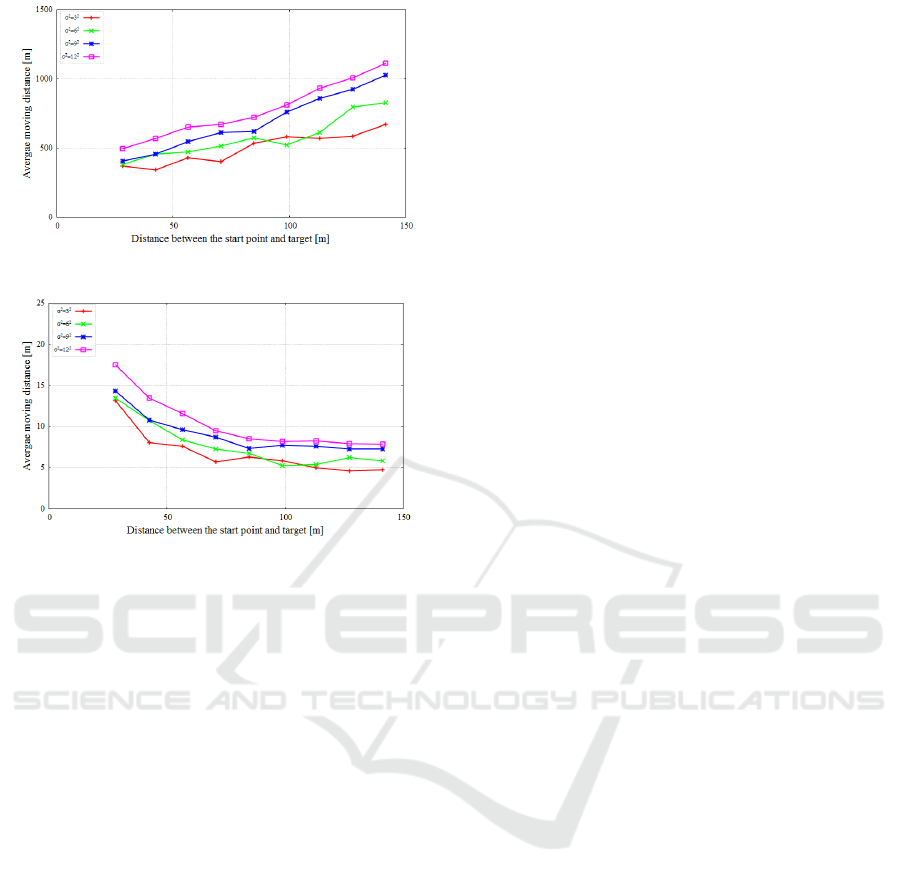
Figure 6: Average MN moving distance.

Figure 7: Ratio between moving distance and the distance

between the start point and target.

the target. As the start point comes closer to the TN,

this ratio increases to be greater than 10. As can be

seen, the MN could approach the TN efﬁciently when

the MN started at a point that was distant from the

TN.

4.6 Movement Locus

Example of movement loci of the averagemoving dis-

tance when the MN approached per σ

in Eq.(8) are

shown in Fig. 8. In these samples, the MN started

from {x,y} = {100,100} on the x− y plane.

5 DISCUSSION

As shown in Table 4, the MN could enter limen and

approach the TN when the PSN is used. We identi-

ﬁed that using PSN reduced the probability of incor-

rect approach determination (Fig 3 and 4). The PSN

was designed as a protection feature to determine the

approach to or departure from the TN. The value of

PSN varied depending on the environment. The PSN

should be small if the environment is favorable, e.g.,

in Eq.(8). In fact, the failure rate of σ

equal to 3

was the least, which is conﬁrmed in Table 4. There-

fore, the PSN was designed to use the value obtained

by testing α at 0.05 and SD

considering the environ-

ment, and the maximum PSN value was selected from

the two. Thus, the PSN of N1 was a variable value,

which chose the maximum value of 5 or SD

. The

MN could successfully approach the TN within limen

when using N1; thus, we can conﬁrm that the moving

distances demonstrate a proportionate relationship to

the distance between the start point and the target, as

shown in Fig. 6. On the other hand, when the MN

approached the TN, the MN demonstrated a moving

distance of approximately 6 ∼ 7 times he distance

between the start point and the target when the start

point was more distant from the TN. However, the

MN demonstrated a moving distance approximately

10 times greater when the start point was close to the

TN than when the start point was distant from the

TN, as shown in Fig. 7. This is a limitation of us-

ing a PSN of N1; however, this result shows that ap-

proach/departure determination works well with the

PSN values based on varying RSSI value.

6 CONCLUSION

In this paper, we have proposed an ap-

proach/departure determination method based

on varying RSSI values. The proposed method was

evaluated using computer simulation. A key concept

of this method is the use of a PSN as a protection

feature. The PSN was implemented to determine

approach/departure and was set to a maximum value

of either SD

of the deviation or α of the signiﬁcance

level as 0.05. In our evaluation, an MN and a TN were

positioned on an x − y plane with two-dimensional

lattice. The moving direction changed when de-

parture was determined, and remained unchanged

when approach was determined. As a result, we can

conﬁrm that the MN could successfully enter into

limen (i.e., a distance threshold), which means that

the MN approached the TN when the PSN was used.

In the future, we plan to device a method for

approach/departure determination that considers ge-

ographical and environment conditions during a nat-

ural disaster. The primary study target is wireless de-

vices, which communicates directly; however, it can

be expected approach in the wide-area by using ad-

hoc communication because numerous wireless de-

vices can collaborate to increase the range of commu-

nication. In addition, a quicker approach can be ex-

pected because of collaboration among a greater num-

ber of wireless devices.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

176

(a) σ

= 3

(b) σ

= 6

= 9

(d) σ

= 12

Figure 8: Examples of MN’s movement loci.

REFERENCES

Capkun, S., Hamdi, M., and Hubaux, J.-P. (2002). Gps-

free positioning in mobile ad hoc networks. Cluster

Computing, 5(2):157–167.

Carr, J. J. (1993). Directional or omnidirectional antenna.

Joe Carr’s Receiving Antenna Handbook, Hightext.

Fall, K. and Varadhan, K. The ns manual. notes

and documentation on the software ns2-simulator.

https://www.isi.edu/nsnam/ns, 2002.

Friis, H. T. (1946). A note on a simple transmission for-

mula. proc. IRE, 34(5):254–256.

Harker, K. W. (2008). What You Need to Get Started in

ARDF. Amateur Radio Direction Finding in Texas,

http://www.texasardf.org/.

Jacobson, V. (1988). Congestion avoidance and control.

In ACM SIGCOMM computer communication review,

volume 18, pages 314–329. ACM.

Li, X., Mitton, N., Simplot-Ryl, I., and Simplot-Ryl, D.

(2012). Dynamic beacon mobility scheduling for sen-

sor localization. Parallel and Distributed Systems,

IEEE Transactions on, 23(8):1439–1452.

Mao, G., Anderson, B. D., and Fidan, B. (2007). Path loss

exponent estimation for wireless sensor network lo-

calization. Computer Networks, 51(10):2467–2483.

Mase, K. and Sakata, S. (2007). AdHoc Networks and

Mesh Networks. Corona publishing CO., LTD. (In

Japanese).

Niculescu, D. and Nath, B. (2001). Ad hoc positioning sys-

tem (aps). In Global Telecommunications Conference,

2001. GLOBECOM’01. IEEE, volume 5, pages 2926–

2931. IEEE.

Niculescu, D. and Nath, B. (2003). Ad hoc position-

ing system (aps) using aoa. In INFOCOM 2003.

Twenty-Second Annual Joint Conference of the IEEE

Computer and Communications. IEEE Societies, vol-

ume 3, pages 1734–1743. IEEE.

Pathirana, P. N., Bulusu, N., Savkin, A. V., and Jha, S.

(2005). Node localization using mobile robots in

delay-tolerant sensor networks. Mobile Computing,

IEEE Transactions on, 4(3):285–296.

Porcino, D. and Hirt, W. (2003). Ultra-wideband radio tech-

nology: potential and challenges ahead. Communica-

tions Magazine, IEEE, 41(7):66–74.

Priyantha, N. B., Miu, A. K., Balakrishnan, H., and Teller,

S. (2001). The cricket compass for context-aware mo-

bile applications. In Proceedings of the 7th annual in-

ternational conference on Mobile computing and net-

working, pages 1–14. ACM.

Rappaport, T. S. et al. (1996). Wireless communications:

principles and practice, volume 2. prentice hall PTR

New Jersey.

Stevens, S. S. (1946). On the theory of scales of measure-

ment.

Toh, C. K. (2001). Ad hoc mobile wireless networks: pro-

tocols and systems. Pearson Education.

Approaching a Target using a Protection Feature based on Received Signal Strength Indicator

177