
An Off-line Analytical Approach to Identify Suitable Management
Policies for Autonomic Cloud Architecture
Marwah Alansari and Behzad Bordbar
School of Computer Science, University of Birmingham, Birmingham, U.K.
Keywords:
Coloured Petri-Nets, Autonomic Cloud Platform, Management Policies, Rules-set, Formal Analysis, Cost
Analysis, Modelling.
Abstract:
Delivering cloud services with better quality-of- service demands infrastructures which are autonomic and
self- manageable. In particular, there is a clear scope for developing automated methods for enforcing suitable
management policies that would run such infrastructures. An example of a management policy is the one that
governs the triggering of migration of virtual machines to manage energy consumption. Although there is
extensive research on developing novel methods of implementing such policies in an autonomic manner, the
identification of suitable policies in terms of cost reduction has received less attention. This requires an analy-
sis of two given sets of policies to identify which one is more suitable. This paper presents a method involving
Coloured Petri Nets for an offline modelling and analysis of an autonomic cloud platform which executes
sets of policies. We use traces of execution in Petri Nets for calculating minimum cost associated to each set
of policies. Petri Net models can generate infinite traces because of the appearance of loops. However, as
migration of virtual machines entails cost, many of the infinite traces will not result in the identification of the
minimal cost. This paper presents an analytical method using Integer Programming to find the minimum cost
of energy consumption for a given policy. We evaluated our approach with the help of an energy management
case study.
1 INTRODUCTION
Delivering cloud services with better quality-of-
service demands infrastructures which are autonomic
and self- manageable. Manual methods for managing
the deployed cloud services would not benefit cloud
providers to achieve their objectives because of the
large size of cloud-infrastructure, as well as the regu-
lar changes in business requirements. Therefore, there
are some autonomic management techniques making
a use of rule-based systems as suggested in (Borgetto
et al., 2012; ?; Alansari and Bordbar, 2013). Such
frameworks have been used for automatically trigger-
ing a dynamic action, such as the live-migration of
a virtual machine, by using different types of man-
agement policies. The management policies can use
constraints, or can be time based, or a combination of
both types (Alansari and Bordbar, 2014).
Autonomic cloud platforms which are governed
by such a combination of policies are very complex
because of the interacting rule sets. These rule sets
may involve a comparison between monitored param-
eters with given threshold values, and also may use
a set of Boolean constraints (Alansari and Bordbar,
2014). Therefore, studying the effectiveness of man-
agement policies in terms of cost saving and iden-
tifying the most appropriate policy before execution
is difficult. Thus, a model-based approach using the
Coloured Petri Nets (CPN) technique is proposed in
(Alansari and Bordbar, 2014). The proposed method
is aimed at defining a formal model for an autonomic
cloud platform which includes a migration action as
a dynamic action. The formal description model for
both cloud platform and policy is denoted as the CPN
Cloud. Each generated CPN Cloud model is simu-
lated to produce a set of traces of execution for 24
hours. At each sampled trace, the Cost Calculating
Method (SM) for computing the costs of both energy
consumption and the migration of a virtual machine
(VM) is applied to assess the overall cost of a policy
(Alansari and Bordbar, 2014).
We investigated some of CPN Cloud models pro-
duced by modelling approach suggested in (Alansari
and Bordbar, 2014). We noticed that the traces
of executions for such models might have complex
structures and might also include various loops. As
232
Alansari, M. and Bordbar, B.
An Off-line Analytical Approach to Identify Suitable Management Policies for Autonomic Cloud Architecture.
In Proceedings of the 6th International Conference on Cloud Computing and Services Science (CLOSER 2016) - Volume 2, pages 232-239
ISBN: 978-989-758-182-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

a result, the Cost Calculating Method proposed in
(Alansari and Bordbar, 2014), does not consider com-
plex cases. Hence, in this paper, we extend the off-
line cost analysis approach developed in (Alansari and
Bordbar, 2014) to consider the time intervals. This
can be achieved by formulating a set of equations of
Integer Programming solved by the Modified Simplex
algorithm (FrontlineSolvers, 2015). The purpose is to
provide comprehensive cost estimation values which
cover all the possible cases that might be found in a
trace generated from a CPN Cloud model. Further-
more, we solved the problem of including loop traces
inside traces of execution. This can be accomplished
by proposing a theory which relates the migration cost
to the loop traces. The objective of this theory is to
find the loop traces that would be discarded during
the process of the cost calculation.
The paper is organised as follows; Section 2 in-
cludes an overview of Coloured Petri Nets (CPN) and
the investigated related work in computing optimal
cost from Petri-nets models. Section 3 presents a sce-
nario for an autonomic cloud platform. The mod-
elling concept for cloud platform and policies is ex-
plained in Section 4. The description of the problem
addressed in this paper is expressed in Section 4.1.
Section 5 presents the proposed method for calculat-
ing the cost using Integer Programming. Section 6
contains the evaluation of the proposed solution us-
ing the scenario presented in Section 3. Finally, the
conclusion is presented in Section 7.
2 BACKGROUND AND RELATED
WORK
2.1 Coloured Petri-Nets (CPNs)
Petri Nets (PNs) are graphical and mathematical lan-
guages used for modelling a wide range of systems.
Through the years, several representations and exten-
sions to the classical Petri Nets have been introduced.
One of the existing Petri Net types is the Coloured
Petri Nets (CPN) (Jensen and Kristensen, 2009) (Cal-
lou et al., 2008).
In CPN, any model consists of a set of places
represented as circles and a set of transitions repre-
sented as bars. Places and transitions are connected
by arrows which contain expressions. Furthermore,
in CPN models some transitions may have guards,
which are conditional expressions used to increase the
control of firing transitions. The guards are written
between square brackets. In addition, a CPN model
has a set of tokens, which in CPN context are called
the colour set, with a data type similar to the place
type. In order to execute the model, there must be
a set of initial markings, which represent the values
of the tokens at each place before running the model
(For more information about CPN formal representa-
tion see (Jensen and Kristensen, 2009)).
2.2 Computing the Optimal Total Cost
in Petri-Nets
Calculating the optimal cost has been studied in var-
ious researches for different types of Petri Net mod-
els particularly in Priced Time Petri Net (PTPN) and
Time Petri Net (TPN). As stated in a study by Ab-
dulla and Mayr (Abdulla and Mayr, 2009), the cost
to reach a final marking from an initial marking is
computable if non-negative cost values are associated
with places and transitions in both PTPN and TPN.
They provide a mathematical formula for computing
the total cost along a path in the reachability graph
which is denoted as Cost(M
0
→ M
f
) (Abdulla and
Mayr, 2009)(Abdulla and Mayr, 2011). In (Abdulla
and Mayr, 2009) and (Abdulla and Mayr, 2011), the
minimal reachable cost in PTPN and TPN is com-
putable if it is transformed to a cost threshold prob-
lem. As a result, we conclude that the optimal cost
can be computed in PTPN if it becomes bounded,
contains set of reachable final markings and also is
associated with cost thresholds variables.
In (Li and Hadjicostis, 2011), the optimal cost
is estimated by using a recursive algorithm for com-
puting the cost at each node in the produced trellis.
Then, the node that has the least cost is determined
at each level in the graph (Li and Hadjicostis, 2011).
The recursive algorithm proposed in (Li and Hadji-
costis, 2011) can be useful to compute the minimal
cost in some Petri Net models. However, the algo-
rithm would not suitable for computing the minimum
cost from the reachability graph generated from CPN
Cloud models studied in our research. The reason
is that our CPN Cloud model is a dynamic platform
which has unfixed cost values along the markings.
3 A SCENARIO FOR AN
AUTONOMIC MANAGEMENT
IN CLOUD PLATFORM
Let us consider a cloud platform consisting of four
private hosts located in different locations and one
public host, as seen in Figure 1. Two private hosts
are located in Europe, whereas the remaining are in
Asia. Furthermore, the platform also has some Ama-
An Off-line Analytical Approach to Identify Suitable Management Policies for Autonomic Cloud Architecture
233

Table 1: Rules-set templates for expressing Time-based Rules for both Policy A and Policy B.
Time-based Policy A Time-based Policy B
• RuleSet 1: (Applied between Private Hosts)
– When Private Host(x) can accept Migrated VM and Time is
after 10.00 and Private Host(y) can migrate VM
then
Allow only one VM to be migrated between Private Host(x)
and Private Host(y) every ∆
time
.
• RuleSet 2:( Applied between Private Host and Public Host)
– When Public Host(x) can accept Migrated VM and Time is
after 10.00 and Private Host(y) can Migrate
then
Allow VM to be Migrated to Public Host(x) every ∆
time
.
• RuleSet 3: ( Applied at Public Host )
– When Time is after 10.00 at Public Host(x)
then
Allow VM to be Migrated to Private Hosts from Pub-
lic Host(x) every ∆
time
.
• RuleSet 4: (Applied between Private Hosts)
– When Private Host(x) can accept Migrated VM and Time is
between 16.00 and 7.00 and Private Host(y) can migrate VM
then
Allow only one VM to be migrated between Private Host(x)
and Private Host(y) every ∆
time
.
• RuleSet 5:( Applied between Private Host and Public Host)
– When Public Host(x) can accept Migrated VM and Time is
between 16.00 and 23.00 and Private Host(y) can Migrate
then
Allow VM to be Migrated to Public Host(x) every ∆
time
.
• RuleSet 6: ( Applied at Public Host )
– When Time is after 23.00 at Public Host(x)
then
Allow VM to be Migrated to Private Hosts from Pub-
lic Host(x) every ∆
time
.
Figure 1: A scenario for an autonomic management via trig-
gering virtual machine migration in a cloud platform.
zon instances, which are located in the USA. All hosts
in the platform are allowed to only migrate one VM
to available hosts at a time. The running virtual ma-
chines in the platform are used for executing com-
putational applications submitted by cloud consumers
(Alansari and Bordbar, 2014). The cloud provider that
owns this architecture is willing to restrict the live mi-
gration action among the hosts using different sets of
policies. All the policies are composed of constraints
and time-based rule sets. The constraint policies are
applied at the hosting node level which analyse the
status of the node using measurement values such as
SLA Violation Rate, Resource Consumption and En-
ergy Consumption. The following is an example of a
constraints policy used in the scenario:
1. RuleSet 1:
When Violation Rate is High or CPU Usage is High or CPU Usage is
Low
then Migrate Smallest VM Running in Host
2. RuleSet 2:
When Violation Rate is Normal and CPU Usage is Normal
then Accept Migrated VM
Moreover, in this scenario, there are two types of
time- based policies that might be used by the cloud
provider. Policy A uses random time constraints that
allow the trigger of the migration action at any time
after 10:00 between all the hosting nodes. Policy B
has fixed time constraints which only permit the mi-
gration during the off-peak time which will be be-
tween 16:00 and 7:00 among private hosts, and from
16:00 to 23:00 between private and public nodes. Ta-
ble 1 is a sample of a rule set used for expressing time
intervals in both Policy A and Policy B.
Before executing policies explained in Table 1 in
real cloud platform, such policies can be modelled
and be analysed in terms of saving energy consump-
tion cost via Coloured Petri Nets (CPN). Briefly, the
approach of using Coloured Petri Nets for modelling
cloud infrastructure with policies will be explained in
Section 4.
4 COLOURED PETRI-NETS FOR
MODELLING MANAGEMENT
POLICIES
Figure 2 is a model of the CPN Cloud for the sce-
nario explained in Section 3. In this CPN model,
places can be represented as hosts for running virtual
machines. Dynamic migration action is modelled as
transitions between places which are in blue colour.
In addition, constraint policies can be a part of inter-
CLOSER 2016 - 6th International Conference on Cloud Computing and Services Science
234

Figure 2: The Coloured Petri Nets model for the scenario.
nal transitions occurring at places, which are referred
to as monitoring transitions. These monitoring transi-
tions are fired periodically with a time delay referred
to as @MointoringTime. The monitoring transitions
appear in grey colour in Figure 2. On the other hand,
the time-based policy is modelled as a guard at each
migration transition. Examples of time-based policies
are those explained in Section 3.
The proposed CPN Cloud model in (Alansari and
Bordbar, 2014) has become a tool that can be used to
assess policies in terms of cost savings. The compar-
ison depends on simulating the Coloured Petri Nets
model to partially generate traces of execution. Then,
the cost is computed by applying the modified Cost
Calculation Method proposed in (Abdulla and Mayr,
2013) which is considered a simple method. The
outcome of such an approach is obtaining the esti-
mated total cost of energy consumption and migration
cost from a single trace σ from the sampled graph.
This calculation method is applied to all traces in the
graph (Alansari and Bordbar, 2014)(a detailed expla-
nation about the Cost Calculation Method is provided
in (Alansari and Bordbar, 2014)).
4.1 The Description of the Problem
From CPN Cloud model that is presented in Figure 2,
we partially generated a reachability graph. A sam-
ple of such graph are shown in Figure 3. In Figure
3, these traces represent the possible execution during
24 hours which is generated using CPN Tool (Jensen
and Kristensen, 2009). Focusing on the highlighted
trace, any single trace can be described in a format as
presented on the right hand side of Figure 3. In a trace
σ, the squares represent the markings which can be ei-
ther a marking resulting from triggering a monitoring
transition or a marking generated from firing a migra-
tion transition. These markings contain the computed
cost values for all running hosting nodes in a cloud
platform. In addition, the trace σ also has arrows
which are annotated with (t
i
, θ
i
). In this form, the
notation θ
i
represents the time unit for firing a transi-
tion. Formally, the trace can be described as follows:
σ := M
0
(t
0
,θ
0
)
−→ M
1
(t
1
,θ
1
)
−→ M
2
(t
2
,θ
2
)
−→ . . .
(t
n−1
,θ
n−1
)
−→ M
n
0 ≤ θ
0
≤ θ
1
≤ θ
2
. . . ≤ θ
n−1
< 24 (1)
As mentioned in the previous section, by applying
the Cost Calculation Method in (Alansari and Bor-
dbar, 2014), we can obtain the estimated cost val-
ues which are Energy Consumption and Migration
Costs. However, there are some CPN Cloud models
that have migration transitions restricted to time in-
tervals, such as the model of the CPN Cloud for the
scenario explained in Section 3. This means that in a
trace σ, a migration transition t
i
is fired with a time
delay d
i
which is between the allowed time-interval
[D
Mini
, D
Maxi
]. The Simple Cost Calculation Method
relies on using CPN simulator to select the time de-
lay for firing a migration transition. However, in case
of using time-interval [D
Mini
, D
Maxi
] for firing a mi-
gration transition t
i
, there is a time delay d
i
where the
cost of energy consumption between the marking M
i
and M
i+1
can be the minimum. As a results, the Sim-
ple Cost Calculation Method explained in (Alansari
and Bordbar, 2014), is extended to compute the min-
imum energy consumption cost between the mark-
ings. This can be achieved by finding the optimal or
near-optimal time delays for firing migration actions
in traces associated with time-intervals.
5 THE IMPROVED COST
CALCULATION METHOD (IM)
Our solution starts by computing both Energy Cost
and Migration Cost at each marking M
i
in a trace
σ using both Equation 3 and Equation 5 mentioned
in our previous research in (Alansari and Bordbar,
2014). Then, we formulate a set of Integer Program-
ming equations for obtaining the minimum energy
consumption cost.
5.1 Computing the Overall Cost in the
Trace
Lets consider that the generated trace σ has the fol-
lowing format:
σ := M
0
(t
0
,θ
0
)
−−−→
d
0
M
1
(t
1
,θ
1
)
−−−→
d
1
M
2
(t
2
,θ
2
)
−−−→
d
2
. . .
M
n−l
(t
n−1
,θ
n−1
)
−−−−−−→
d
n−1
M
n
0 ≤ θ
0
≤ θ
1
≤ θ
2
. . . ≤ θ
n−1
< 24 (2)
An Off-line Analytical Approach to Identify Suitable Management Policies for Autonomic Cloud Architecture
235

Figure 3: A sample of a reachability graph (left hand-side) and a sample of a trace extracted (right-hand-side).
which each M
i
is a marking resulted from firing t
i
with a delay time unit d
i
. Each M
i
happens at time
θ
i
. To compute the total cost in trace σ such that each
ti is fired with time delay d
i
which has the minimum
ECost(M
i
), we define the following objective func-
tion:
OverallCost(σ) = Minimize(
n−1
∑
i=0
d
i
∗ ECost(M
i
)
+ TCost(t
i
)) (3)
subject to the following constraints:
1. In case the firing transition t
i
is a migration tran-
sition, then:
D
Mini
≤ d
i
≤ D
Maxi
.
2. In case t
i
is a monitoring transition, then:
d
i
= @MonitoringTime ≤ 24.
3. θ
i+1
= d
i
+ θ
i
≤ 24
4. θi , θ
i+1
, d
i
> 0, θ
i
< θ
i+1
5. θ
0
= 0 and θ
n
= 24
6. d
i
, θ
i+1
, θ
i
are integers
In our solution, we consider computation for a day
(i.e., 24 hours). Yet, the computation can be easily
adjusted for days, weeks or seasons. Both D
Mini
and
D
Maxi
are integer values extracted from the manage-
ment policy used to limit the variable d
i
. The variable
@MonitoringTime represents the delay-time unit for
monitoring transitions which will be assigned in CPN
Cloud model before extracting the traces. θ
i
is the
time for firing the transitions in a trace σ and θ
i+1
is
the next time unit after firing a transition t
i
. In this
method, we assume that each fired monitoring transi-
tion has no cost. As a result, in Equation 3, the ob-
tained cost value for any monitoring transition will be
equal to 0.
The value of OverallCost(σ) is obtained using
Modified Simplex Algorithm uses the Branch and
Bound Method (FrontlineSolvers, 2015). The objec-
tive is to find the feasible integer values for time-delay
d
i
. Since the CPN Cloud model considers discrete
time not continuous time. Using such algorithm, the
total cost along σ can be computed by fining the best
time-delay d
i
for firing each migration transition t
i
. In
case Modified Simplex does not find a feasible solu-
tion in a trace σ, we assign for each d
i
the value D
mini
.
5.2 A Special Case: Handling Traces
with Loops
In the previous section, we mentioned a method of
calculating the minimal cost for a given finite trace
σ consisting of transitions fired using time-intervals.
However, it is possible that some traces involve peri-
odic behaviours which appear in these traces as loops.
This is depicted in Figure 4, from the trace shown in
the figure, infinite traces can be obtained by repeating
the loop involving the markings M
2
, M
3
and M
4
.
It is possible for each given number of iterations of
the loop to obtain a trace and apply the method of the
previous section to calculate the minimum cost. The
trace would repeat the markings involved in the loop.
Clearly, the length of the traces can increase as we
can include an arbitrary number of repetitions of each
loop. At first glance, it might be the case that we need
to identify the minimal cost over an infinite number of
traces. However, with each iteration on a loop, there
are associated costs with the traces. This is because
the migration of the virtual machine accumulates cost.
For a sufficiently large number of migration costs, the
Figure 4: An example of a trace with a loop.
CLOSER 2016 - 6th International Conference on Cloud Computing and Services Science
236

trace will be large enough to be discarded from the
calculation, when we are looking for a solution with a
minimal cost.
Lemma 1. Assume that σ is a trace of execution such
that σ has a loop. i.e. σ has the following sub-
sequence:
λ = M
k−1
(t
k−1
,θ
k−1
)
−−−−−−→
d
k−1
M
k
(t
k
,θ
k
)
−−−→
d
k
M
k+1
. . .
(t
l−1
,θ
l−1
)
−−−−−−→
d
l−1
M
l
such that M
l
= M
k−1
and Cost(σ) ≥
N × LoopCost(λ) in which N is the num-
ber of repetitions of the sequence (∗) and
LoopCost(λ) =
∑
l
i=k
TCost(t
i
)
Sketch of The Proof: The amount of energy as-
soicated with λ consists of the amount of energy con-
sumed of running virtual machines at all hosts in CPN
Cloud model. (i.e.) The cost at M
i
where k − 1 ≤
i ≤ l − 1 plus the cost of the migration when the
transitions t
k−1
,t
k
, . . . , t
l−1
are fired. LoopCost(λ) =
∑
l
i=k
TCost(t
i
) captures only the cost migration. If
there are N repetitions of the loop, we end up with
N × LoopCost(λ) with at least the cost assoicated
with migration for N iterations of the loop.
Theorem 1. Assume L represents the set of all loops
with at least one migration transition with a non-
negative cost. Suppose C
min
= min{LoopCost(λ)|λ ∈
L} repeating the smallest value for all the cost of mi-
gration within a loop. Suppose that σ
s
is an arbitrary
finite trace of execution starting from the initial mark-
ing and executing for 24 hours. If q is the smallest
number that q ×C
min
≥ TCost(σ
s
), then the minimum
cost will be
Min{Cost(σ)|σ is a trace with at most q
repetitions of each loop} (4)
Proof. For any trace σ with more than q repetitions
of a loop L, the cost of σ will be grater than or equal
Cost(σ
s
). Hence, traces will be discarded as it will
result in a minimum cost of energy.
Using the above theorem, we need to calculate
the minimum cost with the help of a finite number
of traces. As a result, if any graph resulting from the
CPN Cloud model consists of a set of traces includ-
ing loops, a finite set of traces executing the loops
should be generated. This can be done by repeating
the loops N repetitions. Then, the cost is computed
using the Improved Method explained in Section 5.
In addition, the cost of migration for traces with loops
should be considered. We stop computing the cost for
traces consisting of loops when the cost values be-
come greater than the cost of a trace with the smallest
repetition number for the loop sequence.
Figure 5: The sequence of execution graph for CPN model
for Policy A.
6 THE EVALUATION OF THE
METHOD
The proposed solution is evaluated by analysing and
comparing a number of modelled policies in the CPN
Cloud model. The CPN tool(Jensen and Kristensen,
2009) is used to generate Coloured Petri Net models
for all tested policies mentioned in Section 3. Then,
a set of sequence of executions for each model is cre-
ated. The cost of energy consumption and the migra-
tion cost which are associated with the markings are
also computed during the process of generating the
sequence graphs using the ML Function in the CPN
tool. After that, Integer Programming equations are
formulated and solved using the Modified Simplex al-
gorithm (FrontlineSolvers, 2015) which is provided
in Microsoft Excel Software. Both the modelling and
analysis processes were done on a Samsung laptop
which has 2.40GHz Intel(R) Core(TM) processor and
6GB memory.
We used the CPN tool to create the models for
Policy A and Policy B. The workload for the models
is simulated to be generated randomly using the ML
function. The traces of execution graphs for the mod-
els are shown in Figure 5 and Figure 6. In all graphs,
the values inside the markings are the cost of energy
consumption for four private hosts. The time intervals
which are applied at each migration transition are lo-
cated at the edges between the markings. We notice
that the graph in Figure 5 has two traces containing
loop traces. For the loop traces, we applied the theo-
rem explained in Subsection 5.2. We noticed that the
overall cost values for each of the traces with loops
are higher than similar traces without executing the
loop sub-traces. Therefore, we discard all the loop
An Off-line Analytical Approach to Identify Suitable Management Policies for Autonomic Cloud Architecture
237
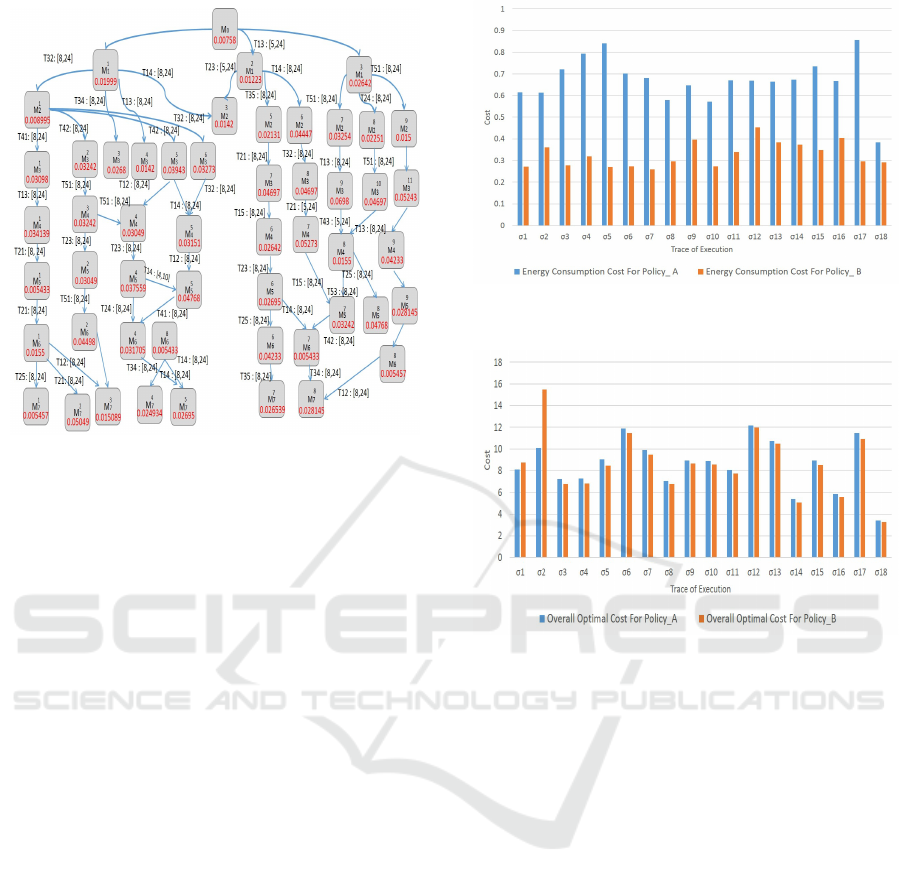
Figure 6: The sequence of execution graph for CPN model
for Policy B.
traces generated in the graph of Policy A from our
calculation.
6.1 Results and Discussion
The graphs shown in Figure 5 and Figure 6, there are
18 traces generated. We applied the Cost Calculation
Method explained in Section 5 to all generated traces.
We obtained the minimum cost of Energy Consump-
tion, Total Migration Cost and Optimal Overall Cost
at each generated trace for all the graphs. To com-
pare both Energy Consumption and The Overall Cost
for all the policies, we selected 18 traces from each
generated graph ignoring all the loop traces. The de-
tailed results produced from the analysis method are
displayed in Figure 7 and Figure 8.
Figure 7 illustrates the Optimal Energy Consump-
tion Cost for 18 traces generated from each of the
traces of execution graphs presented in Figures 5 and
6. Generally, the figures show that each trace for Pol-
icy B has an Optimized Energy Consumption Cost
value which is less than the traces in Policy A, since
Policy A allows the migration to be triggered at any
time using random time intervals. In contrast, the mi-
gration action in Policy B is restricted to the off-peak
time which is from 16:00 until 21:00 mapped as [8-
24] in some of the traces of the graph of Policy B
(See Figure 6).
Figure 7, we can analyse the cost of each trace
for each policy individually. For instance, we can see
that trace σ
18
has the lowest Optimized Energy Con-
sumption Cost among traces of Policy A. Whilst trace
σ
7
has the least Optimized Energy Consumption Cost
Figure 7: The optimal energy consumption cost for 18
traces from the sequence of execution graphs.
Figure 8: The optimal overall cost for 18 traces from the
sequence of execution graphs.
among the traces of Policy B which is nearly 0.26. In
addition, we can notice that there are some traces of
Policy A that have nearly the same cost values which
are reasonably high such as σ
17
, σ
5
, σ
4
and σ
3
.
Figure 8 presents the Optimal Overall Cost af-
ter accumulating the Migration Cost values of each
trace to its Optimized Energy Consumption Cost. We
found that there are changes in cost values since some
traces required the triggering of migration transitions
which means their migration costs are high. As a re-
sult, the figures for each trace of execution for both
Policy A and Policy B are roughly similar.
6.2 Comparing the Improved Method
with the Simple Method
To study the effectiveness of the proposed method
on the computed cost values, we compared this
method with the Simple Method proposed method in
(Alansari and Bordbar, 2014). For all traces of both
Policy A and Policy B graphs the Simple Method are
applied. During this process, we ignored the Migra-
tion Cost values computed from both methods be-
CLOSER 2016 - 6th International Conference on Cloud Computing and Services Science
238

Figure 9: A comparison between the two methods of calcu-
lating the cost energy consumption in traces.
cause these values are fixed. On the other hand, we
focused on the computed Energy Consumption Cost
values from both methods. As shown in Figure 9 that
the Improved Method produces averages of Energy
Consumption Cost for both Policy A and Policy B
which are lower than the values given by the Simple
Method. Thus, the Improved Method is more accurate
in estimating the cost of Energy Consumption which
can be suitable for analysis of some types of manage-
ment policies. However, if the objective is to speed
up the process of calculating the cost, or if time de-
lays are not of much concern to cloud providers, then
the Simple Method can be applicable in such types of
management policies.
7 CONCLUSION
Management policies that would be executed in a
cloud platform can be assessed in terms of Energy
Cost saving before execution via Coloured Petri Nets.
By using the Improved Cost Calculation Method sug-
gested in this paper, the estimated energy consump-
tion and the migration costs can be obtained. The
Improved Cost Calculation Method provides a deep
analysis for both cost values which are extracted from
the traces of execution graph of CPN Cloud models.
The method uses a set of Integer Programming equa-
tions which are solved via the Modified Simplex al-
gorithm. The objective is to find traces which have
minimum energy cost values and the best time for fir-
ing migration actions during 24 hours. Coloured Petri
Nets can be a powerful tool for modelling and anal-
ysis of autonomic Cloud platforms and management
policies. If Cloud CPN models are combined with the
off-line cost analysis method suggested in this paper,
various set of policies can be assessed before real im-
plementation.
REFERENCES
Abdulla, P. and Mayr, R. (2009). Minimal cost reachabil-
ity/coverability in priced timed petri nets. In de Al-
faro, L., editor, Foundations of Software Science and
Computational Structures, volume 5504 of Lecture
Notes in Computer Science, pages 348–363. Springer
Berlin Heidelberg.
Abdulla, P. A. and Mayr, R. (2011). Computing optimal
coverability costs in priced timed petri nets. In Logic
in Computer Science (LICS), 2011 26th Annual IEEE
Symposium on, pages 399–408.
Abdulla, P. A. and Mayr, R. (2013). Petri nets with time and
cost. arXiv preprint arXiv:1302.3291.
Alansari, M. and Bordbar, B. (2014). Modelling and analy-
sis of migration policies for autonomic management
of energy consumption in cloud via petri-nets. In
Proceedings of the The International Conference on
Cloud and Autonomic Computing. IEEE.
Alansari, M. M. and Bordbar, B. (2013). An architectural
framework for enforcing energy management policies
in cloud. 2013 IEEE Sixth International Conference
on Cloud Computing, 0:717–724.
Borgetto, D., Maurer, M., Da-Costa, G., Pierson, J.-M.,
and Brandic, I. (2012). Energy-efficient and sla-aware
management of iaas clouds. In Proceedings of the
3rd International Conference on Future Energy Sys-
tems: Where Energy, Computing and Communication
Meet, e-Energy ’12, pages 25:1–25:10, New York,
NY, USA. ACM.
Callou, G. R. d. A., Maciel, P. R. M., de Andrade, E. C.,
Nogueira, B. C. e. S., and Tavares, E. A. G. a. (2008).
A coloured petri net based approach for estimating ex-
ecution time and energy consumption in embedded
systems. In Proceedings of the 21st Annual Sym-
posium on Integrated Circuits and System Design,
SBCCI ’08, pages 134–139, New York, NY, USA.
ACM.
FrontlineSolvers (2015). Excel solver - inte-
ger programming. [Online] Available from:
http://www.solver.com/excel-solver-integer-
programming, [Accessed: 12
th
October 2015].
Jensen, K. and Kristensen, L. M. (2009). Coloured Petri
Nets: Modelling and Validation of Concurrent Sys-
tems. Springer.
Li, L. and Hadjicostis, C. N. (2011). Least-cost planning se-
quence estimation in labelled petri nets. Transactions
of the Institute of Measurement and Control, 33(3-
4):317–331.
Maurer, M., Brandic, I., and Sakellariou, R. (2013). Adap-
tive resource configuration for cloud infrastructure
management. Future Generation Computer Systems,
29(2):472 – 487.
An Off-line Analytical Approach to Identify Suitable Management Policies for Autonomic Cloud Architecture
239
