
Automatic Generation of Fuzzy Membership Functions using
Adaptive Mean-shift and Robust Statistics
Hossein Pazhoumand-Dar, Chiou-Peng Lam and Martin Masek
School of Computer and Security Science, Edith Cowan University, Perth, Australia
Keywords: Fuzzy Membership Functions, Variable Bandwidth Mean-shift, Fuzzy Logic, Activities of Daily Living,
Abnormality Detection, Robust Statistics.
Abstract: In this paper, an unsupervised approach incorporating variable bandwidth mean-shift and robust statistics is
presented for generating fuzzy membership functions from data. The approach takes an attribute and
automatically learns the number of representative functions from the underlying data distribution. Given a
specific membership function, the approach also works out the associated parameters. The investigation
here examines the application of approach using the triangular membership function. Results from
partitioning of attributes confirm that the generated membership functions can better separate the underlying
distributions when compared to a number of other techniques. Classification performance of fuzzy rule sets
produced using four different methods of parameterizing the associated attributes is examined. We observed
that the classifier constructed using the proposed method of generating membership function outperformed
the 3 other classifiers that had used other methods of parameterizing the attributes.
1 INTRODUCTION
Eliciting representative membership functions (MFs)
for data is one of the fundamental steps in
applications of fuzzy theory as the success of many
fuzzy approaches depends on the membership
functions used. However, there are no simple rules,
guidelines, or even consensus among the community
on how to choose the number, type, and parameters
of membership functions for any application or
domain (Medasani et al., 1998). Several methods for
the automatic generation of MFs have been proposed
in the literature and the choice of function has been
linked to the problem and the type of data available.
However, in most of these techniques, the number of
fuzzy sets has to be provided empirically.
Furthermore, the range for membership functions
generated by many existing techniques does not
address the impact of outliers and noisy
measurements in data.
In this paper, we propose a hybrid approach that
incorporates variable bandwidth mean-shift (VBMS)
and robust statistics for automatic generation of
representative MF(s) for an attribute. The analysis of
the underlying data distribution is unsupervised as
the proposed approach first determines the number
of modes from the probability density function
(PDF) and then uses this value as the number of
clusters for a multimodal data distribution. The
approach overcomes the problems associated with
some of the existing approaches by
determining the number of representative MFs
for the attribute from the underlying data
distribution automatically
automatically handling noise and outliers in the
attribute feature space
The rest of this paper is organised as follow: Section
2 briefly reviews relevant literature on MF
generation techniques. Some preliminary concepts
are described in Section 3. Section 4 describes the
proposed approach. The experimental evaluation of
our technique is presented in Section 5 followed by
conclusions and future directions in Section 6.
2 BACKGROUND
Many techniques have been proposed to generate
fuzzy membership functions from an attribute. Three
questions that have to be addressed are: (1) number
of fuzzy sets to be defined for the dataset, (2) shape
of the membership functions, and (3) parameters
defining each membership function.
160
Pazhoumand-Dar, H., Lam, C-P. and Masek, M.
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics.
DOI: 10.5220/0005751601600171
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 160-171
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Typically, techniques have used manual
partitioning of attributes, mostly based on expert
knowledge, and adopted a pre-determined number of
membership functions (Seki, 2009) to partition the
data space for the attribute by (usually evenly-
spaced) MFs. However, manual approaches suffer
from the deficiency that they rely on subjective
interpretations from human experts.
Given a labelled dataset, evolutionary methods
can also be utilized to generate MFs. Moeinzadeh et
al., (2009) applied Genetic Algorithm (GA) and
Particle Swarm Optimization (PSO) for the
adjustment of MF parameters to increase degree of
membership of data to their classes for classification
problems. Authors in (Amaral and Crisóstomo,
2001) applied GA for evolving parameters
associated with MFs in a fuzzy logic controller for a
helicopter. Initial guesses for the MFs are made by
the expert and the GA adjusts the MF parameters to
minimise the movement of a hovering helicopter. In
the classification method proposed by Tang et al.
(2014), a fitness function quantifies how well the
crisp values of attributes are classified into MFs and
the GA process evolves over time by searching the
best set of MF parameters which optimises result of
the fitness function.
Takagi and Hayashi (1991) also proposed the use
of artificial neural networks (ANN) for the
construction of membership functions. Their
approach takes raw data (say, in a control problem),
apply a conventional clustering algorithm to group
the data into clusters and apply an ANN to this
clustered data to determine the membership of a
pattern within particular fuzzy sets.
However, for situations where the training data is
not labelled, MF generation techniques generally
involve unsupervised clustering of data using a
specific distance measure and then the parameters of
detected clusters (mean, variance, etc.) are used to
generate MFs. For example, techniques
(Pazhoumand-Dar et al., 2015) have used the Fuzzy
C-Means (FCM) clustering algorithm (Kuok et al.,
1998) to cluster a particular attribute into specific
number of clusters. Cluster boundaries and the
location of the centre were then used to determine
the cluster membership function parameters. Doctor
et al., (2014) presented a fuzzy approach to model an
occupant behaviour in a residential environment.
They used a Double Clustering technique
(Castellano et al., 2002) combining FCM and
agglomerative hierarchical clustering for extracting a
predefined number of MFs from the user’s recorded
input/output data.
The disadvantage associated with most of these
methods is that the number of fuzzy sets must be
predefined. However, we usually do not know an
optimal number of representative MFs for a
particular attribute. In addition, outliers in data are
included in range of MFs generated by many of
these techniques. New robust techniques that can
determine number of representative MFs
automatically would address some of these
limitations.
3 PRELIMINARY CONCEPTS
This section provides a review on related techniques
and concepts used in the proposed approach. The
variable bandwidth mean-shift strategy is first
described, and is then followed by a review of the
skewness adjusted boxplot technique.
3.1 Variable Bandwidth Mean-Shift
Algorithm
VBMS proposed by Comaniciu et al., (2001) is a
nonparametric clustering technique which does not
require the number of clusters to be defined. It takes
multidimensional data with an unknown density
and estimates the density at each point by taking the
average of locally-scaled kernels centered at each of
the data points, and tries to map each data point to
its corresponding mode. The output of this technique
is locations of modes detected in and the cluster of
data associated with each mode. Usually the kernel
K is taken to be a radially symmetric, nonnegative
function centered at zero such that
‖
‖
).
More specifically, given the data points
1,…,, steps for the VBMS algorithm are as
follows:
1. Use the plug-in rule (Sheather and Jones, 1991)
to find an initial bandwidth
for the kernel
and estimate PDF of data using Eq. (1).
̅
1
(1)
Plug-in rule is a bandwidth selection technique for
kernel density estimation of a data distribution. It
involves using a kernel function to estimate the PDF
of data. Estimation is performed per different values
for the bandwidth of the kernel function, and the
bandwidth that minimises an error function is
selected.
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
161

2. Obtain
1
1
log ( ( )
i
N
N
i
f
x
e
3. Compute the adaptive bandwidth
for each
data point
using Eq. (2).
1/2
0
() [ ]
()
i
i
hx h
fx
(2)
In Eq. (2),
is a fixed bandwidth obtained from the
plug-in rule (in step 1) and is a proportionality
constant which divides the range of density values
into low and high densities. When the local density
for a given data point
is low (i.e.,
̅
),
increases relative to
implying more
smoothing in the estimated density for the point
.
For data points where their estimated density
̅
is greater than the bandwidth becomes narrower.
2
2
2
1
2
1
()
1
N
i
N
i
d
i
i
i
i
d
i
i
i
xx
x
g
h
h
mx
xx
g
h
h
(3)
where d is the dimension of the data and
4. Choose the location of an unprocessed data as
the initial location of the kernel and compute
mean shift vector represented in Eq. (3)
iteratively till convergence.
5. Record the location of kernel at convergence as
the location of a mode of PDF, and group all data
points covered by the kernel, during its
successive locations, as the cluster associated
with the mode.
6. Repeat step 4 to 5 until no unprocessed data is
left.
More details on VBMS can be found in (Sheather
and Jones, 1991).
3.2 The Skewness Adjusted Boxplot
Technique
The skewness adjusted boxplot (SAB) technique is a
graphical tool (with a robust measure of skewness)
used in robust statistics (RS) for the purpose of
outlier detection (Rousseeuw and Hubert, 2011).
Given a continuous unimodal data, SAB first
calculates a robust measure of skewness (i.e.,
medcouple (MC) (Brys et al., 2004)) of the
underlying data distribution. Then it outputs a
normal range for the data which excludes possible
outliers from the normal data.
More specifically, if
1,…, is a
univariate data, medcouple (MC) of data is
calculated as
(, )
xm x
inj
MC h x x
ij
med
(4)
where for all
the kernel function is given
by:
,
(5)
In Eq. (5),
is the median of data points. If
, let
...
be the indices of the
data points which are associated with the median
. The kernel is then defined as Eq. (6).
,
1,
1
0,
1
1,
1
(6)
In case the distribution is skewed to the right, MC
gets a positive value up to +1. MC becomes negative
(up to -1) in a left-skewed distribution. Finally, a
symmetric distribution has a zero MC.
Once the value of MC is obtained for the data,
SAB calculates the normal range (NR) for the data as
13
13
()
(3MC)
-4MC
(-3MC) (4MC)
[Q -1.5 e IQR ;Q + 1.5 e IQR] if MC 0
NR=
[Q -1.5 e IQR ;Q + 1.5 e IQR] otherwise
(7)
where
and
are the first and the third quartiles
of the data and
. For a left-skewed
distribution (with a MC <0), the cut-off interval for
the distribution will be the upper range shown in Eq.
(7). The lower range in Eq. (8) is for right-skewed
distributions having a positive MC.
Once NR is determined for the distribution, all
observations outside the interval will be marked as
potential outlier. Note that by using different ranges
for different types of skewed distributions, we allow
the cut-off interval to be asymmetric around the
median of distribution.
4 THE PROPOSED APPROACH
The proposed approach takes an attribute and
automatically defines a number of associated MFs as
linguistic variables. Let an attribute take a series of
crisp numerical values
1,…, and these
data points belong to an unknown probability
density function (PDF) f. The two-step procedure of
the proposed approach for generating MFs for the
attribute is as follows
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
162
Step 1. use VBMS to find modes (local maxima) of
f representing the attribute and cluster of
data points associated with each mode
Step 2. use skewness adjusted boxplot technique
(Hubert and Vandervieren, 2008) to obtain
the normal range of data for each cluster
(where there are no outliers), and
accordingly define a MF for the cluster.
The output of Step 1 is the location of modes of f
denoted as
and the cluster of data
associated with each mode.
When an attribute has a multimodal PDF and
each mode may be associated with a different
density distribution, one fixed global bandwidth is
not optimal for estimating the location of modes in
PDF, and thus local bandwidths should be computed
(Comaniciu et al., 2001). Using VBMS, we
determine a local bandwidth for each data point in a
way that points corresponding to tails of the data
distributions receive a bigger bandwidth than data
points lying in large density region of distributions
and hence the estimated density function for tails of
the distributions is smoothed more.
In Step 2, we use the output from Step 1, the
number of modes as the number of required MFs
representing the attribute and for each cluster of data
associated with a mode, we define a MF. We first
use the SAB technique to determine the normal
range (NR) for the cluster (see Section 3.2) and we
denoted this as
,
.
The output of Step 2 for each attribute is a tuple
(X, m
1
, m
2
, … , m
nc
) as linguistic variables, where X
stands for the attribute name and m
i
stands for an
MF defined over the universe of discourse for the
attribute and nc stands for the number of modes
identified in Step 1.
Various forms of MFs, together with their
corresponding parameters, can be used in the
proposed approach to characterise the identified
clusters. In this paper we first explored using
triangular membership functions (TMFs) because of
their simplicity of calculation and ability to represent
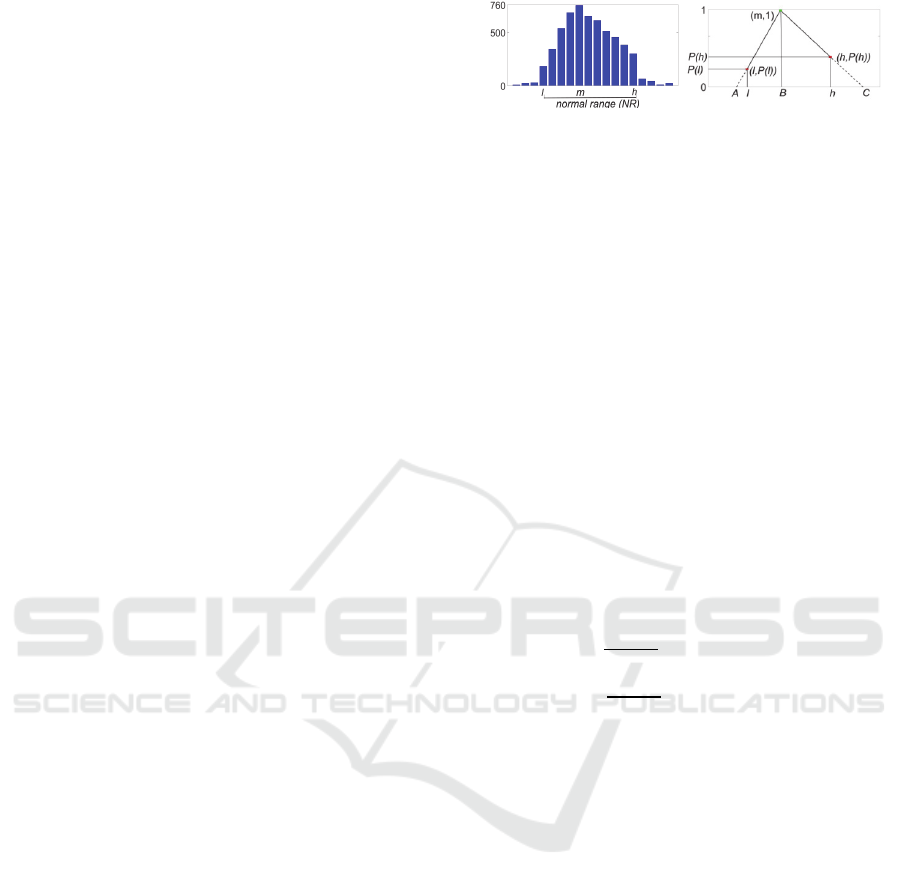
skewed distributions. As shown in Figure 1(b),
parameters of TMF are defined by a triad ,,,
with point representing the left foot of TMF, is
the location of the center, and is the location of the
right foot.
To define a TMF for a detected cluster we use
NR
,
( is the lower and is higher limit for the
normal range, respectively) associated with the
cluster, and the cluster mode, , to determine its
parameters ,,. This is illustrated using an
example shown in Figure 1.
(a) (b)
Figure 1 (a): The histogram of a detected data cluster from
Step 1. The vertical axis shows the number of
observations. (b) The corresponding TMF defined for the
cluster.
Figure 1(a) showed the histogram associated
with the cluster, with the detected mode and
normal range
,
shown, in Figure 1 (a). A
probability density distribution (PDF) is first
obtained from this histogram. Figure 1 (b) shows the
corresponding TMF defined for the cluster with
as the center point for the TMF. Next, using the
generated PDF, we calculate the probability density
of lower bound () and higher bound () of the
cluster, denoted by and
inFigure1b,
respectively. Then, we find the parameter A for the
TMF by extrapolating the two points (, 1) and (,
). In the same manner, we find the parameter C
by extrapolating the two points (, and (,
1). Now, TMF is defined using Eq. (8).
0
0
(8)
Figure 2 (a) and (b) shows examples of histograms
for attributes with a unimodal and bimodal
distributions, respectively. Each distribution of data
associated with a detected mode is shown with a
different colour. In case of Figure 2 (a), VBMS
associates all the data pints with the only mode
detected in the PDF whereas for Figure 2 (b), two
separate distributions as shown in blue and red
colours have been detected. The corresponding
normal range and the location of mode detected for
each of the distributions in Figure 2 (a) and (b) are
shown in Figure 2 (c) and (d), respectively. In Figure
2 (c), the detected lower and upper bounds for the
distribution are shown by the two vertical black
lines, respectively, and the range between these two
lines forms the normal range for the cluster
associated with the distribution. All the data points
shown by the red dots outside the detected normal
range are marked as outlier. As can be observed
from Figure 2 (c), the distance of the lower limit to
the mode of distribution is larger than that between
the mode and the upper limit, thus reflecting the
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
163
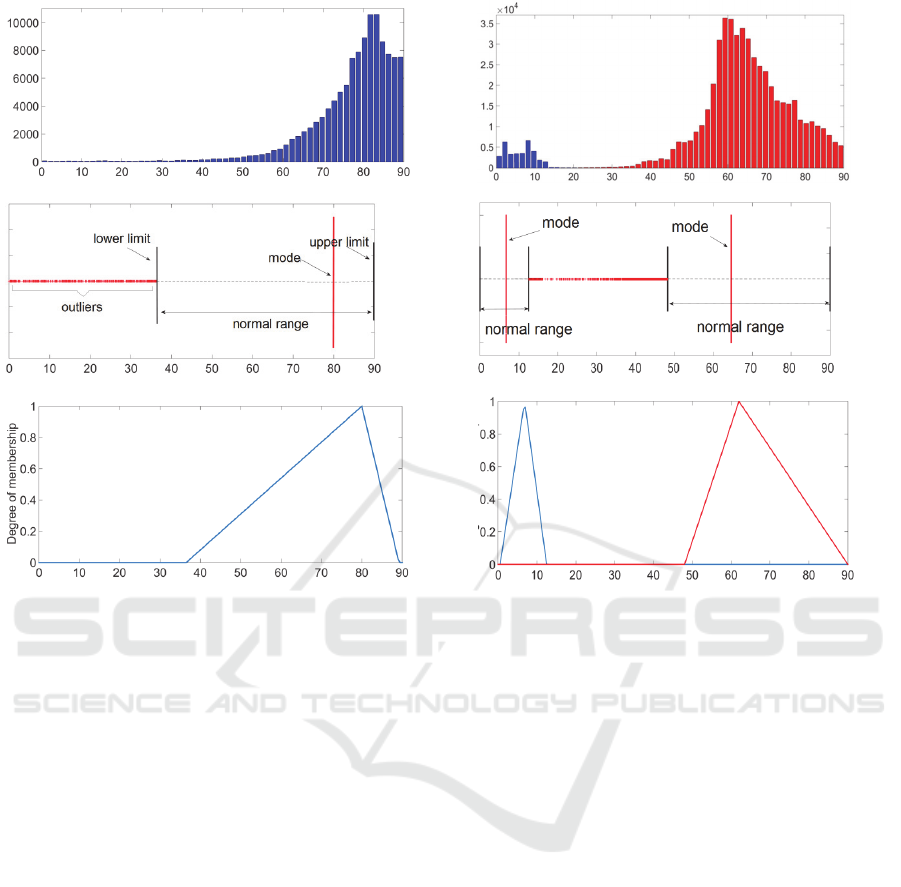
(a) (b)
(c) (d)
(e) (f)
Figure 2 (a) and (b): examples of attributes with a unimodal and bimodal distributions, respectively. (c) and (d) the
corresponding normal range and the location of mode detected for each of these distributions, respectively, and (e) and (f)
the corresponding TMFs.
skewness of the underlying distribution in Figure 2
(a). In Figure 2 (c) and (d), the data points inside
each normal range are kept as a cluster, and data
points that are outside of the detected normal ranges
are considered in this technique as being outliers and
will be eliminated. Figure 2 (e) and (f) show TMFs
representing the distributions in Figure 2 (a) and (b)
obtained from the procedure described in Step 2 of
the proposed approach.
5 EXPERIMENTAL RESULTS
Our evaluation consists of comparison between the
proposed approach and two other techniques in
terms of (i) parameterising MFs for attributes with
different distributions, and (ii) classification
performance of a fuzzy rule set that was developed
using the parameterised output of each of the 3
techniques.
5.1 Dataset
We evaluated the effectiveness of the proposed
approach using attributes associated with a dataset
for classification activities of daily living (ADLs), as
previously used in (Pazhoumand-Dar et al., 2015).
This dataset is collected via multiple Kinect
cameras, each installed in a different area of a single
monitored house. Data was collected from this house
for a period of five weeks, during which a single
occupant undertook activities typical of a retired
elderly person. From each Kinect, observations for
activities undertaken are taken at one-second
intervals and ones in which a person is detected are
stored. The entire dataset consisted of more than two
million observations. The attributes we extracted
from this dataset were the occupant’s Centre of
Gravity pixel location ,, Aspect Ratio (AR)
of the 3D axis-aligned bounding box, and
Orientation ().
The dataset for each location was partitioned into
a training set and an unseen test set. The training set
for each location consisted of nearly one million
observations of behaviour patterns associated to
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
164

typical (or normal) ADLs of the occupant. The test
set holds some sequences of normal behaviour (i.e.
typical ADLs) and abnormal events (e.g. occupant
lying on the floor of the kitchen).
The system used for the gathering of data
consisted of Windows 8.1 notebook PCs, with one
notebook per Kinect device. Custom data collection
code was written in C# under the Microsoft .Net
framework. Data analysis was subsequently
performed in MatLab™.
5.2 Comparison of Techniques for
Parameterizing Attributes with
Different Characteristics
Attributes with different data distribution were used
to compare the parameterisation results between the
proposed approach (VBMS–RS) and two other
techniques: (i) using MS (instead of VBMS) in Step
1 of the proposed approach followed by the
procedure of robust statistics in Step 2 (MS-RS), and
(ii) using the Fuzzy-C-Means (FCM) clustering
algorithm to generate a fixed number of membership
functions over the domain of a particular attribute
without the use of robust statistics. For each
particular attribute, we empirically set this number
for FCM according to the number of modes in the
attribute probability density function, as discussed in
the following sections. In each case, comparisons are
made through the clusters and TMFs produced by
each of the 3 techniques.
5.2.1 Attribute with Separated Distributions
One example with separated distributions is for the
attribute associated with the living room dataset,
as shown in Figure 3.
Figure 3: A bimodal distribution for the attribute
associated with the living room dataset.
The reason is that, as shown in Figure 4 (a) and
(b), the living room was occupied mainly for sitting
at a computer desk (the left distribution) and using
the sofa for watching TV (the distribution to the
right) and as a result, values for are mostly
concentrated around two separate regions in feature
space of Xc (i.e., 150 and 325), respectively.
(a)
(b)
Figure 4: (a) Sitting at a computer desk, and (b) watching
TV while sitting on a sofa in the living room. The body of
the occupant is masked by its binary silhouette obtained
from the Kinect SDK and the numbers in the vertical and
horizontal axis indicate pixel location.
It should be remarked that all the attributes in
this dataset were obtained from depth maps and their
corresponding binary mask of the occupant. The
colour images shown in Figure 4 are only to
visualise the living room area for the readers and the
attributes for the two observations shown in Figure 4
were actually obtained from the two depth maps
shown in Figure 5, respectively.
(a) (b)
Figure 5: The corresponding depth maps of images shown
in Figure 4.
Figure 6 (a) illustrates the results of using
VBMS–RS for parameterising distributions of Xc
from the living room. Each underlying distribution
of data associated with a detected mode is shown
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
165
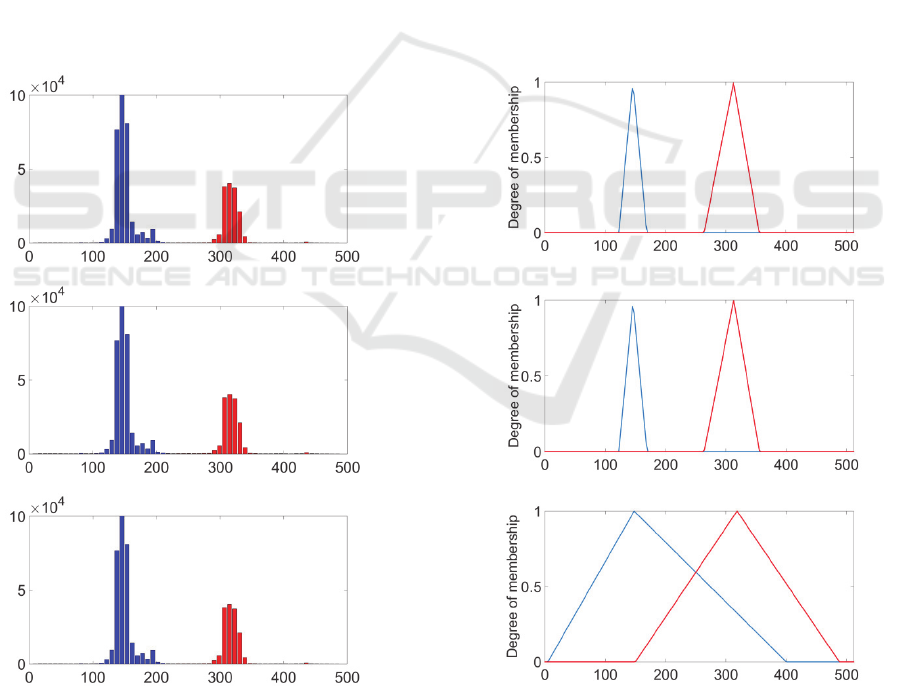
with a different colour.
VBMS–RS could separate correctly this attribute
feature space into two main underlying distributions.
The distribution to the right in Figure 6 (a) is in the
shape of reverse-J (skewed to the left), and the
corresponding TMF defined by VBMS–RS
represents only the range for the normal data points
associated with this distribution.
To further evaluate VBMS-RS, we replaced
VBMS with MS in Step 1 of the proposed approach
and repeated the experiment. By comparing the
results, we observed that where the distributions in
the attribute feature space are separated distinctly,
both methods work equally well. However, MS–RS
requires an empirical input, the bandwidth
parameter, whereas for VBMS in the proposed
approach, the initial bandwidth is derived from the
data automatically (see Section 3.1).
In the comparison using FCM, we empirically set
the number of membership functions to be 2 (as this
is obvious from a visual examination of the data). As
shown with blue and red colours, Figure 6 (e)
demonstrates that FCM correctly separated the
attribute into two distributions in the attribute feature
space. As a result, the two TMFs in Figure 6 (f) were
generated to represent the two distributions detected
in the attribute feature space, respectively. Since
FCM does not use robust statistics, the resulting
parameterization of the TMFs is not the same as the
proposed approach. More specifically, TMFs
generated by FCM have a wider support and hence
represent a wider area outside the normal range for
the two main distributions in Figure 6 (e). As a
result, the TMFs generated by FCM will be
representing many rare observations (outliers)
around the main distributions. For example, they
give membership values 0.17 and 0.83 to the outlier
point (380) so that the sum of memberships of this
point is one. This is in contrast to TMFs generated
by VBMS-RS which give zero membership to this
outlier point.
VBMS-RS
(a) (b)
MS-RS
(c) (d)
FCM
(e) (f)
Figure 6: Different techniques for parameterising the two underlying distributions present in Figure 3. The different colors
in each of (a), (b), and (c) show range for clusters obtained using the 3 different techniques. (b), (d), and (f) show the
corresponding TMFs.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
166

5.2.2 Attribute with a Unimodal
Distribution
One example of the attributes that have unimodal
skewed distribution is the AR attribute from the
dining room, as illustrated in images on the left hand
side of Figure 7 (i.e., 7 (a), 7 (c), and 7 (e)). The
overall distribution shown in those images illustrates
the skewed distribution for AR. Different colors in
each of the images indicate the distributions related
to the clusters that have been obtained using the 3
different techniques. Figure 7 (b), (d), and (f) show
results of generating TMFs for the distribution of the
AR attribute using the 3 different techniques. As
shown in Figure 7 (a), VBMS-RS correctly
associated all data points with the only mode in the
distribution. However, as shown in Figure 7 (c), MS-
RS has broken the distribution into two clusters.
This difference is mainly because in VBMS, points
that correspond to the tails of the underlying density
will get a broader neighbourhood and a smaller
importance. So, they will be included to main
structures and hence, tail of distributions will not be
broken into pieces. This is unlike MS, where it
assigns a fixed global bandwidth to all data points
and hence all points receive the same importance
when estimating the PDF of data.
As the distribution is unimodal, input value for
the number of clusters in FCM was set to 1. From
Figure 7 (e) we can see that although FCM has
grouped all data points in the distribution into the
stipulated one cluster, the support of the generated
TMF in Figure 7 (f) is much broader than TMF
generated by VBMS-RS which might lead to non-
specific responses for classification of the attribute
values (i.e., every point is considered to be in the
set). Also, when the application of generating TMFs
is for classification of outliers, the generated TMF in
this example is representing many rare observations
(outliers) located between 4 and 6, and hence will be
not able to correctly classify a new abnormal
observation within that boundary.
However, the TMF resulted from the proposed
approach is not representing any data point for
outside the normal range [0.5 , 3.5] and therefore,
VBMS-RS method can obtain better classification
results for normal points and better accuracy for
handling outlier observations.
VBMS-RS
(a) (b)
MS-RS
(c)
(d)
FCM
(e) (f)
Figure 7: Using the 3 different techniques for parameterising distribution of the AR attribute for the dining room dataset.
(a), (c), and (e) show the range for clusters obtained using the 3 different techniques, and (b), (d), and (f) show the
corresponding TMFs.
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
167

5.2.3 Attribute with Multimodal
Distribution
An example of an attribute with multimodal
distribution is Xc from the kitchen dataset. From the
ground truth in examining the video data for this
attribute there were three distinct places for Xc
where the occupant performed most of the activities
in the kitchen. As a result, PDF for this attribute has
3 modes, each associated with a particular
distribution and the 3 distributions overlap.
Results of parameterising this attribute using the
3 different techniques are shown in Figure 8. Input
value for the number of clusters to be created by
FCM was set to 3. It is clear from the results in
Figure 8 that, VBMS-RS partitions the feature space
into the right number of membership functions
whereas using MS-RS and FCM were unable to
separate the mixed distributions correctly. The
difference between results for VBMS-RS and MS-
RS is due to the fact that, using VBMS, the data
points lying in large density regions will get a
narrower neighbourhood since the kernel bandwidth
is smaller, but are given a larger importance. So
when main distributions are mixed in the attribute
feature space, VBMS can better separate those
structures than MS. This finding is consistent with
Comaniciu et al., (2001).
From Figure 8 (f) FCM has partitioned the
attribute feature space to be represented by three
TMFs. However, the parameters for these three
TMFs are different to those of the results from
VBMS-RS. The reason is that FCM aims to
minimise the distance of data points from their
respective cluster centres. As a result the locations of
centre of clusters are not always corresponding to
the modes in distribution of data. Furthermore, as
seen in Figure 8 (e), distributions with their modes
located on pixel location 150 and 200, respectively,
are represented by the same TMF. Hence, TMFs
generated by this technique are not accurately
representing data distributions in this attribute
feature space.
5.3 Results on Classification Accuracy
using TMFs Produced by Different
Techniques
The characteristics of MFs generated by a particular
technique have a direct impact on performance of
the corresponding fuzzy rule set for classification
purposes. In other words, a better technique to
estimate the underlying distributions for attributes
can lead to more representative MFs and hence a
better classification accuracy of the corresponding
fuzzy rule set. To investigate this, we conducted
experiments in which we applied the output of the 3
different MF generation techniques, including the
proposed approach, to obtain a fuzzy rule set for the
application of detecting abnormal activities in
ADLs. As we had data from 5 rooms and each room
was associated with 4 attributes with different
number of modes in their corresponding PDF, we
empirically set the number of clusters for FCM to a
specific number (i.e., 3) to suite across all situations,
a technique used typically by existing fuzzy
approaches (Tajbakhsh et al., 2009). To obtain the
classifier, we extracted the attributes (described in
Section 5.1) from the training dataset associated
with each location and developed the fuzzy system
using the approach from (Pazhoumand-Dar et al.,
2015). A brief description of this approach is
described below:
The unsupervised ADLs monitoring approach
proposed by (Pazhoumand-Dar et al., 2015) uses a
set of attributes derived from Kinect camera
observations and consists of two phases: training and
monitoring.
During the training phase, the system first learns
“normal” behaviour patterns of the occupant as a set
of fuzzy rules. For each monitored location, normal
behaviour patterns are learnt by finding frequent
occurrences of attributes via the use of a fuzzy
association rule mining algorithm (Kuok et al.,
1998). The antecedent part of each rule in the
resulting fuzzy rule set for each monitored location
represents a combination of fuzzy linguistic values
describing a frequent behaviour of the occupant. The
normal duration of that frequent behavior is shown
in the consequent part of the rule.
The monitoring phase takes the fuzzy rule set
obtained from the training phase as input, and for
each location, it classifies the current behaviour of
the occupant as abnormal if it is not in the set of
frequent behaviours. For more detail, we refer the
reader to (Pazhoumand-Dar et al., 2015).
Table 1 compares classification accuracy for
fuzzy rules obtained using the output of the 4
different MF generation techniques. More
specifically, 40 sequences of different scenarios for
normal and abnormal behaviour in the unseen test
set (20 sequences for each category of normal and
abnormal behaviour, respectively) were used to
evaluate the accuracy of the fuzzy rule set obtained
using the output of a particular technique and the
resulting classification accuracy is reported in Table
1.
From Table 1 it can be observed that when we
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
168

use MS-RS to obtain TMFs for fuzzy rules, 6 of the
test sequences, mostly representing an abnormal
behaviour, were classified incorrectly. This is
mainly because MS couldn’t distinctly separate
overlapped distributions in feature space of
attributes. Therefore, for some attributes two or
more behaviour patterns belonging to different
overlapped distributions were represented by the
same TMF and hence represented by the same fuzzy
rule. For example, distributions of AR for crouching
on the kitchen floor (to pick up an object) and
bending down (to manipulate objects inside the
kitchen cabinet), while belonging to different main
distributions in the attribute feature space,
considered as belonging to the same cluster, and
hence, the corresponding fuzzy rule set was not able
to label a sequence for spending a long time sitting
on the kitchen floor as abnormal behaviour.
Classification that results from using FCM to
generate TMFs produced accuracy of 78%. This is
mostly because the test sequences involving normal
behaviour patterns that were slightly different from
their corresponding training patterns were
misclassified by this classifier as abnormal. This was
mainly because FCM broke main distributions for
some attributes into pieces and consequently, for a
particular activity, when most of training values
belonged to a particular part of the distribution and
the values for test sequences fell into another part of
the distribution, the corresponding fuzzy rule for the
activity could not be able to trigger and hence less
accuracy of the classifier.
We also evaluated the classification accuracy of
the fuzzy rules obtained by applying the proposed
approach without robust statistics and results are
shown Table 1 denoted by VBMS. We observed that
many test sequences for abnormal behaviour have
been labeled as normal. In those sequences, the
values of attributes were well outside of the normal
range for the main distributions in the feature space
of attributes. However, since the range of generated
TMFs was wider than the range of main
distributions, they included many outlier
observations, and hence, outlier observations in each
of those test sequences triggered a corresponding
rule for a normal behaviour in the rule base to be
VBMS-RS
(a) (b)
MS-RS
(c) (d)
FCM
(e) (f)
Figure 8: Results for using the 3 different techniques for parameterising distribution of Yc associated with the kitchen
dataset. (a), (c), and (d) show the range for clusters obtained using the 3 different techniques, and (b), (d), and (f) show the
corresponding TMFs.
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
169

fired and resulted in the test sequence being labelled
normal.
Table 1: Results of using the output of different MF
generation techniques to obtain a fuzzy rule set for the
application of detecting abnormal activities in ADLs.
Method
Normal
behaviour
Abnormal
behaviour
Overall
accuracy
FCM with 3
clusters
70% 85% 78%
MS-RS 90% 80% 85%
VBMS 100% 35% 68%
VBMS-RS 100% 85% 92.5%
From the last row of Table 1 we see that the rule
set obtained from the results of VBMS-RS could
classify 37 test sequences correctly and hence an
accuracy of 92.5%. We observed that for almost all
attributes, using the combination of VBMS and
robust statistics yields in the resulting TMFs
representing only the normal range for the main
distributions in the attributes. Therefore, while
outlier observations for abnormal behaviours were
classified correctly, attribute values during most of
sequences for normal behaviour were within the
bounds associated with the generated TMFs, and
hence, those sequences triggered a rule
corresponding to a normal behaviour to fire.
6 CONCLUSIONS
In this paper, we presented an unsupervised MF
generation method which learns the number of
representative MFs for a dataset from the underlying
data distribution automatically and sets up
parameters associated with each MF. We performed
comparisons between the results of the proposed
approach and other techniques. In term of
partitioning a particular attribute, results confirmed
that the proposed approach generates membership
functions that can separate the underlying
distributions better. In comparing the results of
different parameterization techniques in building
fuzzy rules for classification of ADLs, we observed
that the proposed approach allows us to achieve a
better classification accuracy, thus showing a better
performance for the proposed approach. Future work
will involve extending the approach to address
different types of membership functions.
REFERENCES
Amaral, T. G. & Crisóstomo, M. M. Automatic helicopter
motion control using fuzzy logic. Fuzzy Systems,
2001. The 10th IEEE International Conference on,
2001. IEEE, 860-863.
Brys, G., Hubert, M. & Struyf, A. 2004. A robust measure
of skewness. Journal of Computational and Graphical
Statistics, 13.
Castellano, G., Fanelli, A. & Mencar, C. 2002. Generation
of interpretable fuzzy granules by a double-clustering
technique. Archives of Control Science, 12, 397-410.
Comaniciu, D., Ramesh, V. & Meer, P. The variable
bandwidth mean shift and data-driven scale selection.
Computer Vision, 2001. ICCV 2001. Proceedings.
Eighth IEEE International Conference on, 2001. IEEE,
438-445.
Doctor, F., Iqbal, R. & Naguib, R. N. 2014. A fuzzy
ambient intelligent agents approach for monitoring
disease progression of dementia patients. Journal of
Ambient Intelligence and Humanized Computing, 5,
147-158.
Hubert, M. & Vandervieren, E. 2008. An adjusted boxplot
for skewed distributions. Computational statistics &
data analysis, 52, 5186-5201.
Kuok, C. M., Fu, A. & Wong, M. H. 1998. Mining fuzzy
association rules in databases. ACM Sigmod Record,
27, 41-46.
Medasani, S., Kim, J. & Krishnapuram, R. 1998. An
overview of membership function generation
techniques for pattern recognition. International
Journal of approximate reasoning, 19, 391-417.
Moeinzadeh, H., Nasersharif, B., Rezaee, A. &
Pazhoumand-Dar, H. Improving classification
accuracy using evolutionary fuzzy transformation.
Proceedings of the 11th Annual Conference
Companion on Genetic and Evolutionary Computation
Conference: Late Breaking Papers, 2009. ACM, 2103-
2108.
Pazhoumand-Dar, H., Lam, C. P. & Masek, M. A Novel
Fuzzy Based Home Occupant Monitoring System
Using Kinect Cameras. IEEE 27th International
Conference on Tools with Artificial Intelligence, 2015
Vietri sul Mare, Italy. in press.
Rousseeuw, P. J. & Hubert, M. 2011. Robust statistics for
outlier detection. Wiley Interdisciplinary Reviews:
Data Mining and Knowledge Discovery, 1, 73-79.
Seki, H. 2009. Fuzzy inference based non-daily behavior
pattern detection for elderly people monitoring system.
Engineering in Medicine and Biology Society, 2009.
EMBC 2009. Annual International Conference of the
IEEE. IEEE.
Sheather, S. J. & Jones, M. C. 1991. A reliable data-based
bandwidth selection method for kernel density
estimation. Journal of the Royal Statistical Society.
Series B (Methodological), 683-690.
Tajbakhsh, A., Rahmati, M. & Mirzaei, A. 2009. Intrusion
detection using fuzzy association rules. Appl. Soft
Comput., 9, 462-469.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
170

Takagi, H. & Hayashi, I. 1991. NN-driven fuzzy
reasoning. International Journal of Approximate
Reasoning, 5, 191-212.
Tang, K., Man, K. & Chan, C. Fuzzy control of water
pressure using genetic algorithm. Proceedings of the
Safety, Reliability and Applications of Emerging
Intelligent Control Technologies, 2014. 15-20.
Automatic Generation of Fuzzy Membership Functions using Adaptive Mean-shift and Robust Statistics
171
