
A Novel Algorithm for String Matching with Mismatches
Vinod-prasad P.
Sur College of Applied Sciences, Ministry of Higher Education, Muscat, Oman
Keywords: Pattern Matching in Strings, String Matching with Mismatches, Similarity Search.
Abstract: We present an online algorithm to deal with pattern matching in strings. The problem we investigate is
commonly known as ‘string matching with mismatches’ in which the objective is to report the number of
characters that match when a pattern is aligned with every location in the text. The novel method we
propose is based on the frequencies of individual characters in the pattern and the text. Given a pattern of
length M, and the text of length N, both defined over an alphabet of size σ, the algorithm consumes O(M)
space and executes in O(MN/σ) time on the average. The average execution time O(MN/σ) simplifies to
O(N) for patterns of size M ≤ σ. The algorithm makes use of simple arrays, which reduces the cost overhead
to maintain the complex data structures such as suffix trees or automaton.
1 INTRODUCTION
Similarity search is a fundamental problem in
pattern recognition. Similarity searches allow for
some mismatches between the text and the pattern.
Searching for similar patterns is common in DNA
sequence analysis, data mining, search engines, and
many other applications. The term ‘distance’ is used
quite often when comparing two strings for
similarity. One of the simplest distance-metric is the
Hamming distance. The hamming distance between
two equal length strings is the number of mismatch
symbols at corresponding locations. In literature,
this problem is sometimes also called ‘string
matching with k-mismatches’.
1.1 String Matching with K
Mismatches
Let R and S be two non-empty equal-length strings
of size M such that R = r
0
r
1
…r
M-1
and S = s
0
s
1
….s
M-1
. Then, the Hamming distance between R
and S is given by ham(R, S) = number of all
locations i where r
i
≠ s
i
such that 0 ≤ i ≤ M-1.
Modern applications require large databases to be
searched for regions that are similar to a given
pattern. In such a context, the ‘k-mismatch’ problem
can be stated as follows: Given the text T = t
0
t
1
...t
N-1
of size N, and the pattern P = p
0
p
1
….p
M-1
of size M
such that M ≤ N. Both text and the pattern are
defined over alphabet λ. Let hd
i
be the Hamming
distance such that hd
i
=ham(P, t
i
t
i+1
…t
i+M-1
), where,
0 ≤ i ≤ (N−M). Then, for a given integer k such that
0≤ k ≤ M, report all locations i in T where hd
i
≤ k.
To solve the ‘k-mismatch’ problem, Landau and
Vishkin (1986) proposed a suffix-tree-based
algorithm. A suffix tree is created using the text and
the pattern in O(N+M) time and space, before
applying searches to report k-mismatches in O(kN)
time. For suffix trees, see (McCreight, 1976),
(Ukkonen, 1995), and (Gusfield, 1999). The Tarhio
and Ukkonen (1993) algorithm requires the pattern
to be preprocessed in O(kσ) space and O(M+kσ)
time, and then reporting k-mismatches in O(kN(k/σ
+1/(M-k))) time. The algorithm (Tarhio et al., 1993)
is based on (Boyer and Moore, 1977), and
(Horspool, 1980). The Galil and Giancarlo (1986)
algorithm runs in O(kN) time and O(M) space. Amir,
Lewenstein, and Porat (2004) provide O (N√k log k)
time algorithm to solve the same problem.
1.2 String Matching with Mismatches
For k=M, the ‘k-mismatch’ problem becomes
independent of k, and hence can be stated as: Given
the text T= t
0
t
1
….t
N-1
, and the pattern P=p
0
p
1
….p
M-
1
. For every i in T such that 0 ≤ i ≤ (N−M), output
the Hamming distance hd
i
such that hd
i
=ham(P, t
i
t
i+1
…t
i+M-1
). In this case, the objective is to report all
mismatches (0 to M) from every alignment location
in the text. Therefore, the problem is commonly
known as ‘string matching with mismatches’. Using
638
P., V-p.
A Novel Algorithm for String Matching with Mismatches.
DOI: 10.5220/0005752006380644
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 638-644
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

a linked list, Baeza-yates and Perleberg (1996)
proposed O(N+Nf
max
) time and O(2M + σ) space
algorithm, where f
max
is the frequency of the most
commonly occurring character in the pattern. Based
on the Boolean convolution of the pattern and the
text, Abrahamson (1987) solves the problem in
O(N√(M log M)) time and O(N) space. Recently,
Nicolae and Rajasekaran (2013) have shown that for
pattern matching with wild-cards, the algorithm
(Abrahamson, 1987) can be modified to obtain an
O(N√(g log M)) time, where g is the number of non-
wild-card positions in the pattern. The algorithm
Clifford and Clifford (2007) is also based on
convolution, which takes O(Nlog(M)) time. A
randomized algorithm Kalai (2002), which is based
on (Karp and Rabin, 1987), consumes O(Nlog(M))
time. Atallah, Chyzak, and Dumas (2001)
approximate the number of mismatches from every
alignment in O(rN log(M)) time, where r is the
number of iteration algorithm has to make.
In literature, string-processing algorithms have
made extensive use of suffix trees, suffix arrays, and
automata. Most of these methods are covered
Crochemore, Hancart, and Lecroq (2007). Algorithms
based on automata give the best worst-case time
O(N). However, exponential time and space
dependence on M and k limits its practicality see
Navarro (2001). Therefore, automaton based
algorithms best suited to short patterns with low
error rates Navarro (2001). Suffix trees on the other
hand, consume space linear to the size of the text,
which may be a challenge when dealing with the
large text.
Breaking the trend, in this paper, we follow a
novel approach to solve the ‘string matching with
mismatches’ problem. The method we propose is
based on the frequencies of individual characters in
the pattern and the text, which is completely
different from the other methods proposed in the
past. The algorithm we propose avoids all complex
data-structures, yet achieves average case O(N) time
for patterns of length ≤ σ. The rest of the paper is
structured as follows: - In section 2, we introduce
few terms and notations used in this paper. To create
a theoretical base for the algorithm, the lemma,
corollaries, and examples are given in section 3. In
section 4, an algorithm is provided to pre-process the
pattern, which is a prerequisite for the main
algorithm given in section 5. For a better
understanding of the algorithm, the run-time
behavior of the algorithm is also described in the
same section. In section 6, we discuss the time and
space requirements of the algorithms. Using real-life
data, experimental results are provided in section 7.
Finally, we conclude our work in section 8.
2 PRELIMINARIES
The symbol ‘λ’ represents the alphabet -a finite non-
empty ordered set of characters, such that |λ|=σ is
the size of the alphabet. We use the symbols T and P
to represent non-empty text and pattern strings of
length N and M respectively. Both T and P are
defined over the alphabet λ. T[i] or t
i
represents the
i
th
character of T, where ‘i’ is referred to as shift,
location, or index in T. Throughout the paper, we
have used a phrase extensively “Number of matches
of P at shift t in T”, which refers to the total number
of the characters that match when pattern P is
aligned with shift t in T. In the algorithm, we refer to
this as the number of hits at shift t in T by the pattern
P. Note, for a clear relationship among the lemma,
corollaries, examples, and the algorithms we
consider the number of character matches (not
mismatches).
3 LEMMA
Consider the text T = t
0
t
1
t
2
t
3
t
4
t
5
= DBCDAB of
size N=6, and the pattern P = DABCD of size M=5.
It is easy to see that one character match may be
found provided that P is aligned at location -4 in T
(assume that there is such a location). Similarly, a
three character match may be found when P is
aligned at locations -1 and 3 in T. Traditionally,
pattern P is aligned with all locations i in T such that
0 ≤ i ≤ N-M. However, considering i’s in the
extended range (1-M) ≤ i ≤ (N-1) may also provide
useful information, particularly when the pattern and
the text are almost same in length, and the character
matches exist at opposite ends of the strings being
matched. Therefore, with the extended search space,
the ‘string matching with mismatches’ problem can
be re-formulated as:-
Given a text T and a pattern P. For every i in T
such that (1-M) ≤ i ≤ (N−1), output the Hamming
distance hd
i
such that hd
i
= ham (P, t
i
t
i+1
...t
i+M-1
),
where, t
i
=null if i < 0 or i ˃ N-1. Now, for the text
and the pattern given above, we are in a position to
say that the hamming distance between P and t
-1
t
0
t
1
t
2
t
3
= 3, i.e., hd
-1
= ham(P, t
-1
t
0
t
1
t
2
t
3
) = 3.
Similarly, hd
3
= ham(P, t
3
t
4
t
5
t
6
t
7
) = 3. The
algorithm given in section 5 solves the problem
outlined above with the extended search space.
A Novel Algorithm for String Matching with Mismatches
639
3.1 The Set Intersection Lemma
Let T be a text of length N, and P be a pattern of
length M such that: T = T[0….N-1], and P =
P[0….M-1]. For each shift j in P, we define a set R
j
such that: R
j
= { i – j | T[i]=P[j],
∀
0 ≤ i ≤ N-1 }.
Further, let S be a set such that S= R
0
∩ R
1
∩ R
2
…∩
R
M-1
. Then, every element t
∊
S represents an exact
match of P at shift t in T, and the cardinality |S|
represents the number of occurrences of P in T.
Proof: The given lemma has a simple and
straightforward proof. Let P is present in T at shift t.
Then, we have to show that t
∊
S. Let P appears in T
at shift t, that means all M characters of pattern P =
P[0…M-1] can be successfully matched with
T[t, t+1…t+M-1]. Hence,
∀
j in P, T[ t+j] = P[j].
Now, from the definition of R
j
,
∀
j in P we have:
R
j
= { ( t + j ) - j } = { t }
⇒
for all j in P, we have
t
∊
R
j
⇒
t
∊
S. Further, since t
∊
S represents an
exact match of P in T at shift t ⇒ |S|= Number of
occurrences of P in T. Therefore, if R
0
∩ R
1
∩
R
2
……∩ R
M-1
= S = { } then, exact match of P is not
available in T. Notice, since 0 ≤ i ≤ N-1, and
0 ≤ j ≤ M-1
⇒
each element of R
j
lie in the range
(1-M) ≤ t ≤ N-1.
Example 1: Let T = CABABABCBA be a text
array of size 10, and P = ABAB be a pattern array of
size 4.
For each shift j in P, we create a set R
j
such that
R
j
={ i – j | T[i] = P[j],
∀
0 ≤ i ≤ 9 }. Which gives:
R
0
= {1, 3, 5, 9}, R
1
= {1, 3, 5, 7}, R
2
= {-1, 1, 3, 7},
and R
3
= {-1, 1, 3, 5}. Hence, R
0
∩ R
1
∩ R
2
∩ R
3
= S
= {1, 3}. Which confirms two (|S|) occurrences of P
in T at shift 1, and 3.
Corollary 1: Given the M sets R
j
defined as
above. Let f
t
be the frequency of occurrence of an
integer ‘t’ in all sets. Then, f
t
represents the number
of characters that match at corresponding locations
when P is aligned with shift t in T.
Proof: As we proved already, t
∊
S represents
exactly M character matches of P at shift t in T.
therefore, each t
∊
R
j
represents a single character
match of P ⇒ the frequency of integer t = f
t
=
Number of characters, that match at corresponding
locations when P is aligned at shift t in T.
Example 2: Consider example 1, the integer 5
appears in three sets: R
0
, R
1
, and R
3
. Hence, the
frequency of integer 5 = f
5
= 3. This confirms a three
characters match of P when P is aligned with shift 5
in T ⇒ hamming distance hd
5
= M – f
5
= 4 – 3 = 1.
Similarly, f
7
=2 and f
-1
=2 reveal two characters
match, when P is aligned with locations 7 and -1 in
T respectively.
Observation 1(a): As we proved in the lemma,
for an exact match of P at shift t in T, the integer t
must be present in all M sets, i.e., f
t
= M.
(b) Since, f
t
represents the number of characters
that match ⇒ M – f
t
represents the Hamming
distance, i.e. the number of mismatches, when the
pattern P is aligned with shift t in T i.e.
hd
t
= ham(P, T[t] T[t+1]...T[t+M-1] ) = M – f
t
.
Observation 2: The lemma and examples given
above may suggest that the method under
consideration requires the entire text to be available
before we create the sets. However, this is not the
case. Consider example 1 again, to identify the first
match at shift 1 in T, we do not require all elements
of R
j
at once. Let us assume that we receive the text
in the form of a stream of characters, and that we
have just received T[0..5]. Applying the set
intersection lemma for the given fragment of text,
we get: R
0
={1, 3, 5}, R
1
={1, 3}, R
2
={-1, 1, 3}, and
R
3
={-1,1}. Thus, we find that: R
0
∩ R
1
∩ R
2
∩ R
3
= S
= {1}, which confirms the first exact match of
P=ABAB at shift 1 in T. Moreover, the double
repetition of -1 and 3 reveals two characters match,
when P is aligned at shifts -1 and 3 in T[0..5].
Example 3: Let’s now discuss the practical
aspect of the method. Consider the text
T=SKRFCTHZCTZCFTYCTZGHTTCTHZTHZFC
THZCTZC of size 38, and the pattern P =
FCTHZCTZCF of size 10.
Table 1: Sets showing integer frequencies.
Pattern
Char
Shift
in T
(i)
Shift
in P
(j)
Set R
j
F
3, 12, 29,
38
0 R
0
= 3, 12, 29, 38
9 R
9
= -6, 3, 20, 29
C
4, 8, 11,
15, 22, 30,
34, 37
1 R
1
= 3, 7, 10, 14, 21,
29, 33, 36
5 R
5
= -1, 3, 6, 10, 17,
25, 29, 32
8 R
8
= -4, 0, 3, 7, 14,
22, 26, 29
T
5, 9, 13,
16, 20, 21,
23, 26, 31,
35
2 R
2
= 3, 7, 11, 14, 18,
19, 21, 24, 29, 33
6 R
6
= -1, 3, 7, 10, 14,
15, 17, 20, 25, 29
H
6, 19, 24,
27, 32
3 R
3
= 3, 16, 21, 24,
29
Z
7, 10, 17,
25, 28, 33,
36
4 R
4
= 3, 6, 13, 21, 24,
29, 32
7 R
7
= 0, 3, 10, 18, 21,
26, 29
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
640

The first column of table 1 summarizes all
unique pattern characters. The second and the third
columns of the table represent the shifts of the
corresponding pattern character in the text and in the
pattern respectively. Each row of the last column
represents set R
j
as defined in the lemma. As noted
above, the frequency of occurrence f
t
of an integer
‘t’ represents the number of characters that match
when P is aligned at shift t in T. For example, f
3
= f
29
= 10=M represent 10 characters match (exact match)
of P at alignment locations 3 and 29 in T. Therefore,
we simply need a mechanism to count the number of
occurrences of individual t’s in the last column of
the table. This can be done using an array of size N,
with all array cells having an integer count, which is
set to 0 initially. Then, for each t
∊
R
j
in the last
column, the count of array[t] is incremented by one.
In other words, each t
∊
R
j
induces a hit at index t in
the array, which increments the hit-count at array[t].
Henceforth, we call the array as ‘hit []’, and the
algorithm as hit-index.
Observation 3: The method described above has
two issues. First, as shown in lemma, each ‘t’ in the
set R
j
lie in the range (1-M) ≤ t ≤ N-1). For example,
f
-1
= 2 in the table suggest that a two character match
may be found if P is aligned at location -1 in T.
However, for integer t < 0 ‘hit [t]’ does not exist. As
a solution, we assume the initial index of the text file
to be M rather than 0. This amplifies each i of the
table 1 by M ensuring all t > 0 in the last column.
Now, since each t is hyped by M, the hit-count at
hit[t] represents the number of character matches at
alignment location t-M rather than t in the text. That
means the hit-count at hit[0] represents the number
of characters that match when P is aligned at
location –M in T. The second issue is the size of the
array ‘N’, which is undesirable for the modern
databases. In section 5 we have shown that how this
issue can be resolved using an array of size 2M.
4 PATTERN PREPROCESSING
The algorithm given in section 5 requires all shifts of
a character to be retrieved quickly from the pattern.
To process the pattern, an array of pointers
shift [max_ASCII+1] is used, where max_ASCII is
the maximum possible ASCII code of a character in
the alphabet, which is typically 127 or 255. Each
pointer in the array points to a linked list that stores
all shifts of a particular character in the pattern.
Initially, all linked lists are empty. While reading the
pattern from left to right, a node containing its shift
is created. Then, based on the ASCII value of the
character, the node is mapped to a particular linked
list. For example, let ‘m’ be the shift of a character
in the pattern that is being read, and let ‘j’ be its
ASCII value. For this character, a node containing
integer ‘m’ is created and then inserted at the
beginning of the linked list pointed by shift[j].
Example 4: Let P=FCTHZCTZCF be a pattern of size
10. The ASCII codes of the pattern characters are:- F=70,
C=67, T=84, H=72, and Z=90. The shift[] is shown in
figure 1.
---------------------------------------------------------------
Input: pattern characters. Output: A shift array, such
that each cell of the array points to a list that stores
all shifts of a particular character in the pattern.
----------------------------------------------------------------------
Let ‘node’ be a structure with two
fields: integer s, and node type
pointer *next
node *shift[max_ASCII +1]
integer j, m = 0
for j = 0 to max_ASCII do
shift[ j ] = NULL
end for
while ( Not end of the pattern ) do
j = ASCII(patten character)
node *ptr = new node
ptr → s = m++
ptr→ next = shift [j]
shift[j] = ptr
end while
Figure 1: The Shift array.
5 ALGORITHM ‘HIT-INDEX’
The challenge of the algorithm is to get the work
done using an array of size 2M. As explained in the
observation 3, the variable D is set to M, which is
the presumed beginning of the text. With the arrival
of each text character, D is incremented by 1.
A Novel Algorithm for String Matching with Mismatches
641

Corresponding to the size of the array 2M, the
variable D is allowed to take values up to 3M-1,
beyond which it is again reset to M. The algorithm
reads a text character, and based on the ASCII value
of the character, a particular list is chosen from the
‘shift[]’ array. For each shift ‘s’ in the list, a hit-
index ‘t’ is computed, which is kept < 2M using
modulus operator. Each ‘t’ so computed increments
the hit-count at ‘hit[t]’.
---------------------------------------------------------------
Input: Pattern in the form of a ‘shift[]’ array, and a
stream of text characters. Output: the number of
characters that match when the pattern P is aligned
from every location i in the text T such that (1-M) ≤
i ≤ (N-1). The algorithm reads the text character by
character, without any upper limit on N.
‘node’ is a structure with two fields:
integer s, and node type pointer *next
integer i=-M, D = M, j, t
integer hit[2M]
for j=0 to 2M-1 do
hit[j]=0 /* initialize */
end for
/* read text*/
while(Not end of the text) do
j = ASCII(text character)
node *ptr = shift[j]
while(ptr != NULL) do
t = (D - (ptr → s))%2M
hit[t]++
ptr = ptr→ next
end while
Print i, hit[D-M]
hit[D-M] = 0 /* reset */
i++ D++
if(D = = 3M)
D = M
end while /* text is over */
for j = 0 to M-1 do
Print i, hit[D-M]
i++ D++
if(D = = 3M)
D = M
end for
The printing of the hit-count in the array lags M
locations behind the character being read. Therefore,
the remaining M hit-counts are printed when the text
input is over. Table 2 given below simulates the run
time behavior of the algorithm for a pattern
P=ABBA of size M=4. For the given pattern, the
two linked lists in the shift array are: A= {3→0},
and B = {2→1}. The algorithm use an array integer
of size 2M=8. All hit-counts in the array are
initialized to 0. Let T be the text such that
T = BBABAABBACAAB. The algorithm begins
with printing the hit-counts from hit[0], which
corresponds to the alignment location –M in the
text. Since all t > 0, the hit-count at hit[0] is always
0, refer to observation 3. Therefore, for the first
alignment at -M, the output is always 0. Each pair (i,
c) in the last column represents the number of
character matches ‘c’ when P is aligned at location
‘i’ in the text. Please view the table growing top-
down with respect to each incoming text character.
For each incoming text character, the algorithm
performs three actions: a) generate the ‘hit-
indexes’(t), b) for each t, increment the hit-count at
hit [t], and c) print, and then reset the hit-count at
hit[D-M].
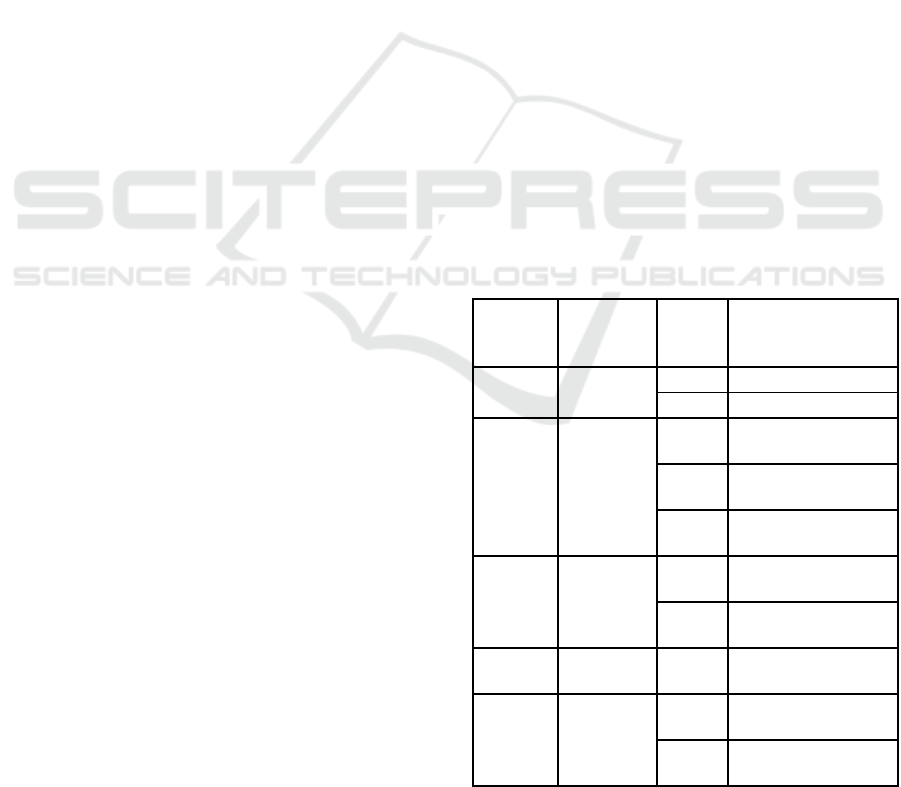
Table 2: Run Time Behavior.
i, T D t Workspace: array hit [8]
i,
hit
[D-
M]
0 1 2 3 4 5 6 7
0 0 0 0 0 0 0 0
-4 #
-3 #
-2 #
-1 #
0 B 4 2, 3 0 0 1 1 0 0 0 0
-4,
0
1 B 5 3, 4 0 0 1 2 1 0 0 0
-3,
0
2 A 6 3, 6 0 0 1 3 1 0 1 0
-2,
1
3 B 7 5, 6 0 0 0 3 1 1 2 0
-1,
3
4 A 8 5, 0 1 0 0 0 1 2 2 0 0, 1
5 A 9 6, 1 1 1 0 0 0 2 3 0 1, 2
6 B 10 0, 1 2 2 0 0 0 0 3 0 2, 3
7 B 11 1, 2 2 3 1 0 0 0 0 0 3, 0
8 A 4 1, 4 2 4 1 0 1 0 0 0 4, 2
9 C 5 --- 0 4 1 0 1 0 0 0 5, 4
10A 6 3, 6 0 0 1 1 1 0 1 0 6, 1
11A 7 4, 7 0 0 0 1 2 0 1 1 7, 1
12B 8 6, 7 0 0 0 0 2 0 2 2 8, 2
# 9 0 0 0 0 0 0 2 2 9, 0
# 10 0 0 0 0 0 0 2 2
10,
2
# 11 0 0 0 0 0 0 2 2
11,
2
# 4 0 0 0 0 0 0 2 2
12,
0
Let us consider first two characters of the text.
For the first character ‘B’, the algorithm retrieves its
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
642

shifts from the shift array to produce two hit-indexes
t = 4 - 2 = 2, and t = 4–1 = 3. Hence, the hit-count at
hit[2] and hit[3] is incremented from 0 to 1.
Thereafter, the hit-count at hit[0] is printed, and then
reset to 0. In the table, cells receiving hits are
underlined, while the resetting is indicated by a
strikethrough. For the next character ‘B’, the
algorithm hits at locations 3 and 4. As a result, the
hit-count at hit[3] and hit[4] is incremented to 2 and
1 respectively. For all other locations, the hit-count
remains the same. This time, the algorithm prints the
hit-count at hit [1], before it is reset to 0. As the
process continues, D takes values up to 3M-1 (11),
beyond which D is reset to M=4. The printout lags
‘M’ locations behind the character being read;
therefore, the last M rows of the table show hit-
counts without any input.
6 TIME AND SPACE ANALYSIS
In the preprocessing phase, insertion of a node in the
beginning of the linked list costs O(1) time. Hence,
for a pattern of size M, the pattern processing time is
O(M). Since a total of M nodes are inserted in the
shift array of size max_ASCII + 1, the pattern
preprocessing phase consumes O(max_ASCII +M)
memory, where max_ASCII is the maximum ASCII
code of a character in the alphabet, which is
typically 128 or 256. An additional array of size 2M
is used in the search phase, which gives the total
run-time space requirement to be
O(max_ASCII + M) + O(2M) i.e. O(M). Thus, the
total run-time memory requirement of the algorithm
is independent of N, which is one of the desired
issues when working with the large databases.
Let’s discuss the time consumed in the search
phase. The outer while-loop of the algorithm
hit-index given in section 5 reads a text character T
i
,
and then retrieves all shifts of T
i
from the shift array.
That means for each text character T
i
, the inner
while-loop runs fT
i
times, where fT
i
is the frequency
of T
i
in the pattern. Assuming a uniform character
distribution, the average frequency of a character in
the pattern can be given by M / σ, where, σ is the
size of the alphabet. For a text of size N, this gives
the average case execution time to be O(N (M / σ)).
Therefore, for a pattern of size M such that M ≤ σ,
the expected execution time is O(N). The worst case
time O(NM) is reached in a rare situation when a
single letter is repeated N and M times in both text
and the pattern, e.g., T=AAAA, and P=AAA.
7 EXPERIMENTAL RESULTS
To conduct our experiments, we have used natural
language as a dataset. For natural language, we use a
plain text version of the eBook “Pride and
Prejudice” (Austen, 1813) retrieved from the project
Gutenberg. The file has 704146 characters (0.7
million approx.). Ten different patterns of varying
sizes were chosen from the different locations in the
file. Fig. 2(a) given below shows the total number of
induced ‘hits’ for the corresponding size of the
pattern. Each ‘hit’ can be treated as a character
comparison. Notice, corresponding to the largest
pattern size M=100, the number of induced ‘hits’ is
roughly equal to 6N. The execution time to process
these patterns is shown in fig. 2(b). The experiments
were conducted on a 64 bit machine, Windows 8.1,
Intel® Core™ i3-3120M, CPU @2.5 GHz, RAM 4
GB, using MinGW, GNU gcc version 4.6.2. The
theoretical average execution time of the algorithm
is O(N (M / σ)). Therefore, keeping the database
unchanged, a 10 times increase in the size of the
pattern, we expect a similar 10 times increase in the
execution time. However, fig. 2(b) shows far more
encouraging results. One final point, while
conducting these experiments, the algorithm
consumed just 0.3 MB of RAM space, which
remains constant throughout the execution.
8 CONCLUSIONS
The completely new method we have proposed in
this paper could be useful for researchers in the field
of string matching. Text processing algorithms have
seen widespread use of complex data structures.
However, there are situations when the price paid in
using these data structures dominates the overall
gains. In this paper, we provide a highly practical
algorithm that do not make use of such data
structures, neither do we create indexes over the
text, yet achieve O(N) average case time for patterns
of size less than σ. Experiments have shown that
larger patterns can also be dealt by the algorithm
without performance deterioration. The proposed
solutions are easy to implement with minimal effort
and resources.
ACKNOWLEDGEMENTS
We thank the Ministry of Higher Education, Oman
for providing with resources to conduct this work.
A Novel Algorithm for String Matching with Mismatches
643
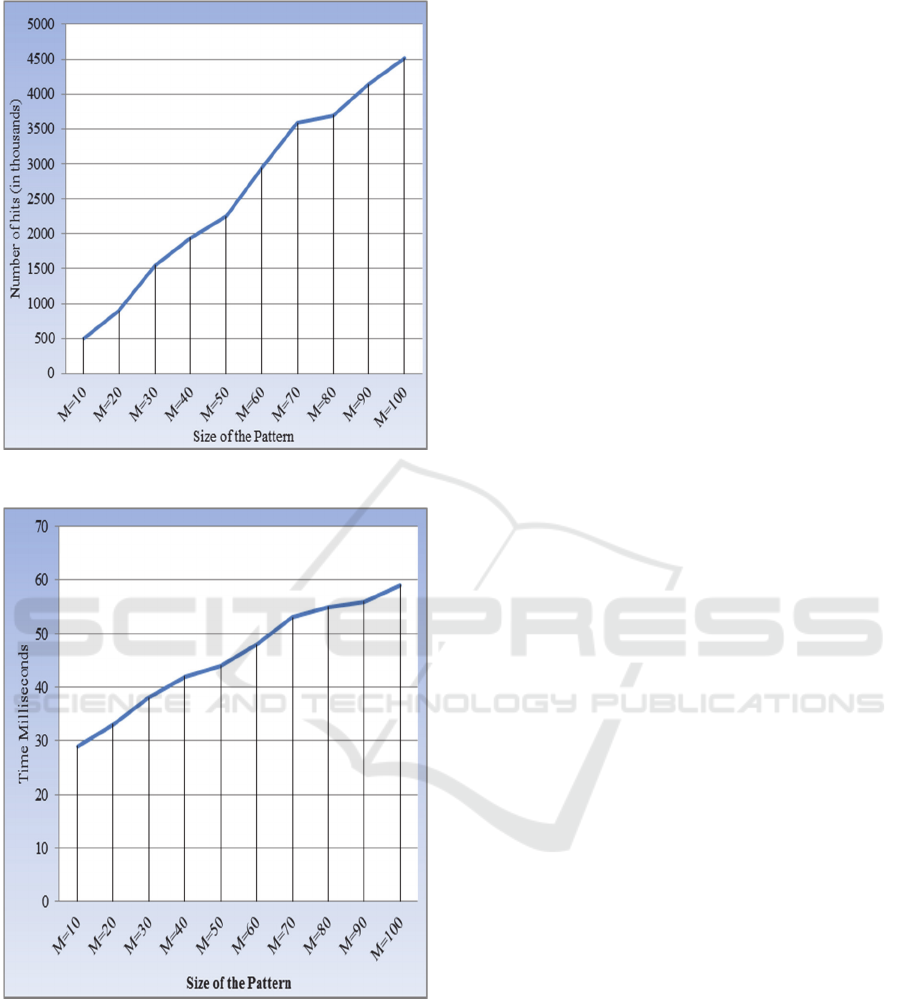
Figure 2(a): Number of hits (in thousands).
Figure 2(b): Execution Time.
REFERENCES
Abrahamson, K., (1987). Generalized string matching,
SIAM Journal of Computing, 16 (6), 1039–1051.
Amir, A., Lewenstein M., and Porat E. (2004) A Faster
algorithms for string matching with k mismatches.
Journal of Algorithms, 257-275.
Atallah, J., Chyzak F., and Dumas P. (2001). A
randomized algorithm for approximate string
matching, Algorithmica, 29(3), 468-486.
Austen, J., (1813). Pride and prejudice, Retrieved from
https://www.gutenberg.org/ebooks/1342.
Baeza-Yates, R., Perleberg, H. (1996) Fast and practical
string matching. Information Processing Letters, 59,
21-27.
Boyer, R., Moore, S., (1977). A fast string searching
algorithm. Communications of the ACM, 20, 762–
772.
Clifford, P., Clifford, R., (2007). Simple deterministic
wildcard matching, Information Processing Letters,
101(2), 53 – 54.
Crochemore M., Hancart, C., Lecroq T., (2007).
Algorithms on Strings, Cambridge University Press.
Galil, Z., Giancarlo, R., (1986). Improved string matching
with k mismatches, SIGACT News, 17(4), 52–54.
Gusfield, D., (1999). Algorithms on strings, trees and
sequences. Cambridge University Press,
Horspool, N., (1980). Practical fast searching in strings.
Software Practice and Experience, 10, 501–506.
Kalai, A., (2002). Efficient pattern-matching with don’t
cares, SODA, 655–656.
Karp, R., Rabin, M., (1987). Efficient randomized pattern-
matching algorithms. IBM Journal Research and
Development, 31, 249-60.
Landau, G., Vishkin, U., (1986). Efficient string with k
mismatches. Theoretical Computer Science, 43, 239-
249.
McCreight, E., (1976). Space-economical suffix tree
construction algorithm, Journal of ACM, 23, 262-272.
Navarro, G., (2001). A guided tour to approximate string
matching. ACM Computing Surveys, 33(1), 31–88.
Nicolae, M., Rajasekaran, S., (2013). On String Matching
with Mismatches, retrieved from
http://arxiv.org/pdf/1307.1406.pdf.
Tarhio, J., Ukkonen, E., (1993). Approximate Boyer–
Moore string matching. SIAM Journal of Computing,
2, 243–260.
Ukkonen, E. (1995). On-line construction of suffix trees,
Algorithmica, 41, 249-260.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
644
