A Discrete Event Simulation Approach for Quantifying Risks in

Manufacturing Processes

Renaud de Landtsheer

, Gustavo Ospina

, Philippe Massonet

, Christophe Ponsard

Stephan Printz

, Lasse H

artel

and Johann Philipp von Cube

CETIC Research Centre, Charleroi, Belgium

Institute for Management Cybernetics (IfU), RWTH Aachen University, Aachen, Germany

Fraunhofer Institute for Production Technology (IPT), Aachen, Germany

Keywords:

Discrete Event Simulation, Manufacturing, Supply Chain, Procurement Risks, Risk Management.

Abstract:

Nowadays supply chains have to face an increasing number of risks related to the globalisation, especially

impacting the procurement processes. Even though tools are available to help companies in addressing those

risks, most companies, even larger ones, still have problems to adequately quantify the risks and assess to

what extend an alternative could address them. The aim of our work is to provide companies with a software

supported methodology to quantify such risks and elaborate adequate risk mitigation strategies at an optimal

cost. Based on a survey conducted about the risk management practices and needs within companies, we

developed a tool that enables a constant focus on risks by enabling the easy expression of key risks together

with the process model and hence help to focus the granularity of the model at the right level. A model-based

simulator can then efﬁciently evaluate these risks thanks to well-known Monte-Carlo simulation techniques.

Our main technical contribution lies in the development of an efﬁcient discrete event simulation (DES) engine

together with a query language which can be used to measure business risks based on simulation results.

We demonstrate the expressiveness and performance of our approach by benchmarking it on a set of cases

originating from the industry and covering a large set of risk categories.

1 INTRODUCTION

Companies are faced with increasing procurement

risks in the context of globalisation. Those risks can

be related to many different factors such as the geo-

graphic location, the political and economic situation.

Assessing those risks alone is also a difﬁcult task as

the risks can reveal themselves at the end of the pro-

duction chain and it requires also to consider to some

extend the impact of internal risks such as the com-

plexity of the manufacturing process (which could de-

crease the capacity to adapt to a supplier failure) or

the level of optimisation in place (which would rise

the impact in case of disruption).

Helping company managers to take the right deci-

sions in the presence of such risks is not an easy task.

Analytic reasoning is quickly impractical and model-

based simulation has proved a very relevant approach

(Deleris and Erhun, 2005). Procurement risks put ex-

tra challenges as they occur at one end of the process

but can sometimes only be measured at the other end,

so they require to embrace the whole manufacturing

process. Addressing this challenge is precisely the

scope of our work, with a focus on small and medium

enterprises in the ﬁeld of mechanical engineering.

Our ultimate goal is to produce a user-friendly

tooled methodology that will guide the user through

the whole process of risk assessment. In order to

reach this goal, our work is structured as follows:

• First, a taxonomy of supplier and internal risks

has been identiﬁed, starting from the simplest risk

of shortage of raw material, which can eventually

drain the whole process chain to more elaborated

risks related to the kind of order policy used.

• Second, a survey was conducted on the state of

practice of risk evaluation in industrial context

(Printz et al., 2015b). The results of this survey

showed that nearly 66% of the companies perform

risk evaluation, although only 10% rely on dedi-

cated software tooling. This means that in practice

risks are evaluated by an individual estimation of

the cost factor and the probability of occurrence.

In general, estimation quality increases by includ-

Landtsheer, R., Ospina, G., Massonet, P., Ponsard, C., Printz, S., Härtel, L. and Cube, J.

A Discrete Event Simulation Approach for Quantifying Risks in Manufacturing Processes.

DOI: 10.5220/0005752403130322

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 313-322

ISBN: 978-989-758-171-7

313

ing historical data in the estimation. However, re-

lying on historical data and estimating the impact,

like delivery timings, quality of the materials is

not possible either in the case of changing sup-

pliers or adding parallel processes in the chain.

Based on the requirements identiﬁed in the con-

ducted survey a software based risk management

framework has been deﬁned.

• Third, we developed a modelling and simulation

toolset to identify risks, quantify them and decide

on design alternatives that can help to mitigate

them. The main technical scope of the present pa-

per is to detail our framework and show how it

helps focusing the modelling on the risks to stay

efﬁcient in the modelling time, simulation time

and result analysis time.

• Fourth, we are also validating our work with a

group of companies that are already trying our

tool through an easy to use web interface. Al-

though this validation is not yet complete, we

could already benchmark our approach on a num-

ber of industry cases and assess the expressiveness

and performance of our approach.

Our modelling framework includes concepts such

as storages where items can be stored or retrieved

with a maximum capacity, as well as several types of

production processes with different timing and failure

behaviours. In addition, we deﬁned a query frame-

work on models that is fully declarative and includes

arithmetic, temporal and logic operators as well as ba-

sic probes on the elements of our factory model (con-

tents of a storage, whether a process is running or

not, etc). Based on this query language, the toolset

is able to calculate the probabilities of different sce-

narios (e.g. delay in deliveries, defective parts or poor

quality) and their impact, based on a timed model of

the considered factory processes.

The approach of monetary risk quantiﬁcation is

based on an approach developed in the Q-Risk project

(von Cube et al., 2014). The simulation toolkit relies

on the discrete event simulation module of the OscaR

framework for its base simulation layer, and adds ded-

icated abstractions, dedicated to the timed modelling

of factories, and the modelling of risk-related queries

(OscaR, 2012).

Our main contribution lies risk-driven dimension

of our framework but also to the attention to usability.

Its design is based on a number of trade-offs between

expressiveness and simplicity of the modelling lan-

guage, as well as efﬁciency of the simulation engine.

The paper is structured as follows: section 2

presents the context of our work; section 3 presents

our modelling language for representing factories;

section 4 presents our query language that can serve

to evaluate risks; section 5 illustrates how complex

risks can be included in our query language; section 6

shows the benchmarking of our simulation tool both

on the expressiveness and performance dimensions;

section 7 discusses some related work; section 8 con-

cludes the paper.

2 BACKGROUND

In order to assess and quantify different kind of risks

in manufacturing processes, we model the manufac-

turing process as a ﬂow graph. This models captures

both the key procurement step but also the production

process itself. In particular, the resource storage place

(like warehouses or stockrooms) and the raw mate-

rials ﬂow through basic processes will be explained

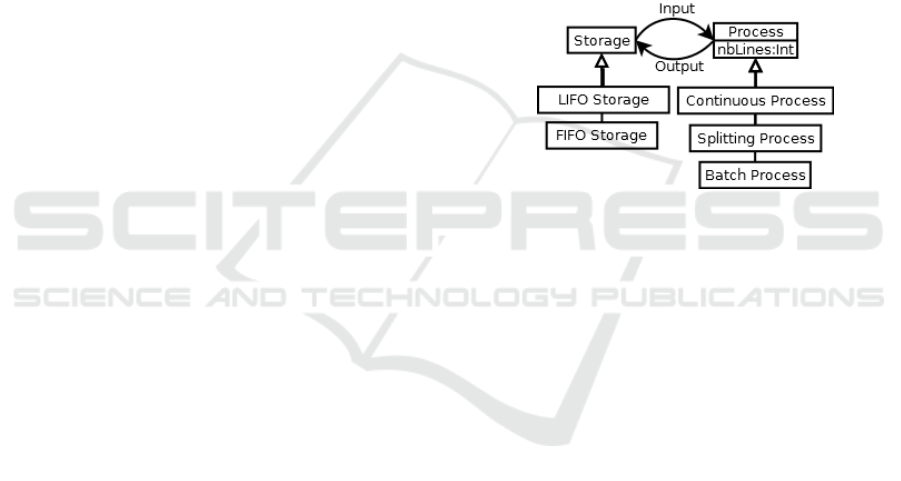
in section 3.1. The main graphical notations imple-

mented by the graphical part of framework are shown

in Figure 1 which is a model used later in our bench-

marking. Notations are quite self explanatory: a sup-

plier is a little truck, storage types are represented by

different variant of cylinder (the one with vertical bars

can overﬂow) and processes are depicted with the in-

dustry icon (also with some variants: multiple hori-

zontal lines means parallel batches, the cross means

possible failure, the rounded, the rounded box depict

a conveyor belt).

Figure 1: Beer game model.

The operation of the whole manufacturing process

can be described as a sequence of timed events. For

instance, in a simulation of a single factory, the ﬁrst

events are fetching some materials of a storage that

will be worked by a process. This fetch can trigger

a new order to a supplier if the storage level reached

some threshold, according to a supply chain policy.

In the rest of this section, we will ﬁrst remind the

reader about the nature of risks and the goal of risk

management, then we will give some details about

Discrete Event Simulation and why it is an adequate

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

314

framework to model the operations of manufacturing

processes and gather relevant data to quantify risks

(Romeike, 2004).

2.1 Risks and Risk Management

In order to develop a Discrete Event Simulation ap-

proach to quantify the impact of risks in manufactur-

ing enterprises, the nature of risk and the underlying

process of risk management needs to be understood in

detail.

2.1.1 Risk

Risks strongly affect enterprises business success di-

rectly being related to costs, effort and yield (Zsi-

disin and Ritchie, 2009). Thereby, risk is under-

stood as an event likely to occur with an undesired

consequence. The most common and for the ap-

proach most convenient categories of risks are the

cause and impact-oriented deﬁnition. The root-cause-

oriented approach considers uncertainty of informa-

tion validity as risk (Siepermann, 2008). Consider-

ing the chance not meeting a planned target is un-

derstood as impact-oriented risk deﬁnition. However,

only combining both categories of risk lead to the nec-

essary scope of information needed to properly man-

age risks. Hence, risk needs to be understood as cer-

tain likelihood to miss a deﬁned target. Hence, the

concept of risk is deﬁned through three components:

the hazards, or potential dangers, the consequences of

those hazards, and their predicted frequency, or like-

lihood (Sutton, 2015). A ”natural” quantiﬁcation of

the hazard associated to a risk is the product of all the

quantiﬁed consequences by the likelihood. A cyber-

netic model of procurement based hazards and their

management is presented in (Printz et al., 2015a).

Risk likelihoods can be modeled with probability

distributions (Artikis and Artikis, 2015), as the oc-

currence of a risk hazard in a process or system is

naturally uncertain. In (Zio, 2013), a theory of prob-

abilistic risk analysis is developed, associated to the

concept of system reliability. As risk is deﬁned as the

deviation from a planned value, statistical measures

can thus be applied to operationalise and compare

the possible magnitude of such deviations (Gleißner,

2012). Evaluation of the risk analysis and the reliabil-

ity of a system can be done with Monte-Carlo meth-

ods (Deleris and Erhun, 2005).

2.1.2 Risk Management

The main objective of risk management lies in the as-

surance of major corporate goals under consideration

of risk policy strategies. Hence, risks affecting long

lasting business success need to be controlled. How-

ever, enterprises will never be able to totally eliminate

risks and will always have to consider a certain degree

of residual risk (Finke et al., 2010). One key task of

risk management is to identify and analyze risks as

early as possible to take cost optimal risk treating ac-

tions (Zsidisin and Ritchie, 2009).

The basic process of risk management (Figure 2)

is described in the standards ISO 31000 and ONR

49000 ff. IEC 31010 provides an overview of cor-

responding risk management methods and techniques

along the process.

Figure 2: Risk management process.

2.2 Discrete Event Simulation

There are two main approaches for representing the

time if we want to simulate the behaviour of a sys-

tem: the ﬁrst approach is to use a continuous time, in

which the events affecting the system occurs in time

“ticks” which are proportional to the actual expected

time of operation for the system. The other approach

is to have a discrete time, and concentrate the simula-

tion only in the operational events instead of the time

events. This is the basis of Discrete Event Systems

(DES).

In the literature (Brailsford et al., 2014; Byong-

Kyu and Donghun, 2013), the main components of

a DES model are described as: entities, which are

the items that are ﬂowing and transformed through

the simulation, queues, representing storage devices

or other areas in which entities wait to be used, activ-

ities, that actually perform some work on the entities,

and resources, a special kind of entities that are re-

quired to operate activities.

DES models deﬁne events as discrete points of

time in which the system state changes. The simu-

lation of the model becomes the checking of a queue

of the different events triggered, the “next-in-time” at

the ﬁrst place. Checking an event can trigger other

events in the queue. For instance, checking the event

of starting an activity will trigger the events of fetch-

ing the corresponding entities needed to perform the

activity, and ending the activity. The event of activity

failure can also be triggered with a given probability.

A Discrete Event Simulation Approach for Quantifying Risks in Manufacturing Processes

315

Several software solutions exist to support DES

based modelling for a variety of applications. Among

the commercial software, we can cite AnyLogic

(AnyLogic, 2015), Arena (Rockwell Automation,

2015) and Plant Simulation (Siemens, 2015).

3 A SIMULATION META-MODEL

FOR FACTORIES

All the main elements of manufacturing processes are

represented in our simulation meta-model, which al-

lows us to deﬁne concrete models that are simulated

in a Discrete Event Simulation engine. In addition

to this, we designed a query language over concrete

simulations in order to collect and analyse data.

3.1 Modeling Factory Processes

This section introduces the basic blocks for represent-

ing factories. In our approach, factories are modeled

as ﬂows of items through processes and stocks.

Storages represent any kind of stock device or

room place for raw materials, like a warehouse, a

barrel, a silo or a dumpster. They have a maximum

capacity. When this capacity is reached, they either

overﬂow, or block the upfront processes, depending

on the setting of the storage. If a full stock can over-

ﬂow, any unloading material on that stock is lost.

Batch processes are factory processes that work

in a batch fashion; supplies are collected from vari-

ous stocks, then the process runs for some time, and

ﬁnally the produced outputs are dispatched to their re-

spective stocks before this whole cycle starts again.

Continuous processes are factory processes that

typically run on a conveyor belt. Items are continu-

ously picked from input stocks and undergo the pro-

cess immediately on a physical end of some machine,

pass through the machine in a queue, and when they

reach the other end of the machine, the resulting items

are dispatched to their respective stocks. A simple ex-

ample is a conveyor belt that passes through a bakery

oven; raw pastries are set on one end of the conveyor

belt; they go through the oven and are cooked when

they reach the other end of conveyor belt where then

are dispatched to their output storage.

Splitting processes are similar to batch processes,

except that they have several sets of outputs and when

it completes, one set of output is selected and the pro-

duced items are dispatched to the stocks associated

to the selected output. This represents a quality as-

surance process whose items ﬂow is split into two (or

more) separated ﬂows, based on the result of the qual-

ity assurance analysis.

Parallel processes are variant of the above pro-

cesses where several lines of the same process are run-

ning in parallel. Basically, all processes introduced

here above have a parameter specifying the number

of process lines running in parallel.

Items ﬂowing in processes and stocks are indistin-

guishable at a given point of the factory, since they all

share the same part number. Yet, they have some in-

trinsic features: some items might come from a given

process, others might be made out of poor quality

supplies, etc. These intrinsic features can inﬂuence

on the behavior of some processes, such as the split-

ting process representing a quality assurance process.

This notion of intrinsic features lead us to distinguish-

ing between two different types of storage, namely:

First In-First Out (FIFO) storage and Last In-First Out

(LIFO) storage.

Figure 3: Concepts of our process modelling languages.

3.2 Process Activation and Supply

Chain Policies

Supply chain policies are also integrated in our model

of the factory, together with activation policies that

are able to turn a process on or off, depending on the

demand for the output stock. To model these two con-

cepts, we introduce the notion of activable and acti-

vation. An activable is something that can be enabled

through an activation. We also associate a magnitude

with the activation, that is, an integer. An activable

can be a process, or a supply order. In the case of a

process, the activation represent the number of batch

that the process is allowed to execute. In the case of

an order, the magnitude represent the number of or-

dered items.

In our model, an order is a stationary activable ob-

ject that represents a class of order that can be passed.

The order is passed when the modeled order object is

activated.

Activables can be activated based on various rules

that are also part of our modelling framework. There

are three types of activation rules, namely: regular ac-

tivations that perform the activation on a regular basis,

based on a period of time; order-based activations that

perform the activation when an order is received; and

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

316

Figure 4: Concept for modelling activation rules.

stock monitoring activation that perform the activa-

tion when the stock level gets below some threshold.

3.3 Modelling Intrinsic Item Features

To represent these intrinsic features, we introduce the

notion of item class , representing the set of intrinsi-

cally identical items. Item classes are characterized

by a set of boolean attributes. A global set of at-

tribute is deﬁned for the whole simulation model, and

each piece has its own combination of attribute val-

ues, deﬁning the item class to which it belongs.

When an item ﬂows through a process, the pro-

cess can update the attribute of the item, to reﬂect that

the process was applied to this item. Similarly, when

an item ﬂows through a splitting process, the selected

output can be speciﬁed according to the attributes of

the item. At this point, we had to set a trade-off be-

tween expressiveness of the modelling language, its

simplicity, and the efﬁciency of the simulation. Our

trade-off is to consider that processes can update the

class of items through three basic operations: setting

an attribute, clearing an attribute, or loading a con-

stant set of attribute. At the level of the simulation

engine, any combination of these operations can be

aggregated into two efﬁcient bit-wise operations per-

formed using bit masks representing attributes.

Another restriction that we have implemented is to

consider how the class of items produced by a process

are linked to the classes of potentially several inputs

of this process. Our choice is to consider the union

of all attributes of all inputs performed for starting a

batch of the process, and set this union as the start

class of the whole batch. The class transformation

function of the process is then applied on this class,

and every item output by the process from this batch

share the same output class computed by this class

transform function.

4 PERFORMING QUERIES OVER

SIMULATIONS

The goal of our approach is to perform risk-related

queries on factory simulations. These queries are

meant to be performed on single runs of simulation

occurring inside the Monte-Carlo engine which ag-

gregates the queries results over the runs. It can then

be queried afterwards e.g. for mean, median, ex-

tremes, variance of these queries over the runs.

Our query language can roughly be split into

six sets of operators, namely: probes on processes,

probes on storages, logic operators, temporal logic

operators, arithmetic operators, and temporal arith-

metic operators. Arithmetic and logic operators differ

by their their return types; they return numeric and

boolean values, respectively.

Since this query language runs over simulated

time, we take the convention that the value of the

queries are computed at the end of the trace on which

they are evaluated. We deﬁne the operator of our lan-

guage together with their semantics by using the |=

notation: t |= P is the value of expression P when

evaluated at position t of the current trace.

Some fragments of the queries are evaluated

throughout the simulation. We take the convention

that they are evaluated at the end of each discrete sim-

ulation step, after all events happening at this point in

time are performed.

Some temporal operators refer to the previous po-

sition in time, denoted as prev(t), notably to compute

deltas or assess changes. These should be used with

care since we are in an event-based model of time, so

adding such operators in the query will add extra time

events in the simulation.

4.1 Probes for Processes

The probes on processes are atomic operators that ex-

tract basic metrics from processes of the simulation

model. Suppose that p is such a process, the follow-

ing probes are supported:

• t |= running(p) true if the process is running at

time t, false otherwise.

• t |= completedBatchCount(p) the total number of

batches performed by the process between the be-

ginning of the trace, and time t.

• t |= startedBatchCount(p) the number of batches

started by the process between the beginning of

the trace, and time t. For a process with multiple

lines, it sums up the started batches of each line.

• t |= totalWaitDuration(p) the total duration where

the process was not running between the start of

A Discrete Event Simulation Approach for Quantifying Risks in Manufacturing Processes

317

the trace, and time t. for a process with multiple

lines, it sums up the waiting time of each line.

• t |= anyBatchStarted(p) true if a batch as started

by the process at time t

4.2 Probes for Storages

The probes on storages are atomic operators that ex-

tract basic metrics from storages of the simulation

model. Suppose that s is such a storage:

• t |= empty(s) true if the storage s is empty at time

t, false otherwise.

• t |= content(s) the number of items in the storage

s at time t.

• t |= capacity(s) the maximal capacity of s. This is

invariant in time.

• t |= relativeCapacity(s) the relative content of

storage s at time t, that is: the content of the stock

divided by the capacity of the storage.

• t |= totalPut(s) the number of items that have been

put into s between the beginning of the simulation

and time t, not counting the initial ones.

• t |= totalFetch(s) the number of items that have

been fetched from s between the beginning of the

simulation and time t.

• t |= totalLostByOverﬂow(s) the number of items

that have been lost by overﬂow from s between

the beginning of the trace, and time t. If s is a

blocking storage, this number will always be zero.

4.3 Operators

Logical Operators

• t |= true the constant true.

• t |= false the constant false.

• t |=!l the negation operator.

• t |= l

op l

where op is one of {&,k} repre-

sent conjunction, and disjunction operators, re-

spectively, returning their conventional results.

• t |= a

comp a

where comp is one of {<,>, ≤,≥

,=, 6=} represent comparison operators over nu-

merical values, returning their standard results.

Temporal Logic Operators

• t |= hasAlwaysBeen l true if for each t

in [0;t],

|= l

• t |= hasBeen l true if there is a t

in [0;t] such that

|= l

• t |= l

since l

true if there is a position t

in [0;t]

such that t

|= l

and for each position t in [t,t] ,

t |= l

• t |= @l true if both t |= l and prev(t) |=!l.

• t |= changed(e) e might be a logic or arithmetic

expression; this evaluate to true when t |= e and

prev(t) |= e have different values.

Arithmetic Operators

• t |= n where n is a numerical literal represents a

literal constant value

• t |= a

op a

where op is one of {+,−, ∗,/} repre-

sent the classical arithmetic operators over numer-

ical values, returning their conventional results.

• t |= −a represents the unary negation.

Temporal Arithmetic Operators

• t |= delta(a1) is a shorthand for t |= a prev(t) |= a

• t |= cumulatedDuration(b) let be T =

)kt

= prev(t

)&t

|= b&t

|= b the ac-

cumulated duration of b is the sum over the

couples (t

) in T of t

• t |= time evaluates to t.

• t |= min(a) the minimum over all the values of

|= a with t

in in [0;t]

• t |= max(a) the maximum over all the values of

|= a with t

in in [0;t]

• t |= avg(a) the average of all the values of t

|= a

with t

in in [0;t]

• t |= integral(a) the integral of t

|= a dt

with t

[0;t]. The integral is computed through the trape-

zoidal rule taking the events as discretisation base.

5 EXPRESSING RISKS AS

QUERIES

Using our query language, we can estimate quantities

that can be related to risk on the ”normal” operation

of a factory. Before, we need to identify the risks we

want to quantify. Some of those risks are dependent

on one speciﬁc factory or stock, whereas some other

risks are more general and inﬂuences a subset or the

whole model.

Risks Speciﬁc to Stocks. In overﬂowing stocks,

we are interested in measuring the risk of los-

ing pieces, that are measured by the probe

totalLostByOver f low(stock). This allow us to

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

318

see if it is needed to adapt the capacity of the

stock service. It is also possible that a stock is

over-sized, that is, the maximum contents of the

stock along the simulation are too low with re-

spect to its capacity. This can be measured with

the probe max(relativeCapacity(stock)) and verify

whether that value is higher than an acceptable per-

centage of the stock capacity.

Risks Speciﬁc to Processes. In complex mod-

els, we are interested in processes that do not

work enough in the simulation, or even processes

that do not work at all. The percentage of idle

time for a process p is measured by the probe

mul t(div(totalWaitDuration(p),currentTime),100).

To detect whether the process p did not operate

at all in the simulation, we can use the probe

hasAlwaysBeen(!anyBatchStarted(p)).

Factory-speciﬁc Risks. We can check on failing

processes the relative percentages of material that

were successfully produced or had to be wasted. For

example, if a failing process p with a probability of

success of 80% is supposed to produce 5 units of raw

material in stock a or waste 10 units to stock b at

failure, checking that the materials put on each stock

after the simulation, correspond to the expected per-

centage can be expressed with the complex probes

div(totalPut(a), 5 ∗ completedBatchCount(p)) and

div(totalPut(b), 10 ∗ completedBatchCount(p)).

6 BENCHMARKING

In order to assess the approach, we took a benchmark-

ing approach based on a set of representative models.

This section ﬁrst describes our implementation, then

the set of models before detailing the benchmarking

results on our two main contributions:

1. Expressiveness: show that all the risks identiﬁed

in the cases can easily be captured by the mod-

eling primitives and measurement probe, either

based on the set of generic probes identiﬁed so

far or by writing case speciﬁc probes.

2. Performance: show that running probes does not

degrade signiﬁcantly the performance of the sim-

ulation engine.

6.1 Implementation

Our simulator is implemented using the OscaR DES

module (OscaR, 2012) and is written in Scala.

A modelling web front-end was developed with

JavaScript technology, mainly Bootstrap, JQuery and

JointJS. The lightweight Scalatra web framework was

used to wrap up the simulator as a set of web services.

All the elements of the factory feature optimal

O(1) complexity for their update operations, with an

additional cost factor for the attribute manipulations,

although these are collapsed into a constant number of

bitwise operations. Queries are evaluated incremen-

tally during the simulation, by performing timely in-

spection of the internal state of the simulation model,

so that the trace is actually not generated. Complex

queries are split into sub-expressions that must be up-

dated at each step of the simulation, such as integrals,

and sub-expressions that only require a single evalua-

tion at the end of the trace, such as a constant weight-

ing factor on the integral. This keeps the overhead of

our query language under control.

6.2 Benchmark Models

We selected four representative models out of a set of

about 20 examples inspired by classic academic cases

(with speciﬁc complex aspects) to anonymous cases

collected in the industry. The cases also vary in the

level of use of random variables. We describe relevant

modelling aspects of each supply chain together with

speciﬁc risk issues associated with each model.

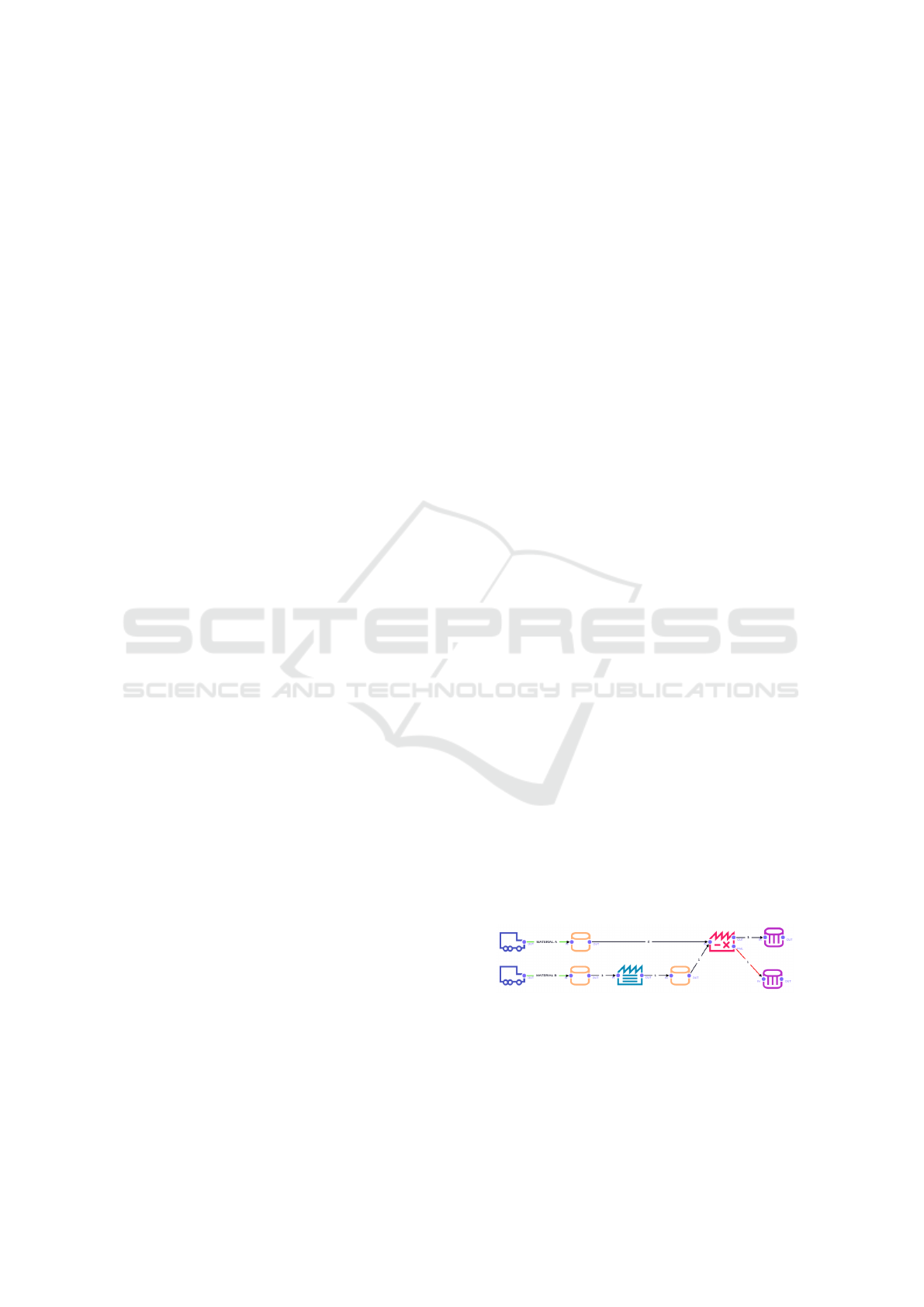
First Case: A Simple Assembler Factory. This

case, illustrated in Figure 5, models a simple fac-

tory that builds an industrial produce using two kinds

of parts, A and B. Each part has its supplier which

feeds the stocks when they become lower than a given

threshold. For part A, the supplier policy is to reﬁll

the stock to its maximum capacity. For part B, the

policy is the delivery of a ﬁxed amount of material.

Part B must be preprocessed before assembly. The

factory combines two units of part A and with one unit

of preprocessed part B with 80% of products passing

the quality tests. so the assembly process can be rep-

resented by a failing single batch process. The goal is

to assess if the input stocks are kept within safe limits

to cope with production demand.

Figure 5: Model 1: a simple assembler factory.

Second Case: A Beer Game Model. Our second

case model is a classical problem called ”beer game”

(Klimov and Merkuyev, 2006). It is long linear sup-

ply chain going from the beer factory to the ﬁnal re-

tailer, passing by distributors and wholesalers. The

A Discrete Event Simulation Approach for Quantifying Risks in Manufacturing Processes

319

beer factory is considered here as a supplier and single

batch processes are used to represent external sources

of delay in the transport. Intermediary stocks also

add extra delays. The continuity of retailing, distribu-

tion and wholesaler processes is modeled by conveyor

belts. The resulting model is shown in ﬁgure 1. The

goal is to assess where potential bottleneck can occur.

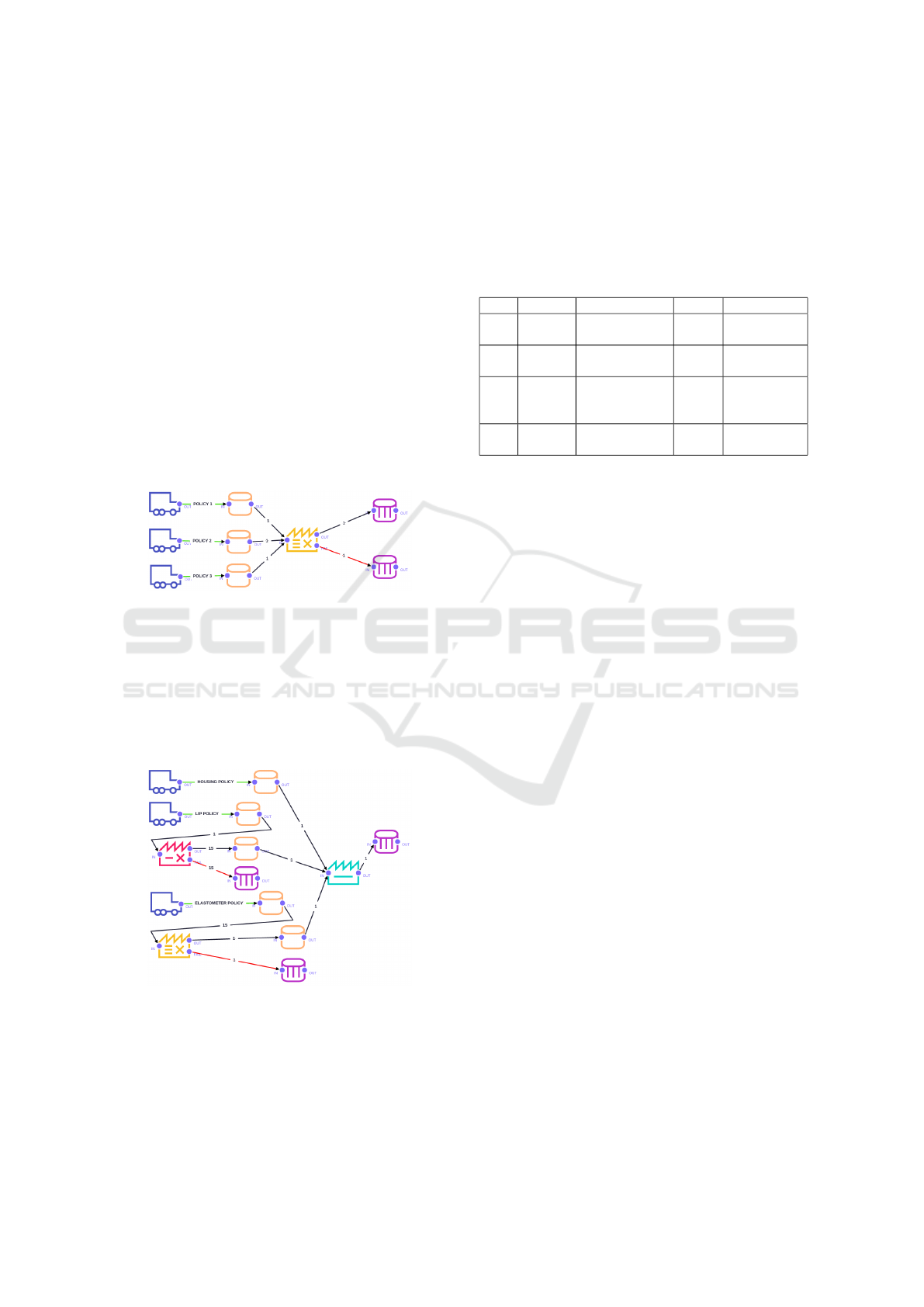
Third Case: Multiple Suppliers. This case is in-

spired by a real industrial case, where the manufactur-

ing involves three different materials having their own

supplier and reﬁll policy, with random delays belong-

ing to a gaussian probability distribution. 90% of pro-

duces built by a batch in the factory fulﬁll the quality

requirements. We want to evaluate the effects of dif-

ferent supplying policies in order to ensure the supply

chains operates at optimal capacity while minimising

the frequency of orders.

Figure 6: Model 3: multiple suppliers.

Fourth Case: A Complex Assembly Process. Our

last case is inspired also in an industrial case of a fac-

tory where complex parts are assembled from 3 dif-

ferent materials following a complex process. Two of

the parts are preprocessed on factory units that can fail

(10% of failures for the ﬁrst one, 40% for the second

one). The process is shown in ﬁgure 7.

Figure 7: Model 4: complex assembly process.

6.3 Expressiveness Analysis

We identiﬁed a number of basic probes relating to

risks directly related to model element. Such probes

are automatically generated. SO, for each stock, we

generate three different probes for measuring the av-

erage and maximum contents of the stock and verify

whether the stock is full or overﬂowing. For each pro-

cess, we generate a probe for measuring the amount

of time in which the process was idle or blocked in

the simulation.

Table 1: Benchmarking table for expressiveness.

Name Size Risk Type #probes Comments

M1 9 (2/2/5) Full stock

Process failure

20 Simple manu-

facturing

M2 17

(1/7/9)

Blocked process

Process failure

36 Beer game

M3 8 (3/1/5) Full stock, Pro-

cess failure

Supplier failure

20 Multiple

suppliers

M4 14

(3/3/8)

Stock losses 31 Complex part

assembly

In addition, the user can specify extra probes

to express business speciﬁc risks that are typically

more complex queries on the model. Table 1 sum-

marises some model characteristics like size (suppli-

ers/processes/storages), risks and number of probes.

To assess expressiveness, we considered a single

probe which actually proved enough to cover the tar-

geted risks when used with basic probes. In the two

last models, we could also explore risk mitigation

strategies.

• In the ﬁrst case, assessing the stocks of raw

materials were full could be achieved the probe

cumulatedDuration(relativeContent(stockA) =

1). For most time in the simulation, the stocks

were full while the assembler process worked

was at full capacity.

• In the second case, we looked at the relative idle

times in the process chain. We noticed that the

distribution process, just after the fabrication, is

the only one that blocks waiting for goods.

• In the third case, we both looked at process idle

time (basic probe) and the average contents of

stocks using the probe avg(content(st)). This

helped us discovering the best threshold to trigger

order while minimising idle time.

• In the fourth case, a full stock was blocking the

production. We mitigate the problem by experi-

menting with overﬂowing storage to estimate the

right size to avoid the overﬂowing, using the

probe totalLostByOver f low(lipStorage).

6.4 Performance Analysis

We performed a Monte Carlo simulation on each case,

using a time limit of 10000 units and 2000 iterations

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

320

to have a good precision. The results in table 2 are the

computed average. We performed the benchmarks on

an Intel Core i7-4600U CPU at 2.10GHz with 8 GB

of RAM. Only a single core is currently used. The

simulation was triggered from the web interface on

the same machine as the server.

Table 2: Benchmarking table for performance.

Name No probes Std probes All probes Overhead

M1 7,3 ms 11,9 ms 12,5 ms 71,2%

M2 11,3 ms 17,6 ms 17,8 ms 57,5%

M3 25,8 ms 29,2 ms 34,2 ms 32,6%

M4 6,8 ms 13,3 ms 13,4 ms 97,1%

The overhead in the simulation with probes varies

from 32,6% in Model 3 to 97,1% in Model 4. Model

3 has the longest run time, because of the randomness

in the delays of supplying induced by the probability

distributions associated to suppliers. Model 4 has the

shortest run time because the simulation stops at an

early time, due to a full intermediary stock. In this

case the relative overhead is bigger because the load

is totally only probes evaluation while the model is

stuck given the efﬁciency of the DES engine.

Globally, overhead are quite acceptable. Some

improvements have still possible in the context of in-

tegration with a web application, especially to op-

timise the network requests between the web inter-

face and the simulator and make that interface more

responsive. The total simulation time allows to run

thousands of simulations in a few minutes and to ex-

plore risk mitigation alternatives within an hour.

7 RELATED WORK

A typical risk assessment conducted on a given fac-

tory plan is reported in (Schmitt and Singh, 2009)

base on the Arena simulation tool, featuring DES and

Monte Carlo methods as in our work. It stresses the

importance of conducting stress-tests using such sim-

ulation platforms. Its focus is mainly on the disrup-

tion risk while our work can cope with other class of

risks like quality. Our framework provides an added

abstraction layer that can cut down the cost of per-

forming these important stress tests, and make them

achievable by smaller industries.

A similar analysis has been performed on a beer

supply chain in (Klimov and Merkuyev, 2006), whose

model was presented in section 6.2. This analysis

leads to an evaluation of inventory excessive accumu-

lation, a back ordering. Again, no dedicated tooling

was used for representing factories at a higher level,

leading to high costs for conducting such evaluation

in an industrial setting while our tooling could cope

with using the available primitives.

Another simulation-based risk assessment is re-

ported in (Finke et al., 2010). It features an aerospace

company with very low production volumes, and

leads to the elaboration of a dedicated simulation en-

gine. The engine was ﬁrst developed with a purely

deterministic behavior, and then enriched with fail-

ure models and stochastic aspects. It showed of great

value to the company even though mainly focusing on

disruption risks, it helped the company to develop a

risk mitigation procedure. Our framework has a sim-

ilar purpose and try to propose a good compromise

between genericity and efﬁciency.

(Almeder et al., 2009) presents a general frame-

work that combines optimisation and DES for sup-

porting operational decisions for supply chain net-

works. Their idea is to iterate between a simulation

phase in which some parameters are estimated, and an

optimisation phase, that adapts the decision rules for

the simulation. Our current work does not cover the

minimization of the risk. The tool is rather designed

to ease the identiﬁcation of risk controls by the risk

manager. We plan to address optimisation in a later

phase, based on the optimisation engines also present

in the OscaR framework (OscaR, 2012).

8 CONCLUSIONS

This paper presented a Discrete Event Simulation Ap-

proach, supported by a toolset that helps to build a

model of a supply chain with the goal to express and

assess risks on them with a speciﬁc focus on procure-

ment risks. The assessment is conducted using an

Monte-Carlo based simulation engine that can also be

used to further explore risk mitigation strategies.

Our strength is to support a declarative and easy

to use graphical modeling language for representing

factory processes and stocks, together with a declar-

ative query language for deﬁning metrics to be mea-

sured while simulating the behaviour of the modeled

system. We could successfully benchmark our ap-

proach both from the expressiveness and performance

perspectives on several typical examples of factories,

together with their supply chain policies.

Of course, further work is required to fully align it

with industrial needs. Our current step is the internal

validation with a number of companies by putting the

tool in the hands of the risk managers on a pilot case.

We already identiﬁed a number of requests about:

• extension to the modeling language, e.g. to sup-

port the notion of shared resource among pro-

cesses and have a statistic model of process fail-

A Discrete Event Simulation Approach for Quantifying Risks in Manufacturing Processes

321

ures and breakdowns. More specialised processes

allowing controlled fork/join are also required.

• identiﬁcation of model parameters easing the

manual (and later optimised) exploration of risk

mitigation strategies.

• availability of a company library of speciﬁc risks

and related probes

• produce speciﬁc reporting (e.g. business continu-

ity plans). We have already explored some work

in this direction (Arenas et al., 2015).

• possibly support model reﬁnements and granular-

ity of simulation. However our aim is not to cap-

ture the full reality but what will help assessing

identiﬁed risks.

• parallelisation in case of need of faster simulation

times. This is easy to implement.

Our framework combining usability, expressive-

ness and efﬁciency is an important milestone in our

work to raise the awareness of companies, especially

of smaller size, w.r.t. the need to evaluate their pro-

curement risks and elaborate their supplying policies

in the most optimal way. We believe it can be used to

manage more general risks. Our design ideas can also

be used to improve other risk management tools. Our

framework is available online (SimQRi, 2015) and is

planned for Open Source release.

ACKNOWLEDGEMENTS

This research was conducted under the SimQRi

research project (ERA-NET CORNET, Grant No.

1318172). The CORNET promotion plan of the Re-

search Community for Management Cybernetics e.V.

(IfU) has been funded by the German Federation of

Industrial Research Associations (AiF), based on an

enactment of the German Bundestag.

REFERENCES

Almeder, C., Preusser, M., and Hartl, R. F. (2009). Simula-

tion and optimization of supply chains: alternative or

complementary approaches? In G

unther, H. O. and

Meyr, H., editors, Supply Chain Planning. Springer-

Verlag.

AnyLogic (2015). AnyLogic Multimethod Simulation Soft-

ware. http://www.anylogic.com.

Arenas, A. E., Massonet, P., and Ponsard, C. (2015). Goal-

oriented requirement engineering support for business

continuity planning. In Proceedings of MReBA’15,

Stockholm, Sweden.

Artikis, C. and Artikis, P. (2015). Probability Distributions

in Risk Management Operations. Springer, London.

Brailsford, S., Churilov, L., and Dangerﬁeld, B. (2014).

Discrete-Event Simulation and Systems Dynamics for

Management Decision Making. Wiley.

Byong-Kyu, C. and Donghun, K. (2013). Modeling and

Simulation of Discrete-Event Systems. Wiley.

Deleris, L. and Erhun, F. (2005). Risk management in sup-

ply networks using Monte-Carlo simulation. In 2005

Winter Simulation Conference, Orlando, USA.

Finke, G. R., Schmitt, A., and Singh, M. (2010). Modeling

and simulating supply chain schedule risk. In 2010

Winter Simulation Conference, Baltimore, USA.

Gleißner, W. (2012). Quantitative methods for risk manage-

ment in the real estate development industry. In Jour-

nal of Property Investment & Finance, volume 30(6),

pages 612–630.

Klimov, R. A. and Merkuyev, Y. A. (2006). Simulation-

based risk measurement in supply chains. In 20th

European Conference on Modelling and Simulation

(ECMS 2006), Bonn, Germany.

OscaR (2012). OscaR: Scala in OR.

https://bitbucket.org/oscarlib/oscar.

Printz, S., von Cube, J. P., Vossen, R., Schmitt, R.,

and Jeschke, S. (2015a). Ein kybernetisches mod-

ell beschaffungsinduzierter st

org

oßen. In Exploring

Cybernetics - Kybernetik im interdisziplinren Diskurs.

Springer Spektrum.

Printz, S., von Cube, P., and Ponsard, C.

(2015b). Management of procurement risks

on manufacturing processes - survey results.

http://simqri.com/uploads/media/Survey Results.pdf.

Rockwell Automation (2015). Arena Simulation Software.

https://www.arenasimulation.com.

Romeike, F. (2004). Der prozess der risikosteuerung und -

kontrolle. In Romeike, F., editor, Erfolgsfaktor Risiko-

Management, pages 236–243. Gabler, Wiesbaden.

Schmitt, A. and Singh, M. (2009). Quantifying supply chain

disruption risk using Monte Carlo and discrete-event

simulation. In 2009 Winter Simulation Conference,

Austin, USA.

Siemens (2015). Plant Simulator.

http://goo.gl/NK7yWg.

Siepermann, M. (2008). Risikokostenrechnung: Erfolgre-

iche Informationsversorgung und Risikopr

avention.

Erich Schmidt, Berlin.

SimQRi (2015). Online SimQRi tool.

https://simqri.cetic.be.

Sutton, I. (2015). Process Risk and Reliability Management.

Elsevier, second edition.

von Cube, J. P., Abbas, B., Schmitt, R., and Jeschke, S.

(2014). A monetary approach of risk management in

procurement. In 7th Int. Conf. on Production Research

Americas’ 2014, pages 35–40, Lima, Peru.

Zio, E. (2013). The Monte Carlo Simulation Method for

System Reliability and Risk Analysis. Springer, Lon-

don.

Zsidisin, G. A. and Ritchie, B. (2009). Supply Chain Risk:

A Handbook of Assessment, Management, and Perfor-

mance. Springer.

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

322