Using Conspiracy Numbers for Improving Move Selection

in Minimax Game-Tree Search

Quang Vu

, Taichi Ishitobi

, Jean-Christophe Terrillon

and Hiroyuki Iida

School of Information Science, JAIST, 1-1 Asahidai, 923-1292, Nomi, Ishikawa, Japan

Institute of General Education, JAIST, 1-1 Asahidai, 923-1292, Nomi, Ishikawa, Japan

Keywords:

Conspiracy Number, Evaluation Function, Move Selection, Minimax Search.

Abstract:

In a two-person perfect-information game, Conspiracy Number Search (CNS) was invented as a possible

search algorithm but did not ﬁnd much success. However, we believe that the conspiracy number, which is

the core of CNS, has not been used to its full potential. In this paper, we propose a novel way to utilize the

conspiracy number in the minimax framework. Instead of using conspiracy numbers separately, we combine

them together. An example way of combining conspiracy numbers with the evaluation value is suggested.

Empirical results obtained for the game of Othello show the potential of the proposed method.

1 INTRODUCTION

In a two-person perfect-information game, it is com-

mon to employ a minimax-based procedure to esti-

mate the current game situation as well as decide the

next move based on that information. A minimax-

based search produces a search tree, using an eval-

uation function to estimate the value of leaf nodes

and use those value to determine the value of the root

node(Shannon, 1950)(Turing et al., 1953). For most

games, the size of the tree renders the search inefﬁ-

cient. As a result, many algorithms such as alpha-beta

pruning (Knuth and Moore, 1975) and SSS* (Stock-

man, 1979) have been invented to solve this prob-

lem. Most algorithms focus on selectively choos-

ing appearing paths to search while ignoring a large

portion of the tree (for example, singular extensions

(Anantharaman et al., 1990) and null move (Beal,

1990)(Goetsch and Campbell, 1990)). However, the

effectiveness of these algorithms also depends on the

quality of the evaluation function, because no matter

how fast the algorithm is, it cannot search the whole

tree. It needs to stop at some points and use static

evaluation values. As a result, a weak evaluation func-

tion may remove the branch with the best move and

bias the search toward non-optimal moves.

Conspiracy Number Search (CNS) (McAllester,

1988) was invented as a game-independent best-ﬁrst

search which expands the game tree non-uniformly

to establish a stable value for the root node. The

algorithm was based on the concept of conspiracy

numbers which, in a sense, show how unlikely the

root value would change to a certain value. Conspir-

acy numbers were also used in alpha-beta-conspiracy

(McAllester and Yuret, 2002); theirs usage were dif-

ferent and less computationally intensive. However,

both algorithms were not very successful (Schaeffer,

1990), and conspiracy numbers did not receive much

attention after that. Recently, the conspiracy number

was investigated again, but for another usage (Khalid

et al., 2015). In our opinion, the failure of these pre-

vious methods occurred because their methods used

conspiracy numbers separately. A single conspiracy

number would not have much information about the

game situation, so it is not beneﬁcial to decide based

on it. In this paper, we propose a new method of com-

bining the conspiracy numbers to evaluate the game

situation. It is shown that the proposed method has a

potential to improve the evaluation accuracy.

The structure of this paper is as follows. Section 2

presents related works in this domain and the basic

idea of conspiracy numbers is described in section 3.

Then we propose our new method in section 4, and

experiments which we performed and their results are

shown together with some discussion in section 5. Fi-

nally, concluding remarks are given in section 6.

2 RELATED WORKS

In this section, we describe in more details about

conspiracy numbers and their application in previous

400

Vu, Q., Ishitobi, T., Terrillon, J-C. and Iida, H.

Using Conspiracy Numbers for Improving Move Selection in Minimax Game-Tree Search.

DOI: 10.5220/0005753004000406

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 2, pages 400-406

ISBN: 978-989-758-172-4

methods.

2.1 Conspiracy Number

In (McAllester, 1988), conspiracy numbers are the

measurement of the difﬁculty of changing the mini-

max root value of a given tree. The conspiracy num-

ber of a particular value v in a given tree is the mini-

mum number of leaf nodes that have to change their

values (called conspirators) so that the value of the

root node will change to v.

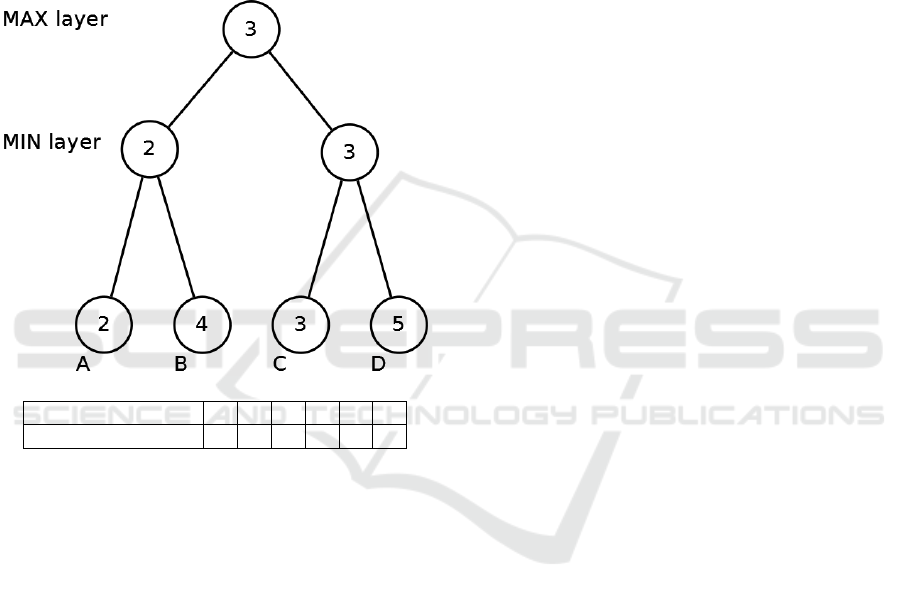
Root value 1 2 3 4 5 6

Conspiracy number 2 1 0 1 1 2

Figure 1: A simple minimax tree. The table shows conspir-

acy numbers for several values. CN(3) = 0 because 3 is the

value of the root node, so we do not need to change any-

thing. To change the root’s value to 2, at least node C or D

needs to change to 2. To change to 1, node A or B and node

C or D need to change to 1.

Let T denote a node with minimax value m. The

conspiracy number CN(T, v) can be deﬁned recur-

sively as follows:

• A a leaf node, because there is no more search,

the only conspirator is the node itself. However,

if it is also a terminal node (an ending position),

its value cannot be changed. So:

CN(T, v) =











0 if v = m

1 if v 6= m

∞ if terminal node

(1)

• At a max node, in order to increase its value, at

least one of its children needs to increase its value.

Meanwhile, to decrease its value, all of its chil-

dren need to decrease their values. Therefore, we

have two cases:

CN ↑ (T, v) =

(

0 if v ≤ m

min

all children T

CN ↑ (T

, v) if v > m

(2)

CN ↓ (T, v) =







∑

all children T

CN ↓ (T

, v) if v < m

0 if v ≥ m

(3)

• At a min node, a similar scheme is applied:

CN ↑ (T, v) =







0 if v ≤ m

∑

all children T

CN ↑ (T

, v) if v > m

(4)

CN ↓ (T, v) =

(

min

all children T

CN ↓ (T

, v) if v < m

0 if v ≥ m

(5)

2.2 Conspiracy Number Search

Conspiracy number search was described in

(McAllester, 1988). It is a selective search that

explores the game tree non-uniformly to determine

the value of the root node. It maintains a range

of possible values and keeps expanding the tree

until a certain degree of conﬁdence is reached. The

conﬁdence is measured by the width of a possible

values’ range W and a minimum value for conspiracy

numbers T . The purpose of the search is to raise

the conspiracy numbers of unlikely values to greater

than T in order to reduce the range of possible values

to below W . At each turn, CNS tries to disprove

either the highest or lowest possible value, which has

the highest conspiracy numbers, by expanding one

of its conspirators. Then, it recalculates conspiracy

numbers and repeats the process until the desired

conﬁdence is obtained.

Using the example in Figure 1, we will demon-

strate how CNS works. Let W be 1, which means that

the search will only stop when there is only 1 value

in the possible range. Let T be 1, which means that

any value which has more than 1 conspirators is con-

sidered unlikely. The range of possible values in our

example would be 2 − 5, which is larger than our de-

sired range W . To reduce it, CNS choose to raise the

conspiracy number of either 2 or 5. If it selects 2,

whose conspirators is either node C or node D, CNS

will expand both node C and D. Figure 2 shows a pos-

sible result after expanding C.

CNS had been analyzed in several papers such

as (Elkan, 1989), (Schaeffer, 1990), (VanderMeulen,

1990), (Klingbeil and Schaeffer, 1990) and (Lister

Using Conspiracy Numbers for Improving Move Selection in Minimax Game-Tree Search

401

Figure 2: The tree in Figure 1 after expanding node C. Now,

to change value of node C to 2, both node E and F need to

change to 2. So the conspirators of 2 are node D or node E

and F. Next, node D will be selected to expand.

and Schaeffer, 1994), which showed some drawbacks

and proposed some improvements to CNS, but CNS

did not enjoy much success or attention afterward.

2.3 Other Directions

Alpha-Beta Conspiracy search (ABC), another algo-

rithm based on the conspiracy number, was intro-

duced in (McAllester and Yuret, 2002). ABC uses

2 values of conspiracy numbers to guide the search;

hence, it is less computationally expensive than CNS.

However, to our knowledge, not much analysis or ap-

plication has been done with ABC.

Later, conspiracy numbers inspired works on

proof-number search (PNS) (Allis et al., 1994) which

was very successful at solving games (Schaeffer et al.,

2007). PNS is applicable in AND/OR tree (Kishimoto

et al., 2012), in which a node only has 3 possible val-

ues: true, false or unknown. In a game situation, these

values can represent a win, a lost or undetermined, re-

spectively. The purpose of PNS is to determine the

outcome of the game as fast as possible by searching

branches that have high chance of establishing result

ﬁrst. PNS does not require an evaluation function; it

only requires the rules of the game to determine the

outcome at ending positions. However, while it is ca-

pable to solve end-game positions (Seo et al., 2001),

PNS cannot make decision at the opening or the mid-

dle of a game.

In (Khalid et al., 2015), another usage of conspir-

acy numbers is investigated. The authors suggest that

the ﬂow of conspiracy numbers can indicate critical

positions which can be used to determine a change in

strategy, speculative plays or early resignation.

3 IMPROVING MOVE

SELECTION WITH

CONSPIRACY NUMBERS

In this section, we will note some important aspects

of conspiracy numbers and introduce our method.

3.1 Important Characteristics of

Conspiracy Numbers

There are 2 important characteristics of conspiracy

numbers. First, they increase asymmetrically with re-

spect to the search depth. Assume that the root node

is a max node, if the search depth is one, from Equa-

tion (2) and (3), it can be seen that for values higher

the root value, their conspiracy numbers will be 1

(only one of its children need to change to a higher

value). Meanwhile, for values lower than root value,

their conspiracy numbers could be higher (all of its

children with higher value than the root value need to

change). If the root node is a min node, the oppo-

site is true. Therefore, we only consider conspiracy

numbers with even search depth, so that their values

would be balanced for both higher values and lower

values.

Another important property of conspiracy num-

bers is that they increase monotonically. Let m denote

the root value. If v

< v

< m, CN(v

) ≥ CN(v

) >

CN(m) = 0. Also if m < v

< v

, 0 = CN(m) <

CN(v

) ≤ CN(v

). Figure 3 illustrates this property.

Figure 3: A simple example shows the relation between

evaluation values and conspiracy numbers. m denotes the

root value.

3.2 Combining Conspiracy Numbers

The above characteristics give us the intuition that

Conspiracy Numbers for a game situation can be

viewed as the probability distribution of evaluation

value for that situation. A value with high conspir-

acy number indicates that it is difﬁcult to achieve

that value and vice versa. From that intuition, we

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

402

Figure 4: Evaluation values and inverted conspiracy num-

bers. Conspiracy numbers are the same as in Figure 3. We

consider CN(m) to be 1 instead of 0 for easier computation.

think that we can combine conspiracy numbers to

better understand game situations. It is also a dif-

ferent approach toward conspiracy numbers since to

our knowledge, previous methods only use conspir-

acy number of a single (as in CNS) or two (as in ABC

search) evaluation values to determine the direction of

the search.

Let v denote the current minimax value of a game

situation. For any value x, CN(x) is the conspiracy

number of x (either CN ↑ (x) or CN ↓ (x)). Then, in-

tuitively, we choose

CN(x)

to represent the probability

of changing to x. The graph of

CN(x)

is shown in Fig-

ure 4. To combine these numbers, we treat CN() as

a continuous function, and

CN(x)

would resemble the

probability distribution of the evaluation value. We

then calculate a value which we call the ”Conspiracy

Adjusted Evaluation Value” (CAEV) as follows:

∞

−∞

CN(x)

∞

−∞

CN(x)

(6)

The numerator represents the expected value if we

consider

CN(x)

as the probability of having x as the

evaluation value. The denominator

∞

−∞

CN(x)

dx is

presented to normalize the new value. Our hypoth-

esis is that the CAEV would be a better measure of

the game position than evaluation value alone.

The CAEV cannot be calculated exactly because

CN() is not a real continuous function. Therefore, we

approximate it using the following procedure:

• First, the evaluation range is divided into small

segments.

• Second, conspiracy numbers for the start and end

positions of each segment are calculated.

• Then, in each segment, we consider CN() to be a

linear function and calculate Equation (6) for that

segment.

• The summation of these values is the approxima-

tion of CAEV.

The detail of the procedure can be found in the Ap-

pendix.

4 EXPERIMENT

We conducted some experiments to assess the effec-

tiveness of the new measure. In this section, we de-

scribe the experiments and discuss about their results.

4.1 Experimental Design

The game of Othello is chosen as our test bed. We

use game transcripts from the United States 2015 Na-

tional Open tournament (United States Othello Asso-

ciation, 2015). For our experiments, we propose a

method which corporate CAEV and alpha-beta search

as in Algorithm 1. Algorithm 2 shows the pseudo

code for minimax procedure (which is implemented

as negamax) in Algorithm 1.

Algorithm 1: Func CN(node, cn depth, ab depth).

minimax(node, cn depth)

for all child in node.children do

child.eval = CAEV (child)

end for

return get best move(node.children)

Algorithm 2: Func minimax(node, depth).

if node.is terminal() or depth = 0 then

node.eval ← al phabeta(node, ab depth)

return

end if

node.eval ← −∞

for all child in node.children do

minimax(child, depth − 1)

node.eval ← max(node.eval, −child.eval)

end for

Figure 5 illustrates the structure of our method.

It consists of 2 layers. The top layer is a game tree

generated by minimax algorithm; CAVE is applied

to this tree. The leaf nodes of this tree are eval-

uated by an alpha-beta procedure. In the pseudo-

code, cn depth denotes the depth of the minimax layer

while ab depth denotes the depth of the alpha-beta

layer. So a player with cn depth = 0 will be iden-

tical to an alpha-beta player, while if ab depth = 0,

it will be a minimax player with CAEV applied. For

short, we will denote a player as CN(x, y) with x being

Using Conspiracy Numbers for Improving Move Selection in Minimax Game-Tree Search

403

Figure 5: Structure of our proposed player which consists of

a layer of minimax above a layer of alpha-beta. The CAEV

will be applied to the minimax layer.

cn depth and y being ab depth. We compare 3 play-

ers: CN(5, 0), CN(3, 2) and CN(0, 5) to identify the

inﬂuence of CAEV on a minimax-based player. Also,

2 evaluation functions are prepared for these players

to identify the effect of different evaluation functions.

Details on these evaluation functions can be found in

the Appendix.

Each player will play 20 games with other players.

A game will start from a random position between

move 5 and move 10 of a game from a set of ran-

domly selected games in the tournament. In addition,

to ensure fairness, for each selected game, each player

will start ﬁrst once, which means that there will be 40

matches between each player pairs. For each match,

the winner gets 1 point, the loser gets 0 point, while

each player will get 0.5 point in case of a draw.

4.2 Experimental Results

First, we performed matches between players with the

same evaluation function. Their results are shown in

Table 1 and Table 2. Then, matches between play-

ers with different evaluation functions was played and

their results are shown in Table 3.

Table 1: Results of matches between players using EV1.

Note that the results are symmetric.

CN(5, 0) CN(3, 2) CN(0, 5)

CN(5, 0) - 19.5 - 20.5 19 - 21

CN(3, 2) 20.5 - 19.5 - 18 - 22

CN(0, 5) 21 - 19 22 - 18 -

From Table 1, we cannot observe much inﬂuence

of CAEV on players with EV1. Most of the matchup

are seemingly equal. But for EV2, We can see that

the CAEV indeed has a remarkable effect on the per-

formance of the players. As shown in Table 2, players

with higher cn depth perform better.

Table 2: Comparison between players with EV2.

CN(5, 0) CN(3, 2) CN(0, 5)

CN(5, 0) - 23 - 17 28 - 12

CN(3, 2) 17 - 23 - 22 - 18

CN(0, 5) 12 - 28 18 - 22 -

Table 3: Comparison between players with EV1 and EV2.

In the column are players with EV1, while in the row are

players with EV2.

EV2

CN(5,0) CN(3,2) CN(0,5)

EV1

CN(5,0) 25 - 15 19 - 21 15 - 25

CN(3,2) 23 - 17 27 - 13 25 - 15

CN(0,5) 22 - 18 25.5 - 14.5 20.5 - 19.5

To ﬁnd the difference between the 2 evaluation

functions, we let players with EV1 compete with

players with EV2. The results are shown in Table 3.

Although the results look complicated, it is clear that

players with EV1 performs better than players with

EV2 since most players with EV1 won over players

with EV2. Among them, CN(3,2) with EV1 achieves

the best results (second row). However, there are still

ambiguity, such as indicated by the fact that CN(5, 0)

with EV1 lost against CN(0, 5) (alpha-beta player)

with EV2 while both CN(3, 2) and CN(0, 5) did not,

and for EV2, the player with more cn depth obtains

worst results, which contradict with the results in Ta-

ble 2. Further investigation is needed to clarify the

effects of CAEV and to know the best way to utilize

it.

5 CONCLUDING REMARKS

We have presented a move selection policy which in-

corporates conspiracy numbers. The novel idea of our

method is treating conspiracy numbers as a whole,

contrasting with previous methods which treat con-

spiracy numbers separately for each individual evalu-

ation value. By doing so, we can better understand a

game situation and make better decisions.

A simple method using the proposed idea was sug-

gested. The method combines conspiracy numbers

into evaluation values by an integration method and

using the new value to select moves. Our experiments

show that the value can have huge improvement on

certain evaluation functions.

To clearly understand the effects of the proposed

idea, more experiments are required. For example,

another evaluation function or another domain should

be tested. We expect that the effect would be greater

on weak evaluation functions than on strong evalua-

tion functions. Also, we could change the function

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

404

CN(x)

. It was chosen based on intuition, and since it is

an approximation, other functions may also perform

well.

The method also has some drawbacks. The most

notable one is the expensive cost of building a mini-

max tree which is inherited from conspiracy number.

If we could calculate or approximate conspiracy num-

bers without the need of a minimax tree, we could use

the method much more freely, such as using alpha-

beta or other fast game playing algorithms.

ACKNOWLEDGEMENTS

The authors thank the anonymous referees for their

insightful and detailed comments. This research is

funded by a grant from the Japan Society for the Pro-

motion of Science, in the framework of the Grant-

in-Aid for Challenging Exploratory Research (grant

number 26540189).

REFERENCES

Allis, V., van der Meulen, M., and van den Herik, J. (1994).

Proof-number search. Artiﬁcial Intelligence, 66(1):91

– 124.

Anantharaman, T., Campbell, M. S., and Hsu, F.-h. (1990).

Singular extensions: Adding selectivity to brute-force

searching. Artiﬁcial Intelligence, 43(1):99–109.

Beal, D. F. (1990). A generalised quiescence search algo-

rithm. Artiﬁcial Intelligence, 43(1):85–98.

Elkan, C. (1989). Conspiracy numbers and caching for

searching and/or trees and theorem-proving. In IJCAI,

pages 341–348.

Goetsch, G. and Campbell, M. S. (1990). Experiments with

the null-move heuristic. In Computers, Chess, and

Cognition, pages 159–168. Springer.

Khalid, M. N. A., Yusof, U. K., Iida, H., and Ishitobi,

T. (2015). Critical position identiﬁcation in games

and its application to speculative play. In Interna-

tional Conference on Agents and Artiﬁcial Intelli-

gence (ICAART-2015).

Kishimoto, A., Winands, M. H., M

uller, M., and Saito, J.-T.

(2012). Game-tree search using proof numbers: The

ﬁrst twenty years. ICGA Journal, 35(3):131–156.

Klingbeil, N. and Schaeffer, J. (1990). Empirical re-

sults with conspiracy numbers. Computational Intel-

ligence, 6(1):1–11.

Knuth, D. E. and Moore, R. W. (1975). An analysis of

alpha-beta pruning. Artiﬁcial intelligence, 6(4):293–

326.

Lister, L. and Schaeffer, J. (1994). An analysis of the con-

spiracy numbers algorithm. Computers & Mathemat-

ics with Applications, 27(1):41 – 64.

McAllester, D. A. (1988). Conspiracy numbers for min-max

search. Artiﬁcial Intelligence, 35(3):287 – 310.

McAllester, D. A. and Yuret, D. (2002). Alpha-beta-

conspiracy search. ICGA Journal, 25(1):16 – 35.

Schaeffer, J. (1990). Conspiracy numbers. Artiﬁcial Intelli-

gence, 43(1):67 – 84.

Schaeffer, J., Burch, N., Bj

ornsson, Y., Kishimoto, A.,

uller, M., Lake, R., Lu, P., and Sutphen, S. (2007).

Checkers is solved. science, 317(5844):1518–1522.

Seo, M., Iida, H., and Uiterwijk, J. W. (2001). The PN*-

search algorithm: Application to tsume-shogi. Artiﬁ-

cial Intelligence, 129(1):253–277.

Shannon, C. (1950). Programming a computer for playing

chess. Philosophical Magazine, 41(314):256 – 275.

Stockman, G. C. (1979). A minimax algorithm better than

alpha-beta? Artiﬁcial Intelligence, 12(2):179–196.

Turing, A. M., Bates, M., Bowden, B., and Strachey, C.

(1953). Digital computers applied to games. Faster

than thought, 101.

United States Othello Association (2015). 2015 national

open transcripts.

VanderMeulen, M. (1990). Conspiracy-number search.

ICCA Journal, 13(1):3–14.

APPENDIX

CAEV. Here is the procedure to calculate the

CAEV of a node.

Algorithm 3: Func CAEV (node).

ev ← node.eval

sum ← 0

for v = ev − RANGE + ST EP; v <= ev+RANGE;

v+ = ST EP do

sum+ = intgr(v − ST EP,

CN(v−ST EP)

, v,

CN(v)

)

end for

return sum

In the above procedure, RANGE is the maximum

distance of the evaluation value to the current value

of the root. We do not need to calculate the maxi-

mum or minimum possible evaluation values because

such values would have very high conspiracy num-

bers, which means that their inverse will be extremely

small and can be disregarded. ST EP is the segments’

length; a smaller ST EP indicates a better approxima-

tion and thus a higher computational cost. In our ex-

periments, we set RANGE to 1000, which is equal to

the difference of 1 corner stone in our evaluation func-

tion, and ST EP to 50. The function intgr(x,fx,y,fy)

will calculate the integral from x to y of a straight line

which goes through (x, f x) to (y, f y).

Using Conspiracy Numbers for Improving Move Selection in Minimax Game-Tree Search

405

Evaluation Function. In our experiment, we use

2 simple evaluation functions which relies on sev-

eral features of the game with hand-tuned weight.

The functions are symmetric in relation to the side to

move. For the ﬁrst evaluation function (EV1), the in-

cluded features are the differences between 2 players

in the number of corners, mobility (the number of

moves), the number of discs, the number of next-to-

open-corner discs and the number of frontier discs

(discs next to an open cell).

Algorithm 4: Evaluation Function 1.

return 1000*corners + 100*mobility -

200*next to corners - 100*frontier discs +

1*discs

The second evaluation function (EV2) is simpler

than the ﬁrst one. It only depends on the number of

corners, the mobility and the number of discs.

Algorithm 5: Evaluation Function 2.

return 1000*corners + 100*mobility + 1*discs

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

406