Distributionally Robust Games with Risk-averse Players

Nicolas Loizou

School of Mathematics, University of Edinburgh, Edinburgh, U.K.

Keywords:

Game Theory, Equilibrium, Distributionally Robust Optimization, Conditional Value at Risk.

Abstract:

We present a new model of incomplete information games without private information in which the players

use a distributionally robust optimization approach to cope with the payoff uncertainty. With some speciﬁc

restrictions, we show that our “Distributionally Robust Game” constitutes a true generalization of three popular

ﬁnite games. These are the Complete Information Games, Bayesian Games and Robust Games. Subsequently,

we prove that the set of equilibria of an arbitrary distributionally robust game with speciﬁed ambiguity set can

be computed as the component-wise projection of the solution set of a multi-linear system of equations and

inequalities. For special cases of such games we show equivalence to complete information ﬁnite games (Nash

Games) with the same number of players and same action spaces. Thus, when our game falls within these

special cases one can simply solve the corresponding Nash Game. Finally, we demonstrate the applicability

of our new model of games and highlight its importance.

1 INTRODUCTION

The classical, complete-information ﬁnite games as-

sume that the problem data (in particular the payoff

matrix) is known exactly by all players. In a now fa-

mous result((Nash et al., 1950), (Nash, 1951)), Nash

has shown that any such game has an equilibrium in

mixed strategies. More speciﬁcally, in his formulation

Nash assumed that all players are rational and that all

parameters(including payoff functions) of the game

are common knowledge. With these two assumptions,

the players can predict the outcome of the game. For

this reason each player given the other players strate-

gies is in a position to choose the mixed strategy that

gives him the maximum proﬁt. A tuple of these strate-

gies is what we call “Nash Equilibrium”.

The existence of equilibria in mixed strategies was

later extended to a class of incomplete information

ﬁnite games by Harsanyi (Harsanyi, 1968), who as-

sumed that the payoff matrix is not known exactly but

rather represents a random variable that is governed

by a probability distribution known to all players. In

particular, Harsanyi assumed that a full prior distri-

butional information for all parameters of the game

is available and that all players use this information

in order to compute the payoff functions of the game.

This computation is made using the Bayes’ rule. For

this reason these games are called “Bayesian Games”

and their equilibrium “Bayesian Nash Equilibrium”.

In 2006, Aghassi and Bertsimas (Aghassi

and Bertsimas, 2006) proposed a new class of

distribution-free ﬁnite games where the payoff matrix

is only known to belong to a given uncertainty set.

This model relaxes the distributional assumptions of

Harsanyi’s Bayesian games, and it gives rise to an al-

ternative distribution-free equilibrium concept. Fur-

thermore, in this model of games the players use a

robust optimization approach to the uncertainty and

this is assumed to be a common knowledge. That is,

given the other players strategies each player tries to

maximise his worst case expected payoff (worst case

is taken with respect to the uncertainty set). The using

of the robust optimization approach is the reason for

calling these “Robust Games” and their equilibrium

“Robust Optimization Equilibrium”.

More recently, Qu and Goh (Qu and Goh, 2012)

proposed a distributional robust version of the ﬁnite

game where they only consider the case in which the

players are risk neutral and they focus on an applica-

tion of supply chain. This model later was extended

to continuous games from Sun and Xu (Sun and Xu,

2015). The approach of these papers is in contrast to

our framework of modelling the players as each seek-

ing to minimize his worst case CVAR expected loss.

Moreover they offer no ideas on computation of their

equilibria.

In this paper we present a new model of incom-

plete information games without private information

186

Loizou, N.

Distributionally Robust Games with Risk-averse Players.

DOI: 10.5220/0005753301860196

In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 186-196

ISBN: 978-989-758-171-7

in which the players use a distributionally robust op-

timization approach to cope with payoff uncertainty.

In our model players only have partial information

about the probability distribution of the uncertain pay-

off matrix. This information is expressed through a

commonly known ambiguity set of all distributions

that are consistent with the known distributional prop-

erties. Similar to the robust games framework, play-

ers in distributionally robust games adopt a worst

case approach. Only now the worst case is com-

puted over all probability distributions within the am-

biguity set. More speciﬁcally we use a worst case

CVaR(Conditional Value at Risk) approach. This al-

lows players to have several risk attitudes which make

our model even more coveted since in real life appli-

cations players rarely are risk neutral.

For classical work on slightly related game mod-

els we refer the reader to (Hayashi et al., 2005) and

(Nishimura et al., 2012). The recent paper (Singh

et al., ) also deals with similar model of games but

in contrast to our approach the authors focused on the

existence of equilibrium.

The remainder of this work is organized as fol-

lows: Section 2 introduces our notation as well as def-

initions that are used through the paper. Section 3 pro-

poses and analyses our new model for Distributionally

Robust Games. After formulating the model, we show

that any other ﬁnite game can be expressed as a dis-

tributionally robust game. In Section 4, we prove the

equivalence of the set of equilibria of a distribution-

ally robust game and the component-wise projection

of the solution set of multi-linear system of equations

and inequalities. Section 5 shows the equivalence of

distributional robust games and Nash games in special

cases. Sections 6 and 7 are devoted to an illustrative

example and numerical experiment, respectively. Fi-

nally, conclusions and future directions are drawn in

Section 8.

All proofs are relegated to the appendix.

2 NOTATIONS-DEFINITIONS

The following notational conventions are used in this

paper. Boldface upper case letters will denote matri-

ces and boldface lower case letters will denote vec-

tors. To denote uncertainty we will use the tilde (˜·)

in which the input parameter (·) can be either scalar,

vector, or matrix and the check (ˇ·) will indicate the

nominal counterpart of the uncertain coefﬁcient ˜·. Fi-

nally, vec(A) denotes the column vector obtained by

stacking the row vectors of the matrix A one on top

of the other.

With

P ∈ R

N×

∏

i=1

we denote the payoff matrix of a

complete information game (ﬁxed matrix) while with

P the uncertainty matrix of the incomplete informa-

tion games.

In particular,

( j

, j

,.... j

)

denotes the payoff to player

i when player k ∈ {1,2,....N} plays action j

∈

{1,2,....,a

} and S

= {x

∈ R

≥ 0,

∑

1} expresses the set of all possible mixed strategies

of player i over all actions {1,2, ...a

}. Moreover, let

(P ;x

,...x

) indicate the expected payoff of

player i when the payoff matrix is given by P and

player k ∈ {1, 2,....N} plays mixed strategy x

∈ S

That is,

(P ; x

,...x

) =

∑

...

∑

...

∑

( j

, j

,.... j

)

∏

i=1

(1)

Finally, in this paper, we use exactly like Bertsimas

and Aghassi (Aghassi and Bertsimas, 2006) the fol-

lowing shorthands:

−i

= (x

,.., x

i−1

i+1

,...x

)

−i

) = (x

,.., x

i−1

i+1

,...x

)

S =

∏

i=1

, S

−i

∏

k=1,k6=i

and the following deﬁnitions for the equilibrium in

Nash games, Bayesian Games and Robust Games:

The tuple of strategies (x

,...x

) ∈ S is:

• Nash Equilibrium iff for each player i ∈

{1,2....N}:

∈ argmax

∈S

(

P ;x

−i

) (2)

• Bayesian Nash Equilibrium iff for each player

i ∈ {1, 2....N}:

∈ argmax

∈S

(

P ;x

−i

)] (3)

• Robust Optimization Equilibrium iff for each

player i ∈ {1, 2....N},

∈ argmax

∈S

[ inf

P ∈U

(

P ;x

−i

)] (4)

3 THE NEW MODEL

In this section we present the new model of incom-

plete information games without private information

Distributionally Robust Games with Risk-averse Players

187

in which the players use a distributionally robust op-

timization approach to cope with payoff uncertainty.

We also show that under speciﬁc assumptions about

the ambiguity set and the values of risk levels, Distri-

butionally Robust Game constitutes a true generaliza-

tion of Nash, Bayesian and Robust Games.

We introduce the new model of Distributionally

Robust Games by ﬁrst giving the two important deﬁ-

nitions of Best Response and Distributionally Robust

Optimization Equilibrium and explain them later in

details.

Deﬁnition 3.1. In the distributionally robust model,

for the case without private information, players i’s

best response to the other players strategies x

−i

∈ S

−i

must belong to:

argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ;x

−i

)] (5)

Deﬁnition 3.2. (x

,...x

) ∈ S is said to be a

Distributionally Robust Optimization Equilibrium of

the corresponding game with incomplete information

iff ∀i ∈ {1,2,..N},

∈ argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ;x

−i

)] (6)

Our approach can be considered a concept closely

related to both Harsanyi’s Bayesian Games (Harsanyi,

1968) and Robust Games (Aghassi and Bertsimas,

2006). In more detail, in Bayesian Games we as-

sume that all players of the game know the exact dis-

tribution of the payoff matrix. Now, in the Distri-

butionally Robust approach the players do not know

the exact distribution. Instead, they are only aware

of a commonly known ambiguity set F of all possi-

ble probability distributions Q that satisfy some spe-

ciﬁc properties. These distributions have no restric-

tion in their form. That is, the ambiguity set may

consists of both, discrete and continuous distributions

of the payoff matrix. In addition, similar to the ro-

bust games framework, we assume that each player

adopts a worst case approach to the uncertainty. Only

now the worst case is computed over all probability

distributions within the set F . For this formulation

which is similar to distributionally robust optimiza-

tion concept we named these games Distributionally

Robust Games(DRG) and we refer to their equilib-

ria as Distributionally Robust Optimization Equi-

libria (DROE).

3.1 CVAR and Main Assumptions

Deﬁnition 3.3. (Conditional Value at Risk)

CVaR

of a loss distribution L is the expected value of

all losses that exceed (1 − ε)-quantile of the distribu-

tion. This can be formalized as:

Q-CVaR

(L) = min

ζ∈R

ζ +

[L − ζ]

(7)

where [x]

= max{x,0}.

Conditional Value at Risk(CVaR) is one of the

most popular quantile-based risk measures because

of its desirable computational properties (Rockafellar

and Uryasev, 2000),(Artzner et al., 2002). Exactly

for these properties we chose to introduce CVaR in

the formulation of the new model.

Using Q-CVaR

, we allow the players to have several

risk attitudes which is a major difference compared

to all other ﬁnite games (Nash, Bayesian and Robust

Games) in which the players are always risk neutral.

Important hypothesis is that risk attitude is a ﬁxed

characteristic of each player and it cannot be changed

depending the game. It is not a notion like the mixed

strategy that a player can choose in order to achieve

his best response and minimise his loss. More

speciﬁcally, the parameter ε

∈ (0,1) determines

the risk-aversion of each decision-maker. In detail,

if player i has risk level ε

= 1 this means that he

is risk neutral since the Conditional Value at Risk

is equal to the expected value of his loss function

(Q-CVaR

= E

). On the other hand if ε

≤ 1 the

player is risk averse and as ε

−→ 0 the risk aversion

of the player becomes larger.

Conclusively, as parameter ε

decreases, the value

of Q-CVaR

increases and the risk aversion of the

player becomes larger and vice versa.

With the introduction of a risk measure in our model

we take into account not only that each player

wishes to maximize his gain (minimize loss) but also

how much she/he is willing to risk to achieve this

maximum value (minimum value).

Assumption of the New Model: The risk

attitude of each player is assumed to be common

knowledge. That is, each player knows how much

risk averse are the other players and that all other

players know that he knows.

In general, CVaR can be calculated from either

the probability distribution of gains or the probability

distribution of losses. In this paper we decide to

follow the original formulation of Rockafellar and

Uryasev (see (Rockafellar and Uryasev, 2002) and

(Rockafellar and Uryasev, 2000)) and calculate

CVAR from the distribution of losses.

For this reason, in deﬁnitions (3.1) and (3.2)

we use the expected loss function of player i,

−π

(P ;x

−i

). Loss distributions are also re-

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

188

sponsible for the use of argmin

∈S

sup

Q∈F

instead of

argmax

∈S

inf

Q∈F

that we use in robust games.

Finally, in the formulation of the DRG we make two

more assumptions.

Assumption: The players commonly know the

ambiguity set of all possible distributions (discrete

and continuous) of the payoff matrix.

Assumption: Each player adopts, like Robust

games, a worst case approach to the uncertainty, only

now the worst case is computed over all probabil-

ity distributions within the set F . In particular we

assume that all players use a worst case CVaR ap-

proach.

3.2 Generalization of all other Games

From the formulation of the DRG (deﬁnitions of best

response and equilibrium) we can easily understand

that only two are the parameters that are amenable to

change. These are, risk level ε

of each player i and

the ambiguity set F . In particular, we assume that pa-

rameter ε

which shows the risk level of each player

can take any value in the interval (0, 1) and we make

no assumptions for the ambiguity set. That is, de-

pending on the game that one faces she/he can choose

the more suitable properties that the distributions of

the ambiguity set must satisfy. Hence, if we assume

some extra constraints for parameter ε

and set F , the

previous general formulation can become very spe-

ciﬁc.

Let’s assume that all players i ∈ {1, 2,...N} have

the same risk level, ε

= 1 ∀i ∈ {1, 2,...., N}. Then

from the deﬁnition of CVaR we obtain the following

∀i ∈ {1, 2,....,N}:

Q-CVaR

[−π

(

P ; x

−i

)] = Q-CVaR

[−π

(

P ; x

−i

)]

= E

[−π

(

P ; x

−i

)]

(8)

Therefore the deﬁnition of best response (3.1) be-

comes:

argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ; x

−i

)] = argmin

∈S

sup

Q∈F

[−π

(

P ; x

−i

)]

= argmin

∈S

sup

Q∈F

[−π

[

P ]; x

−i

)]

= argmax

∈S

inf

Q∈F

[π

[

P ]; x

−i

)]

(9)

The equality in the second line in the above expres-

sion follows from the linearity of expectation operator

and the linearity of π

[π

(

P ;x

−i

)] = [π

[

P ];x

−i

)]

where E

[

P ]is the component-wise expected value

P . The equality in the third line is due to the fol-

lowing properties of linear functions:

max f (x) = − min[− f (x)]

and

z ∈ argmin

x∈S

f (x) = z ∈ argmax

x∈S

− f (x).

Now, using the assumption that ε

= 1 ∀i ∈

{1,2, ...N} and by choosing the right properties for

the probability distributions of the payoff matrix we

can specify our formulation and create the desire

games.

Theorem 3.1. In the DRG, players i’s best response

to the other players strategies x

−i

∈ S

−i

must belong

to:

argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ; x

−i

)] (10)

If we assume that ε

= 1 ∀i ∈ {1, 2,...N}, then:

1. If F = {Q : E

[

P ] = Ψ} the set of DROE is

equivalent to that of a classical Nash Game.

2. If the ambiguity set is singleton, that is, F = {Q},

the DRG have the same equilibria with a related

ﬁnite Bayesian Game.

3. If F = {Q : Q[W · vec(E

[

P ]) ≤ h] = 1} the set

of DROE is equivalent to that of the classical Ro-

bust Game.

4 COMPUTING SAMPLE

EQUILIBRIA OF DRG

To examine if one speciﬁc tuple of strategies is equi-

librium is a typically elementary procedure in any

kind of game. However, to ﬁnd the set of all equilibria

of a game, with complete or incomplete information,

is a very difﬁcult task.

In this section, we present Theorem (4.1), in which

we show that for any ﬁnite distributionally robust

game with a speciﬁed ambiguity set and with no pri-

vate information the set of equilibria is a projection

of the solution set of multilinear system of equalities

and inequalities. The projection is like in (Aghassi

and Bertsimas, 2006), the component wise one into a

lower dimensional space.

Theorem 4.1. (Computation of Equilibria in Distri-

butionally Robust Finite Games)

Consider the N-player distributionally robust

game in which i ∈ {1,2,...,N} has action set

Distributionally Robust Games with Risk-averse Players

189

{1,2, ...,a

}, 1 < a

< ∞, in which the ambiguity set

is:

F = {Q : Q[

P ∈ U] = 1, E

[vec

P ] = m, E

[



vec(

P ) − m



] ≤ s}

(11)

where U = {P : W · vec(P ) ≤ h} is bounded and polyhe-

dral set, and in which there is no private information.

The following two conditions are equivalent.

Condition 1) (x

,....x

) is an equilibrium of the dis-

tributionally robust game.

Condition 2) For all i ∈ {1,2,....N} there exists

,ζ

,ρ

∈ R, γ

∈ R

, ξ

,θ

∈ R

and

,λ

,κ

,δ

,ν

,τ

,φ

∈ R

∏

i=1

, such that

, x

, ....x

,α

,ζ

,ρ

,γ

,β

, λ

, κ

, δ

, ν

, τ

, f

, φ

, g

, ξ

, θ

)

satisﬁes:

sγ = ρ

, e

= 1,

− m

+ m

+ h

≥ 0, ρ

≤ f

−i

)

+ κ

− γ

e ≤ 0, δ

+ ν

− γ

e ≤ 0

− m

+ m

+ h

+ ζ

≥ 0

−δ

+ ν

+ W

− β

− Y

−i

= 0

−e

− e

≤

s, −τ

− f

−τ

+ φ

≤ σ

m, τ

+ φ

≤ −σ

W τ

≥ −σ

h, W f

≥ −h

−f

+ g

≤ m, f

+ g

≤ −m

−λ

+ κ

+ W

− β

= 0,

,κ

,δ

,ν

≥ 0, θ

,ξ

,φ

≤ 0

γ ≥ 0,

(12)

where Y

−i

) ∈ R

∏

i=1

)×a

denotes the matrix

such that

vec(P )

−i

= π

(P ;x

−i

), (13)

parameter ε

denotes the risk level of player i and

1−ε

is a ﬁxed number ∀i ∈ {1, 2,....N}.

5 THE AMBIGUITY SET

In all DRG that we develop in this paper the ambigu-

ity set have the following form:

F = {Q : Q[W · vec(

P ) ≤ h] = 1, E

[vec

P ] = m, E

[



vec(

P ) − m



] ≤ s}

(14)

This, combined with different risk levels ε

for

player i ∈ {1, 2,..N} allows several variations of each

distributionally robust game. By changing the values

of ambiguity set’s uncertain parameters W,h, m and

s and by assuming each time different risk attitudes

for the players the set of DROE which constitute the

solution of our problem can change dramatically.

At this point, we present the role of each uncertain

parameter of the ambiguity set (14).

Matrix W ∈ R

(m×N

∏

i=1

)

and vector h ∈ R

are

the two variables which represent the uncertainty

polyhedral set in which the uncertain values of the

payoff matrix should belong. The maximum distance

of all possible vec(

P ) from the average vector m

is denoted by scalar s. Finally, m ∈ R

∏

i=1

is the

vector that denotes the expected value of vec(

P ) for

each distribution that belongs to the ambiguity set.

Important assumption: Vector m must belong to the

bounded uncertainty polyhedral set of the payoff

matrix

P . Otherwise the ambiguity set F will be

empty.

Special Cases of Distributionally Robust Games:

Under certain conditions (special cases), the set of

equilibria of distributionally robust ﬁnite game with

ambiguity set like (14) is equivalent to that of a

related ﬁnite game with complete payoff information

(Nash Game) and with the same number of players

and the same action spaces. Thus, when our game

falls within these special cases one can simply solve

the corresponding Nash Game.

The special cases of such games are studied in the

next three propositions.

Proposition 5.1. The set of equilibria of a distribu-

tionally robust game in which all players are risk neu-

tral (ε

= 1, ∀i ∈ {1,2, ..N}) is equivalent to the set of

equilibria of a Nash Game with ﬁxed payoff matrix Ψ

where vec(Ψ) = m. (m is the average vector of the

ambiguity set (14). )

Proposition 5.2. The set of equilibria of a distribu-

tionally robust game in which the parameter s of the

ambiguity set (14) is equal to zero(s=0) is equivalent

to the set of equilibria of a Nash Game with ﬁxed pay-

off matrix M where vec(M ) = m. (m is the average

vector of the ambiguity set (14). )

Proposition 5.3. The set of equilibria of a distribu-

tionally robust game that has as a support a single

point is equivalent to the set of equilibria of a Nash

Game with ﬁxed payoff matrix the one that corre-

sponds to this single point. Single point is named the

unique payoff matrix which created from speciﬁc val-

ues of the matrix W and vector h of the ambiguity

set. The values of matrix W and vector h are se-

lected in order to make the uncertainty set U = {P :

W · vec(P ) ≤ h} singleton.

6 ILLUSTRATIVE EXAMPLE

Having presented our distributionally robust games

model we will now illustrate our approach with one

concrete example.

Distributionally Robust Inspection Game (DRIG)

Problem Description:

The DRIG is a two player game in which the row

player is the employee (possible actions:Shirk or

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

190

Table 1: Normal Form Representation of DRIG.

Inspect NotInspect

Shirk (0,−

h) (w, -w)

Work (w − ˜g, ˜v − w −

h) (w − ˜g, ˜v − w)

Work) and the column player is the employer(with

possible actions Inspect or not Inspect). The two play-

ers choose their actions simultaneously and then they

receive the payoffs corresponding to the combination

of their strategies. When the employee works he has

cost ˜g and his employer has proﬁt equal to ˜v. Each

inspection costs to the employer

h but if he inspects

and ﬁnds the employee shirking then he does not pay

him his wage w. In all other cases employee’s wage

is paid. All values except the payment w of the em-

ployee are uncertain.

In the classical complete information Inspection

game the parameters ˜g, ˜v and

h are ﬁxed ( ˜g = ˇg, ˜v =

ˇv,

h =

h) and in the robust approach ( ˜g, ˜v,

h) ∈ [g,g] ×

[v,v] × [h,h] (Aghassi and Bertsimas, 2006).

In our new, distributionally robust approach, players

have partial information about the probability distri-

butions of the uncertain variables ˜g, ˜v and

h (about the

probability distribution Q of the payoff matrix

P ). In

particular, the players do not know the exact distri-

bution of the payoff matrix. They are only aware of

a commonly known ambiguity set F of all possible

probability distributions Q that satisfy some speciﬁc

properties. Subsequently, all players adopt a worst

case CVaR approach to the uncertainty which is com-

puted over all probability distributions within the set

F . The introduction of the CVaR in the formulation

of the game allows the two players to have different

risk attitudes. Finally, the risk levels of the players

are assumed to be common knowledge and none of

the two players has private information.

For example, we may consider the DRIG in which the

ambiguity set is given by:

F = {Q : Q[( ˜g, ˜v,

h) ∈ U ] = 1, E

[vec(

P )] = m, E

[



vec(

P ) − m



] ≤ s}

(15)

Where:U = [g, g] × [v, v] × [h,h] , s ≥ 0, and

P =



(0,−

h) (w, −w)

(w − ˜g, ˜v − w −

h)) (w − ˜g, ˜v − w)



(16)

Important assumption: Vector m of the second

constraint of the ambiguity set must belong to the

bounded polyhedral uncertainty set of payoff matrix

P. For the DRIG, m ∈ [g,g] × [v, v] × [h,h]. Other-

wise the ambiguity set will be empty.

7 NUMERICAL EXPERIMENT

In this section, we experimentally evaluate the new

model of games described in this paper. In the interest

of brevity, we only present one experiment. For more

examples, experiments and detailed explanation of

our computational method we refer the reader to

chapter 5 of (Loizou, 2015).

The Experiment:

Fixed Ambiguity Set - Several Risk Levels

What would happen to the number of equilibria

and to the payments of the two players when the

ambiguity set is kept ﬁxed while the values of players’

risk levels are varied.

Computational Method:

The method that we use to approximately compute the

DROE and the players’ payoffs at each equilibrium of

any DRG is developed as follows:

1. Check if the ambiguity set of the DRG can be ex-

pressed like the general form of equation (14).

(The ambiguity set of DRIG has this property.)

2. Estimate the multi-linear system of equali-

ties and inequalities whose dimension-reducing

component-wise projection of the feasible solu-

tion set is equivalent with the set of equilibria of

the DRG (see theorem (4.1))

3. Find the feasible solutions of the multi-linear sys-

tem and for each solution keep the components

that correspond to the strategies of the players

(projection of the solution). Additionally, com-

pute the players’ payoffs at each equilibrium.

These are achieved using the YALMIP modelling

language (L

ofberg, 2004), in Matlab 2014b.

All numerical evaluations of this chapter were

conducted on a 2.27GHz, Intel Core i5 CPU 430

machine with 4GB of RAM.

More speciﬁcally, in the experiment of this sec-

tion we assume that the uncertain parameters of the

costs ( ˜g, ˜v,

h) must belong to [8,12] × [16,24] × [4, 6]

and that the payment w of the employee is ﬁxed

at w=15. In addition, we assume that average

vector m of the ambiguity set is the one that

corresponds to the nominal

version of the game

m = m

= (0, −5,15, −15,5, 0,5, 5)

and without

loss of generality that the maximum distance s of the

third constraint of the ambiguity set is s = 4.

With “nominal” we mean that the average vector takes

the value of vec(P ) when the uncertain parameters ˜g, ˜v and

h are equal to the mid points of their intervals ( ˜g = 10, ˜v =

20,

h = 5 and w = 15).

Distributionally Robust Games with Risk-averse Players

191

Therefore, since all variables of the ambiguity set are

kept ﬁxed

, we can derive that the ambiguity set of

the form (14) is kept ﬁxed in this experiment . The

only variables that are allowed to change are the risk

levels ε

and ε

of the two players.

The following tables and ﬁgures illustrate the number

of equilibria and the players’ payoffs at these equilib-

ria for the aforementioned ﬁxed ambiguity set while

the players’ risk levels change.

In particular Table 2 shows the equilibria of the pre-

viously described game when player 1 is risk neutral

(ε

= 1) and player 2 has several risk attitudes. The

players’ payoffs at equilibria for each combination of

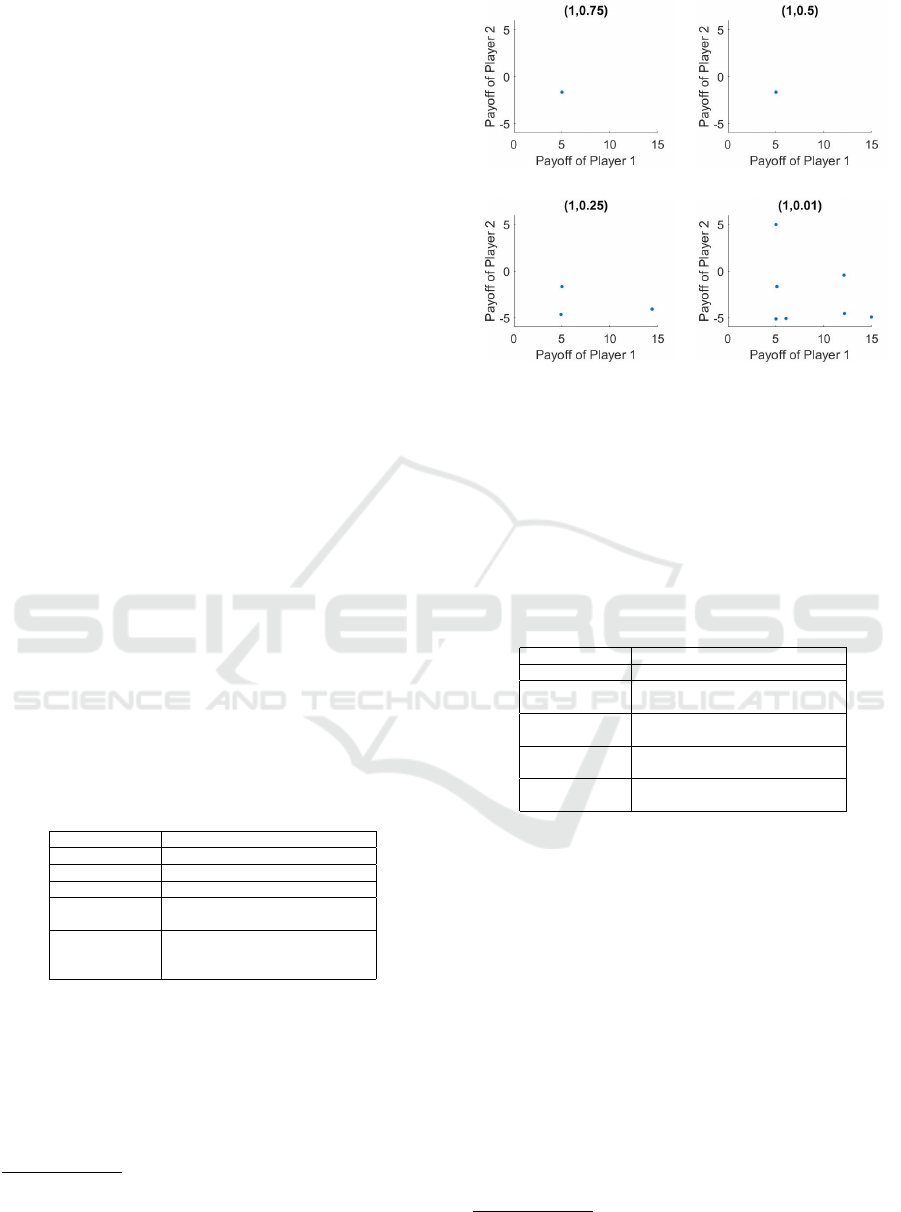
the risk levels are given in Figure 1.

Notice that the ﬁrst line of the Table 2 and Table

3 corresponds to the special case in which the two

players of the game are risk neutral(ε

= 1,ε

= 1).

This means that instead of solving the DRIG using the

aforementioned computational method we can simply

solve the corresponding Nash Game with ﬁxed payoff

matrix M where vecM = m:

M =



(0,−5) (15,−15)

(5,0) (5,5)



(17)

This Complete Information Game has unique equilib-

rium equal to (1/3,2/3). That is, the employee(row

player) shirks(plays action 1) with probability x

1/3 and the employer(column player) inspects(plays

action 1)with probability x

= 2/3.

Table 2: DRIG: The equilibria for different values of Risk

levels when the vector m of the ambiguity set take the nom-

inal value and the maximum distance is s = 4. Player 1 is

risk neutral. His risk level is kept ﬁxed (ε

= 1) while player

2 has several levels of risk aversion.

Risk Levels Equilibria

= 1,ε

= 1 (1/3,2/3)

= 1,ε

= 0.75 (0.333, 0.66)

= 1,ε

= 0.5 (0.333, 0.66)

= 1,ε

= 0.25 (0.333,0.66)(0.8179,0)

(0.9342,0.7069)

= 1,ε

= 0.01 (1,0),(0,0.66),

(1,0.66),(1,0.1941) (0.333,0.66),

(0.9654,0.1387),(1,0.59)

Subsequently, Table 3 shows the equilibria of the

previously described game when player 2 is risk neu-

tral (ε

= 1) and player 1 has several risk attitudes.

The players’ payoffs at equilibria for each combina-

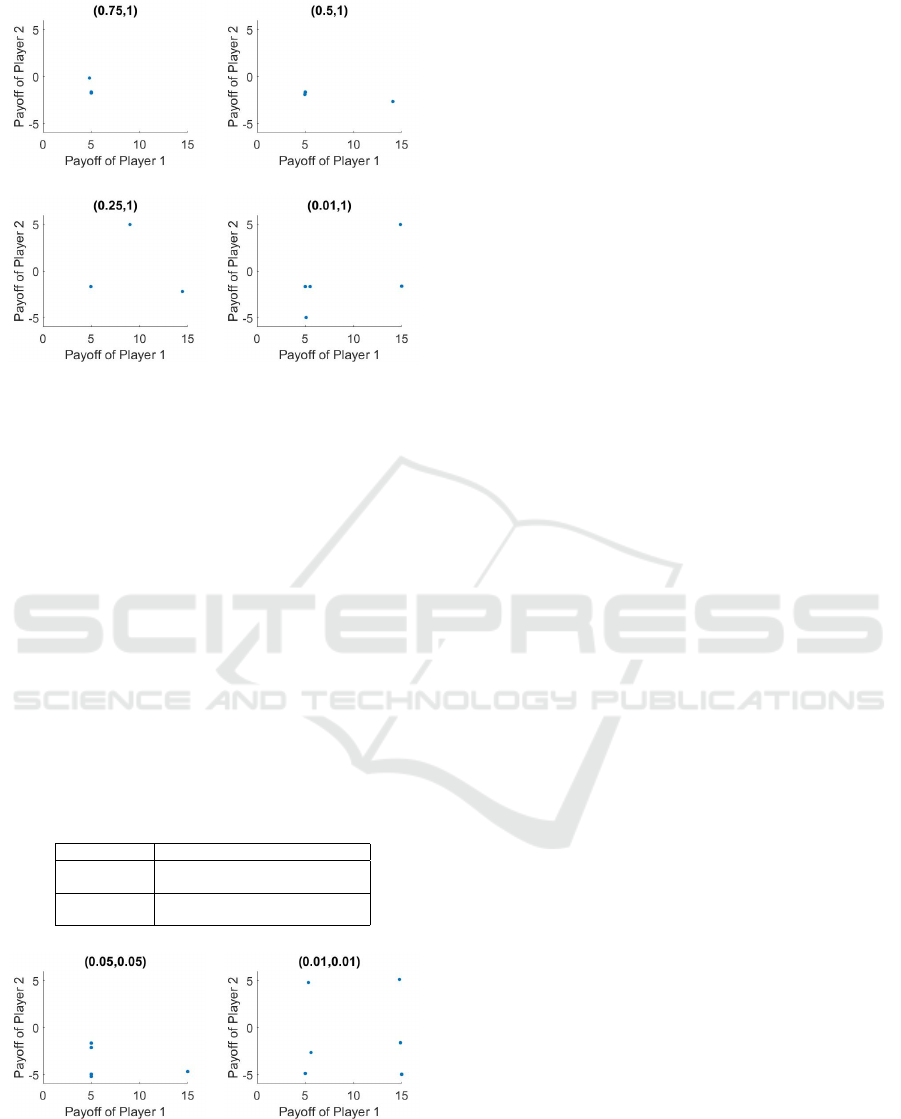
tion of the risk levels are given in Figure 2.

Discussion of the Results:

In standard optimization problems we know that as

The matrix W and vector h of the ﬁrst constraint of the

ambiguity set are also ﬁxed because the uncertain parame-

ters of the payoff matrix ( ˜g, ˜v,

h) belong in a speciﬁc ﬁxed

uncertainty set

(a) (b)

Figure 1: Graph representation of the payoffs of the two

players at equilibria for different risk levels. Risk level of

player 1 is kept ﬁxed (ε

= 1) while player 2 has several

levels of risk aversion. The title of each sub-ﬁgure denotes

the risk levels of the two players: (Players 1’s risk level,

Players 2’s risk level).

Table 3: DRIG: The equilibria for different values of Risk

levels when the vector m of the ambiguity set take the nom-

inal value and the maximum distance is s = 4. Player 2 is

risk neutral. His risk level kept ﬁxed (ε

= 1) while player

1 has several levels of risk aversion.

Risk Levels Equilibria

= 1,ε

= 1 (1/3,2/3)

= 0.75,ε

= 1 (0.333,0.666),(0.35,0.665),

(0.2583,0.96)

= 0.5,ε

= 1 (0.333,0.666),(0.5379,0),

(0.3842,0.66)

= 0.25,ε

= 1 (0.4427,0),(0.333,0.666),

(0,0.3467)

= 0.01,ε

= 1 (0,0),(1,1), (0.333,0.666),(0.33,0),

(0.335,1)

the decision maker becomes more risk averse his pay-

off always decreases. From the previous Figures 1

and 2 we can conclude that in game theory situation

this is not always the case. We can not have a gen-

eral rule, since now the nature of the problem is more

complicated.

In the DRG we assume that players are rational, so

they can predict the outcome of the game and choose

the strategies that form an equilibrium. For this rea-

son, a difference at risk attitude of a player does not

change only his decision but also the decisions of his

opponents.

. Hence, with increasing of risk aversion

of one player the players’ payoffs at equilibria may

both increase or decrease depending the game. For

example, in Figure 1 at Subﬁgure (d) where the risk

levels are (1,0.01) we can observe that for some equi-

in DRG, risk attitude is assumed to be common knowl-

edge

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

192

(a) (b)

Figure 2: Graph representation of the payoffs of the two

players at equilibria for different risk levels. Risk level of

player 2 is kept ﬁxed (ε

= 1) while player 1 has several

levels of risk aversion. The title of each sub-ﬁgure denotes

the risk levels of the two players: (Players 1’s risk level,

Players 2’s risk level).

libria the players have large payments and for some

others very low.

To verify that in the DRIG we can not have a gen-

eral rule about what happen in the payoffs of the two

players when they choose to play strategies that form

equilibria we also present Table 4 and Figure 3 witch

illustrate the payoffs of the two players at equilib-

ria when both of them are risk averse. More specif-

ically when their risk levels are ε

= ε

= 0.05 and

= ε

= 0.01

Table 4: DRIG: Equilibria when the players’ risk levels are

= ε

= 0.05 and ε

= ε

= 0.01.

Risk Levels Equilibria

= ε

= 0.05 (1,0.66),(1,1)(0.95,0),

(0.43,1),(0.333,0.666)

= ε

= 0.01 (1,0),(0,0),(0.332,0),

(0.5303,1),(1,0.78)

(a) (b)

Figure 3: Graph representation of the players’ payoffs at

equilibria when their risk levels are ε

= ε

= 0.05 and ε

= 0.01.The title of each sub-ﬁgure denotes the risk levels

of the two players: (Players 1’s risk level,Players 2’s risk

level).

8 CONCLUSIONS

This paper combines Game Theory and Distribution-

ally Robust Optimization to propose a novel model of

incomplete information games without private infor-

mation in which the players use distributionally ro-

bust optimization to cope with payoff uncertainty.

We showed that for speciﬁc ambiguity sets and risk

levels, distributionally robust games constitute a true

generalization of Nash games, Bayesian Games and

Robust Games. Thus, any ﬁnite game of these three

categories can be expressed as a distributionally ro-

bust game.

Subsequently, we proved that the set of equilibria of

an arbitrary distributionally robust game with spec-

iﬁed ambiguity set and without private information

can be computed as the component-wise projection of

the solution set of a multi-linear system of equations

and inequalities. For special cases of such games we

also showed equivalence to complete information ﬁ-

nite games (Nash Games) with the same number of

players and same action spaces.

Finally to concretize the idea of a distributionallly ro-

bust game we presented Distributionally Robust In-

spection Game. We experimentally evaluated the new

model of games and we studied how the number of

equilibria and the players’ payments change when the

ambiguity set is ﬁxed and the risk levels of the players

are varied.

Our approach opens up many avenues for further de-

velopment and research. For instance, the work of this

paper can be generalized to the case of distribution-

ally robust games involving potentially private infor-

mation. Furthermore, interesting results might arise if

we try to make similar work for more general classes

of ambiguity sets.

ACKNOWLEDGEMENTS

The author is very grateful to Wolfram Wiesemann

for helpful discussions and remarks. NL acknowl-

edges support by the Leventis Foundation and Laura

Wisewell Fund. Most of this work was done while at

Imperial College London.

REFERENCES

Aghassi, M. and Bertsimas, D. (2006). Robust game theory.

Mathematical Programming, 107(1-2):231–273.

Artzner, P., Delbaen, F., Eber, J.-M., and Heath, D. (2002).

Coherent measures of risk1. Risk management: value

at risk and beyond, page 145.

Distributionally Robust Games with Risk-averse Players

193

Harsanyi, J. C. (1967,1968). Games with incomplete infor-

mation played by “bayesian” players, i-iii. Manage-

ment science, 14:159–182,320–334,486–502.

Hayashi, S., Yamashita, N., and Fukushima, M. (2005). Ro-

bust nash equilibria and second-order cone comple-

mentarity problems. Journal of Nonlinear and Convex

Analysis, 6(2):283.

ofberg, J. (2004). Yalmip: A toolbox for modeling and

optimization in matlab. In Computer Aided Control

Systems Design, 2004 IEEE International Symposium

on, pages 284–289. IEEE.

Loizou, N. (2015). Distributionally robust game theory.

arXiv preprint arXiv:1512.03253.

Nash, J. (1951). Non-cooperative games. Annals of mathe-

matics, pages 286–295.

Nash, J. F. et al. (1950). Equilibrium points in n-person

games. Proceedings of the national academy of sci-

ences, 36(1):48–49.

Natarajan, K., Pachamanova, D., and Sim, M. (2009). Con-

structing risk measures from uncertainty sets. Opera-

tions Research, 57(5):1129–1141.

Nishimura, R., Hayashi, S., and Fukushima, M. (2012).

Semideﬁnite complementarity reformulation for ro-

bust nash equilibrium problems with euclidean un-

certainty sets. Journal of Global Optimization,

53(1):107–120.

Qu, S. and Goh, M. (2012). Distributionally robust games

with an application to supply chain. Harbin Institute

of Technology.

Rockafellar, R. T. and Uryasev, S. (2000). Optimization of

conditional value-at-risk. Journal of risk, 2:21–42.

Rockafellar, R. T. and Uryasev, S. (2002). Conditional

value-at-risk for general loss distributions. Journal of

banking & ﬁnance, 26(7):1443–1471.

Singh, V. V., Jouini, O., and Lisser, A. Existence of

nash equilibrium for distributionally robust chance-

constrained games.

Sion, M. et al. (1958). On general minimax theorems. Pa-

ciﬁc J. Math, 8(1):171–176.

Sun, H. and Xu, H. (2015). Convergence analysis for distri-

butionally robust optimization and equilibrium prob-

lems. Mathematics of Operations Research.

Wiesemann, W., Kuhn, D., and Sim, M. (2014). Distribu-

tionally robust convex optimization. Operations Re-

search, 62(6):1358–1376.

APPENDIX

Proof of Theorem 3.1: Using equation (9) we obtain

the following results:

For Nash Games: If F = {Q : E

[

P ] = Ψ}

∈ argmax

∈S

inf

Q∈F

[π

[

P ]; x

−i

)] = argmax

∈S

inf

Q∈F

[π

(Ψ;x

−i

)]

= argmax

∈S

[π

(Ψ;x

−i

)]

(18)

which is equivalent to the formulation of Nash Equi-

librium (see equation (2)).

For Bayesian Games: If the ambiguity set is single-

ton, that is F = {Q}.

∈ argmax

∈S

inf

Q∈F

[π

(

P ; x

−i

)] = argmax

∈S

[π

(

P ; x

−i

)]

(19)

which is equivalent to the formulation of Bayesian

Nash Equilibrium (see equation (3)).

For Robust Games: If F = {Q : Q[E

[

P ] ∈ U] = 1}

where U = {P : W · vec(P ) ≤ h}, then:

∈ argmax

∈S

inf

Q∈F

[π

[

P ]; x

−i

)] = argmax

∈S

inf

S∈U

[π

(

S;x

−i

)]

(20)

where

S = E

[

P ];

which is equivalent to the formulation of Robust

Optimization Equilibrium Games (see equation (4)).

Proof of Theorem 4.1: By the Formulation of the

DRG Condition 1 is equivalent to

∈ argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ;x

−i

)] ∀i ∈ {1,2, ...., N}

(21)

From (Rockafellar and Uryasev, 2000) and (Rockafel-

lar and Uryasev, 2002) we know that :

Q-CVaR

[−π

(

P ; x

−i

)] = min

∈R

[−π

(

P ; x

−i

) − ζ

]

(22)

where [x]

= max{x,0}.

Therefore equation (21) is equivalent to:

∈ argmin

∈S

sup

Q∈F

min

∈R

[−π

(

P ; x

−i

) − ζ

]

∀i ∈ {1,.., N}

(23)

From Saddlepoint theorem ( Sion’s minimax theorem

(Sion et al., 1958) ) we could exchange the order of

supremum and inﬁmum(minimum)

resulting:

∈ argmin

∈S

min

∈R

sup

Q∈F

[−π

(

P ; x

−i

) − ζ

]

∀i ∈ {1,..N}

(24)

From the moment problem theory,

sup

Q∈F

[−π

(

P ;x

−i

) − ζ

]

can be cast as

the following problem:

maximize

[−π

(P ;x

−i

) − ζ

]

dµ(vec(P ))

subject to µ ∈ M

∏

i=1

dµ(vec(P )) = 1

vec(P )dµ(vec(P )) = m

vec(P ) − m

dµ(vec(P )) ≤ s,

(25)

We can use Sion’s minimax theorem since the function

under consideration is convex-concave in its two arguments

Q ∈ F and ζ

∈ R

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

194

where M

∏

i=1

is the set of non-negative mea-

sures supported on R

∏

i=1

There is a duality theory for moment problems(see

(Wiesemann et al., 2014) and (Natarajan et al., 2009))

which implies that the following dual problem attains

the same optimal value:

min α

+ m

+ sγ

s.t α

∈ R, β

∈ R

∏

i=1

, γ

∈ R

+ vec(

P )



vec(

P ) − m



≥ [−π

(

P ; x

−i

) − ζ

]

(26)

Where the last inequality must be satisﬁed for all

P ∈ U.

By replacing the deﬁnition of [·]

min α

+ m

+ sγ

s.t α

∈ R, β

∈ R

∏

i=1

, γ

∈ R

+ vec(

P )



vec(

P ) − m



≥ −π

(

P ;x

−i

) − ζ

+ vec(

P )



vec(

P ) − m



≥ 0.

(27)

Where the last two inequalities must be satisﬁed for

all P ∈ U.

Substituting this dual formulation of

sup

Q∈F

[−π

(

P ;x

−i

) − ζ

]

into (24), we

obtain the following which we call Main Problem.

The projection of the solution set of this problem will

be the set of the equilibria that we desire.

min

,ζ

,α

,β

,γ

(α

+ m

+ sγ

)

s.t α

∈ R, β

∈ R

∏

i=1

, γ

∈ R

,ζ

∈ R

∈ S

+ vec(

P )



vec(

P ) − m



≥ −π

(

P ; x

−i

) − ζ

+ vec(

P )



vec(

P ) − m



≥ 0.

(28)

Where the last two inequalities must be satisﬁed for

all P ∈ U.

This is now a ‘classical robust optimisation prob-

lem’ and we use standard duality techniques to

simplify the semi-inﬁnite constraints. We know

that: f (p) ≥ k, ∀p ∈ U ⇔ min

p∈U

f (p) ≥ k Therefore,

using this the two robust constraints of the linear pro-

gram (28) become:

min

P ∈U

[α

+ vec(P )

vec(P ) − m

+ π

(P ; x

−i

)] ≥ −ζ

(29)

and

min

P ∈U

[α

+ vec(P )

vec(P ) − m

] ≥ 0 (30)

The left hand sides of the constraints (29) and (30)

are equivalent to the following problems (31) and

(32) respectively.

min

vec(P )

+ vec(P )

vec(P ) − m

+ π

(P ; x

−i

)

subject to W · vec(P ) ≤ h.

(31)

and

min

vec(P )

+ vec(P )

vec(P ) − m

subject to W · vec(P ) ≤ h.

(32)

In turn these programs are equivalent to:

min

vec(P ),η

+ vec(P )

+ γ

∏

i=1

∑

j=1

+ vec(P )

−i

s.t W · vec(P ) ≤ h

≥ vec(P )

− m

∀ j = 1, 2, ...N

∏

i=1

≥ m

− vec(P )

∀ j = 1, 2, ...N

∏

i=1

(33)

and

min

vec(P ),η

+ vec(P )

+ γ

∏

i=1

∑

j=1

subject to W · vec(P ) ≤ h

≥ vec(P )

− m

∀ j = 1, 2, ...N

∏

i=1

≥ m

− vec(P )

∀ j = 1, 2, ...N

∏

i=1

(34)

where η

= |vec(P )

− m

|, ∀ j = 1,2, ...N

∏

i=1

and Y

−i

) is as deﬁned in (13).

The dual problems of (33) and (34) are respectively

the following:

max

,β

,θ

− m

+ m

+ h

−δ

+ ν

+ W

− β

− Y

−i

= 0

+ ν

− γ

e ≤ 0

≥ 0, ν

≥ 0, θ

≤ 0.

(35)

max

,κ

,ξ

− m

+ m

+ h

−λ

+ κ

+ W

− β

= 0

+ κ

− γ

e ≤ 0

≥ 0, κ

≥ 0, ξ

≤ 0.

(36)

We know that:∃p ∈ U : f (p) ≥ K ⇔ max

p∈U

f (p) ≥

K. Subsequently, we substitute the last two prob-

lems (35) and (36) in the Main Problem (28).

Therefore for each player i ∈ {1, 2,...N}, ∃ α

,γ

,ζ

∈

R,β

,λ

,κ

,δ

,ν

∈ R

∏

i=1

and ξ

,θ

∈ R

such

that (x

,β

,λ

,κ

,δ

,ν

,θ

,α

,γ

,ζ

) is a mini-

mizer of:

min

,α

,β

,γ

,ζ

,λ

,κ

,ξ

,δ

,ν

,θ

sγ

= 1

− m

+ m

+ h

≥ 0

−λ

+ κ

+ W

− β

= 0

+ κ

− γ

e ≤ 0

− m

+ m

+ h

+ ζ

≥ 0

−δ

+ ν

+ W

− β

− Y

−i

= 0

+ ν

− γ

e ≤ 0

≥ 0, κ

≥ 0, ξ

≤ 0

≥ 0, ν

≥ 0, θ

≤ 0

≥ 0, γ

≥ 0.

(37)

Distributionally Robust Games with Risk-averse Players

195

whose dual is:

max

,ρ

, f

,φ

−e

− e

≤

−τ

− f

−τ

+ φ

≤ σ

+ φ

≤ −σ

W τ

≥ −σ

−f

+ g

≤ m

+ g

≤ −m

W f

≥ −h

≤ f

−i

)

≤ 0, g

≤ 0.

(38)

Condition 2 follows from strong linear programming

duality. The reverse direction (Condition 2 =⇒

Condition 1) is also holds as all steps of our proof are

based on the equivalence of the two parts.

Proof of Proposition 5.1: The second constraint of

the ambiguity set F is E

[vec

P ] = m. Therefore if

we denote with Ψ the matrix for which vec(Ψ) = m

then Ψ = E

[

P ] and with use of equation (9):

∈ argmax

∈S

inf

Q∈F

[π

[

P ]; x

−i

)] = argmax

∈S

inf

Q∈F

[π

(Ψ;x

−i

)]

= argmax

∈S

[π

(Ψ;x

−i

)]

(39)

which is equivalent to the formulation of Nash

Equilibrium (see equation (2)).

Proof of Proposition 5.2: For s = 0 the third

constraint of the ambiguity set (14) becomes:

[



vec(

P ) − m



] ≤ 0. Then, since all val-

ues inside the expectation operator E

are posi-

tive we have that E

[



vec(

P ) − m



] = 0 and that



vec(

P ) − m



= 0] = 1 which is equivalent to

Q[vec(

) − m

= 0] = 1, ∀i ∈ {1, 2,...R

∏

i=1

(40)

Therefore if s −→ 0 the third constraint of the am-

biguity set is equivalent to: Q[vec(

P ) − m = 0] = 1

which means that vec(

P ) = m for all distributions of

the ambiguity set. Therefore:

F = {Q : Q[W · vec(

P ) ≤ h] = 1, E

[vec

P ] = m, Q[vec(

P ) = m] = 1}

= {Q : Q[vec(

P ) = m] = 1}

(41)

Using the deﬁnition of Nash Equilibrium we can ﬁnd

now the equivalence between our game and a Nash

Game.

∈ argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ; x

−i

)] = argmin

∈S

[−π

(M; x

−i

)]

= argmax

∈S

[π

(M; x

−i

)]

(42)

where vec(M) = m.

Proof of Proposition 5.3: The uncertainty set U is a

singleton. Therefore the ﬁrst constraint of the ambi-

guity set (14) is equivalent to: Q[

P = C] = 1 where

C denotes the support single point, the only matrix of

set U. Thus the ambiguity set becomes:

F = {Q : Q[

P = C] = 1, E

[vec

P ] = m, Q[vec(

P ) = m] = 1}

(43)

where vec(C) = m.

Using this, the desired result follows:

argmin

∈S

sup

Q∈F

Q-CVaR

[−π

(

P ; x

−i

)] = argmin

∈S

Q-CVaR

[−π

(C;x

−i

)]

= argmin

∈S

[−π

(C;x

−i

)]

= argmax

∈S

[π

(C;x

−i

)]

(44)

ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems

196