
Promoting Cooperation and Fairness in Self-interested
Multi-Agent Systems
Ted Scully
1
and Michael G. Madden
2
1
Cork Institute of Technology, Cork, Ireland
2
National University of Ireland, Galway, Ireland
Keywords:
Cooperation, Multi-Agent System, Coalitions, Negotiation, Protocol.
Abstract:
The issue of collaboration amongst agents in a multi-agent system (MAS) represents a challenging research
problem. In this paper we focus on a form of cooperation known as coalition formation. The problem we con-
sider is how to facilitate the formation of a coalition in a competitive marketplace, where self-interested agents
must cooperate by forming a coalition in order to complete a task. Agents must reach a consensus on both the
monetary amount to charge for completion of a task as well as the distribution of the required workload. The
problem is further complicated because different subtasks have various degrees of difficulty and each agent is
uncertain of the payment another agent requires for performing specific subtasks. These complexities, cou-
pled with the self-interested nature of agents, can inhibit or even prevent the formation of coalitions in such a
real-world setting. As a solution, an auction-based protocol called ACCORD is proposed. ACCORD manages
real-world complexities by promoting the adoption of cooperative behaviour amongst agents. Through exten-
sive empirical analysis we analyse the ACCORD protocol and demonstrate that cooperative and fair behaviour
is dominant and any agents deviating from this behaviour perform less well over time.
1 INTRODUCTION
Coalition formation is one of the fundamental re-
search problems in multi-agent systems (Wooldridge,
2011). Coalition formation represents an important
means of MAS cooperation, which has associated
benefits such as enabling agents to take advantage of
their complementary capabilities, resources and ex-
pertise.
Multi-agent coalition formation represents a fun-
damental means of MAS cooperation. We consider
the problem of coalition formation in a dynamic real-
world context. The real-world problem domain that
we address consists of a marketplace populated by
self-interested agents, where each agent represents an
individual firm. In this marketplace, a task consisting
of multiple subtasks is proposed to all agents. We as-
sume that no agent is capable of individually perform-
ing an entire task. Therefore, in order to successfully
perform a task, agents must cooperate by forming a
coalition.
Successfully forming a coalition in such an envi-
ronment represents a significant research challenge.
Firstly, an agent must determine the optimal set of
agents with whom to enter into a coalition. Secondly,
if a coalition of agents is to successfully form, its
member agents must reach a consensus on the amount
to charge for completion of the task as well as the dis-
tribution of the required workload.
As we have done in previous work (Scully and
Madden, 2014), we incorporate a number of real-
world difficulties into our problem domain, to ensure
its practical applicability. We assume that agents do
not possess perfect information about one another;
rather, each agent is unsure of the value (monetary
or otherwise) that other agents place on specific sub-
tasks. An emergent difficulty is that agents may ar-
tificially inflate the financial reward they require for
performing a subtask within a coalition.
We incorporate an additional real-world complex-
ity into our problem domain with the assumption that
subtasks may have various levels of difficulty. It is re-
alistic to expect that agents performing the more diffi-
cult subtasks will expect to receive a higher financial
reward. This may lead to an increased level of com-
petition for the more difficult subtasks, which in turn
could lead to a scenario where agents are unable to
reach agreement on the distribution of tasks within a
coalition. We refer to the occurrence of such a sce-
nario as deadlock.
172
Scully, T. and Madden, M.
Promoting Cooperation and Fairness in Self-interested Multi-Agent Systems.
DOI: 10.5220/0005754001720180
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 172-180
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

We propose that the occurrence of deadlock and
the artificial inflation of financial rewards can be
avoided if the agents involved were to act in a fair and
cooperative manner. In the context of this work, an
agent exhibits fair behaviour if it honestly calculates
the financial reward for all member agents of a coali-
tion (including itself) on the basis of its personal be-
liefs. An agent is cooperative if it agrees to participate
in any coalition proposal irrespective of the subtask
it is asked to perform, assuming the financial reward
it receives for performing that subtask is adequate.
Cooperation allows us to avoid deadlock as an agent
will participate in a coalition, even though it may not
be optimal from that agent’s perspective. While the
adoption of cooperative and fair behaviour would al-
low agents to successfully form coalitions, the diffi-
culty remains that such agents are self-interested and
have to be motivated to adopt these behaviours.
We progress our previous research (Scully and
Madden, 2014) by considering two variations of the
ACCORD protocol:
1. Public ACCORD, in which each agent is required
to reveal to all others how much it would charge
for each subtask; this is analogous to an open cry
auction
2. Private ACCORD, in which agents do not have to
reveal monetary information; this is analogous to
a sealed bid auction.
2 ACCORD
In this section, we describe the ACCORD(An Auction
Integrated Coalition Formation Protocol For Dynamic
Multi-Agent Environments) protocol, which will en-
able agents to form coalitions while simultaneously
governing agent behaviour by promoting the adoption
of cooperative and fair behaviour. We consider two
variants, Public ACCORD and Private ACCORD.
2.1 Motivation for Two Versions of
ACCORD Protocol
At a fundamental level, the ACCORD protocols are
a type of auction, which are extended specifically for
the purpose of facilitating coalition formation. Before
presenting the ACCORD protocols in detail we con-
sider the issue of information privacy. Should agents
be allowed to retain as much private subtask infor-
mation as possible or should they be required to di-
vulge some of this information to the other agents in
the environment? It is interesting to note that an auc-
tion protocol can be categorised on the basis of its ap-
proach to the issue of information privacy. An auction
can be classified as either an open-cry auction, where
participants divulge private information to the public,
or a sealed-bid auction, where information remains
relatively private and is only shared with the auction-
eer. Consequently, from the perspective of providing
a coalition formation protocol, we propose that both
approaches (public and private) constitute valid solu-
tions depending on the prevailing view of information
privacy. Therefore, we provide two versions of AC-
CORD. One version requires the public revelation of
private monetary information while the other allows
each agent to retain a significant amount of their pri-
vate information.
The first approach, which we refer to as Public
ACCORD, requires each agent to reveal the mone-
tary amount it would charge for completion of each
subtask that it is interested in performing (see Section
2.3).
While in certain environmentsagents may be will-
ing to reveal private information, it is also reasonable
to assume that in some scenarios agents would pre-
fer not to divulge a full price list to competing agents.
Therefore, our second approach requires an interested
agent to propose a monetary amount to another agent
on the basis of its own private information. We refer
to this protocol as Private ACCORD, which is pre-
sented in more detail in Section 2.4.
2.2 Problem Description
The ACCORD environment contains a set of self-
interested service agents A = {a
1
, a
2
, . . . , a
m
} and an
auctioneer agent. The set S = {s
1
, s
2
, . . . , s
h
} consists
of all valid subtasks that can be performed in this mar-
ket. Any agent a
i
∈ A is capable of performing a cer-
tain set of subtasks S
a
i
, such that S
a
i
⊆ S. In addition,
a
i
maintains a set of private valuations for all possi-
ble subtasks. The function mn() denotes the monetary
valuation that a
i
places on any subtask. For example,
a
i
’s private valuation of subtask s
g
is mn(i, s
g
).
In order to perform a task, a
i
must cooperate with
one or more agents in the form of a coalition. A coali-
tion is represented by the tuple hC, salloc, palloci.
The members of the proposed coalition are contained
in the set C, such that C ⊆ A. In order for a coali-
tion to form successfully, the agents in C must reach
an agreement on the distribution of subtasks and fi-
nances within the coalition. The subtask distribution
is specified by the allocation function salloc(). For
any agent a
i
∈ C, salloc(a
i
) returns the subtask(s)
within the coalition that a
i
is to perform. The finan-
cial distribution is specified by the allocation func-
tion palloc(). Therefore, the monetary amount that a
i
Promoting Cooperation and Fairness in Self-interested Multi-Agent Systems
173

would receive for performing its specified subtask(s)
within the coalition is palloc(a
i
).
2.3 Protocol Description of Public
ACCORD
Public ACCORD can be subdivided into the following
eight stages:
1. Task Submission. A customer submits a task T
consisting of multiple subtasks to the auctioneer,
such that T ⊆ S. Subsequently, the auctioneer will
send notification of T to each agent a
i
.
2. Bidder Participation. Each agent a
i
will inform
the auctioneer of whether or not it is willing to
participate in the protocol. It is logical that a
i
will
participate iff:
∃ s
x
: s
x
∈ S
a
i
∧ s
x
∈ T
In order for a
i
to indicate its willingness to par-
ticipate in the protocol it must submit its offers
to the auctioneer. The subtask and monetary of-
fers from a
i
in relation to T are denoted by the
set B
T
a
i
= {S
T
a
i
, P
T
a
i
}. The set S
T
a
i
= {s
′
1
, s
′
2
, . . . , s
′
q
}
contains the subtasks in T that a
i
is capable of per-
forming.
The set P
T
a
i
contains a
i
’s private monetary valua-
tion for each subtask specified in S
T
a
i
. Therefore,
P
T
a
i
= {mn(i, s
′
1
), . . . mn(i, s
′
q
)}.
3. Auction Commencement. The auctioneer main-
tains a record, B
T
, of the subtask and monetary
capabilities of all agents willing to participate in
the protocol. When the auctioneer receives a re-
ply, B
T
a
i
, from a
i
it adds it to the record B
T
.
Once all replies have been collected the auction-
eer will commence a first-price sealed bid auction
for T. Subsequently, the auctioneer sends notifi-
cation of the auction deadline coupled with B
T
to
each agent a
i
that is willing to participate in the
protocol.
4. Coalition Proposal. Agents participating in the
protocol will propose coalitions to each other in
a peer-to-peer manner. Therefore, an a
i
will ini-
tially perform coalition calculation in order to
determine the optimal coalition proposal CP
a
i
=
hC, salloc, palloci. In order to construct such
a coalition proposal, a
i
must consider both the
monetary demands and subtask capabilities of all
agents. Fortunately, on receipt of B
T
, a
i
is aware
of the subtasks in T that all other agents can per-
form as well as the monetary amount each agent
will charge for completion of these subtasks.
We also assume that a
i
maintains a private estima-
tion of the level of cooperation exhibited by other
agents. It is reasonable to expect that a
i
will incor-
porate these cooperation ratings into its coalition
calculation process. For example, it would be less
likely to include an agent that constantly refuses
all coalition proposals compared to an agent that
regularly demonstrates a high willingness to ac-
cept proposals.
Once a
i
has determined the optimal member
agents C = {a
′
1
, a
′
2
, . . . , a
′
n
} it can construct and
send CP
a
i
to each member agent in C.
5. Proposal Response. An agent a
v
will assess any
coalition proposal CP
a
i
that it receives. It will is-
sue either an accept or reject notice to the propos-
ing agent. ACCORD does not control the means
by which a
v
evaluates a coalition proposal. How-
ever, it is reasonable to assume that a
v
will con-
sider both the subtask(s) and the monetary award
it is offered in CP
a
i
. It is also reasonable to expect
that a
v
will assess the value of participating in a
coalition with the other member agents in C.
6. Coalition Proposal Result. After sending a pro-
posal a
i
must await the replies from the potential
member agents of the coalition. The two possible
outcomes of this stage are:
• The failure to form the proposed coalition CP
a
i
.
If a
i
receives one or more rejections from the
member agents in C the coalition cannot be
formed. It must subsequently inform all agents
inC of the unsuccessful completion of coalition
formation. If adequate time remains before the
auction deadline expires a
i
can recommencethe
coalition proposalstage and attempt to form an-
other coalition.
• The successful formation of the proposed coali-
tion CP
a
i
. If a
i
receives an acceptance from
each of the potential member agents then the
coalition formation process has been success-
ful. It subsequently notifies each member agent
that the proposed coalition has been success-
fully formed.
7. Bid Submission. If a
i
successfully forms the pro-
posed coalition CP
a
i
it will subsequently enter the
coalition as a bid in the auction. Each agent is lim-
ited to submitting a single bid. Therefore, after a
i
has submitted a bid, it can only participate in the
proposal response stage. That is, it can only ac-
cept or reject coalitions proposed by other agents.
Once the auctioneer receivesCP
a
i
, it calculates the
total monetary reward required by the coalition to
perform T as
∑
n
d=1
palloc(a
′
d
). Subsequently, the
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
174

auctioneer records this as a sealed-price bid in the
auction.
8. Winner Notification. Once the auction deadline
expires, the auctioneer calculates the lowest mon-
etary bid. The member agents of the correspond-
ing coalition are notified that they have been suc-
cessful in obtaining the contract to collectively
perform T.
2.4 Protocol Description of Private
ACCORD
Private ACCORD facilitates agent-based coalition
formation while also placing emphasis on the reten-
tion of private information. Private ACCORD can be
subdivided into the same eight stages used to illus-
trate Public ACCORD. However, only two of these
stages differ from the formal description of Public
ACCORD. We confine our description of Private AC-
CORD to these two stages.
(2) Bidder Participation. In order for an agent a
i
to
indicate its willingness to participate in the Pri-
vate ACCORD protocol it must submit a list of its
subtask capabilities to the auctioneer. The agent
does not provide it’s private monetary valuation
to the auctioneer.
The subtask capabilities of a
i
for T are denoted by
B
T
a
i
= {S
T
a
i
}. As before, the set
S
T
a
i
= {s
′
1
, s
′
2
, . . . , s
′
q
}
denotes the subtasks that a
i
can perform.
(4) Coalition Proposal. Agents participating in the
protocol will propose coalitions to each other
in a peer-to-peer manner. Each agent a
i
, must
first perform coalition calculation in order to de-
termine its optimal coalition proposal CP
a
i
=
hC, salloc, palloci.
In order to construct such a coalition proposal, a
i
will need to consider both the monetary demands
and subtask capabilities of other agents. On re-
ceipt of B
T
, a
i
is aware of the subtasks in T that
all other agents can perform. However, because
perfect information is not available, a
i
is uncertain
of the monetary amount each agent will require as
payment for performing a given subtask.
Each agent a
i
must maintain a matrix of expected
payments for each subtask for each agent. Ini-
tially a
i
may base the monetary price of a sub-task
to other agents as equal to its own cost for per-
forming that sub-task. However, we also assume
that a
i
has basic learning abilities that allow it to
improve the accuracy of its estimations through
repeated interaction with other agents.
It is also reasonable to assume that a
i
will main-
tain a private estimation of the level of cooper-
ation exhibited by other agents. Therefore, the
cooperation rating of all participating agents is
also considered when performing coalition calcu-
lation.
Once a
i
has determined the optimal member
agents C = {a
′
1
, a
′
2
, . . . , a
′
n
} it can construct and
send CP
a
i
to each member agent in C.
2.5 Motivating Cooperation and
Fairness in the ACCORD Protocols
Cooperation is not an intrinsic attribute of a self-
interested agent. Therefore, for successful coalition
formation to occur, it is necessary to motivate a self-
interested agent to cooperate. The proposed coalition
formation protocols impose the restriction that each
agent can only submit a single bid to the auction for
a task. However, throughout the duration of the auc-
tion, an agent may receive numerous coalition pro-
posals, originating from other agents, for the same
task. Upon receipt of such a proposal an agent has
the opportunity to participate in another coalition by
issuing an acceptance. If the coalition is successfully
formed, the agent increases the probability that it will
be a member of the winning coalition. Therefore, we
hypothesise that a higher probability of success pro-
vides the agents participating in the ACCORD proto-
cols with the motivation to cooperate.
Self-interested agents attempt to maximise their
own profit. Therefore, ACCORD must ensure that
agents are fair and will not artificially inflate their own
financial rewards. Agents are provided with two dis-
incentives against acting selfishly. Firstly, by acting
selfishly, an agent reduces its probability of winning
the auction, since the more an agent inflates its finan-
cial reward the less probable it is that its bid will win
the auction. Secondly, by acting selfishly, an agent
reduces its appeal to others as a potential coalition
partner. When performing coalition calculation it is
logical to assume that an agent will attempt to min-
imise the total price charged by the coalition. There-
fore, selfish agents with inflated monetary require-
ments are less probable to be chosen as coalition part-
ners. Therefore, we hypothesise that a lower proba-
bility of success provides agents participating in the
ACCORD protocols with a disincentive against acting
selfishly.
Promoting Cooperation and Fairness in Self-interested Multi-Agent Systems
175

3 EMPIRICAL EVALUATION
The objective of this empirical evaluation is to un-
dertake a comparative analysis between Public and
Private ACCORD. We have developed a simulation
testbed to evaluate the protocols. Each experiment
measures the performance of agents adopting differ-
ent behaviours in the ACCORD simulation environ-
ment. Section 3.2 presents a brief summary of the
results of Public ACCORD. A more comprehensive
analysis of the Public ACCORD results can be found
in (Scully and Madden, 2014). Section 3.3 and 3.4
assess the impact of adopting uncooperative and self-
ish behaviour in Private ACCORD and contrast this
with the results observed from the Public ACCORD
protocol.
3.1 Experimental Methodology
Each experiment is run on 10 randomly generated
datasets. A dataset is comprised of 50 tasks, which are
auctioned in sequential order. Each task consists of 8
subtasks, chosen randomly from a set of 20 possible
subtasks. The duration of each auction is 4 minutes.
If two bids of equal value are submitted, a winner is
chosen randomly.
We referred to deadlock a situation where a subset
of agents, attempting to form a coalition, are unable
to reach agreement due to a high level of competition
for performing specific subtasks. There may be one or
more subtasks that multiple agents are capable of per-
forming and they are unable to find a resolution. We
simulate such an environment by ensuring that each
agent is capable of performing a large number of the
possible subtasks. For each new dataset a population
of 20 service agents is generated. Each agent is capa-
ble of performing 8 subtasks. By allowing each agent
to perform 8 out of the possible 20 subtasks, a high
level of competition and consequently deadlock regu-
larly occurs in our simulation environment.
The monetary amount each agent will charge for
subtask completion must also be generated. For each
subtask s
z
∈ S (where S is the set of all possible
subtasks), we have randomly selected a mean cost,
V
s
z
, with a uniform distribution between 10 and 99.
To simulate uncertainty of information, each agent
chooses the monetary amount it will charge for com-
pletion of s
z
by using a Normal distribution with a
standard deviation of 2 and a mean equal to V
s
z
.
For each of the 10 datasets generated, the perfor-
mance of 4 differing behaviour types (described later)
is contrasted. Within the simulated marketplace of 20
agents, each agent will exhibit 1 of the 4 behaviours
(5 agents for each behaviour). The subtask capabil-
ities are also represented equally amongst agents ex-
hibiting differing behaviours. This allows us to com-
pare the performance of different behaviour types in
an unbiased manner.
The result of a single experiment is arrived at
by combining the results obtained from 10 randomly
generated datasets. After each task in a dataset is auc-
tioned, the accummulated financial reward obtained
by each agent type is recorded. Therefore, the results
of a single experiment are derived by summing the
accumulated financial reward received by each agent
type across the 10 datasets.
We characterise each agent with a function accept-
ing two parameters, λ(α, β). The level of coopera-
tion exhibited by an agent is denoted by α, such that
0 ≤ α ≤ 1, α ∈ R. The level of selfishness displayed
by an agent is defined by β, such that 0 ≤ β ≤ 4, β ∈ Z.
A fair coalition proposal offers an agent an ade-
quate financial reward for performing a specific sub-
task. An adequate financial reward is greater than or
equal to the true reward the agent would expect to
receive for performing the subtask. If an agent re-
ceives a fair coalition proposal, it must subsequently
decide whether it will cooperate and join the proposed
coalition. It bases this decision on its value of α.
The parameter α represents the minimum fraction of
the most financially rewarding subtask that an agent
is willing to accept. For example, consider the task
Tr(A, D), which consists of the sub-tasks Sr(A, B),
Sr(B,C) and Sr(C, D). Assume that agent t
1
with an
α value of 0.5 expects a monetary reward of 15 units
for performing Sr(A, B) and 40 units for performing
Sr(C, D). Therefore, its α value dictates that it will
not accept a coaliton proposal that offers less than 20
(0.5 ∗ 40). Higher values of α imply lower coopera-
tion. If t
1
in our above example had an α value of
0.8 then it would only accept a coalition proposal that
offered it greater than or equal to 32 (0.8∗ 40).
An agent can exhibit selfish behaviour by artifi-
cially inflating its own financial rewards. The value
of β signifies the amount by which an agent increases
its financial reward. For example, assume the agent
t
1
with β = 0 expects a financial reward of 40 units
for performing Sr(C, D). If the configuration of t
1
is
changed so that it has β = 1 it would now expect a
financial reward of 41 units for performing Sr(C, D).
Agents with β = 0 exhibit fair behaviour because they
do not artificially inflate their own financial rewards.
3.2 Fair and Cooperative Behaviour in
Public ACCORD
We initially present the effect of different levels of
selfishness (β) in Public ACCORD. We perform 4
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
176

0
20
40
60
80
100
120
5 10 15 20 25 30 35 40 45 50
Normalised Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Coop Selfish λ(0, 1)
Coop Selfish λ(0, 2)
Coop Selfish λ(0, 3)
Coop Selfish λ(0, 4)
Figure 1: Overview of Fair (β = 0) and Selfish (β > 0) Be-
haviour for Public ACCORD.
experiments that contrast the performance of fair
(β = 0) and selfish (β > 0) agents. In Experiment 1
we contrast the performance of selfish agents where
β = 1 with fair agents (β = 0). The 4 agent types
that populate the marketplace are Cooperative Fair
(λ(0, 0)), Cooperative Selfish (λ(0, 1)), Uncoopera-
tive Fair (λ(1, 0)) and UncooperativeSelfish (λ(1, 1)).
The details for Experiments 2 — 4 are the same,
except that selfish agents use β = 2 in Experiment 2,
β = 3 in Experiment 3 and β = 4 in Experiment 4.
An overview of the results obtained by coopera-
tive agents in the Experiments 1 — 4 are presented
in Figure 1. The performance of the Cooperative
Fair λ(0, 0) agent type over Experiments 1 — 4 is
normalised as 100%. Figure 1 measures the perfor-
mance of the Cooperative Selfish agent types (λ(0, 1),
λ(0, 2), λ(0, 3), λ(0, 4)) in the Experiments 1-4 as a
percentage of the performance of the CooperativeFair
agent type. The Cooperative Fair λ(0, 0) agent type
exhibits the best performance. It is evident that an in-
crease in the value of β corresponds to a decrease in
performance.
To investigate the effect of different levels of co-
operation (α), Experiments 5 — 8 are performed.
The objective of these experiments is to contrast the
performance of cooperative (α = 0) and uncoopera-
tive (0 < α ≤ 1) agents. In Experiment 5, we ex-
amine the performance of uncooperative agents that
use α = 0.25 with cooperative agents (α = 0). The
4 agent types that populate the marketplace for Ex-
periment 5 are Cooperative Fair λ(0, 0), Cooperative
Selfish λ(0, 2), Uncooperative Fair λ(0.25, 0) and Un-
cooperative Selfish λ(0.25, 2). The details for Exper-
iments 6 — 8 are the same, except that uncooperative
agents use α = 0.5 in Experiment 6, α = 0.75 in Ex-
periment 7 and α = 1 in Experiment 8.
Figure 2 contains an overview of the results ob-
tained by fair agents in the Experiments 5 — 8. As
a fair agent reduces its value of α it experiences a
0
20
40
60
80
100
120
5 10 15 20 25 30 35 40 45 50
Normalised Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Uncoop Fair λ(0.25, 0)
Uncoop Fair λ(0.50, 0)
Uncoop Fair λ(0.75, 0)
Uncoop Fair λ(1, 0)
Figure 2: Overview of Cooperative (α = 0) and Uncooper-
ative (0 < α ≤ 1) Behaviour for Public ACCORD.
0
20
40
60
80
100
5 10 15 20 25 30 35 40 45 50
Cumulative Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Coop Selfish λ(0, 1)
Uncoop Fair λ(1, 0)
Uncoop Selfish λ(1, 1)
Figure 3: Comparing Performance of Fair (β = 0) and Self-
ish (β = 1) Behaviour for Private ACCORD.
corresponding degradation in performance. This re-
sult demonstrates the dominance‘of cooperative be-
haviour (α = 0) in Public ACCORD.
3.3 Fair/Selfish Behaviour in Private
ACCORD
The experiments undertaken in this section investi-
gate the effect of different levels of selfish behaviour
(β) amongst agents participating in Private ACCORD.
Experiments 9 — 12 are executed in the Private AC-
CORD environment. As in Section 3.2 these exper-
iments contrast the performance of fair (β = 0) and
selfish (β > 0) agents. The agent population setup for
Experiments 9 — 12 is the same as the setup used for
Experiments 1 — 4 respectively. For example, selfish
agents use β = 1 in Experiment 9, β = 2 in Experi-
ment 10, β = 3 in Experiment 11 and β = 4 in Exper-
iment 12.
The results obtained from Experiment 9 are de-
picted in Figure 3. The Cooperative Fair (λ(0, 0))
agent type significantly outperforms all other agent
types. The cooperative fair agents outperforms all
other agent types in the Experiments 10-12. These ex-
Promoting Cooperation and Fairness in Self-interested Multi-Agent Systems
177
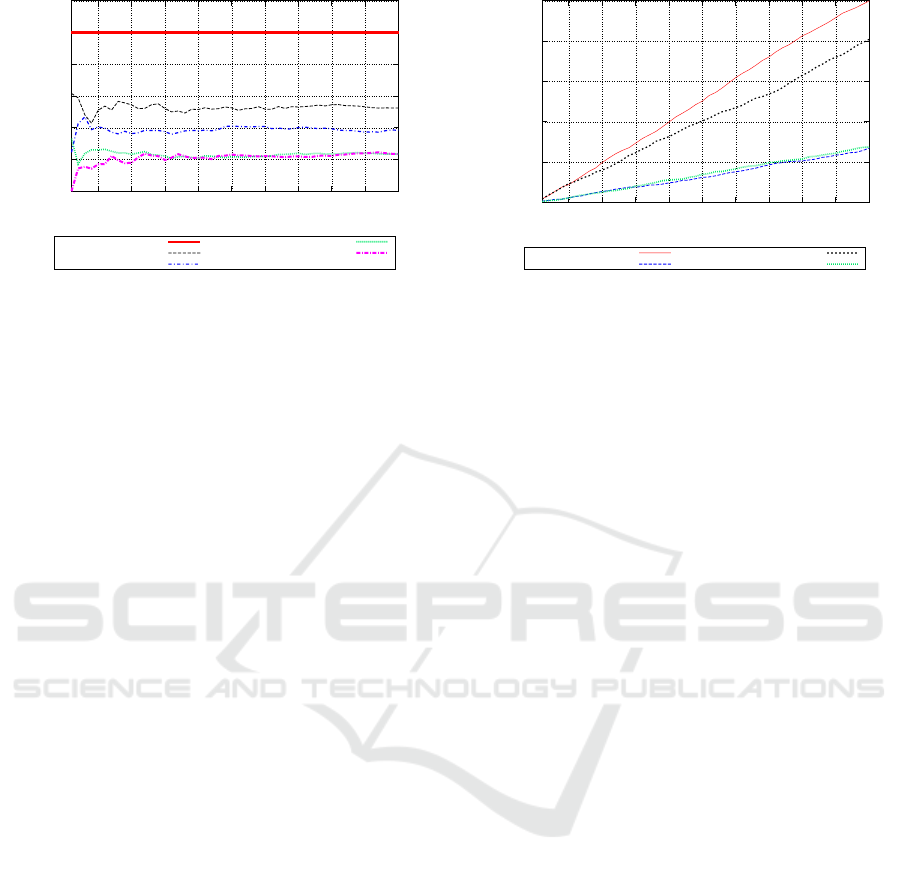
0
20
40
60
80
100
120
5 10 15 20 25 30 35 40 45 50
Normalised Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Coop Selfish λ(0, 1)
Coop Selfish λ(0, 2)
Coop Selfish λ(0, 3)
Coop Selfish λ(0, 4)
Figure 4: Overview of Fair (β = 0) and Selfish (1 ≤ β ≤ 4)
Behaviour for Private ACCORD.
periments also show a reduction in the performanceof
the selfish agent types as the value of β is increased.
Figure 4 presents an overview of the results ob-
tained by cooperative agents in Experiments 9 — 12.
The results confirm that the performance of an agent
type decreases as it increases its value of β. It is also
interesting to compare the overview of selfish varia-
tion in Private ACCORD (Figure 4 ) with that of self-
ish variation in Public ACCORD (Figure 1). The self-
ish agent types in Private ACCORD outperform their
equivalent agents in Public ACCORD, confirming that
selfish behaviour is more severely punished in Public
ACCORD than in Private ACCORD. It can also be ob-
served that the initial period of instability experienced
by agents in Figure 1 is also present in Figure 4. How-
ever, not only is the duration of the instability experi-
enced in Figure 4 longer than that experienced in Fig-
ure 1 but the degree of variance present is also more
severe. This period of instability is attributed to the
learning process that each agent must undergo. That
is, each agent must learn about the other agents with
whom they share the market-place. However, in Pub-
lic ACCORD each agent is already aware of the price
other agents require for performing specific subtasks.
Therefore, an agent need only learn about the level
of cooperation exhibited by other agents. However,
agents participating in Private ACCORD are unaware
of the financial demands of other agents and conse-
quently face a more complicated and time consuming
learning task. This is reflected in the increased insta-
bility present in Figure 4.
3.4 Cooperative/Uncooperative
Behaviour in Private ACCORD
In order to assess the impact of varying levels of un-
cooperative behaviour in Private ACCORD, 4 experi-
ments (numbered 13 — 16) are performed. The agent
population setup for these experiments is the same
0
20
40
60
80
100
5 10 15 20 25 30 35 40 45 50
Cumulative Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Coop Selfish λ(0, 2)
Uncoop Fair λ(0.25, 0)
Uncoop Selfish λ(0.25, 2)
Figure 5: Comparing Performance of Cooperative (α = 0)
and Uncooperative (α = 0.25) Behaviour for Private AC-
CORD.
as for Experiments 5 — 8. The only difference is
that Experiments 13 — 16 are run on the Private AC-
CORD simulation environment instead of the Public
ACCORD environment. Uncooperative agents use,
α = 0.25 in Experiment 13, α = 0.5 in Experiment
14, α = 0.75 in Experiment 15 and α = 1 in Experi-
ment 16.
The results obtained from Experiment 13 are de-
picted in Figure 5. As with the previous experi-
ments the Cooperative Fair (λ(0, 0)) agent type out-
performs all other agent types. It is interesting to con-
trast the results of this experiment with those obtained
from the equivalent experiment (Experiment 5) per-
formed on the Public ACCORD simulation environ-
ment. The uncooperative agent types (λ(0.25, 0) and
λ(0.25, 2)) perform better when participating in Pri-
vate ACCORD (Experiment 13) than they do in Pub-
lic ACCORD (Experiment 5). This indicates that un-
cooperative behaviour is less advantageous in Public
ACCORD than it is in Private ACCORD.
The results of experiments 14 — 16 reveal that the
cooperative fair agents remain dominant, while also
showing a gradual degradation in the performance of
the the uncooperative agents as they increase their
value of of α.
An overview of the results obtained by fair agents
in the Experiments 13 — 16 are presented in Figure
6. On examination of Figure 6 it is apparent that a sig-
nificant period of instability occurs at the commence-
ment of each of the experiments. The Cooperative
Fair (λ(0, 0)) agent type is outperformedbriefly by the
Uncooperative Fair (λ(0.25, 0)) agent type at the be-
ginning of Experiment 13. The performance of each
agent type stabilises over the duration of the experi-
ment. While the initial instability in Figure 6 is an
undesirable attribute of Private ACCORD, it is still
necessary in order for each agent to learn about the
other agents in the market-place and identify potential
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
178
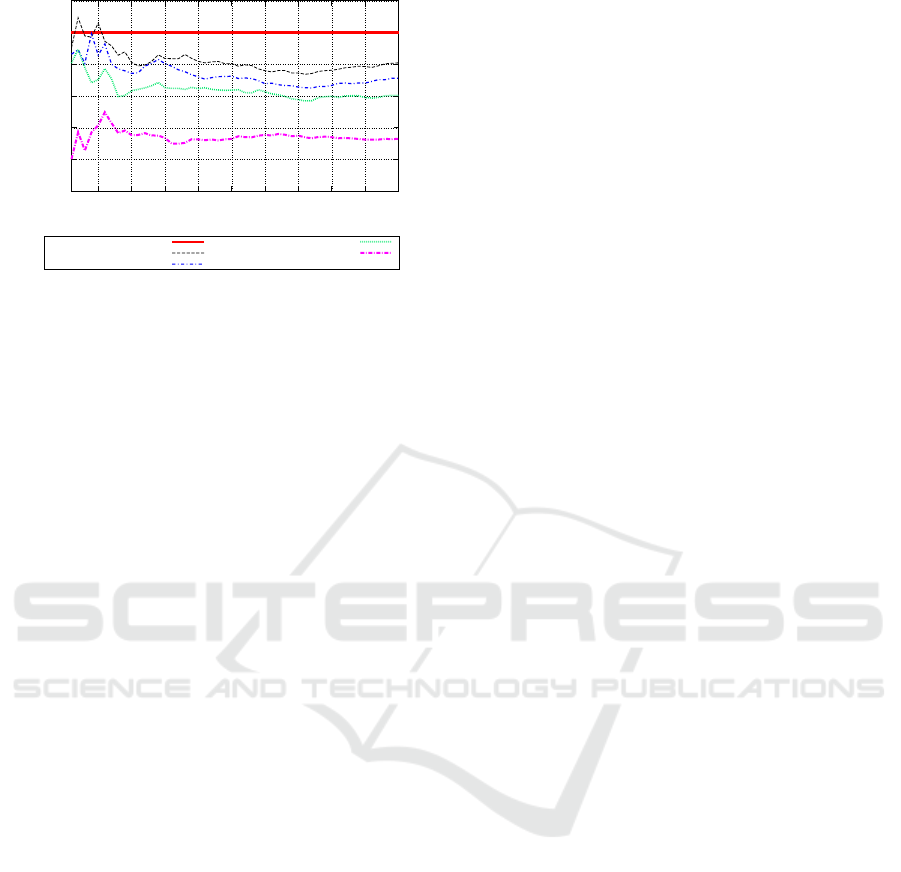
0
20
40
60
80
100
120
5 10 15 20 25 30 35 40 45 50
Normalised Financial Reward (%)
Number of Tasks
Coop Fair λ(0, 0)
Uncoop Fair λ(0.25, 0)
Uncoop Fair λ(0.50, 0)
Uncoop Fair λ(0.75, 0)
Uncoop Fair λ(1, 0)
Figure 6: Overview of Cooperative (α = 0) and Uncooper-
ative (0 < α ≤ 1) Behaviour for Private ACCORD.
partners. Apart from initially being outperformed the
Cooperative Fair (λ(0, 0)) agent type still proves to be
dominant. The instability present in Figure 6 is more
severe than that present in Figure 2, which presents an
overview of uncooperative behaviour in Public AC-
CORD. This is consistent with our previous observa-
tion that Private ACCORD experiences greater initial
instability than Public ACCORD (Section 3.3).
It is also interesting to compare the instability that
occurs in Figure 6 and in Figure 4, which presents an
overview of selfish behaviour in Private ACCORD.
The instability present in Figure 4 is visibly less se-
vere than that encountered in Figure 6. This indicates
that learning to identify uncooperative agents repre-
sents a more difficult task than learning to identify
selfish agents. This is to be expected because of the
inherent inconsistency of uncooperative behaviour.
While a selfish agent behaves selfishly all the time,
uncooperative agents may only exhibit uncooperative
behaviour occasionally (an agent with α = 0.25 may
rarely adopt uncooperative behaviour).
As expected, Figure 6 demonstrates that as an
agent increases its level of uncooperative behaviour
its performance degrades. By comparing the results
of Figure 6 and Figure 2, which assesses the impact
of uncooperative behaviour in Public ACCORD, we
can conclude that agents adopting uncooperative be-
haviour achieve a higher level of performance when
participating in Private ACCORD than they do in
Public ACCORD. This confirms that uncooperative
behaviour is less severely punished in Private AC-
CORD than in Public ACCORD.
4 RELATED RESEARCH
A important research objective in multi-agent systems
is to enable self-interested agents to successfully form
coalitions. A coalition of agents can jointly perform
a complex task, which the individual member agents
would be unable to complete in isolation (Ye et al.,
2013). Coalition formation research in MAS’s can be
broadly classified into either macroscopic or micro-
scopic coalition formation(Vassileva et al., 2002).
The macroscopic approach examines the entire
agent population and research work in this area has
focused on the development of techniques to calcu-
late the optimal coalition structure, which is the di-
vision of all agents in the environment into exhaus-
tive and disjoint coalitions (Sen and Dutta, 2000),
(Bachrach et al., 2013), (Rahwan and Ramchurn,
2009), (Iwasaki et al., 2013), (Dan et al., 2012), (Xu
et al., 2013). This work typically assumes any given
coalition has a fixed determinable value, which is uni-
versally known by all agents (Sandholm and Lesser,
1997). This assumption conflicts with one of the real-
world difficulties we incorporated into our problem
domain, namely, that agents may maintain differing
values for any subtasks, which also means they may
have differing values for any coalition.
In the microscopic approach to coalition forma-
tion each agent will reason about the process of form-
ing a coalition based on its personal information and
its perspective of the system. The work in this area
can be divided into cooperative and self-interested
multi-agent environments. Significant research at-
tention has been focused on the development of dis-
tributed coalition formation protocols for cooperative
agent environments (Toˇsi´c and Ordonez, 2012), (Ye
et al., 2013), (Smirnov and Sheremetov, 2012).
Microscopic coalition formation has also been
studied in the context of hedonic games. In such an
environment self-interested agent achieve a specific
level of satisfaction based on the coalition they join.
A number of distributed protocols have been proposed
to facilitate coalition formation in such environments
(Ghaffarizadeh and Allan, 2013), (Aziz et al., 2011),
(Genin and Aknine, 2011). A solution to a hedonic
game is the exhaustive decomposition of all agents in
an environment into coalitions.
Research has been carried out on the topic of
coalition formation in self-interested buyers markets.
One such example is the development of coalition for-
mation protocols that enable buyers, interested in pur-
chasing the same or similar products, to form coali-
tions (Tsvetovat and Sycara, 2000) (Shehory, 2000).
These protocols facilitate coalition formation, how-
ever the market that they address differs significantly
from that considered in this paper as the agents are
not in direct competition with one another.
Promoting Cooperation and Fairness in Self-interested Multi-Agent Systems
179

5 CONCLUSIONS
This paper has introduced Public and Private AC-
CORD to facilitate the process of coalition forma-
tion in dynamic real-world environments. In order
to evaluate these protocols we developed a simula-
tion testbed that was used to contrast the performance
of agents adopting different behaviours. The results
demonstrate that cooperative and fair behaviour is
dominant in our empiricial environment. This solves
the problem of artificial inflation of financial rewards
and provided a mechanism of forming coalitions that
would not suffer from deadlock.
It was also found that deviant behaviour (uncoop-
erative or selfish behaviour) was more severely pun-
ished in Public ACCORD. It was also observed that an
initial period of instability was experienced in both
Public and Private ACCORD, which corresponds to
the duration of the agent learning process. Because
Public ACCORD requires the revelation of private in-
formation, the initial instability it experienced was not
as severe as that experienced in Private ACCORD.
There is wide range of possible research avenues
for the ACCORD protocols. An undesirable property
of these protocols is the presence of an initial period
of instability. This has been attributed to the learning
process that each agent must undergo. Such instabil-
ity could potentially be exploited by uncooperative or
selfish agents. Sen & Dutta encounter a similar prob-
lem with their method of reciprocative-based cooper-
ation and effectively employed a reputation mecha-
nism as a solution. An interesting area of future work
would be to incorporate a similar reputation mecha-
nism into the ACCORD protocols. It would also be
worthwhile to observe the level of instability that oc-
curs in Public and Private ACCORD for large agent
populations. For example, is it possible that the pe-
riod of instability will increase inline with the size of
the agent population?
REFERENCES
Aziz, H., Brandt, F., and Seedig, H. (2011). Stable partitions
in additively separable hedonic games. Autonomous
Agents and Multiagent Systems, 1:183–190.
Bachrach, Y., Kohli, P., Kolmogorov, V., and Zadimoghad-
dam, M. (2013). Optimal Coalition Structure Genera-
tion in Cooperative Graph Games Finding the Optimal
Coalitional Structure. In Twenty-Seventh AAAI Con-
ference on Artificial Intelligence, pages 81–87.
Dan, W., Cai, Y., Zhou, L., and Wang, J. (2012). A Co-
operative Communication Scheme Based on Coalition
Formation Game in Clustered Wireless Sensor Net-
works. IEEE Transactions on Wireless Communica-
tions,, 11(3):1190 – 1200.
Genin, T. and Aknine, S. (2011). Constraining Self-
Interested Agents to Guarantee Pareto Optimal-
ity in Multiagent Coalition Formation Problem.
IEEE/WIC/ACM International Conferences on Web
Intelligence and Intelligent Agent Technology, pages
369–372.
Ghaffarizadeh, A. and Allan, V. (2013). History Based
Coaliton Formation in Hedonic Conext Using Trust.
International Journal of Artificial Intelligence & Ap-
plications, 4(4):1–8.
Iwasaki, A., Ueda, S., and Yokoo, M. (2013). Finding the
Core for Coalition Structure Utilizing Dual Solution.
IEEE/WIC/ACM International Joint Conferences on
Web Intelligence (WI) and Intelligent Agent Technolo-
gies (IAT), pages 114–121.
Rahwan, T. and Ramchurn, S. (2009). An anytime algo-
rithm for optimal coalition structure generation. Jour-
nal of Artificial Intelligence, 34:521–567.
Sandholm, T. and Lesser, V. (1997). Coalitions Among
Computationally Bounded Agents. Artificial Intelli-
gence: Special Issue on Economic Principles of Multi-
Agent Systems, 94:99–137.
Scully, T. and Madden, M. (2014). Facilitating Multi-
Agent Coalition Formation through Cooperation in
Self-Interested Environments. In Proceedings of Eu-
ropean Conference on Multi-Agent Systems. Springer.
Sen, S. and Dutta, P. (2000). Searching for optimal coalition
structures. Proceedings Fourth International Confer-
ence on MultiAgent Systems, pages 287–292.
Shehory, O. (2000). Coalition Formation for Large-Scale
Electronic Markets. In Proceedings of the Fourth In-
ternational Conference on MultiAgent Systems, pages
167–174. IEEE Computer Society.
Smirnov, A. and Sheremetov, L. (2012). Models of coali-
tion formation among cooperative agents: The current
state and prospects of research. Scientific and Techni-
cal Information Processing, 39(5):283–292.
Toˇsi´c, P. and Ordonez, C. (2012). Distributed protocols
for multi-agent coalition formation: a negotiation per-
spective. Active Media Technology, pages 93–102.
Tsvetovat, M. and Sycara, K. (2000). Customer Coalitions
in the Electronic Marketplace. In Fourth International
Conference on Autonomous Agents, pages 263–274.
Vassileva, J., Breban, S., and Horsch, M. (2002). Agent
Reasoning Mechanism for Long-Term Coalitions
Based on Decision Making and Trust. Computational
Intelligence, 18(4):583–595.
Wooldridge, M. (2011). Computational aspects of cooper-
ative game theory. Agent and Multi-Agent Systems:
Technologies and Applications, 6682.
Xu, B., Zhang, R., and Yu, J. (2013). Improved
Multi-objective Evolutionary Algorithm for Multi-
agent Coalition Formation. Journal of Software,
8(12):2991–2995.
Ye, D., Zhang, M., and Sutanto, D. (2013). Self-Adaptation-
Based Dynamic Coalition Formation in a Distributed
Agent Network: A Mechanism and a Brief Survey.
Parallel and Distributed Systems, 24(5):1042–1051.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
180
