Motion Artifact Reduction in Photoplethysmography using Bayesian
Classification for Physical Exercise Identification
Giorgio Biagetti, Paolo Crippa, Laura Falaschetti, Simone Orcioni and Claudio Turchetti
DII – Dipartimento di Ingegneria dell’Informazione, Universit`a Politecnica delle Marche,
Via Brecce Bianche 12, I-60131 Ancona, Italy
Keywords:
Photoplethysmography, PPG, Motion Artifact Reduction, Heart Rate, Bayesian Classification, Identification,
GMM, Expectation Maximization, Karhunen-Lo`eve Transform.
Abstract:
Accurate heart rate (HR) estimation from photoplethysmography (PPG) recorded from subjects’ wrist when
the subjects are performing various physical exercises is a challenging problem. This paper presents a frame-
work that combines a robust algorithm capable of estimating HR from PPG signal with subjects performing a
single exercise and a physical exercise identification algorithm capable of recognizing the exercise the subject
is performing. Experimental results on subjects performing two different exercises show that an improvement
of about 50% in the accuracy of HR estimation is achieved with the proposed approach.
1 INTRODUCTION
Photoplethysmography (PPG) is a non invasive tech-
nique to estimate the heart rate (HR) by measuring
the blood flow at the surface of the skin. In wearable
devices for fitness and/or daily activities this signal
needs to be monitored when motion is always present.
The subjects’ hand movements during intensive
physical exercise cause a strong motion artifact (MA)
that corrupts PPG signal, making HR monitoring
from wrist devices a challenging problem.
Many signal processing techniques have been pro-
posed to remove MA from raw PPG signal. The
most common are: independent component analysis
(Kim and Yoo, 2006), adaptive filtering techniques
(Foo, 2006; Gibbs et al., 2005), Kalman filtering
(Lee et al., 2010), wavelet based methods (Raghuram
et al., 2010), empirical mode decomposition (Raghu-
ram et al., 2014; Raghuram et al., 2012). More re-
cently combinations of a number of techniques have
been successfully used (Ram et al., 2012; Zhang et al.,
2015).
However,although an HR estimation with an aver-
age absolute error less than 2 beats per minute (BPM)
can be obtained by these latest techniques, such a
performance is limited to PPG signals recorded from
subjects during fast running.
Thus accurate HR estimation from PPG recorded
from subjects’wrist when the subjects are perform-
ing various physical exercises, such as fast running,
weightlifting, or jumping, remains a challenge.
This paper focuses on this aspect, namely MA re-
duction in PPG when subjects perform various phys-
ical exercises. In particular a physical exercise iden-
tification algorithm, based on Bayesian classification
and truncated Karhunen-Lo`eve transform (KLT) rep-
resentation, which is able to recognize the physical
exercise the subject is performing, is adopted to this
end. This algorithm is combined with a robust arti-
fact reduction algorithm, CARMA (Bac`a et al., 2015),
which can be optimized for a single physical exercise
by setting a specific tracking model. Once a set of
different tracking models are derived, the exercise the
subject is performing is automatically selected by the
identification algorithm.
The rest of the paper is organized as follows. Sec-
tion 2 reviews the CARMA algorithm. Section 3 re-
ports the physical exercise identification algorithm.
Section 4 describes the framework adopted for MA
reduction combining both CARMA and the physical
exercise identification algorithm. Section 5 discusses
experimental results. Conclusion is given in the last
section.
2 CARMA ALGORITHM
The CARMA algorithm has proven to be very effec-
tive for HR monitoring from PPG signals with sub-
jects performing a single physical exercise.
Biagetti, G., Crippa, P., Falaschetti, L., Orcioni, S. and Turchetti, C.
Motion Artifact Reduction in Photoplethysmography using Bayesian Classification for Physical Exercise Identification.
DOI: 10.5220/0005755304670474
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 467-474
ISBN: 978-989-758-173-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
467

FFT
Peak
Finder
FFT
Peak
Finder
Motion Artifact
Removal
Tracker
SVD SVD SVD
Filtering
Windowing
Hankel
FFT
Peak
Finder
HR
1
g
2
g
x
y
z
Figure 1: Flow chart of CARMA algorithm (g
1
and g
2
are
the PPG channels, x, y, z are the 3-axial accelerometer sig-
nals).
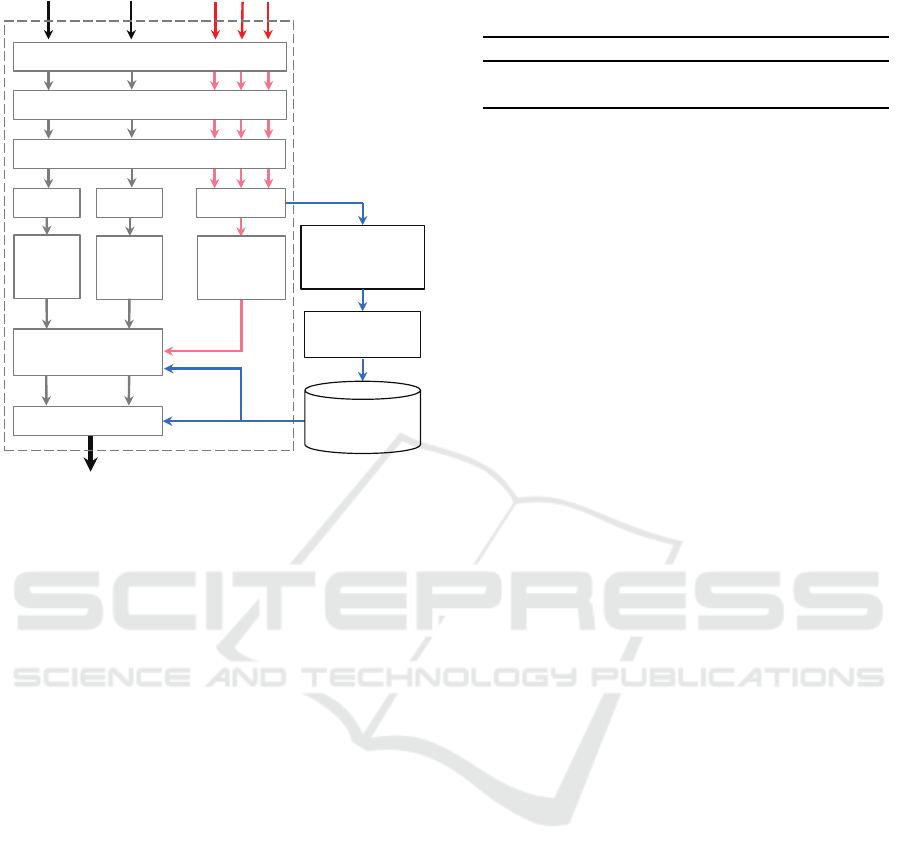
A flow chart of the algorithm is shown in Fig. 1.
It consists of the following steps: i) pre-processing
of PPG and accelerometer signals, ii) singular value
decomposition (SVD), iii) peak detection of the FFTs,
iv) MA reduction, v) tracking of the HR.
2.1 Review of Subspace Decomposition
Approach and Tracking
Given the accelerometer signals x,y,z the main objec-
tive of the algorithm is to determine the correspond-
ing subspace hSi they belong to, that is a basis S
that generates hSi. To this end let X =
h
x
(1)
... x
(L)
i
,
Y =
h
y
(1)
... y
(L)
i
, Z =
h
z
(1)
...z
(L)
i
be the Hankel
data matrices of the three signals respectively, then
the complete matrix of sample signals
H = [XY Z] (1)
can be approximated by the SVD as
H
∼
=
P
∑
i=1
λ
i
s
i
r
T
i
, (2)
where λ
i
are the singular values in decreasing order
and s
i
, r
i
the corresponding left and right singular vec-
tors.
This approximation is equivalent to assume the
signals are in the subspace
hSi = span(s
1
... s
P
) , (3)
generated by the basis S = [s
1
... s
P
] where s
1
... s
P
are
the most significative components of the motion sig-
nal, and hSi represents the subspace of motion signals
(SMS).
Considering the following model for the PPG sig-
nal
g = m+ e , (4)
where e is the HR signal, m the artifact and g the PPG
signal, as m belongs to the subspace hSi, then the cor-
responding Hankel data matrix G can be written as
G = SA+ E . (5)
Assuming the component SB of E belonging to
the subspace hSi is negligible when comparing with
the artifact component SA, that is
E ≃ S
⊥
B
⊥
, (6)
where S
⊥
= [s
P+1
,...s
N
] is orthogonal to S, it results
G = SA+ E ≃ SA+ S
⊥
B
⊥
. (7)
Now let
G = UΣV
T
(8)
be the SVD of G, where U = [u
1
...u
N
], V =
[v
1
...v
L
], and Σ is the matrix of singular values, then
the two components SA, E can be derived by selecting
the vectors u
i
that are the closest to the subspace hSi.
In order to define a physically meaningful distance
between these vectors, both s
i
and u
i
are characterized
by the central frequency of their main spectral peak,
and the distance between a vector u
i
and the subspace
hSi is defined as the shortest distance between the vec-
tor u
i
and any of the s
i
.
The set (u
i
1
...u
i
Q
) is then chosen such that the
corresponding distances are below a given threshold
ϑ, so that the subspace

U
q

= span(u
i
1
...u
i
Q
) is the
closest to the artifact subspace hSi.
As a consequence the following decomposition
G = [U
q
U
d
]

Σ
q
0
0 Σ
d

V
T
q
V
T
d

= U
q
Σ
q
V
T
q
+U
d
Σ
d
V
T
d
, (9)
with U
q
=

u
i
1
...u
i
Q

, U
d
=

u
i
Q+1
...u
i
N

, holds.
Assuming the vectors

u
i
1
...u
i
Q

belong to the
subspace hSi and posing
Σ
q
V
T
q
=
h
b
(1)
...b
(L)
i
(10)
it follows that every column of the matrix
U
q
Σ
q
V
T
q
=
h
U
q
b
(1)
...U
q
b
(L)
i
(11)
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
468

belong to hSi. Finally, comparing (7) with (9) yields
(
SA ≃ U
q
Σ
q
V
T
q
E ≃ U
d
Σ
d
V
T
d
. (12)
Having derived the representation of E, then the
HR can be found as the dominant frequency of the
first column of U
d
alone.
Whilst the artifact removal so performed is usu-
ally very good, a frequency tracking algorithm is nec-
essary to further reduce HR estimation error and to
combine the signals from the two available PPG chan-
nels.
First a check is made to determine if the extracted
frequency is a harmonic of the HR, and it is halved
or doubled according to the result being more likely.
This is done exploiting a rough estimate of the joint
probability density function (pdf) of the HR versus
the motion artifact frequency (MAF).
Then, to select the best of the two PPG channels,
the one that is closest to the previous estimate is cho-
sen. Let e
t−1
be the previous HR estimate, the current
estimate e
t
is found by
e
t
= κe
t−1
+ (1− κ) f
t
, (13)
where f
t
is the frequency of the selected peak, κ ∈
[0,1] is a weighting factor that increases as the dis-
tance of f
t
from e
t−1
increases and can be adjusted
to filter out spurious estimates while simultaneously
tracking relatively rapid HR variations.
The algorithm previously reviewed behaves well
for a single physical exercise, however it fails when
subjects perform various physical exercises, as it will
be shown in Sect. 5. To remove this limitation a set
Γ of different tracking models, specifically optimized
for various physical exercises, can be derived and au-
tomatically selected by a physical exercise identifica-
tion algorithm.
3 PHYSICAL EXERCISE
IDENTIFICATION
The algorithm developed in this section follows the
approach reported in (Biagetti et al., 2015) as it was
successfully adopted in the field of speaker identifica-
tion.
3.1 Bayesian Classification
Let us refer to a frame ξ[n], n = 0,...,N − 1, contain-
ing features extracted from the accelerometer signals.
We assume that the observations for all physical
exercises that need to be identified, are acquired and
divided in two sets, W for training and Z for testing.
For Bayesian classification, a group of Γ exer-
cises is represented by the probability density func-
tions (pdfs)
p
γ
(ξ) = p(ξ | θ
γ
) , γ = 1,2,··· ,Γ , (14)
where θ
γ
are the parameters to be estimated during
training, ξ ∈ W . Thus we can define the vector
p = [p
1
(ξ),··· , p
Γ
(ξ)]
T
. (15)
The objective of classification is to find the model θ
γ
corresponding to the exercise γ which has the maxi-
mum a posteriori probability for a given frame ξ ∈ Z.
Formally:
b
γ(ξ) = argmax
1≤γ≤Γ

p(θ
γ
| ξ)

= argmax
1≤γ≤Γ

p(ξ | θ
γ
)p(θ
γ
)
p(ξ)

. (16)
Assuming equally likely exercises (i.e. p(θ
γ
) =
1/Γ ) and noting that p(ξ) is the same for all exercise
models, the Bayesian classification is equivalent to
b
γ(ξ) = argmax
1≤γ≤Γ

p
γ
(ξ)

. (17)
Thus Bayesian identification reduces to solving the
problem stated by (17).
The most generic statistical model one can adopt
for p(ξ | θ
γ
) is the Gaussian mixture model (GMM)
(Reynolds and Rose, 1995). The GMM for the single
exercise is a weighted sum of F components densities
and given by the equation
p(ξ | θ) =
F
∑
i=1
α
i
N (ξ | µ
i
,C
i
) (18)
where α
i
, i = 1,... , F are the mixing weights, and
N (ξ | µ
i
,C
i
) represents the density of a Gaussian dis-
tribution with mean µ
i
and covariance matrix C
i
. It
is worth noting that α
i
must satisfy 0 ≤ α
i
≤ 1 and
∑
F
i=1
α
i
= 1.
θ (the index γ is omitted for the sake of notation
simplicity) is the set of parameters needed to specify
the Gaussian mixture, defined as
θ = {α
1
,µ
1
,C
1
,..., α
F
,µ
F
,C
F
} . (19)
The usual choice for solving estimate of the mix-
ture parameters is the expectation maximization (EM)
algorithm.
The EM algorithm is based on the interpretation
of W as incomplete data and H as the missing part
of the complete data X = {W ,H }. In general the
EM algorithm computes a sequence of parameter esti-
mates

ˆ
θ(p) , p = 0, 1,...

by iteratively performing
two steps:
Motion Artifact Reduction in Photoplethysmography using Bayesian Classification for Physical Exercise Identification
469

• Expectation step: compute the expected value of
the complete log-likelihood, given the training set
W and the current parameter estimate
ˆ
θ(p). The
result is the so-called auxiliary function
Q

θ|
ˆ
θ(p)

= E

log[p(W ,H |θ)]|W ,
ˆ
θ(p)

.
(20)
• Maximization step: update the parameter estimate
ˆ
θ(p+ 1) = argmax
θ

Q

θ|
ˆ
θ(p)

(21)
by maximizing the Q-function.
Recently, Figuereido et al. (Figueiredo and Jain,
2002) suggested an unsupervised algorithm for learn-
ing a finite mixture model from multivariate data, that
overcomes the main lacks of the standard EM ap-
proach, i.e. sensitiveness to initialization and selec-
tion of number F of components.
This algorithm integrates both model estimation
and component selection, i.e. the ability of choos-
ing the best number of mixture components F accord-
ing to a predefined minimization criterion, in a single
framework.
3.2 Bayesian Classification by
Truncated KLT Representation
For a sampling rate of 125 Hz a good choice of N is
400 (Zhang et al., 2015). Although the Figuereido’s
EM algorithm behaves well with multivariate random
vectors, a too large amount of training data would be
necessary to estimate the pdf p(ξ | θ
γ
) and, in any
case, with such a dimension the estimation problem
is impractical.
In order to face the problem of dimensionality, the
usual choice (Jain et al., 2000) is to reduce the vector
ξ to a vector k
M
of lower dimension by a linear non-
invertible transform H (a rectangular matrix) such that
k
M
= H ξ , (22)
where ξ ∈ R
N
, k
M
∈ R
M
, H ∈ R
M× N
, and M ≪ N.
It is well known that, among the allowable linear
transforms H : R
N
→ R
M
, the Karhunen-Lo`eve trans-
form truncated to M < N orthonormal basis functions,
is the one that ensures the minimum mean square er-
ror.
To this end, let us consider the vector ξ[n], n =
0,... , N − 1, as an observation of the N × 1 real
random vector ξ = [ξ
1
,..., ξ
N
]
T
with autocorrelation
function R
ξξ
.
Once R
ξξ
is estimated, an orthonormal set
{φ
1
,..., φ
N
}, can be derived so that the KLT of ξ is
given by the couple of equations (Fukunaga, 1990)
k = Φ
T
ξ , (23)
ξ = Φ k , (24)
where k = [k
1
,..., k
N
]
T
is the transformed random
vector.
In order to reduce the dimension of such a repre-
sentation, let us rewrite (24) as:
ξ = Φ k = Φ
M
k
M
+ Φ
η
k
η
= ξ
M
+ η
ξ
, (25)
where Φ = [Φ
M
, Φ
η
], being Φ
M
= [φ
1
,..., φ
M
] the
eigenvectors corresponding to the most significative
eigenvalues, k
M
∈ R
M
.
In (25)
ξ
M
= Φ
M
k
M
(26)
is the truncated expansion, and
η
ξ
= Φ
η
k
η
(27)
is the error or residual.
The truncation is equivalent to the approximations
ξ ≈ ξ
M
, k ≈ k
T
=

k
M
0

, (28)
thus, as k
M
is given by
k
M
= Φ
T
M
ξ , (29)
comparing with (22) yields H = Φ
T
M
.
Given a group of Γ exercises, let us define the pdfs
p
γ
(k
T
) = p(k
T
| θ
γ
) , γ = 1,2,...,Γ , (30)
where k
T
is the truncation of k. Consequently the vec-
tor
˜p = [p
1
(k
T
),..., p
Γ
(k
T
)]
T
(31)
represents an approximation of the vector p in (15).
Thus (17) becomes:
b
γ(ξ) = argmax
1≤γ≤Γ

p
γ
(k
T
)

. (32)
However, due to truncation, we have
p
γ
(k
T
) = p
γ
(k
M
) δ(k
η
) , (33)
so it results
b
γ(ξ) = argmax
1≤γ≤Γ

p
γ
(k
M
) δ(k
η
)

= argmax
1≤γ≤Γ

p
γ
(k
M
)

. (34)
As you can see comparing (34) with (17), the dimen-
sionality of classification problem is reduced from N
to M, with M < N.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
470

FFT
Peak
Finder
FFT
Peak
Finder
Motion Artifact
Removal
Tracker
HR
SVD SVD SVD
Filtering
Windowing
Hankel
FFT
Peak
Finder
Singular Value
Spectrum
Normalization
Bayesian
Classifier
CARMA
Parameters
Table
1
g
2
g
x
y
z
Figure 2: Flow chart of proposed framework (g
1
and g
2
are the PPG channels, x, y, z are the 3-axial accelerometer
signals).
4 COMBINING CARMA AND
PHYSICAL EXERCISE
IDENTIFICATION
ALGORITHMS
A schematic diagram of the framework adopted for
MA reduction combining both CARMA and physical
exercise identification algorithm, is shown in Fig. 2.
By denoting with H
t
∈ R
N×3L
the data matrix of
the accelerometer signals at each time instant t the HR
h
t
is estimated, in order to apply the physical exercise
identification algorithm, a feature vector ξ
t
has to be
derived from this matrix.
We noticed that different types of exercises lead to
different distributions of the energy of the accelerom-
eter signals among its eigenvectors. Thus, a suit-
able candidate for identifying the type of exercise
is the normalized spectrum of singular values Λ =
[λ
1
...λ
N
], so as to avoid dependence on the intensity
of the exercise. Therefore we choose ξ
t
= Λ
t
/||Λ
t
||
where || · || represents the norm of a vector.
This normalized singular value spectrum can eas-
ily be computed immediately after having performed
the SVD on the accelerometer signals, and used as
input to the Bayesian classifier after a KLT-based di-
mensionality reduction from N = 400 to M = 10. The
output of the classifier is used to choose the param-
Table 1: Performance (sensitivity, specificity, precision, and
accuracy) of the exercise type identifier evaluated on the
whole testing set.
class sens. spec. prec. acc.
1 84.94% 92.02% 93.56% 87.94%
2 92.02% 84.94% 81.74% 87.94%
eters of both the MA remover and the HR tracker,
by looking them up on a hand-tuned table carefully
written for each exercise type. For instance, exer-
cises involving running require stronger MA removal,
thus the dimension of SMS P is set to 10 for them,
and just to 2 for other types. Running also require
second-harmonic detection, while this is unnecessary
for other exercises. A number of other tracking pa-
rameters need also be tuned accordingly.
Since the detection of the exercise type is per-
formed for every frame, the tracking parameters are
adjusted on the fly and the subject is free to move
from one exercise to another, and the system will try
to follow.
5 EXPERIMENTAL RESULTS
The experiments were carried out on datasets
recordedwhen subjects performed two different phys-
ical exercises. A total of 23 signals were available
(Zhang et al., 2015), 12 recorded while subjects per-
formed running drills (classified as type 1 exercise),
11 recorded while subjects performed a mixture of
other activities (classified as type 2 exercise). Of
these, the first 6 of each class were used for train-
ing the classifier, the others for testing purposes. The
signals, sampled at 125 Hz were processed using a
sliding window 8s long (corresponding to W = 1000
samples), shifted by 2 s for each frame. The Han-
kel matrices were built using N = 400 so that L =
W − N + 1 = 601.
A first test was devoted to check the effectiveness
of the chosen motion eigenvalue spectrum as a signif-
icant feature to discriminate the exercise type. Re-
sults are shown in Table 1, and we deem an accu-
racy approaching 88% to be satisfactory, especially
since in many signals there are tails where the sub-
ject stood essentially still, making classification there
quite pointless. For reference, the two classes were
modeled using just 5 and 6 Gaussians in the GMM.
The final test involved executing the complete al-
gorithm on all the available data. The average HR
error for each signal is reported in Table 2. The up-
per two blocks report results obtained without using
the automatic classifier, and setting the tracking pa-
rameters to those optimized for class 1 and class 2
Motion Artifact Reduction in Photoplethysmography using Bayesian Classification for Physical Exercise Identification
471

0 50 100 150 200 250 300
frequency [min
-1
]
0
50
100
150
200
class 2, signal 8
time [s]
0 50 100 150 200 250 300
mode
1
2
classifier disabled - mode forced to 1
0 50 100 150 200 250 300
frequency [min
-1
]
0
50
100
150
200
class 1, signal 7
time [s]
0 50 100 150 200 250 300
mode
1
2
classifier disabled - mode forced to 1
Figure 3: Example of tracking obtained with CARMA
alone.
respectively. The bottom block reports the results ob-
tained with the proposed automatic classifier. As can
be seen, it nearly always succeeds in selecting the best
of the two results.
Moreover, Figs. 3 and 4 show the algorithm track-
ing capabilities respectively without and with auto-
matic parameter selection for a couple of significant
cases.
In these figures, black lines represent the reference
(true) HR obtained by simultaneous ECG recordings,
the green lines are the estimate obtained by the pro-
posed algorithm. Colored stars represent the frequen-
cies of the spectral peaks extracted from the singular
vectors (only first two are shown) which remain after
MA removal. These are the values the tracking algo-
rithm tries to follow. Blue circles are the MA frequen-
cies (only the strongest is shown). The bottom pane
of each figure shows the automatically identified ex-
ercise type for each input frame. As can be seen, most
errors occur only during the initial stage of the exer-
cise or when the subject is at rest (low or null MA
frequency).
0 50 100 150 200 250 300
frequency [min
-1
]
0
20
40
60
80
100
120
140
160
180
200
class 2, signal 8
time [s]
0 50 100 150 200 250 300
mode
1
2
0 50 100 150 200 250 300
frequency [min
-1
]
0
20
40
60
80
100
120
140
160
180
200
class 1, signal 7
time [s]
0 50 100 150 200 250 300
mode
1
2
Figure 4: Example of tracking obtained combining
CARMA and exercise identification algorithm.
As can be seen e.g. in the top plot of Fig. 3, with-
out the classifier the tracker might be driven off-track
when the subject performs a different exercise, lead-
ing to huge errors. This does not happen with the
classifier enabled, as can be seen in the top plot of
Fig. 4. Unfortunately, there can be some points where
the classification fails (bottom plot of Fig. 4), but this
does not cause the tracker to go completely astray and
the loss in accuracy is contained.
A summary of the results, reporting the average
tracking error over the whole datasets, are shown in
Table 3.
These results clearly show that once the mode is
set (corresponding to a tracking model specifically
optimized for a single physical exercise) the mini-
mum mean error the CARMA algorithm is able to
reach is 10.25 BPM (with mode set to 1), while us-
ing the physical exercise identification algorithm the
mean error drastically drops to 5.60 BPM.
Of course, the automatic exercise classifier cannot
be expected to improve tracking results for the class
of signals that matches the one for which the fixed-
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
472

Table 2: Average tracking error for the different signals. Shaded cells represents signals that were also used in the training of
the classifier.
class
Heart Rate Error [BPM] — without classifier — mode fixed at 1
1 2 3 4 5 6 7 8 9 10 11 12
1 2.58 1.48 1.40 2.47 1.54 3.24 1.01 1.19 0.93 6.28 1.68 3.30
2
4.01 30.16 54.94 14.24 25.20 6.63 4.15 38.20 16.10 3.66 1.03
class
Heart Rate Error [BPM] — without classifier — mode fixed at 2
1 2 3 4 5 6 7 8 9 10 11 12
1 15.01 21.91 41.52 3.62 1.53 37.71 3.51 21.01 0.98 67.50 1.70 4.41
2
8.50 20.70 2.85 9.05 23.09 6.62 3.48 3.98 18.12 3.37 1.01
class
Heart Rate Error [BPM] — with automatic classifier
1 2 3 4 5 6 7 8 9 10 11 12
1 3.37 2.79 1.76 2.49 1.54 3.44 1.28 1.84 0.96 6.65 1.64 3.41
2
8.32 13.65 2.86 9.06 23.88 7.15 3.63 3.98 17.58 3.38 1.02
Table 3: Performance of the HR tracker evaluated on the
whole dataset with the original CARMA algorithm and with
and without the addition of the exercise type classifier. Data
are in beats per minute.
class
mode 1
error
mode 2
error
automatic
error
1 2.26 18.37 2.60
2 18.03 9.16 8.59
mean 10.15 13.77 5.60
mode algorithm was optimized, though a minor im-
provement was still achieved for class 2, which com-
prises a variety of exercises which might sometimes
resemble running (class 1). For the first class, only a
minor increase in the average error occurs do to a few
misclassified frames, but the average error of the two
classes still manifest a significative improvement.
6 CONCLUSIONS
In this paper we propose a general framework to
reduce MA in PPG when subjects perform various
physical exercises.
Experimental results show that currently adopted
algorithms for artifact removal behave well when sub-
jects perform a single exercise, while fail when sub-
jects perform various physical exercises.
Using the physical exercise identification algo-
rithm proposed in this work gives a significative im-
provement (more than 50%) in the average error of
the HR estimation for different classes of exercises.
REFERENCES
Bac`a, A., Biagetti, G., Camilletti, M., Crippa, P.,
Falaschetti, L., Orcioni, S., Rossini, L., Tonelli, D.,
and Turchetti, C. (2015). CARMA: A robust motion
artifact reduction algorithm for heart rate monitoring
from PPG signals. In 23rd European Signal Process-
ing Conference (EUSIPCO 2015), pages 2696–2700.
Biagetti, G., Crippa, P., Curzi, A., Orcioni, S., and
Turchetti, C. (2015). Speaker identification with short
sequences of speech frames. In 4th International
Conference on Pattern Recognition Applications and
Methods (ICPRAM 2015), volume 2, pages 178–185.
Figueiredo, M. A. F. and Jain, A. K. (2002). Unsuper-
vised learning of finite mixture models. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
24(3):381–396.
Foo, J. Y. A. (2006). Comparison of wavelet transforma-
tion and adaptive filtering in restoring artefact-induced
time-related measurement. Biomedical Signal Pro-
cessing and Control, 1(1):93–98.
Fukunaga, K. (1990). Introduction to statistical pattern
recognition. Academic Press.
Gibbs, P. T., Wood, L. B., and Asada, H. H. (2005). Active
motion artifact cancellation for wearable health mon-
itoring sensors using collocated MEMS accelerome-
ters. In Smart Structures and Materials, volume 5765,
pages 811–819. International Society for Optics and
Photonics.
Jain, A. K., Duin, R. P. W., and Mao, J. (2000). Statistical
pattern recognition: A review. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 22(1):4–
37.
Kim, B. S. and Yoo, S. K. (2006). Motion artifact reduction
in photoplethysmography using independent compo-
nent analysis. IEEE Transactions on Biomedical En-
gineering, 53(3):566–568.
Lee, B., Han, J., Baek, H. J., Shin, J. H., Park, K. S., and Yi,
W. J. (2010). Improved elimination of motion artifacts
from a photoplethysmographic signal using a Kalman
smoother with simultaneous accelerometry. Physio-
logical Measurement, 31(12):1585.
Raghuram, M., Madhav, K. V., Krishna, E. H., Koma-
lla, N. R., Sivani, K., and Reddy, K. A. (2012).
Motion Artifact Reduction in Photoplethysmography using Bayesian Classification for Physical Exercise Identification
473

HHT based signal decomposition for reduction of mo-
tion artifacts in photoplethysmographic signals. In
IEEE Int. Instrumentation and Measurement Technol-
ogy Conf. (I2MTC), pages 1730–1734.
Raghuram, M., Madhav, K. V., Krishna, E. H., and Reddy,
K. A. (2010). Evaluation of wavelets for reduction of
motion artifacts in photoplethysmographic signals. In
10th Int. Conf. Information Sciences Signal Process-
ing and their Applications (ISSPA), pages 460–463.
Raghuram, M., Sivani, K., and Reddy, K. A. (2014). E2MD
for reduction of motion artifacts from photoplethys-
mographic signals. In Int. Conf. Electronics and Com-
munication Systems (ICECS), pages 1–6.
Ram, M. R., Madhav, K. V., Krishna, E. H., Komalla, N. R.,
and Reddy, K. A. (2012). A novel approach for motion
artifact reduction in PPG signals based on AS-LMS
adaptive filter. IEEE Transactions on Instrumentation
and Measurement, 61(5):1445–1457.
Reynolds, D. and Rose, R. (1995). Robust text-independent
speaker identification using Gaussian mixture speaker
models. IEEE Transactions on Speech and Audio Pro-
cessing, 3(1):72–83.
Zhang, Z., Pi, Z., and Liu, B. (2015). TROIKA: A gen-
eral framework for heart rate monitoring using wrist-
type photoplethysmographic signals during intensive
physical exercise. IEEE Transactions on Biomedical
Engineering, 62(2):522–531.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
474