XML Labels Compression using Prefix-encodings

Hanaa Al Zadjali and Siobhán North

Department of Computer Science, The University of Sheffield, Sheffield, U.K.

Keywords: XML Labels, XML Compression, Encoding Methods, Prefix Encoding.

Abstract: XML is the de-facto standard for data representation and communication over the web, and so there is a lot

of interest in querying XML data and most approaches require the data to be labelled to indicate structural

relationships between elements. This is simple when the data does not change but complex when it does. In

the day-to-day management of XML databases over the web, it is usual that more information is inserted over

time than deleted. Frequent insertions can lead to large labels which have a detrimental impact on query

performance and can cause overflow problems. Many researchers have shown that prefix encoding usually

gives the highest compression ratio in comparison to other encoding schemes. Nonetheless, none of the

existing prefix encoding methods has been applied to XML labels. This research investigates compressing

XML labels via different prefix-encoding methods in order to reduce the occurrence of any overflow problems

and improve query performance. The paper also presents a comparison between the performances of several

prefix-encodings in terms of encoding/decoding time and compressed code size.

1 INTRODUCTION

Due to its flexible, self-describing nature, eXtensible

Mark-up Language (XML) has become the de-facto

standard for data representation and transformation

over the web but, again due to its self-describing

nature, it is verbose. Moreover, throughout the

lifecycle of an XML document there can be arbitrary

insertions of new nodes. Various methods have been

proposed to improve the storage and retrieval of XML

data in a dynamic environment. Among them a

variety of dynamic XML labelling schemes intended

to speed up query processing. Unfortunately, almost

all the existing dynamic labelling schemes suffer

from a linear growth rate of label size under

arbitrary/frequent node insertions which may cause

an overflow problem.

The aim of this paper is to study the possibility of

compressing XML labels to reduce the occurrence of

any overflow problems. Although several encoding

methods have been applied by existing XML

labelling schemes to store XML labels, prefix-

encoding techniques were not among them.

Therefore, this paper tests and compares the

performance of many prefix encoding methods in

terms of compressing XML labels.

This paper is structured as follows: Section 2

briefly describes XML labelling schemes and section

3 considers how the generated labels are encoded in

different label storage schemes. Section 4 defines the

overflow problem. Section 5 describes various prefix-

encoding methods used for compressing XML labels

to overcome the limitation of the current label storage

schemes. The experimental validation of the

performance of these prefix-encoding techniques in

terms of encoding/decoding time and compressed

code size is illustrated in section 6. Finally section 7

concludes this paper with the results.

2 XML LABELLING SCHEMES

An XML document can be represented as an ordered

tree structure in which nodes represent elements and

edges represent the structural relationships (e.g.

Parent/Child and Ancestor/Descendant). An XML

labelling scheme assigns a unique identifier to each

node in such a way that structural relationships

between nodes can be determined directly from these

labels, ideally all structural relationships.

In general, XML labelling schemes can be

classified into four categories: interval-based, prefix-

based, multiplicative, and hybrid labelling schemes.

With the available data on frequently updated XML

applications it is difficult to determine in advance the

number of possible future updates and consequently

Zadjali, H. and North, S.

XML Labels Compression using Preﬁx-encodings.

In Proceedings of the 12th International Conference on Web Information Systems and Technologies (WEBIST 2016) - Volume 1, pages 69-75

ISBN: 978-989-758-186-1

the initial size of intervals in interval-based labelling

schemes which leave space for insertions. Whereas

constructing labels in multiplicative labelling schemes

which can easily cope with insertions and hybrid

labelling schemes are computationally expensive and

complex (Haw and Lee, 2011). For these reasons,

prefix based labelling approaches appear to be more

suitable for dynamic XML data (Sans and Laurent,

2008). Therefore, this research concerns prefix

labelling schemes where the labelling summarizes both

the position of the node in the tree and also maintains

the document order during updating.

The first prefix labelling scheme which

considered document order was introduced by

(Tatarinov et al., 2002) and is called Dewey labelling

scheme. It assigns integer labels based on the Dewey

decimal classification system for libraries. Although

this scheme is the most widely used (He, 2015) in

XML query processing since it easily identifies the

structural relationship between XML nodes, it does

not support node insertion.

Recently many prefix-based XML labelling

schemes have been proposed in the literature to support

node insertions amongst them the SCOOTER labelling

scheme (O’Connor and Roantree, 2012). Unlike

Dewey, SCOOTER labels are based on quaternary

strings and represent node order lexicographically

rather than numerically. However, like all dynamic

labelling schemes, SCOOTER suffers from what is

called the overflow problem in certain circumstances

(Ghaleb and Mohammed, 2013).

3 ENCODING METHODS

A key factor for all dynamic XML labelling schemes

is how their labels are physically encoded, decoded

and stored in a computer. In the logical representation

of prefix labelling schemes there is always a delimiter

“.” but this delimiter is encoded and stored separately

from the label value (Li et al., 2008). Therefore, the

logical interpretation of a label in the computer

immediately affects the label size on disk as well the

computational cost of encoding/decoding between

the logical and physical representations (O’Connor

and Roantree, 2013).

All existing dynamic labels storage schemes can

be categorised into four classes: length fields, control

tokens, separators, and prefix-free codes.

3.1 Length Field

Concept of a length field is a field to store the length

of a node label (as a fixed length bit number) directly

before the node label value. The length of labels can

vary widely depending on the node’s position within

the XML tree. Since XML trees are arbitrarily wide

and arbitrarily deep there restriction on the number of

nodes might be inserted later, as a consequence in a

dynamic XML the number of node insertions is

limited to the capacity of the fixed length field

yielding to the overflow problem.

3.2 Control Tokens

Control tokens are tokens used to indicate the position

of a label value within a specific-level interval and

these tokens are used to determine how the

subsequent bit sequence of the label value is

interpreted. An example of control tokens is UTF-8

(Yergeau, 2003) which is employed by the Dewey

labelling scheme to encode Dewey labels, where each

component of Dewey path is encoded in UTF-8 and

then concatenated together in the same path order

(Tatarinov et al., 2002). However, this encoding

method causes overflow when a code value goes

beyond 2

3.3 Separator

In prefix based labelling schemes a separator “.” is

usually encoded and stored separately from the label

itself. In a separator storage scheme a predefined bit

sequence is reserved as a delimiter and not a part of

the label value. For instance, the quaternary encoding

QED (Li and Ling, 2005) and SCOOTER (O’Connor

and Roantree, 2012) employed their own separator

storage scheme in which the digit “0” is used only for

separators and therefore the separator code size

remain constant no matter how big the label size

might become. This approach results in slow bit-by-

bit or byte-by-byte comparison operation during

decoding because of the process needed to recognize

bit “0” or “00” as a separator rather than the binary

representation of the code itself. Consequently, it

degrades query performance.

3.4 Prefix-free Codes

Prefix-free codes are based on the (Elias, 1975)

proposition that a prefix set S is said to be a prefix

code if and only if no member of S is the beginning

of another. A prefix-free code approach often requires

fewer bits to represent a label than a control token

scheme since the prefix-free codes can be adjusted

according to the number of members within a prefix

set (Härder et al., 2007). An example of a dynamic

labelling scheme that uses prefix-free codes is

WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies

ORDPATH (O'Neil et al., 2004). However, the

ORDPATH compression technique makes the

decoding process in ORDPATH more time

consuming.

4 OVERFLOW PROBLEM

There are two main reasons that cause re-labelling

nodes when XML is updated (O’Connor and

Roantree, 2013). The first reason is when arbitrary

dynamic node insertions are not enabled by the node

insertion algorithms within a labelling scheme, such

as in Dewey labelling scheme (Tatarinov et al., 2002).

The other reason is the overflow problem produced

by a labelling scheme due to the label storage scheme

used for encoding XML labels, such as in ORDPATH

(O'Neil et al., 2004) and SCOOTER (O’Connor and

Roantree, 2012).

The overflow problem relates to the label storage

scheme used to encode and store label values. If there

is insufficient storage space to accommodate a new

node label, a part of the new label might be lost

resulting in incorrect and possibly duplicate labels.

This is referred to as an overflow problem. When the

problem occurs the entire tree has to be re-labelled; a

costly process which is always undesirable. It is to

avoid re-labelling that so many dynamic labelling

schemes have been devised.

Node labels are stored either as fixed-length or

variable length binary numbers at implementation.

Fixed-length labels are not scalable as the whole tree

has to be re-labelled when all the assigned bits have

been used up otherwise overflow will occur. On the

other hand, using variable length necessitates the use

of length field storage scheme which also subject to

overflow as described in section 3.1.

Prefix labelling schemes; in particular, suffer

from the overflow problem since they are structured

so that the label of every ancestor is included in each

label. This has the advantage of speeding up the

identification of relationships between nodes but at a

cost in label size.

This research investigates the possibility of

reducing the overflow or complete re-labelling

occurrences by compressing label size. Several

alternative prefix encoding methods have been

investigated to this end.

5 PREFIX ENCODING

METHODS

One of the most popular data compression techniques

currently is prefix coding (Karpinski and Nekrich,

2009). A prefix code is a variable-size code suitable

for coding a set of integers whose size is unknown

beforehand. Many researchers such as (Walder et al.,

2012) and (Bača et al., 2010) have shown that prefix

encoding approaches give highest compression ratio

in comparison to other encoding schemes.

In this paper several prefix coding approaches are

used for first time to compress XML nodes labels,

where each component of a label path is encoded

separately and then concatenated (the separators are

omitted).

5.1 Fibonacci of Order m ≥ 2

Based on Fibonacci numbers (F

), the Generalised

Fibonacci code of order

m ≥ 2 was introduced in

(Apostolico and Fraenkel, 1987) and states that for

each non-negative integer value

N there is exactly one

unique binary code of the form:

=







,



∈



0,1



,0≤≤





(1)

Such that there is no (

m) consecutive 1-bits within

the summation result of Fibonacci numbers of order

m; whereas each Fibonacci code ends up with exactly

(m) consecutive 1-bits.

O’Connor used Fibonacci-Zeckendorf principle

(O’Connor and Roantree, 2013) for encoding and

decoding the length field of a label value.

Nevertheless, Fibonacci-Zeckendorf representation

only compresses the length field part of the encoded

labels and so the labels codes still subject to overflow

in case of frequent nodes insertions.

5.2 Lucas Coding

Lucas numbers (L

) introduced by Edouard Lucas

(MacTutor, 1996) based on Fibonacci sequence

properties and so coding theorems for Lucas numbers

correspond to Fibonacci coding (of order 2)

theorems. Equation 2 below represents the

Zeckendorf theorem for Lucas numbers applied in

this paper. Although the Lucas coding algorithm

exists, no one has implemented it for encoding. In this

paper, the Lucas coding method is applied (for first

time) to compress XML labels.

=











,



∈



0,1





(2)

XML Labels Compression using Preﬁx-encodings

suchthat









=0,



 ≥ 0









= 0

5.3 Elias-delta Coding

Introduced by Peter Elias (Elias, 1975), the Elias-

delta code is one of the most commonly used prefix

codes defined as follow: for each positive integer

value N the Elias-delta code E(N) = S(N) ⊕ L(N) ⊕

B’(N) ; where:“⊕”means concatenation.

B(N) is the

binary representation of

N excluding insignificant 0-

bits (at the left of the binary number) and

B’(N) is

B(N) without the foremost 1-bit (most-left 1-bit).

L(N) is the length of B(N); i.e. number of bits of B(N),

and S(N)

is a sequence of 0-bits of size equals to the

length of

L(N) -1.

(Williams and Zobel, 1999) applied Elias-delta

codes to store integers in compressed form in order to

improve the performance of disk access and data

retrieval. Elias-delta was also utilised by (Scholer et

al., 2002) for compressing inverted indices to speed

up the query performance and query evaluation.

5.4 Elias-Fibonacci of Order 2

Elias-Fibonacci code introduced by (Walder et al.,

2012) as a combination of Elias-Delta code and

Fibonacci of order 2 code and it is defined as follow:

(

)

=F

(



)

L

(

)

B(N)

(3)

Where B

(

)

is binary representation of N, L(N)

is the length of B

(

)

, and F

(



)

L

(

)

 is Fibonacci of

order 2 of L(N). (Bača et al., 2010) applied Elias-

delta, Fibonacci of order 2 and order 3, and Elias-

Fibonacci codes for the compression of XML node

streams arrays.

5.5 Elias-Fibonacci of Order 3

In this paper a new Elias-Fibonacci (m>2) is

proposed to encode XML labels. The method is

basically to code

L(N) in Fibonacci of order (m>2)

instead of order 2 in Elias-Fibonacci coding method

(see equation 4).

(

)

=F

(



)

L

(

)

 B

(

)

,m>2

(4)

The aim of this is to study the effect of increasing

the order number into the encoding time and

generated code size.

6 IMPLEMENTATION

AND RESULTS

Three different real XML benchmark datasets

(Miklau, 2015) were used to test the efficiency of the

prefix coding methods presented in section 5. Table 1

illustrates the characteristics of the datasets used from

which Dewey labels (type integer) and SCOOTER

labels (type string) were generated separately using a

SAX parser. Dewey/SCOOTER labels for each

dataset were compressed and decompressed by the 6

different prefix encoding methods presented earlier.

To improve the compression performance of the

SCOOTER labels, the label’s components were also

coded as long integers. Moreover, the original

encoding methods proposed by the designers of

Dewey and SCOOTER labelling schemes were also

applied (i.e. UTF8 for Dewey and QED for

SCOOTER labels) for comparison.

Table 1: XML benchmarks datasets properties.

XML

dataset

File

size

Max

depth

Max

breadth

Total

elements

Nasa 23MB 8 80396 476646

Treebank 82 MB 36 144493 2437666

DBLP 127MB 6 328858 3332130

6.1 Encoding and Decoding Time

The encoding/decoding process for each prefix

coding method were implemented (repeated 20 times

after excluding at least the first 4 runs to avoid cache

memory and verify the accuracy and reliability of the

results) for every Dewey/SCOOTER label set and the

execution time in mill-seconds was calculated.

Figures 1-4 shows the average encoding and decoding

time comparison. Due to limited space, compression/

decompression results of SCOOTER labels as strings

are not included in the figures.

Overall the encoding/decoding time of Dewey

and SCOOTER labels were slowest for the Treebank

dataset, which has the deepest XML tree. SCOOTER

labels are computed based on the node child count

and so the more children per node exist (i.e. wider

XML tree as in DBLP dataset) the bigger self-label

value is. For integers SCOOTER labels Fibonacci and

Lucas methods have given the slowest encoding time

for DBLP whilst these methods failed to encode

SCOOTER string labels for DBLP because the huge

label size caused overflow. Overall, for SCOOTER

WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies

labels the original QED achieved the fastest encoding

time of all 6 prefix-encoding methods.

The Kruskal-Wallis test (non-parametric test

equivalent to ANOVA) was carried out on average

encoding/decoding time and the p-value obtained was

p < 0.001, suggesting there is a very strong evidence

of difference between at least two prefix-encoding

methods. Then the “pairwise comparisons” via

Manny-Whitney test showed that there was very

strong evidence (p<0.001, adjusted using the

Bonferroni correction) of a difference between most

of the groups.

In terms of encoding time there was no evidence

of difference between Elias-Delta and the newly

implemented Elias-Fibonacci of order 3. The overall

time for Elias-Delta has a smaller median value in

comparison to the other prefix coding methods.

Alternatively, the Manny-Whitney test has shown

that there is no evidence of difference between

Fibonacci of order 2, Fibonacci of order 3, and Lucas

coding. Moreover, Fibonacci of order 2 and Lucas

produced the same median value (of decoding time)

and that is smaller than other prefix-encodings. In

practice, the decoding process is usually done more

often than encoding. Therefore, for faster XML query

processing Fibonacci coding is preferable to other

encoding methods.

Figure 1: Average encoding timefor Dewey labels.

Figure 2: Average encoding time for SCOOTER labels.

Figure 3: Average decoding time for Dewey labels.

Figure 4: Average decoding time for SCOOTER labels.

6.2 Code Size

The average, maximum, and total code sizes of all the

Dewey/SCOOTER labels within a dataset were

computed. Figures 5 and 6 illustrates the total code

size (in Kbyte) for all the prefix coding methods for

each dataset. All the prefix-encoding methods applied

have generated smaller codes in comparison to the

original UTF8 coding for Dewey labels, but for

SCOOTER labels the original QED encoding gave

the smallest codes of all prefix-encodings.

The size of self-label values in a label set has an

impact on the size of the compressed code. For

instance, label sets with shorter self-labels such as

Dewey labels for the NASA and Treebank datasets

using Fibonacci order 2 generated the smallest code.

As self-label values gets bigger (e.g. in SCOOTER

labels), Fibonacci of order 3 produced the most

compressed code. In general, Fibonacci coding

generates the most compressed codes in comparison

to the other prefix-encoding methods applied in this

paper. For smaller self-labels values Fibonacci of

order 2 is better, whereas Fibonacci of order 3 is

recommended for larger self-labels values.

XML Labels Compression using Preﬁx-encodings

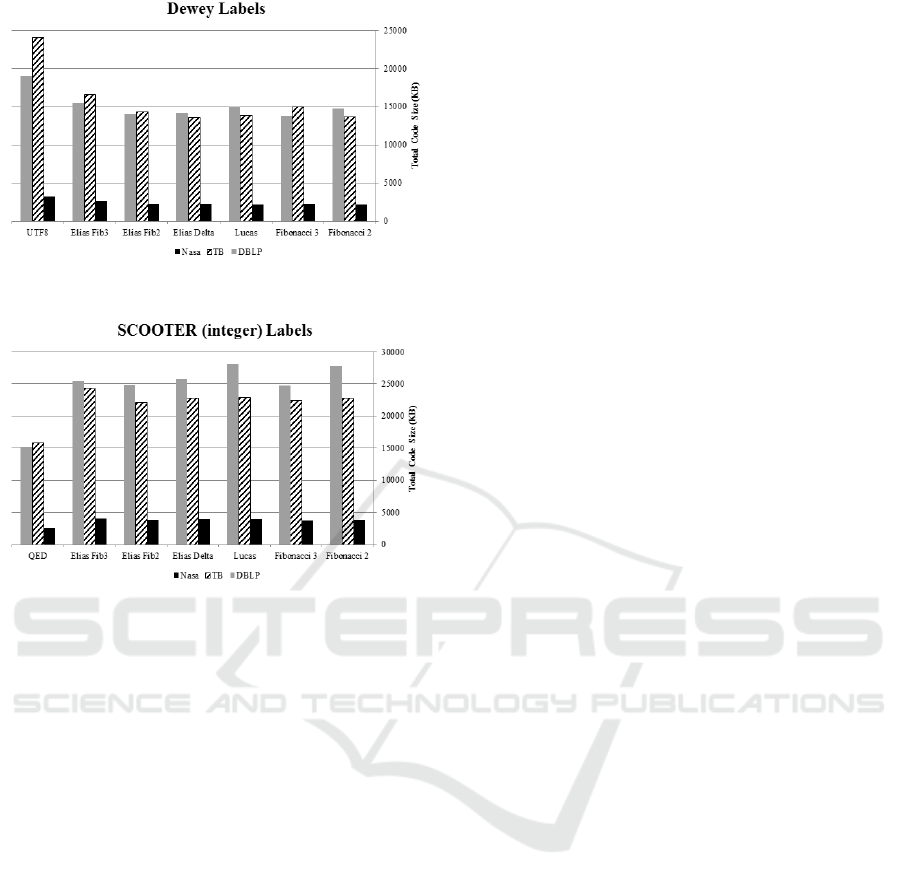
Figure 5: Total code size (KB) for Dewey labels.

Figure 6: Total code size (KB) for SCOOTER labels.

6.3 Dataset Size

To study the effect of the dataset size on the

compression process Treebank and DBLP file sizes

were reduced to 23MB (to be the same as the NASA

file size) but their XML tree properties were

preserved as described in table 1. The compression

and decompression methods were measured over

these datasets and the results were consistent with the

original ones. In conclusion, the XML tree’s shape

(depth and breadth) influences the compression time

and code size but not the XML document size.

7 CONCLUSION AND FUTURE

WORK

In this paper, various prefix coding methods were

applied for the first time for compressing XML labels.

Among these coding methods Lucas coding was

implemented for first time and Elias-Fibonacci of

order m > 2 was also considered. The compression

process was conducted on three real XML benchmark

datasets. The results shown the structure of an XML

tree representation of a dataset affects the

performance of the compression methods but not the

XML document size. Among the prefix-encoding

methods studied Elias-Delta achieved the fastest

encoding time on average whilst Fibonacci of order 2

had the best decoding time and Fibonacci of order 3

produced the most compressed codes. Consequently,

Fibonacci coding is recommended for encoding XML

labels since it generates smaller code and produces

faster decoding in comparison to other encoding

methods presented in this paper.

REFERENCES

Apostolico, A. & Fraenkel, A. S. 1987. Robust

Transmission Of Unbounded Strings Using Fibonacci

Representations. Information Theory, Ieee

Transactions On, 33, 238-245.

Bača, R., Walder, J., Pawlas, M. & Krátký, M. Year.

Benchmarking The Compression Of Xml Node

Streams. In: Database Systems For Advanced

Applications, 2010 Berlin Heidelberg. Springer, 179-

190.

Elias, P. 1975. Universal Codeword Sets And

Representations Of The Integers. Information Theory,

Ieee Transactions On, 21, 194-203.

Ghaleb, T. A. & Mohammed, S. Year. Novel Scheme For

Labeling Xml Trees Based On Bits-Masking And

Logical Matching. In: 2013 World Congress On

Computer And Information Technology (Wccit),, 22-24

June 2013 2013 Tunisia, Sousse. Ieee, 1-5.

Härder, T., Haustein, M., Mathis, C. & Wagner, M. 2007.

Node Labeling Schemes For Dynamic Xml Documents

Reconsidered. Data & Knowledge Engineering, 60,

126-149.

Haw, S.-C. & Lee, C.-S. 2011. Data Storage Practices And

Query Processing In Xml Databases: A Survey.

Knowledge-Based Systems, 24, 1317-1340.

He, Y. Year. A Novel Encoding Scheme For Xml

Document Update-Supporting. In: International

Conference On Advances In Mechanical Engineering

And Industrial Informatics (Ameii), 2015 Zhengzhou.

Atlantis Press.

Karpinski, M. & Nekrich, Y. 2009. A Fast Algorithm For

Adaptive Prefix Coding. Algorithmica, 55, 29-41.

Li, C. & Ling, T. W. 2005. Qed: A Novel Quaternary

Encoding To Completely Avoid Re-Labeling In Xml

Updates. Proceedings Of The 14th Acm International

Conference On Information And Knowledge

Management. Bremen, Germany: Acm.

Li, C., Ling, T. W. & Hu, M. 2008. Efficient Updates In

Dynamic Xml Data: From Binary String To Quaternary

String. The Vldb Journal—The International Journal

On Very Large Data Bases, 17, 573-601.

Mactutor. 1996. Edouard Lucas Http://Www-

Groups.Dcs.St-And.Ac.Uk/~History/Biographies/

Lucas.Html [Online]. [Accessed 7/May/2015].

WEBIST 2016 - 12th International Conference on Web Information Systems and Technologies

Miklau, G. 2015. Xml Data Repository Http://Www.Cs

.Washington.Edu/Research/Xmldatasets/ [Online].

[Accessed February 2015].

O'neil, P., O'neil, E., Pal, S., Cseri, I., Schaller, G. &

Westbury, N. 2004. Ordpaths: Insert-Friendly Xml

Node Labels. Proceedings Of The 2004 Acm Sigmod

International Conference On Management Of Data.

Paris, France: Acm.

O’connor, M. & Roantree, M. 2012. Scooter: A Compact

And Scalable Dynamic Labeling Scheme For Xml

Updates. Database And Expert Systems Applications.

Springer Berlin Heidelberg.

O’connor, M. & Roantree, M. 2013. Fiblss: A Scalable

Label Storage Scheme For Dynamic Xml Updates.

Advances In Databases And Information Systems.

Springer Berlin Heidelberg.

Sans, V. & Laurent, D. 2008. Prefix Based Numbering

Schemes For Xml: Techniques, Applications And

Performances. Proc. Vldb Endow., 1, 1564-1573.

Scholer, F., Williams, H. E., Yiannis, J. & Zobel, J. 2002.

Compression Of Inverted Indexes For Fast Query

Evaluation. Proceedings Of The 25th Annual

International Acm Sigir Conference On Research And

Development In Information Retrieval. Tampere,

Finland: Acm.

Tatarinov, I., Viglas, S. D., Beyer, K., Shanmugasundaram,

J., Shekita, E. & Zhang, C. 2002. Storing And Querying

Ordered Xml Using A Relational Database System.

Proceedings Of The 2002 Acm Sigmod International

Conference On Management Of Data. Madison,

Wisconsin: Acm.

Walder, J., Krátký, M., Bača, R., Platoš, J. & Snášel, V.

2012. Fast Decoding Algorithms For Variable-Lengths

Codes. Information Sciences, 183, 66-91.

Williams, H. E. & Zobel, J. 1999. Compressing Integers For

Fast File Access. The Computer Journal, 42, 193-201.

Yergeau, F. 2003. Utf-8, A Transformation Format Of Iso

10646 Via Https://Tools.Ietf.Org/Html/Rfc3629

[Online]. [Accessed January 2015].

XML Labels Compression using Preﬁx-encodings