Comparing Machine Learning Techniques in a

Hyperemia Grading Framework

L. S. Brea

, N. Barreira

, A. Mosquera

, H. Pena-Verdeal

and E. Yebra-Pimentel

Department of Computer Science, Univ. A Coruna, A Coru˜na, Spain

Department of Electronics and Computer Science, Univ. Santiago de Compostela, Santiago de Compostela, Spain

Department of Applied Physics, Univ. Santiago de Compostela, Santiago de Compostela, Spain

Keywords:

Image Processing, Medical Imaging, Pattern Recognition.

Abstract:

Hyperemia is the occurrence of redness in a certain tissue. When it takes place on the bulbar conjunctiva,

it can be an early symptom of different pathologies, hence, the importance of its quick evaluation. Experts

grade hyperemia as a value in a continuous scale, according to the severity level. As it is a subjective and

time consuming task, its automatisation is a priority for the optometrists. To this end, several image features

are computed from a video frame that shows the patient’s eye. Then, these features are transformed to the

grading scale by means of machine learning techniques. In previous works, we have analysed the performance

of several regression algorithms. However, since the experts only use a ﬁnite number of values in each grading

scale, in this paper we analyse how classiﬁers perform the task in comparison to regression methods. The

results show that the classiﬁcation techniques usually achieve a lower training error value, but the regression

approaches classify correctly a larger number of samples.

1 INTRODUCTION

Hyperemia is the occurrence of an abnormal hue of

red in a tissue. One of the areas that can be affected

is the bulbar conjunctiva, where it can be an early

symptom of pathologies such as conjunctivitis, aller-

gies, contact lens complications, or dry eye syndrome

(Rolando and Zierhut, 2001). Specialists measure hy-

peremia as a degree in a continuous scale. Scales

are collections of pictures or photographies that rep-

resent different levels of severity. The clinician com-

pares the patient’s eye with the images, and assigns a

level. In this paper, we work with two of the available

scales: Efron (5 levels of severity, shown in Fig. 1)

and CCLRU (4 levels, depicted in Fig. 2). Specialists

grade using not only the 4-5 prototype levels, but also

decimal values indicating how much a patient’s eye

distances from the model.

Figure 1: Efron severity levels. Photographic scale.

In order to perform the evaluation, experts take

into account several parameters. Some examples

Figure 2: CCLRU severity levels. Drawing scale.

are the general hue of the conjunctiva, the number

of blood vessels, or their width. The task is time-

consuming and presents high intra and inter expert

subjectivity. This arises the need of its automatisation.

There are few approaches that tackle the problem of

automatic hyperemia computation. Different frame-

works have been developed, but there are some steps,

such as the determination of the region of interest,

that are not automatic (Yoneda et al., 2012; Rodriguez

et al., 2013). There are several works that propose

features that need to be calculated in order to perform

the grading (Papas, 2000; Wolffsohn and Purslow,

2003). There are also different works that depict the

construction and validation of grading scales (Efron

et al., 2001; Fieguth and Simpson, 2002), analysing

how specialists tend to choose the values they assign.

One of the most important steps is the transfor-

mation from the image features to the grading scale

values. This transformation can be performed using

regression methods, as both the feature scale and the

Brea, L., Barreira, N., Mosquera, A., Pena-Verdeal, H. and Yebra-Pimentel, E.

Comparing Machine Learning Techniques in a Hyperemia Grading Framework.

DOI: 10.5220/0005756004230429

In Proceedings of the 8th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2016) - Volume 2, pages 423-429

ISBN: 978-989-758-172-4

423

expert grading are continuous. However, in practice

specialists do not use all the values in a continuous

scale, but have a tendency to assign certain grades

more frequently, such as integer and half-integer val-

ues (Schulze et al., 2007). Those values are taken

as references even when they assign other amounts.

This give us the possibility to apply classiﬁcation al-

gorithms by performing an initial division of the val-

ues in classes. In this work, we analyse how classiﬁer

methods are able to perform the transformation of the

image features into grading scale values. We compare

the results achieved by these methods to different re-

gression techniques.

The paper is structured as follows: Section 2 ex-

plains the approaches we have selected as well as the

experiments, Section 3 shows the results, and Sec-

tion 4 discusses the conclusions and future lines of

research.

2 METHODOLOGY

Specialists grade hyperemia by analysing a video of

the patient’s eye. For the automatisation of the pro-

cess, we receive this video as input and perform four

steps to obtain the value in the grading scale as the

output. First, the input video is analysed in order to

select the frame that is the most suitable for grading

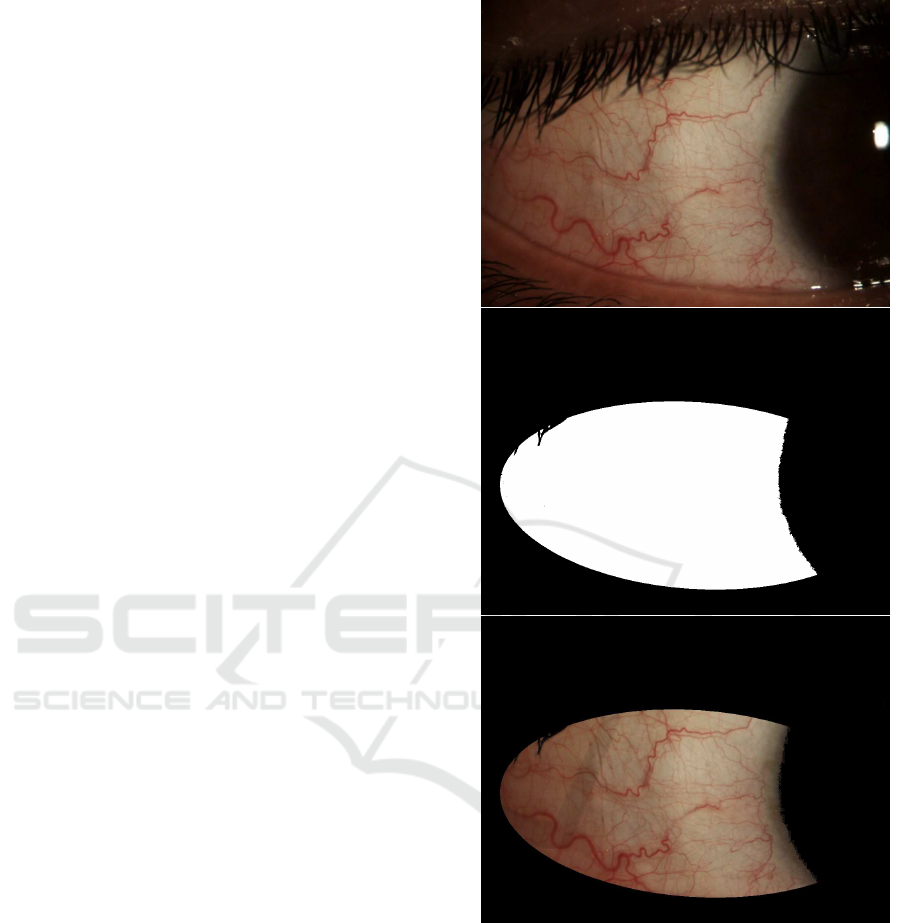
(S´anchez et al., 2015a). Then, a region of interest

comprising only the bulbar conjunctiva is delimited

by means of an elliptical mask and thresholding oper-

ations. It is depicted in Fig. 3 how the mask removes

the iris and pupil area, the eyelids, and the eyelashes.

Next, several image features are computed and, last,

these features are transformed into the grading value

(S´anchez et al., 2015b). This work is focused in the

ﬁnal step of the process. This section presents the

image features we worked with as well as the classi-

ﬁcation and regression approaches used.

2.1 Feature Computation

Specialists take different parameters into account

when performing hyperemia grading. This way, ex-

pert knowledge is the ﬁrst issue we have to face, as it

is difﬁcult to explain and understand which features

are relevant. For example, the amount of red value

in the image implies a higher hyperemia level, but it

does not have the same relevance if that redness cor-

responds to vessel or background areas. We also have

to take into account the general tonality of the image,

as the illumination is not constant for all the image

set. This lead us to implement measures that com-

pare the red value to other colours. We have to simu-

Figure 3: Region of Interest of the conjunctiva.

late the expert perception so that we also test several

colour spaces, such as RGB, HSV, and L*a*b*, in or-

der to determine which one offers the best representa-

tion. Moreover,experts look at the vessel quantity and

width too, as hyperemia is produced by blood vessel

engorgement.

After consulting past works on the subject (Papas,

2000; Wolffsohn and Purslow, 2003) and talking to

optometrists, we computed 25 image features:

• Vessel count f

. The image is scanned horizon-

tally in ten rows equally separated and the number

of vessels that are cut is counted.

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

424

• Vessel occupied area f

. The number of vessel

pixels is divided by the ROI size.

• Relative vessel redness f

and relative image red-

ness f

. (RGB) Sum of red channel values divided

by all the channels’ values for all the vessel pixels

or the whole image pixels, respectively.

• Difference red-green in vessels f

and in the im-

age f

(RGB). Sum of differences between red

and green channels divided by all the channels’

values for all the vessel pixels or the whole image

pixels, respectively.

• Difference red-blue in vessels f

and in the image

(RGB). Sum of differences between red and

blue channels divided by all the channels’ values

for all the vessel pixels or the whole image pixels,

respectively.

• Red hue value f

(HSV). Sum of the red compo-

nent of the hue channel for all the pixels divided

by the ROI size.

• Percentage of vessels f

. The number of vessel

pixels is divided by the total pixels and multiplied

by 100 as it was originally proposed in (Papas,

2000).

• Percentage of red in vessels (RGB f

, HSV f

Sum of red value for all the vessel pixels divided

by the number of vessel pixels.

• Redness in neighbourhood (HSV), f

. Besides

taking into accountthe current pixel, the hue value

is also analysed in the neighbouring pixels. The

whole image is analysed.

• a-channel in vessels f

and in the image f

(L*a*b*). Sum of the values of the a-channel in

each pixel corresponding with a vessel divided by

the ROI size, or sum through all the pixels of the

image.

• Yellow in background (RGB, HSV, L*a*b*) f

. Sum of yellow value for those pixels cor-

responding to conjunctiva (areas without vessels)

divided by the ROI size.

• Red in background (RGB, HSV, L*a*b*), f

-f

Sum of white value for those pixels corresponding

to conjunctiva divided by the ROI size.

• White in background (RGB, HSV, L*a*b*), f

. Sum of red value for those pixels correspond-

ing to conjunctiva divided by the ROI size.

• Vessel width, f

. Vessel widths are measured in

ten circumferences centered at the corner of the

eye and with radius ranging from h/2∗ n to h/2,

where h is the height of the image and n the num-

ber of circumferences, by means of an active con-

tour algorithm (V´azquez et al., 2013). The mean

vessel width is selected as the representative fea-

ture.

In features based on vessels, a Canny ﬁlter is applied

to locate the vessel boundaries (Canny, 1986). The

ﬁlter performance was previously evaluated by manu-

ally segmenting 106 vessels from our image set. 94%

of these vessels were correctly extracted by the auto-

matic method. In order to obtain the values for the

red hue in HSV, we measure the H-channel and check

the value |H − 128|, as H-channel range is 0 to 255

and the purest red is in 0 and 255. For a-channel in

L*a*b*, positive values mean that there is red hue,

while the negative ones correspond to green colour.

RGB values are directly obtained by accessing the ap-

propriate channel.

2.2 Hyperemia Grading

One of the most important and overlooked steps in

hyperemia grading is the transformation from the im-

age features to the grading scale. This procedure in-

volves ﬁnding the relationship between feature values

and the given scale. It was originally approached with

regression methods in (S´anchez et al., 2015b). Even

though both scales are in theory continuous, several

researches have study how in reality experts only ap-

ply a certain set of values in their gradings. Hence, in

this work we are applying classiﬁer models and com-

paring its performance with regression methods.

Classiﬁer models present certain beneﬁts if com-

pared with regression techniques. For example, some

regression methods require to assume the data follows

a certain distribution or structure, such as linear re-

gression. Other more complex methods, like artiﬁcial

neural networks, model well convoluted relationships

but at the cost of being opaque. This is an issue spe-

cially when we are interested in understanding the un-

derlying relationship and not only in training a system

that achieves good predictions.

In order to apply classiﬁcation techniques to con-

tinuous data, we need to group the values in classes.

The ﬁrst decision we have to face is how to imple-

ment this division. We performed experiments with

three assumptions:

• Using integer and half-integer values. This ap-

proach is supported by those works that conclude

that experts usually grade taking this characteris-

tic values as a reference (Schulze et al., 2007).

• Using one decimal. This is the maximum preci-

sion of human experts when grading.

• Using integer, half and quarter values. We decided

to include this approach in order to check how the

values evolve with the gap between classes.

Comparing Machine Learning Techniques in a Hyperemia Grading Framework

425

For each of these assumptions, we applied a set of

classiﬁers, chosen in order to cover the different types

of machine learning algorithms:

• Bayes Network (BN) (Friedman et al., 1997;

Jensen, 1996).

• Naive Bayes (NB) (John and Langley, 1995).

• Support Vector Machine (SVM) (Chang and Lin,

2011).

• Sequential Minimal Optimisation (SMO) (Platt

et al., 1999; Keerthi et al., 2001; Hastie et al.,

1998).

• Instance Based (IB1 and IB3) (Aha et al., 1991).

• Decision Table (DT) (Kohavi, 1995).

• One Rule (OR) (Holte, 1993).

• Decision Tree (J48) (Quinlan, 2014).

• Random Forest (RF) (Breiman, 2001).

Regarding the regression methods we also se-

lected the following approaches:

• Instance Based (IBR) (Aha et al., 1991).

• Linear Regression (LR).

• Support Vector Regresion (SVR) (Smola and

Sch¨olkopf, 2004).

• M5P (Wang and Witten, 1996; Quinlan et al.,

1992).

• Multi Layer Perceptron (MLP) (Baum, 1988).

• Radial Basis Function Network (RBFN) (Buh-

mann, 2000).

3 RESULTS

Our data set consisted of 105 videos of the bulbar

conjunctiva. These videos have been ﬁlmed by the

Optometry Group (University of Santiago de Com-

postela) following a standardised acquisition proto-

col. The videos belong to different patients. Even

though each person could present a different distribu-

tion of vessels in the conjunctiva, a extremely high

number is considered unusual and labelled with high

values in the scale.

For each video, the best frame is selected, result-

ing in an image of 1024× 768 px that shows a side

view of the eye, from the pupil to the corner of the

eye or the lacrimal. The images had been graded by

two optometrists twice. The mean value for the two

gradings was computed for each specialist and then,

the mean value from both specialists is used as target.

Due to the subjectivity of the problem, it is difﬁcult to

ﬁnd how the expert’s gradings and the image features

are related. Figures 4 and 5 depict the issue of the in-

tra expert subjectivity. Both gradings were performed

months apart, and we can observe how the given val-

ues vary. Moreover, this variation is not consistent, as

the expert assigned higher values on the second grad-

ing for the lower levels of severity but lower ones for

the most severe conjunctivas.

Figure 4: Intra expert differences in CCLRU scale.

Figure 5: Intra expert differences in Efron scale.

Figures 6 and 7 show the inter expert differences

in both scales. We can notice how the experts per-

form different when grading near the various levels

of severity. In fact, if we compare the gradings of

the two experts, we obtain a RMSE of 0.4705 for the

Efron scale and 0.4743 for the CCLRU scale.

Figure 6: Inter expert differences in CCLRU scale.

We divided the continuous output in classes sep-

arated a certain step (0.5, 0.25, and 0.1). The meth-

ods were trained using 10-fold cross validation. We

computed the success rate during the training. For the

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

426

Figure 7: Inter expert differences in Efron scale.

regression methods, as they provide a continuous re-

sult, an instance was accounted as correctly classiﬁed

if the closest deﬁned class to this output value was

the expected one. We used the data mining software

Weka (Hall et al., 2009). In order to select the pa-

rameters for each classiﬁer, empirical tests were con-

ducted. The systems conﬁgurations were the follow-

ing:

• BN: search algorithm is K2 (Cooper and Her-

skovits, 1991). Alpha value for the estimator is

0.5.

• SVM: type = C-SVC, kernel = radial basis func-

tion.

• SMO: Pearson universal kernel (ω = 1.0, σ =

1.0).

• IB1: neighbours = 1.

• IB3: neighbours = 3.

• DT: the evaluation measure is the RMSE.

• J48: conﬁdence factor for pruning = 0.25, mini-

mum instances per leaf = 2.

• RF: number of trees = 100.

• IBR: neighbours = 3.

• SVR: type = ε-SVR

• M5P: minimum instances per leaf = 4.

• MLP: hidden layers = [40 16], learning rate = 0.3,

training epochs = 500.

Tables 1, 2 and 3 depict the results obtained for

both scales and all the methods. The root mean

squared error (RMSE) was obtained during the train-

ing stage for the whole image set.

We can observe how the error value is higher as

the step becomes wider, but the number of correctly

classiﬁed images is also larger. This was expected,

as a misclassiﬁcation generates a worse error when

the gap between values is broader. SMO classiﬁer

achieves consistently good results. Some of the meth-

ods obtain a perfect classiﬁcation on the test set in

some of the test cases, such as RF with step=0.25.

Table 1: Classiﬁcation results (step=0.5).

Efron CCLRU

SR RMSE SR RMSE

BN 46.7 0.3073 53.3 0.3254

38.1 0.3551 43.8 0.3755

SVM 41.9 0.3593 44.8 0.3973

SMO

48.6 0.286 56.2 0.3086

IB1 40.0 0.3651 51.4 0.3725

IB3

41.0 0.2959 44.8 0.3207

DT 46.7 0.2714 54.3 0.294

OR 35.2 0.3794 45.7 0.3938

J48

39.0 0.354 53.3 0.3401

RF 41.0 0.2751 58.1 0.2831

IBR 46.7 0.4213 56.2 0.353

54.3 0.404 55.2 0.3478

M5P 47.6 0.3801 58.1 0.3224

MLP

36.2 0.4882 50.5 0.4223

RBF 40.0 0.4683 49.5 0.3809

SVR

41.9 0.4945 44.8 0.3997

Table 2: Classiﬁcation results (step=0.25).

Efron CCLRU

SR RMSE SR RMSE

BN 20.0 0.2365 32.4 0.2701

NB 21.9 0.2816 31.4 0.2994

SVM

21.0 0.305 25.7 0.3381

SMO 21.0 0.2249 36.2 0.252

IB1 27.6 0.2918 31.4 0.3248

IB3

15.2 0.2441 24.8 0.2688

DT 21.0 0.2234 33.3 0.2463

24.8 0.2975 25.7 0.3381

J48 28.6 0.2776 31.4 0.3052

18.1 0.2264 35.2 0.246

IBR 25.7 0.3846 39.1 0.3006

LR 34.3 0.3753 28.7 0.2991

M5P

28.6 0.3772 34.3 0.2956

MLP 31.4 0.4465 35.2 0.3472

RBF

20.0 0.4433 25.7 0.3619

SVR 21.0 0.4722 25.7 0.3809

However, our main goal is to achieve a lower RMSE,

as the number of correctly and incorrectly classiﬁed

images can be misleading. For example, an overﬁtted

model will present good results in these parameters

but with a higher RMSE.

Regarding the differences between both types of

methods, we can perceive how the regression meth-

ods achieve, with the exception of SMO classiﬁer,

better results, as they classify correctly a larger num-

ber of images. However, training error is higher also

for regression methods. This happens because almost

all regression predictions have at least a slight error,

since the model does not predict the exact output.

We also have to take into account that a high

Comparing Machine Learning Techniques in a Hyperemia Grading Framework

427

Table 3: Classiﬁcation results (step=0.1).

Efron CCLRU

SR RMSE SR RMSE

BN 9.5 0.1516 11.4 0.1738

9.5 0.2014 14.3 0.2221

SVM 10.5 0.209 12.4 0.2378

SMO

7.6 0.1731 11.4 0.152

IB1 10.5 0.209 20.0 0.2272

IB3

9.5 0.1675 13.3 0.1852

DT 9.5 0.1517 10.5 0.1734

OR 13.3 0.2056 11.4 0.239

J48

8.6 0.1911 9.5 0.2176

RF 6.7 0.1574 17.1 0.1741

IBR 11.4 0.3711 14.3 0.2932

16.2 0.3728 15.2 0.2836

M5P 18.1 0.3416 15.2 0.2727

MLP

9.5 0.4188 14.3 0.3251

RBF 8.6 0.4402 4.8 0.3545

SVR

7.6 0.4677 7.6 0.376

number of images are classiﬁed in contiguous classes

which, in the case of step=0.1 is still an accurate clas-

siﬁcation. Figures 8, 9, 10, and 11 depict how the

success rate varies if we take into account the in-

stances that are classiﬁed in neighbouring classes. In

these ﬁgures, the x-axis shows the tolerance margins

whereas the y-axis shows the percentage of correct

classiﬁcations in that margin.

We can observe how in the CCLRU scale the

methods are able to classify more instances with

lower margin levels, while in the Efron scale only one

Figure 8: Evolution of the success rate in the classiﬁcation

techniques (EFRON scale).

Figure 9: Evolution of the success rate in the regression

techniques (EFRON scale).

Figure 10: Evolution of the success rate in the classiﬁcation

techniques (CCLRU scale).

Figure 11: Evolution of the success rate in the regression

techniques (CCLRU scale).

method achieves 90% of success rate for the maxi-

mum margin. The approaches that achieve the better

results are the regression techniques for both scales.

We can conclude that our system behaves like an

expert, as with a ±0.5 margin it is able to classify cor-

rectly 90% of the instances in the Efron scale. In the

CCLRU scale the results are better, as a ±0.4 margin

is enough to achieve more a 90% of success rate. We

think that this happens due to the nature of the proto-

types of each scale, since the Efron scale is made of

pictures whereas the CCLRU scale contains real eye

photographies. In consequence, gradings are easier

in the later scale, which is consistent with the system

behaviour.

4 CONCLUSIONS

The apparition of hyperemia in the bulbar conjunc-

tiva can be an early indicator of several pathologies,

such as conjunctivitis or dry eye syndrome. The pro-

cess that clinicians perform is tedious and subjective,

hence the importance of its automatisation in order to

provide objective and repeatable results. The present

work was focused in the transformation from the sev-

eral image features computed from a video frame of

the patient eye to a value in two given scales, Efron

and CCLRU. We performed severalexperimentscom-

paring the behaviour of classiﬁcation and regression

techniques under different divisions of the data. Re-

ICAART 2016 - 8th International Conference on Agents and Artiﬁcial Intelligence

428

sults show that the system behaves like an expert, and

that regression methods perform better in both scales.

Future work will tackle the study of the evolution

of a patient, allowing us to measure the ratio of ap-

pearance of new vessels and other associated changes

that occur in the conjunctiva.

REFERENCES

Aha, D. W., Kibler, D., and Albert, M. K. (1991).

Instance-based learning algorithms. Machine learn-

ing, 6(1):37–66.

Baum, E. B. (1988). On the capabilities of multilayer per-

ceptrons. Journal of complexity, 4(3):193–215.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Buhmann, M. D. (2000). Radial basis functions. Acta Nu-

merica 2000, 9:1–38.

Canny, J. (1986). A computational approach to edge detec-

tion. Pattern Analysis and Machine Intelligence, IEEE

Transactions on, (6):679–698.

Chang, C.-C. and Lin, C.-J. (2011). LIBSVM: A library

for support vector machines. ACM Transactions on

Intelligent Systems and Technology, 2:27:1–27:27.

Cooper, G. F. and Herskovits, E. (1991). A bayesian

method for constructing bayesian belief networks

from databases. In Proceedings of the Seventh con-

ference on Uncertainty in Artiﬁcial Intelligence, pages

86–94. Morgan Kaufmann Publishers Inc.

Efron, N., Morgan, P. B., and Katsara, S. S. (2001). Valida-

tion of grading scales for contact lens complications.

Ophthalmic and Physiological Optics, 21(1):17–29.

Fieguth, P. and Simpson, T. (2002). Automated measure-

ment of bulbar redness. Investigative Ophthalmology

and Visual Science, 43(2):340–347.

Friedman, N., Geiger, D., and Goldszmidt, M. (1997).

Bayesian network classiﬁers. Machine learning, 29(2-

3):131–163.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: an update. ACM SIGKDD explorations

newsletter, 11(1):10–18.

Hastie, T., Tibshirani, R., et al. (1998). Classiﬁcation by

pairwise coupling. The annals of statistics, 26(2):451–

471.

Holte, R. C. (1993). Very simple classiﬁcation rules per-

form well on most commonly used datasets. Machine

learning, 11(1):63–90.

Jensen, F. V. (1996). An introduction to Bayesian networks,

volume 210. UCL press London.

John, G. H. and Langley, P. (1995). Estimating continuous

distributions in bayesian classiﬁers. In Proceedings

of the Eleventh conference on Uncertainty in artiﬁcial

intelligence, pages 338–345. Morgan Kaufmann Pub-

lishers Inc.

Keerthi, S. S., Shevade, S. K., Bhattacharyya, C., and

Murthy, K. R. K. (2001). Improvements to platt’s smo

algorithm for svm classiﬁer design. Neural Computa-

tion, 13(3):637–649.

Kohavi, R. (1995). The power of decision tables. In Ma-

chine Learning: ECML-95, pages 174–189. Springer.

Papas, E. B. (2000). Key factors in the subjective and objec-

tive assessment of conjunctival erythema. Investiga-

tive Ophthalmology and Visual Science, 41(3):687–

691.

Platt, J. et al. (1999). Fast training of support vector ma-

chines using sequential minimal optimization. Ad-

vances in kernel methodssupport vector learning, 3.

Quinlan, J. R. (2014). C4. 5: programs for machine learn-

ing. Elsevier.

Quinlan, J. R. et al. (1992). Learning with continuous

classes. In 5th Australian joint conference on artiﬁcial

intelligence, volume 92, pages 343–348. Singapore.

Rodriguez, J. D., Johnston, P. R., Ousler III, G. W., Smith,

L. M., and Abelson, M. B. (2013). Automated grad-

ing system for evaluation of ocular redness associated

with dry eye. Clinical ophthalmology (Auckland, NZ),

7:1197.

Rolando, M. and Zierhut, M. (2001). The ocular surface

and tear ﬁlm and their dysfunction in dry eye disease.

Survey of Ophthalmology, 45, Supplement 2(0):S203

– S210.

S´anchez, L., Barreira, N., Garc´ıa-Res´ua, C., and Yebra-

Pimentel, E. (2015a). Automatic selection of video

frames for hyperemia grading. Eurocast 2015, pages

165–166.

S´anchez, L., Barreira, N., Pena-Verdeal, H., and Yebra-

Pimentel, E. (2015b). A novel framework for hyper-

emia grading based on artiﬁcial neural networks. In

Advances in Computational Intelligence, pages 263–

275. Springer.

Schulze, M. M., Jones, D. A., and Simpson, T. L. (2007).

The development of validated bulbar redness grading

scales. Optometry & Vision Science, 84(10):976–983.

Smola, A. J. and Sch¨olkopf, B. (2004). A tutorial on

support vector regression. Statistics and computing,

14(3):199–222.

V´azquez, S. G., Barreira, N., Penedo, M. G., Pena-Seijo,

M., and G´omez-Ulla, F. (2013). Evaluation of SIRIUS

retinal vessel width measurement in REVIEW dataset.

In Proceedings of the 26th IEEE International Sym-

posium on Computer-Based Medical Systems, Porto,

Portugal, June 20-22, 2013, pages 71–76.

Wang, Y. and Witten, I. H. (1996). Induction of model trees

for predicting continuous classes.

Wolffsohn, J. S. and Purslow, C. (2003). Clinical monitor-

ing of ocular physiology using digital image analysis.

Contact Lens and Anterior Eye, 26(1):27–35.

Yoneda, T., Sumi, T., Takahashi, A., Hoshikawa, Y.,

Kobayashi, M., and Fukushima, A. (2012). Auto-

mated hyperemia analysis software: reliability and re-

producibility in healthy subjects. Japanese journal of

ophthalmology, 56(1):1–7.

Comparing Machine Learning Techniques in a Hyperemia Grading Framework

429