Teachers’ Experiences of the Integration of 21st Century Learning in

the Mathematics Classroom – The Bridge21 Model in Action

Aibhin Bray

Centre for Research in IT in Education (CRITE), School of Education and School of Computer Science & Statistics,

Trinity College Dublin, Dublin, Ireland

Keywords: Continuous Professional Development, 21st

Century Learning, Post-Primary Education, Mathematics

Education.

Abstract: Current research indicates a need for ongoing support and continuous professional development (CPD) for

teachers in order to facilitate the development of 21st Century pedagogies and the integration of technology,

as well as to scaffold their changing role in the classroom. This article describes a particular model of 21st

Century teaching and learning and an associated approach to CPD, with a particular focus on mathematics

education. A qualitative, case study approach has been taken in order to explore the teachers’ experiences of

using the model of teaching and learning, as well as their perceptions of the students’ experiences. A total of

15 teachers who attended a Contextual Mathematics module on the CPD course provided consent for their

data to be used in this study and a constant comparative analytic technique has been used to analyse their

written reflections. Results indicate that the approach has the potential to address many of the difficulties

associated with 21st Century teaching and learning identified in the literature review.

1 INTRODUCTION

There is no single, universally recognised definition

of 21

Century skills or of the types of teaching and

learning required to achieve them. However, in their

comparative analysis of international frameworks for

Century competences, Voogt and Roblin (2012)

identify a common recognition of the development of

skills relating to communication and collaboration,

problem-solving and creativity, as well as

technological fluency, as being fundamentally

important. Many of these skills can be defined as

higher-order thinking and learning skills, or “life-

skills”, and they are seen as being transversal (not

subject-specific) and multi-dimensional, impacting

on attitudes and knowledge (Dede, 2010a; Voogt and

Roblin, 2012).

Although a general recognition of the benefit of

these skills is not new, an approach to education that

emphasises the importance of acquiring them in an

integrated manner throughout curricular activities,

combined with the potential of technology to assist in

their realisation, can be viewed as innovative

(Conole, 2008; Dede, 2010a; 2010b; Voogt and

Roblin, 2012). Meaningful incorporation of such 21

Century Learning (21CL) skills in mainstream

curricula however, may require a change in

pedagogic focus. Such a change would require a shift

in teaching and learning approaches, de-emphasising

the more traditional, procedural activities still

common in educational practice, and increasing

emphasis on the more complex skills that require an

understanding of ‘why’ as well as ‘how’ the routine

procedures should be used (Conneely et al., 2013;

Dede, 2010b; Fullan and Langworthy, 2014; Voogt

and Roblin, 2012). The role of technology in 21CL is

perceived as important, in that it requires the

development of specific competences regarding the

effective use, management and evaluation of

information across many different platforms (Martin

and Grudziecki, 2006; Voogt and Roblin, 2012).

It is generally recognised that 21CL can be best

supported through pedagogic approaches such as

Inquiry-Based Learning (IBL), Problem-Based

Learning (PBL), and collaboration, as well as a more

formative approach to assessment (Conneely et al.,

2013; Conole, 2008; Fullan and Langworthy, 2014;

Voogt and Roblin, 2012). Some of these approaches

as well as barriers to, and possible facilitation of, their

implementation are discussed in the following

sections.

Bray, A.

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action.

In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 219-230

ISBN: 978-989-758-179-3

219

2 LITERATURE REVIEW

European research (Commission of the European

Communitities, 2008; Euler and Maaß, 2011) has

highlighted a need for appropriate structure, support

and scaffolding in order to create opportunities for

young people to develop key 21CL competences

within the school environment. It is recognised

however, that this is not a straightforward task.

Indeed, the PRIMAS report (Euler and Maaß, 2011)

has acknowledged that although many teachers wish

to develop teaching and learning strategies that

incorporate skills associated with 21CL, they are

hampered by numerous factors outside of their

control, including the restraints of current practices in

curriculum and assessment, and a lack of relevant

continuous professional development (CPD) for

teachers.

Euler and Maaß (2011) identify three levels of

problems associated with the implementation of a

21CL approach to teaching and learning: the

overarching school system; a lack of resources

including CPD; and teachers’ beliefs. The macro-

level issues identified by Euler and Maaß, relating to

policies, curriculum, and assessment, while

fundamental, are not addressed in detail in this

research.

At the meso- and micro-levels, problems relating

to classroom management and the difficulties that

teachers may have in redefining their role, have been

identified as contributing to the gap between the

intended curricula, which tend to recognise the

importance of 21

Century skills, and that which is

actually implemented (Conneely et al., 2013; Euler

and Maaß, 2011; Voogt nd Roblin, 2012). Not only

are teachers expected to facilitate the acquisition of

Century skills among their students, but they are

also expected to possess the skills themselves (Voogt

and Roblin, 2012). Discussion alone is not sufficient

to address these issues, rather a shift in the beliefs and

practices of policy-makers and practitioners is

required (Dede, 2010b). Educators need to be

provided with adequate support and CPD in order to

master the necessary skills and teaching strategies,

but also to ‘unlearn’ the beliefs and assumptions that

underpin the traditional industrial-model of

classroom practice (Conneely et al., 2013; Dede,

2010b; Voogt and Roblin, 2012).

It has been suggested that an approach to CPD that

presents teaching as a problem-solving activity, or

‘research-in-action’, may be particularly appropriate

for linking teaching practice with children’s learning

(Commission of the European Communitities, 2008).

This has clear links with the approach described in

this research.

3 BRIDGE21 AND CPD

One of the findings that has emerged throughout the

analysis of the literature, is a need for ongoing

support and continuous professional development

(CPD) for teachers in order to facilitate the

development of 21

Century pedagogies and the

integration of technology, as well as to scaffold their

changing role in the classroom (Conneely et al., 2013;

Dede, 2010a; Maaß nd Artigue, 2013; Voogt and

Roblin, 2012). This paper describes the

implementation of a structured CPD module that has

been incorporated into a larger Postgraduate

Certificate (PG Cert) course in 21

Century Teaching

and Learning for post-primary school teachers,

coordinated by the School of Education in Trinity

College Dublin (Bridge21, 2014). This course began

in September 2014 and the first cohort of teachers

have recently completed the programme.

Bridge21 offers a structured pedagogic model for

the integration of 21CL in classrooms, and supports

an innovative approach to CPD, strongly influenced

by the Japanese model of Lesson Study that uses an

iterative cycle of goal setting, planning, teaching and

observation, review, and revision (Lewis et al., 2009).

Groups of teachers form communities of practice to

engage in a process of systematic examination of their

practice, with the goal of becoming more effective

teachers and optimising their lessons (Maaß and

Artigue, 2013; Takahashi nd Yoshida, 2004).

The initial experience for teachers engaging with

the Bridge21 CPD model involves active

participation in immersive and authentic activities,

which enables them to understand the power of the

approach at a personal level. Throughout the process,

participants are provided with the resources, practical

designs and collegial support that Donnelly et al.,

(2011) highlight as necessary conditions to motivate

change amongst teachers.

The Contextual Mathematics module on the PG

Cert requires each of the attending teachers to

complete an assignment that involves the creation and

implementation of a 21CL activity in their school,

with a standard class. The activity should use the

Bridge21 model of 21CL (Section 4) and a set of

design heuristics (Section 5) developed for the

creation of contextual, 21CL mathematics learning

activities (Bray et al., 2013; Bray and Tangney,

2013b; 2014; Tangney et al., 2015). The written part

of the assignment involves a description of the

activity, highlighting the basic and transversal skills

CSEDU 2016 - 8th International Conference on Computer Supported Education

220

that are covered, as well as a reflection on their own,

and the students’ experiences of the process.

A total of 22 teachers attended the contextual

mathematics module which forms the basis of this

study. These teachers came from a wide range of

schools and had levels of teaching experience ranging

from 3 to 19 years. In a number of cases, two or three

of the teachers came from the same school, which

promoted greater levels of collaboration in the design

and implementation of their activities, and also

strengthened the communities of practice within the

schools. Fifteen of the teachers provided consent for

their work to be included in this research. This paper

provides an analysis of their work, placing particular

emphasis on their reflections on the process, and their

experiences with it.

4 THE BRIDGE21 MODEL

Bridge21 (www.bridge21.ie) is a model of

collaborative, project-based learning that has been

developed at the authors’ institution (Lawlor et al.,

2010; Lawlor et al., 2015). Initially established in

2007 as part of an outreach programme, the Bridge21

model has been developed throughout the intervening

years and is currently being trialled in a number post-

primary schools as part of a systemic process of

reform of the Irish education system (Conneely et al.,

2015; Department of Education and Skills, 2012;

Lawlor et al., 2015). The Bridge21 activity model is

inspired by the concept of Design Thinking (Brown,

2008), and brings together many of the elements of

Figure 1: The Bridge21 Activity Model.

21CL in a structured manner, scaffolding teachers’

introduction of the pedagogical approach. A Bridge21

learning experience involves a number of steps

(Figure 1):

1. Set-Up: Ice breaker and team formation.

2. Warm-Up: Divergent thinking activity.

3. Investigate: Explanation of the problem context.

4. Plan: Group planning.

5. Create: An iterative process

a. Exploration with resources.

i. In the field.

ii. In the classroom.

b. Modelling and Calculation:

i. Analysis and Synthesis.

6. Present: Competition and/or Presentations.

7. Reflect: Reflection and Discussion.

In addition to the activity process, Bridge21 observes

a particular model of collaboration and group work

influenced by the World Organisation of the Scout

Movement (Bénard, 2002), which emphasises mixed-

ability groups and individual, as well as group

reflection. The role of the teacher is to act as a guide

and mentor, scaffolding and orchestrating the

learning. The physical learning space is configured to

support an inquiry-based, technology-mediated, and

collaborative approach to learning. The Bridge21

approach to CPD involves teacher participation in a

full cycle of the activity model prior to the

collaborative development of their own activities and

their delivery in the classroom.

5 THE DESIGN HEURISTICS

In the Contextual Mathematics module, the use of a

particular set of Design Heuristics for the creation of

contextual 21CL mathematics activities is advocated.

These heuristics have been developed and refined by

the author over the course of the last three years. The

theoretical foundations of the set of Design Heuristics

were developed from an extensive literature review

(Bray and Tangney, 2013a; 2014; Tangney et al.,

2015). Particular attention was paid to the Realistic

Mathematics Education, or RME (Freudenthal, 1991)

approach to mathematics education, which, since its

inception in the 1960s has become internationally

influential in curriculum design (Clements et al.,

2013).

In conjunction with the theoretical foundations

stemming from the literature, an iterative process of

activity design, pilot activities and in-school

interventions were used to refine the Design

Heuristics (Bray et al., 2013; Bray et al., in press;

Bray and Tangney, 2013a; 2014). The primary

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action

221

concepts that underpin the heuristics can be

summarised as follows:

1. “Activities should follow a 21CL model such as

Bridge21: they should be collaborative and team-

based in accordance with a socially constructivist

approach to learning.

2. They should make use of a variety of technologies

(digital and traditional) suited to the task, in

particular, non-specialist mobile technology such

as smartphones and digital cameras that students

have to hand. Emphasis should be placed on the

transformative, as well as the computational,

capabilities of the technology.

3. Task design should prioritise guided-discovery,

involving problem-solving, investigation and

sense-making, and a move from concrete to

abstract concepts. Tasks should be open-ended,

allowing for different trajectories and solutions;

they should have a “low-floor” and “high-

ceiling”, such that all students will be able to

engage meaningfully with the problem, with the

potential for more interested/able students to push

its boundaries.

4. The context of the problem, and the learning

experience, should be interesting and

immersive/real, adapting the environment and

class routine as appropriate;

5. Presentation, competition and reflection can be

used for assessment purposes.” (Bray & Tangney,

In Press)

Activities designed in accordance with these

heuristics, and implemented using the Bridge21

approach have been associated with increases in

students’ levels of engagement with mathematics, and

their attitudes to using technology for its learning

(Bray et al., in press; Bray and Tangney, In Press).

6 METHODOLOGY AND

RESEARCH QUESTIONS

The work presented here is framed as an exploratory

case study, which aims to investigate teachers’

experiences of the creation and implementation of

mathematics activities designed in accordance with

the Design Heuristics and the Bridge21 methodology.

The research design is a single case study, with

multiple embedded units, each consisting of one of

fifteen teachers’ implementations of an activity in

their school, and subsequent reflection on the process.

The context is Post-Primary Education – Authentic

Setting (the researcher is not an observer), and the

case relates to teacher experiences and their

perceptions of their students’ engagement (Figure 2).

The written assignments, which include a description

and rationale for the design of the learning

experience, content and skills to be covered, evidence

to demonstrate student learning, and a personal

reflection on the experience, form the basis of the data

for analysis. As described in section 7, a constant

comparative analytic technique was used to highlight

the emerging themes (Strauss and Corbin, 2008).

Figure 2: Case Study Model.

The specific aims of this exploratory case study are:

1. To explore the experiences of teachers in the

creation and implementation of such activities,

with particular emphasis on their perceived

barriers to, and benefits of, the approach.

2. To explore the teachers’ perceptions of their

students’ experiences with the activities.

The data that has been collected for this exploratory

study is purely qualitative and comes from the written

reports of the teachers. Not all of the teachers

provided authorisation for their work to be included

in this research - the total number of assignments that

have been analysed is fifteen.

7 THE MATHS LEARNING

ACTIVITIES

A number of the teachers worked collaboratively on

the design of the activities, and joint implementation

was permitted for teachers at the same school. In total,

11 different activities were created by the 15 teachers.

The teacher-designed activities were conducted with

students across four different year groups, ranging in

age from 12 – 16. All of the activities were creative,

contextual and transformative in their use of

technology (Puentedura, 2006).

Context: Post-Primary Education -

Authentic Setting

Case: Teacher Experience

Teacher 1

Teacher

Teachers

...

Teacher

CSEDU 2016 - 8th International Conference on Computer Supported Education

222

Table 1: Teachers' Activities.

Activity Class Description

Heights with

Helium

Transition Year

(age 15/16)

A helium balloon and technology was used to find the measure of certain heights around our school.

This meant dealing with only two variables, Height and Time and being able to use the free video

analysis software Kinovea (www.kinovea.org) to obtain these variables and a Spreadsheet to graph

the data.

Functions in

context: analysing

trajectory.

Year

(age 13/14)

Each team of students take video clips of attempts to throw a ball into a basket. They then use

appropriate software to analyse the trajectory of a successful shot. Using a suitable graph, they

compare successful and unsuccessful shots.

Distance, Speed and

Time

Year

(age 14/15)

Students ask themselves “how fast am I running?” Based on their introduction to Kinovea and their

knowledge of Microsoft Excel, they are asked to answer this question and illustrate their answers

in the form of graphs and tables.

Statistics/

Height/Distance,

Speed and Time

Year

(age 12/13)

Working in groups, students are tasked with comparing the speed of the shortest and tallest

members of their group over a specified distance. The data collected, and analysis of their findings,

will be done using Kinovea.

Egg Drop

Challenge

Transition Year

(age 15/16)

Teams of four students work to design a method of safely dropping an egg from a first floor window.

They use smart phones, digital camera and iPads to visually record the activity. They generate data

from the activity and use a video App and maths analysis software to provide mathematical evidence

for their approach.

Quadratic

equations, functions

and algebra.

Transition Year

(age 15/16)

The students are asked to plot the quadratic function for the flight of their shot in a football crossbar

challenge. The students are dived into groups of 3-4 students. Each group works with the tracker

software to analyse the shot that is closest to hitting the crossbar. The students use the software

Kinovea and excel to find and plot the flight of their shot. The students are asked to analyse the graph

produced.

Children’s Birthday

Party

Year

(age 13/14)

Given an advertisement for a party hire company, the students use GeoGebra to explore different

combinations of tables etc. to get the best value for money.

Speed, Distance,

Time

Transition year

(age 15/16)

The students are presented with the problem ‘Who is the fastest in the class?’ In their groups they must

produce a method of experiment and a Microsoft excel presentation of their results.

Shoot a basket!

Year

(age 13/14)

In groups, the students develop different ways to analyse and make ‘real’ quadratic functions through

group work and peer teaching and learning. Students learn to select, create, and use many new forms

of technology, such as GeoGebra and Tracker (physlets.org/tracker). The groups will be briefly

introduced to the programmes but need to decide if it will help answer the question, “What makes a

successful shot successful?” As the students gain experience working with the programmes, they

become more aware of the technology available around them.

Speed\Distance\

Time, Statistics

Year

(age 12/13)

The students undertake a study to determine if the speed of the ball affects the chances of scoring goal.

Speed Camera

Year

(age 13/14)

In groups students are required to use technology to analyse the speed of cars passing by the school.

They represent the data using an appropriate chart and come up with a hypothesis as to whether

different coloured cars are more prone to breaking the speed limit based on their data.

Transition year is a one-year school programme in which the focus is on personal, social, vocational and educational development,

providing opportunities for students to experience diverse educational inputs in a year that is free from formal examinations.

The majority of the activities focussed on the

mathematics involved in data collection and

representation, patterns, and linear and quadratic

functions. In all cases this was reported as being the

first experience that the students had of generating

their own functions using “real” data that they had

collected empirically. Brief descriptions of the

activities are provided in Table 1.

Of particular relevance to this research are the

written reflections from the teachers’ assignments,

which provide insight into their experiences with the

implementation of contextual mathematics learning

activities and into the barriers to, and benefits of, the

approach.

8 ANALYSIS OF RESULTS

The results are drawn from a qualitative analysis of

the teachers’ reflections and a constant comparative

approach to the analysis of the data has been taken.

The steps in this process follow the procedure

outlined by Glaser (1965) and Strauss and Corbin

(2008). Constant comparison is a method of reducing

qualitative data to codes emerging from within the

original source, while retaining much of the richness

of the original data. Thus, the results of the analysis

can be used to create a rich picture of the teachers’

experiences, potentially identifying any common

themes or categories.

8.1 Generation of Initial Codes and

Categories

NVivo10 software was used to facilitate the process

of coding and theming. After the first five

assignments were analysed, a total of 23 codes were

identified. These fell into the two main categories of

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action

223

Barriers, with five associated codes, and Benefits,

with 18 associated codes. All segments of text

associated with each of these codes were re-examined

and compared before moving on to the next set of

assignments, of which the next four led to the addition

of five new codes, four under the category of

Benefits, and one under Barriers. At this point, the

process of memoing – keeping detailed notes on the

thought process involved behind the coding – was very

useful for highlighting areas that could potentially

benefit from re-organisation (Figure 3). In particular,

the codes associated with the category of Benefits

seemed to be developing into a number of

subcategories, some relating to teachers and some to

students, some to the development of key skills, and so

on.

The remaining six assignments only led to the

generation of two more codes, leading to the tentative

conclusion that a reasonable level of saturation of

codes may have been reached (Strauss and Corbin,

2008).

Figure 3: Sample Memo.

All of the text was re-examined after each session

of analysis, and particularly after the addition of new

codes, in order to compare the coded text within their

assigned nodes and also to identify whether they

could be associated with any other codes. This

process of constant evaluation and comparison has

led to a rigorous association of codes and text.

8.2 The Reduction of Codes

Once the initial development of codes and categories

was completed, the process of reducing and merging

the codes, and developing sub-categories began. This

involved an examination of the codes and the coded

segments in order to determine whether there was any

crossover of themes.

Figure 4: Barriers Category.

The Barriers category had significantly fewer

references than Benefits, and included student

abilities, teams, technical difficulties (at individual

and school level), and time constraints (Figure 4).

Table 2: Matrix Coding of Task Design and Perceived Benefits.

CSEDU 2016 - 8th International Conference on Computer Supported Education

224

(In Figures 4, 5 and 6, Sources refers to the

number of individual teachers whose data were

categorised at the related code, while References

relates to the overall number of coded segments.)

The category of Benefits had a total of 295

references, in comparison to only 37 in the Barriers

category. At this point in the analysis, a number of

subcategories were confirmed in the Benefits

category. These related to benefits to the students

(key skills, other outcomes, associated task attributes)

and benefits to the teachers (change in beliefs, teacher

as facilitator, and teacher as learner).

8.3 Analysis of Relationships

The process of analysis of relationships used the

coding matrix facility of NVivo10. Analysis focused

on the relationships between the teachers’ perceptions

of the task design elements that had an impact on

themselves and on their students, and their perceived

benefits. No associations between task attributes and

barriers were identified. Table 2, above, provides a

numerical analysis of the number of times that

segments of text were co-coded with a particular

aspect of task design and a perceived benefit. The

most significant elements (most frequently coded) of

the task design columns and perceived benefits

columns have been highlighted.

Using the sum functionality at the end of each row

and column, it is clear that the fact that the tasks were

student-led has had the most significant impact on

perceived benefits, particularly on the sense of

student ownership or autonomy, on their conceptual

understanding, and on engagement. The student-led

approach also seems to be significant in effecting a

change in the role of the teacher in the classroom.

Peer learning and the contextual nature of the task

design appear to have had beneficial effects on the

students and teachers, particularly in the areas of

collaboration, communication and engagement.

In terms of perceived benefits, it appears that the

task design has had most impact on student

engagement, with the tasks set in contexts that were

meaningful to the students and the student-centred

nature of the activities appearing to have the greatest

effect.

Conceptual understanding is highlighted as the

second highest co-coded perceived benefit, and this

seems to be related to tasks that are set in contexts that

are meaningful to the students, as well as the student-

led nature of the learning

9 FINDINGS

The findings that have emerged through analysis of

the relationships between task design and the

perceived benefits of the approach, go some way to

confirm the link between the approach to

mathematics teaching and learning and increases in

student engagement emerging from earlier research

(Bray et al., in press; Bray and Tangney, In Press). In

particular, there is an apparent link between the

student-led, contextual and meaningful approach to

activity design, and a perception of increased

engagement, conceptual understanding, and

confidence. However, in addition to these

relationships, a number of findings have emerged

relating to the teachers’ perceptions of the barriers to

the implementation of activities of this kind, and also

of the benefits that engagement with these tasks can

engender.

9.1 Barriers

The CPD model presented here, has addressed some

of the barriers to the integration of technology and the

implementation of new teaching and learning

strategies highlighted in the literature review, such as

a need for a structured and supportive approach

(Conneely et al., 2013; Dede, 2010a; Euler and Maaß,

2011; Means, 2010; Voogt and Roblin, 2012).

However, many of the more systemic barriers remain,

and have been identified by the teachers. The most

significant of these relates to time constraints and the

difficulty that implementing a project-based, inquiry

activity in a series of 40 minute classes, which was

identified as a problem in 10 of the 15 assignments

(Note: teacher initials have been used to code

quotations): “Having a longer block of time would

have been more productive, having to stop after 40

minutes and then pick up again a day or two later was

inconsistent, especially when we were running into

problems” (AH)

Technical barriers were an issue for nine of the

teachers, with five identifying personal difficulties

with the technology, which would be easily

rectifiable on a re-run of the project: “The camera we

were using ran out of battery power during the

penalty shoot outs... More cameras would need to be

made available, especially if more teachers were to

start working with this approach.” (WMI)

Eight of the teachers identified technical barriers

at the school level, which primarily related to

inadequate access to the technology: “Resourcing

fully functioning laptops could be a challenge - I need

to ensure that the limited number of laptops are

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action

225

available for at least three class periods.” (IS)

Other barriers that were identified by the teachers

referred to lower than expected levels of students’

technical expertise, and difficulties relating to the

development of well-functioning teams.

9.2 Benefits

The perceived benefits associated with the approach

far outweigh the barriers, and can be broken down

into benefits for teachers and benefits for students.

9.2.1 Benefits to Teachers

The teachers perceived a number of changes to their

beliefs and to their role in the classroom.

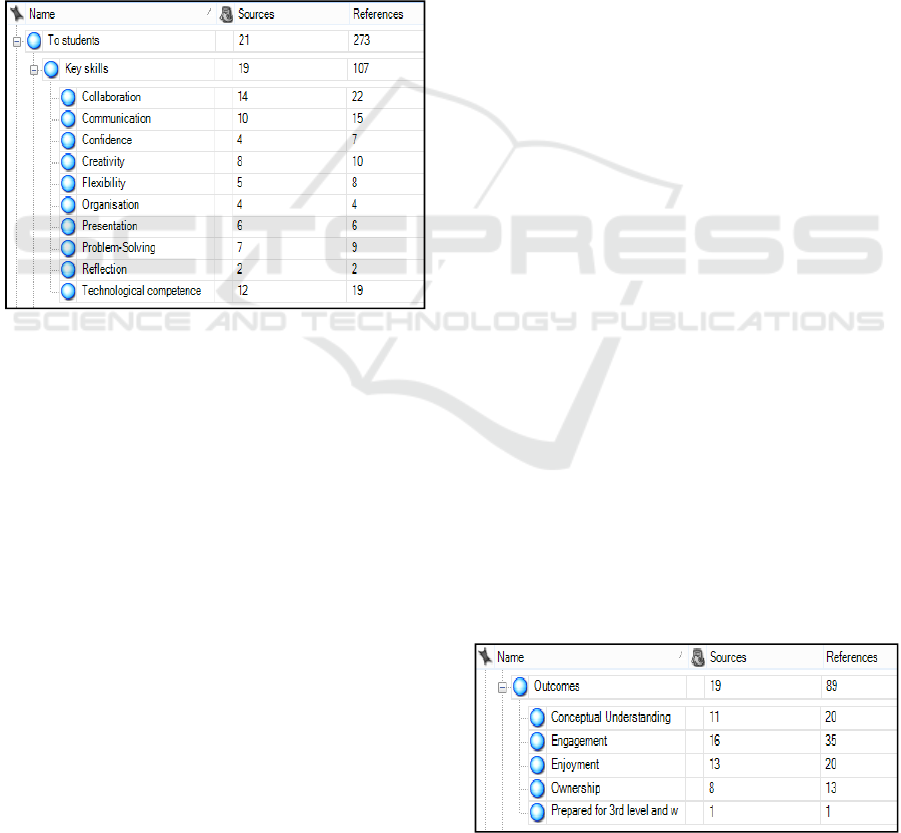
Figure 5: Key Skills.

Two of the teachers in particular discussed the

impact that teaching in this way has had on their

beliefs about mathematics teaching:

“After trying this, my eyes have been opened to the

possibilities of covering the curriculum, but by

changing the setting of the learning, you can teach a

lot more effectively to an audience who are stimulated

and engaged.” (JPF)

“I will be honest that I found it more difficult to

change my teaching style when it came to Maths. I

was teaching the way I was taught, which was with

very little understanding.” (MC)

It appears that the role of the teacher in the

classroom is significantly affected through the

implementation of these activities. The change in role

from transmitter of information to facilitator of

learning was not a comfortable one for some of the

teachers; however, in all cases, it was hailed as a

positive development, empowering the students to

take ownership of their own progress. “I decided to

tell the students of how this was as much of a learning

curve to me as it was to them. This was because I

really did feel that they would lose confidence in me

if they felt that I was trying to teach them rather than

facilitate them. This seemed to empower them as they

felt that even though I wasn’t part of their team, I was

learning and teaching with them.” (MC)

In addition to the change in role from teacher to

facilitator, six of the teachers also identified

themselves as co-learners in the classroom, both in

terms of learning about the technology with and from

the students, and learning about how to make

activities of this kind more successful in the future.

9.2.2 Benefits to Students

The benefits to the students have been deconstructed

into the subcategories of ‘key skills’, ‘other

outcomes’ and ‘associated task attributes’. The

relationships between the task attributes and the

perceived benefits of the approach have already been

discussed in section 7.3. This section will therefore

focus on the perceived benefits of the approach to

students, without dwelling on their associations with

the task design.

The key skills subcategory is made up of the

codes listed in Figure 5. It is clear from this figure that

the most common skills that were developed relate to

collaboration and communication, technological

confidence and creativity and problem-solving. The

students generally seemed to enjoy working in teams

and learning with and from their peers. Many of the

teachers recognised the potential that technology has

to facilitate a deeper understanding of the

mathematics involved in the activities, as well as

increasing the students’ technological skills.

“The resounding theme of the [student] reflection

was that they could really engage with one another

and more importantly that they could engage more

with the abstract topics of maths because of their

ability to use technology in everyday maths.” (DR)

In addition to the development of key skills, a

number of other beneficial outcomes emerged

through students’ participation in the activities

in figure 6.

Figure 6: Other Beneficial Outcomes.

CSEDU 2016 - 8th International Conference on Computer Supported Education

226

An increase in student engagement relating both

to how they felt about the subject (affective

engagement) and how they behaved in the classroom

(behavioural engagement) (Pierce, Stacey, &

Barkatsas, 2007), was evident through the teachers’

reflections. Comments such as those provided below,

clearly illustrate the sense of engagement and

motivation experienced by students and teachers

alike.

“All the team members were fully engaged in the

activity; their pride in and ownership of their

learning was clearly expressed… It’s really

heartening to encounter such a level of motivation

and commitment.” (DD)

“Please let’s do more of this stuff! It’s brought Maths

to life! I really get it now! J” (Student)

“This project was a thoroughly enriching experience

for both the students and teachers assisting them.”

(DOC)

“After this contextual Maths workshop, they asked for

a Maths club. To me that is success!” (MC)

There is a high level of cross-coding of segments

of text coded as engagement and as enjoyment.

However, a deeper analysis of the text coded at

enjoyment indicates that this code is particularly

closely related to affective engagement. Any

segments that are coded at enjoyment and not at

engagement relate specifically to the idea of having

fun in the class, both from the point of view of the

students, and the teachers:

“This project has highlighted one of the most

enjoyable pieces of technology that I have used in my

teaching career” (IB)

“I feel that the students enjoyed this realistic,

contextualized activity and by taking part they have

taken a step forward in developing their

technological skills, becoming better problem solvers

and gaining attributes in working as part of a team.”

(AH)

“The students also had fun, which they said that they

thought they would never be able to say about

Maths.” (MC)

An increase in students’ conceptual understanding

and confidence was identified in nine of the analysed

reports. This appears to be particularly closely

associated with the contextual and meaningful nature

of the tasks, a relationship that is clearly captured in

the following: “I am sure that none of these students

will ever forget how they deepened their

understanding of quadratic functions: the next time

they video a friend kicking a football or teeing off in

golf they will visualise that ball moving across the

Cartesian plane, describing a smooth parabola.”

(DD)

In addition, the open-ended task design and the

student-led approach within the classrooms appears

to have led to a deepening of the students’

understanding: “The open-ended nature of the activity

produced a new energy in the teams: they were not

working to find one answer (already known to me) but

were engaged in a meaningful exploration of the

topic.” (DD)

Seven of the reports refer to the increased sense

of student ownership of their work, leading in turn to

pride, engagement and motivation.

“Students came into their own when given the

opportunity to work as a group and they seemed to

grow as individuals even in the short space of time

while working in groups with their peers” (DR)

“Moreover, I feel that if I had taken over this aspect

of the project… I would be impacting on their self-

efficacy.” (DF)

By handing the responsibility for the learning to

the students, they were seen to develop as individuals

and as members of a group, with the apparent increase

in levels of motivation and pride in their learning

leading to higher levels of conceptual understanding.

“All the participants felt that they had created their

own quadratic function and understood that it could

be mathematically analysed.” (DD)

In summary, these findings provide a

compellingly positive picture of the approach to the

development and implementation of mathematics

learning activities that correspond to the design

heuristics described in this research.

10 DISCUSSION

The analysis of teachers’ reflections described in this

paper has provided an opportunity to explore various

aspects of the participants’ experiences of the

Contextual Mathematics module on the Postgraduate

Certificate, thereby addressing the research aims

identified in section 5. In particular, analysis of the

data has permitted:

• Examination of the experiences of teachers in the

creation and implementation of such activities,

paying particular attention to the barriers to, and

benefits of, the approach.

• Exploration of the teachers’ perceptions of their

students’ experiences with the activities.

These topics have been explored throughout this

research. This discussion will explore aspects of the

reflections that mirror concerns that emerged in the

literature review, and will also set out the primary

limitations of the exploratory study.

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action

227

10.1 Addressing the Issues

Throughout the analysis of the teachers’ reports, it

was interesting to see that many of the problems

associated with mathematics education that had been

identified through the literature review, were also

highlighted by the teachers taking part in this module.

The predominantly formulaic approach to text-book

questions (Boaler, 1993) was identified by one

teacher as an area that the approach advocated in the

CPD module, had the potential to address.

“These problems involved being given the function,

algebraically or graphically, and all the information

required to answer some fairly predictable questions.

There was never any redundant information either:

just enough and not too much to apply the usual

procedures… I considered that setting the students

the task of creating their own quadratic curve would

give them a real sense of ownership and a greater

insight into the nature of quadratic functions.” (DD)

The teachers’ reflections indicate a belief that this

approach may go some way to address the

fragmented, and de-contextualised nature that

frequently pervades school mathematics (Albert and

Kim, 2013; Dede, 2010a).

“It was useful for students to see different aspects of

Maths used in one place rather than the disjointed

treatment that they usually receive in a text book.”

(WMI)

In addition, as observed by Oldknow (2009), the

use of personal devices, such a mobile phones, to

generate mathematical models, contextualised the

mathematics for the students, providing a relevance

and meaning to the topic:

“For students, to discover that they can take their

ubiquitous phone out of their pocket and create a

mathematical model of an everyday event grounds

Maths in the real world.” (DD)

The issues surrounding teachers’ beliefs and their

changing role in the classroom can also be seen to be

addressed through the structured, immersive and

supportive nature of the CPD program. The provision

of a specific pedagogical structure (Bridge21) and set

of lesson design heuristics provide the teachers with

an approach that has been tested and shown to work.

The teachers all seemed to have been empowered by

this, and were confident to approach their classes in a

different way. The results appear to have been

beneficial for both teachers and students.

“I have worked with this particular class group on

two other 21

Century Teaching and Learning

Assignments. Their development throughout the

course of the year has been astounding. The flair with

which they now competently and confidently use

technology to gather and analyse information, and

present their findings is very impressive. This project

was a thoroughly enriching experience for both the

students and teachers assisting them.” (DOC)

10.2 Limitations

It is clear from this analysis that the approach to the

creation and implementation of mathematics learning

activities that has been developed in this research has

the potential to address many of the issues that were

highlighted in the literature review. However, it is

important to identify the limitations of this study.

Firstly, the sample that is used in this exploratory

study consists of teachers who have opted to be a part

of the research, and who are participants on a CPD

course that they have chosen to attend. It is therefore

a self-selecting sample and cannot be seen as

representative.

Another point that needs to be highlighted is that

the reflective pieces provided by the teachers were all

submitted for assessment purposes. There is a

possibility that the participants therefore emphasised

the positive aspects of their experiences more than the

negative. This is a limitation of the study to date,

which future work will aim to overcome through

interviews with participants and their students and

non-participant observation of the classes.

Another drawback of this exploratory study is its

small size. The analysis of fifteen teachers’ reports is

unlikely to permit the generation of any substantive

theory. However, the consistency of the results do

allow the generation of hypotheses and research

questions to follow up on the initial, very promising,

findings.

11 CONCLUSIONS

This study will require further expansion in order to

fully examine the emerging themes. It is a very

encouraging however, to see such positive results

emerging from the work with teachers. In particular,

the following quote from one of the attendees on the

Contextual Mathematics module highlights the

teachers’ understanding of the intention behind this

research.

“The importance of 21

Century teaching and

learning and indeed the B21 model can be seen by

Green and Hannon who state, “In an economy driven

by knowledge rather than manufacturing, employers

are already valuing very different skills, such as

creativity, communication, presentation skills and

team building. Schools are at the frontline of change

CSEDU 2016 - 8th International Conference on Computer Supported Education

228

and need to think about how they can prepare young

people for the future workplace” (2007, p. 15). As

such a huge emphasis is being placed on STEM

subjects/activities in schools, RME in conjunction

with the B21 model helps to contextualise maths for

our students, increasing their engagement and

allowing them to use technology in a meaningful

way.” (MC)

REFERENCES

Albert, L. R., & Kim, R. (2013). Developing creativity

through collaborative problem solving. Journal of

Mathematics Education at Teachers College, 4(2), 32 -

38.

Bénard, D. (2002). A method of non-formal education for

young people from 11 to 15. Handbook for Leaders of

the Scout Section. World Scout Bureau, Geneva.

Boaler, J. (1993). Encouraging the transfer of ‘school

’mathematics to the ‘real world’ through the integration

of process and content, context and culture.

Educational studies in mathematics, 25(4), 341-373.

Bray, A., Oldham, E., & Tangney, B. (2013). The Human

Catapult and Other Stories – Adventures with

Technology in Mathematics Education. 11th

International Conference on Technology in

Mathematics Teaching (ICTMT11), 77 - 83.

Bray, A., Oldham, E., & Tangney, B. (in press).

Technology-Mediated Realistic Mathematics

Education and the Bridge21 Model: A Teaching

Experiment. Ninth Congress of European Research in

Mathematics Education (CERME9).

Bray, A., & Tangney, B. (2013a). Mathematics, Pedagogy

and Technology - Seeing the Wood From the Trees. 5th

International Conference on Computer Supported

Education (CSEDU 2013), 57 - 63.

Bray, A., & Tangney, B. (2013b). Mathematics,

Technology Interventions and Pedagogy. Eighth

Congress of European Research in Mathematics

Education (CERME8), 2774 - 2776.

Bray, A., & Tangney, B. (2014). Barbie Bungee Jumping,

Technology and Contextual Learning of Mathematics.

6th International Conference on Computer Supported

Education (CSEDU 2014), 3, 206 - 213.

Bray, A., & Tangney, B. (In Press). Enhancing Student

Engagement through the Affordances of Mobile

Technology: A 21st Century Learning Perspective on

Realistic Mathematics Education. Mathematics

Education Research Journal.

Bridge21. (2014). Postgraduate Certificate in 21st Century

Teaching and Learning Course Handbook 2014/2015.

Dublin: Trinity College Dublin.

Brown, T. (2008). Design thinking. Harvard business

review, 86(6), 84.

Clements, M. A., Keitel, C., Bishop, A. J., Kilpatrick, J., &

Leung, F. K. S. (2013). From the few to the many:

Historical perspectives on who should learn

mathematics. In M. A. Clements, A. J. Bishop, C.

Keitel, J. Kilpatrick, & F. K. S. Leung (Eds.), Third

International Handbook of Mathematics Education (pp.

7 - 40). New York: Springer.

Commission of the European Communitities. (2008).

Improving competences for the 21st Century: An

Agenda for European Cooperation on Schools

(SEC(2008) 2177). Retrieved from http://eur-

lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2

008:0425:FIN:EN:PDF.

Conneely, C., Girvan, C., & Tangney, B. (2015). An

Exploratory Case Study into the Adaption of the

Bridge21 Model for 21st Century Learning in Irish

Classrooms. In D. Butler, K. Marshall, & M. Leahy

(Eds.), Shaping our Future: How the lessons of the past

can shape educational transformation (pp. 348-381).

Dublin: Liffey Press.

Conneely, C., Lawlor, J., & Tangney, B. (2013).

Technology, Teamwork and 21st Century Skills in the

Irish Classroom. In K. Marshall (Ed.), Shaping our

Future: How the lessons of the past can shape

educational transformation. Dublin: Liffey Press.

Conneely, C., Murchan, D., Tangney, B., & Johnston, K.

(2013). 21 Century Learning - Teachers' and Students'

Experiences and Views of the Bridge21 Approach

within Mainstream Education. Society for Information

Technology & Teacher Education International

conference (SITE), 5125 - 5132.

Conole, G. (2008). New schemas for mapping pedagogies

and technologies. Ariadne(56), 2.

Dede, C. (2010a). Comparing frameworks for 21st century

skills. In J. Bellanca & R. Brandt (Eds.), 21st century

skills: Rethinking how students learn (pp. 51-76).

Bloomington, IN: Solution Tree Press.

Dede, C. (2010b). Technological supports for acquiring

21st century skills. International Encyclopedia of

Education, 158-166. Retrieved from

https://ejournal.narotama.ac.id/files/Technological%20

Supports%20for%20Acquiring%2021st%20Century%

20Skills.pdf.

Department of Education and Skills. (2012). A Framework

for Junior Cycle. Retrieved from Dublin:

www.juniorcycle.ie/NCCA_JuniorCycle/media/NCC

A/Documents/JC-Framework_FINAL_02oct12.pdf.

Donnelly, D., McGarr, O., & O’Reilly, J. (2011). A

framework for teachers’ integration of ICT into their

classroom practice. Computers & Education, 57(2),

1469-1483.

Euler, M., & Maaß, K. (2011). Report about the survey on

inquiry-based learning and teaching in the European

partner countries. Retrieved from Freiburg:

http://www.primas-project.eu/

Freudenthal, H. (1991). Revisiting mathematics education:

China lectures (Vol. 9). Dordrecht/Boston/London:

Springer.

Fullan, M., & Langworthy, M. (2014). A rich seam: How

new pedagogies find deep learning (Vol. 100). London:

Pearson.

Glaser, B. G. (1965). The Constant Comparative Method of

Qualitative Analysis. Social Problems, 12(4), 436-445.

Teachers’ Experiences of the Integration of 21st Century Learning in the Mathematics Classroom - The Bridge21 Model in Action

229

Green, H., & Hannon, C. (2007). Their Space. Education

for a Digital Generation. Retrieved from London:

www.demos.co.uk/files/Their%20space%20-

%20web.pdf.

Lawlor, J., Conneely, C., & Tangney, B. (2010). Towards a

pragmatic model for group-based, technology-

mediated, project-oriented learning–an overview of the

B2C model. In M. D. Lytras, P. Ordonez De Pablos, D.

Avison, J. Sipior, Q. Jin, W. Leal, L. Uden, M. C.

Thomas, S., & D. G. Horner (Eds.), Proceedings of the

2010 TechEduca Conference (pp. 602-609). Athens.

Lawlor, J., Marshall, K., & Tangney, B. (2015). Bridge21 –

Exploring the potential to foster intrinsic student

motivation through a team-based, technology mediated

learning mode. Technology, Pedagagy and Education,

in press, 1-20.

Lewis, C. C., Perry, R. R., & Hurd, J. (2009). Improving

mathematics instruction through lesson study: A

theoretical model and North American case. Journal of

Mathematics Teacher Education, 12(4), 285-304.

Maaß, K., & Artigue, M. (2013). Implementation of

inquiry-based learning in day-to-day teaching: a

synthesis. ZDM, 45(6), 779-795.

Martin, A., & Grudziecki, J. (2006). DigEuLit: concepts

and tools for digital literacy development. Innovation in

Teaching And Learning in Information and Computer

Sciences, 5(4), 249-267.

Means, B. (2010). Technology and education change:

Focus on student learning. Journal of research on

technology in education, 42(3), 285-307.

Oldknow, A. (2009). Their world, our world—bridging the

divide. Teaching Mathematics and its Applications,

28(4), 180-195.

Pierce, R., Stacey, K., & Barkatsas, A. (2007). A scale for

monitoring students’ attitudes to learning mathematics

with technology. Computers & Education, 48(2), 285-

300.

Puentedura, R. (2006). Transformation, Technology, and

Education. Retrieved from

http://hippasus.com/resources/tte/

Strauss, A. L., & Corbin, J. M. (2008). Basics of Qualitative

Research: Techniques and Procedures for Developing

Grounded Theory 3e (3rd ed.). Thousand Oaks, CA:

Sage Publications, Inc.

Takahashi, A., & Yoshida, M. (2004). Lesson-Study

Communities. Teaching Children Mathematics, 10(9),

436-437.

Tangney, B., Bray, A., & Oldham, E. (2015). Realistic

Mathematics Education, Mobile Technology & The

Bridge21 Model for 21st Century Learning - A Perfect

Storm. In H. Crompton & J. Traxler (Eds.), Mobile

Learning and Mathematics: Foundations, Design, and

Case Studies (pp. 96 - 106). Oxon, UK: Routledge.

Voogt, J., & Roblin, N. P. (2012). A comparative analysis

of international frameworks for 21st century

competences: implications for national curriculum

policies. Journal of Curriculum Studies, 44(3), 299-

321.

CSEDU 2016 - 8th International Conference on Computer Supported Education

230