
HMM-based Transient and Steady-state Current Signals Modeling for
Electrical Appliances Identification
Mohamed Nait-Meziane
1
, Abdenour Hacine-Gharbi
2
, Philippe Ravier
1
, Guy Lamarque
1
,
Jean-Charles Le Bunetel
3
and Yves Raingeaud
3
1
PRISME Laboratory, University of Orl
´
eans, 12 Rue de Blois, 45067 Orl
´
eans, France
2
LMSE Laboratory, University of Bordj Bou Arr
´
eridj, Elanasser, 34030 Bordj Bou Arr
´
eridj, Algeria
3
GREMAN Laboratory, UMR 7347 CNRS - University of Tours, 20 Avenue Monge, 37200 Tours, France
Keywords:
Electrical Appliances Identification, Energy Disaggregation, Harmonic Analysis, Hidden Markov Mod-
els (HMM), Non-Intrusive Load Monitoring (NILM), Parameter Relevance, Short-Time Fourier Se-
ries (STFS), Smart Grids, Transient and Steady-state Electrical Signal Analysis.
Abstract:
The electrical appliances identification problem is gaining a rapidly growing interest these past few years due
to the recent need of this information in the new smart grid configuration. In this work, we propose to construct
an appliance identification system based on the use of Hidden Markov Models (HMM) to model transient and
steady-state electrical current signals. For this purpose, we investigate the usefulness of different choices for
the proposed identification system such as: the use of the transient and the steady-state current signals, the use
of even and odd-order harmonics as features, and the optimal number of features to take into account. This
work also discusses the choice of the Short-Time Fourier Series (STFS) coefficients as adapted features for
the representation of transient and steady-state current signals.
1 INTRODUCTION
The way power grids work to provide the needed elec-
trical energy has changed a lot in the last few years.
Classically, in the power grid, the energy goes only
one way, i.e. from the power stations (usually ther-
mal) to the consumers. With the advent of the idea of
exploiting renewable energy resources (wind power,
solar power, hydropower, etc.) the flow of energy in
the power grid can no longer go only one way. A con-
sumer having a wind turbine, solar cells, or other
renewable-based energy generation systems becomes
also an energy producer and this gives rise to a decen-
tralized energy production. Also, in this new config-
uration, the energy production is no longer based on
one energy source (thermal) but it can be generated
using different, eventually renewable, energy sources.
These new mutations created the need for an upgrade
to the power grid and the result is what we call a smart
grid.
As defined in (Gellings, 2009): “a smart grid is the
use of sensors, communications, computational abil-
ity and control in some form to enhance the overall
functionality of the electric power delivery system.”
Adding these features to a power grid allows a bet-
ter monitoring and a continuous supervision of the
energy flow. The energy sensors (or energy meters)
along with their communication and computational
capabilities are the basic building block of a smart
grid. An energy meter allows the access to the energy
consumption information of the appliance or group of
appliances it measures.
The importance of energy metering and detailed
electrical consumption information has been dis-
cussed in several previous works (Fischer, 2008)
(Darby, 2006) (Darby, 2010) (Hancke et al., 2012).
The impact of this information on the consumer be-
havior has been studied in (Chakravarty and Gupta,
2013) where the results showed that on average the
consumers that used a solution that allowed the break
down of the energy consumption consumed on aver-
age 14% less energy than the consumers that did not
use it. According to (Carrie Armel et al., 2013), the
benefits of appliance-level electrical consumption in-
formation over global consumption fall into three cat-
egories: (1) benefits to the consumer through possi-
ble energy savings thanks to the consumption feed-
back, (2) research and development benefits since the
feedback allows the understanding of appliance en-
ergy consumption profiles and then redesigning ap-
670
Nait-Meziane, M., Hacine-Gharbi, A., Ravier, P., Lamarque, G., Bunetel, J-C. and Raingeaud, Y.
HMM-based Transient and Steady-state Current Signals Modeling for Electrical Appliances Identification.
DOI: 10.5220/0005759506700677
In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 670-677
ISBN: 978-989-758-173-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

pliances for energy efficiency, and (3) utility and pol-
icy benefits such as allowing for improved load fore-
casting (Feinberg and Genethliou, 2005) and energy
demand prediction which is very important when it
comes to decision making and taking economically
reliable actions either by utilities or governments.
2 GENERAL BACKGROUND FOR
ELECTRICAL APPLIANCES
IDENTIFICATION
To break down the global energy consumption into
its different constituent parts (for example, the whole
home energy consumption into the appliance-level
energy consumption) three approaches can be consid-
ered: intrusive, semi-intrusive, and non-intrusive ap-
proaches.
Intrusive Load Monitoring (ILM) approaches are
based on the use of distributed sensing meters to sup-
port control, monitor and intervention of such de-
vices (Burbano Acu
˜
na, 2015). As stated by (Parson,
2012) different forms of ILM can be found:
• Electrical sub-metering: one energy meter is used
for each appliance
• Smart appliances: the appliances have communi-
cating chips that allows them to self-report their
energy consumption to a central unit
• Electrical probing: transmitting an electrical sig-
nal into the households mains circuit and analyz-
ing the return signal
The ILM do not seem to be viable solutions since
they assume the installation of different energy meters
in different household locations which is not easy to
do and most of the time costly. Semi-Intrusive Load
Monitoring (SILM) is somehow a relaxed version of
the ILM, where instead of using energy meters one
per appliance, we use one energy meter to measure a
group of appliances (Tang et al., 2014). SILM share
the same drawbacks of the ILM but with less intru-
sion. Very little information can be found, in the lit-
erature, on SILM and this may be because they are
usually confused with ILM approaches.
Non-Intrusive Load Monitoring (NILM) is a field
where the main concern is to break down an ag-
gregated energy consumption into its different con-
stituent parts in a non-intrusive way using only one
energy meter. For example, instead of introducing
different energy meters put all around the household
we only put one energy meter at the main breaker
panel level. The work on this field started with Hart
in the late 1980s (Hart, 1989) (Hart, 1992) where he
proposed to use the (real) power consumption varia-
tion to identify household appliances. Even though
some other work was done in this field after Hart
between the early 1990s and the late 2000s (Sul-
tanem, 1991) (Leeb et al., 1995) (Cole and Al-
bicki, 1998) (Drenker and Kader, 1999) (Chan et al.,
2000) (Baranski and Voss, 2003) (Laughman et al.,
2003) (Ting et al., 2005) (Patel et al., 2007) (Chang
et al., 2008) it was not until around five years ago
that this field started to gain a rapidly growing inter-
est. A state of the art for the NILM techniques can be
found in (Najmeddine et al., 2008) (Du et al., 2010)
and (Zeifman and Roth, 2011). In (Carrie Armel
et al., 2013) the authors gave a table that summa-
rizes some of the works done in the NILM field up
to 2012. They organized them in a chronological or-
der and gave some details on the used methods, data
types, appliance types, data frequency, and other in-
teresting characteristics.
In this study we propose the use of Hidden
Markov Models (HMM) for transient electrical sig-
nals modeling and classification. The obtained fea-
tures are to be used eventually as a complementary
information that helps a NILM system identify home
appliances. Previous work on NILM using HMM was
done by (Zia et al., 2011) (Beckel et al., 2012) (Par-
son, 2012) and more recently by (Ridi and Hen-
nebert, 2014) and (Parson et al., 2014). In these stud-
ies, the authors applied their proposed approaches on
low-frequency sampled signals (for example, (Beckel
et al., 2012) used the REDD dataset
1
with 1 Hz
sampling frequency signals and (Ridi and Hennebert,
2014) used the ACS-F1 dataset
2
that has 10 Hz sam-
pling frequency signals). In our study, we propose
the use of HMM on high-frequency sampled signals
and we use for this purpose the recently released
PLAID dataset (PLAID, 2015). It is worth mention-
ing that the lack of a proper database that is informa-
tive, diverse, and scalable (Lai et al., 2012) of high-
frequency sampled electrical signals for appliances
hindered a lot the development of high-frequency
NILM. This was one of the concerns that have been
discussed by the NILM community during the 2nd
European NILM workshop (July, 2015) held in Lon-
don
3
.
In the literature, and to the best of our knowl-
edge, the authors of (Thiruvaran et al., 2013) are the
only ones, to date, that have done a study on high-
frequency sampled signals (10 kHz) using HMM.
In (Thiruvaran et al., 2013) the authors proposed to
1
http://redd.csail.mit.edu/
2
http://www.wattict.com/web/index.php/databases/acs-
f1
3
http://www.nilm.eu/
HMM-based Transient and Steady-state Current Signals Modeling for Electrical Appliances Identification
671

use the Short-Time Fourier Transform (STFT) and
Wavelet Tranform (WT) coefficients as features for
their identification system and as a dataset they col-
lected measurements of current and voltage wave-
forms for four different appliances (a fluorescent
lamp, an incandescent lamp, a computer monitor, and
a motor). To acquire the waveforms, these four ap-
pliances were used to form switching-on sequences
(24 possible sequence in total). For example, as a se-
quence we can imagine: the fluorescent lamp is first
turned-on, then the incandescent lamp, then the com-
puter monitor and then the motor. Finally, they an-
nounced accuracies of 97.9% when using the STFT
features and 93.75% when using the WT features. In
our study, we propose to consider not only the tran-
sient but also the steady-state and we quantify the use-
fulness of the transient part over the steady-state part
for appliance recognition. Also, the accuracies ob-
tained in (Thiruvaran et al., 2013) can not quantify the
real recognition accuracy of the HMM-based system
due to the small size of the used dataset. This is why
the use of the PLAID dataset should allow more reli-
able results. Along with this, we propose in our study
the evaluation of the harmonic-order on the recogni-
tion accuracy of the proposed HMM-based system
instead of just taking into account all the harmon-
ics. Another difference compared to the work done
in (Thiruvaran et al., 2013) is that the PLAID dataset
signals are electrical signals of individual appliances.
That means that each signal was acquired with only
one appliance operating alone. Analyzing such sig-
nals should allow the determination of intrinsic high-
frequency characteristic features for the different ap-
pliances that can be used afterwards as a complemen-
tary information in a larger recognition system with
data fusion capabilities.
3 HARMONIC ANALYSIS
There are different ways to analyze the harmonic con-
tents of a signal. The most known method is the use of
the Fourier Transform (FT). For a discrete-time signal
s[n] we define the Discrete Fourier Transform (DFT)
as follows (Mallat, 1999):
S [k] =
L−1
∑
n=0
s[n]exp
− j2πkn
L
, k = 0, . .., L − 1
(1)
where L is the length of s[n] in samples. The com-
putation of the harmonic content of s[n] using Equa-
tion 1 starts to become heavier as L becomes bigger
and bigger even when using fast algorithms like the
Fast Fourier Transform (FFT), especially, when the
dataset is big and a lot of signals have to be analyzed.
Since the electrical current signals are periodic (the
steady-state signals), we propose to exploit this char-
acteristic to improve the computational time using the
Fourier Series (FS) decomposition instead of the FT.
The FS are particular instances of the FT for Dirac
sums (Mallat, 1999). This means that to get the FT
of a periodic signal we only have to compute its FS
coefficients. For the periodic signal s[n], the Discrete
FS (DFS) decomposition is:
s[n] =
N−1
∑
k=0
C
k
exp
j2πkn
N
, (2)
where N is the period of s[n] in samples and
C
k
=
1
N
N−1
∑
n=0
s[n]exp
− j2πkn
N
, k = 0, . .., N − 1
(3)
are the DFS coefficients of s[n]. Even though, Equa-
tions 1 and 3 look similar (up to a factor), the main
difference is the number of samples over which the
sum is computed. By summing over the signal pe-
riod N (usually < L) instead of over the whole signal
length we gain in computational time.
The DFS coefficients C
k
, k = 1, ..., N − 1
(Equation 3) correspond to the fundamental fre-
quency of the periodic signal (k = 1) and its har-
monics. For the steady-state electrical current signals
these frequencies appear to represent most, if not all,
of the information contained in the signal. Hence, this
is another reason that justifies the use of the DFS in-
stead of the DFT.
For transient electrical current signals, however,
the periodicity property is lost and strictly speaking
we are not allowed to use Equations 2 and 3. Nev-
ertheless, we think that even for the transient signals,
the important of the signal information is contained
around the fundamental frequency and its harmonics.
That is why we chose to represent the transient signals
also using the DFS coefficients.
Since our approach is based on dividing the elec-
trical current signals (transient and steady-state) into
overlapping windows and computing the DFS on each
window, the obtained coefficients can be called Short-
Time Fourier Series (STFS) coefficients. Hence, for
the remainder of the paper we will use the notation
STFS instead of DFS. Each STFS coefficients’ vec-
tor (computed on a window) is called an observation.
Thus, each waveform (an electrical current signal) is
represented by a sequence of vectors considered as a
sequence of observations for the HMM-based classi-
fication.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
672

4 EXPERIMENTAL RESULTS
AND DISCUSSION
The appliance identification system is mainly based
on three things: a dataset, a feature extraction (even-
tually feature selection) algorithm, and a classifier.
As dataset we chose the PLAID dataset for which
we give a brief description in the next sub-section.
This dataset contains current and voltage waveforms
(sometimes instantaneous power) of different appli-
ances. For our study, we have decided to only use
the current waveforms as an appliance signature for
two main reasons. The first one is that the voltage
waveform does not change much for the different ap-
pliances and hence does not add much information to
the identification system. Actually, from a theoretical
point of view, the voltage waveform is not supposed
to change. We expect the voltage waveform to always
be a sine wave with a fixed frequency equal to the
power line frequency of 50 or 60 Hz (depending on
the considered country) and a fixed root-mean-square
(rms) voltage. Even though this is not a hundred per-
cent true (since there are always fluctuations in the
power grid characteristics) we can assume to a certain
degree that it is the case in practice. The second rea-
son is that we found on the dataset a lot of voltage
waveforms that are incorrectly calibrated (i.e. having
incorrect amplitude values that diverge a lot from the
standard rms value of the grid voltage).
The used feature extraction algorithm is based on
the STFS already discussed in section 3 and the con-
sidered features are the magnitudes of the STFS co-
efficients. For the classifier we chose to use Hid-
den Markov Models (HMM) for their capabilities to
model dynamic time variations of signals.
An HMM is a finite state machine which changes
state once every time unit (the value of the time unit
depends on the observed phenomenon). Each time t
that a state j is entered, an observation vector o
t
is
generated from a probability density b
j
(o
t
). The tran-
sition from state i to state j is also probabilistic and is
governed by the discrete probability a
i j
. The emission
likelihood b
j
for state j and observation o
t
at time t is
done by a Gaussian Mixture Model (GMM) (Hacine-
Gharbi et al., 2012):
b
j
(o
t
) =
M
∑
m=1
c
m
N (o
t
;µ
µ
µ
m
,Σ
m
), (4)
where N (o; µ,Σ) is the value in o of a multivariate
Gaussian with mean µ
µ
µ and covariance Σ. M Gaussians
are used in a mixture, each weighed by c
m
.
The classifier is based on modeling each appliance
type by an HMM using the Hidden Markov Model
Toolkit (HTK) library (Young et al., 2009). The train-
ing is done in several steps by applying the embed-
ded Baum–Welch reestimation (HEREST command).
For the identification step we used the Viterbi algo-
rithm (HVITE command). More details on the al-
gorithms used for training and identification can be
found in (Young et al., 2009). For our identification
system, we chose to model each appliance type us-
ing 3 states, and each state using 3 Gaussian mix-
tures. Each waveform was subdivided into overlap-
ping windows and from each window N features can
be extracted (even though in practice we only choose
a reduced number to work with, see the end of sub-
section 4.4). The window size was fixed to 16.7 msec
(500 samples at 30 kHz frequency) that corresponds
to the 60 Hz cycle-time and the overlapping to 50%
of the window size.
The identification results are evaluated using the
Classification Rate (CR) defined as:
CR(%) =
T − M
T
× 100, (5)
where T is the total number of tested waveforms
(each one representing an appliance) given to the in-
put of the classifier and M is the number of misclassi-
fied tested waveforms.
4.1 Summary of the PLAID Dataset
The Plug Load Appliance Identification Dataset
(PLAID) is a public dataset of electric signatures.
These signatures are current and voltage measure-
ments taken during the summer of 2013 in Pittsburgh,
Pennsylvania, USA, from 55 households. This dataset
contains 11 appliance types and for each appliance
from three to six instances (the dataset contains a to-
tal of 1074 instances). Each signature of the dataset
is a few-second-long signal containing the turn-on
transient (when available, since for some appliances
like the “Fridge” for example, which is usually work-
ing all the time, the turn-on transient is not always
present) and a portion of the steady-state part (that
corresponds to the steady consumption phase). These
signals are sampled at a 30 kHz rate. Table 1 summa-
rizes the appliances found on the dataset: the differ-
ent appliance types and the number of instances for
each type. For more details on the dataset please refer
to (Gao et al., 2014). Finally, it is worth pointing out
that the values of the number of instances we found
in the dataset for each appliance type were most of
the time different than the ones given in (Gao et al.,
2014). The total number of instances in the dataset is
also different. This might be due to an update of the
dataset after the publication of the paper (Gao et al.,
2014).
HMM-based Transient and Steady-state Current Signals Modeling for Electrical Appliances Identification
673

Table 1: Summary of the appliances found on the PLAID
dataset.
Appliance type Number of instances
Air Conditioner 66
Compact Fluorescent
Lamp
175
Fan 115
Fridge 38
Hairdryer 156
Heater 35
Incandescent Light
Bulb
114
Laptop 172
Microwave 139
Vacuum cleaner 38
Washing Machine 26
Total 1074
4.2 PLAID Dataset Subdivision for
Training and Tests
In this work, the dataset is divided into a training set
that allows the learning of appliances HMM mod-
els and a test set for the performance evaluation of
the identification system. It is considered that all the
houses (55 in total) have examples in the training and
in the test sets. In order to study the effect of the num-
ber of waveform versions belonging to training and
test sets, we proposed four subdivisions. In the first
one, we take for each house, at most one version of the
reference signal corresponding to a particular appli-
ance and the other versions are kept for testing. This
subdivision gives us 230 training waveforms and 844
test waveforms. The other subdivisions are obtained
by changing the maximum number of waveform ver-
sions to put in the training set from 2 to 4. Thus, we
got the four subdivisions shown in Table 2, where sbi
Table 2: Different tested subdivisions of the dataset
sb # sb1 sb2 sb3 sb4
NTR 230 441 648 848
NTEST 844 633 426 226
indicates the subdivision with “i” waveform versions
in the training set. NTR is the number of the consid-
ered training waveforms and NTEST is the number
of the considered test waveforms. For the following
sub-sections, the results are given for each one of the
above mentioned subdivisions.
4.3 Transient vs. Steady-state Electrical
Signals Usefulness for Appliance
Identification
The goal of the experiment done in this sub-section is
to study the usefulness of the transient and the steady-
state parts of the electrical current signals for the iden-
tification task of the different appliances. This ex-
periment required us to segment the PLAID dataset
waveforms each into a transient part and a steady-
state part. This segmentation was done by character-
izing the transient part as the one with the large energy
variation compared to the steady-state part. For the
performance evaluation, the classification rate CR us-
ing the transient part (TP), steady-state part (SSP) and
the overall part (OP) was computed. This evaluation
takes into account the different dataset subdivisions
mentioned in sub-section 4.2. Note that in this exper-
iment, we only used 10 STFS coefficients. Table 3
gives the CR for each subdivision sbi each time con-
sidering a different waveform part (OP, TP and SSP).
Table 3: Transient vs. Steady-state CR evaluation.
sb # sb1 sb2 sb3 sb4
CR (%), OP 86.02 87.36 87.56 88.50
CR (%), TP 88.98 91.15 90.85 92.48
CR (%), SSP 86.61 88.94 86.62 88.50
From these results, we can say that the use of the
transient part is the one that gives the best CR. More-
over, the results show that the computational time
when using only the transient part is much lower com-
pared to the others. For example, in the case of sb2,
the running test time was 218 seconds for TP, 418 sec-
onds for SSP, and 436 seconds for OP. The hardware
used for the experiment is a computer with an Intel
Core i5 processor and 4 GB of RAM memory.
Thereby, the use of the transient should allow the
construction of an appliance identification system that
is fast and accurate which justifies its usefulness for
the appliance identification task. In order to improve
the identification, we studied further the harmonic
analysis by taking into account the harmonic order
(even or odd) and the optimal number of STFS co-
efficients to choose. The details are given in the next
sub-sections.
4.4 Even vs. Odd Harmonic Order for
Appliance Identification
The experiment presented in this sub-section allows
the study of the harmonic order (even or odd or-
der) relevance for the appliance identification task.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
674
This experiment is similar to the one done in sub-
section 4.3 but we only consider the transient part,
following the results of sub-section 4.3. For the per-
formance evaluation, we compared the identification
system CR when using even harmonics only, odd har-
monics only, and when using both. For each one of
these configurations, we used the corresponding first
5 STFS coefficients as features (i.e, first 5 even har-
monics, first 5 odd harmonics, and first 5 harmon-
ics independently of the order, respectively). Table 4
gives the obtained CR for each tested configuration.
From Table 4, we can deduce the following conclu-
Table 4: Even vs. Odd CR evaluation.
sb #
sb1 sb2 sb3 sb4
CR (%),
(even+odd)
88.98 91.15 90.85 92.48
CR (%),
even
63.63 64.45 64.79 63.27
CR (%),
odd
90.05 89.57 89.44 90.71
sions:
• The odd-order harmonics give the best perfor-
mance results no matter the considered subdivi-
sion w.r.t. the even-order harmonics
• The even-order harmonics give the worst perfor-
mance results
• Adding the even-order harmonics to the odd-order
harmonics feature vector does not seem to im-
prove a lot the CR
To conclude, the coefficients of the fundamental and
its odd harmonics are the most useful for the appli-
ance identification task. This can be explained by the
half-wave symmetry usually found in electrical sig-
nals (i.e. for a periodic signal g(t) with period T , we
have g(t) = −g(t ±T /2)) (Nait Meziane et al., 2015).
This half-wave symmetry causes the even order coef-
ficients to have null values.
4.5 Optimal Number of Harmonics for
Appliance Identification
A very important parameter to take into account is the
optimal number (the smallest) of STFS coefficients to
consider in order to guarantee the best CR. To get
an insight on what this optimal number is, we eval-
uated the identification system using various feature
vector (STFS coefficients number) sizes. We only
considered the odd harmonics coefficients from 1 to
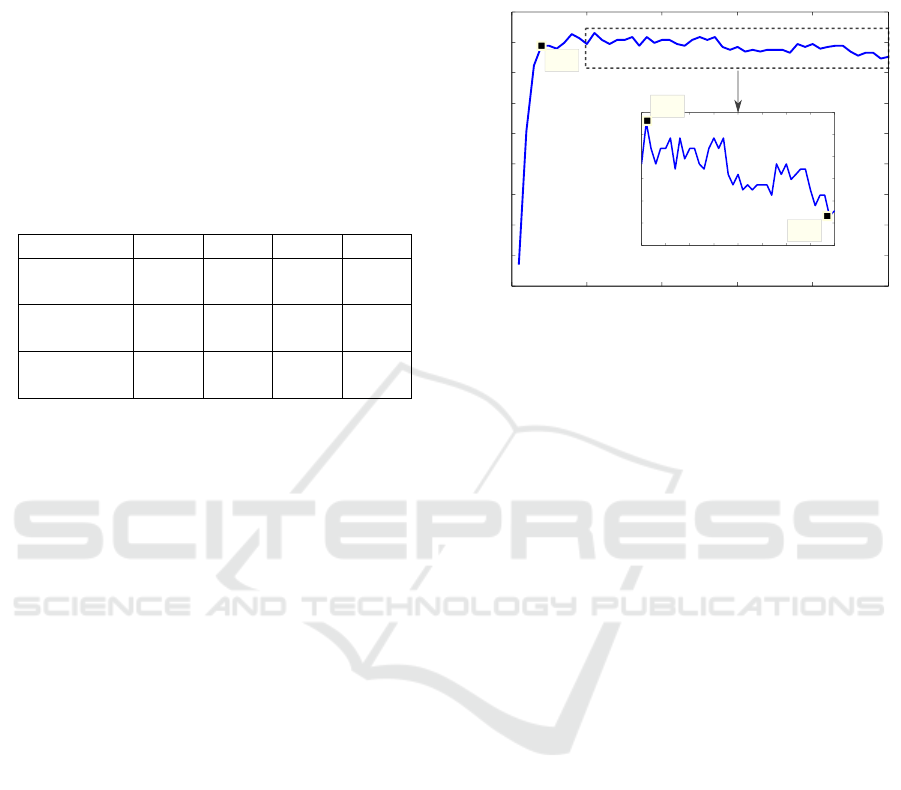
50. Figure 1 gives the obtained results. This figure
shows the CR function of the odd harmonics number
taken into account for the identification. The results
show that no significant improvement is noticed when
taking more than 4 odd harmonics.
0 10 20 30 40 50
50
55
60
65
70
75
80
85
90
95
X: 4
Y: 89.44
Number of considered odd harmonics
CR (%)
10 15 20 25 30 35 40 45 50
86
87
88
89
90
91
92
X: 11
Y: 91.55
Number of considered odd harmonics
X: 49
Y: 87.32
X: 11
Y: 91.55
CR (%)
Figure 1: CR function of the considered odd harmonics
number.
Moreover, after reaching a peak value (when tak-
ing 11 odd harmonics) and after fluctuating around
a more or less stable value (when taking up to 27
odd harmonics) that is smaller than the peak value,
the CR starts decreasing (see the zoom on Figure 1)
as we start taking more and more coefficients. This
phenomenon is very known in pattern recognition and
is called the curse of dimensionality or peaking phe-
nomenon (Jain et al., 2000). The dimension of the
feature vector depends on the dimension of the dataset
used. To avoid this problem, and as a rule of thumb,
we usually say that the number of training data points
should be an exponential function of the feature vec-
tor dimension (Jain et al., 2000).
5 CONCLUSIONS
In this paper, we have discussed the use of HMM
models to solve the electrical appliance identification
problem based on high-frequency sampled signals.
We have evaluated the usefulness of different choices
for the identification system (the use of transient vs.
steady-state signals, even vs. odd-order harmonics as
features, and the optimal feature vector size). We
conclude from this study that the combined use of
the transient part of the electrical current signals with
only a few odd-order harmonics allows to construct an
appliance identification system that is accurate, fast,
and less complex in terms of memory occupancy and
computations. In future work, and for more complete
results, the use and comparison of different types of
classifiers and different features may be considered.
HMM-based Transient and Steady-state Current Signals Modeling for Electrical Appliances Identification
675

ACKNOWLEDGEMENTS
The authors would like to thank the R
´
egion Centre-
Val de Loire (France) for their financial support of the
project MDE-MAC3 (Contract n
◦
2012 00073640)
under which this study was conducted.
REFERENCES
Baranski, M. and Voss, J. (2003). Nonintrusive appliance
load monitoring based on an optical sensor. In Power
Tech Conference Proceedings, 2003 IEEE Bologna,
volume 4, pages 8–pp. IEEE.
Beckel, C., Kleiminger, W., Staake, T., and Santini, S.
(2012). Improving device-level electricity consump-
tion breakdowns in private households using on/off
events. ACM SIGBED Review, 9(3):32–38.
Burbano Acu
˜
na, M. D. (2015). Intrusive and non-intrusive
load monitoring (a survey). Latin-American Journal
of Computing, Systems Engineering, National Poly-
technic School, Ecuador, 2(1).
Carrie Armel, K., Gupta, A., Shrimali, G., and Albert, A.
(2013). Is disaggregation the holy grail of energy effi-
ciency? the case of electricity. Energy Policy, 52:213–
234.
Chakravarty, P. and Gupta, A. (2013). Impact of energy dis-
aggregation on consumer behavior. In UC Berkeley:
Behavior, Energy and Climate Change Conference.
Chan, W., So, A. T., and Lai, L. (2000). Harmonics load
signature recognition by wavelets transforms. In Elec-
tric Utility Deregulation and Restructuring and Power
Technologies, 2000. Proceedings. DRPT 2000. Inter-
national Conference on, pages 666–671. IEEE.
Chang, H.-H., Lin, C.-L., and Yang, H.-T. (2008). Load
recognition for different loads with the same real
power and reactive power in a non-intrusive load-
monitoring system. In Computer Supported Coopera-
tive Work in Design, 2008. CSCWD 2008. 12th Inter-
national Conference on, pages 1122–1127. IEEE.
Cole, A. I. and Albicki, A. (1998). Algorithm for non-
intrusive identification of residential appliances. In
Circuits and Systems, 1998. ISCAS’98. Proceedings
of the 1998 IEEE International Symposium on, vol-
ume 3, pages 338–341. IEEE.
Darby, S. (2006). The effectiveness of feedback on energy
consumption. A Review for DEFRA of the Literature
on Metering, Billing and direct Displays, 486:2006.
Darby, S. (2010). Smart metering: what potential for house-
holder engagement? Building Research & Informa-
tion, 38(5):442–457.
Drenker, S. and Kader, A. (1999). Nonintrusive monitor-
ing of electric loads. Computer Applications in Power,
IEEE, 12(4):47–51.
Du, Y., Du, L., Lu, B., Harley, R., and Habetler, T. (2010).
A review of identification and monitoring methods
for electric loads in commercial and residential build-
ings. In Energy Conversion Congress and Exposition
(ECCE), 2010 IEEE, pages 4527–4533. IEEE.
Feinberg, E. A. and Genethliou, D. (2005). Load forecast-
ing. In Applied mathematics for restructured electric
power systems, pages 269–285. Springer.
Fischer, C. (2008). Feedback on household electricity con-
sumption: a tool for saving energy? Energy efficiency,
1(1):79–104.
Gao, J., Giri, S., Kara, E. C., and Berg
´
es, M. (2014). Plaid:
A public dataset of high-resolution electrical appli-
ance measurements for load identification research:
Demo abstract. In Proceedings of the 1st ACM Con-
ference on Embedded Systems for Energy-Efficient
Buildings, BuildSys ’14, pages 198–199, New York,
NY, USA. ACM.
Gellings, C. W. (2009). The smart grid: enabling energy
efficiency and demand response. The Fairmont Press,
Inc.
Hacine-Gharbi, A., Ravier, P., Harba, R., and Mohamadi, T.
(2012). Low bias histogram-based estimation of mu-
tual information for feature selection. Pattern Recog-
nition Letters, 33(10):1302 – 1308.
Hancke, G. P., Hancke Jr, G. P., et al. (2012). The role of
advanced sensing in smart cities. Sensors, 13(1):393–
425.
Hart, G. (1989). Residential energy monitoring and com-
puterized surveillance via utility power flows. Tech-
nology and Society Magazine, IEEE, 8(2).
Hart, G. (1992). Nonintrusive appliance load monitoring.
Proc. of the IEEE, 80(12):1870–1891.
Jain, A. K., Duin, R. P. W., and Mao, J. (2000). Statistical
pattern recognition: A review. Pattern Analysis and
Machine Intelligence, IEEE Transactions on, 22(1):4–
37.
Lai, P.-h., Trayer, M., Ramakrishna, S., and Li, Y. (2012).
Database establishment for machine learning in nilm.
In Proceedings of the 1st International Non-Intrusive
Load Monitoring Workshop.
Laughman, C., Lee, K., Cox, R., Shaw, S., Leeb, S., Nor-
ford, L., and Armstrong, P. (2003). Power signa-
ture analysis. Power and Energy Magazine, IEEE,
1(2):56–63. Read.
Leeb, S., Shaw, S., and Jr, J. K. (1995). Transient event de-
tection in spectral envelope estimates for nonintrusive
load monitoring. Power Delivery, IEEE Transactions
on, 10(3):1200–1210.
Mallat, S. (1999). A wavelet tour of signal processing. Aca-
demic press.
Nait Meziane, M., Ravier, P., Lamarque, G., Abed-Meraim,
K., Le Bunetel, J.-C., and Raingeaud, Y. (2015). Mod-
eling and estimation of transient current signals. In
Signal Processing Conference (EUSIPCO), 2015 Pro-
ceedings of the 23rd European, pages 2005–2009.
Najmeddine, H., El Khamlichi Drissi, K., Pasquier, C.,
Faure, C., Kerroum, K., Diop, A., Jouannet, T., and
Michou, M. (2008). State of art on load monitoring
methods. In Power and Energy Conference, 2008.
PECon 2008. IEEE 2nd International, pages 1256–
1258. IEEE. Read.
Parson, O. (2012). Using hidden markov model variants for
non-intrusive appliance load monitoring from smart
meter data.
ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods
676

Parson, O., Ghosh, S., Weal, M., and Rogers, A. (2014). An
unsupervised training method for non-intrusive appli-
ance load monitoring. Artificial Intelligence.
Patel, S. N., Robertson, T., Kientz, J. A., Reynolds, M. S.,
and Abowd, G. D. (2007). At the flick of a switch:
Detecting and classifying unique electrical events on
the residential power line (nominated for the best pa-
per award). In UbiComp 2007: ubiquitous computing,
pages 271–288. Springer. Read.
PLAID (2015). PLAID: the Plug Load Appliance
Identification Dataset. [Online] Available from:
http://plaidplug.com. [Accessed: 22nd October 2015].
Ridi, A. and Hennebert, J. (2014). Hidden markov models
for ilm appliance identification. Procedia Computer
Science, 32:1010–1015.
Sultanem, F. (1991). Using appliance signatures for mon-
itoring residential loads at meter panel level. Power
Delivery, IEEE Transactions on, 6(4):1380–1385.
Tang, G., Wu, K., and Lei, J. (2014). Semi-intrusive load
monitoring for large-scale appliances. In Interna-
tional Workshop on Non-Intrusive Load Monitoring
(NILM 2014).
Thiruvaran, T., Phung, T., and Ambikairajah, E. (2013). Au-
tomatic identification of electric loads using switching
transient current signals. In TENCON Spring Confer-
ence, 2013 IEEE, pages 252–256. IEEE.
Ting, K., Lucente, M., Fung, G. S., Lee, W., and Hui, S.
(2005). A taxonomy of load signatures for single-
phase electric appliances. In IEEE PESC (Power Elec-
tronics Specialist Conference), pages 12–18. Read.
Young, S., Evermann, G., Gales, M., Hain, T., Kershaw, D.,
Liu, X., Moore, G., Odell, J., Ollason, D., Povey, D.,
Valtchev, V., and Woodland, P. (2009). The HTK book
(for HTK Version 3.4).
Zeifman, M. and Roth, K. (2011). Nonintrusive appli-
ance load monitoring: Review and outlook. Con-
sumer Electronics, IEEE Transactions on, 57(1):76–
84. Read.
Zia, T., Bruckner, D., and Zaidi, A. (2011). A hidden
markov model based procedure for identifying house-
hold electric loads. In IECON 2011-37th Annual Con-
ference on IEEE Industrial Electronics Society, pages
3218–3223. IEEE.
HMM-based Transient and Steady-state Current Signals Modeling for Electrical Appliances Identification
677
