Uncertain Marking for Dealing with Partial Parallelization in Business

Processes

Leiliane Pereira de Rezende

1,2,∗

, St

ephane Julia

and Janette Cardoso

Computing Faculty, Federal University of Uberl

andia - UFU, Uberl

andia, MG, Brazil

DMIA Department, Institut Sup

erieur de l’A

eronautique et de l’Espace - ISAE, Toulouse, France

Keywords:

WorkFlow Net, Possibilistic Petri Net, Deviations, Process Monitoring.

Abstract:

In this paper, an approach based on WorkFlow nets and possibilistic Petri nets is proposed for dealing with ﬂow

deviations in business processes. Routing patterns existing in business processes are modeled by WorkFlow

nets. Possibilistic Petri nets with uncertainty in the marking and the transition ﬁring are considered to express

in a more realistic way the ordering of human activities during real time execution of the process model.

Combining both formalisms, a kind of possibilistic WorkFlow net is obtained. An example of ﬂow deviations

due to human behavior at a process monitoring level is presented.

1 INTRODUCTION

An organization produces value for its customers by

executing various business processes (BP) which rep-

resent the sequences of activities that have to be ex-

ecuted within an organization to treat speciﬁc cases

and to reach well deﬁned goals (van der Aalst and

Hee, 2004). Due to complexity and variety of BP,

contemporary organizations use information technol-

ogy to support activities which may include the au-

tomation of their processes.

A workﬂow process corresponds to the automa-

tion of a BP, in whole or part, during which docu-

ments, information or tasks are passed from one par-

ticipant to another for a particular form of action, ac-

cording to a set of procedural rules. A Workﬂow Man-

agement System (WFMS) is a system that completely

deﬁnes, manages and executes workﬂow processes

through the execution of software whose sequence of

activities is driven by a computer representation of the

workﬂow process logic (Members, 1994).

Many papers have already considered Petri net

theory as an efﬁcient tool for the modeling and anal-

ysis of WFMS (van der Aalst, 1998) (van der Aalst

and Hee, 2004) (Soares Passos and Julia, 2009). The

WorkFlow nets (WF-nets) (acyclic Petri net models

used to represent BP) are deﬁned in (van der Aalst

and Hee, 2004).

The ﬁrst author received CAPES Scholarship - Proc.

◦

. 99999.001925/2015-06

Soundness property is an important criterion

which needs to be satisﬁed when treating workﬂow

processes. In fact, good properties of well-deﬁned

formal models such as WF-nets can easily be proved

when BP are following a rigid structure that does not

allow for deviations from the process description dur-

ing real time execution. Although the explicit or-

dering of activities makes the coordination of activ-

ities relatively easy to understand, even for a non-

technical stakeholder, it was shown that BP do not

easily map to a rigid modeling structure (Kapuruge

et al., 2010). Consequently, they are implemented

such that they “ﬁt the system”, which can cause var-

ious problems (Pesic, 2008). First, considering that

some activities executed in a BP depend on human

resources which do not necessarily respect the rigor-

ous deﬁnition of workﬂow processes, manual inter-

ventions become increasingly frequent as human em-

ployees attempt to manipulate workﬂow inputs and

outputs to conform with changes in workplace prac-

tices. Second, these manual interventions reduce pro-

ductivity and increase processing time. Since it is un-

dertaken in an ad-hoc manner, manual handling in-

curs an added penalty: the corrective actions under-

taken are not added to organizational memory and, as

a consequence, natural process evolution is not incor-

porated into future iterations of the process (Adams,

2010).

Attempts at incorporating a certain level of ﬂex-

ibility in process deﬁnition have already been pro-

posed by several authors.

118

Rezende, L., Julia, S. and Cardoso, J.

Uncertain Marking for Dealing with Partial Parallelization in Business Processes.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 118-125

ISBN: 978-989-758-187-8

Adams et al., in (Adams et al., 2005) and (Adams

et al., 2006), deﬁned the worklet approach as an

extensible repertoire of self-contained sub-processes

aligned to each task, from which a dynamic runtime

selection is made depending on the context of the par-

ticular work instance. In addition, in (Adams, 2007)

and (Adams et al., 2007), an extensible repertoire

of self-contained exception-handling processes called

“exlets” was incorporated in the worklet approach.

However some good properties can be lost due to the

dynamic changes.

In (Pesic and van der Aalst, 2006) and (Pesic et al.,

2007), a declarative constraint-based approach that

allows a process instance to deviate from the origi-

nal behavior at runtime by adding/removing or soft-

ening/hardening the constraints and their mapping to

process deﬁnitions is proposed. In (van der Aalst

et al., 2009), an approach based on constraints that

implicitly speciﬁes the execution procedure, i.e., any-

thing is possible as long as it is not explicitly forbid-

den is proposed. The problem with these approaches

is that the sequencing of single activities speciﬁed for

a certain process type is only limited to the satisfac-

tion of predetermined constraints.

In (Mohammed et al., 2007), two process models

coexist during the monitoring of the BP. The ﬁrst one

corresponds to the expected behavior of the process

and the second one, based on the visible actions of

human actors, is built dynamically. The two process

models are then permanently compared and analyzed

in order to detect possible deviations. The problem

in dealing with two models is that the monitoring ac-

tivity can easily be overloaded implying a decrease in

the system’s performance.

In (Zazworka et al., 2009), the deviations and non-

conformities between a planned and executed process

are detected during the development of the software.

In (Thompson and Torabi, 2009), a kind of declar-

ative implicit model, essentially based on rules, is

used to detect inconsistencies (non-conformant states

in the process) and to accept possible deviations (non-

conformant transitions between activities). The limi-

tation of the methodology is that the speciﬁed rules

only detect the non-conformance of the process but

do not help in an explicit manner for the real time

process monitoring.

Some authors, such as (Rozinat and van der Aalst,

2008)(Munoz-Gama, 2010)(van der Aalst et al.,

2012), evaluated the level of conformance between

the process model and the execution log of the pro-

cess. For this, they developed metrics for measuring

the relationship between predeﬁned process models

and actual results presented in the form of event logs.

The problem with this approach is that the veriﬁcation

is carried out after the process execution.

A very promising alternative for dealing with ﬂex-

ibility in BP seems to be those approaches based on

uncertain knowledge as that presented in (Cmpan and

Oquendo, 2000). The model of the process is then

given through fuzzy sets and possibilistic distribu-

tions.The advantage of fuzzy and possibility reason-

ing is the ability to naturally represent uncertain and

imprecise information that exists when activities are

executed by human employees.

One of the ﬁrst studies which combines fuzzy and

possibilistic representation of information with the

precise structure of a Petri net when considering dis-

crete event systems is that described in (Cardoso et al.,

1999). The main feature of possibilistic/fuzzy Petri

nets is to allow one to reason about the aspects of un-

certainty and change in dynamic discrete event sys-

tems. Most of the examples presented by the authors

of possibilistic Petri net were applied to ﬂexible man-

ufacturing systems.

In this paper, an approach based on WF-nets and

possibilistic Petri nets is proposed to deal with ﬂexi-

bility in BP. In particular, a kind of possibilistic Work-

Flow net will be deﬁned to treat deviations incurred

by manual interventions of the human employees dur-

ing real time execution of the process model.

The remainder of this paper is as follow: in section

2, the deﬁnition of WF-nets and soundness correct-

ness criterion are provided. In section 3, an overview

of possibilistic Petri nets is given. In section 4, the

possibilistic WorkFlow net is presented and a sample

business process model illustrates the approach. Fi-

nally, section 5 concludes this work with a short sum-

mary, an assessment based on the approach presented

and an outlook on future work proposals.

2 WORKFLOW NET

A Petri net that models a workﬂow process is called

a WorkFlow net (WF-net) (van der Aalst and Hee,

2004). A WF-net needs to possess the following prop-

erties (van der Aalst, 1998):

• It has only one source place, named Start and only

one sink place, named End. These are special

places, such that the place Start has only outgoing

arcs and the place End has only incoming arcs.

• A token in Start represents a case that needs to be

handled and a token in End represents a case that

has been handled.

• Every task t (transition) and condition p (place)

should be on a path from place Start to place End.

Uncertain Marking for Dealing with Partial Parallelization in Business Processes

119

As previously mentioned, a task can be associated

to a transition in a WF-net. However, in order to ex-

plicitly indicate the beginning and the end of each task

in execution, two sequential transitions plus a place

to model a task is used. The ﬁrst transition represents

the beginning of the task, the place the task, and the

second transition represents the end of the task (Wang

et al., 2009).

Figure 1: WorkFlow net model of a task.

As shown in ﬁgure 1, transition B represents the

beginning of a task execution; E represents the end

of the task execution. Place A

represents the task in

execution. From a reachability analysis perspective,

ﬁgure 1 can be reduced to a single transition, which

represents the entire task execution as a single logic

unit.

Soundness is a correctness criterion deﬁned for

WF-nets and is related to its dynamics. A WF-net is

sound if, and only if, the following three requirements

are satisﬁed (van der Aalst and Hee, 2004):

• For each token put in the place Start, one and only

one token appears in the place End.

• When the token appears in the place End, all the

other places are empty for this case.

• For each transition (task), it is possible to move

from the initial state to a state in which that tran-

sition is enabled, i.e. there are no dead transitions.

A method for the qualitative analysis of WF-nets

(soundness veriﬁcation) based on the proof trees of

linear logic is presented in (Soares Passos and Julia,

2009) and another based on a reachability graph is

presented in (van der Aalst et al., 2011).

3 POSSIBILISTIC PETRI NET

Possibilistic Petri nets are derived from Object Petri

nets (Sibertin-Blanc, 2001). As characterized in the

approach presented in (Cardoso, 1999), a possibilis-

tic Petri net is a model where a marked place corre-

sponds to a possible partial state, a transition to a pos-

sible state change, and a ﬁring sequence to a possible

behavior. The main advantage in working with pos-

sibilistic Petri nets is that they allow for the updating

of a system state at a supervisory level with ill-known

information without necessarily reaching inconsistent

states.

A possibilistic Petri net model associates a possi-

bility distribution Π

(p) to the location of an object o,

p being a place of the net. Π

(p) = 1 represents the

fact that p is a possible location of o, and Π

(p) = 0

expresses the certainty that o is not present in place p.

Conventionally, a marking in a possibilistic Petri net

is then a mapping:

M : O × P −→ {0, 1}

where O is a set of objects and P a set of places. If

M(o, p) = 1, there exists a possibility of there being

the object o in place p. On the contrary, if M(o, p) =

0, there exists no possibility of there being o in p. A

marking M of the net allows one to represent:

• A certain marking: each token is located in only

one place (well-known state). Then M(o, p) = 1

and ∀p

6= p, M(o, p

) = 0.

• An uncertain marking: each token location has a

possibility distribution over a set of places. It can-

not be asserted that a token is in a given place,

but only that it is in a place among a given set

of places. For example, if there exists a possi-

bility at a certain time of having the same ob-

ject o in two different places, p

and p

, then

M(o, p

) = M(o, p

) = 1.

A possibilistic marking will correspond in practice

to knowledge concerning a situation at a given time.

In a possibilistic Petri net, the ﬁring (certain or

uncertain) of a transition t is decomposed into two

steps:

• Beginning of a ﬁring: objects are put into out-

put places of t but are not removed from its input

places.

• End of a ﬁring: that can be a ﬁring cancellation

(tokens are removed from the output places of t)

or a ﬁring achievement (tokens are removed from

the input places of t).

A certain ﬁring consists of a beginning of a ﬁring

and an immediate ﬁring achievement. An uncertain

ﬁring (or a pseudo-ﬁring) that will increase the un-

certainty of the marking can be considered only as

the beginning of a ﬁring (there is no information to

conﬁrm whether the normal event associated with the

transition has actually occurred or not). To a certain

extent, pseudo-ﬁring is a way of realizing forward de-

duction.

The interpretation of a possibilistic Petri net is de-

ﬁned by attaching to each transition T an authoriza-

tion function η

,...,x

deﬁned as follows:

,...,x

: T −→ {False,Uncertain, True}

where x

, ..., x

are the variables associated with the

incoming arcs of transition T (when considering the

underlying Object Petri net).

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

120

If o

, ..., o

is a possible substitution for x

, ..., x

for ﬁring t, then several situations can be considered:

• t is not enabled by the marking but the associated

interpretation is true; an inconsistent situation oc-

curs and a special treatment process of the net is

activated;

• t is enabled by a certain marking and the inter-

pretation is true; then a classical ﬁring (with cer-

tainty) of an object Petri net occurs;

• t is enabled by a certain marking and the interpre-

tation is uncertain; then the transition is pseudo-

ﬁred and the imprecision is increased;

• t is enabled by an uncertain marking; if the inter-

pretation is uncertain, t is pseudo-ﬁred;

• t is enabled by an uncertain marking and the inter-

pretation is true: a recovery algorithm, presented

in (Cardoso et al., 1989), is called and a new com-

putation of the possibility distribution of the ob-

jects involved in the uncertain marking is realized

in order to go back to a certain marking.

Concepts concerning possibilistic Petri nets will

be illustrated through a practical example in section

4 POSSIBILISTIC WORKFLOW

NET FOR THE PARTIAL

PARALLELIZATION OF A

SEQUENTIAL PROCESS

If a Petri net is used as a model for Business Pro-

cesses in a WFMS, transitions will represent the state

changes of the process. In particular, each event oc-

curring during the execution of the process (begin-

ning and ending of activities) will be associated with

a transition as a boolean variable. Such a variable will

be essentially seen as an external value corresponding

to a message received from an activity (or send to an

activity). Possibly, internal values depending on cer-

tain token attributes will enable some transitions too.

Petri net models can be directly executed using a

specialized inference mechanism called “token player

algorithm” that allows for a simpliﬁed monitoring of

the represented process model. A classical “token

player algorithm”, as the one deﬁned in (Cardoso and

Valette, 1997), is only based on events under those

conditions normally expected. If an unexpected event

occurs, the process stops or needs to be repaired man-

ually.

As pointed out in the introduction, the explicit

ordering of activities makes the coordination of ac-

tivities relatively easy to understand even for a non-

technical stakeholder, however, due to rigid structure

of workﬂow processes, several manual interventions

have become increasingly frequent as human employ-

ees attempt to manipulate workﬂow inputs and out-

puts to conform with changes in workplace practices.

From this, some deviations may occur between the

model of the process and the real process execution.

A classic deviation may be the initialization of an ac-

tivity before the end of a previous one due to a dead-

line for example.

If inevitable system changes are handled haphaz-

ardly without being added to organizational memory

in order that they be considered part of the evolution-

ary process, they can lead to major work disruptions

increasing dissatisfaction to a point at which the entire

system implementation is considered as a failure. In

order to handle the changes during real process execu-

tion and register them in the organizational memory,

a model of the process based on the routing structure

of WF-nets and on uncertain marking along with the

ﬁring of possibilistic Petri nets is proposed for dealing

with the deviations incurred by manual interventions

by human employees during its real time execution.

A simple ordering process, presented in (Weske,

2007), will be used to illustrate the approach. This

process features a sequence of activities. Firstly, the

order is stored. After, the inventory is checked, the

invoice is sent, the funds are received and the ship-

ment is prepared. Finally, the goods are shipped and

the process terminates with the archiving of the or-

der. The possibilistic WF-net with objects in Figure 2

represents such a model.

< c > is an object belonging to the class “Order”,

as well as variable x and all the model’s places. Each

transition has an interpretation and an action attached

to it deﬁned by the designer. The interpretation is

used to manage the occurrence of each event in the

system by imposing restrictions on the ﬁring of tran-

sitions. The action is an application that involves the

attributes or methods of formal variables associated

with incoming arcs allowing for the modiﬁcation of

some speciﬁc attributes. However, in the model pre-

sented, the actions are not represented given that they

do not interfere in understanding the approach. The

true and uncertain interpretations are represented, re-

spectively, by the letters T and U. Note that when the

representation of the uncertain interpretation is omit-

ted in the model, such interpretation is always evalu-

ated as false. On the other hand, the false interpreta-

tion is evaluated as true when both the true interpreta-

tion and the uncertain interpretation are evaluated as

false. The element τ represents the current time.

The conditions correspond to the folloing interpre-

Uncertain Marking for Dealing with Partial Parallelization in Business Processes

121

Figure 2: A BP model using possibilistic WF-net.

tations:

• “sgBA1”, “sgBA2”, “sgBA3”, “sgBA4”, “sgBA5”,

“sgBA6” and “sgBA7” represent, respectively, the

beginning of the tasks “store order”, “check in-

ventory”, “send invoice”, “receive funds”, “pre-

pare shipment”, “ship goods” and “archive”;

• “sgEA1”, “sgEA2”, “sgEA3”, “sgEA4”,

“sgEA5”, “sgEA6” and “sgEA7” represent,

respectively, the end of the tasks “store order”,

“check inventory”, “send invoice”, “receive

funds”, “prepare shipment”, “ship goods” and

“archive”;

• t

max

BA4

, t

max

BA5

and t

max

BA6

are maximum points

in the timescale associated to a speciﬁc activity

which indicate the maximum time allowed for the

initialization of a task;

• t

max

EA3

, t

max

EA4

, t

max

EA5

and t

max

EA6

are maximum

points in the timescale associated to a speciﬁc ac-

tivity, which indicates the maximum time allowed

to begin the conclusion of a task.

Due to the somewhat cautious policy realized by

the BP, the normal expected behavior of the process

is to execute all activities in sequence such that for an

activity to start, it must wait for the end of the previ-

ous one. For example, the activity “prepare shipment”

) starts only after receiving the funds (activity A

In consequence, BP instances based on this process

model might suffer from long processing times, re-

sulting in insufﬁcient customer satisfaction.

An abnormal behavior will happen if, disregarding

the rigid sequencing of the activities but considering

a maximum time allowed to start or ﬁnish an activ-

ity, the activities A

and A

, for example, start before

the end of the activity A

, allowing a lower processing

time and sufﬁcient customer satisfaction. In this case,

some pseudo-ﬁring will have to occur and the impre-

cision linked to some objects will increase. In doing

so, some of the sequential activities, speciﬁed through

the rigid structure of the sequential WF-net of ﬁgure

2, will be partially executed in parallel.

The general behavior of a WFMS contingent on

possibilistic WF-net models will be based on the pos-

sibilistic token player given by the activity diagram in

Figure 3.

To illustrate a possible abnormal behavior, the fol-

lowing values are considered: t

max

EA3

= 24, t

max

BA4

25, t

max

EA4

= 49, t

max

BA5

= 50, t

max

EA5

= 74, t

max

BA6

75 and t

max

EA6

= 90. In addition, it is assumed that the

conditions become true on the following dates: sgBA

at τ = 0, sgEA

at τ = 4, sgBA

at τ = 7, sgEA

τ = 19, sgBA

at τ = 20, sgEA

at τ = 23, sgBA

τ = 24, sgEA

at τ = 85, sgBA

at τ = 86, sgEA

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

122

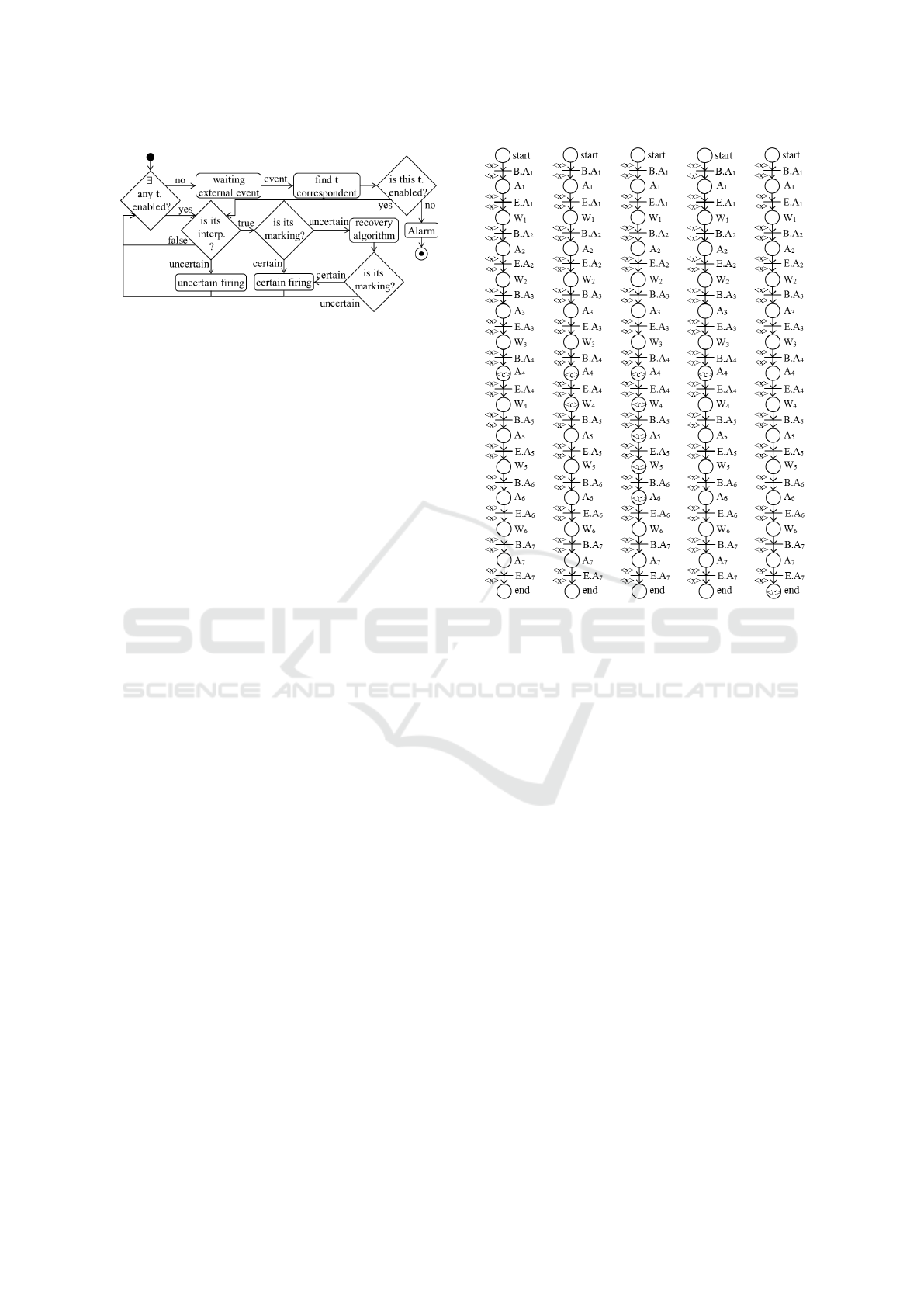
Figure 3: Possibilistic token player algorithm.

τ = 87, sgBA

at τ = 88, sgEA

at τ = 89, sgBA

τ = 90 and sgEA

at τ = 100.

Taking into consideration the values deﬁned above

(the maximum points and the conditions), the follow-

ing scenario will occur:

• at the following times τ = 0, τ = 4, τ = 7, τ = 19,

τ = 20, τ = 23 and τ = 24, the transitions B.A

E.A

, B.A

, E.A

, B.A

, E.A

and B.A

are re-

spectively ﬁred with certainty given that they are

enabled by a certain marking and the interpreta-

tion attached to them is true (η

<c>

(t) = true). The

resulting state of the process after this ﬁring se-

quence is shown in Figure 4(a).

• at current time τ = 49, the transition E.A

is en-

abled by a certain making and its interpretation is

uncertain (η

<c>

(E.A

) = uncertain). Then, E.A

is pseudo-ﬁred (Figure 4(b));

• at the following times τ = 50, τ = 74 and τ = 75,

the transitions B.A

, E.A

and B.A

are respec-

tively pseudo-ﬁred given that they are enabled by

uncertain markings and the interpretation attached

to them is uncertain (η

<c>

(t) = uncertain). The

resulting state of the process after this ﬁring se-

quence is shown in Figure 4(c);

• at current time τ = 85, the transition E.A

is en-

abled by an uncertain marking and its interpreta-

tion becomes true (η

<c>

(E.A

) = true). This situ-

ation occurs because the notiﬁcation of the receipt

of the funds arrived late and the activities A

and

started before it ended, so as not to increase

the processing time of the process such that cus-

tomer satisfaction is not affected. Consequently,

the recovery algorithm described in Algorithm 1

is called to cancel some pseudo-ﬁred transitions.

After the execution of the recovery algorithm, the

transition E.A

can be ﬁred with certainty given

that it is enabled by a certain marking (Figure

4(d)) and its interpretation is true. It is important

to note that if the marking is not certain after the

processing of the algorithm, the transition E.A

cannot be ﬁred with certainty and the process in-

stance must wait for a new event in order that the

(a)

τ = 24

(b)

τ = 49

(c)

τ = 75

(d)

τ = 85

(e)

τ = 100

Figure 4: Simulation results of the scenario.

process state can go back to a certain marking;

• ﬁnally, at the following times τ = 86, τ = 87,

τ = 88, τ = 89, τ = 90 and τ = 100, the transitions

B.A

, E.A

, B.A

, E.A

, B.A

and E.A

are re-

spectively ﬁred with certainty given that they are

enabled by certain markings and the interpretation

attached to them is true (η

<c>

(t) = true). The

resulting state of the process, after this ﬁring se-

quence, is shown in Figure 4(e).

Figure 5(a) depicts the possibility distributions of

instance < c > as functions of time relative to the sce-

nario described above(the black lines represent a pos-

sibility equal to 1 and the bright lines a possibility

equal to 0). Note that the activities A

and A

after the

execution of the recovery algorithm do not spend all

the processing time predeﬁned because they have al-

ready been initialized. In addition, observing the pos-

sibility distributions of instance < c >, it is easy to

verify that the activities A

, A

and A

were pseudo-

parallelized during the time period between 49 and 85

even with the fact that in the process model they are

strictly described in a pure sequential way.

In order to show the difference in the processing

time spent when the process model is strictly executed

Uncertain Marking for Dealing with Partial Parallelization in Business Processes

123

(a) Pseudo-parallelized (b) Strictly sequential

Figure 5: Possibility distributions of object location < c >.

Algorithm 1: Recovery algorithm.

Inputs:

WN: WF-net with an uncertain marking

t: transition

Output:

WN: WF-net with a new marking

1. if t was pseudo-ﬁred

2. then LP ← (t•)

3. cancel the ﬁring of t

2. else LP ← φ

4. while LP 6= φ do

5. p ← LL[0]

6. while ∃ t

∈ (p•) | t

was pseudo-ﬁred do

7. LP ← LP ∪ (t

•)

8. cancel the ﬁring of t

sequentially, Figure 5(b) depicts the possibility distri-

butions of instance < c > as functions of time consid-

ering the same processing time that each task spent

during its execution in the scenario described above.

Comparing both ﬁgures (Figure 5(a) and 5(b)), it is

easy to see that the processing time spent by the ﬁrst

is 33% lower than the second one.

Considering the change patterns suitable for pro-

viding ﬂexibility in time execution proposed by We-

ber et al. in (Weber et al., 2008), the proposed ap-

proach incorporates, during real time execution, the

adaptation pattern “Parallelize Process Fragments”.

5 CONCLUSIONS

In this article, a possibilistic WorkFlow net model was

presented with the purpose of dealing with deviation

situations in BP. Combining the routing structure of

WF-nets and the uncertain reasoning of possibilistic

Petri nets, the authors presented an approach that can

deal with deviation situations that can be reached dur-

ing the real time execution when human behaviour is

considered. Such an approach was applied to an ex-

ample of a simple ordering process.

Other studies that deal with the problem of devia-

tions in workﬂow processes create new structures dur-

ing the execution process, which can lose the good

properties of the process or only detect the devia-

tions after the conclusion of the process. Comparing

these studies with the approach presented in this pa-

per, the main advantage is that the good properties of

the model will be preserved because the structure in

the process (the different routing patterns) will not be

altered during the real time execution. Some devia-

tions will be allowed and recorded in the organiza-

tional memory for being posteriorly considered in the

process evolution. However, the allowed deviations

will be limited due to the possibilistic behavior.

As a future work proposal, it will be interesting to

deal with fuzzy time information in an explicit way

in the structure of a WF-net as the one presented in

(Cardoso, 1999). The use of fuzzy dates can allow

a ﬂexible control of a time schedule describing the

causality relations between the events and improving

the updating process. Such an approach should be

interesting at the monitoring level in order to diminish

the imprecision of human intervention.

In addition, in order to validate experimentally

such an approach, the model of the possibilistic Work-

Flow net will have to be implemented on a Petri net

software tool allowing for the programming of transi-

tion pseudo ﬁring. It seems that the CPN Tools soft-

ware resources (Beaudouin-Lafon et al., 2001) should

be able to implement in a simple way some of the ba-

sic behaviors of a possibilistic token player given that

they combine advanced interaction techniques into a

consistent interface for editing, simulating, and ana-

lyzing Coloured Petri Nets. Such an implementation

should prove the gain in the overall process perfor-

mance.

ACKNOWLEDGEMENTS

The authors would like to thank Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior

(CAPES), Fundac¸

ao de Amparo a Pesquisa do Estado

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

124

de Minas Gerais (FAPEMIG) and Conselho Nacional

de Desenvolvimento Cientﬁco e Tecnolgico (CNPq)

for ﬁnancial support.

REFERENCES

Adams, M. (2007). Facilitating Dynamic Flexibility and

Exception Handling for Workﬂows. PhD thesis,

Queensland University of Technology.

Adams, M. (2010). Chapter 4: Dynamic workﬂow. In Mod-

ern Business Process Automation: YAWL and its Sup-

port Environment, pages 123–145.

Adams, M., Hofstede, A. H. M. t., Edmond, D., and van der

Aalst, W. M. P. (2005). Facilitating ﬂexibility and

dynamic exception handling in workﬂows through

worklets. In CAiSE, volume 161, pages 45–50.

Adams, M., Hofstede, A. H. M. t., Edmond, D., and van der

Aalst, W. M. P. (2006). Worklets: A service-oriented

implementation of dynamic ﬂexibility in workﬂows.

In Proceedings of the OTM, volume 4275, pages 291–

308.

Adams, M., Hofstede, A. H. M. t., van der Aalst, W. M. P.,

and Edmond, D. (2007). Dynamic, extensible and

context-aware exception handling for workﬂows. In

OTM, volume 4803, pages 95–112.

Beaudouin-Lafon, M., Mackay, W., Jensen, M., Andersen,

P., Janecek, P., Lassen, M., Lund, K., Mortensen, K.,

Munck, S., Ratzer, A., Ravn, K., Christensen, S., and

Jensen, K. (2001). Cpn/tools: A tool for editing and

simulating coloured petri nets etaps tool demonstra-

tion related to tacas. In Tools and Algorithms for the

Construction and Analysis of Systems, volume 2031,

pages 574–577.

Cardoso, J. (1999). Time fuzzy petri nets. In Fuzziness in

Petri Nets, pages 115 – 145.

Cardoso, J. and Valette, R. (1997). Redes de Petri.

DAUSFC.

Cardoso, J., Valette, R., and Dubois, D. (1989). Petri nets

with uncertain markings. In Applications and Theory

of Petri Nets, volume 483, pages 64 – 78.

Cardoso, J., Valette, R., and Dubois, D. (1999). Possibilistic

petri nets. IEEE Transactions on SMC, Part B, 29:573

–582.

Cmpan, S. and Oquendo, F. (2000). Dealing with software

process deviations using fuzzy logic based monitor-

ing. SIGAPP Appl. Comput. Rev., 8:3–13.

Kapuruge, M., Han, J., and Colman, A. W. (2010). Sup-

port for business process ﬂexibility in service compo-

sitions: An evaluative survey. In Australian Software

Engineering Conference, pages 97–106.

Members, W. M. C. (1994). Glossary – a workﬂow manage-

ment coalition speciﬁcation. Technical report, Coali-

tion, Workﬂow Management.

Mohammed, K., Redouane, L., and Bernard, C. (2007). A

deviation-tolerant approach to software process evo-

lution. In IWPSE, pages 75–78.

Munoz-Gama, J. (2010). Algorithms for process confor-

mance and process reﬁnement. Master’s thesis, Uni-

versitat Polit

ecnica de Catalunya.

Pesic, M. (2008). Constraint-based Workﬂow Management

Systems: Shifting Control to Users. PhD thesis, Eind-

hoven University of Technology.

Pesic, M., Schonenberg, M., Sidorova, N., and van der

Aalst, W. M. P. (2007). Constraint-based workﬂow

models: Change made easy. In OTM, volume 4803,

pages 77–94.

Pesic, M. and van der Aalst, W. M. P. (2006). A declarative

approach for ﬂexible business processes management.

In BPM Workshops, volume 4103, pages 169–180.

Rozinat, A. and van der Aalst, W. M. P. (2008). Confor-

mance checking of processes based on monitoring real

behavior. Information Systems, 33:64–95.

Sibertin-Blanc, C. (2001). Cooperative objects: Princi-

ples, use and implementation. In Concurrent Object-

Oriented Programming and Petri Nets, volume 2001,

pages 216–246.

Soares Passos, L. and Julia, S. (2009). Qualitative analysis

of workﬂow nets using linear logic: Soundness veriﬁ-

cation. In IEEE SMC, pages 2843 –2847.

Thompson, S. and Torabi, T. (2009). An observational ap-

proach to practical process non-conformance detec-

tion. In ICADIWT, pages 62–67.

van der Aalst, W. M. P. (1998). The application of petri nets

to workﬂow management. Journal of Circuits Systems

and Computers, 8:21–66.

van der Aalst, W. M. P., Adriansyah, A., and van Dongen, B.

(2012). Replaying history on process models for con-

formance checking and performance analysis. WIREs:

Data Mining and Knowledge Discovery, 2:182–192.

van der Aalst, W. M. P. and Hee, K. v. (2004). Workﬂow

Management: Models, Methods, and Systems. MIT

Press.

van der Aalst, W. M. P., Pesic, M., and Schonenberg, H.

(2009). Declarative workﬂows: Balancing between

ﬂexibility and support. Computer Science - Research

and Development, 23:99–113.

van der Aalst, W. M. P., van Hee, K. M., ter Hofstede, A.

H. M., Sidorova, N., Verbeek, H. M. W., Voorhoeve,

M., and Wynn, M. T. (2011). Soundness of workﬂow

nets: Classiﬁcation, decidability, and analysis. Form.

Asp. Comput., 23:333–363.

Wang, J., Tepfenhart, W. M., and Rosca, D. (2009). Emer-

gency response workﬂow resource requirements mod-

eling and analysis. IEEE Transactions on SMC, Part

C, 39:270–283.

Weber, B., Reichert, M., and Rinderle-Ma, S. (2008).

Change patterns and change support features - enhanc-

ing ﬂexibility in process-aware information systems.

Data and Knowledge Engineering, 66:438–466.

Weske, M. (2007). Business Process Management: Con-

cepts, Languages, Architectures. Springer-Verlag

New York, Inc.

Zazworka, N., Basili, V. R., and Shull, F. (2009). Tool sup-

ported detection and judgment of nonconformance in

process execution. In ESEM, pages 312–323. ACM /

IEEE Computer Society.

Uncertain Marking for Dealing with Partial Parallelization in Business Processes

125