Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in

Business Processes

Leiliane Pereira de Rezende

1,2

, St

ephane Julia

and Janette Cardoso

Computing Faculty, Federal University of Uberl

andia - UFU, Uberl

andia - MG, Brazil

DMIA Department, Institut Sup

erieur de l’A

eronautique et de l’Espace - ISAE, Toulouse, France

Keywords:

WorkFlow Net, Possibilistic Petri Net, Cancellation Features, Reset Arcs, Process Monitoring.

Abstract:

In this paper, an approach based on WorkFlow nets and possibilistic Petri nets is proposed for dealing with

the cancellation features in business processes. Routing patterns existing in business processes are modeled

by WorkFlow nets. Possibilistic Petri nets with uncertainty in the marking and the transition ﬁring are used

to deal with all possible markings when cancellation behaviour is considered. Combining both formalisms, a

kind of possibilistic WorkFlow net is obtained. An example of a simpliﬁed version of a credit card application

process is presented.

1 INTRODUCTION

Organizations are increasingly using Workﬂow Man-

agement Systems (WFMS) to reduce costs and im-

prove the performance and efﬁciency of important

business processes (BP). BP represent the sequences

of activities that have to be executed within an organi-

zation to treat speciﬁc cases and to reach well deﬁned

goals (van der Aalst and van Hee, 2004). In the ﬁeld

of systems engineering, modeling plays a key role for

understanding and controlling the behavior of the cor-

responding systems. WFMS are used for the model-

ing, analysis, enactment, and coordination of struc-

tured BP by groups of people (van der Aalst, 2000).

A workﬂow process corresponds to the automation of

a business process, in whole or part, during which

documents, information or activities are passed from

one participant to another for a particular form of ac-

tion, according to a set of procedural rules (Members,

1994).

Many researchers, such as (van der Aalst, 1998)

(van der Aalst and van Hee, 2004) (Soares Passos

and Julia, 2009), have indicated the Petri net theory

as an efﬁcient tool for the modeling and analysis of

WFMS’s. In particular, an acyclic Petri net model

used to represent a BP, the so-called WorkFlow nets

(WF-nets), was proposed in (van der Aalst and van

Hee, 2004). When considering the WF-nets, the main

The ﬁrst author received CAPES Scholarship - Proc. n

◦

99999.001925/2015-06.

property that has to be proven to guarantee the cor-

rectness notion of the process model is the soundness

property (van der Aalst and van Hee, 2004).

An important concept in WFMS is cancellation

when the execution of some activities may lead to

the termination of other activities in certain circum-

stances (van der Aalst et al., 2003). Cancellation can

be triggered by either a customer request (e.g., a cus-

tomer wishes to cancel a purchase) or by exceptions

(e.g., an order cannot be processed due to insufﬁcient

information). In general, cancellation results in one

of two outcomes: disabling some scheduled activities

or stopping currently running activities (Wynn et al.,

2009).

In order to model cancellation in a process model,

reset nets were proposed. They are Petri nets extended

with special arcs (reset arcs) that can clear the tokens

in selected places, i.e., everything is removed from

these places for a particular instance (Dufourd et al.,

1998). Reset nets have a natural application in busi-

ness process modeling, where possible cancellation

of activities needs to be modeled explicitly, and in

WFMS where such process models with cancellation

behaviors have to be enacted correctly (Wynn et al.,

2009).

The reset nets are apparently an innocent exten-

sion of Petri nets but they have rather dramatic con-

sequences. Simple questions such as reachability be-

come undecidable for reset nets with more than two

reset arcs (Araki and Kasami, 1976) (Dufourd et al.,

1998) (Dufourd et al., 1999) (Hofstede et al., 2010).

126

Rezende, L., Julia, S. and Cardoso, J.

Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in Business Processes.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 126-133

ISBN: 978-989-758-187-8

 2016 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

Consequently, the soundness property is also unde-

cidable for reset WF-net as proven in (van der Aalst

et al., 2009). This shows that, although cancellation

regions form a very useful modeling construct, in-

creasing the expressive power of Petri nets, they com-

plicate to a certain extent the process of veriﬁcation of

workﬂow models (Verbeek et al., 2007). Considering

this, Wynn et al., in (Wynn et al., 2009), proposed a

set of reduction rules for workﬂow nets with reset nets

to facilitate the veriﬁcation of workﬂow models. The

inspiration for such rules came from earlier reduction

rules for Petri nets without reset arcs. Typically, a

reduction rule will decrease the number of elements

under consideration by removing certain transitions

and/or places in the net while preserving some inter-

esting properties (Verbeek et al., 2010). However, a

reset arc can never be abstracted entirely from a re-

set net. That is, if a net contains reset arcs, it is not

possible to obtain a reduced net without any reset arc

(Wynn et al., 2009). In addition, model translations

normally introduce lots of “dummy” transitions that

do not correspond to real events.

Note that it is far from trivial to express the de-

sired behavior without reset arcs given that, to re-

move them, all possible markings should be consid-

ered, making the process model completely unread-

able and intractable (van der Aalst et al., 2009). Tak-

ing this into account, an approach based on WF-nets

and on possibilistic Petri nets is proposed to deal with

all possible markings when the reset arcs are disre-

garded through the use of pseudo-ﬁrings. In particu-

lar, a kind of possibilistic WorkFlow net will be de-

ﬁned to consider, even without being explicitly enu-

merated, all the possible cancellation situations dur-

ing real time execution of the process model. In ad-

dition, such an approach will preserve the decidabil-

ity of the good properties of the model, such as the

soundness property, given that the reset arcs are not

consider in the process model.

The remainder of this paper is as follow: in section

2, the deﬁnition of WF-nets and soundness property

are provided. In section 3, an overview of possibilis-

tic Petri nets is given. In section 4, the possibilistic

WorkFlow net is presented and a simpliﬁed version

of a credit card application process illustrates the ap-

proach. Finally, section 5 concludes this work with a

short summary, an assessment based on the approach

presented and an outlook on future work proposals.

2 WORKFLOW NET

A Petri net that models a workﬂow process is called a

WorkFlow net (WF-net) (van der Aalst and van Hee,

2004). A WF-net needs to possess the following prop-

erties (van der Aalst, 1998):

• It has only one source place, named Start and only

one sink place, named End. These are special

places, such that the place Start has only outgoing

arcs and the place End has only incoming arcs.

• A token in Start represents a case that needs to be

handled and a token in End represents a case that

has been handled.

• Every activity t (transition) and condition p

(place) should be on a path from place Start to

place End.

As previously mentioned, an activity can be asso-

ciated to a transition in a WF-net. However, in or-

der to explicitly indicate the beginning and the end of

each activity in execution, two sequential transitions

plus a place to model an activity is used. The ﬁrst

transition represents the beginning of the activity, the

place the activity, and the second transition represents

the end of the activity (Wang et al., 2009).

Figure 1: WorkFlow net model of an activity.

As shown in ﬁgure 1, transition B represents the

beginning of an activity execution; E represents the

end of the activity execution. Place A

represents the

activity in execution. From a reachability analysis

perspective, ﬁgure 1 can be reduced to a single transi-

tion, which represents the entire activity execution as

a single logic unit.

Soundness is a correctness criterion deﬁned for

WF-nets and is related to its dynamics. A WF-net is

sound if, and only if, the following three requirements

are satisﬁed (van der Aalst and van Hee, 2004):

• For each token put in the place Start, one and only

one token appears in the place End.

• When the token appears in the place End, all the

other places are empty for this case.

• For each transition (activity), it is possible to

move from the initial state to a state in which that

transition is enabled, i.e. there are no dead transi-

tions.

A method for the qualitative analysis of WF-nets

(soundness veriﬁcation) based on the proof trees of

linear logic is presented in (Soares Passos and Julia,

2009) and another based on a reachability graph is

presented in (van der Aalst et al., 2011).

Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in Business Processes

127

3 POSSIBILISTIC PETRI NET

Possibilistic Petri nets are derived from Object Petri

nets (Sibertin-Blanc, 2001). As characterized in the

approach presented in (Cardoso, 1999), a possibilis-

tic Petri net is a model where a marked place corre-

sponds to a possible partial state, a transition to a pos-

sible state change, and a ﬁring sequence to a possible

behavior. The main advantage in working with pos-

sibilistic Petri nets is that they allow for the updating

of a system state at a supervisory level with ill-known

information without necessarily reaching inconsistent

states.

A possibilistic Petri net model associates a possi-

bility distribution Π

(p) to the location of an object o,

p being a place of the net. Π

(p) = 1 represents the

fact that p is a possible location of o, and Π

(p) = 0

expresses the certainty that o is not present in place p.

Conventionally, a marking in a possibilistic Petri net

is then a mapping:

M : O × P −→ {0, 1}

where O is a set of objects and P a set of places. If

M(o, p) = 1, there exists a possibility of there being

the object o in place p. On the contrary, if M(o, p) =

0, there exists no possibility of there being o in p. A

marking M of the net allows one to represent:

• A certain marking: each token is located in only

one place (well-known state). Then M(o, p) = 1

and ∀p

6= p, M(o, p

) = 0.

• An uncertain marking: each token location has a

possibility distribution over a set of places. It can-

not be asserted that a token is in a given place,

but only that it is in a place among a given set

of places. For example, if there exists a possi-

bility at a certain time of having the same ob-

ject o in two different places, p

and p

, then

M(o, p

) = M(o, p

) = 1.

A possibilistic marking will correspond in practice

to knowledge concerning a situation at a given time.

In a possibilistic Petri net, the ﬁring (certain or

uncertain) of a transition t is decomposed into two

steps:

• Beginning of a ﬁring: objects are put into out-

put places of t but are not removed from its input

places.

• End of a ﬁring: that can be a ﬁring cancellation

(tokens are removed from the output places of t)

or a ﬁring achievement (tokens are removed from

the input places of t).

A certain ﬁring consists of a beginning of a ﬁring

and an immediate ﬁring achievement. An uncertain

ﬁring (or a pseudo-ﬁring) that will increase the un-

certainty of the marking can be considered only as

the beginning of a ﬁring (there is no information to

conﬁrm whether the normal event associated with the

transition has actually occurred or not). To a certain

extent, pseudo-ﬁring is a way of realizing forward de-

duction.

The interpretation of a possibilistic Petri net is de-

ﬁned by attaching to each transition an authorization

function η

,...,x

deﬁned as follows:

,...,x

: T −→ {False,Uncertain, True}

where x

, ..., x

are the variables associated with the

incoming arcs of transition t (when considering the

underlying Object Petri net).

If o

, ..., o

is a possible substitution for x

, ..., x

for the ﬁring of t, then several situations can be con-

sidered:

• t is not enabled by the marking but the associated

interpretation is true; an inconsistent situation oc-

curs and a special treatment process of the net is

activated;

• t is enabled by a certain marking and the inter-

pretation is true; then a classical ﬁring (with cer-

tainty) of an object Petri net occurs;

• t is enabled by a certain marking and the interpre-

tation is uncertain; then the transition is pseudo-

ﬁred and the imprecision is increased;

• t is enabled by an uncertain marking; if the inter-

pretation is uncertain, t is pseudo-ﬁred;

• t is enabled by an uncertain marking and the inter-

pretation is true: a recovery algorithm, presented

in (Cardoso et al., 1989), is called and a new com-

putation of the possibility distribution of the ob-

jects involved in the uncertain marking is realized

in order to go back to a certain marking.

Concepts concerning possibilistic Petri nets will

be illustrated through a practical example in section

4 POSSIBILISTIC WORKFLOW

NET FOR CANCELLATION

As pointed out in the introduction, cancellation is an

important concept in WFMS’s, which captures the in-

terference of an activity in the execution of others in

certain circumstances. In order to elaborate such a

concept, in (Dufourd et al., 1998), reset arcs were in-

troduced into the process model, thus allowing for an

increase to its expressive power and to cancel the ex-

ecution of the activities that belong to cancellation re-

gion. However, reachability and, consequently, the

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

128

soundness property are undecidable for Petri nets (or

WF-nets) with reset arcs.

To consider the concept of cancellation, such that

the reachability and soundness property continue de-

cidable, a model of the process based on WF-nets and

on possibilistic Petri nets is proposed. Such a model,

through the use of pseudo-ﬁrings, will then be able

to deal with several markings that must be considered

when the reset arcs are not considered.

The notions of cancellation activity and cancel-

lation case can be generalized to the notion of the

cancellation region, whereby an arbitrary region of a

workﬂow speciﬁcation can be subjected to a cancel-

lation action (Wynn, 2006). In the model proposed

in this paper, if an activity belongs to a cancellation

region, its beginning and end transition will have a

certain and uncertain interpretation attached to each.

However, if an activity does not belong to a cancella-

tion region, its beginning and end transition will only

have a certain interpretation attached to each. The cer-

tain interpretation is related to the beginning and end

conditions of an activity and the uncertain interpreta-

tion to a cancellation event. Note that if the process

model has more than one cancellation region, the un-

certain interpretation will be a disjunction of the can-

cellation events related to each region.

To illustrate the approach, a simpliﬁed version of

a credit card application process, presented in (Wynn

et al., 2009), will be used. The process starts when

an applicant submits a credit card application (with

the proposed amount). Upon receiving an application

(ra), a credit clerk checks whether the submitted ap-

plication is complete (cc). If not, the clerk requests

additional information from the applicant (rmi) and

waits (WT) until this information is received (ri) be-

fore proceeding. At the same time, a timer is set (to)

so that if a certain period elapses before requested in-

formation is received, another request for information

is sent again. For a complete application, the clerk

ﬁrst checks the requested loan amount (cla). It is then

followed by additional checks to validate the appli-

cants income and credit history. Different checks are

performed depending on whether the requested loan is

large (pcl) or small (pcs). The validated application is

then passed on to a manager to make a decision (md).

In the case of an acceptance, the credit card approval

activity can start (sa). The applicant is notiﬁed of the

decision (na) and, at the same time, he/she is asked for

his/her preference on any extra features (wef). The

applicant can choose extra features such as rewards

program or secondary cardholders (cf) before a credit

card is produced and delivered (dcc). This indicates

the completion of the approval activity (ca) and the

process ends. For a rejected application, the applicant

is notiﬁed of the rejection (nr) and the process ends.

An interesting feature of this process is that an ap-

plicant can request to cancel an ongoing application

(ON) at any time after it was received (ra) and before

the manager makes a decision (md), i.e., the activities

cc, rmi, ri, to, cla, pcs and pcl belong to a cancel-

lation region and the activity pcr is responsible for

capturing the withdrawal of an ongoing application.

The possibilistic WF-net with objects in Figure

2(a) depicts the credit card application process. The

symbol < c > is an object belonging to the class

“Credit”, as well as variables x and y, and all the

model’s places. Each transition has an interpretation

and an action attached to it deﬁned by the designer.

The interpretation is used to manage the occurrence

of each event in the system by imposing restrictions

on the ﬁring of transitions. An action is an applica-

tion that involves some speciﬁc methods applied on

the attributes of the formal variables associated with

the incoming arcs, allowing for the modiﬁcation of

some speciﬁc attributes of the object < c >. How-

ever, in the process model presented in this article,

the actions will not be described given that they do

not interfere in the understanding of the approach.

Knowing that the activities cc, rmi, ri, to, cla, pcs

and pcl belong to a cancellation region, their begin-

ning and end transitions will have a certain and uncer-

tain interpretation attached to each of them. All the

other activities (ra, pcr, md, nr, sa, na, we f , dcc, c f

and ca) will have only a certain interpretation. Table

1 shows the authorization functions (η) for each tran-

sition belonging to the possibilistic WF-net shown in

Figure 2(a). The certain and uncertain interpretations

attached to each transition by the authorization func-

tion are respectively represented by the columns with

the subscription “true if ” and “uncertain if ”. The

false interpretation is not represented in Table 1, but it

is evaluated as true when the certain and uncertain in-

terpretations are evaluated as false at the same time or,

otherwise, it is evaluated as false. Finally, if a transi-

tion does not have an uncertain interpretation attached

to it, the space concerning the uncertain interpretation

in Table 1 is empty.

The conditions used in the interpretation of the

transitions correspond to the following interpreta-

tions:

• “begRA”, “begCC”, “begRMI”, “begRI”,

“begTO”, “begCLA”, “begPCS”, “begPCL”,

“begMD”, “begNR”, “begSA”, “begNA”,

“begW EF”, “begDCC”, “begCF” and “begCA”

represent, respectively, the beginning of the

execution of the activities ra, cc, rmi, ri, to, cla,

pcs, pcl, md, nr, sa, na, we f , dcc, c f and ca;

• “endRA”, “endCC”, “endRMI”, “endRI”,

Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in Business Processes

129

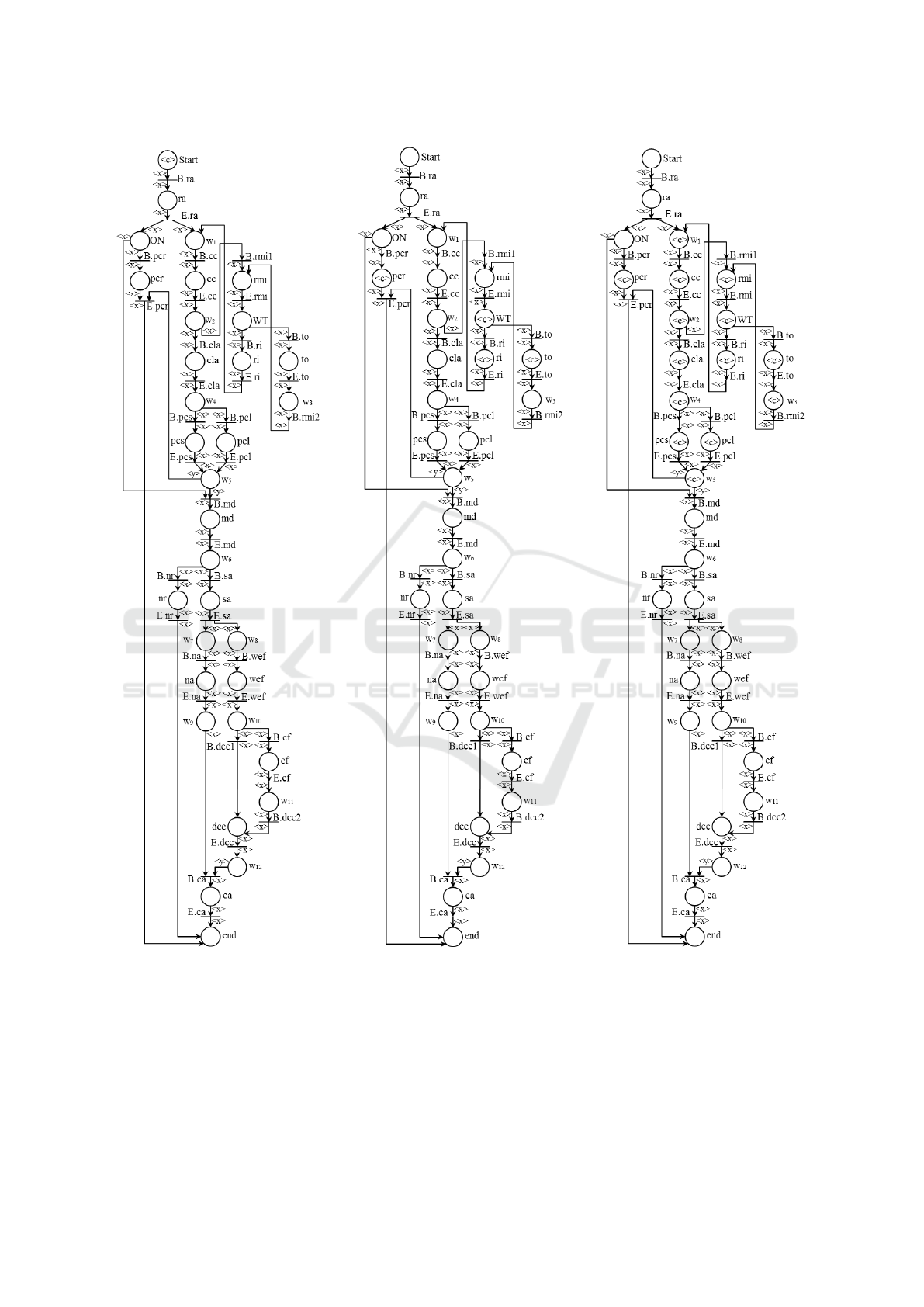
(a) Credit card application process

modeled by a possibilistic WF-net.

(b) The uncertain marking obtained

after the pseudo-ﬁring of B.ri and

B.to.

after the pseudo-ﬁring of the transi-

tions.

Figure 2.

“endT O”, “endCLA”, “endPCS”, “endPCL”,

“endMD”, “endNR”, “endSA”, “endNA”,

“endW EF”, “endDCC”, “endCF” and “endCA”

represent, respectively, the end of the execution

of the activities ra, pcr, cc, rmi, ri, to, cla, pcs,

pcl, md, nr, sa, na, we f , dcc, c f and ca;

• “cancel” represents the request of an applicant to

cancel an ongoing application.

Considering the process model represented in Fig-

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

130

Table 1: Authorization functions of the transitions.

true if uncertain if

(B.ra) = x.begRA

(E.ra) = x.endRA

(B.pcr) = cancel

(E.pcr) = cancel

(B.cc) = x.begCC ∧ ¬cancel cancel

(E.cc) = x.endCC ∧ ¬cancel cancel

(B.rmi1) = x.begRMI ∧ ¬cancel cancel

(B.rmi2) = x.begRMI ∧ ¬cancel cancel

(E.rmi) = x.endRMI ∧ ¬cancel cancel

(B.ri) = x.begRI ∧ ¬cancel cancel

(E.ri) = x.endRI ∧ ¬cancel cancel

(B.to) = x.begT O ∧ ¬cancel cancel

(E.to) = x.endTO ∧ ¬cancel cancel

(B.cla) = x.begCLA ∧ ¬cancel cancel

(E.cla) = x.endCLA ∧ ¬cancel cancel

(B.pcs) = x.begPCS ∧ ¬cancel cancel

(E.pcs) = x.endPCS ∧ ¬cancel cancel

(B.pcl) = x.begPCL ∧ ¬cancel cancel

(E.pcl) = x.endPCL ∧ ¬cancel cancel

(B.md) = x.begMD ∧ ¬cancel

(E.md) = x.endMD

(B.nr) = x.begNR

(E.nr) = x.endNR

(B.sa) = x.begSA

(E.sa) = x.endSA

(B.na) = x.begNA

(E.na) = x.endNA

(B.we f ) = x.begW EF

(E.we f ) = x.endW EF

(B.dcc1) = x.begDCC

(B.dcc2) = x.begDCC

(E.dcc) = x.endDCC

(B.c f ) = x.begCF

(E.c f ) = x.endCF

(B.ca) = x.begCA

(E.ca) = x.endCA

ure 2(a), an object in the place md indicates that the

application was validated and passed on to a manager

to make a decision, thus disabling any request on the

part of the applicant to cancel it. However, an object

in the place pcr indicates that the application received

a request for withdrawal and, consequently, all activ-

ities that belong to the cancellation region must be

stopped if they are currently executing or disabled if

they are scheduled.

If the applicant does not request the cancellation

of the application, all the transition ﬁrings will be cer-

tain and all the markings will be precise. However, if

the applicant makes a request for cancellation, some

pseudo-ﬁring will have to occur until that the transi-

tion E. pcr is enabled by a uncertain marking and the

process can be canceled correctly.

The general behavior of a WFMS based on pos-

sibilistic WF-net models will be based on the possi-

bilistic token player, given by the activity diagram in

Figure 3.

Figure 3: Possibilistic token player algorithm.

To illustrate a possible cancellation request, let us

assume that the activities ra, cc and rmi have already

been executed, i.e., the transitions B.ra, E.ra, B.cc,

E.cc, B.rmi and E.rmi have already been ﬁred with

certainty. If the applicant requests the cancellation of

the application, i.e., the condition “cancel” is true, the

following scenario will occur:

• the transition B.pcr is enabled by a certain mak-

ing and its interpretation is true (η

<c>

(B.pcr) =

true). Then, B. pcr is ﬁred with certainty, i.e. the

object < c > is removed from the place ON, a new

object < c > is produced in the place pcr and the

actions associated to the transition (when they ex-

ist) are executed;

• the authorization functions (η

<c>

) attached to

transitions B.cc, E.cc, B.cla, E.cla, B. pcs, E.pcs,

B.pcl, E.pcl, B.rmi1, E.rmi, B.ri, E.ri, B.to, E.to

and B.rmi2 are all evaluated as uncertain. How-

ever, only the transitions B.ri and B.to can be

pseudo-ﬁred as they are the only ones enabled by

the object < c >. Then, both B.ri and B.to are

pseudo-ﬁred and, consequently, copies of the ob-

ject < c > are produced in the places ri and to,

respectively. Note that the object < c > is not

removed from the place W T (uncertain marking)

(Figure 2(b));

• considering the new marking, the transitions E.ri

and E.to are enabled by an uncertain marking and

the interpretation attached to them is uncertain

(η

<c>

(E.ri) = η

<c>

(E.to) = uncertain). Then,

they are pseudo-ﬁred and copies of the object

< c > are produced in the places w

and w

, re-

spectively;

• considering the evolution of the marking, the

following transitions B.cc, B.rmi2, E.cc, B.cla,

E.cla, B.pcs, B.pcl and E.pcs will be pseudo-

ﬁred given that the interpretation attached to them

is uncertain, therefore, they will be enabled by an

uncertain marking. Consequently, copies of the

object < c > will be produced in the places cc,

rmi, w

, cla, w

, pcs, pcl and w

, respectively;

Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in Business Processes

131

• the transitions B.rmi1, E.rmi and E.pcl are

enabled by an uncertain marking and the

interpretation attached to them is uncertain

(η

<c>

(B.rmi1) = η

<c>

(E.rmi) = η

<c>

(E.pcl) =

uncertain). However, such transitions cannot be

ﬁred due to the existence of the object < c >

in their output places (rmi, W T and w

, respec-

tively) which, through their deﬁnition, prohibit

the pseudo-ﬁring as explained in (Cardoso et al.,

1989);

• the actual marking of the process model is shown

in Figure 2(c). For this marking, the transi-

tion E.pcr is enabled by an uncertain mark-

ing and the interpretation attached to it is true

(η

<cc>

(E.pcr) = true). This situation occurs

because the applicant requested the cancellation

of the application and all activities between ra

and md must be canceled or disabled. Conse-

quently, to go back to the certain marking, the

recovery algorithm, presented in (Cardoso et al.,

1989), is called. Such an algorithm will achieve

the pseudo-ﬁring of the transitions E.pcs, B.pcs,

E.cla, B.cla, E.cc, B.cc, E.ri and B.ri and can-

cel the pseudo-ﬁring of the transitions B.pcl, B.to,

E.to and B.rmi2. After the execution of the recov-

ery algorithm, the transition E.pcr can be ﬁred

with certainty given that it is enabled by a cer-

tain marking and its interpretation is true. There-

fore, allowing for the execution of the actions at-

tached to it and thus, ﬁnalize the cancellation re-

quest and the workﬂow process (only the place

end is marked at the end of the cancellation). Note

that no action attached to a transition pseudo-ﬁred

is executed, even if its ﬁring is achieved.

Through the use of pseudo-ﬁrings, a ﬁring se-

quence is deﬁned, which will transform the mark-

ing until the object < c > is localized in the place

. Then, the process can be ﬁnalized with success

through the certain ﬁring of the transition E.pcr af-

ter the execution of the recovery algorithm. The ex-

istence of this ﬁring sequence is guaranteed by the

soundness property, which ensures that there does not

exist dead transitions in this WF-net.

5 CONCLUSIONS

In this article, a possibilistic WorkFlow net model was

presented with the purpose of dealing with cancella-

tion features in business processes. Combining the

routing structure of WF-nets and uncertain reasoning

of possibilistic Petri nets, the authors presented an

approach that is able to treat the cancellation events

through of the use of pseudo-ﬁring, which give a de-

scription of a set of possible markings that are all

reachable markings of the underlying WF-net. Such

an approach was applied to an example of a simpliﬁed

version of a credit card application process.

Other studies that deal with the problem of cancel-

lation use reset arcs in the process model. Such arcs

have as a consequence the loss of decidability over

some important structural properties, such as reacha-

bility. To avoid this loss, other works proposed tech-

niques for reducing the size of the net and conse-

quently the quantity of reset arcs. However, a reset

arc can never be abstracted entirely from a reset net,

consequently, the structural properties continue being

undecidable. In addition, lots of “dummy” transitions

that do not correspond to real events can be introduced

to the process model. Comparing these studies with

the approach presented in this paper, the main advan-

tage is that, as the reset arcs are not used in the process

model, the decidability of the structural properties of

the model, such as soundness property, are guaran-

teed. Furthermore, all the scenarios that correspond to

a cancellation situation are considered during the real

time execution, even without being explicitly enumer-

ating in the process model.

As a future work proposal, the quality of this ap-

proach should be explicitly validated through a kind

of experimental approach that allows for the program-

ming of transition pseudo ﬁring. It would seem that

the CPN Tools software resources (Beaudouin-Lafon

et al., 2001), developed by the computing science

group of Aarhus University in Denmark, allows in

particular for the use of complex function calculus as-

sociated with the model’s arcs. This should be able to

program in a simple way some of the basic behaviors

of a possibilistic token player implementing cancel-

lation scenarios. In addition, it will be interesting to

model and test a larger business process with more

than one cancellation region.

ACKNOWLEDGEMENTS

The authors would like to thank Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior

(CAPES), Fundac¸

ao de Amparo a Pesquisa do Estado

de Minas Gerais (FAPEMIG) and Conselho Nacional

de Desenvolvimento Cient

ıﬁco e Tecnol

ogico (CNPq)

for ﬁnancial support.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

132

REFERENCES

Araki, T. and Kasami, T. (1976). Some decision problems

related to the reachability problem for petri nets. The-

oretical Computer Science, 3:85 – 104.

Beaudouin-Lafon, M., Mackay, W., Jensen, M., Andersen,

P., Janecek, P., Lassen, M., Lund, K., Mortensen, K.,

Munck, S., Ratzer, A., Ravn, K., Christensen, S., and

Jensen, K. (2001). Cpn/tools: A tool for editing and

simulating coloured petri nets etaps tool demonstra-

tion related to tacas. In Tools and Algorithms for the

Construction and Analysis of Systems, volume 2031,

pages 574–577. Springer Berlin Heidelberg.

Cardoso, J. (1999). Time fuzzy petri nets. In Fuzziness in

Petri Nets, pages 115 – 145. Springer.

Cardoso, J., Valette, R., and Dubois, D. (1989). Petri nets

with uncertain markings. In Applications and Theory

of Petri Nets, volume 483, pages 64 – 78.

Dufourd, C., Finkel, A., and Schnoebelen, P. (1998). Reset

nets between decidability and undecidability. In Pro-

ceedings of the 25th International Colloquium on Au-

tomata, Languages and Programming, volume 1443,

pages 103–115.

Dufourd, C., Jan

car, P., and Schnoebelen, P. (1999). Bound-

edness of reset p/t nets. In International Colloquium

on Automata, Languages and Programming, volume

1644, pages 301–310.

Hofstede, A. H. M. t., van der Aalst, W. M. P., Adams, M.,

and Russell, N., editors (2010). Modern Business Pro-

cess Automation - YAWL and its Support Environment.

Springer Science & Business Media.

Members, W. M. C. (1994). Glossary – a workﬂow manage-

ment coalition speciﬁcation. Technical report, Coali-

tion, Workﬂow Management.

Sibertin-Blanc, C. (2001). Cooperative objects: Princi-

ples, use and implementation. In Concurrent Object-

Oriented Programming and Petri Nets, volume 2001,

pages 216–246.

Soares Passos, L. and Julia, S. (2009). Qualitative analysis

of workﬂow nets using linear logic: Soundness veriﬁ-

cation. In Systems, Man and Cybernetics, 2009. SMC

2009. IEEE International Conference on, pages 2843

–2847.

van der Aalst, W. M. P. (1998). The application of petri nets

to workﬂow management. Journal of Circuits Systems

and Computers, 8:21–66.

van der Aalst, W. M. P. (2000). Workﬂow veriﬁcation:

Finding control-ﬂow errors using petri-net-based tech-

niques. In Business Process Management, Models,

Techniques, and Empirical Studies, pages 161–183.

van der Aalst, W. M. P., Hofstede, A. H. M. t., Kie-

puszewski, B., and Barros, A. P. (2003). Workﬂow

patterns. Distrib. Parallel Databases, 14:5–51.

van der Aalst, W. M. P. and van Hee, K. (2004). Workﬂow

Management: Models, Methods, and Systems. MIT

Press.

van der Aalst, W. M. P., van Hee, K., Hofstede, A. H. M. t.,

Sidorova, N., Verbeek, H., Voorhoeve, M., and Wynn,

M. (2009). Soundness of workﬂow nets with reset

arcs. In Transactions on Petri Nets and Other Mod-

els of Concurrency III, volume 5800, pages 50–70.

van der Aalst, W. M. P., van Hee, K. M., Hofstede, A. H.

M. t., Sidorova, N., Verbeek, H. M. W., Voorhoeve,

M., and Wynn, M. T. (2011). Soundness of workﬂow

nets: Classiﬁcation, decidability, and analysis. Form.

Asp. Comput., 23:333–363.

Verbeek, H., van der Aalst, W. M. P., and Hofstede, A.

H. M. t. (2007). Verifying workﬂows with cancella-

tion regions and or-joins: An approach based on re-

laxed soundness and invariants. The Computer Jour-

nal, 50:294–314.

Verbeek, H., Wynn, M., van der Aalst, W. M. P., and Hof-

stede, A. H. M. t. (2010). Reduction rules for re-

set/inhibitor nets. Journal of Computer and System

Sciences, 76:125 – 143.

Wang, J., Tepfenhart, W. M., and Rosca, D. (2009). Emer-

gency response workﬂow resource requirements mod-

eling and analysis. IEEE Transactions on SMC, Part

C, 39:270–283.

Wynn, M., Verbeek, H., van der Aalst, W. M. P., Hofst-

ede, A. H. M. t., and Edmond, D. (2009). Soundness-

preserving reduction rules for reset workﬂow nets. In-

formation Sciences, 179:769–790.

Wynn, M. T. K. (2006). Semantics, Veriﬁcation, and Im-

plementation of Workﬂows with Cancellation Regions

and OR-joins. PhD thesis, Queensland University of

Technology.

Possibilistic WorkFlow Nets for Dealing with Cancellation Regions in Business Processes

133