
An Interval Type-2 Fuzzy Logic System for Assessment of Students’
Answer Scripts under High Levels of Uncertainty
Ibrahim A. Hameed
1,*
, Mohanad Elhoushy
2
, Belal A. Zalam
2
and Ottar L. Osen
1
1
Department of Automation Engineering (AIR), Faculty of Engineering and Natural Sciences,
Norwegian University of Science and Technology (NTNU), Larsgårdsvegen 2, 6009 Ålesund, Norway
2
Department of Industrial Electronics and Control Engineering, Faculty of Electronic Engineering,
Menofia University, 32952 Menouf, Egypt
Key
words: Students’ Evaluation, Uncertainty, Interval Type-2 (IT2) Fuzzy Sets, Type Reduction, Footprint of
Uncertainty (FOU).
Abstract: The proper system for evaluating the learning achievement of students is the key to realizing the purpose of
education and learning. Traditional grading methods are largely based on human judgments, which tend to
be subjective. In addition, it is based on sharp criteria instead of fuzzy criteria and suffers from erroneous
scores assigned by indifferent or inexperienced examiners, which represent a rich source of uncertainties,
which might impair the credibility of the system. In an attempt to reduce uncertainties and provide more
objective, reliable, and precise grading, a sophisticated assessment approach based on type-2 fuzzy set
theory is developed. In this paper, interval type-2 (IT2) fuzzy sets, which are a special case of the general
T2 fuzzy sets, are used. The transparency and capabilities of type-2 fuzzy sets in handling uncertainties is
expected to provide an evaluation system able to justify and raise the quality and consistency of assessment
judgments.
1 INTRODUCTION
As highlighted by Boud (1988), assessment methods
and requirements probably have a greater influence
on how and what students learn than any other
factor. This influence may become of greater
importance than the impact of teaching materials
itself. A high quality, reliable and transparent
assessment system supports and improves student
lifelong learning and ensures that all students receive
fair treatment in order not to limit students' present
and future opportunities. The evaluation of a
students’ learning achievement is done over years
and provides the basis for certification of individual
achievement, therefore, it should regularly reviewed
and improved to ensure that the systems are
educationally beneficial to all students (Saleh and
Kim, 2009; Hameed, 2011). Students’ evaluation
and scoring are largely based on human judgments,
which tend to be subjective, and hence represents a
rich source of uncertainties. Assessment process, as
well, is suffering from uncertainty due to assigning
erroneous grades and indifferent and inexperienced
practices. Uncertainty is an attribute of information
(Zadeh, 2005). More often than not, the decision-
relevant information is subjected to uncertainty
arising from different sources. Consequently,
decisions involve an undeniable amount of risk
(Daradkeh et al., 2013).
In an attempt to reduce the uncertainty in the
students’ assessment process, several attempts have
been made in the last decade to use fuzzy set theory
in educational evaluation. Biswas (1995) presented
two methods for students’ answerscripts evaluation
using fuzzy sets; a fuzzy evaluation method and a
generalized fuzzy evaluation method and a matching
function. Echauz and Vachtsevanos (1995) proposed
a fuzzy logic system for translating traditional scores
into letter-grades. Law (1996) built a fuzzy structure
model for education grading system with its
algorithm to aggregate different test scores in order
to produce a single score for individual student.
Wilson, Karr and Freeman (1998) presented an
automatic grading system based on fuzzy rules and
genetic algorithms. Chen and Lee (1999) presented
two methods for applying fuzzy sets to overcome the
problem of rewarding two different fuzzy marks the
same total score that could arise from Biswas’
40
Hameed, I., Elhoushy, M., Zalam, B. and Osen, O.
An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 40-48
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

method. Ma and Zhou (2000) proposed a fuzzy set
approach to assess the outcomes of student-centered
learning using the evaluation of their peers and
lecturer.
Weon and Kim (2001) presented an evaluation
strategy based on fuzzy MFs. They pointed out that
the system for students’ achievement evaluation
should consider the three important factors of the
questions that the students answer: the difficulty, the
importance, and the complexity. Weon and Kim
used singleton functions to describe the factors of
each question reflecting the effect of the three
factors individually, but not collectively. Wang and
Chen (2008) presented a method for evaluating
students’ answerscripts using fuzzy numbers
associated with degrees of confidence of the
evaluator. Bai and Chen (2008b) pointed out that the
difficulty factor is a very subjective parameter and
may cause an argument about fairness in evaluation.
Bai and Chen (2008a) proposed a method to
automatically construct the grade MFs of fuzzy rules
for evaluating student’s learning achievement. Bai
and Chen (2008b) proposed a method for applying
fuzzy MFs and fuzzy rules for the same purpose. To
solve the subjectivity of the difficulty factor of
Weon and Kim’s method (2001), they obtained the
difficulty as a function of accuracy of the student’s
answer script and time consumed to answer.
However, their method still has the subjectivity
problem, since the results in scores and ranks are
heavily depend on the values of several weights that
are determined by the subjective knowledge of
domain experts.
Saleh and Kim (2009) proposed three nodes
fuzzy logic approach based on Mamdani’s fuzzy
inference engine and the center of gravity (COG)
defuzzification technique as an alternative to Bai and
Chen’s method (2008b). The transparency and
objective nature of the fuzzy system makes their
method easy to understand and enables teachers to
explain the results of evaluation to persuade skeptic
students. Hameed (2011) proposed using Gaussian
MFs as an alternative of the triangle MFs used in
Saleh and Kim (2009). A sensitivity study showed
that using Gaussian MFs with standard deviation
higher than 0.4 provide more reliable and robust
evaluation system which is able to provide new
ranking orders without changing students’ scores.
In this paper, a type-2 fuzzy logic (T2FL) system
is proposed. The general framework of T2 fuzzy
reasoning allows handling much of the uncertainty
inherited in students’ evaluations systems. T2FL has
better capabilities in reducing the amount of
uncertainty in a system due to its ability in handling
linguistic uncertainties by modeling vagueness and
unreliability of information (Liang and Mendel,
2000). In this paper, a new implementation of the
three-nodes fuzzy evaluation system presented in
Saleh and Kim (2009) and Hameed (2011) using
T2FSs will be presented. An example will be given
to highlight the differences between traditional,
T1FSs- and T2FSs-based approaches.
The paper is organized as follows: a review of
some existing evluation approaches is presented in
Section 2. The proposed inteleval type-2 fuzzy logic
based evalaution system is presented in Section 3. In
Section 4, results of the appraoches presented in
Sections 2 and 3 applied to a real world example are
presnted. Comaprsons between different approahces,
concluding remarks and future work are presnted in
Section 5.
2 REVIEW OF EVALUATION
METHODS
2.1 Classical Approach
Assume that there are n students to answer m
questions. Accuracy rates of students’ answerscripts
(student’s scores in each question divided by the
maximum score assigned to this question) are the
basis for evaluation. We get an accuracy rate matrix
of dimension m x n,
A = [a
ij
], m x n,
where
]1,0[∈
ij
a
denotes the accuracy rate of
student j on question i. Time rates of students (the
time consumed by a student to solve a question
divided by the maximum time allowed to solve this
question) is another basis to be considered in
evaluation. We get a time rate matrix of dimension
m x n,
T = [t
ij
], m x n,
where
]1,0[∈
ij
t
denotes the time rate of student j
on question i. We are given a grade vector
G = [g
i
], m x 1,
where
]100,1[∈
i
g
denotes the assigned maximum
score of question i satisfying
∑
=
=
m
i
i
g
1
100
.
Based on the accuracy rate matrix A and the grade
vector G, we obtain the total score vector of
dimension n x 1,
An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty
41
S = A
T
G = [s
j
], n x 1, (1)
where s
j
]100,0[∈
is the total score of student j
which is obtained by
s
j
=
∑
=
⋅
m
i
iij
ga
1
(2)
The classical rank of students is then obtained by
sorting values of S in a descending order. In this
approach, the time used in solving each question is
not considered
2.2 Three-nodes Fuzzy Evaluation
Approach
The system consists of three nodes, the difficulty
node, the cost node, and the adjustment node, as it is
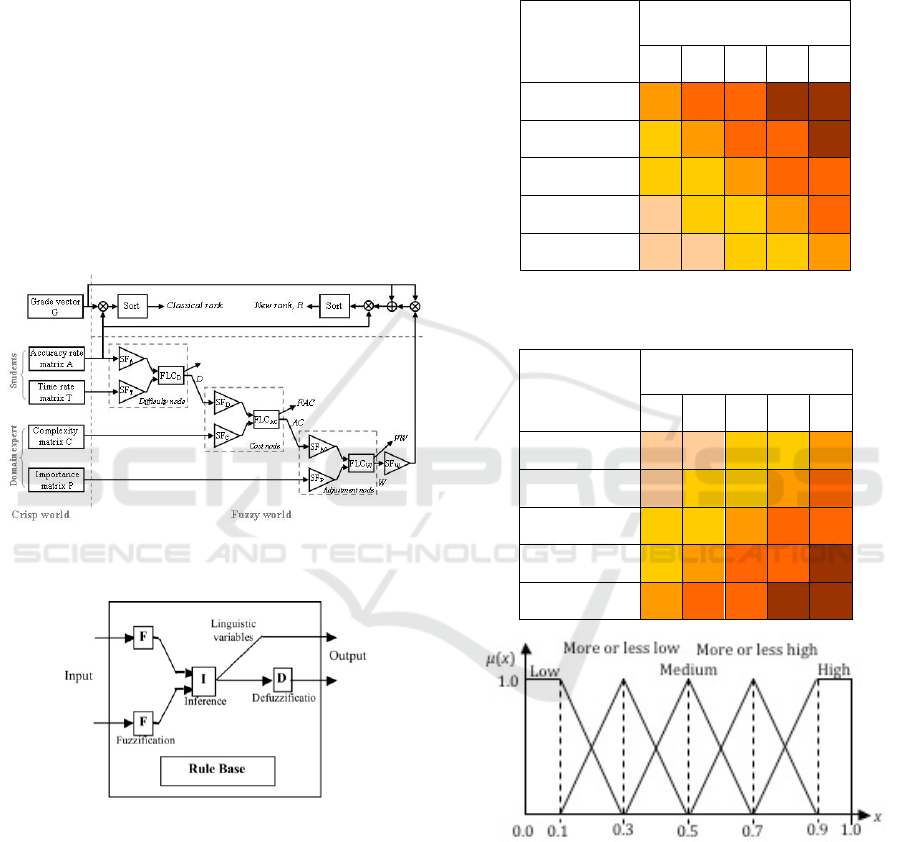
shown in Figure 1 (Saleh and Kim, 2009).
Figure 1: Block diagram of the three nodes fuzzy
evaluation system.
Figure 2: Node representation as a fuzzy logic controller.
Input to the system, in the left part of the figure,
is given either by exam results or domain expert.
Each node of the system behaves like a fuzzy logic
controller (FLC) with two scalable inputs and one
output, as it is shown in Figure 2. It maps a two-to-
one fuzzy relation by inference through a given rule
bases, shown in Tables 1 & 2 where 1, 2, 3, 4 and 5
stands for the five linguistic labels or levels low,
more or less low, medium, more or less high and
high. Fuzzy sets (FSs) are sets whose elements have
degrees of membership, and were first introduced by
Zadeh in 1965 as an extension of the classical notion
of set (Zadeh, 1965). The inputs are fuzzified based
on the predefined defined levels (fuzzy sets) shown
in Figure 3.
Table 1: A fuzzy rule base to infer the difficulty.
Accuracy
Time rate
1 2 3 4 5
1 3 4 4 5 5
2 2 3 4 4 5
3 2 2 3 4 4
4 1 2 2 3 4
5 1 1 2 2 3
Table 2: A fuzzy rule base to infer the cost and
adjustment.
Difficulty/
Cost
Complexity/
Importance
1 2 3 4 5
1 1 1 2 2 3
2 1 2 2 3 4
3 2 2 3 4 4
4 2 3 4 4 5
5 3 4 4 5 5
Figure 3: Triangular membership functions of the five
levels (i.e., five MFs).
In the first node, both inputs are given by exam
result, whereas in the later nodes, one input is the
output of its previous node while a domain expert
gives the other input. The output of each node can be
in the form of a crisp value (defuzzified) or in the
form of linguistic variables (MFs). Each node has
two scale factors (SFs) that can be chosen in a
manner to reflect the degree of importance of each
CSEDU 2016 - 8th International Conference on Computer Supported Education
42

input. Here, SFs are chosen to be equal to 1 to reflect
the equal influence of each input on the output. In
this method, each fuzzy node proceeds in following
four steps.
Step. 1: Fuzzification step in which inputs, if
given in crisp values, the degree to which these
inputs belong to each of the appropriate fuzzy sets is
determined. Triangular MF is the commonly used
due to its simplicity and easy computation. We note
that the same five fuzzy sets, shown in Figure 3, are
applied to represent the accuracy, the time rate, the
difficulty, the complexity, and the adjustment of
questions in the fuzzy domain.
Step. 2: Rule evaluation where the fuzzified
inputs are applied to the antecedents of the fuzzy
rules to obtain a single number that represents the
result of the antecedent evaluation (i.e., rule or firing
strength). The result of the antecedent evaluation is
then applied to the membership function of the
consequent (i.e., rule implication). Two implication
methods are commonly used; clipping where the
consequent membership function is sliced at the
level of the level of the rule firing strength. The
clipped function set loses some information,
however, it is preferred because it involves less
complex computations and generates an aggregated
output surface that is easier to defuzzify (Iancu,
2012). Another method, named scaling, offers a
better approach for preserving the original shape of
the fuzzy set: the original membership function of
the rule consequent is adjusted by multiplying all its
membership degrees by the truth value of the rule
antecedent
Step. 3: Aggregation of rule outputs where the
membership functions of all rule consequents
previously clipped or scaled are combined into a
single fuzzy set. Implication is modeled by means of
minimum operator, and the resulting output MFs are
combined using maximum operator (i.e.
aggregation).
Step. 4: defuzzification in which the aggregated
fuzzy sets are converted into a single crisp output.
The most popular method is the centroid technique
where a point representing the center of gravity
(COG) of the aggregated fuzzy set is found. In this
paper, the center of gravity (COG) method is
applied. The crisp value of question i is then
obtained by
(3)
where integrals are taken over the entire range of the
output and µ(x), and µ(x) is the membership degree
of x. By taking the center of gravity, conflicting
rules essentially are cancelled and a fair weighting is
obtained.
Each of the three nodes follows the above
scheme. The difficulty node has two inputs, the
accuracy rate and the time rate, and one output of the
difficulty. The cost node has two inputs, the
difficulty and complexity, and one output of the
cost. The adjustment node has two inputs, the cost
and the importance, and one output of the
adjustment.
The adjustment vector, W, is then used to obtain
the adjusted grade vector of dimension m x 1,
m x 1, where is the adjusted grade of
question i, and is obtained using the formula:
),1(
~
iii
wgg +⋅=
(4)
It is then scaled to its total grade by using the
formula:
∑∑
⋅=
m
j
j
m
j
jii
gggg
~~~
(5)
Then we obtain the adjusted total scores of
students by,
GAS
T
~
~
=
(6)
The new rank of students is then obtained by
sorting values of
S
~
in a descending order.
2.3 Gaussian based Three Nodes Fuzzy
Evaluation Approach
The three nodes fuzzy evaluation system described
in Section 2.2 is based on the simple triangular-
shaped MF formed using straight lines. Triangular
MFs are defined by three scalar parameters a, b and
c. The parameters a and c locate the feet of the
triangle MF while b locates its peak. There is no way
to get its optimum values, however, they should be
chosen in a manner to provide a satisfying overlap
between different MFs. The simplicity of this
function makes it ideal for control applications
where computational power and resources are
crucial (Zhao and Bose, 2002). However, it was
noted that when theses parameters are changed
slightly, different ranking orders are obtained which
could impair the system’s reliability.
In order to avoid losing reliability and having a
robust evaluation system, it should be able to give
the same ranking orders without changing students’
scores and for various values of these parameters. In
this connection, Gaussian MFs are proposed
(Hameed, 2011). Gaussian MFs are suitable for
problems that require continuously differentiable
curves and smooth transitions between levels,
whereas triangular MFs do not have. Gaussian MFs
∫∫
=
xx
i
dxxdxxxy )()(.
μμ
],
~
[
~
i
gG =
i
g
~
An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty
43

are defined by two parameters; c which locates the
distance from the origin to the center of each MF
and σ which determines its width. Gaussian MFs is
one parameter less than that of the triangular MFs
which will lead to an evaluation system with 15 less
Degrees Of Freedom (DOF) and hence a more
robust performance (Zhao and Bose, 2002).
Gaussian MFs is defined as
(7)
where c
i
is the center (i.e., mean) and σ
i
is the width
(i.e., standard deviation) of the i
th
fuzzy set, which
has by nature, infinite support. Therefore, for
Gaussian MFs with wide widths it is possible to
obtain a membership degree to each fuzzy set
greater than 0 and hence every rule in the rule base
fires. Consequently, the relationship between input
and output can be described accurate enough. Here,
the centers of the five Gaussian MFs are chosen to
be the same as that of the triangular MFs shown in
Figure 3 (i.e. [0.1 0.3 0.5 0.7 0.9]). Gaussian MFs of
the five levels for σ=0.1 are shown in Figure 4.
Figure 4: Gaussian membership functions of the five
levels for σ = 0.1.
From Figure 4 it is obvious that Gaussian MFs
provide more continuous transition from one interval
to another and hence provides smoother control
surface from the fuzzy rules. The Gaussian based
fuzzy evaluation system was able to provide correct
ranking order of students with equal total scores
without changing the total mean scores of all
students and the score of each student for σ ≥ 4.0
(Hameed, 2011; Hameed and Sørensen, 2010).
3 INTERVAL T2FL SYSTEM
BASED EVALUATION SYSTEM
Interval type-2 fuzzy logic systems (IT2 FLSs) have
demonstrated better abilities to handle uncertainties
than their type-1 (T1) counterparts in many
applications (Wu, 2013). The concept of T2FSs was
first introduced by Zadeh in 1975 (Zadeh, 1975) as
an extension of the concept of an ordinary type-1
fuzzy set. Such sets are fuzzy sets whose
membership grades themselves are T1FSs instead of
crisp numbers in T1 FS. Interval type-2 (IT2) FSs
are T2 FSs whose memberships are intervals instead
of T1FSs in a general T2FS (Zadeh, 2005).
T2FSs are useful in such cases when it becomes
difficult to determine exact membership function for
a fuzzy set and hence are useful for incorporating
linguistic uncertainties. Figure 5 shows the
schematic diagram of an IT2 FLS. It is similar to its
T1 counterpart, shown in Figure 2, the major
difference being that at least one of the FSs in the
rule base is an IT2 FS. Hence, the outputs of the
inference engine are IT2FSs. A type-reducer is
needed to convert them into T1FSs before
defuzzification can be carried out (Wu, 2013).
Fuzzifier
Rules
Inference
Defuzzifier
Type Reducer
Output Processing
Fuzzy output setFuzzy input set
Crisp input Crisp output
Type reduced
set
Figure 5: Schematic diagram of IT2 FLS.
Mendel and Liang (1999) demonstrated the first
type-2 fuzzy framework where the information
about the linguistic/numerical uncertainty can be
incorporated. They introduced the concept of
concept of footprint-of-uncertainty (FOU) where the
an interval type-2 membership function (MF) is
characterized by an upper and lower type-1 MFs
bounding the region called FOU, as it is shown in
Figure 6. The internal structure of T2FLS is shown
in Figure 6. A fuzzy logic system can be considered
as T2 when at least one of the antecedents or
consequents of its rule-base’s FSs is T2. As the
outputs of the inference engine are IT2 FSs, a type-
reducer is required to convert its T2FSs into T1FSs
to be defuzzified. A detailed description can be
found in (Mendel, 2001).
(a) (b)
Figure 6: FOU for (a) T2 Gaussian MF, and (b) Triangle
MF.
()
()
,
2
2
1
ii
i
cx
A
ex
σ
μ
−−
=
CSEDU 2016 - 8th International Conference on Computer Supported Education
44

In this paper, the three-nodes fuzzy evaluation
framework shown in Figures 1 and 2 is implemented
using triangle T2FSs shown in Figure 6(b). Five T2
triangle MFs are used to represent the five levels
used to describe each variable, as it is shown in
Figure 7(a). The FOU (i.e., thickness of the MFs) is
provided as an external input by the domain expert
as an estimate of the amount of uncertainty in his/her
knowledge. In this paper, FOU is chosen to be a
number in the range of 0 to 0.3 where 0 refers to
zero uncertainty, 0.1 refers to low uncertainty, 0.2
refers to medium uncertainty and 0.3 refers to high
uncertainty. It is worth noting that the T2 fuzzy
system will converge to its T1 counterpart when
uncertainty measure is set to zero (Hameed, 2009),
as it is shown in Figure 7(a). In this paper, it is
assumed that the domain expert has a medium
degree of uncertainty in his knowledge (i.e.,
FOU≈0.2).
Figure 7: FOU: (a) zero uncertainty (FOU=0), (b) low
uncertainty (0<FOU≤0.1), (c) medium uncertainty
(0.1<FOU≤0.2), and (d) high uncertainty (0.2<FOU≤0.3).
4 RESULTS
In this section, a comparison between the different
evaluation approaches presented in Sections 2 and 3
will be introduced using an example.
4.1 Example
Assume that we have n students laid to an exam of m
questions where n=10 and m=5. The accuracy rate
matrix, A, the time rate matrix, T, and the grade
vector, G, are given as follows (Bai and Chen,
2008b; Saleh and Kim, 2009; Hameed, 2011):
,
61.097.051.039.093.065.081.008.049.093.0
25.09.092.032.002.05.016.018.072.073.0
74.091.042.087.086.017.071.097.069.077.0
53.081.022.004
.016.088.004.014.027.001.0
24.004.023.084.008.011.066.0135.059.0
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=A
,
2.08.02.08.016.0111.00
5.07.08.04.03.01101.02.0
4.01.03.02.019.01.001.00
3.008.02.03.013.09.001
9.04.06.
07.02.07.011.04.07.0
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=T
[]
3025201510=
T
G
Here, A=[a
ij
] and T=[t
ij
] are of n×m dimensions,
where a
ij
∈[0, 1] denotes the accuracy rate of student
j on question i, t
ji
∈[0, 1] denotes the time rate of
student j on question i. G
T
denotes the transpose of
G, where G is of m×1 dimension, G= [g
i
], g
i
∈[1,
100] denotes the assigned maximum score to
question i. Importance and complexity of each
question, I and C, are determined by the domain
expert as follows:
I =
00 0 0 1
0 0.33 0.67 0 0
0 0 0 0.15 0.85
10 0 0 0
0 0.07 0.93 0 0
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
Q
1
Q
2
Q
3
Q
4
Q
5
,
C =
0 0.85 0.15 0 0
0 0 0.33 0.67 0
0 0 0 0.69 0.31
0.56 0.44 0 0 0
000.70.30
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
Q
1
Q
2
Q
3
Q
4
Q
5
.
Matrices I=[i
ik
] and C=[c
ik
] are of dimension
m×l where i
ik
∈[0, 1] denotes the membership value
of question i belonging to the importance level k,
and c
ik
∈[0, 1] denotes the membership value of
question i belonging to the complexity level k.
4.2 Classical Approach
In this approach, total score can be obtained using
formula (1) as follows:
s
1
s
2
s
3
s
4
s
5
s
6
s
7
s
8
s
9
s
10
S
T
= 67.60 54.05 38.40 49.70 49.70 48.80 46.10 52.30 85.95 49.70
⎡
⎣
⎤
⎦
Thus the “classical” ranks of students can then
be obtained by simply sorting S in a descending
order to get:
S
9
> S
1
> S
2
> S
8
> S
4
= S
5
= S
10
> S
6
> S
7
> S
3
,
where S
a
> S
b
means score of student a is higher
than score of student b while S
a
= S
b
means that their
An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty
45

scores are equal.
4.3 Triangle MFs based Fuzzy
Approach
The process starts by averaging the accuracy rate
and answer-time rate matrices A and T, respectively,
for each student to get:
A
T
= 0.45 0.31 0.711 0.47 0.637
⎡
⎣
⎤
⎦
,
T
T
= 0.57 0.48 0.31 0.50 0.57
⎡
⎣
⎤
⎦
.
Based on the fuzzy MFs shown in Figure 3 we
obtain the fuzzy accuracy rate matrix and the fuzzy
time rate matrix as follows:
FA =
0 0.25 0.75 0 0
0 0.95 0.05 0 0
0 0 0 0.945 0.055
0 0.15 0.85 0 0
0 0 0.315 0.685 0
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
,
.
035.065.000
00100
0005.095.00
009.01.00
035.065.000
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=FT
In the first node, both inputs are given by
examination results, whereas in later nodes, one
input will be the output of its previous node and
while a domain expert will provide the other. The
output of each node can be in the form of a crisp
value (defuzzified) or in the form of fuzzy numbers
(i.e., degrees of membership (MFs) of each variable
in the five linguistic levels). Each node has two scale
factors (SFs shown in Figure 1). Here, we let both
scaling factors have the same value of unity
assuming equal influence of each input on the
output.
Each fuzzy node performs Mamdani fuzzy
inference to compute its output given the inputs and
the fuzzy rules (described in Tables 1 and 2). Each
fuzzy node proceeds in a number of steps described
in Section 2.2. By applying FA and FT to the first
node, the difficulty vector, D, and its fuzzy
counterpart, FD. In the same way, the cost vector
will be obtained by applying the difficulty and
complexity to the second node. Finally, the
adjustment vector, W, will be obtained by applying
the cost and importance to the third node as follows:
[]
5.0177.0749.0552.07.0=
T
W
The new scores of students S
1
to S
10
are then
obtained using Equations 3-5 to be 67.151, 53.168,
42.096, 52.190, 48.307, 51.814, 48.474, 49.272,
85.253, 51.493, respectively. The new rank of
students is then obtained by sorting values of
S
ˆ
in a
descending order
S
9
> S
1
> S
2
> S
4
> S
6
> S
10
> S
8
> S
7
> S
5
> S
3
.
4.4 Gaussian MFs based Fuzzy
Approach
By replacing triangle MFs, used in Section 4.3,
which are formed simply using straight lines with
Gaussian MFs with the same center points (i.e.,
mean) as the triangle MFs, as it is shown in Figures
3 and 4 with stand deviation (i.e., width) σ≥4.0, new
scores for the 10 students are obtained where the
mean score is still equal to that of their original
scores obtained using the classical approach. The
new scores of students are then obtained using
Equations 3-5 as:
S
1
S
2
S
3
S
4
S
5
S
6
S
7
S
8
S
9
S
10
ˆ
S
T
= 64.60 54.05 38.40 49.70 49.70 48.80 46.10 52.30 84.95 49.70
⎡
⎣
⎤
⎦
The new rank of students is then obtained by
sorting values of S in a descending
S
9
> S
1
> S
2
> S
8
> S
4
> S
10
> S
5
> S
6
> S
7
> S
3
.
Table 3: Ranking order for different FOU values.
FOU
Rank
1> 2> 3> 4> 5> 6> 7> 8> 9> 10
0 9 1 2 4 6 10 8 5 7 3
0.1 9 1 2 4 6 10 5 8 7 3
0.2 9 1 2 4 6 10 8 7 5 3
0.3 9 1 2 8 5 10 4 6 7 3
4.5 IT2 MFs based Fuzzy Approach
In this Section, IT2 MFs with different value of
FOU (i.e., zero, low, medium and high uncertainty)
as it is shown in Figure 7. The new ranking orders
for different FOU values are shown in Table 3. A
comparing between the ranking orders of the four
types is shown in Table 4.
Table 4: Ranking order for different approaches: class for
classical, T1T for type-1 triangle MFs, T1G for type-1
Gaussian MFs, and T2 for type-2 MFs.
Method
Rank
> 2> 3> 4> 5> 6> 7> 8> 9> 10
Class 9 1 2 8 4= 5= 10= 6 7 3
T1T 9 1 2 4 6 10 8 7 5 3
T1G 9 1 2 8 4 10 5 6 7 3
CSEDU 2016 - 8th International Conference on Computer Supported Education
46

T2 9 1 2 8 5 10 4 6 7 3
5 CONCLUSIONS
As it is shown in Table 1, classical assessment
approach resulted in students of equal scores that
make it difficult to determine a distinguished order
of each student. T1 Triangular FSs overcome the
problem of students of equal scores but at the same
time it changed scores of other students who does
not fall in that category which might spark questions
and make students skeptic about the evaluation
process. On the other hand, T1 Gaussian FSs based
system influenced only that category of students
with equal scores while other students of different
scores are left intact. Similarly, T2 FSs changed only
the scores and hence the rank order of students with
equal scores while the others are left intact. A major
difference between T2 and T1G FSs is that T2
system gave preferences to complexity of questions
over importance and that is clear from GIVING A
higher rank for student S5 who given a higher rank
(rank#5) on account of student S4 who is given a
lower rank (rank#7). On the other side, T1G gave
preferences to importance of questions over its
complexity and that explains why S4 is given higher
rank (rank#5) on account of S5 who has given a
lower rank (rank#7).
The transparency and the human logic nature of
fuzzy logic system make it easy to interpret and
explain why certain scores have changed. The
system inherently has a kind a feedback system to
correct erroneous scores assigned by indifferent or
inexperienced examiners. Easy of implementation of
the proposed system recommended it to spread out
and to be broadly used in other decisions support
systems. In this paper, a collective FOU for all the
fuzzy variables is used to represent a collective
uncertainty in the knowledge of the domain expert.
As a future work, the effect of using various FOU
values for each fuzzy variable such as importance,
complexity, etc. will be investigated. The evaluation
systems proposed in this paper hav been
implemented using the Fuzzy Logic Toolbox™ for
building a fuzzy inference system from
MathWorks™ (Fuzzy Logic Toolbox, 2016).
REFERENCES
Bai, S.-M., Chen, S.-M., 2008a. Automatically
constructing grade membership functions of fuzzy
rules for students’ evaluation. Expert Systems with
Applications, 35(3), 1408-1414.
Bai, S.-M., Chen, S.-M., 2008b. Evaluating students’
learning achievement using fuzzy membership
functions and fuzzy rules. Expert Systems with
Applications, 34, 399-410.
Biswas, R., 1995. An application of fuzzy sets in students’
evaluation. Fuzzy Sets and Systems, 74(2), 187-194.
Boud, D., 1988. Developing student autonomy in learning
(2
nd
ed.), London: Kogan Page.
Chen, S.M., Lee, C.H., 1999. New methods for students’
evaluating using fuzzy sets. Fuzzy Sets and Systems,
104(2), 209–218.
Daradkeh, M., McKinnon, A., Churcher, C., 2013.
Supporting informed decision-making under
uncertainty and risk through interactive visualization.
The Australian Computer Science Communications,
35(5), 23-32.
Echauz, J.R., Vachtsevanos, G.J. 1995. Fuzzy grading
system. IEEE Transactions on Education, 38(2), 158-
165.
Fuzzy Logic Toolbox™ 2.2.7, 2016, retrieved from
http://www.mathworks.com/products/fuzzylogic/ in
February 6
th
2016.
Hameed, I.A., 2009. Simplified architecture of a type-2
fuzzy controller using four embedded type-1 fuzzy
controllers and its application to a greenhouse climate
control system. Proc. IMechE Part I: Journal of
Systems and Control Engineering, 223(5), 619-631.
Hameed, I.A., 2011. Using Gaussian membership
functions for improving the reliability and robustness
of students' evaluation systems. Expert systems with
Applications, 38(6), 7135-7142.
Hameed, I.A., Sørensen, C.G., 2010. Fuzzy Systems in
Education: A More Reliable System for Student
Evaluation, Fuzzy Systems, Azar A. T. (Ed.), ISBN:
978-953-7619-92-3, INTECH, Croatia.
Iancu, I., 2012. A Mamdani type fuzzy logic controller,
Fuzzy Logic - Controls, Concepts, Theories and
Applications, Prof. Elmer Dadios (Ed.), ISBN: 978-
953-51-0396-7, InTech,
John, R.I., 1998. Type-2 fuzzy sets: an appraisal of theory
and applications. International Journal of Uncertainty,
Fuzziness Knowledge-Based Systems, 6(6), 563–576.
Larsen, P.M., 1980. Industrial applications of fuzzy logic
control. International Journal of Man-Machine
Studies, 12(1), 3–10.
Law, C.K., 1996. Using fuzzy numbers in education
grading system. Fuzzy Sets and Systems, 83(3), 311-
323.
Liang, Q., Mendel, J.M., 2000. Interval Type-2 Fuzzy
Logic Systems: Theory and Design. IEEE
Transactions on Fuzzy Systems, 8(5), 535-550.
Ma, J., Zhou, D., 2000. Fuzzy set approach to the
assessment of student-centered learning. IEEE
Transactions on Education, 43(2), 237-241.
Mamdani, E.M., 1974. Applications of fuzzy algorithms
for simple dynamic plants. Proceedings of the
Institution of Electrical Engineers (IEE), 21(2), 1585–
1588.
Mamdani, E.M., Assilian, S., 1975. An experiment in
linguistic synthesis with a fuzzy logic controller.
International Journal of Man-Machine Studies, 7, 1–
13.
An Interval Type-2 Fuzzy Logic System for Assessment of Students’ Answer Scripts under High Levels of Uncertainty
47

Mendel, J.M., 2001. Uncertain Rule-Based Fuzzy Logic
Systems, Prentice-Hall, Upper Saddle River, NJ 07458.
Mendel, J.M., Liang, Q., 1999. Pictorial Comparison of
Type-1 and Type-2 Fuzzy Logic Systems. In:
Proceedings of IASTED International Conference on
Intelligent Systems & Control.
Saleh, I., Kim, S.-I., 2009. A fuzzy system for evaluating
students’ learning achievement. Expert systems with
Applications, 36(3), 6236-6243.
Wang, H.Y., Chen, S.M. 2008. Evaluating students'
answerscripts using fuzzy numbers associated with
degrees of confidence. IEEE Transactions on Fuzzy
Systems, 16(2), 403-415.
Weon, S., Kim, J., 2001. Learning achievement evaluation
strategy using fuzzy membership function.
Proceedings of the 31
st
ASEE/IEEE Frontiers in
Education Conference, Reno: NV.
Wilson, E., Karr, C.L., Freeman, L.M., 1998. Flexible,
adaptive, automatic fuzzy-based grade assigning
system. Proceedings of the North American Fuzzy
Information Processing Society Conference, 334-338.
Wu, D., 2013. Approaches for reducing the computational
cost of interval type-2 fuzzy logic systems: overview
and comparisons. IEEE Transactions on Fuzzy
Systems, 21(1), 80-99.
Zadeh L.A., 1975. The concept of a Linguistic Variable
and Its Application to Approximate Reasoning-I.
Information Sciences, 8, 199-249.
Zadeh, L.A., 1965. Fuzzy sets. Information and Control,
8, 338-353.
Zadeh, L.A., 2005. Towards a generalized theory of
uncertainity (GTU) – an outline. Information Sciences,
172, 1–40.
Zhao, J., Bose, B.K., 2002. Evaluation of membership
functions for fuzzy logic controlled induction motor
drive. In: Proceedings of the 28
th
Annual Conference
of the Industrial Electronics Society, IEEE (IECON
02), 1, 229-234.
CSEDU 2016 - 8th International Conference on Computer Supported Education
48
