Towards High-Quality Parallel Stabilization

Abdelrahman Ahmed and Mohamed S. Shehata

Department of Electrical and Computer Engineering, Memorial University of Newfoundland, St. John’s, Canada

Keywords:

Stabilization, Parallel Architecture, Handheld Devices, UAV.

Abstract:

With the widespread use of handheld devices and unmanned aerial vehicles (UAVs) that has the ability to

record video sequences. Digital video stabilization becomes more important as these sequences are usually

shaky undermining the visual quality of the video. Digital video stabilization has been studied for decades

yielding an extensive amount of literature in the ﬁeld. However, most of them are highly sequential. In this

paper, we present a new parallel technique that exploits the parallel architecture found in modern day devices.

The algorithm divides the frame into blocks and estimates a camera path for each block to better enhance the

estimation of the transformation needed to adjust for the shakiness of the video.

1 INTRODUCTION

The introduction of digital cameras in cell phones and

the spread of unmanned aerial vehicles (UAVs) made

the capture of video sequences much easier. How-

ever, these sequences usually suffer from undesired

high frequency jittering due to the movement of the

camera holder or the movement of the UAV platform.

This jittering result in video sequences with poor vi-

sual quality, plus it undermines the use of other algo-

rithms used for object detection and tracking which

are vital in many video applications (e.g., surveillance

systems, search and rescue .. etc.). The aim of digital

video stabilization is to remove the unwanted jittering

producing sequences with better quality.

Digital video stabilization has been studied for years

in the ﬁeld of computer vision. Generally, Stabiliza-

tion algorithms perform three main operations: 1) Es-

timating the camera motion (shaky path), 2) Estimate

new smooth camera path, 3) Reﬁne the original shaky

path using the smoothed one. Digital video stabi-

lization approaches fall broadly into two categories

based on the motion estimation model: 1) 2D Stabi-

lization, 2) 3D Stabilization. The 2D methods (Mat-

sushita et al., 2006; Grundmann et al., 2011) estimate

a linear transformation either afﬁne or homography

between successive frames. And the camera path is

formed by the concatenation of the linear transfor-

mations. In general these methods are robust and

fast. However, they suffer a limitation as they can-

not deal with the parallax caused by depth informa-

tion in the scene. 3D methods (Liu et al., 2012; Liu

Figure 1: Block diagram of the proposed algorithm.

et al., 2009)on the opposite hand can handle the par-

allax induced by the depth information and produce

highly stable sequences. However, their motion esti-

mation model is complex and less robust than the 2D

methods. Recent approaches tried to combine both

beneﬁts of the 2D and 3D as shown in (Goldstein and

Fattal, 2012) by employing the concepts of epipolar

geometry. However, these methods require tracking

features for long period of time which can be difﬁcult

in sequences with rapid motion or occlusion.

This paper falls in the ﬁrst category aiming to pro-

vide robust and high quality stable sequences from 2D

linear transformations. This paper contribution is in

two folds. 1) We propose a novel algorithm in the

estimation of the frame trajectory. Speciﬁcally, the

proposed algorithm divides the image into blocks and

maintains the trajectory for each block so that each

block has its own camera path, then for any given

frame the paths of its blocks are combined to give

a better estimation for its transformation. Figure 1

summarizes the proposed algorithm. 2) Unlike, most

of the algorithms in the literature, the proposed al-

Ahmed, A. and Shehata, M.

Towards High-Quality Parallel Stabilization.

DOI: 10.5220/0005765306650670

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 667-672

ISBN: 978-989-758-175-5

667

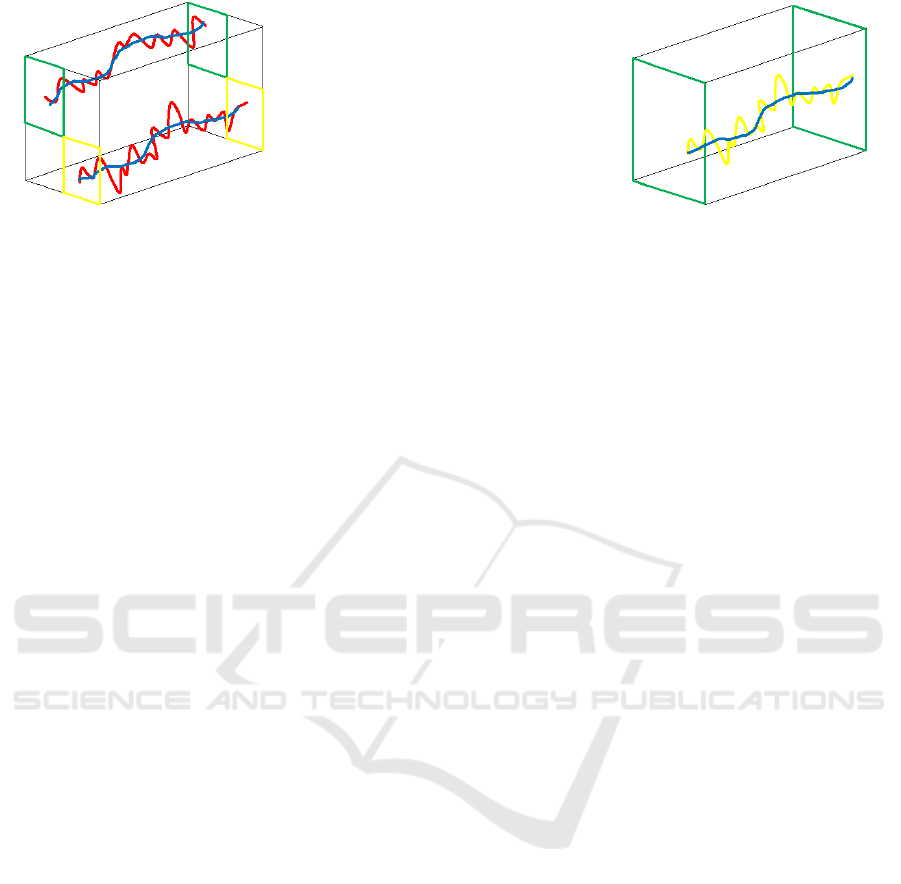
(a) Original block shaky path in red,

smoothed path for the block in blue.

(b) Original frame path in yellow,

smoothed path for the frame in blue.

Figure 2: Camera paths.

gorithm is highly parallelizable exploiting the paral-

lel architecture found in modern computers and hand-

held devices ensuring real time performance. The re-

mainder of this paper is organized as follows: related

work is presented in section 2; a detailed description

of the proposed algorithm is presented in Section 3,

followed by the evaluation criteria and results in Sec-

tion 4. A discussion of the results is presented in sec-

tion 5. Finally, Section 6 concludes the paper and di-

rects future work.

2 RELATED WORK

Stabilization methods can be categorized into two

main categories: 1) 2D Methods, 2) 3D methods.

The 2D methods estimates linear transformations

(afﬁne or homography) between successive frames

and smooth the trajectory over time to produce a sta-

bilized video. Wang et al.(Wang et al., 2011) as-

sumes the motion model ﬁt a polynomial curve e.g.

a cubic curve to smooth the parameters. Irani et

al. (Irani et al., 1994) deals with complex video se-

quences and attempts to estimate a homography trans-

formation which stabilizes a dominant planar region

in the video. Matsushita et al.(Matsushita et al., 2006)

extends the stabilized frames to become full frames

and apply low pass ﬁlter for smoothing the parame-

ters over time. Grundmann et al. (Grundmann et al.,

2011) proposes the application of L1- norm optimiza-

tion model to smooth the camera path to follow cin-

ematography rules. This technique was integrated

into Googles YouTube. 3D methods require the re-

covery of structure from the video sequence includ-

ing 3D camera poses and depth structures. These

structures can computed using Structure from motion

(SFM) techniques (Agarwal et al., 2011; Furukawa

et al., 2010; Jiang et al., 2012; Wu, 2013). Buehler

et al.(Buehler et al., 2001) computes SFM in a gen-

eral un-calibrated camera setting and solved using the

bundle adjustment method (Triggs et al., 2000). Liu

et al. (Liu et al., 2009) proposes a full 3D stabiliza-

tion method by introducing content-preserving warps

for the novel view synthesis. Liu et al. (Liu et al.,

2012) uses a depth camera to recover depth infor-

mation and perform 3D video stabilization. Since

3D reconstruction of a full video is still challenging.

Goldstein and Fattal (Goldstein and Fattal, 2012) uses

the concepts of epipolar geometry to avoid 3D recon-

struction. Wang et al.(Wang et al., 2013) proposes

a new representation of each feature trajectory as a

Bezier curve and then smoothed over time. Liu et

al. (Liu et al., 2011) choose to smooth basis trajecto-

ries of the subspace (Irani, 2002) which are extracted

from long feature tracks of 50 frames or more. This

method achieves high quality stabilization that is sim-

ilar to the full 3D methods, while avoiding the need

of a full 3D reconstruction and using long feature tra-

jectories instead. This technique has been integrated

in Adobe After Effects as a video stabilization func-

tion named Warp Stabilizer. Recently, Liu et al.(Liu

et al., 2013) proposes an extension of the method to

cope with stereoscopic videos. However, the need of

long feature trajectories is difﬁcult to achieve espe-

cially in videos with quickly changing scenes or a lot

of occlusions. Regardless if the algorithms are 2D or

3D, almost all of them are either highly sequential or

ofﬂine stabilizers. Previous work on real-time stabi-

lization as in Wang et al. work (Wang et al., 2011)

the motion model was restricted to translation only.

Litvin et al.(Litvin et al., 2003) the algorithm used

Kalman ﬁltering to extend the model to be a full 2D

afﬁne model with translation and rotation. However,

these techniques sacriﬁce much of the robustness and

visual quality to achieve real time performance. The

proposed method aims at providing parallel, real time

performance without sacriﬁcing loss in the robustness

or the visual quality provided by the ofﬂine stabiliz-

ers. By dividing the frame into blocks and smoothing

their trajectory over time allowing better estimation

for the frame transformation that can adopt with vari-

ous videos.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

668

3 PROPOSED ALGORITHM

The proposed method uses a novel technique to esti-

mate the transformation parameters for a video frame

and smooth the parameters over time in two phases,

as illustrated in Figure 1. The algorithm description

is discussed in the next sections.

3.1 Algorithm Description

Phase I: At each frame, the frame is divided into N

blocks with window overlap of 60% that has been

deﬁned empirically through experiments on various

videos some of which are shown in Figure 4. The

overlap ensures that the features are well tracked

along the boundaries. Then, for each block features

are extracted using good features to track(Shi and

Tomasi, 1994). These features are then tracked in

the same block in the next frame using optical ﬂow

method. An afﬁne transformation denoted by H is

then estimated for each block. The camera path of the

block is then smoothed over time using a Gaussian

low pass ﬁlter with sigma σ

producing a more stable

camera path for that block. So let P

denotes the origi-

nal shaky block path, which is formed by the concate-

nation of the blocks afﬁne transformations over time

as deﬁned by equation 1. The desired (smoothed)

camera path for the block C

is calculated based on

equation 2.

∏

i=0

. (1)

= P

∗ G

(2)

where G

is the Gaussian low pass ﬁlter function with

sigma σ

. Phase II: With each block camera path

smoothed individually from phase I. these paths are

then combined to form an estimate for the transfor-

mation parameters for their corresponding frame. The

paths are combined using another low pass 2D Gaus-

sian with sigma σ

which gives more weight to the

central blocks of the frame as the central blocks of

the frame should contain the dominant motion in the

frame. Let C

t,i

represent the smoothed block path the

frame estimation

is derived by equation 3.

= C

∗W (X, Y ) (3)

where W (X, Y) is the 2D Gaussian window function

with sigma σ

. Then as a ﬁnal step the ﬁnal camera

path for that frame is smoothed within a window of

neighbouring frames using a third low pass Gaussian

ﬁlter with sigma σ

to produce the ﬁnal transforma-

tion parameters for the frame in a similar procedure

to the smoothing of the block path deﬁned by equa-

tion 2. As seen the algorithm is highly parallelizable

as the estimation of the block transformation does not

need any communication or dependency between data

needed by different processors to produce results so

the process can be easily parallelized.

Algorithm 1: The Proposed Algorithm.

1: Input: Input Frame.

2: Divide the frame into blocks(Input frame).

3: for each block i ∈ N Parallel do

4: Extract good features to track.

5: Track the features into previous block.

6: Evaluate good matches.

7: Estimate afﬁne transformation.

8: In case no good transformation can be calcu-

lated, the estimation is replaced by the transfor-

mation of the same block from previous frame.

9: For each block in the neighborhood window,

the trajectory is smoothed using a low pass Gaus-

sian ﬁlter.

10: A new transformation is estimated based on

the smoothed trajectory.

11: end for

12: For each block in the frame, their estimation is

smoothed using a 2D Gaussian kernel to estimate

the transformation for the frame.

13: The trajectory of the frame is then smoothed

based on the Gaussian ﬁlter with the neighboring

frame in the window.

14: The ﬁnal transformation is then estimated based

on the smoothed trajectory of the whole frame.

15: The ﬁnal stabilized frame is computed through

warping the input frame.

16: Output: Stabilized Frame.

3.2 Implementation

In the implementation of the proposed algorithm, the

number of blocks N =16 for videos with frame height

of 720 and width of 1280. The size of the neighbor-

hood used for smoothing was set to 30 in both cases

of smoothing on block and frame level. The sigma of

the Gaussian ﬁlter used in block smoothing is small

=0.3 and σ

= 0.5. Only σ

is set to larger value to

suppress any ﬂuctuations and enforce more smooth-

ness on the path of the camera, so σ

is set to 10.

All the values were set empirically based on experi-

menting with different video sequences. Then Using

OpenMp directives the estimation of the transforma-

tion for each block is done in parallel. The rest of

the implementation for feature extraction, matching

and estimation of transformation and warping of the

frames is based on OpenCV implementation. Algo-

rithm 1 shows a pseudo-code of the implementation.

Towards High-Quality Parallel Stabilization

669

(a) Original Mean of Sequence (b) Our Stabilized Sequence Mean (c) Google’s Youtube Stabilized

Sequence Mean

Figure 3: Sequence Mean Comparison.

4 RESULTS

The proposed algorithm has been tested on both the

datasets provided by (of Central Florida, ) (Grund-

mann et al., 2011) and (Liu et al., 2009). The evalu-

ation criteria are based on (Morimoto and Chellappa,

1998) measuring the average ﬁdelity with equation 4,

the mean of the sequence to assess the visual quality

improvement and also the path of the camera.

PSNR

, I

) = 10 log

(255)

MSE(I

, I

)

(4)

where MSE is the mean squared error measuring the

error per pixel from the optimal stabilized result, and

the 255 represents the maximum intensity a pixel may

have. Figure 3 shows a comparison of the mean of

the stabilized sequence from the results from Googles

YouTube stabilizer at the right and the result from our

proposed algorithm at the middle. by examining the

images, it can be seen that our proposed method can

produce results that are comparable to one the state

of the art stabilization algorithms. However, in se-

quences with high jitter as in the fourth sequence, our

algorithm performs poorly which will be discussed

later in the upcoming section. In Table 1 the value

of the ﬁdelity after the stabilization is signiﬁcantly

higher. In Figures 4-6 the trajectory of the sequence

in Y-axis, X-axis and the rotation angle respectively

plotted with the original trajectory in blue and the

smoothed version in green, it can be clearly seen that

the smoothed trajectory does not suffer the high ﬂuc-

tuations found on the original trajectory.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

670

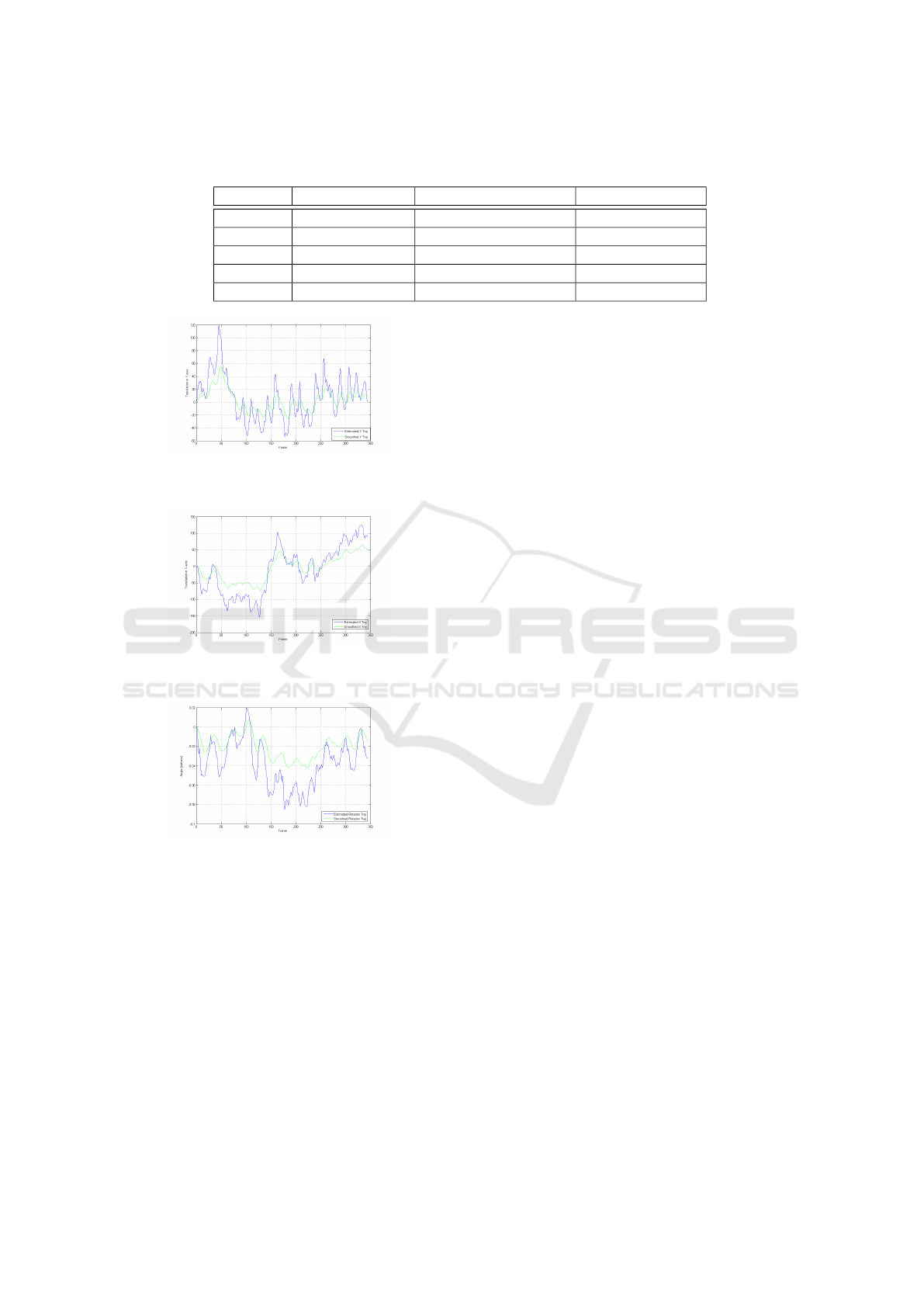
Table 1: Comparison between the ﬁdelity of the original sequence (left) ,using our method (middle) and Stabilized Fidelity

from Google’s Youtube(right).

Sequence Original Fidelity Our Stabilized Fidelity Google’s Youtube

Seq. 1 40 dB 56 dB 53 dB

Seq. 2 45 dB 50 dB 66 dB

Seq. 3 42 dB 60 dB 59 dB

Seq. 4 42 dB 53 dB 77 dB

Seq. 5 34 dB 45 dB 50 dB

Figure 4: Comparison between the original trajectory (blue)

and the smoothed trajectory (green) for Y-direction.

Figure 5: Comparison between the original trajectory (blue)

and the smoothed trajectory (green) for X-direction.

Figure 6: Comparison between the original trajectory (blue)

and the smoothed trajectory (green) for the angle of rota-

tion.

5 DISCUSSION AND

PERFORMANCE ANALYSIS

5.1 Discussion

The proposed algorithm does perform well on short

sequences, However as seen in Figure 3 the mean

sequence still suffers some jittering especially in se-

quence with extreme jittering as maintaining the cam-

era path for each block will tend to make some drifts

in the estimations this can be seen also in Figure 5. as

the smoothing of the X-direction drifting away from

the estimation and instability in both the estimation

and the smoothing increases over time. To overcome

this drawback more constraints will be added to the

system to ensure the calculations in both the block

and frame level. Generally, we ﬁnd that the 3D recon-

struction method gives the best results when success-

ful. However, the proposed method produces videos

with high visual quality and takes beneﬁt of the ro-

bustness and simplicity of 2D methods and not re-

stricted to one type of transformation.

5.2 Runtime Analysis

The proposed algorithm has been tested on the follow-

ing conﬁgurations: Intel Quad Core processor @2.20

GHz. The average running time for the whole algo-

rithm is around 20 fps, taking around more than half

the time needed to process one frame in Phase I. Typ-

ically the running time for this phase increases with

increasing the number of blocks in the frame and with

extending the size of the window used for smoothing.

6 CONCLUSION AND FUTURE

WORK

This paper presented a parallel technique in stabiliza-

tion based on 2D linear transformations with running

time suitable for real time systems and with high vi-

sual quality compared to ofﬂine and 3D stabilizers.

In the future, the algorithm will be tested in more

datasets, plus extending the work to handle feature-

less scenes and longer sequences. Also, the addition

of new constraints on the smoothing function to allow

the process of longer sequences to produce the highest

stabilization quality.

REFERENCES

Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Cur-

less, B., Seitz, S. M., and Szeliski, R. (2011). Build-

Towards High-Quality Parallel Stabilization

671

ing rome in a day. Communications of the ACM,

54(10):105–112.

Buehler, C., Bosse, M., and McMillan, L. (2001). Non-

metric image-based rendering for video stabilization.

In Computer Vision and Pattern Recognition, 2001.

CVPR 2001. Proceedings of the 2001 IEEE Computer

Society Conference on, volume 2, pages II–609. IEEE.

Furukawa, Y., Curless, B., Seitz, S. M., and Szeliski, R.

(2010). Towards internet-scale multi-view stereo. In

Computer Vision and Pattern Recognition (CVPR),

2010 IEEE Conference on, pages 1434–1441. IEEE.

Goldstein, A. and Fattal, R. (2012). Video stabilization us-

ing epipolar geometry. ACM Transactions on Graph-

ics (TOG), 31(5):126.

Grundmann, M., Kwatra, V., and Essa, I. (2011). Auto-

directed video stabilization with robust l1 optimal

camera paths. In Computer Vision and Pattern Recog-

nition (CVPR), 2011 IEEE Conference on, pages 225–

232. IEEE.

Irani, M. (2002). Multi-frame correspondence estimation

using subspace constraints. International Journal of

Computer Vision, 48(3):173–194.

Irani, M., Rousso, B., and Peleg, S. (1994). Recovery of

ego-motion using image stabilization. In Computer

Vision and Pattern Recognition, 1994. Proceedings

CVPR’94., 1994 IEEE Computer Society Conference

on, pages 454–460. IEEE.

Jiang, N., Tan, P., and Cheong, L.-F. (2012). Seeing

double without confusion: Structure-from-motion in

highly ambiguous scenes. In Computer Vision and

Pattern Recognition (CVPR), 2012 IEEE Conference

on, pages 1458–1465. IEEE.

Litvin, A., Konrad, J., and Karl, W. C. (2003). Probabilis-

tic video stabilization using kalman ﬁltering and mo-

saicing. In Electronic Imaging 2003, pages 663–674.

International Society for Optics and Photonics.

Liu, F., Gleicher, M., Jin, H., and Agarwala, A. (2009).

Content-preserving warps for 3d video stabilization.

In ACM Transactions on Graphics (TOG), volume 28,

page 44. ACM.

Liu, F., Gleicher, M., Wang, J., Jin, H., and Agarwala, A.

(2011). Subspace video stabilization. ACM Transac-

tions on Graphics (TOG), 30(1):4.

Liu, F., Niu, Y., and Jin, H. (2013). Joint subspace sta-

bilization for stereoscopic video. In Computer Vi-

sion (ICCV), 2013 IEEE International Conference on,

pages 73–80. IEEE.

Liu, S., Wang, Y., Yuan, L., Bu, J., Tan, P., and Sun,

J. (2012). Video stabilization with a depth camera.

In Computer Vision and Pattern Recognition (CVPR),

2012 IEEE Conference on, pages 89–95. IEEE.

Matsushita, Y., Ofek, E., Ge, W., Tang, X., and Shum, H.-Y.

(2006). Full-frame video stabilization with motion in-

painting. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 28(7):1150–1163.

Morimoto, C. and Chellappa, R. (1998). Evaluation of

image stabilization algorithms. In Acoustics, Speech

and Signal Processing, 1998. Proceedings of the 1998

IEEE International Conference on, volume 5, pages

2789–2792. IEEE.

of Central Florida, U. Ucf aerial action data set.

http://crcv.ucf.edu/data/UCF

Aerial Action.php.

Shi, J. and Tomasi, C. (1994). Good features to track.

In Computer Vision and Pattern Recognition, 1994.

Proceedings CVPR’94., 1994 IEEE Computer Society

Conference on, pages 593–600. IEEE.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (2000). Bundle adjustmenta modern synthesis.

In Vision algorithms: theory and practice, pages 298–

372. Springer.

Wang, Y., Hou, Z., Leman, K., and Chang, R. (2011). Real-

time video stabilization for unmanned aerial vehicles.

In MVA, pages 336–339.

Wang, Y.-S., Liu, F., Hsu, P.-S., and Lee, T.-Y. (2013). Spa-

tially and temporally optimized video stabilization.

Visualization and Computer Graphics, IEEE Transac-

tions on, 19(8):1354–1361.

Wu, C. (2013). Towards linear-time incremental structure

from motion. In 3D Vision-3DV 2013, 2013 Interna-

tional Conference on, pages 127–134. IEEE.

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

672