
Time-to-Contact from Underwater Images
Laksmita Rahadianti, Fumihiko Sakaue and Jun Sato
Departement of Computer Science and Engineering, Nagoya Institute of Technology,
Nagoya-shi, Showa-ku, 466-8555, Japan
Keywords:
Time-to-Contact, Underwater, Scattering Media, Transmission, Red Channel Prior.
Abstract:
In this paper, we propose a method for estimating time-to-contact (TTC) of moving objects and cameras
in underwater environments. The time-to-contact is useful for navigating moving vehicles and for avoiding
collisions in the 3D space. The existing methods calculate time-to-contact from geometric features of objects
such as corners and edges. However, if the cameras and objects are in scattering media, such as fog and water,
the degradation of image intensity caused by light scattering makes it difficult to find geometric features in
images. Thus, in this paper we propose a method for estimating time-to-contact in scattering media by using
the change in image intensity caused by the camera motion.
1 INTRODUCTION
In this paper, we aim to extract 3D information from
images in scattering media, such as underwater im-
ages. In particular, we propose a method for estimat-
ing time-to-contact (TTC) of moving objects in scat-
tering media.
Time-to-contact represents the time remaining be-
fore collision (Cipolla and Blake, 1992; Horn et al.,
2007). In the case of an object moving towards the
camera, or vice versa, time-to-contact is useful for
navigation and collision avoidance of moving vehi-
cles in the 3D space. This method does not need cal-
ibrated cameras, and does not require a full 3D re-
construction of the scene, freeing it from calibration
errors.
The existing methods calculate time-to-contact
from geometric features of objects such as corners
and edges in images (Cipolla and Blake, 1992). How-
ever, if the cameras and objects are in a scattering me-
dia, the degradation of image intensity makes it diffi-
cult to find geometric features in the captured image,
as shown in Fig. 1.
Recently, Watanabe et al. (Watanabe et al., 2015)
proposed a method for estimating time-to-contact
from image intensity. Their method can estimate
time-to-contact without extracting geometricfeatures,
but it only applies to clear environments without light
scattering effects. In situations where the cameras and
objects are in scattering media, the standard photo-
metric model no longer holds, and we need a more
complex model to analyze the photometric properties
(a) Clear air (b) Underwater
Figure 1: Images in clear and scattering media.
(Narasimhan and Nayar, 2003a; Narasimhan and Na-
yar, 2003b; Narasimhan et al., 2005). For scattering
media environments, Jeong et al. (Jeong et al., 2015)
proposed a method for computing time-to-contact
based on a photometric model in scattering media.
However, their method requires a point light source
attached on the camera, and hence it is limited.
In this paper we propose a method for estimating
time-to-contact in scattering media without using ac-
tive light. We consider underwater scattering media
environments, and assume that the scene is illumi-
nated naturally by ambient sunlight. Our approach
utilizes the change in intensity caused by the cam-
era motion, which provides us relative distance be-
tween the camera and the object for estimating time-
to-contact. We use the red channel prior proposed by
Galdran et al. (Galdran et al., 2015), a special case of
the dark channel prior (He et al., 2011), which consid-
ers the quick degradation of intensity in red channel
in under water environments. While previous works
used these priors for recovering clear images from
scattering images, we use these priors for directly es-
timating time-to-contact in scattering media.
Rahadianti, L., Sakaue, F. and Sato, J.
Time-to-Contact from Underwater Images.
DOI: 10.5220/0005766106710678
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 673-680
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
673

2 UNDERWATER IMAGE
FORMATION
Underwater images are blurry and unclear compared
to clear images, due to the microparticles contained
in the water that interfere with the light propagation
from the scene to the imaging device. A microparti-
cle that comes into a light ray’s path may absorb the
light’s intensity (absorption), as well as alter its path
(scattering). The combination of these effects atten-
uate the overall light that is finally captured by the
camera.
The effects of absorption and scattering in under-
water images are characterized by certain coefficients,
which will be referred to as the absorption coefficient
and scattering coefficient. The value of these coeffi-
cients are different depending on the body of water
(Smith and Baker, 1981; Ahn et al., 1992). Addition-
ally, the scattering and absorption coefficients in un-
derwater environments are wavelength dependent.
The final light intensity I observedat the camera in
scattering media consists of three components, which
are the direct component I
d
, the backscattering com-
ponent I
b
, and the forward scattering component I
f
as
follows:
I = I
d
+ I
b
+ I
f
(1)
These three components are depicted in Fig. 2.
It is known that the effects of forward scattering
are small compared to the direct component and
backscattering component (Schechner and Karpel,
2005). Thus, we assume that the effects of I
f
are neg-
ligible, and only consider the direct component I
d
and
the backscattering component I
b
in Eq. (1).
2.1 Direct Component
The direct component I
d
is the light traveling from the
light source that arrives at the object and is reflected
directly back into the camera. This component con-
tains direct information about the target object such
as color and shape. In underwater environments, this
I
d
component becomes attenuated.
The amount of light that is able to arrive at the
camera depends on the transmission τ of the medium.
According to the Beer-Lambert law, the light intensity
will decrease exponentially with respect to distance
traveled, as follows:
τ = e
−c.z
(2)
where z denotes the distance of the object from the
camera, and c is the attenuation coefficient. The coef-
ficient c is the sum of both the absorption coefficient
and the scattering coefficient.
Figure 2: Underwater image formation model.
We can now calculate the direct component of
light based on the transmission of the water. Since
the coefficient c is wavelength dependent, the direct
component can then be calculated as follows:
I
d
(λ) = I
0
(λ).ρ(λ).e
−c(λ)z
(3)
where the term I
0
annotates the intensity of the light
source, and ρ is the reflectance of the object.
2.2 Backscattering Component
The backscattering component I
b
is the light travel-
ing from the light source that encounters a micropar-
ticle and is scattered directly into the camera without
arriving at the object. This does not contain any in-
formation about the object, and results into a veiling
effect. This component reduces image contrast and
obscures geometric features of the object. In natural
underwater environments particularly, the scattering
effects are higher in the longer wavelengths, resulting
in a bluish hue.
In our model we assume the scattering to follow a
single scattering model such as in (Narasimhan et al.,
2005). In the single scattering model, light rays are
scattered to all directions from the microparticle. This
property is represented by using a phase function P .
As in (Narasimhan et al., 2005), we use the first-order
approximation of the phase function, as follows:
P (g, α) =
1
4π
(1+ g.cosα) (4)
where α is the angle between the incoming and re-
flected light ray, and g ∈ (−1, 1) to show the shape of
the phase function.
Using the phase function P (g, α), I
b
can be de-
scribed as follows:
I
b
(λ) =
z
Z
x=0
b(λ).I
0
(λ).P (g, α).e
−c(λ)x
dx (5)
After defining the I
d
and I
b
components, we can
calculate the final amount of light that is captured by
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
674

the camera as the sum of both components as follows:
I(λ) = I
d
(λ) + I
b
(λ)
= I
0
(λ).ρ(λ).e
−c(λ).z
+
z
Z
x=0
b(λ).I
0
(λ).P (g, α).e
−c(λ)x
dx (6)
3 3D INFORMATION IN
UNDERWATER IMAGES
Before further analysis, we attempt to simplify the
physical model in Eq. (6). In reality, the attenua-
tion is wavelength dependent, but since we are using
3-channel RGB images, we simplify the model to the
R, G, and B channels separately. We also solve the
integration in the I
b
component, arriving at Eq. (7).
I
s∈{R,G,B}
= I
0
.ρ
s
.e
−c
s
.z
+
b
s
.P (g, α)
c
s
.I
0
.(1− e
−c
s
.z
)
(7)
Next, we consider the term
b
s
.P (g,α)
c
s
.I
0
in the
backscattering component. This term can also be de-
scribed as the waterlight A. The waterlight A is the
intensity at a point where the light does not carry in-
formation of objects and originates solely from the
scattering effects. Finally, we represent the light re-
flected by the object as the original object color inten-
sity J
s
= I
0
.ρ
s
, and take the transmission τ
s
as Eq. (2)
to arrive at the simplified equation for the observed
light, as follows:
I
s∈{R,G,B}
= J
s
.τ
s
+ A
s
.(1− τ
s
) (8)
Previous publications have used the image forma-
tion model shown in Eq. (8) to try to recover the clear
scene J
s
. This problem is under-constrained if the in-
put is only a single underwater image I
s
, so additional
constraints are necessary to solve the equation.
3.1 Red Channel Prior
Without any other prior information, it is difficult to
extract depth information from a single image. For
foggy images, He et al. (He et al., 2011) proposed a
statistical prior named the Dark Channel Prior (DCP)
based on the physical observation of the image inten-
sities in clear images. The DCP states that in clear
outdoor images, for local patches of non-sky regions,
at least 1 channel in {R, G, B} will have a very low
intensity, as follows:
DCP(x) = min
y∈Ω(x)
min
s∈{R,G,B}
J
s
(y)
≈ 0 (9)
where x denotes the pixel location in the image, and
Ω(x) denotes the local patch of pixels around x.
The DCP was intended for scattering media in
the form of fog and smoke, and is not designed to
handle underwater environments. Due to the wave-
length dependent nature of attenuation in underwater
images, the J
R
channel is often very low in the en-
tire image, making the DCP invalid. In order to han-
dle this, more recent works have proposed modified
priors more suitable for underwater images, such as
the Underwater Dark Channel Prior (UDCP) (Drews
et al., 2013) and Red Channel Prior (RCP) (Galdran
et al., 2015). In our approach we use the Red Channel
Prior.
In order to handle the low R channel intensities,
the RCP (Galdran et al., 2015) replaces J
R
with its
reciprocalchannel 1−J
R
. The RCP states that in clear
non-degraded underwater images, for local patches of
non-water regions, at least 1 channel in {1− R, G, B}
will have a very low intensity, as follows:
RCP(x) = min( min
y∈Ω(x)
(1− J
R
(y)), min
y∈Ω(x)
(J
G
(y)),
min
y∈Ω(x)
(J
B
(y))) ≈ 0
(10)
3.2 Waterlight Estimation
Intuitively, waterlight A can be found at the pixel at
maximum distance from the camera (z → max), and
its color depends only on the scattering effects. As
mentioned in section 3.1, the red channel prior im-
plies that RCP(x) ≈ 0 at minimum distances z → 0
in non-degraded underwater images. Inversely, the
maximum distance and the waterlight can therefore be
found where RCP becomes maximum (Galdran et al.,
2015).
Despite this intuition, in reality the waterlight is
not always correctly found using the above assump-
tion. It is more difficult while dealing with blue ob-
jects that are very similar to the waterlight. To handle
the erroneous estimated waterlight, we follow the so-
lution in (Galdran et al., 2015) by adding a user input
to select a general area of water, then the RCP is used
within that region to find the correct waterlight pixel.
3.3 Transmission Estimation
Based on the red channel prior in section 3.1, we can
now estimate the transmission τ of an underwater im-
age (Galdran et al., 2015). Taking the image intensi-
ties I
s∈{1−R,G,B}
from Eq. (8), we divide them with
the waterlight A as follows:
Time-to-Contact from Underwater Images
675

1− I
R
1− A
R
,
I
G
A
G
,
I
B
A
B
=
τ
R
.
1− J
R
1− A
R
+ (1− τ
R
),
τ
G
.
J
G
A
G
+ (1− τ
G
), τ
B
.
J
B
A
B
+ (1− τ
B
)
(11)
Next we take the local minimum for every channel
in Eq. (11), and take the overall minimum on both
sides of the equation, as follows:
min
min
Ω
(
1− I
R
1− A
R
), min
Ω
(
I
G
A
G
), min
Ω
(
I
B
A
B
)
=
τ. min
min
Ω
(
1− J
R
1− A
R
), min
Ω
(
J
G
A
G
), min
Ω
(
J
B
A
B
)
+1− τ
(12)
where τ in Eq. (12) represents the transmission of the
minimum channel.
Since we have assumed the red channel prior to be
valid in underwater images (RCP ≈ 0), it cancels out
the first term on the right hand side of Eq. (12), and
hence we have:
τ = 1− min
min
Ω
(
1− I
R
1− A
R
), min
Ω
(
I
G
A
G
), min
Ω
(
I
B
A
B
)
(13)
By using Eq.(13) we can estimate the transmission
τ of the minimum channel from the image intensity I
and the waterlight A.
4 TIME-TO-CONTACT FROM
UNDERWATER IMAGES
In the case of an object moving at a constant speed
towards the observer, or vice versa (Horn et al., 2007;
Cipolla and Blake, 1992), time-to-contact can be es-
timated by the ratio between the distance z and the
change in distance ∆z at time t as follows:
TTC =
z
∆z
(14)
From Eq. (14) it is apparent that we need two con-
secutive observationsat time t andt +1 for computing
time-to-contact. In clear environments, it is possible
to use the geometric properties of the observed object
such as height, width or area. Since these geometric
properties change in relation to distance z, they can
be used for computing time-to-contact. However, in
the case of underwater environments, these geomet-
ric properties are more difficult to extract due to the
image degradation. Thus we propose the following
time-to-contact estimation method using image inten-
sity.
Suppose the target object has a surface facing the
camera, we can calculate the time-to-contact of the
object surface as follows. In section 3.3, the red chan-
nel prior is used to estimate the transmission in the
image. Since the distance information is encoded in
the transmission information as shown in Eq. (2), we
can define time-to-contact directly from the 2 consec-
utive observations of transmission.
Based on τ = e
−c.z
, the distance z can be repre-
sented by using the transmission τ as follows:
z =
logτ
−c
(15)
If the camera then moves closer by a distance of
∆z, the distance from the object becomes z − ∆z, and
thus we have:
z− ∆z =
logτ
′
−c
(16)
where τ
′
denotes the transmission at the second obser-
vation. ∆z then can be described by using the trans-
mission as:
∆z =
logτ − logτ
′
−c
(17)
By substituting Eq. (15) and Eq. (17) into Eq.
(14), the time-to-contact can be computed from the
change in transmission estimated from the change in
image intensity caused by the camera motion. The
TTC from transmission can then be written as fol-
lows:
TTC =
logτ
logτ − logτ
′
(18)
5 EXPERIMENTAL RESULTS
In order to evaluate the performance of the proposed
TTC estimation method proposed in section 4, we
conducted a series of experiments using both syn-
thetic and real underwater images.
Note that the proposed estimation method can
compute the time-to-contact from just a single point
on the object surface, but in order to account for the
noise and error we consider an area of points on the
object’s surface. Even so, there is no need for exact
point and line correspondencesbetween observations,
as we only need to track the object area. In our work
we assume that the region of interest (ROI) is prede-
fined.
5.1 Synthetic Images
In the first step of our experiments, a set of synthetic
images was generated simulating an object in an un-
derwater environment at different distances from the
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
676
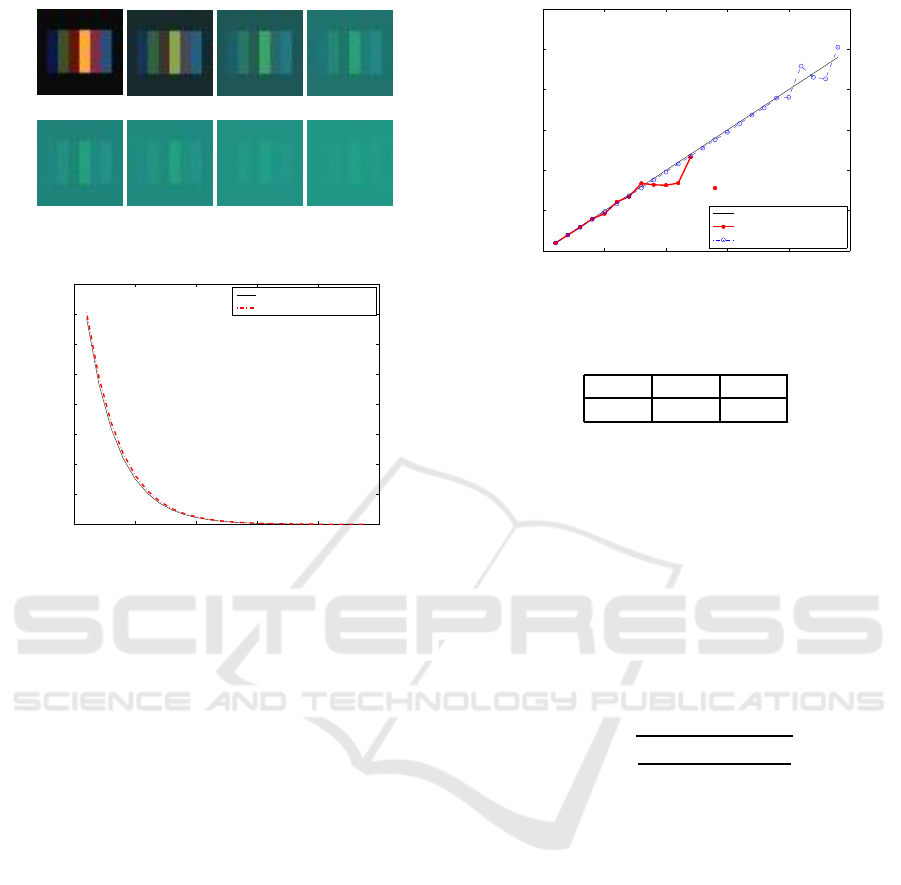
(a) Object
(b) 2m (c) 6m (d) 10m
(e) 14m (f) 16m
(g) 20m
(h) 24m
Figure 3: Synthetic underwater images.
0 5 10 15 20 25
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Distance (m)
Transmission
Real Transmission
Estimated Transmission
Figure 4: Transmission estimated from synthetic underwa-
ter images.
camera. Considering a flat object facing the camera
as shown in Fig. 3(a), we simulated the underwater
scattering effects based on the physical model in Eq.
(6) at distances between 0 to 24 meters (Fig. 3(b)-(h)).
These synthetic images show simulated scattering ef-
fects according to the distance and wavelength.
Before estimating time-to-contact, we first ana-
lyze the estimated transmission in the synthetic un-
derwater images according to Eq. (13). Since the
estimation is pixel-wise, we take the median value
of transmission estimates from the region of interest.
The transmission estimation results compared to the
real transmission can be seen in Fig. 4.
With the transmission accurately estimated, we
then calculated the time-to-contact from the synthetic
underwater images based on the TTC from transmis-
sion method proposed in section 4. Given that the ob-
ject is moving towards the camera at a constant speed
of 1 m/s from the distance of 24 to 1 meters, we cal-
culated the TTC from both 8-bit and 16-bit images, as
shown in Fig. 5.
The results in Fig. 5 show that the proposed
method is able to estimate time-to-contact well. How-
ever, since the estimation fails at smaller distances
when we use 8-bit images due to quantization error,
it is desirable to use 16-bit representations to ensure
robustness.
In the next experiment we once again evaluate the
0 5 10 15 20 25
0
5
10
15
20
25
30
Real TTC
Estimated TTC
Real TTC
Est TTC 8−bit images
Est TTC16−bit images
Figure 5: TTC estimated from transmission using 8-bit and
16-bit synthetic underwater images.
Table 1: Estimation error in synthetic images.
1 m/s 2 m/s 4 m/s
0.63 0.16 0.06
time-to-contact estimation of the proposed TTC from
transmission. Using only 16-bit images, we estimate
the time-to-contact for the object moving at various
speeds. The results are shown in Fig. 6.
The results show that even with the 16-bit im-
ages, the time-to-contact estimation starts to fail at
distances above 23 meters, especially in Fig. 6(a).
This is due to the scattering effects that eliminate al-
most all of the object details in images.
Lastly, we calculate the standard error of the pro-
posed method. The standard error of estimates can be
calculated as:
E =
r
∑
(TTC
e
− TTC
r
)
2
N
(19)
where TTC
e
is the estimated TTC, TTC
r
is the real
TTC, and N is the number of observations. The error
of TTC from transmission using simulated images is
shown in Table 1.
It is apparent that the stability of the time-to-
contact estimation improves at higher speeds, due to
the larger distances between observations. This larger
distance causes a larger observable change in inten-
sity that improves the time-to-contact estimation.
5.2 Real Images
We further evaluate the TTC from transmission
method proposed in section 4 using real images taken
in an experimental underwater environment. The im-
ages were captured using an action camera, which is
designed for capturing high-action shots. The action
camera is shockproof and equipped with a waterproof
case, enabling us to use it to capture stable underwater
images.
Time-to-Contact from Underwater Images
677
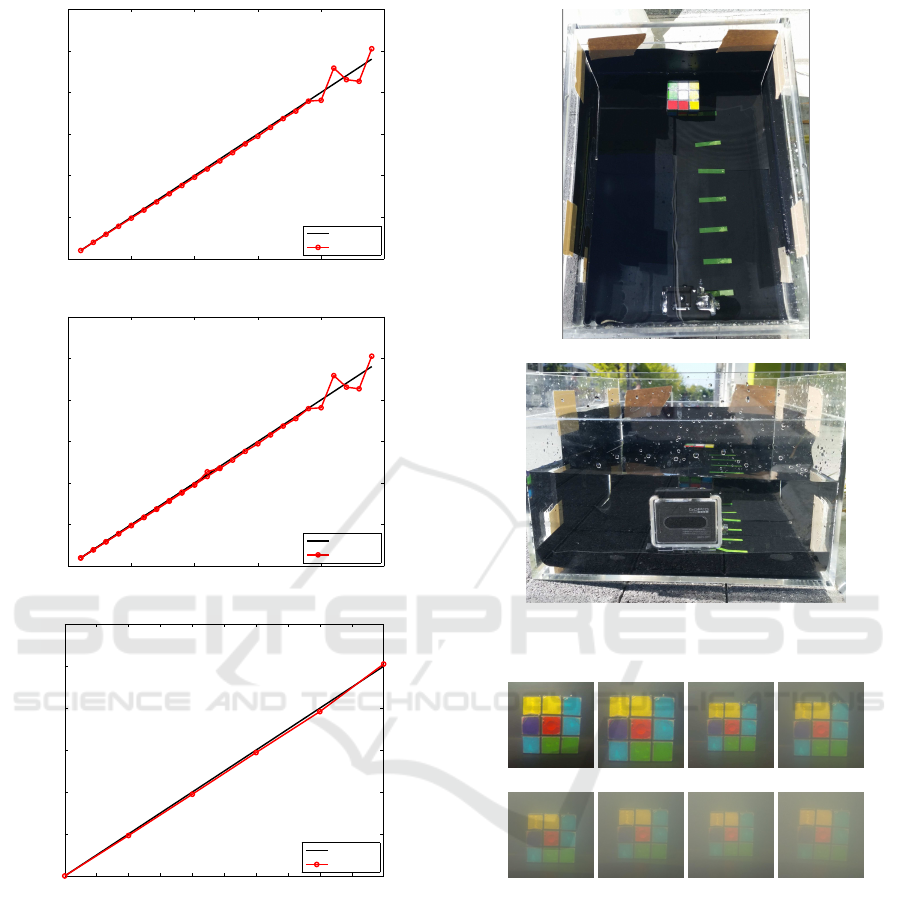
0 5 10 15 20 25
0
5
10
15
20
25
30
Real TTC
Estimated TTC
Real TTC
Est TTC
(a) Speed 1 m/s
0 5 10 15 20 25
0
5
10
15
20
25
30
Real TTC
Estimated TTC
Real TTC
Est TTC
(b) Speed 2 m/s
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
1
2
3
4
5
6
7
Real TTC
Estimated TTC
Real TTC
Est TTC
(c) Speed 4 m/s
Figure 6: TTC estimated from synthetic underwater images
at various speeds.
In order to capture the experimental images, a 30
x 20 x 40 cm aquarium is placed in an sunny out-
door area. There is no additional light source aside
from the natural ambient sunlight. The bottom and
sides of the aquarium are covered with a black rubber
non-reflecting material, in order to ensure the incom-
ing light is coming from above only. The aquarium is
then filled with 10 liters of water and both the camera
and the object are submerged in the water, as shown
in Fig. 7.
To obtain more visible scattering effects, we
(a) Aerial View
(b) Frontal View
Figure 7: Experimental setup.
(a) 6cm (b) 9cm (c) 12cm (d) 15cm
(e) 18cm (f) 21cm
(g) 24cm
(h) 27cm
Figure 8: Captured images of object in 0.02% milk solution.
added turbidity to the water. We captured images us-
ing 2 different water solutions, which was a 0.02%
milk solution with 2 ml of milk dissolved into the wa-
ter, as well as the same milk solution with added blue
food coloring. We then captured images of the object
at distances ranging from 4 cm to 30 cm at an interval
of 1 cm. The resulting images are shown in Fig. 8 and
Fig. 9.
As previously done with the synthetic images, we
first estimated the transmission in the real underwa-
ter images based on Eq.(13). Once again we take the
median value of the transmission estimates in the re-
gion of interest. The results are shown in Fig. 10.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
678

(a) 6cm (b) 9cm (c) 12cm (d) 15cm
(e) 18cm (f) 21cm
(g) 24cm
(h) 27cm
Figure 9: Captured images of object in 0.02% milk solution
plus blue food coloring.
0 5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Distance (cm)
Transmission
Est Transmission 0.02% milk
Est Transmission 0.02% milk+blue
Figure 10: Transmission estimated from real underwater
images.
Without information about the absorption and scatter-
ing coefficients, we cannot compare the results with
the ground truth. However, it can be observed that the
transmission decreases with a slope consistent with an
exponential decay function.
Next, we evaluate the performance of the pro-
posed TTC from transmission method using real im-
ages. The action camera used in this experiment is
only able to capture 8-bit images, but since we are
dealing with small distances, the images are sufficient
for TTC estimation. Using the captured images at dif-
ferent intervals, we simulate the object moving at var-
ious speeds. The TTC estimation results are shown in
Fig. 11.
We can see from Fig. 11 that due to the natural
noise in the real images, the estimation shows a level
of error. However, from the results we can still distin-
guish a slope that follows the correct time-to-contact.
Aside from the natural environmental noise, the er-
ror in estimation could also be caused by human error
during the process of image capture.
Finally, we calculate the standard error of esti-
mates using Eq.(19). The error of TTC from trans-
mission using simulated images is shown in Table 2.
In the case of real images, the time-to-contact estima-
tion also improves at higher speeds.
5 10 15 20 25 30
0
5
10
15
20
25
30
35
Real TTC
Estimated TTC
Real TTC
Est TTC 0.02% milk
Est TTC 0.02% milk + blue color
(a) Speed 1 cm/s
2 4 6 8 10 12 14
2
4
6
8
10
12
14
16
18
20
Real TTC
Estimated TTC
Real TTC
Est TTC 0.02% milk
Est TTC 0.02% milk + blue color
(b) Speed 2 cm/s
1 2 3 4 5 6 7
0
1
2
3
4
5
6
7
8
9
Real TTC
Estimated TTC
Real TTC
Est TTC 0.02% milk
Est TTC 0.02% milk + blue color
(c) Speed 4 cm/s
Figure 11: TTC estimated from real underwater images at
various speeds.
Table 2: Estimation error in real images.
Speed 1 cm/s 2 cm/s 4 cm/s
milk solution 4.48 1.23 0.87
milk + blue color 5.88 2.31 0.91
6 CONCLUSION AND FUTURE
WORK
In this paper, we proposed a novel method for estimat-
ing time-to-contact from underwater images, namely
Time-to-Contact from Underwater Images
679

TTC from transmission. Our method does not require
a dedicated light source nor camera calibration. The
proposed method uses the image intensity and the em-
bedded scattering effects to extract 3D distance infor-
mation from the image.
We have tested these methods using both syn-
thetic and real underwater images. The synthetic im-
ages were generated based on an underwater light
propagation model, and the real underwater images
were taken in an experimental underwater environ-
ment. The proposed method is able to accurately esti-
mate TTC in synthetic underwater images and shows
promising results for real underwater images. The dif-
ference that occurs with the real images is due to the
real natural noise and possibly due to human error in
the image capture process. Even so, the TTC estima-
tion shows a slope that follows the correct TTC val-
ues.
It is mentioned in this paper that the waterlight es-
timation outlined in section 3.2 requires an additional
user input to ensure correct waterlight is used. The red
channel prior assumption used in the waterlight esti-
mation is sometimes hindered by bright areas or ob-
jects with a reflectance similar to the waterlight. This
albedo-airlight ambiguity is an ongoing issue for vi-
sion in scattering media.
For the next step in our work, we will address this
albedo-airlight ambiguity problem in underwater vi-
sion. We aim to arrive at a solution for better wa-
terlight estimation results, which in turn will lead to
an improvedtransmission and 3D distance estimation.
Furthermore, we will examine the possibility of more
novel and improved methods for extracting 3D infor-
mation from underwater images, which can then be
applied to TTC estimation, 3D shape reconstruction,
as well as to other underwater vision applications.
REFERENCES
Ahn, Y.-H., Bricaud, A., and Morel, A. (1992). Light
backscattering efficiency and related properties of
some phytoplankters. Deep Sea Research Part A.
Oceanographic Research Papers, 39(11):1835–1855.
Cipolla, R. and Blake, A. (1992). Surface orientation and
time to contact from image divergence and deforma-
tion. In Proc. European Conference on Computer Vi-
sion (ECCV), pages 465–474.
Drews, P., do Nascimento, E., Moraes, F., Botelho, S., and
Campos, M. (2013). Transmission estimation in un-
derwater single images. In Proc. IEEE International
Conference on Computer Vision Workshops (ICCVW),
pages 825–830. IEEE.
Galdran, A., Pardo, D., Pic´on, A., and Alvarez-Gila, A.
(2015). Automatic red-channel underwater image
restoration. Journal of Visual Communication and Im-
age Representation, 26:132–145.
He, K., Sun, J., and Tang, X. (2011). Single image haze
removal using dark channel prior. In Proc. IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 1956–1963. IEEE.
Horn, B., Fang, Y., and Masaki, I. (2007). Time to con-
tact relative to a planar surface. In Proc. Intelligent
Vehicles Symposium, pages 68–74.
Jeong, W., Rahadianti, L., Sakaue, F., and Sato, J. (2015).
Time-to-contact in scattering media. In Proc. IEEE
Conference on Computer Vision Theory and Applica-
tions, pages 658–663.
Narasimhan, S., Nayar, S., Sun, B., and Koppal, S. (2005).
Structured light in scattering media. In Proc. Interna-
tional Conference on Computer Vision (ICCV), pages
420–427.
Narasimhan, S. G. and Nayar, S. (2003a). Interactive
deweathering of an image using physical models.
In Proc. IEEE Workshop on Color and Photometric
Methods in Computer Vision.
Narasimhan, S. G. and Nayar, S. K. (2003b). Contrast
restoration of weather degraded images. IEEE PAMI,
25(6):713 – 724.
Schechner, Y. Y. and Karpel, N. (2005). Recovery of under-
water visibility and structure by polarization analysis.
IEEE Journal of Oceanic Engineering, 30(3):570–
587.
Smith, R. C. and Baker, K. S. (1981). Optical properties
of the clearest natural waters (200–800 nm). Applied
Optics, 20(2):177–184.
Watanabe, Y., Sakaue, F., and Sato, J. (2015). Time-to-
contact from image intensity. In Proc. IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 4176–4183.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
680
