
Towards Semantical DSMLs for Complex or Cyber-physical Systems
Blazo Nastov
1
, Vincent Chapurlat
1
, Christophe Dony
2
and François Pfister
1
1
LGI2P, Ecole des mines d’Alès, Nîmes, France
2
LIRMM, University of Montpellier, Montpellier, France
Keywords: MDE, Modeling, Models, DSML, Behavior, Dynamic Semantics, Formal Verification, Simulation.
Abstract: MDE is nowadays applied in the context of software engineering for complex or cyber-physical systems, to
build models of physical systems that can then be verified and simulated before they are built and deployed.
This article focuses on DSMLs direct formal verification and simulation of their dynamic semantics. By
“direct”, we mean without transforming the DSML description into an automata-like one. This paper
presents xviCore, a metamdeling language to create DSMLs equipped with an abstract syntax, a concrete
syntax and a dynamic semantics. We exemplify xviCore by an integration of a metamodeling language and
a formal behavioral modeling language, based on the blackboard design pattern. Formal verification
techniques based on the Linear Temporal Logic (LTL) and the Temporal Boolean Difference can be then
applied as demonstrated by the proposed approach.
1 INTRODUCTION
The development of software engineering for
complex or cyber-physical systems currently
deflects a key issue. Within this context, the Model-
Driven Engineering (MDE) provides means for
systems modeling through creation, checking and
manipulation of various models. Models are
nowadays created using Domain Specific Modeling
Languages (DSML). A DSML basic components are
its syntax and semantics (Kleppe, 2007) but current
DSMLs have been more studied from the syntactical
point (syntactical DSMLs) than from the semantical
one that is often neglected or, when needed,
provided by means of translating the DSML into a
third-party formalism. This is a key limitation for
formal verification and simulation (Chapurlat,
2013). According to (Combemale et al., 2009), the
DSML semantical part can be divided into a static
part, representing concept meaning (abstract and
concrete syntaxes) and behavior independent
structural constraints (pre and post conditions,
invariants, etc.) and a dynamic part, dealing with the
way models behave. We focus hereafter on this
dynamic part, usually named “dynamic semantics”
or “behavior”. It can be defined either by using
action languages (e.g., Java) or behavioral modeling
languages (e.g., Statechart), providing respectively
an implementation or an explicit specification.
Nevertheless, to follow the basic MDE
“everything is a model” principle (Bézivin, 2005)
requires a model-based way of specifying behavior.
Languages to model dynamic semantics in this
context and/or dedicated virtual machines for
simulation have already been studied in various
works: Statechart in (Douglass, 2002) or UML
activities in (Scheidgen and Fischer, 2007).
However, using different tools to design syntax and
an automata-like behavior of a language creates a
gap that requires transformation rules between them.
In some works, e.g., (Mayerhofer et al., 2013), the
behavioral modeling language fUML is integrated
into the M3 metamodeling layer. This overcomes
transformation related problems, but formal-
verification related problems remain still a subject of
a debate.
Our global contribution presented in this paper is
a new meta-modeling language, called xviCore,
allowing meta-modelers to build DSMLs (called
xviDSMLs), that along with their syntax and static
semantics part also integrates a dynamic semantics
part and providing solution for direct (without
transformation) models verification and simulation.
Our solution combines, two meta-languages, EMOF
for the specification of the static part, and an original
extension of the behavioral modeling formal
language “Interpreted Sequential Machine” (ISM)
called extended ISM (eISM) for the dynamic part.
Nastov, B., Chapurlat, V., Dony, C. and Pfister, F.
Towards Semantical DSMLs for Complex or Cyber-physical Systems.
In Proceedings of the 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering (ENASE 2016), pages 115-123
ISBN: 978-989-758-189-2
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
115

Thanks to this key extension (that includes a
blackboard-based communication model), dynamic
semantics of an xviDSMLs can be designed,
statically verified and used to simulate models
written using them (called xviModels). xviCore is a
tooled meta-language implemented as an Eclipse-
EMF deployable plug-in.
The remainder of this paper is structured as
follows. Sections 2-3-4 describe our xviCore
solution. Section 2 proposes an overview of the
approach and the rationale for eISM and for its
combination with EMOF. Section 3 presents eISM.
Section 4 explains how the dynamic semantics of an
xviDSML can be verified. A case study example
demonstrating the approach’s applicability is
illustrated in Section 5. Section 6 presents related
works on DSML dynamic semantics. Section 7
concludes and highlights our perspectives.
2 GLOBAL VIEW OF THE
CONTRIBUTION (xviCore)
Our integrated meta-language xviCore (executable
verifiable and interoperable core concepts and
mechanisms) for creating verifiable DSML is
illustrated in Fig. 1. XviCore combines two
metalanguages, EMOF and our extension of the
formal behavioral modeling language “Interpreted
Sequential Machine” (ISM) (Vandermeulen, 1996)
called extended ISM (eISM). Assuming other
metalanguages could have been used, we thereafter
justify this choice. An xviModel is created by an
xviDSML itself created by EMOF for the static part
and eISM for its dynamic semantics.
Figure 1: An overview of xviCore.
The static part description of xviDSMLs is based
on EMOF and does not require additional efforts
(Steinberg et al., 2008). For what concerns the
dynamic semantics, each domain concept has its
own behavior, specified by a behavioral model. The
means for interoperation between different
behavioral models should then be established,
including at least centralized data and event
exchanges between behavioral models assuming
temporal synchronization rules. However,
behavioral modeling languages are not tailored for
such use. We propose hereafter a solution for this
problem based on the blackboard design pattern
integrated to the extension of ISM.
The blackboard design pattern (Engelmore and
Morgan, 1988) is a behavioral pattern “affecting
when and how programs react and perform”. A
“blackboard” is a shared and structured memory that
establishes relationships between independent
modules called “autonomous processes” where each
process is individually able to solve a sub-problem.
Processes can solve a “global problem” when they
are put together, reading and writing data in the
blackboard that is iteratively updated. Each process
has a set of triggering conditions that have to be
satisfied by particular kinds of events, sent by a
controller. The processes synchronization is handled
by a controller that monitors the data stored into the
blackboard and decides which autonomous
processes to prioritize. The controller reacts to
global changes in the blackboard resulting from
external inputs or previously executed processes.
Processes can be simultaneously executed, having a
concurrent access to the relevant blackboard data.
This may produce a situation of deadlock (if two or
more processes are each waiting for the other to
finish, and thus neither ever does) (Lalanda, 1997).
The Fig. 2 shows xviCore that introduces four
main concepts:
1) Controller (C) is used to schedule the execution
of behavioral models (described hereafter) from
an xviDSML according to a logical and periodical
clock taking into account multiscale time and
stability management rules. We propose an
execution algorithm in (Nastov et al., 2015). It
corresponds to the “controller” module of the
blackboard pattern.
2) Blackboard (BB) is a common base of
information where behavioral models write their
output data (O) and read their input data (I),
enabling information exchange. The BB
corresponds to the “blackboard” module on the
blackboard pattern and is formally defined as 5-
uplet ≝
〈
,,,,
〉
where: AT is a set
of “time indication” variables, specifying the
time of adding.
Abstract
syntax
Dynamic
semantics
an xviDSML
Model abstract
syntax
« instanceOf » « instanceOf »
« instanceOf »
« executes »
xviCore - composed of two metalanguages
an xviModel
M3
M2
M1
EMOF:
Object-Oriented
metamodeling language
eISM:
Formal behavioral
modeling language
ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering
116
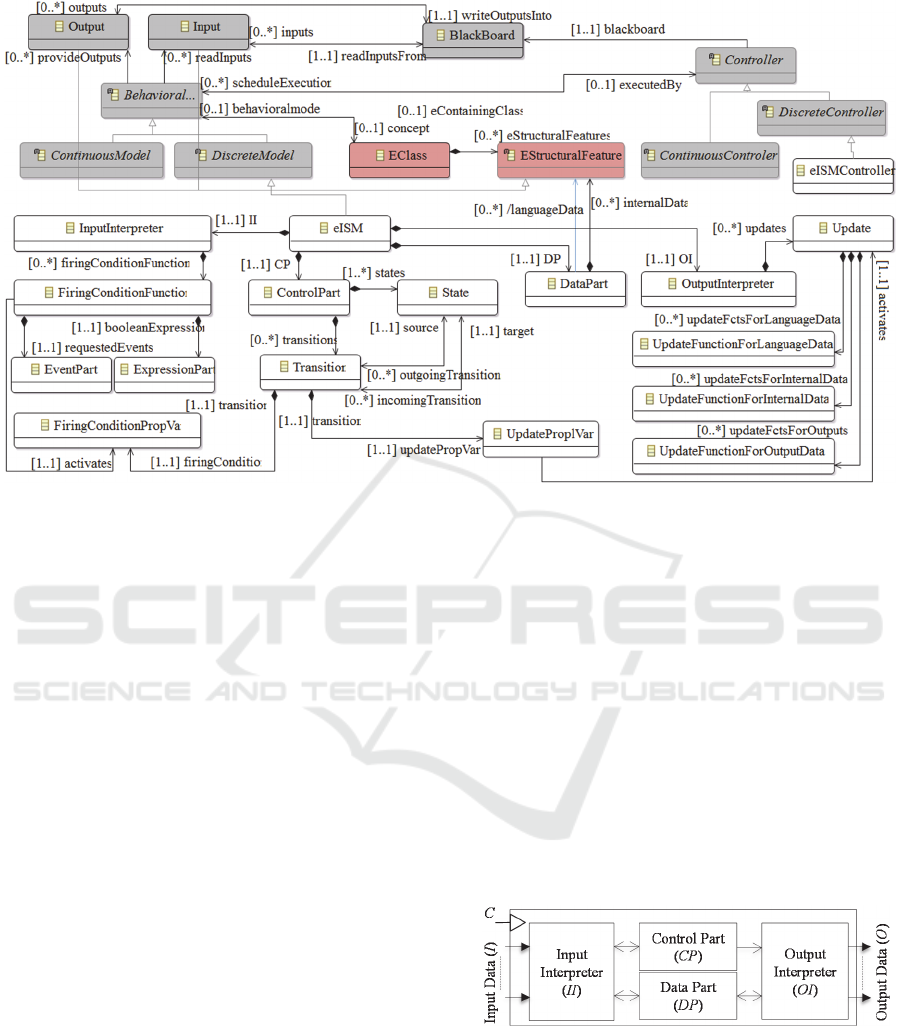
Figure 2: xviCore - in red (a part of) EMOF, in white eISM and in gray the design blackboard pattern.
LT is a set of “lifetime” variables, indicating the
remaining time before updating messages. C is a set
of “content” variables carried out by the messages. S
is a set of “sender” variables specifying the
behavioral model that sent the message and
,..,
is a set of “receivers” variables
indicating the behavioral models that read the
message: ∀
∈,
,..,
.
3) Concept is the core component of xviCore
represented using the EMOF’s EClass. It is used
to model domain concepts for which a behavioral
model might be specified. It does not correspond
to any component of the blackboard design
pattern. We have chosen EMOF’s EClass mainly
for two reasons: (1) EMOF and its realization
Ecore are standardized by the OMG and (2) it is
supported by tools such as Eclipse-EMF under
the Eclipse Public License.
4) Behavioral model represents the behavior of a
domain concept instance of EClass. It
corresponds to the “autonomous processes”
module of the blackboard design pattern.
Behavioral models are designed using a
behavioral modeling language based on
continuous or discrete events hypotheses. In this
article, we focus on discrete behavioral
description, for which we hereafter introduce
eISM an extended version of the Interpreted
Sequential Machine (Vandermeulen, 1996).
eISM behavioral models operate with typed data
and expressions, separating the states/transitions
description from the data specification. This
allows specifying some states using data
variables, reducing consequently their number.
The underlying structure of an eISM behavioral
model is based on the Linear Temporal Logic
(LTL) which is beneficial for formal verification.
3 EXTENDED ISM – eISM
An eISM is composed of four interconnected parts
called: Input Interpreter (II), Output Interpreter (OI),
Control Part (CP) and Data Part (DP) as modeled in
Fig. 2 and illustrated in Fig. 3.
Figure 3: The components (modules) of an eISM model.
The CP is a graph of states and transitions. The
DP holds the model data. The II interprets input data
(gathered into the set I) available in the Blackboard
(BB) and model data from the DP. Interpreted data
takes part in the firing conditions that are associated
with each transition of the CP, consequentially
taking part in the CP’s evolution. The OI is an
Towards Semantical DSMLs for Complex or Cyber-physical Systems
117

interface that interprets the evolution of the CP by
updating the values of the output data (gathered into
the set O) and the values of the model data from the
DP. This model is formalized as a 6-uplet eISM ≝
〈
,,,,,,
〉
where:
a) I is the set of input data available from the BB.
Each input i
i
is defined by a current value
cvalue
i
, a domain definition I
i
and a type I
i
’, such
as I
i
⊆
I
i
’.
b) O is the set of output data that is sent to the BB
by the OI. Each output o
i
is defined by a current
value cvalue
i
, a domain definition O
i
and a type
O
i
’, such as O
i
⊆
O
i
’.
c) The CP (Control Part), is defined as a graph of
states related by labeled transitions and formally
defined as a 5-uplet ≝
〈
,,,,
〉
where:
,…,
is a set of states,
,…,
is a set of state propositional variables,
,…,
is a set of transitions,
,…,
is a set of firing condition propositional variables
and
,…,
is a set of update
propositional variables. Transitions are given in
the following form
,
,
,
. By
hypothesis, there is a unique state s
i
that is active
each moment of the evolution. When the state s
i
is active (otherwise inactive), the propositional
variable associated to that state i.e., s
i
= True
(False otherwise). In addition, firing condition
propositional variables, e
j
∈
E, evaluate to True if
an only if the corresponding firing condition
function e
j
computed by II returns True. A
transition
can be fired by the transition
function
:→ if and only if, the
transition’s firing condition propositional
variable e
i
evaluates to true and the source state
of the transition
is an active state. Firing a
transition activates the output function
:
→. As a consequence to these two functions,
the source state of transition
is deactivated, its
target state is activated and the corresponding
update propositional variable
∈ is set to
True.
d) The DP (Data Part) holds the model data that is
used to specify transitions’ firing condition
functions E and update functions U. It is
formally defined by a 2-uplet ≝
〈
,
〉
where:
,…,
is a set of language
data directly derived from the corresponding
DSML class and
,…,
is a set of
internal (to the eISM model) data, explicitly
needed for the description of firing condition and
update functions. DP’s data elements, from both
LD and ID sets, are defined by a current value
cvalue, a domain definition DP and a type DP’
such that DP⊆DP’.
e) The II (Inputs Interpreter) reads data (input data
from the BB and model data from the DP) and
based on it, evaluates the firing condition
propositional variables that are associated with
transitions of the CP. It is formally defined as 5-
uplet ≝
〈
,,,
,
〉
where
,…,
is a set of firing condition functions
and
,…,
is a set of firing condition
propositional variables. Firing condition
functions are composed of a Boolean expression
part (evaluated using input and model data) and a
requested events part (evaluated using only input
data), formally defined as: ∀
∈,
,
. The firing condition function
evaluates to True, if both parts compute to True,
False if at least one computes to False. Every
firing condition propositional variable is
associated with a firing condition function. This
is formally defined as
:∪∪→
0,1
and ∀ ∈
1,..,
,
1⇔
.
f) The OI (Outputs Interpreter) associates the
update propositional variables with the
corresponding update functions. The evaluation
of update functions impacts on the model data
from the DP and on the output data that is send
to the BB. The OI is illustrated on Fig. 7 and is
formally defined as a 6-uplet ≝
〈
,,,,,
〉
where
,…,
is a
set of update propositional variables and
,…,
is a set of updates. Each update
might be associated with three types of update
functions: update functions for output data
:∪∪→, update functions for
language data
:∪∪→ and update
functions for internal data
:∪∪→
. When an update propositional variable
is
set to true, the corresponding update is activated,
executing simultaneously all associated update
functions.
4 VERIFICATION
Verification of the xviDSML static and dynamic part
must occur, prior to model specification and
simulation. In general, a verification process is
composed, at least, of three components: 1) a formal
specification, on which the verification process is
conducted, 2) formal properties that are verified on
ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering
118

the formal specification during the verification
process and 3) a model-checking verification tool.
We cover hereafter each of these components,
focusing only on verification of the dynamic part.
1) Formal Specification: The underlying structure
of an eISM behavioral model is based on the
Linear Temporal Logic (LTL), defined by a set
of Elementary Valid Formulas (EVF) (Larnac et
al., 1997). EVF are inferred from the PC’s
transitions combined with LTL operators. Let
,
,
,
a transition between
states s
i
and s
j
, associated to an e
j
firing condition
propositional variable and to a u
i
update
propositional variable. T
i
infers as an EVF of the
following form:
∶
∧
⊃
∧
Its interpretation stands as follows: “it is always true
( operator) that if s
i
is the current state (and
therefore s
i
is true) and e
j
is true, then the next state
( operator) will be s
j
(s
j
will be true), and the
current output propositional variable u
i
becomes
true”. The list of all the EVFs gives a symbolic and
equivalent description of the behavior of an eISM
model. Similarly, a Unified Valid Formula (UVF) is
computed by taking EVFs into consideration.
Briefly, the concept of Temporal Event (E
t,
)
describes possible effects of an eISM model
evolution. E
t
can either be a future state (E
t
=s
i
), a
future state within n-time steps (E
t
=
n
s
i
), a future
output propositional variable (E
t
=u
i
), or a future
output propositional variable within n-future steps
(E
t
=
n
u
i
). A Unified Valid Formula (UVF) defines
then conditions that must be satisfied for the
occurrence of a temporal event E
t
:
∶
∧
,
/
∧
⊃
Its interpretation stands as follows: “next temporal
event E
t
(respectively state S
j
or update function u
i
)
is reachable if and only if at least one of the
proposed conditions is verified”. So the calculation
of UVFs consists in manipulating the set of EVFs.
For instance, let’s consider the following EVF
formulas:
-
∶
∧
⊃
∧
-
∶
∧
⊃
∧
The UVF(E
t
) when E
t
= s
j
is then noted:
-
∶
∧
∨
∧
whose interpretation is: “s
j
will be active in the next
step (
s
j
is true), either if
∧
is true or if
∧
is true”.
2) Formal Properties: coherence between the
formal specification and the “to be checked”
formal properties is necessary. Therefore,
properties should also be specified using the
LTL. As an example, the state determinism
hypothesis “at a given time step, there is one and
only one current state” can be specified as the
following LTL formula:
∶
⊃
,∀, ∈
1,..,
,.
3) Tool: An adequate model checking tool is under
construction considering the survey of (Rozier,
2011) on the formal verification technique of
LTL symbolic model checking. As an example
of LTL formulas checking mechanisms, let’s
introduce Temporal Boolean Difference (TBD)
mechanism (Larnac et al., 1997 – Vandermeulen
et al., 1995) inspired by (Kohavi, 1978). This
mechanism is applied on a UVF with respect to a
current state or a firing condition propositional
variable, composing them into a Derived Valid
Formula (DVF):
,
∶
|
⨁
|
The result of an evaluation of
,
can either
be: False – UVF(E
t
) is independent of x. In other
words, the change of value of x has no influence
over the occurrence of E
t
. Not False – in this case,
we obtain a LTL formula which expresses the
sensitivity of UVF(Et) with respect to the changes of
x.
5 CASE STUDY
We demonstrate here the construction of a new toy
xviDSML, called WaterDistrib for modeling water
storage and distribution systems using our approach
xviCore.
Figure 4: a WaterDistrib model – an example of a water
storage and distribution system.
Towards Semantical DSMLs for Complex or Cyber-physical Systems
119
A model created by WaterDistrib is illustrated in
Fig. 4 and simulated using the dynamic semantics of
WaterDistrib allowing experts to observe the
changing water level. It is composed of a water tank,
a water-source that is connected to the tank with
pipes and a control station. A house is supplied with
water thanks to the tank. There are valves on each of
the pipes, controlled (opened or closed) by a control
station, based on the water request and the water
level inside the tank.
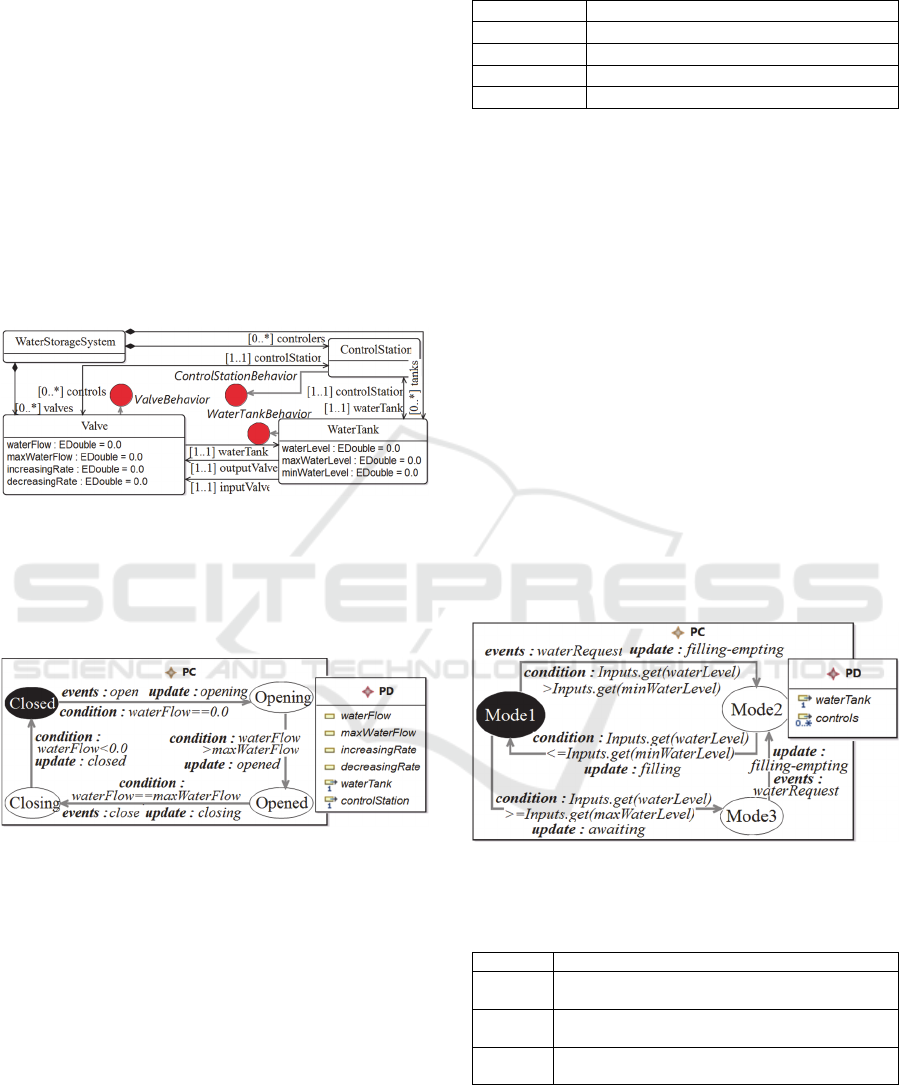
We propose in Fig. 5 a metamodel for
WaterDistrib composed of three principle concepts:
WaterTank, Valve and ControlStation. The red ovals
represent the eISM behavioral models of each of the
concepts as discussed hereafter.
Figure 5: WaterDistrib a new DSML for a water storage
and distribution systems.
The behavior of the concept Valve is composed
of four states: Closed, Opening, Opened and Closing
as illustrated in Fig. 6.
Figure 6: Behavioral model associated to the class Valve.
A valve is initially Closed, not providing any
water flow (update closed is activated, see Table 1),
awaiting a request to open itself. When the open
request arrives, the update opening is activated (see
Table 1) and the valve enters Opening state. Once
the valve’s water flow reaches its maximum value,
the update open is activated (see Table 1) and the
valve enters Opened state. Now the valve awaits a
request to close itself. When the close request
arrives, the update closing is activated (see Table 1)
and the valve enters Closing state. As soon as the
valve’s water flow reaches 0, the update closed is
activated and the valve enters its initial Closed state.
Table 1: Valve’s updates.
Update Language Data
closed waterFlow=0
opening waterFlow+=increasingRate
opened waterFlow=maxWaterFlow
closing waterFlow-=decreasingRate
The behavior of the concept ControlStation is
composed of three states: Mode1, Mode2 and Mode3
as illustrated in Fig. 7. A control station is initially in
the Mode1 state, filling the tank (update filling is
activated, see Table 2) awaiting water request. When
the request arrives and if there is a sufficient water
level in the tank, the filling-empting update is
activated (see Table 2) and the control station enters
Mode2 state. If the tank is empting faster than
filling, when its current water level reaches the
critical min level, the control station enters again
Mode1 state, activating the filling update. For the
sake of simplicity, the case when the tank is filling
faster than empting is not modeled in Fig. 7. When
the station is in Mode1 state, if a water request has
not yet arrived and the tank reaches its critical max
level, the awaiting update is activated (see Table 2).
The control station enters Mode3 state, waiting for a
water request. The request arrival activates the
filling-empting update and the control station enters
Mode2 state.
Figure 7: eISM behavioral models associated to the class
Control Station.
Table 2: Control Station’s updates.
Update Output Data
filling
Outputs.set(waterTank.inputValve, Open)
Outputs.set(waterTank.outputValve, Close)
filling-
empting
Outputs.set(waterTank.inputValve, Close)
Outputs.set(waterTank.outputValve, Open)
awaiting
Outputs.set(waterTank.inputValve, Close)
Outputs.set(waterTank.outputValve, Close)
The next phase consists of checking dynamic
semantics for well-constructiveness. For this
purpose, the formal underlying structure of the eISM
behavioral models should be developed, as
illustrated in Fig. 8.
ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering
120

Figure 13: The underlying formal structure of the eISM
behavioral models associated to the class Valve.
At the upper side of the figure the states, updates
and firing conditions are specified, along with their
corresponding propositional variables. Using these
variables allows the specification of EVFs that are
furthermore used for the specification of the UVFs.
In the same way, one can specify the formal
underlying structure of any eISM model.
Concerning formal properties, let’s consider the
transition exclusion hypothesis: “at any given time
step, for the current active state (which must be
unique), there is one and only one output transition
that can be fired”. In other word, all firing condition
of output transitions of any state from the PC, are to
be exclusive, modelled as:
∀
∈,
∀
∈
,
∧
⨁
/
0
Finally, an adequate model-checker should be used
to verify this property on the formal specification.
6 RELATED WORK
Specifying dynamic semantics in the field of MDE
have been a topic of research for quite some time
now, resulting with a wide diversity of approaches
mainly based either on translational or operational
semantics (Combemale et al. 2009).
The main benefit of translational semantics
approaches is the reuse of appropriate formal tool-
supported target space usually based on Automata-
like formalisms. Among the most popular and
currently used are: StateMate (Harel and Politi,
1998), Uppaal (Larsen et al., 1997), the Finite State
Machine (FSM) model of computation of Ptolemy II
(Lee and John, 1999), the Stateflow module in the
The MathWorks Simulink framework (Boldt, 2007)
and the UML State Machines (Schäfer et al., 2001;
Harel, 1987). However, in comparison with the
proposed approach, several drawbacks are hereafter
highlighted. Translational semantics approaches
require expertise and knowledge in the chosen target
domain and in transformation languages and tools.
Demonstrating the relevance between (source and
target) concepts and their behaviour remain limited,
often impossible, i.e., obtained results are only
available in the target spaces, so they should be
interpreted back to the source space.
Operational semantics allows the specification of
behavior directly on concepts, allowing model
simulation and animation, as early as possible with
minimum of effort, improving system quality and
reducing time-to-market. Action languages can
define operational semantics in ad hoc manner, as a
set of operations associated to each concept of a
DSML. For this matter different types of languages
can be used: object-oriented (e.g., Java), aspect-
oriented (e.g., Kermeta), executable constraint (e.g.,
xOCL (Clark et al. 2008)) or the MOF action
language (Paige et al., 2006). Approaches such as:
Xcore (an extension of EMOF/Ecore) (Clark et al.
2004) or the EPROVIDE framework (Sadilek et
Wachsmuth, 2009), are also worth mentioning. The
latter, for instance, is not related to a single language
allowing the choice between Java, Prolog, ASM or
QVT. However, in comparison to our approach, they
do not follow the basic MDE “everything is a
model” principle (Bézivin, 2005), providing an
implementation of the behavior, instead of an
explicit specification. This principle leverages the
use of modeling languages for the specification of
behavior, named behavioral modeling languages.
Among the commonly used are Statechart or Finite
Automata. But, as previously discussed, there is a
gap between the technical spaces related to such
languages and the MDE that can be bridged by using
transformation techniques. Alternative approaches
bridge this gap by integrating a behavioral modeling
language with a metamodeling language into a
single metamodeling layer promoted at M3. They
propose to use various languages to model behavior,
Statechart in (Douglass, 2002), UML activities in
(Scheidgen and Fischer, 2007) or fUML in
(Mayerhofer et al. 2013) and introduce dedicated
virtual machines for simulation. These approaches
allows to execute (even partial) models, to test them
for correctness as early as possible with very little
effort, eliminating the need to manually write source
code for the model means, removing consequently
developer coding defects and thereby improving
system quality and reducing time-to-market.
Firing condition functions and propositional variables
States/Updates and propositional variables
Elementary Valid Formulas
Unified Valid Formulas
opening: u
1
opened: u
2
closing: u
3
closed: u
4
{waterFlow==0, open}: e
1
{waterFlow>maxWaterFlow, /}: e
2
{waterFlow==maxWaterFlow, close}: e
3
{waterFlow<0, /}: e
4
Closed: s
1
Opening: s
2
Opened: s
3
Closing: s
4
Towards Semantical DSMLs for Complex or Cyber-physical Systems
121

However, in comparison to the proposed approach,
they are not adapted for formal verification of
defined behavior.
7 CONCLUSION AND OUTLOOK
The presented contribution illustrates an original,
formal and tool-equipped approach named xviCore
for verification and simulation purposes of DSML
and models.
xviCore provides the means for expressing
dynamic semantics using formal behavioral
modeling language, i.e., an extended version of the
interpreted sequential machine (ISM), named eISM.
eISM is integrated with the metamodeling language
EMOF, based on the blackboard design pattern. The
resulting executable metamodeling language is
promoted to the M3 layer. The approach also
supports several formal verification techniques for
dynamic semantics based on the Linear Temporal
Logic (LTL) and the Temporal Boolean Difference.
Other contributions remain still a subject of a
debate. To prove the scalability of the approach, we
are currently working on a more complex case study
applied in the field of Systems Engineering. Our
goal is to provide a framework for Systems
Engineering composed of several interconnected
languages. In addition, we aim to integrate xviCore
with a formal property modeling language, initially
proposed in (Chapurlat, 2013), allowing the
specification of structural and behavioral properties
for an xviDSML. At a final stage, we aim at
integrating a behavioral modeling language based on
continuous hypotheses.
REFERENCES
Bézivin, J., 2005. On the unification power of models.
Software & Systems Modeling, vol. 4, no 2, p. 171-
188.
Boldt, R. F., 2007. Combining the Power of MathWorks
Simulink and Telelogic UML/SysML-based Rhapsody
to Redefine MDD. Telelogic White Paper.
Chapurlat, V., 2013. UPSL-SE: A model verification
framework for Systems Engineering. Computers in
Industry, 64(5), 581-597.
Clark, T., Evans, A., Sammut, P., and Willans, J., 2004.
An eXecutable metamodelling facility for domain
specific language design. The 4
th
OOPSLA Workshop
on Domain-Specific Modeling. Technical Report TR-
33, University of Jyva¨skyla¨, Finland.
Clark, T., Sammut, P., and Willans, J. 2008.
Superlanguages: developing languages and
applications with XMF, Ceteva.
Combemale, B., Crégut, X., Garoche, P.-L., and Thirioux,
X., 2009. Essay on Semantics Definition in MDE. An
Instrumented Approach for Model Verification.
Journal of Software, 4(6).
Douglass, B. P., 2002. Real time UML. In the 7th
International Symposium FTRTFT, Oldenburg,
Germany.
Engelmore, R., and Morgan, T. 1988. Blackboard systems,
edited by Robert Engelmore, Tony Morgan. Addison
Wesley Publishing Company.
Harel, D., 1987. Statecharts: A visual formalism for
complex systems. Science of computer programming,
8(3), 231-274.
Harel, D., and Politi, M. 1998. Modeling reactive systems
with statecharts: the STATEMATE approach.
McGraw-Hill, Inc.
IEC 60848, Specification language GRAFCET for
sequential function charts. Second edition, 2000.
Kleppe, A. G., 2007. A language description is more than
a metamodel.
Kohavi, Z., 1978. Switching and Finite Automata Theory.
Tata McGraw Hill, Computer Science Series.
Lalanda, P., 1997. Two complementary patterns to build
multi-expert systems. Pattern Languages of Programs.
Larnac, M., Chapurlat, V., Magnier, J., and Chenot, B.,
1997. Formal Representation and Proof of the
Interpreted Sequential Machine Model.
EUROCAST'97, Las Palmas.
Larsen, K. G., Pettersson, P., and Yi, W., 1997. UPPAAL
in a nutshell. International Journal on Software Tools
for Technology Transfer (STTT), 1(1), 134-152.
Lee, E. A., and John, I. I., 1999. Overview of the ptolemy
project.
Mayerhofer, T., Langer, P., Wimmer, M., and Kappel, G.,
2013. xMOF: Executable DSMLs based on fUML. In
Software Language Engineering (pp. 56-75). Springer
International Publishing.
Nastov, B., Chapurlat, V., Dony, C., and Pfister, F., 2015.
“A Verification Approach from MDE Applied to
Model Based Systems Engineering: xeFFBD Dynamic
Semantics.” In the proceedings of CSD&M, (pp. 225-
238). Springer International Publishing.
Paige, R. F., Kolovos, D. S., and Polack, F. A., 2006. An
action semantics for MOF 2.0. In Proceedings of the
2006 ACM symposium on Applied computing (pp.
1304-1305). ACM.
Rozier, K. Y., 2011. Linear temporal logic symbolic
model checking. Computer Science Review, 5(2), 163-
203.
Sadilek, D. A., and Wachsmuth, G., 2009. Using
grammarware languages to define operational
semantics of modelled languages. In Objects,
Components, Models and Patterns (pp. 348-356).
Springer Berlin Heidelberg.
Schäfer, T., Knapp, A., and Merz, S. 2001. Model
checking UML state machines and collaborations.
Electronic Notes in Theoretical Computer Science,
55(3), 357-369.
Scheidgen, M., and Fischer, J., 2007. Human
ENASE 2016 - 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering
122

comprehensible and machine processable
specifications of operational semantics. In ECMDA-
FA 07, pages 157–171. Springer.
Steinberg, D., Budinsky, F., Merks, E., and Paternostro,
M., 2008. EMF: eclipse modeling framework. Pearson
Education.
Vandermeulen, E., Donagan, H. A., Larnac, M., and
Magnier, J., 1995. The temporal boolean derivative
applied to verification of extended finite state
machine. Computer and Mathematics with
application, Vol 30, n°2.
Vandermeulen, E., 1996. Machine Séquentielle
Interprétée. PhD Thesis University of Montpellier II,
(in French).
Towards Semantical DSMLs for Complex or Cyber-physical Systems
123
