Kalman Filter as Tool for the Real-time Detection of Fast

Displacements by the Use of Low-cost GPS Receivers

Paolo Dabove and Ambrogio Maria Manzino

Environment, Land and Infrastructure Department, Politecnico di Torino, Corso Duca degli Abruzzi 24, Turin, Italy

Keywords: Landslide Monitoring, GNSS NRTK Positioning, Mass-market Receivers, Kalman Filter, Accuracy.

Abstract: In this paper the problem of landslide monitoring and deformation analysis using the Kalman filter and results

obtained from a GPS mass-market receiver in real-time is addressed. Landslide monitoring and deformation

analysis are relevant aspects about the safety of human life in any terrain where landslides can impact human

activity. It is therefore necessary to monitor these effects in order to detect and prevent these risks. Very often,

most of this type of monitoring is carried out by using traditional topographic instruments (e.g. total stations)

or satellite techniques such as GNSS receivers, and many experiments were carried out considering these

types of mass-market instruments. In this context it is fundamental to detect whether or not deformation exists,

in order to predict future displacement. Filtering means are essential to process the diverse noisy

measurements (especially if low cost sensors are considered) and estimate the parameters of interest. In this

paper a particular version of Kalman Filter is considered in order to understand if there are any displacements

from a statistical point of view in real time. The tests, the algorithm and results are herein reported.

1 INTRODUCTION

Deformation monitoring is the act of ordinary and

continuous observation of such variations that are

referred to as “deformation” (Sedlak and Jecny, 2004;

Chrzanowski et al., 1986).

Considering the types of network, deformation

survey techniques are classified as Absolute

Deformation Monitoring (some reference points

located in the area surrounding the object of interest,

i.e. dam, bridge, etc.) and Relative Deformation

Monitoring (where the reference points are located in

the structure and both the object and reference points

are subject to displacement) (Aharizad et al., 2012;

USACE, 2002). Methods of deformation monitoring

have changed considerably in principle over the past

few decades as newer data sources have come to be

used. In sparsely vegetated terrain, landslides are

routinely detected and mapped by a combination of

the interpretation of airphotos or multispectral digital

imagery and selective ground verification (Benoit et

al., 2014). However, it is quite difficult to use these

methods in rugged terrain covered with dense

vegetation. Also, landslide inventory mapping studies

typically focus on outlining boundaries and neglect

the wealth of information revealed by internal

deformation features (Cruden, 1991).

With regard to deformation analysis, it is possible

to consider two main categories (Szostak-

Chrzanowski et al., 2005): geometrical analysis,

which detects the location and the magnitude of the

deformation, and physical interpretation, which

determines the relationship between the deformation

and its causes. In this context, there are four types of

models that allow the analysis of deformation

(Welsch and Heunecke, 2001; Aharizad et al., 2012;

Brückl et al., 2013) These are the static, kinematic,

dynamic and congruence models.

This paper focuses attention on the second type of

model. Kinematic models describe deformation as a

function of time, including velocity and acceleration.

It is also possible to classify data processing

techniques into two main groups. The first consists of

robust methods, such as Iterative Weighted Similarity

Transformation (IWST) and tests (e.g. Chow test,

Chow, 1960; Bellone et al., 2016), while the second

one is composed of non-robust methods, e.g. Kalman

Filter (Li and Kuhlmann, 2008; Tasci, 2010; Simon,

2001; Gülal, 1999; Acar et al, 2004; Masiero et al,

2013). In this study attention is focused on these last

methods, and especially on the Kalman Filter, in

Dabove, P. and Manzino, A.

Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers.

In Proceedings of the 2nd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2016), pages 15-23

ISBN: 978-989-758-188-5

order to perform a 3-D deformation analysis using a

low-cost single-frequency GPS data in real-time.

Some previous studies have also investigated the

accuracy obtainable with geodetic receivers and

antennas (Li and Kuhlmann, 2010 and 2012) while

some of them have also considered the mass-market

ones for landslide monitoring (Janssen and Rizos

2003; Squarzoni et al., 2005; Heunecke et al., 2011).

Those studies used both post-processing (Cina and

Piras, 2014) and real-time (Bellone et al., 2016)

approaches in order to analyze the various types of

landslide phenomena. In both cases, the most notable

feature of these instruments is that they provide

centimeter or sub-centimeter accuracy in real time

when phase ambiguity is adjusted (Manzino and

Dabove, 2013). This is also observed in considering

different GNSS positioning techniques (Othman et al.

2011a; Othman et al. 2011b) such as static (Brunner

et al. 2007), rapid-static (Hastaoglu and Sanli 2011),

and real-time kinematic (RTK - Wang 2011)

positioning.

A practical case study will show the reliability of

the results obtained through the Kalman filter as a

statistical tool to detect and predict displacements in

real-time. A brief comparison of the results obtained

by this method and those obtained with the modified

Chow test (Bellone et al., 2016) will conclude this

work.

2 GNSS INSTRUMENTS

CONSIDERED FOR

LANDSLIDES ANALYSIS

Nowadays, many types of GNSS instruments are

available functioning in a variety of frequencies,

constellations and accuracies obtainable both in real-

time and post-processing (Dabove et al., 2014;

Dabove and Manzino, 2014). As previously stated,

GPS/GNSS instruments are very often used for

landslides monitoring (Eyo Etim et al., 2014) and are

frequently coupled with other instruments such as

theodolite, Electronic Distance Measurement (EDM)

(Günther et al., 2008), levels, total station (Rizzo,

2002), inclinometers (Calcaterra et al., 2012), and

wire extensometers (Bertachini et al. 2009; Coe et al.

2003; Gili et al., 2000; Malet et al., 2002; Moss, 2000;

Tagliavini et al., 2007).

In other studies GPS instruments were integrated

with other surveying techniques, such as terrestrial

laser scanning, Synthetic Aperture Radar (SAR)

interferometry (Peyret et al., 2008; Rott and Nagler

2006), and photogrammetry (Mora et al., 2003), to

investigate landslide phenomena (Wang and Soler,

2012). Some studies have also investigated the

accuracy of low-cost single-frequency GPS receivers

for landslide monitoring (Janssen and Rizos, 2003;

Squarzoni et al. 2005) both in post-processing, (Cina

and Piras, 2014), and in real-time approaches

(Bellone et al., 2016) in order to analyze various types

of landslide phenomena (landslides with low constant

velocity or with an unexpected and sudden

displacement). Considering the first approach, raw

GNSS measurements are acquired and post-

processed in a single- or multi-base solution with one

or more GNSS permanent stations or Virtual Rinex

while, considering the second one, differential

corrections provided by CORSs networks are used to

determine the rover position in real-time. In this paper

we focus our attention only on this last approach,

analysing displacements in real-time.

Table 1: Characteristics of GPS receiver and antenna.

Receiver:

uBlox LEA EVK-5T

Evaluation kit

Antenna:

Garmin GA38

GPS& Glonass L1

Constellation: GPS (50

channels)

Constellation: GPS +

GLONASS

Observations:

C/A L1, Doppler, S/N

Gain 27 dB on the average

Cost: about 250 € Cost: about 50 €

The employment of mass-market receivers and

antennas is due to the fact that there is an high

probability to lose these instruments if an unexpected

displacement occurs: in this context, the amount of

cost is less than 1000 € for each receiver + antenna

that is an order of magnitude less than geodetic

instruments. For this study, an u-blox EVK-5T

receiver (Table 1- left) with an external antenna

(Garmin GA38, Table 1 - right) was used. This

receiver has a cost of about 350 € (including a patch

antenna) while the cost of the Garmin antenna is

about 50 €. One of the features of this receiver is that

it is able to receive in input the differential corrections

obtained from a Continuous Operating Reference

Stations (CORSs) network.

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

3 THE TESTS PERFORMED

The experiments using this mass-market receivers for

Network Real Time Kinematic (NRTK) positioning

were performed within the Regione Piemonte

(http://gnss.regione.piemonte.it/frmIndex.aspx)

CORSs network (Figure 1). The network product

used is the VRS

stream broadcasted by the network

software SpiderNet of the Leica Geosystems

Company.

Figure 1: The GNSS CORSs network of Regione Piemonte.

In previous studies (Bellone et al., 2016) it was

possible to analyze the performances obtainable

considering a static positioning using both real-time

and post-processing approaches with this type of

receiver and antenna.

The antenna was mounted on a sledge (Figure 2)

composed by a complex system of micrometric

screws that allow small and controlled displacements,

in order to verify the quality of the positioning and the

reliability of the statistic tests that were to be

performed.

The movements are set by means of a hand-wheel,

which moves the sledge along the rail. It is therefore

possible with a millimetre tape to obtain direct and

visual information about the movements in order to

compare the imposed movements against those

measured by GNSS instruments. With this sledge,

horizontal and vertical movements up to 1.30 m and

0.4 m respectively are possible.

As stated in previous studies (Cina et al., 2014;

Bellone et al., 2016), there is always a precision of the

sledge movement of about 1mm. Therefore it is

possible to consider this value as the “scale

resolution” of this support.

The patch antenna was mounted on this sledge as

shown in Figure 2. The positioning results were

obtained with a frequency of 1 Hz, considering

displacements equal to 1 cm both in planimetry and

in altimetry which were provided manually at 30

second intervals.

Figure 2: The sledge where the GNSS antenna was

mounted.

To perform the NRTK positioning, the routines

RTKLIB V. 2.4.2 (http://www.rtklib.com/) were used

(Takasu and Yasuda, 2009). This software was

chosen because it supports standard and precise

positioning algorithms with GPS, Global'naja

Navigacionnaja Sputnikovaja Sistema (GLONASS)

and Quasi-Zenith Satellite System (QZSS)

constellations, considering also different positioning

modalities for both real-time and post-processing

approaches: single-point, DGPS/DGNSS, Kinematic,

Static, Moving-baseline, Fixed, etc. Moreover the

software is able to manage both the proprietary

messages (e.g. u-blox LEA-4T, 5T, 6T) and external

communication via serial, TCP/IP, NTRIP etc. of

several GNSS receivers. In particular, the RTKNAVI

tool was used for these experiments. This tool allows

the input of both the raw data (pseudorange and

carrier-phase measurements) of the u-blox receiver

and the stream data coming from a network with

NTRIP authentication (Weber et al., 2006). For this

reason the receiver was connected to a laptop to

enable Internet connection and to store the NMEA

sentences (Manzino and Dabove, 2013). Another

peculiarity of this software is that it allows the fixing

of the phase ambiguity for real-time kinematic

positioning, even if the receiver uses only the L1 GPS

frequency.

Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers

4 THE USE OF KALMAN FILTER

TO DETECT

DISCONTINUITIES

The Kalman Filter (KF) was designed to estimate

linear dynamic systems (Kalman, 1960; Kalman and

Bucy, 1961). According to Grewal and Andrews

(1993), the Kalman Filter is an estimator for what is

called the linear-quadratic Gaussian (according to

Linear Quadratic Gaussian – LQG) (Mäkilä, 2004),

while Maybeck (1979) claims that the Kalman Filter

is simply an optimal recursive data processing

algorithm.

The intuition of this filter is represented by the

possibility of updating an estimate of the least squares

adjustment due to the introduction of new

observations, without recalculating the entire system.

The Kalman filter consists of two steps (Welch

and Bishop, 2003): filtering and smoothing. The first

allows the best parameter estimation at the current

epoch to be determined, while the second, starting

from the last epoch of measurement, allows the best

parameter estimation of the previous epochs to be

determined. For the real-time purposes of this study,

only the filtering process is applicable.Unlike the

sequential least squares method, one characteristic of

the Kalman filter is represented by the fact that it can

be used for dynamic problems (Wei et al., 2010).

For this reason, the vector containing the

parameters to be estimated will be called the state

vector.

This vector, which contains, for example, the

position and speed of an aeroplane, is not the same at

the time i and at the time i-1. It is possible to assume,

however, the existence of a simple relationship (e.g.

linear), among the state parameters of two following

epochs, the said state equation:

|1 1 1|1ii i i i i

xFx





 

(1)

where



is the system transition matrix,

|1ii



and

1| 1ii



are the state vectors at different epochs.

The measurement equation, similar to that

commonly used in the least squares method, should

now be added:

iiii

Hx e

(2)

where

is the measurement vector and

is the

observation matrix at epoch i.

As it is possible to see from (1), the state equation

includes the errors



, which assumes zero mean and

known dispersion matrix



. On the other side, the

measurement equation (2) includes the measurement

errors

, that also, in this case, are assumed to have

zero mean and known dispersion matrix

. Another

hypothesis is given by the fact that it is assumed that

the measurement errors are independent with respect

to the state errors.

Given these preliminary remarks relating to the

classic version of the filter, it is necessary to analyze

in which way the measurement and state equations

can be modified if there is bias. The first applications

dates to Teunissen (1998) and Tiberius (1998) where

the goal was the detection and resolution "on the fly"

of cycle slips, or rather with a moving receiver. The

authors in fact apply to the KF a well-known

procedure that has already been previously applied,

called DIA. The acronym indicates the three steps of

the process: Detection, Identification and Adaptation.

This procedure can also be considered for the

detection of movements or displacements, especially

if these movements are quick (i.e. occuring within

only two epochs), and if the accuracy of the

instruments allows their observation.

In this case, equation (1) can be written as

|1 1|1 1|1ii i i i i

xTx Bb









(3)

|1 | |ii ii ii

yHxCbe







(4)

where

is a vector that identifies the position and

the velocity of the point with respect to the initial

position while

is a scalar value that represents the

difference between the coordinates estimated at

epoch i and i-1. The

term represents the biases,

such that the possible displacements occurred

between two consecutive epochs. If one considers

only the height component (called z) the relationship

can be written as:

and









(5)

where z is the position and v the velocity of the point

(

is the bias of the position and

the bias of the

velocity) considering only the up component. So

110

and

01 01

















(6)

under the hypothesis of a constant and known

velocity motion,

and

become scalar values, then:

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management



= and

100

00100

00010

0001









































(7)

So, equations (1) and (2) can be written as:

|1 1|1

ii i i

ii ii

yH e







 



(8)

with

22 22 22

22 22 22 22

00 00

xx x

xx xx



 







 

where I (in the first equation) represents the identity

matrix and C

εε

is the var-covariance matrix of

parameters. If the mean velocity is set equal to zero,

previous equations can be written as:

|1 1|1

ii i i







 

  

 

 

  

  

 

(9)



|||

ii ii ii

yH e





  





The var-covariance matrices in these experiments are

chosen respectively as:

10 0

010

10 0

010





















(10)

The weights were chosen according to both the

accuracy of the measurements and the expected

displacements (that have an order of magnitude of 1

cm) in an adaptive way.

As it is known, at every period it is possible to test

the predicted residuals. If these last are defined as:





|1iiii

vyH









(11)

with their var-covariance matrix

viiiie

QHQHC 

(12)

it is possible to identify the displacement as an outlier,

according to the



test. The

|ii

represents the var-

covariance matrix of parameters estimated at epoch i.

Since, in this case, there is only one measurement

equation but two unknowns, the DIA does not provide

reliable results, as is known in the literature (Baarda,

1968; Teunissen and Salzmann, 1989; Salzmann

1995). However, by using the Kalman filter, the

solution can also be obtained in this case.

Accordingly, the Thomson test can be used in

order to define if a displacement occurs:

idof







 ~

(13)

where



represents the significance level (in our

case equal to 10 % that represents the probability of

rejecting the null hypothesis when it is true) and

dof

is the degree of freedom of the system, that in this

case can be determined as the trace of the redundancy

matrix





()

ii ee

dof tr R tr I H Q H C





(14)

So if

,idof







it can be assumed that the obtained

values are the positioning results, otherwise there is

the possibility that a displacement occurs. In this case,

,idof







the Minimum Detectable Bias (MDB) is

calculated in order to verify if this value is a real

displacement.

5 DATA PROCESSING AND

RESULTS COMPARED WITH

OTHER METHODS

The method previously described is applied to two

real-time datasets that simulates a landslide. As

previously stated, the system was composed as shown

in Figure 2. The positioning results were obtained

with a frequency of 1 Hz, considering displacements

equal to 1 cm both in planimetry and in altimetry

provided manually every 30 seconds. This can be

seen in Figure 4, where two cases, one with good

(number of satellites greater than 7) and another one

with low (only 5 satellites) satellite visibility, are

considered. The results shown in this paper will refer

only to the second case, that represents the worst

available possibility.

Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers

Figure 3: Altimetric profile of displacements with good

(more than 7 satellites - left) satellite visibility.

Figure 4: Altimetric profile of displacements with poor

(only 5 satellites - right) satellite visibility.

Figure 5: Planimetric trend (up) and estimated bias (down).

The goal is to estimate the most probable value of

the bias (the occurred shift) and to add it to the value

of the bias of the previous period.

As it is possible to see from Figure 5, despite some

errors in the estimation of discontinuities (in the

circle), the solution seems to be correct. If the

detected displacements are analyzed, a success rate of

96.1% is obtained (i.e. real displacements detected

correctly). As well, 1.3% of undetected displacements

(i.e. real displacements not detected) and 2.6% of

false alarms (it means that the filter has declared a

displacement that it has not occurred) are identified.

An example of undetected or correctly detected

displacements can be seen in Figure 7, where also a

summary of obtained results can be found. Must to be

underlined that no significant differences in terms of

success rate can be obtained according to the number

of visible satellites, even if the quality of the

positioning changes as it is possible to see from

Figure 3. The reported tests were made considering

from 5 up to 7 satellites while all results shown in this

work are obtained with a number of satellites equal to

6, that is a reasonable number of satellites visible with

mass-market receivers, also in hard-environment

conditions.

Figure 6: Altimetric trend (up) and estimated bias (down).

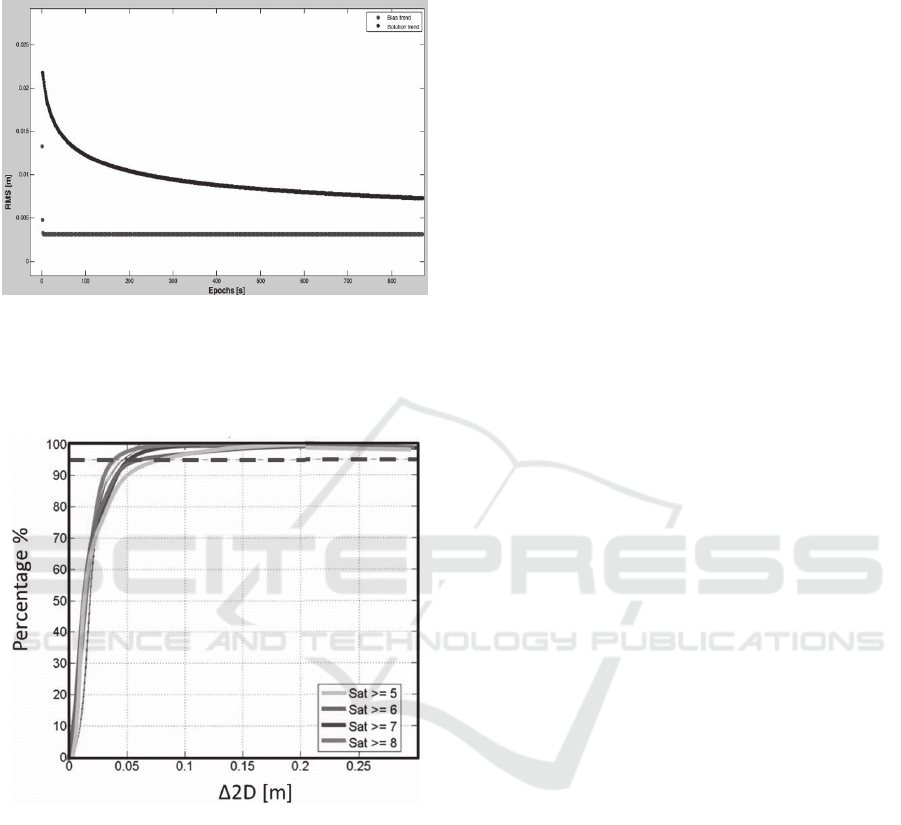
Also the root mean square (RMS) values of the

solution and biases are evaluated. As can be seen

from Figure 8, the accuracy of the solution is very

high. This means that the Kalman filter can be

considered as a useful tool to detect displacements

with this type of receivers and that the tuning of the

filter was correctly achieved.

Figure 7: Results obtained with the Kalman filter.

If the tuning is carried out correctly, this filter

allows both to decrease the accidental error of RTK

positioning and to control the possible gross-errors or

outliers that can be due to a false fix of the phase

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

ambiguity and not to an unexpected displacement (in

this case this error goes to zero at the next epoch).

Figure 8: RMS of estimated biases and solution.

This can be affirmed considering the previous

results (Figure 8) and those obtained if a planimetric

positioning error of 24 hours is considered (Figure 9).

Figure 9: Planimetric positioning error (the dotted line

represents the significance level equal to 95%).

In fact, in the first case the RMS of positioning

(less than 2 cm) is better than those obtained in the

following graph (5 cm at 95% of reliability).

Finally, these results were compared with those

obtained in a previous study based on a modified

Chow test. Applying the methods described in the

literature (Bellone et al., 2016), and considering a 10-

element sample size (meaning that a sample

composed of 10 epochs = 10 seconds of latency of

alarm at 1 Hz of acquisition rate), this method

correctly identified 93.1% of the displacements, with

a very low rate of false alarms equal to 3.3%. Anyway

these values are greater than those estimated with the

Kalman filter, that has shown the best performances

in terms of both false alarms (2.6%) and undetected

displacements (1.3%).

6 CONCLUSIONS

In this study, the Kalman filtering technique has been

applied for kinematic deformation analysis

procedure. A GPS data set that simulates a landslide

movement was collected and the proposed method

has been tested. The two methods (Kalman filter and

modified Chow test) produced comparable results,

even though the proposed version of the Kalman filter

has shown the best performance. Interesting results

have been obtained in real-time also by employing a

mass-market GPS receiver. In this context, the results

have shown the possibility of using this type of

receivers for this kind of application.

The employment of these receivers on a landslide

site could be useful also from an economic point of

view. The total cost of receiver, antenna, transmission

system and power supply (solar panel and battery) is

about € 600. The advantage is that the economic

damage in case of an unexpected event is less than

could occur if a geodetic GNSS instrumentation is

utilized. At the same time, it is possible to calculate

the position of the receivers in a similar way to the

CORS network, with obvious advantages in the

precision and accuracy of the results and the landslide

analysis.

This study has considered static motion but it is

also possible to suppose a motion where the bias is

the change of velocity between two points.

Considering some preliminary results, in this last

case the Kalman filter appears to provide better

results with respect to statistical tests. This aspect will

be investigated subsequently.

REFERENCES

Aharizad, N., Setan, H., Lim, M. 2012. Optimized Kalman

filter versus rigorous method in deformation analysis.

Journal of Applied Geodesy, 6(3-4), 135-142.

Acar, M., Özlüdemir, M. T., Çelik, R. N., Erol, S., Ayan, T.

2004. “Landslide monitoring through kalman filtering:

A case study in Gürpinar”. Proceeding of XXth ISPRS

Congress, Istanbul, Turkey.

Baarda, W. 1968. A Testing Procedure for Use in Geodetic

Networks. Netherlands Geodetic Commission.

Publications on Geodesy - New Series. Vol. 2. No. 5.

Bellone, T., Dabove, P., Manzino, A.M., Taglioretti, C.

2016. Real-time monitoring for fast deformations using

GNSS low-cost receivers. Geomatics, Natural Hazards

Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers

and Risk, 7(2):458-470. Available at:

http://dx.doi.org/10.1080/19475705.2014.966867.

Benoit, L., Briole, P., Martin, O., Thom, C. 2014. Real-time

deformation monitoring by a wireless network of low-

cost GPS. Journal of Applied Geodesy, 1-10.

Bertachini, E., Capitani, A., Capra, A., Castagnetti, C.,

Corsini, A., Dubbini, M., Ronchetti, F. 2009. Integrated

surveying system for landslide monitoring, Valoria

landslide (Appennines of Modena, Italy). Paper

presented at: FIG working week 2009, Eilat, Israel.

Brückl, E., Brunner, F.K., Lang, E., Mertl, S., Müller, M.,

Stary, U. 2013. The Gradenbach Observatory -

monitoring deep-seated gravitational slope deformation

by geodetic, hydrological, and seismological methods.

Landslides 10 (2013): 815 – 829.

Calcaterra, S., Cesi, C., Di Maio, C., Gambino, P., Merli,

K., Vallario, M., Vassallo, R. 2012. Surface

displacements of two landslides evaluated by GPS and

inclinometer systems: a case study in Southern

Apennines, Italy. Nat Hazards 61(1):257–266.

Chrzanowski, A., Chen, Y., Romero, P. and Secord, J.M.

1986. Integration of Geodetic and Geotechnical

Deformation Surveys in the Geosciences.

Tectonophysics, Vol. 130, No. 1-4, November: 369-

383.

Chow, G. C. 1960. Tests of Equality Between Sets of

Coefficients in Two Linear Regressions. Econometrica

28(3): 591–605.

Cina, A., Piras, M. 2014. Monitoring of landslides with

mass market GPS: an alternative low cost solution.

Geomatics, Natural Hazards and Risk. [cited 2014 Feb

24]. Available from:

http://www.tandfonline.com/doi/full/10.1080/1947570

5.2014.889046#.U0-vV6IzfcB.

Coe, J.A., Ellis, W.L., Godt, J.W., Savage, W.Z., Savage,

J.E., Michael, J.A., Kibler, J.D., Powers, P.S., Lidke,

D.J., Debray, S. 2003. Seasonal movement of the

Slumgullion landslide determined from Global

Positioning System surveys and field instrumentation,

July 1998-March 2002. Engineering Geology, 68 (1–2):

67–101.

Cruden, D.M. 1991. A simple definition of a landslide.

Bulletin of the international association of engineering

geology. Bulletin de l’Association Internationale de

Géologie de l’Ingénieur. 43(1):27–29.

Dabove, P., Manzino, A.M., Taglioretti, C. 2014. GNSS

network products for post-processing positioning:

limitations and peculiarities. Applied Geomatics, vol. 6

n. 1, pp. 27-36. - ISSN 1866-9298. Available at:

http://link.springer.com/article/10.1007/s12518-014-

0122-3.

Dabove, P., Manzino, A.M. 2014. GPS & GLONASS

Mass-Market Receivers: Positioning Performances and

Peculiarities. Sensors 2014, 14, 22159-22179.

Eyo Etim, E., Tajul, A.M., Khairulnizam, M.I., Yusuf, D.O.

2014. Reverse RTK Data Streaming for Low-Cost

Landslide Monitoring. Geoinformation for Informed

Decisions. Lecture Notes in Geoinformation and

Cartography

. Springer International Publishing,

Switzerland.

Gili, J.A., Corominas, J., Rius, J. 2000. Using global

positioning system techniques in landslide monitoring.

Eng Geol 55(3):167–192.

Günther, J., Heunecke, O., Pink, S., Schuhbäck, S. 2008.

Developments towards a low cost GNSS Based Sensor

Network for the monitoring of landslides. Paper

presented at:13th FIG International Symposium on

Deformation Measurements and Analysis, Lisbon.

Gülal, E. 1999. Application of Kalman filtering

technique in the analysis of deformation

measurements. Journal of Yıldız Technical University,

(1). (in Turkish).

Hastaoglu, K.O., Sanli, D.U. 2011. Monitoring Koyulhisar

landslide using rapid static GPS: a strategy to remove

biases from vertical velocities. Natural Hazards.

58:1275-1294.

Heunecke, O., Glabsch, J., Schuhbäck, S. 2011. Landslide

Monitoring Using Low Cost GNSS Equipment –

Experiences from Two Alpine Testing Sites. Journal of

Civil Engineering and Architecture. 45:661-669.

Janssen, V., & Rizos, C. (2003). A mixed-mode GPS

network processing approach for deformation

monitoring applications. Survey review, 37(287), 2-19.

Kalman, R.E. 1960. A new approach to linear filtering and

prediction problems. Trans. ASME J. Basic Engr: 35-

45.

Li, L., Kuhlmann, H. 2008. Detection of deformations and

outliers in Real-time GPS measurments by Kalman

Filter Model with Shaping Filter. In: 4th IAG

Symposium on Geodesy for Geotechnical and

Structural Engineering and 13th FIG Symposium on

Deformation Measurements, Lisbon.

Li, L., Kuhlmann, H. 2010. Deformation Detection in the

GPS Real-time Series by the Multiple Kalman Filter

Model. Journal of Surveying Engineering. 136:157-

164.

Li, L., Kuhlmann, H. 2012. Real-time deformation

measurements using time series of GPS coordinates

processed by Kalman filter with shaping filter. Survey

Review, Vol. 44, 326:189-197.

Mäkilä, P.M. 2004. Kalman Filtering and Linear Quadratic

Gaussian Control. Lecture notes for course 7604120,

Part I. Available at:

http://www.dt.fee.unicamp.br/~jbosco/ia856/KF_part1

_Makila.pdf.

Malet, J-P., Maquaire, O., Calais, E. 2002. The use of global

positioning system techniques for the continuous

monitoring of landslides: application to the super-sauze

earth flow (Alpes-de-Haute-Province, France).

Geomorphology

43:33–54.

Manzino, A.M., Dabove, P. 2013. Quality control of the

NRTK positioning with mass-market receivers. Global

Positioning Systems: Signal Structure, Applications

and Sources of Error and Biases. Ya-Hui Hsueh,

Hauppauge NY. Chapter 2. p. 17-40.

Masiero, A., Guarnieri, A., Vettore, A., Pirotti, F. 2013. A

nonlinear filtering approach for smartphone-based

indoor navigation. May 2013, 1-3, Tainan, Taiwan.

Mora, P., Baldi, P., Casula, G., Fabris, M., Ghirotti, M.,

Mazzini, E., Pesci, A. 2003. Global positioning systems

GISTAM 2016 - 2nd International Conference on Geographical Information Systems Theory, Applications and Management

and digital photogrammetry for the monitoring of mass

movements: application to the Ca’ di Malta landslide

(northern Apennines, Italy). Eng Geol 68(1–2):103–

121.

Moss, J.L. 2000. Using the global positioning system to

monitor dynamic ground deformation networks on

potentially active landslides. Int J Appl Earth Obs

Geoinf, 2(1):24–32.

Othman, Z., Wan Aziz, W.A., Anuar, A. 2011. Evaluating

the performance of GPS survey methods for landslide

monitoring at hillside residential area: static vs rapid

static. IEEE 7

international colloquium on signal

processing and its applications, George Town, Penang.

Peyret, M., Djamour, Y., Rizza, M., Ritz, J. F., Hurtrez,

J.E., Goudarzi, M.A., Nankali, H., Chery, J., Le Dortz,

K., Uri, F. 2008. Monitoring of the large slow Kahrod

landslide in Alboz mountain range (Iran) by GPS and

SAR interferometry. Eng. Geol. 100:131-141.

Rizzo, V. 2002. GPS monitoring and new data on slope

movements in the Maratea Valley (Potenza, Basilicata).

Phys Chem Earth, Parts A/B/C 27(36):1535–1544.

Rott, H., Nagler, T. 2006. The contribution of radar

interferometry to the assessment of landslide hazards.

Adv Space Res 37(4):710–719.

Salzmann, M.A. 1995. Real-time adaptation for model

errors in dynamic systems. Bulletin Geodesique, 69:81-

91.

Sedlak, V., Jecny, M. 2004. Deformation measurements on

Bulk Dam of waterwork in East Slovakia. Geology,

Ecology, Mining Service, Vol. L, No. 2, 1-10.

Szostak-Chrzanowski, A., Chrzanowski, A., & Massiéra,

M. (2005). Use of deformation monitoring results in

solving geomechanical problems—case studies.

Engineering Geology, 79(1), 3-12.

Tagliavini, F., Mantovani, M., Marcato, G., Pasuto, A.,

Silvano, S. 2007. Validation of landslide hazard

assessment by means of GPS monitoring technique – a

case study in the Dolomites (Eastern Alps, Italy). Nat.

Hazards Earth Syst. Sci., 7:185-193,

Takasu, T., Yasuda, A. 2009. Development of the low-cost

RTK GPS receiver with the open source program

package RTKLIB. International symposium on

GPS/GNSS, International convention centre, Jeju,

Korea.

Teunissen, P.J.G., Salzmann, M.A. 1989. A recursive slip-

page test for use in state-space filtering. Manuscripta

Geodaetica, 14:383-390.

Wang, G. 2011. GPS landslide monitoring: single base vs.

network solutions—a case study based on the Puerto

Rico and Virgin Islands permanent GPS network. J

Geodetic Sci 1(3):191–203.

Wang, G., Soler, T. 2012. OPUS for horizontal sub-

centimeter accuracy landslide monitoring: case study in

Puerto Rico and Virgin Islands region. J Surv Eng

138(3):11.

Weber, G., Dettmering, D., Gebhard, H. 2006. Networked

transport of RTCM via internet protocol (NTRIP).

International association of geodesy symposia: a

window on the future of geodesy, vol 128.

Welch, G., Bishop, G. 2003. An introduction to the Kalman

Filter. TR95-04, Department of Computer Science,

University of North Carolina at Chapel Hill. Available

at:

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.

1.1.117.6808&rep=rep1&type=pdf.

Welsch, W., Heunecke, O. (2001). Models and terminology

for the analysis of geodetic monitoring observations.

Official report of the ad-hoc committee of FIG working

group, 6, 390-412.

Wei, Z., Dongli, F., Jinzhong, Y. 2010. Adaptive Kalman

Filtering Method to the Data Processing of GPS

Deformation Monitoring. Proceedings of the 2010

International Forum on Information Technology and

Applications - Volume 01 (IFITA '10), Vol. 1. IEEE

Computer Society, Washington, DC, USA, 288-292.

DOI=10.1109/IFITA.2010.18

http://dx.doi.org/10.1109/IFITA.2010.18.

Kalman Filter as Tool for the Real-time Detection of Fast Displacements by the Use of Low-cost GPS Receivers