The Use of the Generalised Knapsack Problem in Computer Aided

Strategic Management

Dorota Kuchta

, Radosław Ryńca

, Dariusz Skorupka

and Artur Duchaczek

Faculty of Computer Science and Management, Wrocław University of Technology,

Smoluchowskiego Street 25, 50-372 Wrocław, Poland

Faculty of Management, The General Tadeusz Kosciuszko Military Academy of Land Forces,

Czajkowskiego Street 109, 51-150 Wroclaw, Poland

Key

words: Portfolio Planning Methods, Strategic Management, Generalised Assignment Problem, General Knapsack

Problem, Computer Decision Aid.

Abstract: There are many methods and tools in the literature that are helpful in strategic management. Some of them

are related to the aspect of sustainability in terms of controlling and balancing the level of fulfilment of the

different, sometimes conflicting, objectives which must be considered while building strategies. These tools

include product portfolio methods. However, their use is often intuitive and detached from the quantitative

aspects of management, such as cost-related restrictions or other quantitative restrictions imposed by the

market or by internal circumstances. This article presents a proposal for the modification of portfolio methods

aimed at enforcing the portfolio’s quantitative aspect through the use of a discrete optimisation problem,

namely the knapsack problem. Interacting with the decision maker, the quantitative parameters of the situation

and the strategic goals are determined. Following this, a proposal solution is generated by a computer system

in which the respective algorithms for the generalised knapsack problem (also called the generalised

assignment problem) are embedded. The decision maker can accept the solution or change the parameters if

the solution does not suit them or if they simply want to have other solutions for comparison. The outline of

the system and the interaction between the decision maker and the system is illustrated by means of an

example of constructing strategies for a university.

1 INTRODUCTION

There are many portfolio planning and control

methods (also known as the growth–share matrices)

in the literature. These methods help to control and

specify companies’ current and future market

position and generally help to make strategic

decisions. They make it possible to assess the

directions in which organisations may develop; in

particular they help to control which products,

technologies, or strategic units the company should

concentrate on and which ones should be abandoned

or treated with less attention. This analysis is a good

basis for strategic planning.

The idea of the application of the matrix methods

consists of defining several (approximately 4–20)

areas in the plane and identifying which areas the

objects to be examined (they may be products,

customers, departments, branches, etc.) belong to for

the time being. Next there is the question of ranking

the areas on the basis of a multicriteria analysis.

Obviously, the areas that have the highest position in

the ranking are usually preferred. Then, the decision

maker should decide whether he or she is happy with

the current distribution of the objects. The answer is

usually negative. To address this problem, the

decision maker has to identify which objects could

and should be moved into which areas and which

objects could and should be abandoned (i.e. taken out

of the matrix (and thus the organisation) completely)

so that the overall situation of the organisation with

respect to the specified criteria becomes better than it

was at the control moment, while the circumstances

in which the organisation is operating are respected.

The practical application of the matrix methods is

usually detached from its quantitative aspect and is

rather intuitive. Not taking the quantitative aspect

explicitly into account may prove decisive to the

credibility of the control and of the selection of

available possibilities for improving the current

Kuchta, D., Ry

nca, R., Skorupka, D. and Duchaczek, A.

The Use of the Generalised Knapsack Problem in Computer Aided Strategic Management.

In Proceedings of the 18th International Conference on Enterprise Information Systems (ICEIS 2016) - Volume 2, pages 39-46

ISBN: 978-989-758-187-8

situation of the organisation. In particular, the aspect

of the cost of potential actions to be taken and its

relation to the projected budget for said actions may

have a decisive influence. Moving objects into

“better” areas requires concrete actions and creates

cost –as may moving objects into “worse” areas (to

make room for other objects), removing objects from

the matrix (i.e. from the organisation), or making an

object stay in the same area in the next period. The

actions are also usually limited by several quantitative

restrictions of an internal or external nature. These

restrictions might, for example, be due to the fact that

a good area will not accept any more objects, as the

market is saturated. There may also be a restriction

related to certain types of actions for which the

organisation may only have a limited quantity of

financial or human resources. Only attempting to take

these restrictions into account in an intuitive way may

mean that the optimal solution (according to the

optimality criteria defined by the decision maker) is

not always determined.

On the other hand, as the application of the matrix

methods in fact reduces itself to answering the

question of how to “pack” the available objects into

the various areas in the matrix in an optimal way, it

seems natural to combine the application of the

matrix methods with the quantitative optimisation

problem of packing, and more exactly with that of

packing several knapsacks (backpacks). This

combined proposal, together with the concept of a

computer system which would support the decision

maker in the control of the current situation and in

strategic decision making, in which the quantitative

restrictions and requirements may be introduced and

interactively modified, is the main product of the

paper. To illustrate the proposal, its application to the

control and to the elaboration of a modification

proposal of a university’s situation is described.

The outline of the paper is as follows. In Section

2 we briefly describe the main matrix methods. In

Section 3 we present the optimisation problem used:

the generalised knapsack problem (also called the

generalised assignment problem) in the form in which

it can be applied to the control of the organisation’s

current situation and to the strategic decision making.

In Section 4 we illustrate the combination of the

matrix methods and the generalised knapsack

problem as well as the concept of the computer

system that supports the proposal by means of an

application to a university’s situation. Screen shots

are shown from the prototype of the system we have

developed. The paper finishes with conclusions.

2 MATRIX METHODS USED IN

STRATEGIC MANAGEMENT

The Boston Consulting Group (BCG) matrix (Udo-

Imeh, Edet and Anani, 2012) is one of the best-known

methods in portfolio analysis. The method helps to

determine the strategic position of the company by

indicating its possibilities for development. The idea

of the BCG method involves the controlling and

planning of a product portfolio or a portfolio of

services in order to ensure a long-term balanced

relationship between the products/services that are

characterised by high competitiveness and

profitability as well as new products/services, often in

the development phase, which are not highly

competitive or profitable. The BCG matrix helps to

determine which products should be withdrawn from

the range of production and which should bring more

profit in the future (Fig.1).

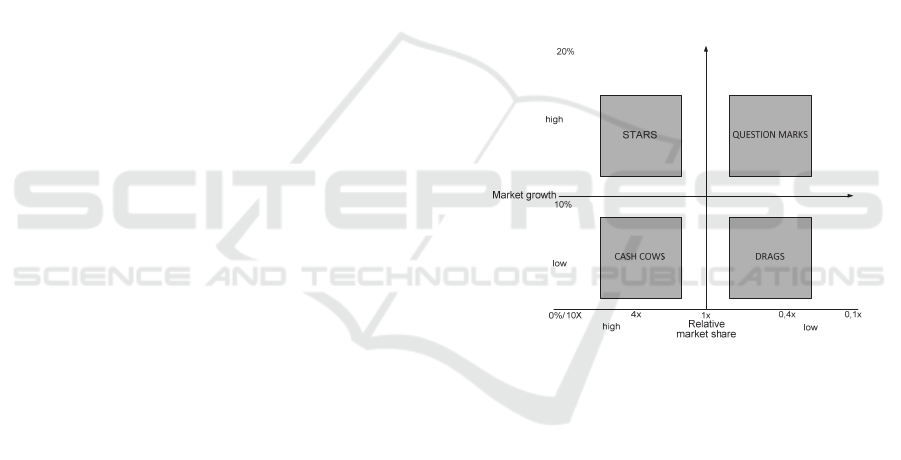
Figure 1: BCG matrix (Adapted from (Porth, 2003)).

As shown in Fig. 1, the BCG matrix is based on

two criteria–relative market share and market growth.

The relative share of the market helps to evaluate the

degree of competitiveness of the company. The

second dimension relates to the attractiveness of the

market in which the company operates. The two

dimensions (criteria) define four areas in the matrix.

In the late 60s and early 70s, when the BCG

method was first presented, the division between the

high and low market growth rate was determined to

be 10%, which is often diminished today to 5% (Udo-

Imeh, Edet and Anani, 2012) and may be changed by

the decision maker.

The second dimension – the relative market share

– allows the decision maker to evaluate the

competitiveness of the products and/or services. This

indicator, because of its specificity, indirectly takes

into account the competition, and, in contrast to the

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

market growth rate, is measured in terms of current

values. “Relative market share“ enables the

competitive position of the company to be compared

with its largest competitor, whose position

determines the limit seen in the matrix.

Products/services placed in Fig. 1 on the left side of

the border reached a leading position in the market.

For example, a share equal to 4 means that the sales

of a particular product are four times greater than the

strongest competitor.

The four areas in the BCG matrix define four

product groups. The first group is called “Stars”,

which represent a valuable investment and have a

good outlook for the future. The second group of

products is “Question marks” (also called “Problem

children”), which are characterised by an unknown

future. Just like “Stars”, these units are characterised

by high market growth. However, the attractiveness

of the market, high returns, and low entry barriers

may allow the competition to gain strength. This

situation requires significant outlays in the fight with

the competition, including marketing activities. A

small market share may be the reason for the late

introduction of these products to the market.

“Question marks” are unprofitable products that

require funding from other sources. The third group

of products, known as “Cash cows” (also called

“Hosts”) is a group of profitable products with an

established competitive position which generate a

financial surplus that can be used to finance other

product groups (especially those which currently do

not generate profitability, but provide opportunities

for development in the future). The low market

growth rate associated with this product group makes

the market less attractive to new investors. The

company has wide discretion in determining the

prices and quantities of products produced, but

significant investments in the modernisation and

improvement of products cannot be made. The last

group of products are so-called “Balls and chains”

(also called “Dogs” or “Pets”).“Dogs” do not

generate high surpluses or incur significant capital

expenditures. They are typically characterised by low

profitability. They are not progressive and do not

bring the profits expected of them (Wilson and

Gilligan, 1992).

Factoring in these considerations, the user

conducts a ranking of the four areas. Seeing the

matrix with the present products located in the

respective areas, the decision maker evaluates the

current situation and plans to take, if possible, actions

to move the selected products from one area to

another one or make the effort the keep them in the

area where they are or to take them out of the

organisation completely. Thus, we are faced with the

problem of packing four knapsacks in an optimal

way; while the knapsack “Balls and chains” should of

course be avoided, the other three knapsacks are more

desirable. All these decisions may be limited by some

quantitative requirements. The decision of where to

put the limits that define the four areas (how to choose

the thresholds for the two criteria) is of a quantitative

nature. These requirements and preferences of the

decision maker will be able to be taken into account

explicitly in the quantitative model that we propose

later in this paper.

Other matrix methods will be described in less

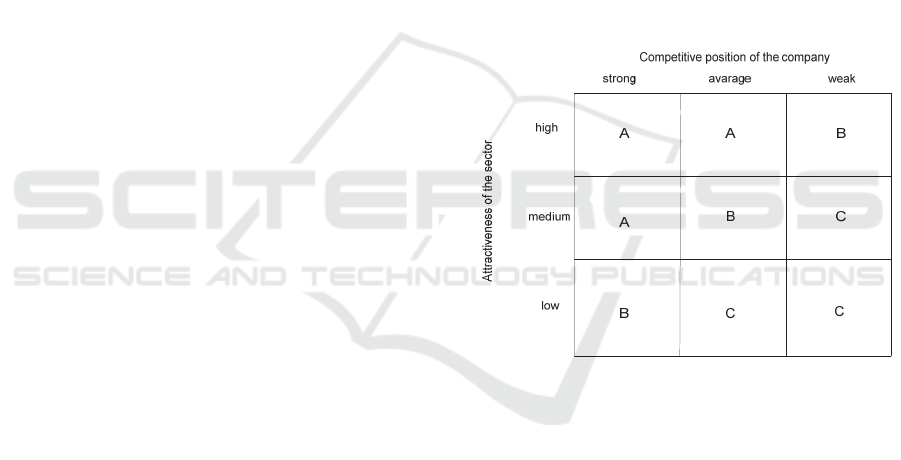
detail. The General Electric(GE)matrix, also called

the McKinsey Matrix or Business –Industry

Attractiveness Matrix (Udo-Imeh et al., 2012), is

based on the assumption that the company should

operate in more attractive sectors and focus on

investing in products that have a strong competitive

position (Fig. 2).

Figure 2: GE matrix (Udo-Imeh et al., 2012).

The GE matrix model is based on two criteria: the

competitive position of the company and the

attractiveness of the sector in which its products are

offered. For each of the variables there are three

options (high, medium, and low) of assessment

provided. In this way 9 areas are distinguished in

which products under evaluation may be placed.

Symbols A,B, and C (Hax and Majluf, 1990) in Fig.2

represent a possible basis for the ranking of the nine

areas (the areas marked with A form the group of

areas with the highest ranking, followed by the areas

marked with B, etc.), whose details will have to be

resolved by the decision maker. All the areas marked

with one letter may also form one area (one knapsack

in our approach). Following this, the decision maker

would have to resolve the optimisation problem of the

optimal packing of the nine areas, where the areas

ranked the highest would be preferred. Our

The Use of the Generalised Knapsack Problem in Computer Aided Strategic Management

proposition in Section 4 would help to formalise this

decision and to find the best possible solution. The

limits (the threshold for the criteria) may also be

defined in a quantitative way, in which case our

proposal would help to examine the sensibility of the

various solutions to the decision of what the notions

“high”, “medium”, and “low” are chosen to mean.

Here fuzzy thresholds may be used.

The ADL matrix, also called the Maturity Matrix

(Mason, 2010), helps to assess company products on

the basis of two criteria – the competitive position of

a product in the sector and the maturity of the sector.

Five different competitive positions and four phases

of the industry life cycle are distinguished, which

gives 20 areas, usually grouped into three categories

– A,B, and C – as in the case of the GE matrix.

The Hofer and Schendel matrix (Ionescu et al.,

2008) is a development of the GE and the ADL

matrix. Its authors suggest that the assessment of

strategic units must take into account the size of their

competitive position and the phase of the business life

cycle that they are in. Hofer and Schendel also

introduce other criteria in order to assess life-cycle

phases, such as the embryonic, market entry, growth

and shocks, maturity, and decline phases. They also

propose various strategic options ranging from

strengthening the market position, through finding a

market niche, to withdrawal from the business.

The Ansoff matrix (Ansoff, 1957) focuses on the

selection of strategic options based on the criteria of

the market and product newness. Ansoff assumes four

possible strategies for business development, i.e.

market development, product development, market

penetration, and product diversification.

To sum up the usage of matrix methods in the

control of a company’s current situation and its

strategic management, we can say that various criteria

and criteria threshold values are used in order to

define areas which we can see as knapsacks

(backpacks).These knapsacks are filled in in the given

moment in a certain way (each product or each

customer belongs to one knapsack). The objective of

the decision maker may be – and usually will be – to

change the assignment of individual objects to the

knapsacks, as some of the knapsacks are considered

to be better and some worse from the point of view of

the overall situation of the organisation. Following

this, the problem of the optimal packing of the

knapsacks in a given situation is in fact considered,

without being explicitly seen and formulated. It is

usually solved intuitively, without explicitly

considering the quantitative limitations. The

approach we propose in Section 4 will make it

possible to formulate an adequate quantitative

optimisation problem, with the participation of the

decision maker, and implement it in a computer

decision support system, which allows better

solutions (because they are formally optimal) to be

obtained.

In the next section we will present the generalised

knapsack problem, also known as the generalised

assignment problem, in the form in which it should be

used in our proposal.

3 GENERALISED KNAPSACK

(ASSIGNMENT) PROBLEM IN

PORTFOLIO ANALYSIS

METHODS

The methods described in the previous section help to

evaluate the current situation of an organisation’s

products, customers, or departments and help users

make decisions about how to improve their

organisation’s current situation. However, in our

opinion they would do this more effectively if the

quantitative aspect, quantitative objectives, and

quantitative requirements were incorporated

explicitly into the methods. The optimisation problem

based on the knapsack (backpack) problem with

multiple knapsacks, also called the generalised

assignment problem, might in our opinion constitute

a useful basis for this step. An incorporation of this

kind, together with a computer system that allows the

decision maker to shape the formulation of the

optimisation model according to his or her wishes,

would constitute a considerable form of assistance in

making strategic decisions.

In the single knapsack problem (Martello and

Toth, 1990), we ask the question of which objects

(each of them having a certain volume and a certain

value) from a given set of objects can be put in the

knapsack, so that their total volume does not exceed

the knapsack capacity and their total value is as high

as possible. If we have several knapsacks (the

problem is then called the generalised knapsack

(assignment) problem (Haddadi and Ouzia, 2004)),

the value of each object may depend on the knapsack

it will be placed in. Next, this assignment of objects

(some of which may remain unassigned because of a

lack of knapsack capacity) to the knapsacks is

explored to determine which assignment would

maximise the total value of the objects placed in the

knapsacks while not exceeding the capacities of the

knapsacks and respecting other constraints. Such an

optimisation problem suits our needs well. We have

various knapsacks–various areas in the matrices, each

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

of which may give another value to the object placed

in it. The volume may be represented in our case by

cost, which would be generated by the decision to

move the item from one knapsack to another, and, if

so desired by the decision-maker, by the decision to

leave an item in the knapsack. The limitations (the

equivalent of the knapsacks’ volumes) would be the

budget available for implementing strategic decisions

or some other limits. For example, we might have a

limited budget or limited competences for certain

types of actions (e.g. promotion actions). The

equivalent of volume may also be simply the number

of objects. This would be the case if the market did

not allow a matrix area to absorb more objects than a

certain number. All constraints of this type and many

more could be introduced into the model and

modified if necessary in cooperation with the decision

maker. The model presented below and implemented

in the computer system prototype we present in the

next section can be expanded in many ways,

including the introduction of fuzzy divisions between

knapsacks/areas and other soft (fuzzy) elements.

The basic model, based on (but not identical to)

the generalised knapsack problem, would be as

follows: we assume that in the matrix we have M

areas or domains, denoted as 



,1,…,.Each

area has a certain ranking position in the eyes of the

decision maker, denoted as 



,   1, … , , while

function R does not have to be injunctive. There are

also N objects



,1,…,. If object 



is in

area



, it has value



, where this value is

determined by experts and takes into account the

ranking of the domains. In some cases we may simply

have 







, 1,…,,1,…,. We also

assume that we have a function that evaluates the

overall situation of the organisation at a given

moment, called the satisfaction function (SF), which

we assume to be as follows:

 

∑∑

















(1)

where

is the binary variable that takes on a value

of 1 if the i-th element is in the j-th area, and takes on

0 if otherwise.

At the moment of the control of the organisation’s

current situation, the decision maker has to identify

the area that each object belongs to at that moment

and calculate the current value of function(1). If the

value of function (1) is satisfactory, there is no

problem to be solved. However, if it is not, we change

the meaning of variables

. They turn into decision

variables:

is equal to1 if the i-th element should be

placed in the j-th area, and equal to 0 otherwise. For





,1,…,, the decision maker has to determine

which areas it might be moved potentially to, and

evaluate for each area the cost of moving object





into area 



,1,…,or of keeping it in this

area. This cost will be denoted as 



, 1,…,,

1, … , . If object 



cannot be moved into area 



the decision maker wants to forbid such a move, then





is given a very high value. Function (1) becomes

an objective function which should be maximised.

We will have in the model the basic constraints of

the generalised knapsack problem (Martello end

Toth, 1990), assuring that no object is placed in more

than one knapsack. The equality sign is also possible,

if we require all the objects to be in one of the

domains, thus if we do not want to eliminate any

object from our activity:

∑





 1for  1, … , 





 (2)

On top of that, all the budgetary or other resource

limit-based constraints have to be identified. For

example, if there is a budget B which can be used for

the realisation of the strategy identified by the

optimisation problem, we will have the constraint:

∑∑

















 (3)

We might also have, for example, a budget





all the activities related to object











beingoneofthenumbers1, … , ). This

might happen, for example, in the case where each

object has a budget assigned to it and no money

transfers among objects are allowed by the

organisation’s management. Then we would have the

constraint:

∑



























 (4)

Another type of constraint could be due to the fact

that it is not possible to place more than a certain

number of objects in a “good” area, as the market

does not allow it. If the area in question has index 



and the limit is 





, we will have the constraint:

∑

















 (5)

Constraints (4) and (5) might have further

variations according to the wishes of the decision

maker. Some of these variations will be illustrated in

the next section.

The solutions of models (1) to (5), found by means

of any software that provides solutions to integer

linear programming problems (for example the free

software “Gusek”, [http://gusek.sourceforge.net/guse

k.html]), will deliver the values of the decision

The Use of the Generalised Knapsack Problem in Computer Aided Strategic Management

variables, which in turn ensuring the highest possible

value of objective function (1) in the given

circumstances. If the decision maker is not happy

with this value, he or she may consider modifying the

model.

The following section contains an example of the

application of the proposed concept to the strategic

management of a Polish university. At the same time

it shows screenshots of the prototype of the proposed

computer system in which our proposal has been

implemented.

4 APPLICATION OF THE

APPROACH AND THE

COMPUTER SYSTEM

CONCEPT

The example discussed here concerns a Polish

university. The university faculties (there are seven of

them, denoted by



,1,…,7) will be the objects

of the analysis and of the strategic decisions. They

can be assessed from the point of view of different

criteria. In the discussed case, we propose the use of

two criteria, i.e. the attractiveness of the faculty and

its profitability (other criteria would be also possible).

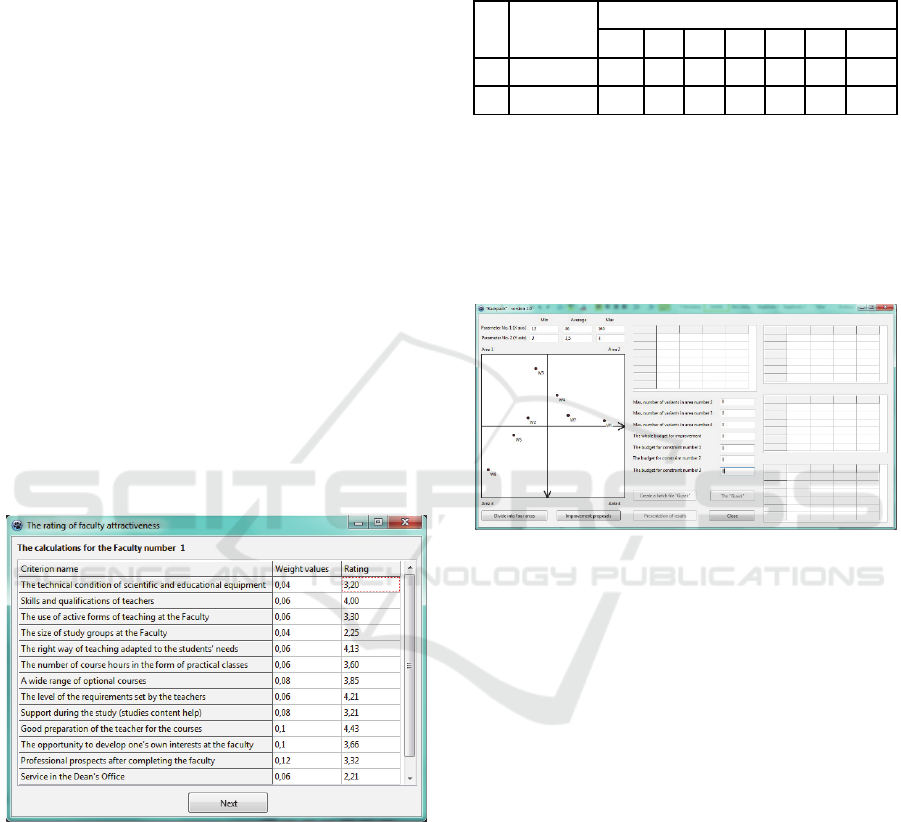
Figure 3: A screenshot showing the assessment of one

faculty’s attractiveness.

While profitability is a rather unanimous measure

(although there are serious problems linked to

university costing (Cox, Downey and Smith, 1999;

Klaus, 2008; Klaus-Rosińska and Kowalski, 2010)),

attractiveness may be measured using various criteria

and from various points of view, which have to be

aggregated in a certain way, e.g. by means of

weighting. Figure 3 gives an idea how this can be

done in the computer system we propose.

We do not enter into details here, although more

on the subject of faculty attractiveness assessment can

be found in (Ryńca, 2014).Here we give the final

results of the calculations:

Table 1: Assessment of the university faculties.

o Criteria

Faculty





























1 attractiveness 3,46 3,44 3,10 3,28 3,56 3,80 3,42

2 profitability 138,6 60,2 68,1 89,9 45,8 19,3 101,56

First, the current university situation was subject

to a control. In the prototype of the computer system,

in which M=4 and the threshold values were chosen

by the decision maker, taking into account Table 1,

we can see the following screen, where all the

faculties have been placed in one of the four areas,

illustrating the current situation of the faculties:

Figure 4: A screenshot showing the positions of the

faculties.

The profitability of the faculties is marked on the

X axis (the horizontal axis), while the attractiveness

of the facilities is displayed on the Y axis (the vertical

axis).

Function R was entered (R(1)=0, R(2)=4, R(3)=5,

R(4)=8), and it was assumed that 







,  

1, … ,7,   1, … ,4. The current value of objective

function (1) was calculated and found to be equal to

22. The maximum possible value of (1) (in the ideal

case where all the faculties are in the 4

area) is 56.

The relation of 22/56 was found to be unsatisfactory.

Thus, the decision maker was asked to use one of the

empty matrices in Figure 4 to define the cost of all the

transfers possible and desirable for the departments

between areas. It was assumed that keeping a

department in an area where it was at that moment

would not generate any cost and that transfers to

lower-rated areas were not allowed. The results

entered by the decision maker are given in Table 2.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems

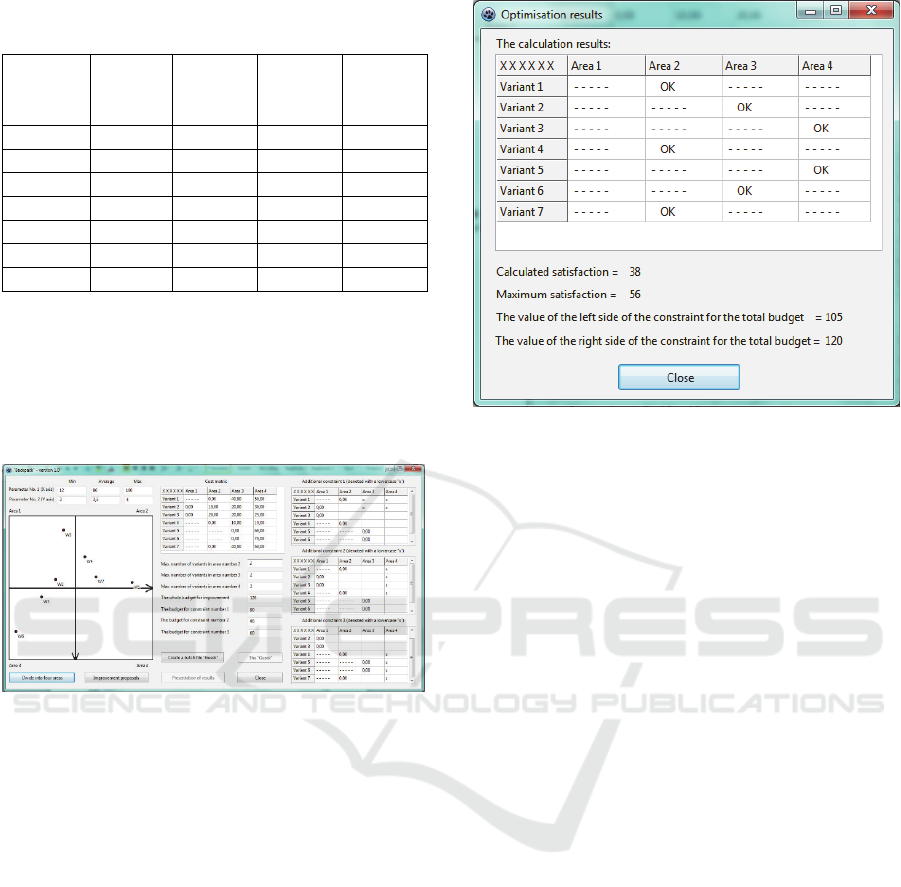
Table 2: Cost of actions which would move a faculty to

a higher-ranked area.

Faculty W

Cost of

moving

to Area 1

Cost of

moving

to Area 2

Cost of

moving

to Area 3

Cost of

moving

to Area 4

---------- 0 40 50

0 10 20 30

0 20 20 25

---------- 0 10 10

---------- ---------- 0 60

---------- ---------- 0 70

---------- 0 40 60

Later, several constraints of the type discussed in

Section 3 were introduced (the basic knapsack

problem constraints (2) are included in the model

automatically). All this can be seen in the next

screenshot of the computer system (see “Cost

matrix”):

Figure 5: A screenshot showing the costs of the transitions

between areas including additional constraints.

The additional constraints seen in Figure 5 are:

 one concerning the total budget for

improvement actions (3)

 those concerning limited budgets for groups

of actions, crossed in the matrices on the

right-hand side of the screen, of type (4) (e.g.

constraint number 1 is 40



50





20



30



90)

 those concerning the absorption possibilities

of the individual areas (of type (5)).

Then a “Gusek” file with the integer linear

programming model is automatically created,

exported, and solved The solution, visible in the right-

hand side of the screen in Figure 6, is then imported

and shown to the decision maker in the system

(Figure 6):

Figure 6: A screenshot showing the optimal solution.

The decision maker can see that it is possible to

improve satisfaction with the university’s position

from 22 to 38, thus from 39% of the ideal satisfaction

to 68%. The total budget for improvements will only

be partially used (due to the other constraints – out of

120 monetary units available, only 105 are needed).

The transfers that should be implemented are marked

with OK in Figure 7. Thus there would finally be no

departments in area 1, which is ranked as the worst

area, departments 



, 



, and 



would be in area 2

(where they were before), departments 



(currently

in area 3) and 



(currently also in area 3) in area 3,

and department 



(currently in area 1) and





(currently in area 3) would be in the best area, area

4. If the decision maker is satisfied with this solution,

he or she may agree to it; otherwise, the model may

be modified.

5 CONCLUSIONS

This paper proposes the calculation of matrix models

known from strategic management, which support the

evaluation of products, units, clients, or units of

organisations, with a quantitative component using

discrete optimisation methods, and proposes

embedding all of this into a computer decision aiding

system, allowing the decision maker to find the best

solution according to his/her criteria. The use of

mathematical models by decision makers forces a

deeper reflection and a more systematic analysis

aimed at a quantitative assessment both of the

parameters of the controlled objects, as well as of the

costs of various activities which may be undertaken

The Use of the Generalised Knapsack Problem in Computer Aided Strategic Management

to implement the adopted strategy. Even if the

quantitative assessment is difficult in some cases, it

fosters an objective analysis. In the case where crisp

values are difficult to give, fuzzy numbers (or even

linguistic expressions, modelled by fuzzy numbers)

can be used. The generalisation of the proposed

concept to the fuzzy case would not be complicated

and is foreseen in future research, as fuzzy versions

of the knapsack problem are discussed in the

literature and corresponding algorithms exist (Lin and

Yao, 2001; Kuchta, 2002; Changdar, Mahapatra and

Pal, 2015).

Undoubtedly, the proposed model requires further

verification in practice and the computer system

prototype requires a large amount of testing. Further

extensions should also be taken into consideration, in

particular the introduction of fuzziness.

As far as the computational aspect is concerned, it

must be noted that the knapsack problem belongs to

computationally difficult problems (Haddadi and

Ouzia, 2004), which means that if it were to deal with

a problem of a large size (usually measured by the

number of evaluated objects) the generation of an

optimal solution may take a long time (this time can

even be hours long). If a given organisation has

several thousand products and wants to generate an

appropriate strategy for them, then the determination

of the solution may take more time. However, there

are numerous references in the literature proposing

approximate algorithms for such cases, which are

much quicker (Haddadi and Ouzia, 2004;

Michalewicz and Fogel, 2004). Additionally, the

control of a company’s current situation and strategy

building is not an everyday activity, so even if it takes

more time, this is usually not a serious obstacle and

the type of free software we propose for use in this

matrix should be satisfactory for practical purposes in

most cases.

REFERENCES

Ansoff, I., 1957. Strategies for Diversification, Harvard

Business Review, Vol. 35 No.5, pp.113–124.

Changdar, C., Mahapatra, G.S., Pal, R.K., 2015. An

Improved Genetic Algorithm Based Approach to Solve

Constrained Knapsack Problem in Fuzzy Environment,

Expert Systems with Applications, Vol. 42, No. 4, pp.

2276–2286.

Cox, K.S., Downey, R.G., Smith, L.G., 1999. ABCs of

Higher Education. Getting Back to the Basics: An

Activity-based Costing Approach to Planning and

Financial Decision Making, Presented at the 39th

Annual Forum of the Association for Institutional

Research, Seattle, WA, USA, 30May–3 June, 1999.

Haddadi, S., Ouzia, H., 2004. Effective Algorithm and

Heuristic for the Generalized Assignment Problem,

European Journal of Operational Research, Vol. 153

No. 1, pp. 184–190.

Hax, A.C., Majluf, N.S., 1990. The Use of Industry

Attractiveness–Business Strength Matrix in Strategic

Planning. In R.G. Dyson (ed.), Strategic Planning:

Models and Analytical Technique(pp.73–92).

Chichester, England: John Wiley & Sons.

Ionescu, F.T., Căescu, Ş.C., Cruceru, A.F., 2008. Business

Portfolio Analysis – Hofer Method, Annals of the

University of Oradea, Economic Science Series, Vol.

17 No. 4, pp. 913–917.

Klaus, A., 2008. Activity based costing - a response to the

increased needs of Polish universities in the field of

information cost. In A. Matysiak (ed.), Prace Naukowe

Uniwersytetu Ekonomicznego we Wrocławiu, Nr. 15.

Rachunkowość zarządcza w warunkach globalizacji

(pp. 152–161).Wrocław, Polska: Wydawnictwo

Akademii Ekonomicznej, (in polish).

Klaus-Rosińska, A., Kowalski, M., 2010. Activity Based

Costing in Universities – A Calculation of Teaching

Costs, Proceedings of the 3rd International Conference

of Education, Research and Innovation

(ICERI2010),Madrid, Spain, 15–17 November, 2010,

pp.1579–1592.

Kuchta, D., 2002. A Generalisation of an Algorithm Solving

the Fuzzy Multiple Choice Knapsack Problem, Fuzzy

Sets and Systems, Vol. 127 No. 2, pp. 131–140.

Lin, F.-T., Yao, J.-S., 2001. Using Fuzzy Numbers in

Knapsack Problems, European Journal of Operational

Research, Vol. 135 No. 1, pp. 158–176.

Martello, S., Toth, P., 1990. Knapsack Problems:

Algorithms and Computer Implementations.

Chichester, England: John Wiley& Sons.

Mason, M., 2010. ADL Matrix by Arthur D. Little. All

About Economies on the Web. Retrieved 8June 2012

from http://www.sayeconomy.com.adl.matrix-by-

arthur-d-little , (access: 13.02.2014).

Porth, S.J., 2003. Strategic Management: A Cross-

Functional Approach, Pearson Education, Inc., Upper

Saddle River, New Jersey.

Michalewicz, Z., Fogel, D.B. (2004), How to Solve It:

Modern Heuristics (2nd ed.). Berlin, Germany:

Springer-Verlag.

Ryńca, R., 2014. Application of selected methods and tools

in the evaluation of universit, Wrocław, Polska:Oficyna

Wydawnicza Politechniki Wrocławskiej, (in polish).

Udo-Imeh, P.T., Edet,W.E. Anani, R.B., 2012. Portfolio

Analysis Models: A Review, European Journal of

Business and Management, Vol. 4 No.18, pp. 101–120.

Wilson, R.M.S., Gilligan, C., 1992. Strategic Marketing

Management: Planning, Implementation and Control.

Oxford, England: Elsevier Butterworth Heinemann.

ICEIS 2016 - 18th International Conference on Enterprise Information Systems