
Towards a Tracking Algorithm based on the Clustering of
Spatio-temporal Clouds of Points
Andrea Cavagna
1
, Chiara Creato
1
, Lorenzo Del Castello
1
, Stefania Melillo
1
, Leonardo Parisi
1,2
and Massimiliano Viale
1
1
Istituto Sistemi Complessi, Consiglio Nazionale delle Ricerche, UOS Sapienza, 00185 Rome, Italy
2
Dipartimento di Informatica, Universit
`
a Sapienza, 00198 Rome, Italy
Keywords:
3D Tracking, Spectral Clustering, Computer Vision.
Abstract:
The interest in 3D dynamical tracking is growing in fields such as robotics, biology and fluid dynamics. Re-
cently, a major source of progress in 3D tracking has been the study of collective behaviour in biological
systems, where the trajectories of individual animals moving within large and dense groups need to be recon-
structed to understand the behavioural interaction rules. Experimental data in this field are generally noisy
and at low spatial resolution, so that individuals appear as small featureless objects and trajectories must be
retrieved by making use of epipolar information only. Moreover, optical occlusions often occur: in a multi-
camera system one or more objects become indistinguishable in one view, potentially subjected to loss of
identity over long-time trajectories. The most advanced 3D tracking algorithms overcome optical occlusions
making use of set-cover techniques, which however have to solve NP-hard optimization problems. Moreover,
current methods are not able to cope with occlusions arising from actual physical proximity of objects in 3D
space. Here, we present a new method designed to work directly on (3D + 1) clouds of points representing the
full spatio-temporal evolution of the moving targets. We can then use a simple connected components labeling
routine, which is linear in time, to solve optical occlusions, hence lowering from NP to P the complexity of
the problem. Finally, we use normalized cut spectral clustering to tackle 3D physical proximity.
1 INTRODUCTION
In recent years the interest in 3D tracking has
grown significantly, both in academic fields as tur-
bulence (Ouellette et al., 2006), biology (Dell et al.,
2014), and social sciences (Moussaid et al., 2012)
and in industrial fields like robotics (Michel et al.,
2007), surveillance (Hampapur et al., 2005), and au-
tonomous mobility (Ess et al., 2010). Advances in
technology contributed to improve the tracking results
in terms of quality of the retrieved trajectories, at the
same time lowering the system requirements. These
progresses allow today the automatic tracking of large
groups of objects in a way that was prohibitive only a
few years back.
A particularly energetic boost of the research into
3D tracking has come from the study of collective
behaviour in biological systems, as bird flocks (At-
tanasi et al., 2015), flying bats (Wu et al., 2011), in-
sect swarms (Straw et al., 2010) (Puckett et al., 2014)
(Cheng et al., 2015) and fish schools (Butail et al.,
2010) (P
´
erez-Escudero et al., 2014). The aim in this
field is to use experimental data about the actual tra-
jectories of individual animals to infer the underlying
interaction rules at the basis of collective motion (Gi-
ardina, 2008). The crucial issue of the tracking algo-
rithm is then to avoid identity switches and minimise
fragmented trajectories, as this may result into a bi-
ased, or even wrong, understanding of the biological
mechanisms.
Data on collective animal behavior are charac-
terized by frequent occlusions lasting up to tens of
frames and by a low spatial resolution such that ani-
mals appear as objects without any recognizable fea-
ture. The latter fact rules out from the outset the use
of any feature-based tracking method (Vacchetti et al.,
2004). Optical occlusions, on the other hand, arise
when two or more targets get close in the 3D space
or in the 2D space of one or more cameras. Individ-
ual targets are not distinguishable anymore and the
identities of the occluded objects are mixed for sev-
eral frames. Occlusions introduce ambiguities which
can result in fragmented trajectories (best case sce-
nario) or identity switches (worst case scenario), de-
pending on the tracking approach used. An effective
tracking method for the study of collective behaviour
must find a way to deal with them.
We can define two types of occlusions: i) ‘simple’
Cavagna, A., Creato, C., Castello, L., Melillo, S., Parisi, L. and Viale, M.
Towards a Tracking Algorithm based on the Clustering of Spatio-temporal Clouds of Points.
DOI: 10.5220/0005770106790685
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 681-687
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
681

2D optical occlusions happen when two (or more) ob-
jects become closer than the optical resolution only in
the camera space; in this case proximity is just an il-
lusion of projection and the objects are not actually
close in real 3D space, so that, in a multi-camera sys-
tems, there will always be one or more cameras in
which the objects are well separated; ii) ‘hard’ 3D oc-
clusions occur when two (or more) objects get into
actual physical proximity in real 3D space; in this
case an optical occlusions is formed in all views of
the multi-camera system.
The most advanced tracking algorithms (Wu et al.,
2011) (Attanasi et al., 2015) (Cheng et al., 2015)
successfully overcome the problem of 2D occlusions
by using weighted set-cover techniques. This how-
ever requires solving a NP-hard optimization prob-
lem, with the consequent limitations on the maximum
size of the studied system. On the other hand, even the
most robust tracking methods do not solve the prob-
lem of occlusions due to actual 3D proximity, hence
incurring into switches of identity. We propose here
a new 3D tracking algorithm – name: Prometheus
– able to: i) solve occlusions due to 2D proximity
making use of a polynomial time connected compo-
nents labeling technique; ii) solve occlusions due to
3D proximity making use of a sophisticated cluster-
ing algorithm based on normalized cut methods.
2 RELATED WORKS
The first 3D tracking algorithms dealing with feature-
less objects were developed in the field of fluid dy-
namics, where the motion of passive tracer particles is
studied to investigate turbulent fluid flows. The most
successful algorithm in this field is the one presented
in (Ouellette et al., 2006), which solves occlusion-
related ambiguities locally in time, potentially pro-
ducing fragmented trajectories. However, in the study
of turbulence one can actually tune the density of trac-
ers, so decreasing the optical density to a point where
this is no longer critical. Clearly, this cannot be done
in biological systems.
More recently the literature about 3D tracking on
animal groups is growing, but the majority of the ex-
isting methods makes strongly use of objects’ features
and therefore they are not suitable for data coming
from large, dense groups in the field. In this case, the
requirement to have the whole group in the common
field of view of all cameras implies a relatively low
resolution at the individual level, making the targets
quite featureless. To the best of our knowledge, the al-
gorithms which best perform tracking of large natural
systems are the ones in (Wu et al., 2011) (bats), (At-
tanasi et al., 2015) (birds, insects) and (Cheng et al.,
2015) (insects). These 3D tracking algorithms fist de-
tect the objects moving in the common field of view of
the camera system via standard background subtrac-
tion and segmentation. Foreground objects are then
linked across cameras connecting 2D objects, projec-
tions at the same instant of time of the same 3D tar-
get in different cameras. Instead, links across time
are defined in the 2D space of each camera or in the
3D space. 2D objects are linked in time when rep-
resenting the projection of the same target at subse-
quent frames time; while 3D reconstructed objects
are linked when representing the three dimensional
reconstruction of the same target at different instant
of time. Depending on whether 2D or 3D links across
time are used, 3D algorithm are classified as tracking-
reconstruction (TR) and reconstruction-tracking (RT)
algorithms (Wu et al., 2009).
TR algorithms use 2D temporal links to create all
the possible 2D paths in each camera. These 2D paths
are then matched across cameras solving a weighted
set-cover problems based on stereometric links. Con-
versely, RT algorithms use links across cameras to
reconstruct all the existent 3D targets and then the
correct trajectories are chosen following 3D tempo-
ral links. In both cases a global multi-linking ap-
proach is necessary to overcome occlusions, as any
one-to-one local linking fails to recover the correct
trajectories, producing highly fragmented and wrong
tracks. The introduction of a global and multi-linking
approach increases the computational complexity of
the problem which has to be formulated as a NP-hard
weighted set-cover. In the general case, the complex-
ity of such a problem cannot be handled and only an
approximation of the optimal solution can be found.
In (Attanasi et al., 2015), the set-cover problem is
approached through a recursive technique, while in
(Wu et al., 2011) a greedy approximation is found. In
(Cheng et al., 2015), instead, the complexity of the
problem is reduced choosing the trajectories globally
in space but not in time.
Neither TR nor RT methods can solve the occlu-
sions due to 3D proximity described in the Introduc-
tion. Note that 3D occlusions occur when the two
objects become closer than the resolution of the 3D
experimental setup, even though they do not literally
occupy the same volume in 3D space. For example, if
the apparatus has an overall resolution (due to lens re-
solving power, atmospheric diffraction, sensor noise,
etc) of 0.2 meters, when two objects in a group be-
come closer than this limit (which may happen due
to inter-individual distance fluctuations), they are in a
3D proximity occlusion. Hence, 3D proximity occlu-
sions are more frequent than what one would naively
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
682

a) b) c)
View 1
View 2
View 3
no occlusion
View 1View 2View 3
3D proximity
View 1View 2View 3
two optical occlusions
Figure 1: The 3D clouds created by Prometheus corresponding to: (a) two targets well separated in all the views; (b) two
targets separated in the 3D space, but forming optical occlusions in two out of three cameras; (c) two targets in actual 3D
proximity (occlusion in all cameras). The two targets are reconstructed as two well-separated 3D clouds when they are not
occluded in at least one camera, while they are reconstructed as a single 3D cloud when in 3D proximity. View 1, View 2 and
View 3 show the image on each camera.
expect.
3 STRUCTURE OF THE
ALGORITHM
The proposed algorithm (name: Prometheus) is a
reconstruction-tracking method, since it first recon-
structs targets in the 3D space and then it retrieves
3D trajectories. However, our method differs from
classic reconstruction-tracking algorithms, as the one
described in (Cheng et al., 2015), because it does not
work on the 2D barycenter of segmented objects and
for this reason it does not need any cumbersome seg-
mentation routine, but only a background subtraction.
The algorithm can be broken into four steps: 1) back-
ground subtraction; 2) creation of the cloud of points;
3) Connected Components Labeling (CCL); 4) Nor-
malized Cut Spectral Clustering (NCSC).
1 - Background Subtraction. This is, of course,
the most standard and by far least demanding part of
the method. In order to discard background pixels, a
background subtraction routine is performed, making
use of a standard sliding window technique. This pro-
cedure is strengthened against image noise applying
standard denoising and thresholding routines (see, for
example, (Sobral and Bouwmans, 2014) for a general
description of background subtraction).
2 - Creation of the Cloud of Points. This mod-
ule is the core of the new method. At each time frame
Prometheus makes use of the geometric constraints
of the camera system (stereometric and epipolar rela-
tions) to match pixels across cameras. In this way, for
every set of pixels matched, it reconstructs the corre-
spondent 3D point in the world space, hence creating
a cloud of 3D points. Using three cameras, this pro-
cess is performed defining triplets of pixels, one for
each camera, that respect the trifocal constraint (Hart-
ley and Zisserman, 2004).
Let us illustrate what this procedure produces
when we are dealing with two different targets (at
fixed time). The easiest case is when the two targets
are well separated in 3D space and they are not op-
tically occluded in any camera view. In this case, of
course, the method produces two separated cloud of
3D points (Fig.1a), each corresponding to one of the
two targets.
View 1
View 2
View 3
CCL
3D+1 cloud
a) b)
Figure 2: 2D occlusion. Left: the temporal evolution of two
moving targets, seen by the three different cameras, forming
an optical occlusion for a few frames in View 1 and View 3.
(a) the (3D + 1) clouds of points created by Prometheus.
(b) the two (3D + 1) clouds of points clustered by the CCL
algorithm, identifying the two objects.
The second case is that of an optical occlusion, i.e.
the targets are well separated in 3D space, but they
form a single object in one (or more) of the 2D views
(Fig.1b – two-cameras occlusion). This is what is nor-
mally hard to solve by segmentation, producing track-
ing ambiguity at this instant of time. However, by
working directly with the cloud of points in 3D space
we see that the two objects become well-separated in
3D, despite some slight shape deformation due to an
epipolar echo of one object onto the other (Fig.1b).
When, on the other hand, the two targets are oc-
Towards a Tracking Algorithm based on the Clustering of Spatio-temporal Clouds of Points
683

View 1
View 2View 3
3D+1 cloud CCL NCSC
a) b) c)
Figure 3: 3D proximity. Left: temporal evolution of two moving targets forming an optical occlusion in all the three cameras
(3D proximity). (a) the (3D + 1) clouds of points created by Prometheus; (b) the outcome of CCL clustering, clearly unable
to retrieve the 3D +1 volumes of the two objects, because they are in physical proximity for a few frames; (c) the result of the
NCSC clustering algorithm: the two objects are correctly clustered and identified.
cluded in all three cameras (Fig.1c), their correspon-
dent volumes are no longer separated in the 3D space
and indeed they become one single 3D cloud. As we
have already said, in this case the two real objects in
3D space are closer than our resolution.
Once all frames are processed, what we have is a
global (3D + 1) cloud representing the volume of
the full spatio-temporal evolution of the targets. As
shown in Figs.2 and 3, the trajectory of each object
appears as a spatio-temporal tube and the challenge
now is to separate volumes corresponding to different
targets. This is what we do by using clustering algo-
rithms.
3 - Connected Components Labeling (CCL).
The (3D + 1) cloud is partitioned in clusters sepa-
rated in the (3D + 1) space. Such spatio-temporal
clustering needs a notion of proximity to connect
points in both space and time. Two 3D points belong-
ing to the same frame are connected if their mutual
distance is smaller than a fixed static threshold; two
3D points belonging to subsequent frames are con-
nected when their mutual distance is smaller than a
fixed dynamic threshold. The (3D + 1) cloud is now
interpreted as a graph and it is clustered by using any
Connected Components Labeling (CCL) technique
(Stockman and Shapiro, 2001).
Fig.2 shows the situation represented by two mov-
ing objects never in physical 3D proximity, but oc-
cluded for a few frames in two of the three cameras.
In this case, the CCL technique successfully separates
the two identities, overcoming the optical occlusion.
We stress that this is exactly the case that needs to be
tackled by multi-path branching and set-cover tech-
niques by other methods, which requires solving an
NP-hard problem. Within Prometheus, on the other
hand, this case is solved by CCL, which is merely
P complex. This advantage may seem minor in the
schematic case of 2 (and it is), but it becomes a sub-
stantial aid when analyzing complex data, as that pre-
sented in the next Section.
When the two targets are in 3D proximity for a
few frames (occlusion in all cameras Fig.3), some 3D
points of one target are linked in both space and time
to 3D points of the other target, connecting the two 3D
volumes corresponding to the different targets, Fig3a.
Hence, in this case the CCL algorithm produces one
single connected component and it fails to solve the
occlusion, as shown in Fig.3b. For this reason we
need to resort to a more sophisticated clustering tech-
nique.
4 - Normalized Cut Spectral Clustering
(NCSC). Consider the schematic case of Fig.3, where
two targets get in 3D proximity for a few frames. The
two 3D volumes describing the spatio-temporal evo-
lution of the two targets are connected by a few links
concentrated around those few frames, while they are
well separated in all the other frames. This suggests
to use both spatial and temporal information to dis-
card links connecting the two different targets, divid-
ing the original cluster into two different connected
components, each representing the dynamic evolution
of one target. The cumulative weakness of the links
connecting the different targets is the key motive to
solve 3D proximity occlusions by spectral clustering.
We work with a technique based on the Normal-
ized Cut Spectral Clustering (NCSC) method intro-
duced in (Shi and Malik, 2000). The NCSC approach
is a substantial improvement on the Minimum Cut
(MC) criterion (Cormen et al., 2009). MC defines
the optimal partition of a graph as the one obtained
by cutting across the minimum number of links; this
favours the formation of small sets of isolated nodes
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
684
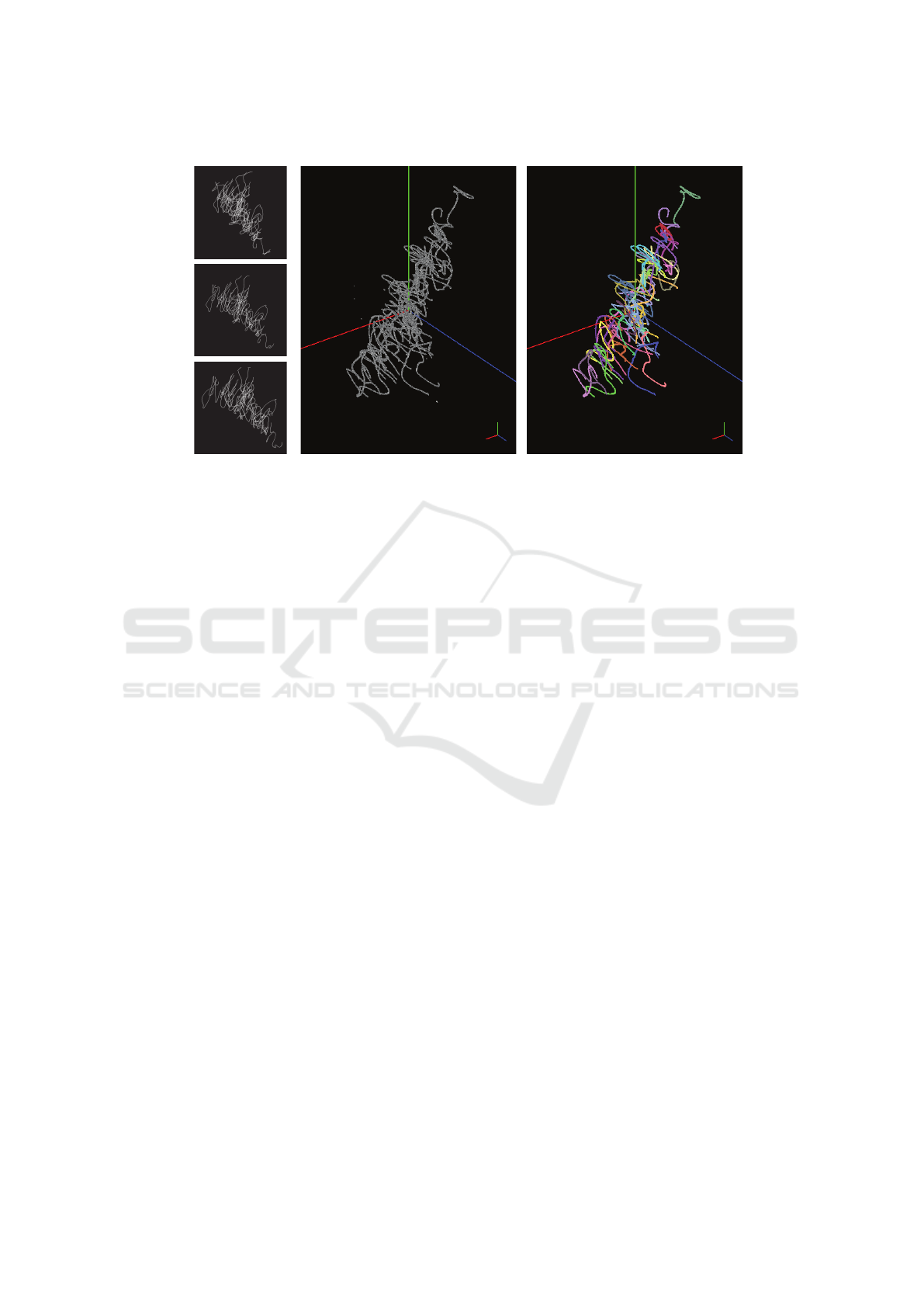
View 1
View 2
View 3
3D+1 cloud
a)
CCL
b)
Figure 4: Test on semi-natural data. Left: temporal evolution of a swarm of 42 midges for 200 frames in the three different
cameras; (a) the (3D + 1) clouds of points; (b) the result of Prometheus.
in the graph. NCSC, on the other hand, optimizes the
balance between cutting a small number of links and
keeping the two clusters as even as possible in terms
of points mass. This means that NCSC will try to min-
imize link-cutting while maximizing the equivalence
in size of the output clusters.
This spirit of NCSC seems very well suited to
deal with the problem of splitting different trajecto-
ries (Fig.3). In general, we want to track a group of
targets all of similar size and shape (which is exactly
the reason why we cannot perform the much-easier
feature-based tracking), evolving for the same num-
ber of frames. For this reason, we expect that differ-
ent targets occupy similar spatio-temporal volumes,
so that NCSC, with its emphasis on creating balanced
clusters, will divide them into the correct trajectories.
We apply NCSC to each multi-object cluster un-
split by CCL due to 3D proximity; we overcome the
NP-complete complexity of NCSC by embedding it in
the real values domain, thus finding a discrete approx-
imation of the optimal solution in polynomial time
(Shi and Malik, 2000). In this respect, we deal with
hard 3D proximity occlusions similarly to what for-
mer methods deal with simple optical occlusions: we
formulate the problem in terms of NP optimization,
whose complexity is then tamed through a P approxi-
mated solution.
As shown in the schematic case of Fig.3c, the nor-
malized cut finds the two correct connected compo-
nents and the two corresponding trajectories are thus
correctly retrieved.
4 TESTING THE ALGORITHM
We performed tests of Prometheus on a semi-natural
data set. We do this (instead of working directly on
raw natural data) in order to have at the same time a
biologically realistic data set and a ground truth with
which comparing our results. Experimental data on
midge swarms (Attanasi et al., 2014), are tracked us-
ing the algorithm described in (Attanasi et al., 2015));
the resulting 3D trajectories are smoothed with 7
points interpolation; moreover, the frame rate is dou-
bled, passing from 170 fps to 340 fps linearly inter-
polating any pair of points. A system of three pinhole
cameras is simulated with the OpenGL library and at
each instant of time the 3D position of each target is
projected on the three sensors. Targets are monochro-
matic spheres of fixed radius, imaged as discs with
Gaussian intensity profile. This procedure results in
a set of images for each of the three cameras, which
is given as an input to Prometheus, together with the
trifocal tensor computed from the mutual positions of
the three cameras (Hartley and Zisserman, 2004).
Fig.4 shows the result of Prometheus on a semi-
natural swarm of 42 midges tracked for 200 frames.
Prometheus successfully solved all the 2D optical oc-
clusions, producing 29 isolated clusters correspond-
ing to the insects which are never occluded in all the
cameras at the same instant of time. We compared
these trajectories with the ground truth and checked
that they are correct. We remark that this result is
achieved without the need of any set-cover technique.
Another 6 clusters produced by CCL correspond
Towards a Tracking Algorithm based on the Clustering of Spatio-temporal Clouds of Points
685

to hybridised objects due to cases of 3D proximity,
which should be tackled again by the NCSC rou-
tine. However occlusions in semi-natural datasets last
longer than the ones the NCSC algorithm can cur-
rently solve, since some temporal constraints are still
not implemented (see next Section).
5 FUTURE WORK
Prometheus can solve 3D proximity occlusions last-
ing a few frames, but it currently does not handle
long-term proximity problems. Fig.5 is a schematic
representation of what may happen during a long-
term 3D proximity occlusion. Two (3D + 1) clouds,
represented as the green and the blue lines, are well
separated except for those frames where the occlusion
occurs; the resulting cloud of points is represented in
the figure as the black circle. The NCSC routine has
to find the partition which minimizes the weight of
the discarded links while maximizing the similarity
on the volumes occupied by the two resulting clusters.
Depending on the time duration of the 3D proxim-
ity, it can either be more convenient for NCSC to cut
along c
1
(correct choice) or along c
2
(wrong choice).
t
a) b)
c1
c2
c1
c2
Figure 5: Long-term 3D proximity. Two (3D + 1) clouds
well separated in time and space, represented in figure as
the green and the blue lines, form an optical occlusion in all
the cameras, due to long-term 3D proximity (black circle in
figure). The dashed lines c
1
and c
2
depicts the two potential
cuts evaluated by the NCSC algorithm. In absence of any
bias differentiating time from space, the choice of the cut
arbitrarily depends on the duration of the 3D proximity.
This happens because, at its present state, the
NCSC module of Prometheus does not differenti-
ate between spatial and temporal dimension: cutting
along time or space does not make any difference,
provided that a right balance between links and mass
is found. Of course, this does not need to be the case:
time has a privileged status in the problem, so that a
priori a cut longitudinal in time has to be preferred
over one transverse in time. Hence, we plan to in-
troduce a time bias in the NCSC linking and splitting
algorithm to overcome this problem.
Secondly, proximity links based on a metric dis-
tance are suitable when the displacement of a single
individual between two consecutive frames is smaller
than the inter objects distance. This limitation can
be overcome speeding up the frame rate. However,
in practice this solution is not always feasible and
we are planning to introduce dynamic predictors in
Prometheus in order to give more robust definition of
temporal links.
6 CONCLUSIONS
Current state-of-the-art tracking algorithms are able
to overcome 2D optical occlusions formulating a NP-
hard weighted set-cover problem, while they are not
able to solve occlusions due to actual 3D proximity.
We presented a new 3D tracking algorithm – name:
Prometheus – that significantly improves this state of
affairs.
Prometheus works directly in 3D, retrieving the
spatio-temporal volume occupied by each target in
(3D + 1) dimensions. It solves 2D occlusions
making use of a linear time connected components
labeling routine, while it overcomes 3D proximity
through a spectral clustering technique based on the
NP-complete normalized cut. In this way, Prometheus
makes NP-Complete what is currently considered im-
possible (actual 3D proximity), while making P what
is currently NP-hard (2D occlusions).
Preliminary tests on a semi-natural data set of in-
sect swarms were performed to check the validity of
the method. These tests confirmed our expectations,
showing that the labeling technique together with the
normalized cut approach is a promising new direction
for a new generation of 3D tracking algorithm.
ACKNOWLEDGEMENTS
This work was supported by the following grants: IIT
– Seed Artswarm; ERC–StG No. 257126; and US-
AFOSR No. FA95501010250 (through the Univer-
sity of Maryland). We thank Irene Giardina for dis-
cussions.
REFERENCES
Attanasi, A., Cavagna, A., Del Castello, L., Giardina, I.,
Jelic, A., Melillo, S., Parisi, L., Pellacini, F., Shen, E.,
Silvestri, E., et al. (2015). Greta - a novel global and
recursive tracking algorithm in three dimensions. Pat-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
686

tern Analysis and Machine Intelligence, IEEE Trans-
actions on, (99).
Attanasi, A., Cavagna, A., Del Castello, L., Giardina, I.,
Melillo, S., Parisi, L., Pohl, O., Rossaro, B., Shen, E.,
Silvestri, E., et al. (2014). Collective behaviour with-
out collective order in wild swarms of midges. PLoS
computational biology, 10(7):e1003697.
Butail, S., Paley, D., et al. (2010). 3d reconstruction of
fish schooling kinematics from underwater video. In
Robotics and Automation (ICRA), 2010 IEEE Interna-
tional Conference on, pages 2438–2443. IEEE.
Cheng, X. E., Qian, Z.-M., Wang, S. H., Jiang, N., Guo, A.,
and Chen, Y. Q. (2015). A novel method for tracking
individuals of fruit fly swarms flying in a laboratory
flight arena. PloS one, 10(6):e0129657.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to Algorithms, Third Edition.
The MIT Press, 3rd edition.
Dell, A. I., Bender, J. A., Branson, K., Couzin, I. D.,
de Polavieja, G. G., Noldus, L. P., P
´
erez-Escudero, A.,
Perona, P., Straw, A. D., Wikelski, M., et al. (2014).
Automated image-based tracking and its application
in ecology. Trends in ecology & evolution, 29(7):417–
428.
Ess, A., Schindler, K., Leibe, B., and Van Gool, L. (2010).
Object detection and tracking for autonomous navi-
gation in dynamic environments. The International
Journal of Robotics Research, 29(14):1707–1725.
Giardina, I. (2008). Collective behavior in animal groups:
theoretical models and empirical studies. HFSP jour-
nal, 2(4):205–219.
Hampapur, A., Brown, L., Connell, J., Ekin, A., Haas, N.,
Lu, M., and Pankanti, S. (2005). Smart video surveil-
lance: exploring the concept of multiscale spatiotem-
poral tracking. Signal Processing Magazine, IEEE,
22(2):38–51.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, ISBN: 0521540518, second edition.
Michel, P., Chestnutt, J., Kagami, S., Nishiwaki, K.,
Kuffner, J., and Kanade, T. (2007). Gpu-accelerated
real-time 3d tracking for humanoid locomotion and
stair climbing. In Intelligent Robots and Systems,
2007. IROS 2007. IEEE/RSJ International Conference
on, pages 463–469. IEEE.
Moussaid, M., Guillot, E. G., Moreau, M., Fehren-
bach, J., Chabiron, O., Lemercier, S., Pettr
´
e, J.,
Appert-Rolland, C., Degond, P., and Theraulaz, G.
(2012). Traffic instabilities in self-organized pedes-
trian crowds. PLoS Comput. Biol, 8(3):e1002442.
Ouellette, N. T., Xu, H., and Bodenschatz, E. (2006).
A quantitative study of three-dimensional lagrangian
particle tracking algorithms. Experiments in Fluids,
40(2):301–313.
P
´
erez-Escudero, A., Vicente-Page, J., Hinz, R. C., Arganda,
S., and de Polavieja, G. G. (2014). idtracker: tracking
individuals in a group by automatic identification of
unmarked animals. Nature methods, 11(7):743–748.
Puckett, J. G., Kelley, D. H., and Ouellette, N. T. (2014).
Searching for effective forces in laboratory insect
swarms. Scientific reports, 4.
Shi, J. and Malik, J. (2000). Normalized cuts and image
segmentation. Pattern Analysis and Machine Intelli-
gence, IEEE Transactions on, 22(8):888–905.
Sobral, A. and Bouwmans, T. (2014). Bgs library:
A library framework for algorithms evaluation in
foreground/background segmentation. In Back-
ground Modeling and Foreground Detection for Video
Surveillance. CRC Press, Taylor and Francis Group.
Stockman, G. and Shapiro, L. G. (2001). Computer Vision.
Prentice Hall PTR, Upper Saddle River, NJ, USA, 1st
edition.
Straw, A. D., Branson, K., Neumann, T. R., and Dick-
inson, M. H. (2010). Multi-camera real-time three-
dimensional tracking of multiple flying animals. Jour-
nal of The Royal Society Interface, page rsif20100230.
Vacchetti, L., Lepetit, V., and Fua, P. (2004). Combining
edge and texture information for real-time accurate 3d
camera tracking. In Mixed and Augmented Reality,
2004. ISMAR 2004. Third IEEE and ACM Interna-
tional Symposium on, pages 48–56. IEEE.
Wu, Z., Hristov, N. I., Kunz, T. H., and Betke, M.
(2009). Tracking-reconstruction or reconstruction-
tracking? comparison of two multiple hypothesis
tracking approaches to interpret 3d object motion
from several camera views. In Motion and Video Com-
puting, 2009. WMVC’09. IEEE Workshop on, pages
1–8. IEEE.
Wu, Z., Kunz, T. H., and Betke, M. (2011). Efficient track
linking methods for track graphs using network-flow
and set-cover techniques. In Computer Vision and Pat-
tern Recognition (CVPR), 2011 IEEE Conference on,
pages 1185–1192. IEEE.
Towards a Tracking Algorithm based on the Clustering of Spatio-temporal Clouds of Points
687
