Efﬁcient Evidence Accumulation Clustering for Large Datasets

Diogo Silva

, Helena Aidos

and Ana Fred

Portuguese Air Force Academy, Sintra, Portugal

Instituto de Telecomunicac

oes, Instituto Superior T

ecnico, Lisboa, Portugal

Keywords:

Clustering Methods, EAC, K-Means, MST, GPGPU, CUDA, Sparse Matrices, Single-Link.

Abstract:

The unprecedented collection and storage of data in electronic format has given rise to an interest in automated

analysis for generation of knowledge and new insights. Cluster analysis is a good candidate since it makes as

few assumptions about the data as possible. A vast body of work on clustering methods exist, yet, typically,

no single method is able to respond to the speciﬁcities of all kinds of data. Evidence Accumulation Clustering

(EAC) is a robust state of the art ensemble algorithm that has shown good results. However, this robustness

comes with higher computational cost. Currently, its application is slow or restricted to small datasets. The

objective of the present work is to scale EAC, allowing its applicability to big datasets, with technology

available at a typical workstation. Three approaches for different parts of EAC are presented: a parallel GPU

K-Means implementation, a novel strategy to build a sparse CSR matrix specialized to EAC and Single-Link

based on Minimum Spanning Trees using an external memory sorting algorithm. Combining these approaches,

the application of EAC to much larger datasets than before was accomplished.

1 INTRODUCTION

The amount and variety of data that exists today has

sparked the interest in automated analysis for gener-

ation of knowledge. Thus, clustering algorithms are

useful to explore the structure of data by organizing it

into clusters. Many clustering algorithms exist (Jain,

2010), but usually they are data dependent. Inspired

by the work on sensor fusion and classiﬁer combi-

nation, ensemble approaches (Fred, 2001; Strehl and

Ghosh, 2002) have been proposed to address the chal-

lenge of clustering a wider spectrum of datasets.

The present work builds on the Evidence Accu-

mulation Clustering (EAC) framework presented by

(Fred and Jain, 2005). The underlying idea of EAC

is to take a collection of partitions, a clustering en-

semble (CE), and combine it into a single partition

of better quality. EAC has three steps: the produc-

tion of the CE, by applying e.g. K-Means, varying

number of clusters (within an interval [K

min

, K

max

]) to

create diversity; the combination of the CE into a co-

association matrix (based on co-occurrences in CE’s

clusters), which can be interpreted as a proximity ma-

trix; and, the recovery of the ﬁnal partition. Single-

Link (SL) and Average-Link have been used for the

recovery, as they operate over dissimilarity matrices.

EAC is robust, but its computational complexity

restricts its application to small datasets. Two ap-

proaches for adressing the space complexity of EAC

have been proposed: (1) exploiting the sparsity of the

co-association matrix (Lourenc¸o et al., 2010) and (2)

consider only the k-Nearest Neighbors of each pattern

in the co-association matrix. The present work aims

to scale the EAC method to large datasets, using tech-

nology found on a typical workstation, which means

optimize both speed and memory usage. Hence, we

speed-up the production of the CE by using the power

of Graphics Processing Units (GPU), deal with the

space complexity of the co-association matrix by ex-

tending the work of (Lourenc¸o et al., 2010) and use

SL to speed-up the recovery, making it applicable to

large datasets by using external memory algorithms.

2 PRODUCTION

We used NVIDIA’s Compute Uniﬁed Device Archi-

tecture (CUDA) to implement a parallel version of K-

Means for GPUs.

2.1 Programming for GPUs with CUDA

A GPU is comprised by multiprocessors. Each multi-

processors contains several simpler cores, which exe-

cute a thread, the basic unit of computation in CUDA.

Silva, D., Aidos, H. and Fred, A.

Efﬁcient Evidence Accumulation Clustering for Large Datasets.

DOI: 10.5220/0005770803670374

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 367-374

ISBN: 978-989-758-173-1

367

Threads are grouped into blocks which are part of the

block grid. The number of threads in a block is typ-

ically higher than the number of cores in a multipro-

cessor, so the threads from a block are divided into

smaller batches, called warps. The computation of

one block is independent from other blocks and each

block is scheduled to one multiprocessor, where sev-

eral warps may be active at the same time. CUDA

employs a single-instruction multiple-thread execu-

tion model (Lindholm et al., 2008), where all threads

in a block execute the same instruction at any time.

GPUs have several memories, depending on the

model. Accessible to all cores are the global mem-

ory, constant memory and texture memory, of which

the last two are read-only. Blocks share a smaller

but signiﬁcantly faster memory called shared mem-

ory, which resides inside the multiprocessor to which

all threads in a block have access to. Finally, each

thread has access to local memory, which resides in

global memory space and has the same latency for

read and write operations.

2.2 Parallel K-Means

Several parallel implementations of K-Means for

GPU exist in the literature (Zechner and Granitzer,

2009; Sirotkovi et al., 2012) and all report speed-

ups relative to their sequential counterparts. Our im-

plementation was programmed in Python using the

Numba CUDA API, following the version of Zech-

ner and Granitzer (2009), with the difference that we

do not use shared memory. We parallelize the label-

ing step, which was further motivated from empirical

data suggesting that, on average, 98% of the time was

spent in the labeling step. Our implementation starts

by transferring the data to the GPU (pattern set and

initial centroids) and allocates space in the GPU for

the labels and distances from patterns to their closest

centroids. Initial centroids are chosen randomly from

the dataset and the dataset is only transferred once.

As shown in Algorithm 1, each GPU thread will com-

pute the closest centroid to each point of its corre-

sponding set, X

T hreadID

, of 2 data points (2 points per

thread proved to yield the highest speed-up). The la-

bels and corresponding distances are stored in arrays

and sent back to the host afterwards for the computa-

tion of the new centroids. The implementation of the

centroid recomputation, in the CPU, starts by count-

ing the number of patterns attributed to each centroid.

Afterwards, it checks if there are any ”empty” clus-

ters. Dealing with empty clusters is important be-

cause the target use expects that the output number

of clusters be the same as deﬁned in the input param-

eter. Centroids corresponding to empty clusters will

be the patterns that are furthest away from their cen-

troids. Any other centroid c

will be the mean of the

patterns that were labeled j. In our implementation

several parameters can be adjusted by the user, such

as the grid topology and the number of patterns that

each thread processes.

Input: dataset, centroids c

, ThreadID

Output: labels, distances

forall x

∈ X

T hreadId

labels

← arg min D(x

, c

);

distances

← D(x

, c

labels

);

end

Algorithm 1: GPU kernel for the labeling phase.

3 COMBINATION

Space complexity is the main challenge building the

co-association matrix. A complete pair-wise n ×n co-

association matrix has O(n

) complexity but can be

reduced to O(

n(n−1)

) without loss of information, due

to its symmetry. Still, these complexities are rather

high when large datasets are contemplated, since it

becomes infeasible to ﬁt these co-association matri-

ces in the main memory of a typical workstation.

(Lourenc¸o et al., 2010) approaches the problem by

exploiting the sparse nature of the co-association ma-

trix, but does not cover the efﬁciency of building a

sparse matrix or the overhead associated with sparse

data structures. The effort of the present work was fo-

cused on further exploiting the sparse nature of EAC,

building on previous insights and exploring the topics

that literature has neglected so far.

Building a non-sparse matrix is easy and fast since

the memory for the whole matrix is allocated and in-

dexing the matrix is direct. When using sparse ma-

trices, neither is true. In the speciﬁc case of EAC,

there is no way to know what is the number of as-

sociations the co-association matrix will have which

means it is not possible to pre-allocate the memory to

the correct size of the matrix. This translates in al-

locating the memory gradually which may result in

fragmentation, depending on the implementation, and

more complex data structures, which incurs signiﬁ-

cant computational overhead. For building a matrix,

the DOK (Dictionary of Keys) and LIL (List of Lists)

formats are recommended in the documentation of the

SciPy (Jones et al., 2001) scientiﬁc computation li-

brary. These were brieﬂy tested on simple EAC prob-

lems and not only was their execution time several or-

ders of magnitude higher than a traditional fully allo-

cated matrix, but the overhead of the sparse data struc-

tures resulted in a space complexity higher than what

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

368

would be needed to process large datasets. For oper-

ating over a matrix, the documentation recommends

converting from one of the previous formats to CSR

(Compressed Sparse Row). Building with the CSR

format had a low space complexity but the execution

time was much higher than any of the other formats.

Failing to ﬁnd relevant literature on efﬁciently build-

ing sparse matrices, we designed and implemented a

novel strategy for building a CSR matrix specialized

to the EAC context, the EAC CSR.

3.1 Underlying Structure of EAC CSR

EAC CSR starts by making an initial assumption on

the maximum number of associations max assocs that

each pattern can have. A possible rule is 3 ×bgs

where bgs is the biggest cluster size in the ensem-

ble. The biggest cluster size is a good heuristic for

trying to predict the number of associations, since it

is the limit of how many associations each pattern will

have in any partition of the clustering ensemble. Fur-

thermore, one would expect that the neighbors of each

pattern will not vary signiﬁcantly, i.e. the same neigh-

bors will be clustered together repeatedly in many

partitions. This scheme for building the matrix uses

4 supporting arrays (n is the number of patterns):

• Indices - stores the columns of each non-zero

value of the matrix;

• Data - stores all the non-zero association values;

• Indptr - the i-th element is the pointer to the ﬁrst

non-zero value of the i-th row;

• Degree - stores the number of non-zero values of

each row.

The ﬁrst two arrays have a length of n ×

max assocs, while the last two have a length of n.

Each pattern (row) has a maximum of max assocs

pre-allocated that it can use to ﬁll with new associ-

ations and discards associations that exceed it. The

degree array keeps track of the number of associa-

tions of each pattern. Throughout this section, the

interval of the indices array corresponding to a spe-

ciﬁc pattern is referred to as that pattern’s indices in-

terval. The end of the indices interval refers to the

beginning of the part of the interval that is free for

new associations. The term ”indices” can refer to the

aforementioned array (indices) or the plural of index

(indices). Furthermore, this method assumes that the

clusters received come sorted in a increasing order.

3.2 Updating the Matrix with Partitions

The ﬁrst partition is inserted in a special way. Since it

is the ﬁrst and the clusters are sorted, it is a matter of

copying the cluster to the indices interval of each of

its member patterns, excluding self-associations. The

data array is set to 1 on the positions where the asso-

ciations were added. Because it is the fastest partition

to be inserted, when the whole ensemble is provided

at once, the ﬁrst partition is picked to be the one with

the least amount of clusters (more patterns per cluster)

so that each pattern gets the most amount of associa-

tions in the beginning (on average). This increases

the probability that any new cluster will have more

patterns that correspond to established associations.

For the remaining partitions, the process is differ-

ent. For each pattern in a cluster it is necessary to add

or increment the association to every other pattern in

the cluster. However, before adding or incrementing

any new association, it is necessary to check if it al-

ready exists. This is done using a binary search in

the indices interval. This is necessary because it is

not possible to index directly a speciﬁc position of a

row in the CSR format. Since a binary search is per-

formed (ns −1)

times for each cluster, where ns is

the number of patterns in any given cluster, the in-

dices of each pattern must be in a sorted state at the

beginning of each partition insertion.

3.3 Keeping the Indices Sorted

The implemented strategy results from the observa-

tion that, if one could know in which position each

new association should be inserted, it would be pos-

sible to move all old associations to their ﬁnal sorted

positions and insert the new ones in an efﬁcient man-

ner with minimum number of comparisons (and thus

branches in the execution of the code). For this end,

the implemented binary search returns the index of

the searched value (key) if it is found or the index for

a sorted insertion of the key in the array, if it is not

found. New associations are stored in two auxiliary

arrays of size max assocs: one (new assoc ids) for

storing the patterns of the associations and the other

(new assoc idx) to store the indices where the new as-

sociations should be inserted (the result of the binary

search). This is illustrated with an example in Fig. 1.

The binary search operation requires each pat-

tern’s indices interval to be sorted. Accordingly, new

associations corresponding to each pattern are added

in a sorted manner. The sorting mechanism looks at

the insertion indices of two consecutive new associ-

ations in the new assoc idx array, starting from the

end. Whenever two consecutive insertion indices are

Efﬁcient Evidence Accumulation Clustering for Large Datasets

369

Figure 1: Inserting a cluster from a partition in the co-

association matrix. The arrows indicate to where the indices

are moved. The numbers indicate the order of the operation.

not the same, it means that old associations must be

moved as seen in the example. More speciﬁcally,

if the i-th element of the new assoc idx array, a, is

greater than the (i −1)-th element, b, then all the old

associations in the index interval [a, b[ are shifted to

the right by i positions. The i-th element will never

be smaller than the (i −1)-th because clusters are

sorted. Afterwards, or when two consecutive inser-

tion indices are the same, the (i −1)-th element of the

new assoc ids is inserted in the position indicated by

a pointer, o ptr. The o ptr pointer is initiazed with the

number of old associations plus the number of new

asociations and is decremented anytime an associa-

tion is moved or inserted. This showed to be roughly

twice as fast as using an implementation of quicksort.

3.4 EAC CSR Condensed

A further reduction of space complexity in the EAC

CSR scheme is possible by building only the up-

per triangular, since this completely describes the co-

association matrix. Thus, the amount of associations

decreases as one goes further down the matrix. In-

stead of pre-allocating the same amount of associa-

tions for each pattern, the pre-allocation follows the

same pattern of the number of associations, effec-

tively reducing the space complexity. The strategy

used was a linear one, where the ﬁrst 5% of patterns

have access to 100% of the estimated maximum num-

ber of associations, the last pattern has access to 5%

of that value and the number available for the patterns

in between decreases linearly from 100% to 5%.

4 RECOVERY

We used Single-Link (SL) for the recovery of the ﬁ-

nal partition. SL typically works over a pair-wise dis-

similarity matrix. An interesting property of SL is its

equivalence with a Minimum Spanning Tree (MST)

(Gower and Ross, 1969). In the context of EAC, the

edges of the MST are the co-associations between the

patterns and the vertices are the patterns themselves.

An MST contains all the information necessary to

build a SL dendrogram. One of the advantages of us-

ing an MST based clustering is that it processes only

non-zero values while a typical SL algorithm will pro-

cess all pair-wise proximities, even if they are null.

4.1 Kruskal’s Algorithm

Kruskal’s algorithm was used for computing the MST.

Kruskal (1956) described three constructs for ﬁnding

a MST, one of which is implemented efﬁciently in the

SciPy library (Jones et al., 2001): ”Among the edges

of G not yet chosen, choose the shortest edge which

does not form any loops with those edges already cho-

sen. Clearly the set of edges eventually chosen must

form a spanning tree of G, and in fact it forms a short-

est spanning tree.” This is done as many times as pos-

sible and if the graph G is connected, the algorithm

will stop before processing all edges when |V |− 1

edges are added to the MST, where V is the set of

edges. This implementation works on a CSR matrix.

One of the main steps of the implementation

is computing the order of the edges of the graph

without sorting the edges themselves, an operation

called argsort. The argsort operation on the ar-

ray [4, 5, 2, 1, 3] would yield [3, 2, 4, 0, 1] since the the

smallest element is at position 3 (starting from 0), the

second smalled at position 2, etc. This operation is

much less time intensive than computing the shortest

edge at each iteration. However, the total space used

is typically 8 times larger for EAC since the data type

of the weights uses only one byte and the number of

associations is very large, forcing the use of an 8 byte

integer for the argsort array. This motivated the stor-

age of the co-association matrix in disk and usage of

an external sorting algorithm.

4.2 External Memory Variant

The PyTables library (Alted et al., 2002), was used

for storing the co-association matrix in graph format,

performing the external sorting for the argsort oper-

ation and loading the graph in batches for process-

ing. This implementation starts by storing the CSR

graph to disk. However, instead of saving the in-

dptr array directly, it stores an expanded version of

the same length as the indices array, where the i-th

element contains the origin vertex (or row) of the i-

th edge. This way, a binary search for discovering

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

370

the origin vertex becomes unnecessary. Afterwards,

the argsort operation is performed by building a com-

pletely sorted index (CSI) of the data array of the CSR

matrix. It should be noted that the arrays themselves

are not sorted. Instead, the CSI allows for a fast index-

ing of the arrays in a sorted manner (according to the

order of the edges). The process of building the CSI

has a low main memory usage and can be disregarded

in comparison to the co-association matrix.

The SciPy implementation of Kruskal’s algorithm

was modiﬁed to work in batches. This was imple-

mented by making the data structures used in the

building of the MST persistent between iterations.

The new variant loads the graph in batches and in a

sorted manner, starting with the shortest edges. Each

batch is processed sequentially since the edges must

be processed in a sorted manner, which means there

is no possibility for parallelism. Typically, the batch

size is a very small fraction of the size of the edges,

so the total memory usage for building the MST is

overshadowed by the size of the co-association ma-

trix. As an example, for a 500 000 vertex graph the

SL-MST approach took 54.9 seconds while the exter-

nal memory approach took 2613.5 seconds - 2 orders

of magnitude higher.

5 RESULTS

Results presented here are originated from one of

three machines, that will be referred to as Alpha,

Bravo and Charlie. The main speciﬁcations of each

machine are as follows:

• Alpha: 4 GBs of main memory, a 2 core Intel i3-

2310M 2.1GHz and a NVIDIA GT520M;

• Bravo: 32 GBs of main memory, a 6 core Intel

i7-4930K 3.4GHz and a NVIDIA Quadro K600;

• Charlie: 32 GBs of main memory, a 4 core Intel

i7-4770K 3.5GHz and a NVIDIA K40c;

5.1 GPU Parallel K-Means

Both sequential and parallel versions of K-Means

were executed over a wide spectrum of datasets vary-

ing number of patterns, features and centroids. All

tests were executed on machine Charlie and the block

size was maintained constant at 512. The sequential

version used a single thread.

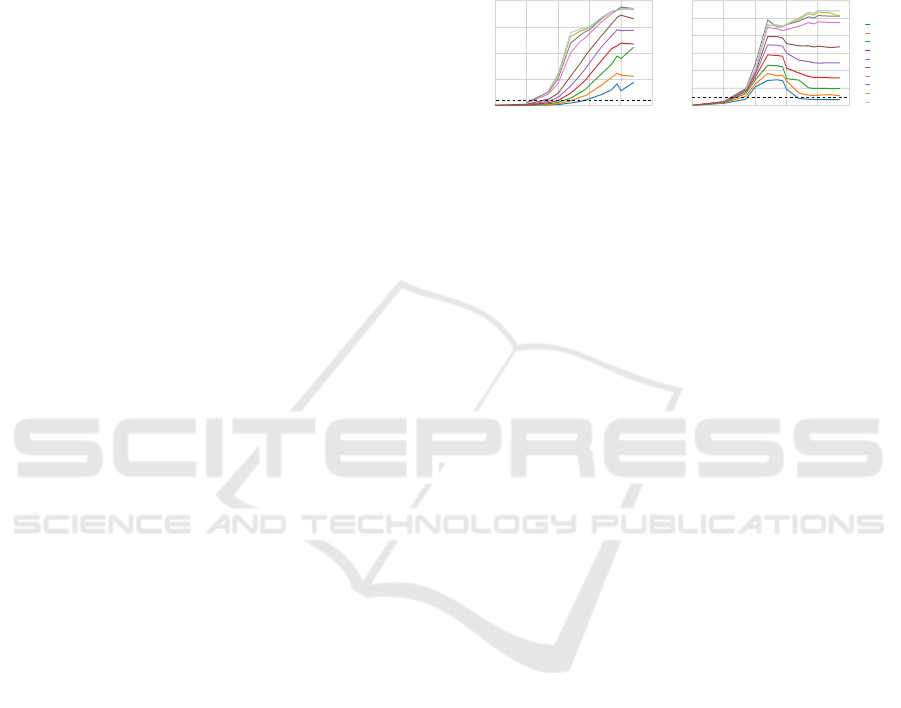
Observing Figures 2A and 2B, it is clear that the

number of patterns, features and clusters inﬂuence the

speed-up. For the simple case of 2 dimensions (Fig

2A), the speed-up increases with the number of pat-

terns. However, there is no speed-up when the overall

complexity of the datasets is low. As the complex-

ity of the problem increases (more centroids and pat-

terns), the speed-up also increases. The reason for this

is that the total amount of work increases linearly with

the number of clusters but is diluted by the number of

threads that can execute simultaneously.

Speed-up

Number of patterns

256

512

1024

2048

Number

of clusters

Speed-up

Number of patterns

(A) Datasets of 2 dimensions (B) Datasets of 200 dimensions

Figure 2: Speed-up of the labeling phase for datasets of (A)

2 dimensions and (B) 200 dimensions, when varying the

number of patterns and clusters. The dotted black line rep-

resents a speed-up of one.

For 200 dimensions (Fig. 2B), the speed-up in-

creased with both the number of patterns and clusters,

as previously. The speed-up obtained is lower than the

low dimensional case, which is consistent with liter-

ature (Zechner and Granitzer, 2009). The speed-up

decreased with an increase of the number of patterns

for a reduced number of clusters. We believe the rea-

son for this might be related to the implementation

itself. Our implementation does not use shared mem-

ory, which is fast.

5.2 Validation with Original

The results of the original version of EAC, imple-

mented in Matlab, are compared with those of the pro-

posed solution. Several small datasets, chosen from

the datasets used in (Lourenc¸o et al., 2010) and taken

from the UCI Machine Learning repository (Lichman,

2013), were processed by the two versions of EAC.

Both versions are processed from the same ensembles

since production is probabilistic, which guarantees

that the combination and recovery phases are equiv-

alent. All processing was done in machine Alpha. Ta-

ble 1 presents the difference between the accuracies

of the two versions. It is clear that the difference is

minimal, most likely due to the original version using

Matlab and the proposed using Python. Moreover, a

speed-up as low as 6 and as high as 200 was obtained

over the original version in the various steps.

5.3 Large Dataset Testing

The dataset used in the following results consists of a

mixture of 6 Gaussians, where 2 pairs are overlapped

and 1 pair is touching. This dataset was sampled into

smaller datasets to analyze different dataset sizes.

Efﬁcient Evidence Accumulation Clustering for Large Datasets

371

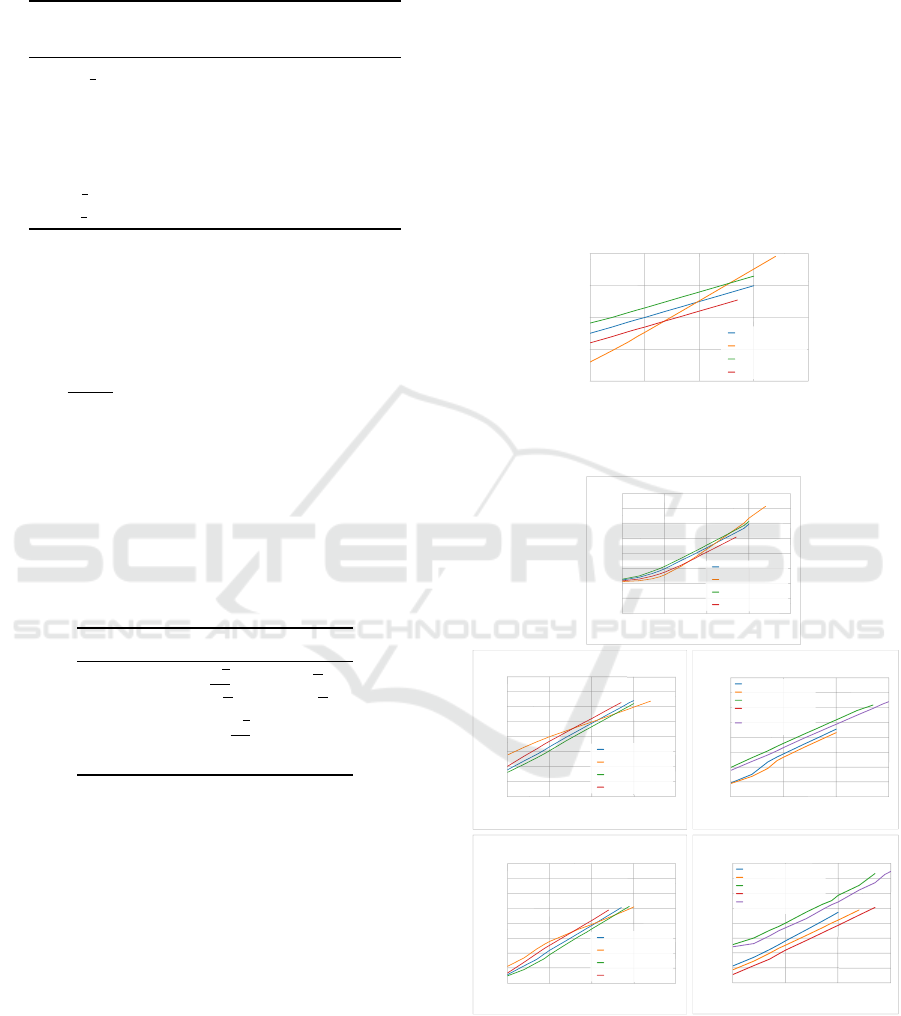
Table 1: Difference between accuracy of the two implemen-

tations of EAC, using the same ensemble. Accuracy was

measured using the H-index (Meila, 2003).

Number of clusters scheme

Dataset Fixed Lifetime

breast cancer 4.94e-06 2.82e-06

ionosphere 1.65e-06 1.45e-06

iris 3.33e-06 3.33e-06

isolet 1.03e-07 4.08e-07

optdigits 3.79e-06 1.48e-06

pima norm 4.16e-07 4.16e-07

wine norm 1.12e-07 1.91e-06

Several rules for computing the K

min

(see Table

2 for details), co-association matrix formats and ap-

proaches for the ﬁnal clustering will be mentioned.

The co-association matrix formats are: full (for fully

allocated n ×n matrix), full condensed (for a fully al-

located

n(n−1)

array to build the upper triangular ma-

trix), sparse complete (for EAC CSR), sparse con-

densed const (for EAC CSR building only the upper

triangular matrix) and sparse condensed linear (for

EAC CSR condensed). The approaches for the ﬁ-

nal clustering are SLINK (Sibson, 1973), SL-MST (for

using the Kruskal implementation in SciPy) and SL-

MST-Disk for a disk-based variant.

Table 2: Different rules for K

min

and K

max

. n is the number

of patterns and sk is the number of patterns per cluster.

Rule K

min

max

sqrt

√

2sqrt

√

n 2

√

sk=sqrt2 sk =

√

1.3K

min

sk=300 sk = 300 1.3K

min

A clustering ensemble was produced for each of

the smaller datasets and for each of the rules. From

each ensemble, co-association matrices were built. A

matrix format was not applicable if it could not ﬁt in

main memory. The ﬁnal clustering was done for each

of the matrix formats. The number of clusters was

chosen with the lifetime criteria (Fred and Jain, 2005).

SL-MST was not executed if its space complexity was

too big to ﬁt in main memory. Furthermore, the com-

bination and recovery phases were repeated several

times, so as to make the inﬂuence of any background

process less salient. For big datasets, the execution

times are big enough that the inﬂuence of background

processes is negligible. All processing was done in

machine Bravo. Similar conclusions were drawn for

a dataset with separated Gaussians.

5.3.1 Execution Times

Execution times are related with the K

min

parameter,

whose evolution is presented in Fig. 3. Rules sqrt,

2sqrt and sk=sqrt2 never intersect but rule sk = 300

intersects the others, ﬁnishing with the highest K

min

Observing Fig. 4A, one can see that the same thing

happens to the production execution time associated

with the sk = 300 rule and the inverse happens to

the combination time (Fig. 4B). A higher K

min

means

more centroids for each K-Means run to compute, so

it is not surprising that the execution time for comput-

ing the ensemble increases as K

min

increases.

Number of samples

min

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

Figure 3: Evolution of K

min

with the number of patterns for

different rules.

(A) Production of the clustering ensemble

-1

-2

-3

Time [s]

Number of samples

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

Number of samples

-1

-2

-3

Time [s]

with different matrix formats

full

full condensed

sparse complete

sparse condensed

const

sparse condensed

linear

(B) Building the co-association matrix

-1

-2

-3

Time [s]

Number of samples

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

Number of samples

-1

-2

-3

Time [s]

(E) Comparison of three methods

for extraction

(D) Extraction with SL-MST

-1

-2

-3

Time [s]

Number of samples

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

SLINK

SL-MST complete

SL-MST-Disk complete

SL-MST condensed

SL-MST-Disk

condensed

Figure 4: Execution time with different rules and variants

for: (A) production of the clustering ensemble; (B,C) build-

ing the co-association matrix; and (D,E) extraction of the

ﬁnal partition with SL.

Fig. 4C shows the execution times on a longitu-

dinal study for optimized matrix formats. It is clear

that the sparse formats are signiﬁcantly slower than

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

372

the fully allocated ones, specially for smaller datasets.

The full condensed usually takes around half the time

than the full, since it performs half the operations.

Idem for both sparse condensed compared to the

sparse complete. The discrepancy between the sparse

and full formats is due to the fact that the former needs

to do a binary search at each association update and

keep the internal sparse data structure sorted.

The clustering times of the different methods of

SL discussed previously (SLINK, SL-MST and SL-

MST-Disk) are presented in Figures 4D and 4E. As

expected, the SL-MST-Disk method is signiﬁcantly

slower than any of the other methods, since it uses

the hard drive which has very slow access times

compared to main memory. SL-MST is faster than

SLINK, since it processes zero associations while SL-

MST takes advantage of a graph representation and

only processes the non-zero associations. In resem-

blance to what happened with combination times, the

condensed variants take roughly half the time as their

complete counterparts, since SL-MST and SL-MST-

Disk over condensed co-association matrices only

process half the number of associations. Although

this is not depicted, SLINK takes roughly the same

time for every rule, which means K

min

has no inﬂu-

ence because SLINK processes the whole matrix, re-

gardless of its association sparsity. The same rationale

can be applied to SL-MST, where different rules can

inﬂuence execution times, since they change the to-

tal number of associations. As with the combination

phase, the sk=300 rule started with the greatest exe-

cution time and decreased as the number of patterns

increased until it was the fastest.

The total execution times presented in Fig. 5 are

for the sparse condensed linear format but the oth-

ers follow the same pattern. When using the SL-MST

method in the recovery phase, the execution time for

three of the rules do not differ much. This is due to

a balancing between a slow down of the production

phase and a speed up of the combination and recovery

phases as K

min

increases at a higher rate for sk = 300

than for other rules. This is not observed for the sqrt

rule as K

min

is always low enough that the total time

is always dominated by the combination and recov-

ery phases. However, when using the SL-MST-Disk

method, the total time is dominated by the recovery

phase. This is clear, since the results in Fig. 5B fol-

low the tendency presented in Fig. 4D.

5.3.2 Association Density

The aforementioned sparse nature of EAC is clear in

Fig. 6A. This ﬁgure shows the association density, i.e.

number of associations relative to the n

associations

in a full matrix. The full condensed has, roughly, a

Number of samples

-1

Time [s]

(A) Recovery phase with SL-MST (B) Recovery phase with SL-MST-Disk

Number of samples

-1

Time [s]

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

Figure 5: Execution times for all phases combined, using

(A) SL-MST and (B) SL-MST-Disk in the recovery phase.

constant density of 50%. Idem for all sparse formats,

as long as no associations are discarded. The den-

sity should decrease as the number of patterns of the

dataset increases, since the full matrix grows quadrat-

ically. Besides, it would be expected that the same as-

sociations would be grouped together more frequently

in partitions and make previous connections stronger

instead of creating new ones, if the relationship be-

tween the number of patterns and K

min

is constant.

Number of samples

-1

-2

-3

Density

1.0

(B) Relationship between max. number

associations and biggest cluster size

Number of samples

-4

1.4

1.8

2.2

2.6

(A) Density of associations relative

to full matrix

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

2sqrt

sk=300, th=30%

sk=sqrt2, th=30%

sqrt

max number biggest

associations / cluster size

Figure 6: (A) Density of associations relative to the full co-

association matrix, which hold n

associations. (B) Maxi-

mum number of associations of any pattern divided by the

number of patterns in the biggest cluster of the ensemble.

Predicting the number of associations is useful for

designing combination schemes that are both memory

and speed efﬁcient. Fig. 6B presents the ratio between

the biggest cluster size and the maximum number of

associations of any pattern. This ratio increases with

the number of patterns, but never exceeds 3. However,

the number of features of the used datasets is small. It

might be the case that this ratio would increase with

the number of features, since there would be more de-

grees where the clusters might include other neigh-

bors. Thus, further studies with a wider spectrum of

datasets should yield more enlightening conclusions.

5.3.3 Space Complexity

The allocated space for the space formats is based on

a prediction that uses the biggest cluster size of the

ensemble. This allocated space is usually more than

what is necessary to store the total number of associa-

tions, to keep a safety margin. Furthermore, the CSR

format, on which the EAC CSR strategy is based, re-

quires an array of the same size of the predicted num-

ber of associations. Still, the allocated number of as-

sociations becomes a very small fraction compared

Efﬁcient Evidence Accumulation Clustering for Large Datasets

373

to the full matrix as the dataset complexity increases,

which is the typical case for using a sparse format.

The actual memory used is presented in Fig. 7. The

data types inﬂuence signiﬁcantly the required mem-

ory. The associations can be stored in a single byte,

since the number of partitions is usually less than 255.

This means that the memory used by the fully allo-

cated formats is n

and

n(n−1)

Bytes for the complete

and condensed versions, respectively. In the sparse

formats, the values of the associations are also stored

in an array of unsigned integers of 1 Byte. However,

an array of integers of 4 bytes of the same size must

also be kept to keep track of the destination pattern

each association belongs to. One other array of inte-

gers of 8 bytes is kept but it is negligible compared to

the other two arrays. The impact of the data types can

be seen for smaller datasets where the total memory

used is actually signiﬁcantly higher than that of the

full matrix. It should be noted that this discrepancy is

not as high for other rules as for sk = 300. Still, the

sparse formats, and in particular the condensed sparse

format, are preferred since the memory used for large

datasets is a small fraction of what would be neces-

sary if using any of the fully allocated formats.

-1

-2

Number of samples

Density

full

full condensed

sparse complete

sparse condensed const

sparse condensed linear

-3

Figure 7: Memory used relative to the full n

matrix. The

sparse complete and sparse condensed const curves are

overlapped.

6 CONCLUSIONS

The main goal of scaling the EAC method for larger

datasets than was previously possible was achieved.

The EAC method is composed by three steps and, to

scale the whole method, each step was optimized sep-

arately. In the process, EAC was also optimized for

smaller datasets. In essence, the main contributions

to the EAC method, by step, were the GPU parallel

K-Means, the EAC CSR strategy and the SL-MST-

Disk. New rules for K

min

were tested and the effects

that these rules have on other properties of EAC were

studied. Together, these contributions allow for the

application of EAC to datasets whose complexity was

not handled by the original implementation.

Further work involves a thorough evaluation in

real world problems. Additional work may include

further optimization of the Parallel GPU K-means by

using shared memory and a better sorting of the co-

association graph in SL-MST-Disk.

ACKNOWLEDGEMENTS

This work was supported by the Portuguese Founda-

tion for Science and Technology, scholarship num-

ber SFRH/BPD/103127/2014, and grant PTDC/EEI-

SII/7092/2014.

REFERENCES

Alted, F., Vilata, I., and Others (2002). PyTables: Hierar-

chical Datasets in Python.

Fred, A. (2001). Finding consistent clusters in data parti-

tions. Multiple classiﬁer systems, pages 309–318.

Fred, A. N. L. and Jain, A. K. (2005). Combining multiple

clusterings using evidence accumulation. IEEE Trans.

Pattern Anal. Mach. Intell., 27(6):835–850.

Gower, J. C. and Ross, G. J. S. (1969). Minimum Spanning

Trees and Single Linkage Cluster Analysis. Journal

of the Royal Statistical Society, 18(1):54–64.

Jain, A. K. (2010). Data clustering: 50 years beyond K-

means. Pattern Recognition Letters, 31(8):651–666.

Jones, E., Oliphant, T., Peterson, P., and Others (2001).

SciPy: Open source scientiﬁc tools for Python.

Lichman, M. (2013). {UCI} Machine Learning Repository.

Lindholm, E., Nickolls, J., Oberman, S., and Montrym, J.

(2008). Nvidia tesla: A uniﬁed graphics and comput-

ing architecture. IEEE micro, (2):39–55.

Lourenc¸o, A., Fred, A. L. N., and Jain, A. K. (2010). On the

scalability of evidence accumulation clustering. Proc.

- Int. Conf. on Pattern Recognition, 0:782–785.

Meila, M. (2003). Comparing clusterings by the variation

of information. Learning theory and Kernel machines,

Springer:173–187.

Sibson, R. (1973). SLINK: an optimally efﬁcient algo-

rithm for the single-link cluster method. The Com-

puter Journal, 16(1):30–34.

Sirotkovi, J., Dujmi, H., and Papi, V. (2012). K-means im-

age segmentation on massively parallel GPU architec-

ture. In MIPRO 2012, pages 489–494.

Strehl, A. and Ghosh, J. (2002). Cluster Ensembles – A

Knowledge Reuse Framework for Combining Multi-

ple Partitions. J. Mach. Learn. Res., 3:583–617.

Zechner, M. and Granitzer, M. (2009). Accelerating k-

means on the graphics processor via CUDA. In IN-

TENSIVE 2009, pages 7–15.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

374