Processing Magnetic Resonance Image Features with One-class

Support Vector Machines

Investigation of the Autism Spectrum Disorder Heterogeneity

Ilaria Gori

1,2

, Alessia Giuliano

1,3

, Piernicola Oliva

2,4

, Michela Tosetti

, Filippo Muratori

Sara Calderoni

and Alessandra Retico

Istituto Nazionale di Fisica Nucleare, Sezione di Pisa, Pisa, Italy

Dipartimento di Chimica e Farmacia, Università di Sassari, Sassari, Italy

Dipartimento di Fisica, Università di Pisa, Pisa, Italy

Istituto Nazionale di Fisica Nucleare, Sezione di Cagliari, Monserrato, Italy

IRCCS Stella Maris, Pisa, Italy

Keywords: Image Processing, Feature Classification, One-class Support Vector Machine, Brain Magnetic Resonance

Imaging (MRI), Autism Spectrum Disorders.

Abstract: Support Vector Machine (SVM) classifiers are widely used to analyse features extracted from brain MRI

data to identify useful biomarkers of pathology in several disease conditions. They are trained to distinguish

patients from healthy control subjects by making a binary classification of image features extracted by

image processing algorithms. This task is particularly challenging when dealing with psychiatric disorders,

as the reported neuroanatomical alterations are often very small and quite un-replicated within different

studies. Subtle signs of pathology are difficult to catch especially in extremely heterogeneous conditions

such as Autism Spectrum Disorders (ASD). We propose the use of the One-Class Classification (OCC) or

Data Description method that, in contrast with two-class classification, is based on a description of one class

of objects only. Then, new examples are tested for their similarity to the examples of this target class, end

eventually considered as outliers. The application of the OCC to features extracted from brain MRI of

children affected by ASD and control subjects demonstrated that a common pattern of features characterize

the ASD population.

1 INTRODUCTION

Several post-processing methods to analyse brain

Magnetic Resonance Imaging (MRI) data have been

developed and implemented so far to obtain

diagnostic models of pathology and useful disease

biomarkers. Machine-learning techniques, e.g. those

based on support vector machines (SVMs) (Vapnik,

1995), have been shown to be valuable tools to make

predictive diagnoses in single subjects in a large

variety of diseases. They can be implemented for

diagnosis prediction, to assess the disease

progression and to evaluate the treatment

effectiveness (Orrù et al., 2012). Conventional

binary (also called two-class) classification

algorithms are applied in most cases. They aim to

classify an unknown object into one of two pre-

defined categories. In the present study we propose

the use of the One-Class Classification (OCC) or

Data Description method (Moya et al., 1993), which,

in contrast to two-class classification, makes a

description of one training class of objects (referred

to as the positive class or target class) and detects

which (new) objects resemble this target class, thus

distinguishing them from examples considered

outliers. Using OCC in standard binary classification

problems, where objects from both the two classes

are at disposal, could result in worse recognition

accuracy, as the complete knowledge encoded in the

available training set is not fully exploited. However,

OCC could provide more robustness in case of

difficulties embedded in the nature of data, since

they seek to describe properties of the target class

instead of minimizing the classification error.

Gori, I., Giuliano, A., Oliva, P., Tosetti, M., Muratori, F., Calderoni, S. and Retico, A.

Processing Magnetic Resonance Image Features with One-class Support Vector Machines - Investigation of the Autism Spectrum Disorder Heterogeneity.

DOI: 10.5220/0005776001110117

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 2: BIOIMAGING, pages 111-117

ISBN: 978-989-758-170-0

111

Table 1: Dataset composition and sample characteristics. Abbreviations: ASD, autism spectrum disorders; NVIQ, non-

verbal intelligence quotient; std, standard deviation.

Variable Subject group, mean ± std [range]

Age (months)

ASD (n=41) Controls (n=40)

49 ± 12 [28-70] 49 ± 14 [24-72]

NVIQ 73 ± 22 [34-113] 73 ± 22 [31-113]

Males (n=21) Females (n=20) Males (n=20) Females (n=20)

Age (months) 50 ± 10 [34-70] 48 ± 13 [28-69] 48 ± 13 [24-70] 50 ± 16 [22-72]

NVIQ 75 ± 22 [40-113] 70 ± 23 [34-113] 73 ± 23 [32-123] 71 ± 24 [31-106]

As a case study, we focused on the analysis of

brain features extracted from MRI data of children

affected by Autism Spectrum Disorders (ASD),

which are complex developmental neuropsychiatric

conditions affecting 1 in 68 children in USA (CDCP,

2014), and characterized by impairment in socio-

communicative abilities, as well as restricted and

stereotyped behaviours. Different approaches have

been proposed to date to explore the genetic, clinical

and neurobiological heterogeneity of ASD. Several

studies aimed to explore the predictive power of

MRI data, to find reliable ASD markers (Ecker et al.,

2010; Jiao et al., 2010; Ingalhalikar et al., 2011;

Calderoni et al., 2012; Zhou et al., 2014; Gori et al.,

2015; Retico et al., 2015).

We propose the implementation of OCC to

region-based characteristics extracted from

structural MRI brain data, in order to measure their

performance in the discrimination of patients with

ASD with respect to controls in the preschool age.

Moreover, we investigate the distribution of

“normal” patterns of brain structure to test its

homogeneity and its potential to enable the

definition of a robust boundary in relation to which

the patients with ASD are classified as outliers.

Should it not be the case, a consistent

neuroanatomical pattern among the ASD patients

would be investigated. Finally, the relative

contribution of the considered brain features to the

decision function is studied to identify the

neuroanatomical regions more involved in the OCC

boundary definition.

2 MATERIALS AND METHODS

2.1 Samples of Subjects and MRI Data

Acquisition

A group of 21 male and 20 female pre-schoolers

with ASD [mean age ± standard deviation = 49 ± 12

months; age range = 28 – 70 months] and a group of

40 control subjects matched by gender, age, non-

verbal IQ (NVIQ), and socioeconomic status were

selected for this case-control study (see Table 1).

Participants in the ASD group were recruited in the

ASD Unit of IRCCS Stella Maris Foundation (Pisa),

a tertiary hospital and research university in Italy.

The control group was composed of 20 pre-

schoolers with idiopathic intellectual disability (ID),

and 20 pre-schoolers without intellectual disability

(noID). Subjects with ID were included within the

control group in order to obtain a match for NVIQ

between patients and controls. T1-weighted MRI

data with voxel size of 1.1x1.1x1.1 mm

were

acquired using a GE 1.5 T Signa Neuro-optimized

System (General Electric Medical Systems).

2.2 Data Preprocessing and Feature

Extraction

The preprocessing of the entire data set included the

volumetric segmentation and cortical reconstruction

by the Freesurfer image analysis suite version 5.1.0,

(http://freesurfer.net/; Fischl et al., 2004). In the

cortical parcellation step, neuroanatomical labels

were assigned to each location on the cortical

surface according to the Desikan–Killiany–Tourville

(DKT) cortical atlas, which divides the cerebral

cortex into 62 structures (31 structures per

hemisphere) (Klein and Tourville, 2012). The

following 5 surface-based features for each structure

are computed: Area (white surface area in mm

);

Vo lu me (gray matter volume in mm

); Thickness

(average cortical thickness in mm); ThicknessStd

(standard deviation of cortical thickness in mm);

Mean-Curv (integrated rectified mean curvature in

-1

). We remark that the Volume is computed

according to a surface-based method, as the average

of the white and pial surface areas, multiplied by the

cortical thickness. In addition we considered the

White Surface Total Area (in mm

) and the Mean

Thickness (in mm) of the cortex in the two

hemispheres, thus obtaining a vector of 314

characteristics for each subject.

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

112

2.3 One-class Feature Classification

Among conventional binary classification

algorithms, Support Vector Machines (SVM) are

quite extensively applied tools (Vapnik, 1995). They

are a supervised binary classification method that

requires a training set of labeled input examples to

learn the differences between the two sample

classes, and a labeled test set to quantify the

classification performance.

In the context of classification of brain images,

each input example is a vector x of features

extracted by each input image. The label y

associated to each input example indicates its

membership, e.g. “1” for vectors belonging to the

patients class, “-1” for controls. Basically, during the

training phase an optimization problem is solved to

identify the largest-margin hyperplane allowing for

an optimal separation of the two classes. The input

vectors contributing to the definition of the

separating hyperplane are called support vectors.

Since data are generally not linearly separable a

regularization parameter C is introduced to control

the trade-off between the number of training errors

and the generalization ability of the classifier. It is

usually set using heuristics or tuned using cross-

validation procedures.

The SVM can then predict the classification of

an unlabeled input vector by checking on which side

of the separating hyperplane the example lies. The

SVM belong to the class of kernel methods, which

depend on data only through dot products. To

achieve good separation results even in case of non-

linearly separable classes, the dot product can be

replaced by a kernel function, which computes a dot

product in some (possibly) higher dimensional

feature space. This allows carrying out a linear

classification in this feature space, without explicitly

mapping in such a feature space the original

observations. The separating hyperplane found in the

feature space corresponds to a non-linear boundary

in the input space. In this case, the prediction of the

class membership of an unlabeled input vector is

performed by mapping it into the feature space, and

checking on which side of the separating hyperplane

the example lies. Among the non-linear kernel

functions the Radial Basis Function (RBF) Kernel is

the most popular. It depends on the Euclidean

distance between the examples and is defined as



(

, 



)

= exp(−|| − 





). The parameter γ

determines the smoothness of the boundary (in the

input space). Like the regularization parameter C,

also this parameter γ is usually set using heuristics or

tuned using cross-validation procedures.

Schölkopf et al., (2000) presented a new

formulation of two-class SVM, where the C

parameter was removed and replaced with a new

parameter ν with a more natural interpretation: it is

an upper bound to the fraction of misclassification

and margin errors and a lower bound on the fraction

of support vectors. For certain parameter settings,

the results of this new algorithm coincide with the

conventional one. Moreover, desirable properties of

previous SVM algorithms are retained. Schölkopf et

al., (2001) modified the previous approach to

address the OCC problem and called the new

algorithm single-class SVM. During the training

phase of a single-class SVM, a hyperplane is placed

such that it separates the target set from the origin

with maximal margin. Similarly to the standard two-

class SVM, when a more flexible data description is

required, an implicit mapping of the data into

another (possibly high dimensional) feature space is

defined, such that the dot product in this feature

space can be computed by evaluating a simple

kernel function. An ideal kernel function would map

the target examples onto a bounded, spherically

shaped area in the feature space and outlier objects

outside this area. The single-class SVM attributes a

new point x to the target or the outlier class by

evaluating which side of the hyperplane it falls on in

feature space. As in two-class algorithm, the

regularization parameter ν

∈

(0, 1] has to be set. It

can be interpreted as an upper bound on the fraction

of training points outside the estimated region, and a

lower bound on the fraction of support vectors.

In this work, we applied single-class SVM with

RBF kernel to the vector of 314 characteristics

extracted for each subject of our datasets. We

performed the single-class classification separately

on the male subset, on the female subset and on the

entire dataset (see Figure 1).

In the linear-kernel classifiers, the entries of the

vector w can be directly considered as the relative

weights of each characteristic for the decision

function (Gori et al., 2015). Conversely, in the non-

linear case (e.g. with the RBF kernel), the

interpretation of the vector w is non-intuitive, since

the separating hyperplane is obtained in the feature

space. We used the approach proposed by Schölkopf

et al., (1999) to approximate the preimages for the

single-class SVM with RBF kernel.

Additionally, to understand which features and

which neuroanatomical regions drive the SVM

boundary definition, we tailored the permutation

testing method (Gori et al., 2015; Gaonkar and

Davatzikos, 2013; Wanh et al., 2007; Mourão-

Miranda et al., 2005) to the case of OCC.

Processing Magnetic Resonance Image Features with One-class Support Vector Machines - Investigation of the Autism Spectrum Disorder

Heterogeneity

113

Figure 1: Schematic representation of analysis method. The regional features are extracted from brain sMRI scan of each

subject using Freesurfer software. Then, the collected sets of features are classified with one-class SVM applying the LPO-

CV procedure. Abbreviations: sMRI, structural Magnetic Resonance; ROI, Region Of Interest.

The performance of the SVM classifiers is evaluated

in terms of the sensitivity and the specificity,

computed by varying the classifier decisional

threshold. These values can be represented in a

curve known as Receiver Operating Characteristic

(ROC) curve (Metz, 2006). The area under the

ROC curve (AUC) is a global index to compare the

performance of different classifiers. To ensure an

unbiased estimate of the OCC SVM performance we

implemented a cross-validation (CV) procedure,

leaving one pair of subjects out at each iteration

(LPO-CV). The difference with respect to a CV

procedure to evaluate binary classification

performance lies only in the training step: we simply

trained the OCC on only one class (target class)

inside the CV, and tested it on the subset of both

classes left out for testing.

3 RESULTS

The Freesurfer pipeline was applied to preprocess

the MRI of each subject. Patients with ASD and

controls were matched on age and NVIQ. To train

and test OCC we used RapidMiner

(http://rapidminer.com/) advanced analytics platform

version 5.3, which includes the single-class SVM as

a part of the LibSVM operator.

We first performed single-class classification by

setting ν=0.1 and γ using heuristics (i.e. as the

inverse of the number of features). Then, we carried

out the optimization of the parameters ν and γ,

within nested LPO-CV loops.

The intuitive approach for transforming a binary

discrimination problem into a single-class task in the

context of highly heterogeneous conditions like

ASD is to use the control class as target class,

figuring that it could enable the definition of a robust

boundary, in relation to which the ASD patients

would be classified as outliers. Consequently, we

first trained a single-class SVM by considering only

control examples to form the decision boundary,

thus discarding information about the ASD class

during the training phase. This would be the optimal

approach if the control class had characteristics of

homogeneity, since the single-class SVM could

capture the control class structure, by adjusting itself

to its properties. This would allow recognizing ASD

examples as outliers, even in case the available ASD

sample is not representative of the real ASD

population, due to the extreme ASD heterogeneity.

However, the results obtained in this case in terms of

AUC were not above the chance level.

Therefore, we repeated the same procedure using

the ASD patient group as the target class to

investigate whether there was a consistent

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

114

neuroanatomical pattern among the ASD patients in

relation to which the controls would be classified as

outliers. The performance achieved by optimizing

the parameters ν and γ was: AUC=0.74 for the male

subset, AUC= 0.68 for the female subset and

AUC=0.64 for the entire dataset.

These results show that the control class does not

have characteristics of homogeneity allowing

recognizing ASD examples as outliers.

Conversely, there is a common structure among

the ASD patients that the single-class SVM could

capture.

We also found a slight performance decrease

when estimating the OCC performance on the entire

dataset, which is not surprising and we ascribed it to

the introduction of the gender as an additional

heterogeneity factor.

In order to evaluate the potential of single-class

SVM with respect to the primary aim of this work,

that is the discrimination of ASD versus controls, we

carried out also the two-class SVM classification

with linear and RBF kernels. The results we

achieved were: AUC of 0.74 for males and 0.58 for

females by using the linear kernel classification, and

0.68 for male subset and 0.65 for females adopting

the RBF kernel.

To understand which of the 314 characteristics

(i.e. which brain regions and which of the 5

computed features) are the most relevant to the

single-class SVM boundary definition, we trained a

OCC SVM with RBF kernel using all the ASD

patient group as the target class (with ν=0.1 and

heuristic γ) and we applied the algorithm proposed

in Schölkopf et al., (1999) to generate the preimage

vector z. Then, we carried out a permutation testing

procedure in the training phase originally tailored to

the OCC with 10000 iterations and with ν=0.1 and

heuristic γ, separately for the male subset, the female

subset and the entire dataset.

We used the Matlab (The MathWorks, Inc.)

interface to the LIBSVM package

(http://www.csie.ntu.edu.tw/~cjlin/libsvm/) to train

the OCC in the permutation testing procedure and

the Statistical Pattern Recognition Toolbox

(http://cmp.felk.cvut.cz/cmp/software/stprtool/index.

html) for Matlab (STPRTool) to generate the

preimage.

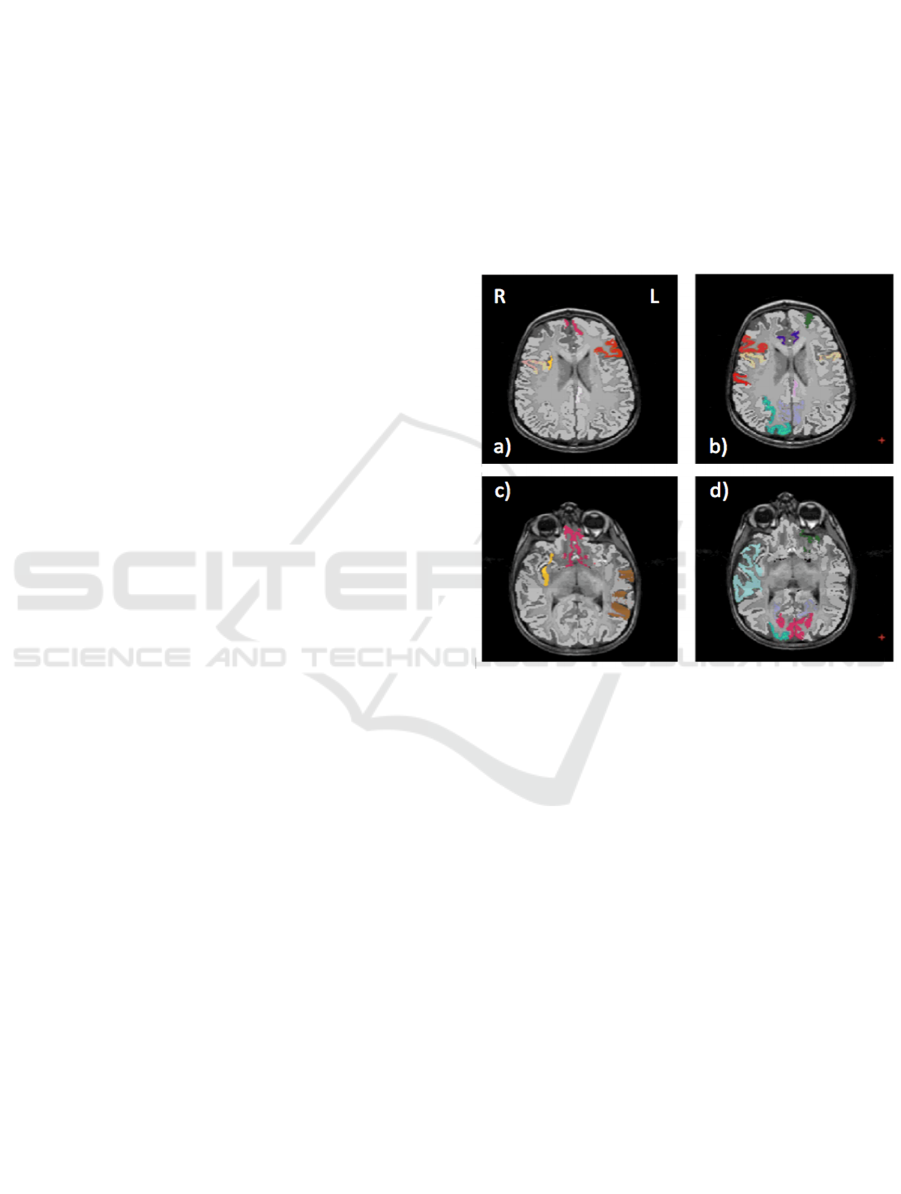
We show in Figure 2 the brain regions most

contributing to the definition of the OCC boundary,

as resulting from the permutation test, for male and

female subsets, respectively. For the male

population the regions visible in Figure 2(a,c) are:

left (L) and right (R) medial orbito frontal cortices,

L pars triangularis, R pars opercularis, middle

temporal cortex and R insula. For the female

population the regions visible in Figure 2(b,d) are: L

and

R caudate anterior cingulate, pars opercularis,

posterior cingulated, cuneus; R pars triangularis

postcentral gyrus, superior temporal cortex and

superior parietal cortex. They are mostly among the

network of structural brain alterations widely

reported in the population with ASD, including

frontal and temporal areas.

Thus, despite the phenotypical heterogeneity in

ASD a common neuroanatomical profile that

underlies the core features could be detected with

the OCC SVM approach.

Figure 2. Brain region most contributing to the definition

of the OCC boundary. For the male population the regions

visible in a) and c) are: left (L) and right (R) medial orbito

frontal cortices (pink), L pars triangularis (red), R pars

opercularis (mustard), middle temporal cortex (brown) and

R insula (yellow). For the female population the regions

visible in b) and d) are: L and R caudate anterior cingulate

(violet), pars opercularis (mustard), posterior cingulate

(light violet), cuneus (magenta); R pars triangularis and

postcentral gyrus (red), superior temporal cortex (light

blue), superior parietal cortex (cyan).

4 CONCLUSIONS

The usefulness of OCC in the biomedical domain

was already proved in a number of applications,

including in the domain of psychiatric disorders

(Mourão-Miranda et al., 2011). However, to the best

of our knowledge, we propose the first application of

OCC to the analysis of MRI data of patients with

ASD.

The aim of this work was to apply OCC not only

Processing Magnetic Resonance Image Features with One-class Support Vector Machines - Investigation of the Autism Spectrum Disorder

Heterogeneity

115

to measure its performance in the discrimination of

ASD versus controls, but also to investigate whether

the distribution of “normal” patterns of brain

structure is enough homogeneous to enable the

definition of a robust boundary, in relation to which

the patients with ASD can be classified as outliers.

As an alternative, a consistent pattern among the

patients with ASD will provide a boundary in

relation to which the controls are classified as

outliers. The latter hypothesis was confirmed by our

results. We found out evidence that the control group

is more heterogeneous and therefore the hypersphere

or decision boundary enclosing most of the controls

contains data in the ASD range. Vice versa, the ASD

group shows a common structure that the SVM OCC

could capture.

The present work is a proof of concept that the

OCC framework can be applied to neuroimaging

data to investigate if consistent patterns of

alterations do exist even in heterogeneous

populations. Despite the results we found need to be

confirmed against a larger population, the approach

we present here is a preliminary step aiming to set

up a strategy to identify common altered features in

specific disorders.

ACKNOWLEDGEMENTS

This work has been partially founded by the Italian

Ministry of Health and the Tuscany Government

(GR2317873, PI: S. Calderoni) and by the National

Institute of Nuclear Physics (nextMR project).

REFERENCES

Calderoni, S., Retico, A., Biagi, L., Tancredi, R.,

Muratori, F., Tosetti, M., 2012. Female children with

autism spectrum disorder: an insight from mass-

univariate and pattern classification analyses.

Neuroimage, 59:1013-1022.

Centers for Disease Control and Prevention, CDCP, 2014.

Prevalence of ASD, MMWR, 63:1-22.

Ecker, C., Marquand, A., Mourão-Miranda, J., Johnston,

P., Daly, E. M., Brammer, M. J., Maltezos,

S., Murphy, C. M., Robertson, D., Williams, S.

C., Murphy, D. G., 2010. Describing the brain in

autism in five dimensions—magnetic resonance

imaging-assisted diagnosis of autism spectrum

disorder using a multiparameter classification

approach. J Neurosci ,30: 10612-10623.

Fischl, B., ,vanderKouwe, A., Destrieux, C., et al, 2004.

Automatically parcellating the human cerebral cortex.

Cereb Cortex, 14: 11-22.

Gaonkar, B., Davatzikos, C., 2013. Analytic estimation of

statistical significance maps for support vector

machine based multi-variate image analysis and

classification. Neuroimage, 78: 270–283.

Gori, I., Giuliano, A., Muratori, F., Saviozzi, I., Oliva, P.,

Tancredi, R., Cosenza, A., Tosetti, M., Calderoni, S.,

Retico, A., 2015. Gray Matter Alterations in Young

Children with Autism Spectrum Disorders: Comparing

Morphometry at the Voxel and Regional Level. J

Neuroimaging, 25(6):866-74. doi: 10.1111/jon.12280.

Ingalhalikar, M., Parker, D., Bloy, L., Roberts, T. P.,

Verma, R., 2011. Diffusion based abnormality

markers of pathology: toward learned diagnostic

prediction of ASD. Neuroimage, 57:918-927.

Jiao, Y., Chen, R., Ke, X., Ch,u K., Lu, Z., Herskovits, E.

H., 2010. Predictive models of autism spectrum

disorder based on brain regional cortical thickness.

Neuroimage, 50:89-599.

Klein, A., Tourville, J., 2012. 101 labeled brain images

and a consistent human cortical labeling protocol.

Front Neurosci, 6:171.

Metz, C. E., 2006. Receiver operating characteristics

analysis: a tool for the quantitative evaluation of

observer performance and imaging systems. J Am

Coll Radiol, 3:413-422.

Mourão-Miranda, J., Bokde, A. L., Born, C., Hampel, H.,

Stetter, M., 2005. Classifying brain states and

determining the discriminating activation patterns:

Support Vector Machine on functional MRI data.

Neuroimage, 28(4):980-95.

Mourão-Miranda, J., Hardoon, D. R., Hahn, T., Marquand,

A. F., Williams, S. C., Shawe-Taylor, J., Brammer,

M., 2011. Patient classification as an outlier detection

problem: An application of the One-Class Support

Vector Machine. Neuroimage, (3-4):793-804.

doi:10.1016/j.neuroimage.2011.06.042.

Moya, M., Koch, M., & Hostetler, L., 1993. One-class

classifier networks for target recognition applications.

In Proceedings World Congress on Neural Networks,

797–801. Portland, OR: International Neural Network

Society.

Orrù, G., Pettersson-Yeo, W., Marquand, A.F., et al.,

2012. Using support vector machine to identify

imaging biomarkers of neurological and psychiatric

disease: a critical review. Neurosci Biobehav Rev

36(4):1140-1152.

Retico, A., Tosetti, M., Muratori, F., Calderoni, S, 2015.

Neuroimaging-based methods for autism

identification: a possible translational application?

Functional Neurology CIC Edizioni Internazionali,

29(4):231-239. ISSN:0393-5264.

Schölkopf, B., Mika, S., Burges, C. C., Knirsch, P.,

Müller, K. R., Rätsch, G., Smola, A. J., 1999. Input

space versus feature space in kernel-based methods.

IEEE Trans Neural Netw, 10(5):1000-17.

Schölkopf, B., Smola, A., J., Williamson, R., Barlett, P.

L., 2000. New Support Vector Algorithms, Neural

Computation, 12:1207-1245.

Schölkopf, B., Platt, J., Shawe-Taylor, J. A. S.,

Williamson, R., 2001. Estimating the support of a

BIOIMAGING 2016 - 3rd International Conference on Bioimaging

116

high-dimensional distribution. Neural Computation,

13:7.

Vapnik, V., 1995. The nature of Statistical Learning

Theory, Berlin.

Wanh, Z., Childress A. R., Wang, J., Detre, J. A., 2007.

Support vector machine learning-based fMRI data

group analysis. Neuroimage, 36(4):1139-51.

Zhou, Y., Yu, F., Duong, T., 2014. Multiparametric MRI

Characterization and Prediction in Autism Spectrum

Disorder Using Graph Theory and Machine Learning.

PLoS ONE 9(6): e90405.

Processing Magnetic Resonance Image Features with One-class Support Vector Machines - Investigation of the Autism Spectrum Disorder

Heterogeneity

117