Geometric Approach to Estimation of Volumetric Distortions
Alexander Naitsat
1
, Emil Saucan
2
and Yehoshua Y. Zeevi
1
1
Electrical Engineering Department, Technion, Haifa, Israel
2
Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
Keywords:
Conformal Geometry, Isometric Distortion, Volume Parameterization, Volumetric Meshes, Geometric
Computing, Computer Graphics.
Abstract:
The problem of measuring geometrical distortions is not trivial for volumetric domains. There exist intrinsic
restrictions and constrains on higher dimensional mappings. Moreover, according to Liouville theorem, most
existing techniques for 2D data can not be directly applied to volumetric objects. In this work we approximate
continuous deformations by piecewise affine functions defined on tetrahedral meshes. Our aim is to study
a few types of geometrical distortions that can be expressed as functions of singular values of a Jacobian.
We employ the proposed methods of estimating conformal and isometric distortions to analyze volumetric
data. In particular, we examine parametrization of tetrahedral models to a ball. Distortions produced by the
resulting spatial mappings depict intrinsic structure of domains, and therefore can be employed in such tasks
as detection of abnormalities and comparison (i.e. similarity assessment) between 3D objects. This geometric
approach and results are highly relevant to various applications in Computer Vision, Computer Graphics, 3D
Printing and Medical Imaging.
1 INTRODUCTION
In mapping between volumetric domains, we are in-
terested in quantifying distortions of the intrinsic geo-
metrical properties, i.e. angles and Euclidean lengths,
referred to as conformal and isometric distortions, re-
spectively. Obeying the condition of angle preserving
transformations, conformal maps are desirable in dig-
ital geometry processing and in computer graphics,
since they do not exhibit shear and, therefore, pre-
serve different vertex properties as well as the topol-
ogy of the mesh itself. They are also instrumental in
image processing and in computer vision.
A conformal mapping f of a domain D ⊂ R
n
is
defined as a smooth bijective function, which at any
point x ∈ D scales the space uniformly in every direc-
tion. This can be stated formally as
kd f
x
· h
1
k = kd f
x
· h
2
k, (1)
where d f
x
denotes the Jacobian matrix at a point x of
a function f : D → R
n
and h
1
,h
2
∈ R
n
are arbitrary
unit vectors. Following this annotation, a conformal
map f (x) is isometric in D if
∀x ∈ D : |detd f
x
| = 1 . (2)
Most of the methods used to construct confor-
mal and almost isometric parametrization of a sur-
face can’t be generalized for dealing with volumes,
due to the classical theorem of Liouville (K
¨
uhnel and
Rademacher, 2007), which states that every confor-
mal mapping of a domain in R
n
,n ≥ 3, is a restric-
tion of M
¨
obius transformation, i.e. a composition of
conformal affine transformations and inversions in a
sphere. Therefore, the problem of computing perfect
conformal functions in higher dimensions is reduced
to minimizing the amount of distortion produced by a
spatial mapping.
Conformal and isometric properties of smooth
mappings in R
n
can be studied by at least two alter-
native approaches. The first approach considers topo-
logical properties of a function along the integrable
curves. The other approach, which we shall employ,
examines the properties of a map in infinitely small
neighborhoods. To this end, we examine the behavior
of a discrete map f in nearest neighborhood repre-
sented by a ring of tetrahedral cells. Our measure-
ments of distortions are based on the singular value
analysis of the Jacobian d f .
The advantage of this method over other tech-
niques that are used in volumetric modeling (e.g. dis-
crete harmonic energy; (Wang et al., 2003)) is that
we can employ the same framework to deal with a
wide range of spatial distortions and energies. For in-
stance, the aspect-ratio distortion (Aigerman and Lip-
Naitsat, A., Saucan, E. and Zeevi, Y.
Geometric Approach to Estimation of Volumetric Distortions.
DOI: 10.5220/0005778201030110
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 105-112
ISBN: 978-989-758-175-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
105

man, 2013), the certain types of rigid and affine en-
ergies (Kovalsky et al., 2014), the n-D comformality
distortion (Lee et al., 2015), the angle and the volume
energies (Paill
´
e and Poulin, 2012) all of which are ex-
pressed as functions of singular values.
While there is an abundance of studies and ap-
plications of conformal mappings in 2D, general
volumetric domains can be mapped only quasi-
conformally. Therefore one of the challenges in 3D
is to measure the minimal conformal distortion asso-
ciated with mapping of one domain into another.
We examine the problem of measuring volumetric
distortions, produced by discrete transformations be-
tween tetrahedral meshes, and addresses issues con-
cerning relations between volumetric distortions and
assessment of geometric similarity between 3D ob-
jects.
2 VOLUMETRIC DISTORTIONS
Let f (x) = Ax + b be a full rank n-dimensional affine
function. A number of geometry processing problems
associated with f are naturally described in terms of
singular values of its linear part. Singular values of a
matrix are non-negative numbers usually denoted by
σ
1
(A) ≥ σ
2
(A) ≥ ... ≥ σ
n
(A); they are unique up to
the order, and satisfy
kAk = σ
1
, `(A) = σ
n
, | det A| =
n
∏
i=1
σ
i
, (3)
where
kAk := max
khk=1
kA · hk, (4)
is also known as the spectral norm of A, and
l(A) := min
khk=1
kA · hk. (5)
The geometrical interpretation is that A transforms
vectors of some unitary basis {v
i
}
i=1,..,n
to the vectors
of other unitary basis {u
i
}
i=1,..,n
, multiplied by the
corresponding singular value σ
i
. Putting these vectors
in rows and columns, respectively, yields a singular
value decomposition (SVD) of A
A = UDiag(σ
1
,...,σ
n
)V
∗
. (6)
The latter plays an important role in image processing
and numerical analysis.
When dealing with volumetric mappings, our pri-
mary interest is in studying distortions of first order
differential properties, such as angles and Euclidean
lengths. This lends itself to the definition of qc (quasi-
conformal) and qi (quasi-isometric) dilatations of a
linear map A, which basically are measures of how
far A is from being conformal and isometric mapping,
respectively. The basic method to assess the degree
of conformality of a linear map A, is to consider the
ratio of singular values
H(A) =
kAk
`(A)
, (7)
also known as the condition number.
A more accurate approach, which follows from
the theory of n-dimensional mappings, is to consider
the following quantity, called qc-dilatation,
K(A) = max

|det(A)|
`(A)
n
,
kAk
n
|det(A)|

. (8)
Quasi-isometric dilatation of a function f is de-
fined as a minimal number C ∈ {1,∞}, such that
1
C
kp
1
− p
2
k ≤ k f (p
1
) − f (p
2
))k ≤ Ckp
1
− p
2
k,
for any p
1
, p
2
∈ D (see (Saucan et al., 2008)). In par-
ticular, for a linear function A, Eq. (4) and Eq. (5)
imply
C(A) = max{`(A)
−1
, kAk}. (9)
Dilatations defined above are related to each other
via the following inequality
K(A) ≤ H
n−1
(A) ≤ C
2(n−1)
(A). (10)
Now, suppose that f is a local diffeomorphism of
an open domain D ⊂ R
n
, that is for each point in D
there is a neighborhood where f is a smooth bijec-
tive mapping with a smooth inverse. We refer to such
mapping simply as a deformation function. Clearly,
d f
x
is a full rank linear transformation, and thus we
define the maximal qc-dilatation of f as
K( f ) = sup
x∈D
K(d f
x
), (11)
and the maximal qi-dilatation as
C( f ) = sup
x∈D
C(d f
x
). (12)
We call a deformation function f qc-mapping if
K( f ) < ∞, and qi-mapping if C( f ) < ∞.
In the sequel we shall assume that n = 3 and that
all the above conditions for f are satisfied. The ba-
sic common method to represent volumetric data in
computer science and engineering is to triangulate a
continuous volume into tetrahedrons. This is a pow-
erful method applicable for various 3D topologies.
Employing this approach to approximate a continuous
deformation f : D → D
0
yields the so-called simplicial
map f
s
.
Let (V,E,F,T ) be a tetrahedral representation of
D, where V , E, F and T are the vertex, edge, face
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
106

(a) Domain (b) Image (c) qc-dilatation K (d) qi-dilatation C
(e) σ
1
(f) σ
3
(in cross section) (g) Image (h) K
Figure 1: Radial stretching of the hexahedral volume of the cube [−1,1]
3
onto the unit ball and onto the round cylinder B ×
[−1,1]. Figures 1(c)-1(f) and 1(h) depict distribution diagrams of the scalar values associated with volumetric distortion: qc
and qi dilatations and singular values σ
i
of a Jacobian. Equivalent tetrahedral meshes are obtained by hexahedral triangulation.
and tetrahedra sets of the mesh, respectively. Then,
for a vertex v ∈ V located at the position x we set
f
s
(v) = f (x). Next, we extent f
s
to the entire do-
main by a piecewise linear extension of the vertex val-
ues (see the exact formula, Eq. (13)). The following
section uses simplicial maps to estimate differential
properties of continuous deformations.
2.1 Computing Singular Values
We can estimate dilatations of a simplicial map f at
vertex v, placed at a position x ∈ R
3
, based on estima-
tion of the Jacobian matrix d f
x
. First, we estimate the
average Jacobian matrix inside a given tetrahedron τ,
denoted by d f
τ
. Then we define the vertex Jacobian
matrix d f
v
as an average over d f
τ
in the neighbouring
tetrahedra.
Let f
(1)
, f
(2)
, f
(3)
be the coordinate components
of the map f , where each one is a function from V to
R. We can express d f
v
as the matrix whose rows are
the average gradient vectors of f
(i)
.
Suppose r is a point inside tetrahedral cell τ,
which consists of vertices v
1
,v
2
,v
3
,v
4
. Let λ
j
be a
face against v
j
. Let s
j
be the vector along the normal
of λ
j
, such that ks
j
k = Area(λ
j
). If v
4
is set to be the
origin of τ, then applying 3D barycentric coordinates
for f yields
f
(i)
(r) =
1
3m(τ)
4
∑
j=1
(v
4
− r) · s
j
f
(i)
(v
j
). (13)
This implies that the gradient is constant inside τ,
hence our estimates yield
∇ f
(i)
(τ) = −
1
3m(τ)
4
∑
j=1
s
j
f
(i)
(v
j
); (14)
and
∇ f
(i)
(v) =
∑
c∈Ring(v)
∇ f
(i)
(c)w(c), (15)
where Ring(v) are the neighbouring tetrahedrons of v,
and w(c) are the chosen normalized weights.
The singular values σ
1
= kd f
v
k and σ
3
= l(d f
v
)
are then approximated as the maximum and minimum
of kd f
v
· h
j
k, sampled at chosen directions h
1
,...,h
m
.
The intermediate singular value is then
σ
2
=
|det(d f
v
)|
σ
1
σ
3
, (16)
where the determinant can be computed directly from
the estimates of the vertex Jacobian. Alternatively, it
may be computed as a weighted average over deter-
minants det(d f
τ
), where the last quantity may be ap-
proximated as a volume ratio between the target and
the source tetrahedra :
|det(d f
τ
)| =
volume( f (τ))
volume(τ)
. (17)
Geometric Approach to Estimation of Volumetric Distortions
107

(a) Domain (b) Image, a = 1 (c) Cross section of the domain (d) a = 1
(e) a = 2 (f) a = 0.5 (g) Mean curvature (h) Dihedral angle (i) qc-dilatation
Figure 2: Parametrization of tetrahedral model mapped into a ball, computed for three different values of parameter a. Figures
2(a), 2(b) and 2(i) depict entire tetrahedral models of the domain and of the image. Figures 2(c)-2(f) show cross sections
delineated by yz plane. Colors depict and correspond to diagrams of cylindrical coordinates of the domain for Figures 2(a)-
2(f), and distribution diagrams of mean curvature and dihedral angles of the boundary and qc-dilations for Figures 2(g)-2(i),
respectively.
(a) (0.2,10) (b) (0.1,20) (c) (0.5,10)
Figure 3: Images of the unit sphere under Ω
A,ω
functions.
The shown pairs of numbers corresponds to the values of A
and ω , respectively.
[See (Naitsat et al., 2015; Naitsat et al., 2014) for de-
tails about estimation of singular values and the Jaco-
bian on tetrahedral and hexahedral meshes.]
Combining the above leads to numerical estimates
of local volumetric distortions at vertex positions. We
denote the corresponding qc and qi dilatations for a
chosen vertex v by K( f , v) and C( f ,v), respectively.
2.2 Bounded Distortion Mappings
A variety of techniques for morphing of polygonal
meshes are used in computer graphics to measure
similarities between objects. Let us consider the fol-
lowing related problem for volumetric domains.
Assume D
1
,D
2
⊂ R
3
are smooth domains that
have the same topology and similar geometrical prop-
erties. Then, according to the basic geometric intu-
ition, there exists a deformation map f : D
1
7→ D
2
with bounded dilatations. The proof and exact condi-
tions required for the existence can be found at (Cara-
man, 1974; V
¨
ais
¨
al
¨
a, 1971). We consider the minimal
conformal and isomtertic distortions that are required
to map one domain into another. The correspond-
ing quantities are called quasi-conformal and quasi-
isometric coefficients of D
1
and D
2
, respectively, and
they are defined as
K(D
1
,D
2
) = inf K( f ), (18)
C(D
1
,D
2
) = infC( f ), (19)
where the infimum is taken over all smooth bijective
mappings f : D
1
→ D
2
.
We expect that the amount of distortion produced
by morphing domain D
1
into D
2
will provide a mea-
sure of resemblance between their geometries. For
instance, if D
2
is image of D
1
under a similarity trans-
formation, then K(D
1
,D
2
) = 1. In a general case
K(D
1
,D
2
) ≥ 1 and it measures how close are these
domains to being conformally-equivalent.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
108

(a) Domain, K (b) image, K (c) domain, C (d) image, C
(e) domain, K (f) image, K (g) domain, C (h) image, C (i) mean curvature on the do-
main’s surface
(j) Domain, K (k) domain, C (l) mean curvature (m) Gaussian curvature
Figure 4: Mapping into a ball of volumes contained inside the wave-like surfaces Ω
A,ω
(S
3
) defined by Eq. (25) for the
following values of the amplitude A and the frequency ω : A = 0.5,ω = 10 for Figures 4(a)-4(i) and A = 0.1, ω = 20 for
Figures 4(j)-4(m). The first two lines alternatively show domain and image of the deformation. Figures 4(a)-4(d) and 4(j)-
4(k) show entire tetrahedral models, while 4(e)-4(h) depict cross sections. The rest of the Figures 4(i), 4(l) and 4(m) are
diagrams of curvature distribution on boundary surfaces.
To access fine geometrical features of the object
from qi-coefficients, we must take into account rela-
tive sizes of the given domains. Let us measure the
size of a domain D
i
by the radios r
i
of the bounding
sphere, i.e, the smallest sphere containing D
i
. Given
a deformation mapping f : D
1
→ D
2
, it is often useful
to consider the so called k-bounded qi-dilation of f
C
0
( f ) =
C( f )
k
, (20)
where k is defined by
k(D
1
,D
2
) = max

r
1
r
2
,
r
2
r
1

. (21)
We define the k-bounded qi-coefficient C
0
(D
1
,D
2
) ac-
cordingly. This approach is important for a general
case. However to make things simpler when dealing
with tetrahedral models, we assume that k(D
1
,D
2
) =
1. This assumption is easily achieved in modeling
tools by scaling the data during the preprocessing.
Dilatation coefficients can be often derived from
comparison between domain’s boundaries. For exam-
ple, consider deformation of a cube onto the round
cylinder shown in Figure 1. This transformation is
a radial stretching of the square in planes R
2
× {z},
with edge 2l into the circle of radius l, which can be
written explicitly in cylindrical coordinates as
(r,ϕ,z) 7→

lr
R(ϕ)
,ϕ,z

, (22)
Geometric Approach to Estimation of Volumetric Distortions
109

where R(ϕ) is a distance from the origin to the bound-
ary of the cube, measured at angle ϕ. Without loss of
generality, we focus on compact domains in R
3
with
non-empty interior that contains the origin.
The mapping (22) for l = 1 can be generalized to
construct parametrization of compact volumes onto
the unit cylinder by
(r,ϕ,z) 7→

r
R(ϕ)

a
,ϕ,z

, (23)
where a > 0 is a chosen parameter.
The same technique of radial stretching can be ap-
plied to produce volumetric parametrization into the
unit ball. Consider a domain D that satisfies the fol-
lowing geometrical condition: for any ζ ∈ ∂D, the an-
gle between the line segment ζ0 and tangent plane at
ζ is larger than or equal to some constant α > 0. We
construct a smooth parametrization of D into the unit
ball written in the spherical coordinates (r,ϕ,θ). First,
set ζ(ϕ, θ) to be the furthest intersection point of ∂D
and the ray along the ϕ,θ direction, then we define the
family of parametrization functions f
a
: D → B
3
by
(r,ϕ,θ) 7→

r
kζ(ϕ,θ)k

a
,ϕ,θ

, (24)
where a > 0 is the same parameter as in Eq. (23).
If the domain is star-shaped, namely if for any x ∈
D: 0x ⊂ D, then the resulting parametrization is onto.
Moreover, Caraman (Caraman, 1974, p. 408) has
shown in this case that f
a
is a qc-mapping and gave
an accurate approximation of K( f
a
) as a function of a
and angle α from the geometrical condition. In partic-
ular, if a → 1 and α → π/2, then K( f
a
) approaches 1,
since the limit function appears to be a uniform scal-
ing of a ball to the unit ball B
3
.
Figures 1 and 2 show cylindrical and spherical
parametrization of models. Both parametrizations ap-
plicable to analysis of volumetric data. However,
parametrization to a cylinder requires an accurate
choice of the rotation axis, where deformation to a
ball is invariant to the initial orientation of objects.
Therefore, this work is focused on radial stretching
into a ball. Figures 2(a)-2(f) depict the geometrical
meaning of the parameter a, which affects the amount
of distortion along the radial axis. In particular, when
a decreases, the interior volume is stretched toward
the surface, while raising values of a squeezes the in-
terior toward the origin. This behavior can be em-
ployed to adjust the amount of local distortions. In
the sequel we assume a = 1, unless stated otherwise.
2.3 Results and Explanations
We present results of numerical computations of volu-
metric distortions for various domains along with the
qualitative interpretation of the outcomes.
Figure 2 summarizes results for the parametriza-
tion of the cat model to the unit ball, represented by
a tetrahedral mesh. Note the correlation between ar-
eas on the surface of higher values of dilatations and
areas of higher values of mean curvature and dihe-
dral angles shown in Figures 2(g) and 2(h). This
phenomenon is further emphasized in Figure 4. The
relation between curvature and measured volumetric
distortions follows from the existence of conformal
and isometric invariants. Similarly, dihedral angle im-
poses tight bounds on qc-coefficients of polyhedral
domains. These facts has been demonstrated for basic
deformations in (Naitsat et al., 2015).
Next, we choose series of symmetrical volumetric
domains D
A,ω
whose boundaries ∂D
A,ω
are set to be
an image of the following wave functions:
Ω
A,ω
(r,ϕ,θ) = (r + A cos(ωϕ)cos(ωθ),ϕ,θ) , (25)
where r is a constant. In other words, we define a si-
nusoid height function on a sphere S
3
r
with amplitude
A and frequency ω (see Figure 3). Our aim is to es-
timate an impact that distinct geometrical features of
a wavelike surface have on the dilatation coefficients.
Although, Eq. (11) and Eq. (12) define K( f ) and
C( f ) as a maximum of the corresponding local dila-
tions, the average value of the volumetric distortion is
more relevant for such practical applications as shape
classification and comparison. Let us denote the aver-
age value of a scalar function F : D ⊂ R
3
→ R by
¯
F =
1
volume(D)
Z
D
F(x)dx (26)
In order to compute
¯
K and
¯
C for a tetrahedral mesh
(V,E,F, T ) of a domain D, we approximate continu-
ous integration as follows :
Z
D
F(x)dx ≈
∑
v∈V
F(v)·volume(Cent(v)), (27)
where Cent(v) is a barycentric cell of a vertex v,
obtained by connecting middle points of edges shar-
ing v. Namely, for each τ ∈ Ring(v) we construct a
sub-tetrahedron by connecting v and middle points of
edges sharing v. Cent(v) is defined as the union of
these sub-tetrahedrons over Ring(v).
Denote by D
A,ω
the volume enclosed by the im-
ages of the unit sphere under Ω
A,ω
. Figure 4 con-
siders deformations f
1
: D
A,ω
→ B
3
defined by Eq.
(24). Observing these figures, we see concentration
of conformal distortion on the surface of the model,
while isometric distortion is spread through the entire
volume. The phenomenon is related to the choice of
a deformation function f
1
from Eq. (24) which is a
uniform scaling when restricted to a radial segment
{(r,ϕ,θ)|r ∈ [0,t]}.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
110

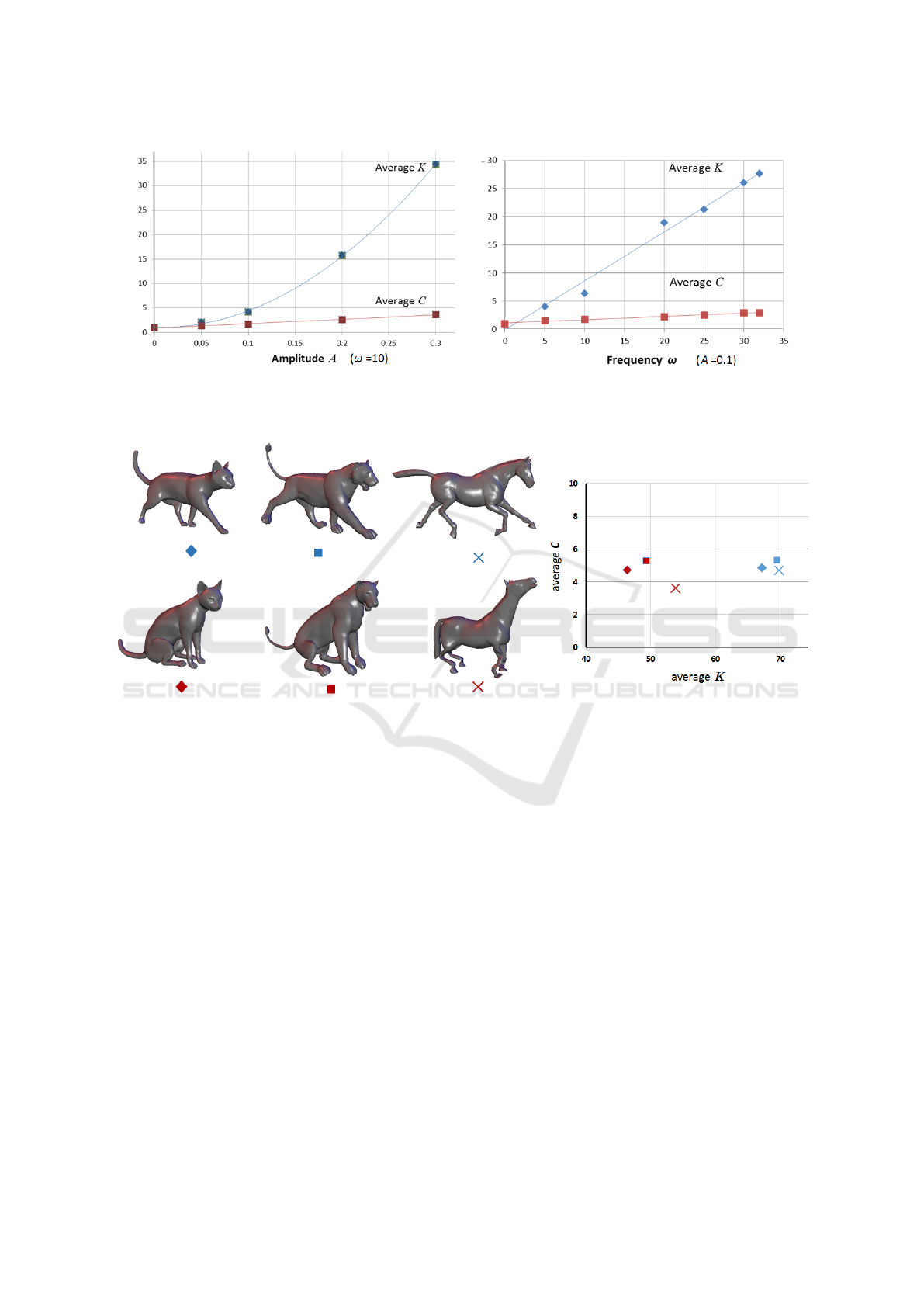
Figure 5: Average qi and qc dilatations
¯
K and
¯
C as a function of the amplitude A and the frequency ω of Ω
A,ω
defined
according to Eq. (25). Dilatations are computed for parametrization (24) of domains D
A,ω
, which are interior volumes of
Ω
A,ω
(S
3
). The results are shown for the constant frequency ω = 10 and the constant amplitude A = 0.1, respectively.
Figure 6: Average volumetric distortions
¯
K and
¯
C produced by parametrization of 3D models into a ball. The corresponding
distances between models in (
¯
K,
¯
C)-plane reveal similarities of global geometrical features. The mesh data used in this
simulation was adopted from (Sumner and Popovi
´
c, 2004).
The corresponding charts in Figure 5 show de-
pendence between the wave parameters and the aver-
age level of volumetric distortions. As expected, for
ω = const, we see that
¯
C has a linear dependence on
the amplitude, while
¯
K appears to be a quadratic func-
tion of A. In contrast, when the amplitude is constant,
both
¯
C and
¯
K are nearly linear functions of ω. This
is because conformal distortion is intensified near the
surface, which for A = const is restrained to the same
area 1 − A ≤ r ≤ 1 + A. 3D shapes can be analyzed
in the spectral domain as a composition of compo-
nents that represent features of high and low frequen-
cies. These features can be estimated by the amount
of distortion required to round the shape. This con-
cept is illustrated in Figure 6 for three pairs of polyg-
onal models. All the pairs, except the last one, are
mutual images under a nearly isometric bending. Av-
erage distortions are measured and displayed on the
(
¯
K,
¯
C)-plane for a deformation map (24) of the en-
closed volumes into a ball. The vertical displacement
of the resulting points in the distortion plane reveals
how far are shapes from being isometrically equiva-
lent, while the Euclidean distance between the points
accesses the resemblance of global features and align-
ment of objects’ medial axes.
3 CONCLUSIONS
This paper presents quantitative method of computing
the major volumetric distortion: qc and qi dilatations.
Our technique is based on estimation of the Jacobian
and the corresponding singular values for a simplicial
map.
Among other applications, our approach can be
used to produce desirable deformations and param-
eterizations of 3D domains, by minimizing the distor-
tion functional
Σ
v∈V
K( f , v) + λC( f , v) , (28)
Geometric Approach to Estimation of Volumetric Distortions
111

under the given conditions. The latest research in
the area (Kovalsky et al., 2014), deals with the min-
imization of the condition number (7), which is not
always sufficiently accurate to properly measure de-
formations in 3D (see (Naitsat, 2015, p. 13) ). We
believe that using our metrics it is possible to achieve
more desirable results.
We have demonstrated in Section 2.2 basic
parametrization techniques for volumetric objects.
Dilatations produced by the corresponding mappings
are tightly related to the distortion of several geomet-
rical properties of a boundary surface, such as curva-
ture and dihedral angles. In particular, we have illus-
trated in Section 2.3 correlations between an average
distortion, the amplitude and the frequency of wave-
like surfaces. These consequences may be targeted
toward spectral analysis of the closed shapes that can
be represented as an image of a sphere under a com-
position
Ω
A
1
,ω
1
◦ Ω
A
2
,ω
2
◦ ... , (29)
which can be considered, in turn, as an analogue of
Fourier series in the spherical coordinates. Likewise,
future analysis may consider distortions produced by
parametrization into non-symmetrical domains and its
relation to global properties of shapes. For example, a
volumetric parametrization into cylinder and shape’s
symmetry relative to the rotation axis.
As has been illustrated in Figure 6, these facts can
be instrumental in quantitative assessment of similar-
ity of objects undergoing elastic deformations. Un-
like most existing algorithms for classification and
comparison of polygonal meshes, our approach can
be applied both for closed simply-connected surfaces
and for volumetric domains with more sophisticated
boundaries.
ACKNOWLEDGEMENTS
This research has been supported by the Israeli Min-
istry of Economics; OMEK consortium and by the
Ollendorff Minerva Center for Vision and Image Sci-
ences.
REFERENCES
Aigerman, N. and Lipman, Y. (2013). Injective and
bounded distortion mappings in 3D. ACM Trans.
Graph, 32(4):106:1–106:14.
Caraman, P. (1974). n-dimensional quasiconformal (QCF)
mappings. Revised, enlarged and translated from
the Roumanian by the author. Editura Academiei
Rom
ˆ
ane, Bucharest, Abacus Press, Tunbridge Wells
Haessner Publishing, Inc., Newfoundland, NJ, 1974.
Kovalsky, S. Z., Aigerman, N., Basri, R., and Lipman, Y.
(2014). Controlling singular values with semidefi-
nite programming. ACM Transactions on Graphics
(TOG), 33(4):68.
K
¨
uhnel, W. and Rademacher, H.-B. (2007). Liou-
ville’s theorem in conformal geometry. Journal de
math
´
ematiques pures et appliqu
´
ees, 88(3):251–260.
Lee, Y. T., Lam, K. C., and Lui, L. M. (2015). Landmark-
matching transformation with large deformation via n-
dimensional quasi-conformal maps. J. Sci. Comput.
(Accepted for publication), pages 1–29.
Naitsat, A. (2015). Quasi-conformal mappings for volu-
metric deformations in geometric modeling. Master’s
thesis.
Naitsat, A., Saucan, E., and Y, Y. Z. (2014). Computing
quasi-conformal maps in 3d with applications to geo-
metric modeling and imaging. In 2014 IEEE Conven-
tion, Israel, pages 1–5.
Naitsat, A., Saucan, E., and Zeevi, Y. Y. (2015). Volu-
metric quasi-conformal mappings - quasi-conformal
mappings for volume deformation with applications to
geometric modeling. In Proceedings of VISIGRAPP
2015, pages 46–57.
Paill
´
e, G.-P. and Poulin, P. (2012). As-conformal-as-
possible discrete volumetric mapping. Computers &
Graphics, 36(5):427–433.
Saucan, E., Appleboim, E., Barak-Shimron, E., Lev, R.,
and Zeevi, Y. Y. (2008). Local versus global in quasi-
conformal mapping for medical imaging. Journal of
Mathematical Imaging and Vision, 32(3):293–311.
Sumner, R. W. and Popovi
´
c, J. (2004). Deformation transfer
for triangle meshes. ACM Transactions on Graphics
(TOG), 23(3):399–405.
V
¨
ais
¨
al
¨
a, J. (1971). Lectures on n-Dimensional Quasicon-
formal Mappings. Springer-Verlag Berlin Heidelberg
New York.
Wang, Y., Gu, X., Yau, S.-T., et al. (2003). Volumetric har-
monic map. In Communications in Information & Sys-
tems, volume 3, pages 191–202. International Press of
Boston.
GRAPP 2016 - International Conference on Computer Graphics Theory and Applications
112