Selective Use of Appropriate Image Pairs for Shape from Multiple
Motions based on Gradient Method
Norio Tagawa and Syouta Tsukada
Graduate School of System Design, Tokyo Metropolitan University, 6-6- Asahigaoka, Hino, Tokyo, Japan
Keywords:
Shape from Motion, Gradient Method, Direct Recovery, Random Camera Motions.
Abstract:
For the gradient-based shape from motion, relative motions with various directions at each 3-D point on a
target object are generally effective for accurate shape recovery. On the other hand, a proper motion size exists
for each 3-D point having an intensity pattern and a depth that varied in each, i.e., a too large motion causes a
large error in depth recovery as an alias problem, and a too small motion is inappropriate from the viewpoint
of an SNR. Application of random camera rotations imitating involuntary eye movements of a human eyeball
has been proposed, which can generate multiple image pairs. In this study, in order to realize accurate shape
recovery, we improve the gradient method based on the multiple image pairs by selecting appropriate image
pairs to be used. Its effectiveness is verified through experiments using the actual camera system that we
developed.
1 INTRODUCTION
3D reconstruction from 2D images is a fundamental
subject in the research field of the computer vision.
There are various clues for reconstruction, for exam-
ple, stereo (Lazaros et al., 2008), motion (Azevedo,
2006), shading (Samaras et al., 2000) and voxel col-
oriing (Seitz and Dyer, 1997). Shape from Motion
(SfM) has attracted attention in particular. For the
gradient-based shape from motion, a large amount
of studies have been performed (Bruhn and Weick-
ert, 2005), (Brox and Malik, 2011), (Ochs and Brox,
2012). To avoid occlusions for point correspondences
between images, we have focused on a monocular
stereo vision. The gradient-based method using the
relation between spatiotemporal differentials of im-
age intensity and an optical flow field has attracted
attention because of its analytic formulation property.
The method is effective for a small motion parallax
between successive two images, hence it cannot exe-
cute high accurate recovery in general.
One strategy for high accuracy is the use of multi-
ple images observed from various viewpoints. When
we use the camera moving continuously around a tar-
get object, corresponding points in an image sequence
are required to be tracked, which is also a difficult
task of the computer vision. Therefore, a method us-
ing multiple images without the tracking is desired.
As such a method, we have proposed the depth re-
covery using random camera rotations imitating fixa-
tional eye movements of a human’s eye ball (Tagawa,
2010). The rotation center of the camera rotations is
set at the back of a lens center. Such a rotation causes
a translational motion of a lens center,which indicates
that depth information can be observed. Since the
camera rotations cause small image motions having
various direction, a lot of image pairs are generated
and can be used simultaneously for the gradient-based
method without point correspondence by tracking.
On the other hand, the accuracy of the gradient-
based method is mainly affected by the equation error
of the gradient equation. The gradient equation is de-
rived as a first order approximation of the intensity
invariant constraint before and after the relative mo-
tion between a camera and a target object. Hence, the
second and more higher order terms corresponds to
the equation error. The degree of the error is deter-
mined by the relation between the size of the optical
flow and the spatial frequency of a dominant intensity
pattern.
To reduce the influence of such an equation er-
ror, the optimal frequency component was extracted
at each pixel and was used for depth recovery(Tagawa
and Koizumi, 2015). In this method, all observed mo-
tions caused by random camera rotations are used at
all pixels by tuning the image resolution to each mo-
tion at every pixel. When a lot of image pairs are
observed and can be used for recovery, the strategy
554
Tagawa, N. and Tsukada, S.
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method.
DOI: 10.5220/0005778805520561
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 554-563
ISBN: 978-989-758-175-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

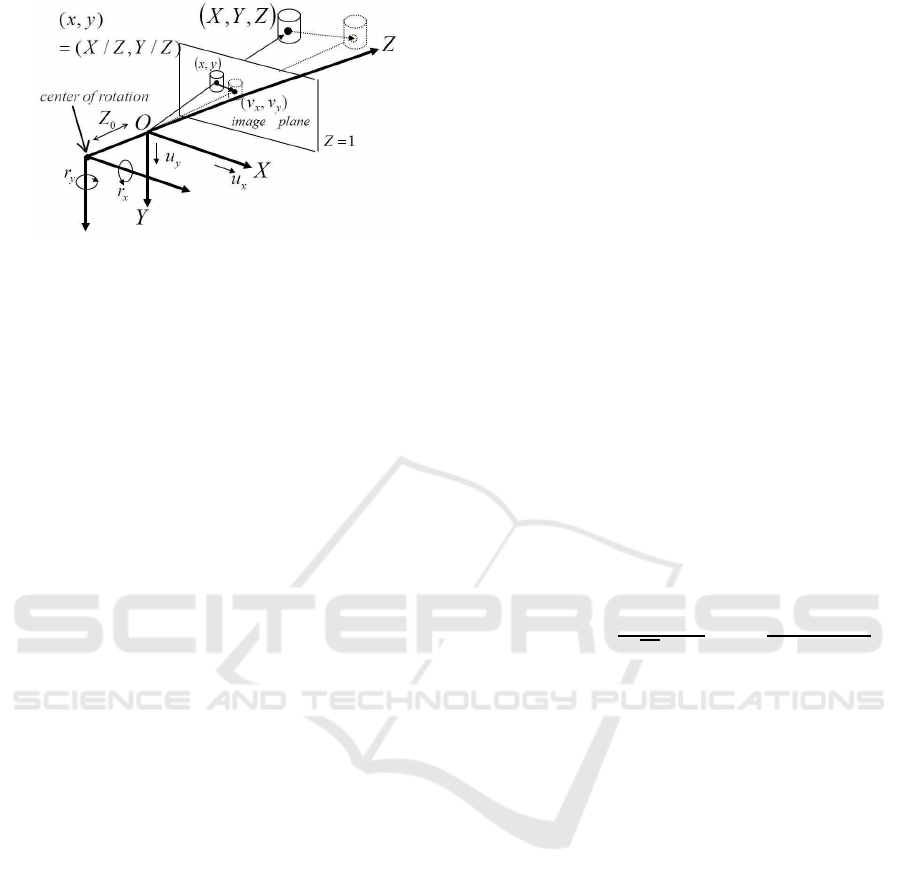
Figure 1: Coordinate system and camera motion model
used in this study.
in which at least one frequency component is used
at every successive image pair (Tagawa and Koizumi,
2015) seems to be redundant, i.e., it is not necessary
to extract the optimal resolution for every motion. It
is expected that the method which selects the appro-
priate image pairs, i.e., appropriate image motions
generally called optical flows, having little high or-
der terms in the gradient equation at every pixel also
can reduce the equation error. In this study, the effec-
tiveness of the selective use of the appropriate image
pairs is confirmed through real image experiments.
In the following, the method (Tagawa, 2010) used
as a fundamental framework in this study is explained
briefly in Sec. 2, and the proposed technique to select
the appropriate image pairs at each pixel is introduced
in Sec. 3. Experimental results using real images are
shown to reveal the effectiveness in Sec. 4, and the
problems left for the future are discussed in Sec. 5.
2 DEPTH FROM MULTIPLE
IMAGES
2.1 Projection and Motion of Camera
The camera coordinate and the camera motion model
are shown in Fig. 1. A perspective projection is
adopted, and a 3D point (X,Y,Z)
⊤
on an object
is projected into an image point x ≡ (x,y,1)
⊤
=
(X/Z,Y/Z,1)
⊤
. A camera rotation center is set at the
back of a lens center with a distance of Z
0
along an op-
tical axis. A rotation identified by a rotational veloc-
ity vector r = [r
X
,r
Y
,r
Z
]
⊤
causes the rotation of a lens
center which is represented with the same value of r.
A translation is not applied explicitly, but the rota-
tion of which the rotation axis is different from a lens
center causes a translation of a lens center implicitly.
The translational velocity vector u = [u
X
,u
Y
,u
Z
]
⊤
is
formulated as follows:


u
X
u
Y
u
Z


=


r
X
r
Y
r
Z


×


0
0
Z
0


= Z
0


r
Y
−r
X
0


. (1)
If we know the value of Z
0
, an absolute shape of an
object can be recovered, although by a general camera
motion only a relative shape is recovered.
Equation 1 indicates that r
Z
is not required to gen-
erate the translation, hence a 2D rotational velocity
r = [r
X
,r
Y
]
⊤
can be redefined and used for recovery.
r
( j)
indicates the discrete value of r in the jth image
pair. Because the use of various optical flows is effec-
tive for the accurate shape recovery, {r
( j)
} is desired
to be a random number series. To avoid feature track-
ing, the camera is required to randomly rotates around
the optical axis without the divergence of the camera
direction. In order to put such a rotation into practice,
the random series of the rotational velocity which cor-
responds to the small rotation between successive im-
ages in a discrete system is required to have a time
correlation. This indicates that the random camera
rotations should be modeled, for example, as an auto-
regressive (AR) series. In this study, for simplicity,
we assume that r
( j)
is a sample of the 2D Gaussian
white random variable.
p({r
( j)
}
M
j=1
|σ
2
r
) =
1
(
√
2πσ
r
)
2M
exp
(
−
∑
M
j=1
r
( j)⊤
r
( j)
2σ
2
r
)
.
(2)
In our experiments, firstly we generate the random
number series of an absolute camera direction accord-
ing to the 2D Gaussian white random variable with an
average of 0 and a variance of σ
2
, and use it to ro-
tate a camera. Therefore, the difference of the camera
direction series, which is treated as an unknown vari-
able, corresponds to r
( j)
. Although {r
( j)
} is a colored
series actually, we approximate its probability density
with Eq. 2 using σ
2
r
= 2σ
2
2.2 Depth Recovery
For the camera motion explained in Sec. 2.1, the op-
tical flow v ≡ [v
x
,v
y
]
⊤
is formulated as follows:
v
x
= xyr
x
−(1+ x
2
)r
y
+ yr
z
−Z
0
r
y
d ≡ v
r
x
−r
y
Z
0
d,
(3)
v
y
= (1+ y
2
)r
x
−xyr
y
−xr
z
+ Z
0
r
x
d ≡ v
r
y
+ r
x
Z
0
d,
(4)
where d ≡ 1/Z is an inverse depth.
The gradient equation, a first-order approximation
of the intensity invariant constraint before and after
the camera motion, is derived as follows:
f
t
= −f
x
v
x
− f
y
v
y
, (5)
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method
555

where f(x,y,t) is an image intensity, and f
x
, f
y
, f
t
are the partial derivatives of f, where (x,y) is a coor-
dinate system in an image plane and t indicates time.
The gradient equation is applied to a successive image
pair, in principle. By substituting Eqs. 3 and 4 into
Eq. 5, the gradient equation for a rigid object with the
camera rotations in Sec. 2.1 is derived.
f
t
= −( f
x
v
r
x
+ f
y
v
r
y
)−(−f
x
r
y
+ f
y
r
x
)Z
0
d ≡−f
r
− f
u
d.
(6)
Using Eq. 6, the inverse depth can be directly recov-
ered without optical flow detection. This scheme is
effective for shape from multiple images, since the in-
verse depth can be considered as a common variable
for all image pairs.
We assume that f
(i, j)
t
, where i and j are a pixel
position and a frame number respectively, includes an
observation error according to the Gaussian distribu-
tion with an average of 0 and a variance of σ
2
o
, but
f
(i, j)
x
and f
(i, j)
y
have no errors. We consider that the
equation error of the gradient equation is dominant in
the error of f
(i, j)
t
.
In addition, {d
(i)
} should be assumed to have lo-
cal correlation spatially, since an object usually has a
smooth structure. As a simple modeling, we use the
following prior of {d
(i)
}.
p(d|σ
2
d
) =
1
(
√
2πσ
d
)
N
exp
(
−
d
⊤
Ld
2σ
2
d
)
, (7)
where d is an N-dimensional vector consisting of
{d
(i)
}, where N indicates the number of pixels, and
L indicates the matrix corresponding to the 2D Lapla-
cian operator, and we control σ
2
d
heuristically in con-
sideration of the smoothness of a recovered depth
map.
Based on the probabilistic models of {r
( j)
},
{f
(i, j)
t
} and { d
(i)
} defined above, we can statisti-
cally estimate the inverse depth map. By applying
the MAP-EM algorithm (Dempster et al., 1977), σ
2
o
and {d
(i)
} are determined as a MAP estimator based
on p(d,σ
2
o
|{f
(i, j)
t
}) and {r
( j)
} is also determined as
a MAP estimator from p({ r
( j)
}|{f
(i, j)
t
},
ˆ
σ
o
2
,{
ˆ
d}), in
which ˆ· means a MAP estimator. It is noted that the
uniform distribution should be used as the prior of σ
2
o
,
because of no information of σ
2
o
in advance. The de-
tails of the estimation algorithm are shown in the lit-
erature (Tagawa, 2010), in which σ
2
r
is also estimated,
but in this study, it is assumed to be known as a setting
value.
3 SELECTION OF IMAGE PAIRS
FOR ACCURATE RECOVERY
Based on the condition that many image pairs are
available, we propose a scheme that at every pixel
we discard the gradient equations, i.e. discard the
image pairs having a large approximation error. In
each pixel, we decide which image pair should be dis-
carded.
At the first step, we focus on an alias problem.
An alias in signal processing is a state caused by a
low sampling rate as compared with the maximum
frequency of signals. In this study, when an image
motion between two images is large against the spa-
tial wavelength of a dominant image intensity pattern,
the direction of the detected optical flow is opposite to
the true direction and causes a large recovery error of
a depth map. In the image region where the alias oc-
curs, the angle between the spatial gradient vectors
of successive image pairs f
(i, j)
s
and f
(i, j+1)
s
, where
f
(i, j)
s
= [ f
(i, j)
x
, f
(i, j)
y
]
⊤
, tends to be large. Therefore,
the angle defined by both vectors can be used to find
the alias region. The image pairs in which the angle is
large should be detected in each pixel and discarded
thresholding.
In the next step, we further select the appropri-
ate image pairs independently in each pixel from the
image pairs remained through the first step described
above in consideration of the amount of nonlinear
terms included in the observation of f
t
. The exact f
t
is represented as follows:
f
t
= −f
x
v
x
− f
y
v
y
−
1
2

f
xx
v
2
x
+ f
yy
v
2
y
+ 2f
xy
v
x
v
y

+···
(8)
After discarding the exceedingly inappropriate image
pairs by the first step, the nonlinear term can be con-
sidered small, and the second order term in Eq. 8 can
be approximated at every pixel i as follows:
−
1
2
n
( f
(i, j)
x
− f
(i, j+1)
x
)v
(i, j)
x
+ ( f
(i, j)
y
− f
(i, j+1)
y
)v
(i, j)
y
o
.
(9)
This representation can be introduced from the fol-
lowing gradient equations with respect to f
x
and f
y
,
f
xx
v
x
+ f
xy
v
y
+ f
xt
= 0, (10)
f
yx
v
x
+ f
yy
v
y
+ f
yt
= 0, (11)
with the approximations of f
xt
≈ f
(i, j+1)
x
− f
(i, j)
x
and
f
yt
≈ f
(i, j+1)
y
− f
(i, j)
y
. Equation 9 can be computed
without detecting the second derivatives of f, which
tend to be noisy.
In this step, we take into account the SNR of f
t
.
When optical flow is small relative to a dominant in-
tensity pattern, the first term in Eq. 8 is likely to be
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
556

small. Inversely when optical flow is large, the term
in Eq. 9 tends to be large. Those means that the SNR
may lowers, if a camera motion is too small or too
large. To estimate the SNR of the observed f
t
, we can
define the measure J
o
as a ratio of the value of Eq. 9
and the first order term of Eq. 8.
J
o
≡
|( f
(i, j)
x
− f
(i, j+1)
x
)v
(i, j)
x
+ ( f
(i, j)
y
− f
(i, j+1)
y
)v
(i, j)
y
|
2|f
(i, j)
x
v
(i, j)
x
+ f
(i, j)
y
v
(i, j)
y
|
.
(12)
It can be easily known that J
o
depends on the direc-
tion of optical flow but is invariant with respect to the
amplitude of optical flow. Additionally, even if the
difference of the spatial gradients f
(i, j)
s
− f
(i, j+1)
s
is
large, when the direction of f
(i, j)
s
− f
(i, j+1)
s
is perpen-
dicular to the direction of optical flow, the value of
J
o
becomes small. Therefore, the value J ≡ |f
(i, j)
s
−
f
(i, j+1)
s
|/|f
(i, j)
s
| can be used as a worst value of J
o
,
which can be computed without the true value of op-
tical flow. In this study, the image pairs for which
the value of J is less than the certain threshold are se-
lected in each pixel to be used for depth recovery.
For the image pairs finally selected independently
in each pixel, the gradient equation including the sec-
ond order term is redefined as follows:
f
(i, j)
t
= −f
(i, j)
x
v
(i, j)
x
− f
(i, j)
y
v
(i, j)
y
−
1
2
n
( f
(i, j)
x
− f
(i, j+1)
x
)v
(i, j)
x
+ ( f
(i, j)
y
− f
(i, j+1)
y
)v
(i, j)
y
o
= −
3f
(i, j)
x
− f
(i, j+1)
x
2
v
(i, j)
x
−
3f
(i, j)
y
− f
(i, j+1)
y
2
v
(i, j)
y
.
(13)
In the following experiments, Eq. 13 is used in-
stead of Eq. 5.
4 EXPERIMENTS
4.1 Camera System
The developed camera system used to perform the ex-
periments of this study is shown in Fig. 2 with a target
object. The camera system can be rotated around the
horizontal axis i.e. X axis and around the vertical axis,
i.e. Y axis. The rotation around the optical axis, i.e. Z
direction, cannot be performed, which is not needed
to obtain the depth information. The parameters of
the system are shown as follows:
• Focal length: 2.8−5.0 mm
• Image size: 2 million (1200×1600) pix.
Figure 2: Camera system with target object.
• Movable range:
X-axis 360 deg., Y-axis (−10, +10) deg.
• Minimum moving unit:
X-axis 1 pulse = 0.01 deg.,
Y-axis 1 pulse = 0.00067 deg.
• Image property: 8 or 12 bit grayscale
While rotating the camera according to the rota-
tion data explained in Sec. 2.1, the computer captures
images automatically.
4.2 Results
We explain the results of the experiments using the
real images captured by the developed camera system.
The images are gray scale and consist of 256 ×256
pixels with 8 bit digitization. An example is shown
in Fig. 3(a). Before experiments, a focal length of
1141 pixel was measured by the conventional calibra-
tion method (Zhang, 2000). Our camera system has
a parallel stereo function, namely the camera can be
moved laterally by a slide system. The depth map re-
covered by the stereopsis is shown in Fig. 3(b). In this
figure, the horizontal axis indicates a position in the
image plane, and the vertical axis indicates a depth
value. The back board of the target object is 191.3
mm away from the lens center and the front board
in the center part is 141.5 mm. In the stereopsis, 10
points in an image were selected as a feature point for
each of back board region and the front board region
respectively, and were used for depth computing. The
average of the depth of each 10 points was computed
to determine the depth of the plane board. Z
0
was also
measured with 38.8 mm using the above depth value
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method
557

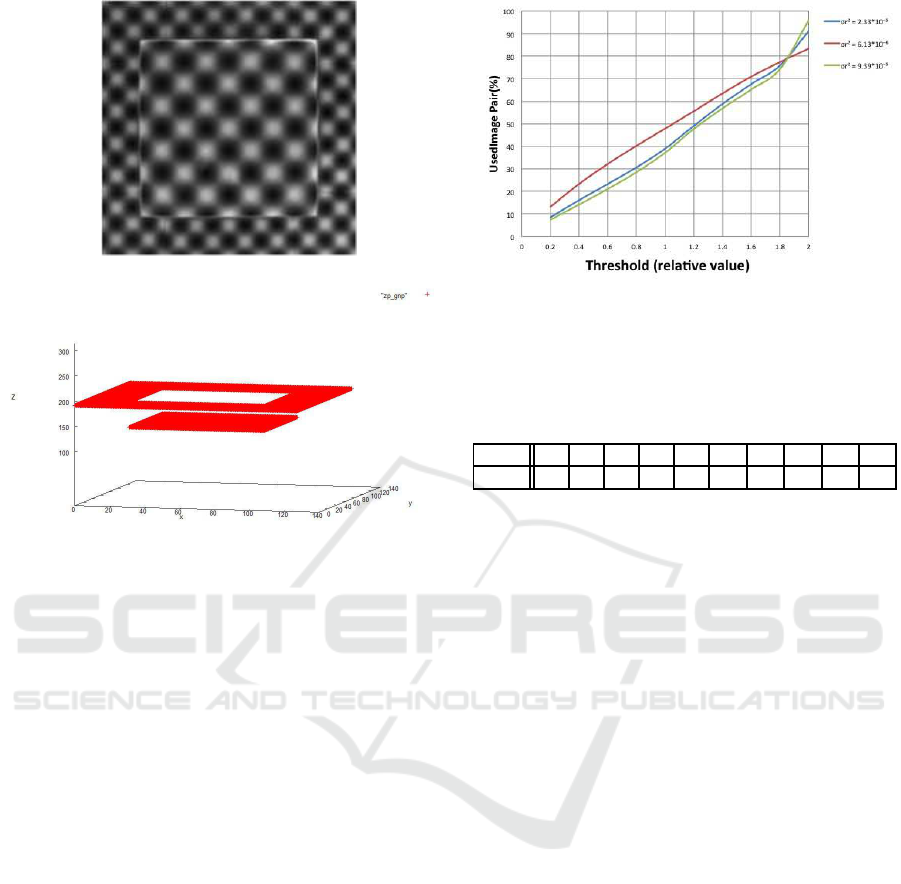
(a)
(b)
Figure 3: Data used for experiments: (a) example of cap-
tured image, (b) depth map recovered by binocular stereop-
sis.
of the object. The calibration algorithm for Z
0
is ex-
plained in the APPENDIX.
100 images were captured for each setting value
of σ
2
r
[rad
2
] and were used for recovery. We varied σ
2
r
as 6.13×10
−6
, 2.32×10
−5
and 9.39×10
−5
, by each
of which the average of the amplitude of the optical
flow approximately coincides with λ/8, λ/ 4 and λ/2
respectively, where λ indicates the wavelength of the
dominant intensity pattern. The smoothness parame-
ter of a depth map, σ
2
d
, was set as 1.0×10
−4
heuristi-
cally.
The combination of two threshold values required
for the two selection steps explained in Sec. 3 re-
spectively has to be carefully examined in the future
study, which includes the determination method of
the threshold values. In this study, we heuristically
use the combination of the threshold values shown in
Table1. The threshold value in the second step cor-
responds to the multiplying factor of the J’s average
about pixels selected by the first step in the region of
the front board of the target. Hence, for example, the
threshold value 2 is equivalent to twice the average.
The J’s average used as an unit as above changes by
the value of σ
2
r
: 0.594 for σ
2
r
= 6.13×10
−6
, 0.963 for
σ
2
r
= 2.33×10
−5
and 1.297 for σ
2
r
= 9.39×10
−5
.
The reason why the threshold value in the first step
is increased depending on the threshold value in the
Figure 4: Relation between usage rate of image pairs and
threshold for J, i.e. for second step. Blue line indicates
σ
2
r
= 6.13×10
−6
, red line indicates σ
2
r
= 2.32×10
−5
and
green line indicates σ
2
r
= 9.39×10
−5
.
Table 1: Combination of threshold values of first and second
steps for image pairs selection.
First
(deg.) 18 36 54 72 90 108 126 144 162 180
Second
(relative) 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
second step is that since the second step selection us-
ing a large threshold value can permit the selection of
the image pairs having a large high-order terms, a se-
vere limit by the first step may removethe effect of the
second step. However, when the limitation achieved
by the first step is loose, the definition of J, which is
introduced by assuming that the higher-order terms in
Eq. 8 is small, may not be reliable.
The relation between the thresholding and the us-
age rate of the image pairs in the experiments is
shown in Fig. 4 for the above mentioned three val-
ues of σ
2
r
. The threshold value of the second step
is used in the horizontal axis. The usage rate in the
vertical axis means the average for all pixels of the
rate of the finally selected image pairs in each pixel.
The usage rate increases in proportion to the thresh-
old value regardless of the value of σ
2
r
. It is noted
that the ratio of the image pairs of which the an-
gle of the spatial gradient vectors is larger than 90
deg. at every pixels with respect to the total num-
ber, i.e. N
2
×(M −1) = 256
2
×99 are 16.6% for
σ
2
r
= 6.13 ×10
−6
, 38.4% for σ
2
r
= 2.32 ×10
−5
and
52.2% for σ
2
r
= 9.39 ×10
−5
. In the future study, we
are planning that in the first step for the image pairs
selection, the image pairs with the angle being larger
than 90 deg. are totally discarded.
It can be confirmed also from Fig. 4 that when we
use image pairs of the same quantity for all three of
σ
2
r
, the selected image pairs for σ
2
r
= 2.32×10
−5
and
σ
2
r
= 9.39×10
−5
may include much high order com-
ponents more than those for σ
2
r
= 2.32 ×10
−5
. This
may cause the difference in the accuracy of recovery
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
558

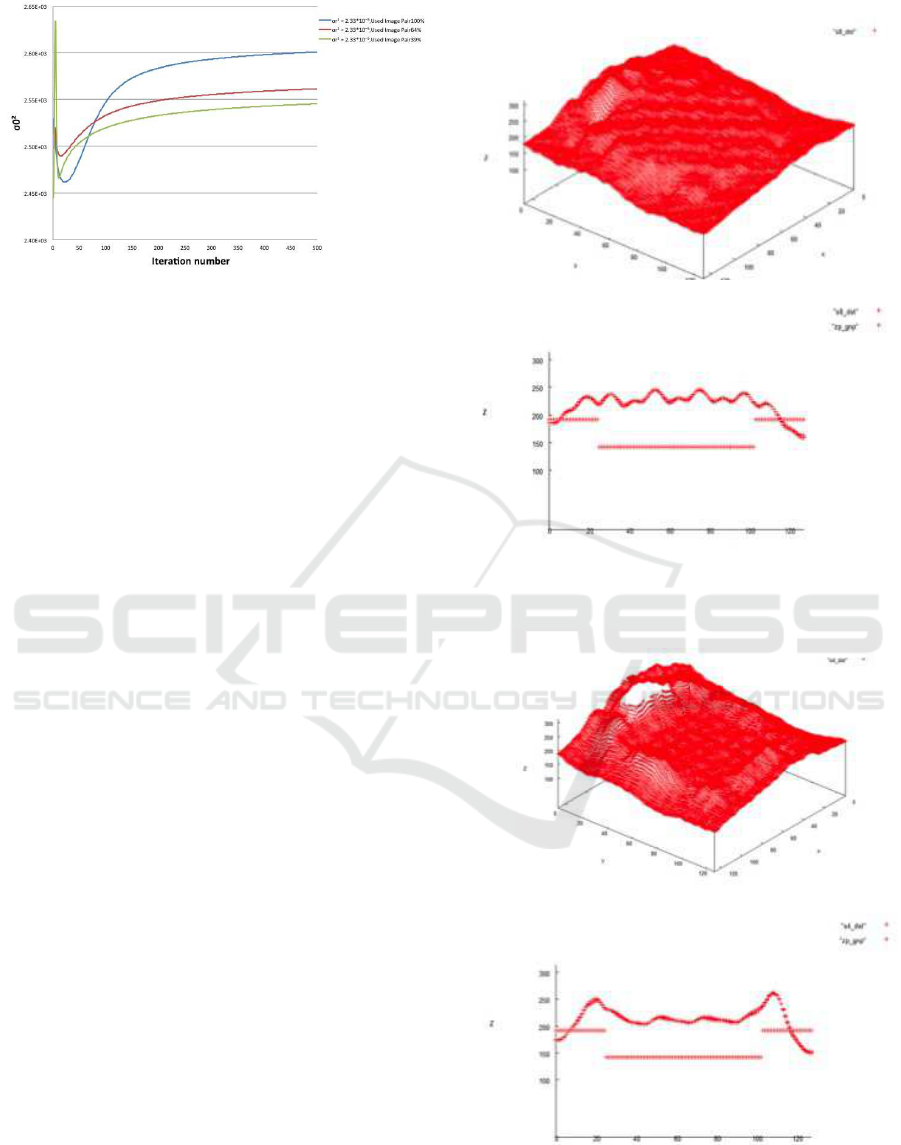
Figure 5: Convergence process of σ
2
o
in iteration of MAP-
EM algorithm with σ
2
r
= 2.32×10
−5
. Blue line indicates
usage rate= 100%, red line indicates usage rate= 64% and
green line indicates usage rate= 39%.
by σ
2
r
.
Figure 5 shows the convergence process of σ
2
o
in
the MAP-EM algorithm with σ
2
r
= 2.32×10
−5
. As a
matter of course, the convergencevalue of σ
2
o
is small
so that the usage rate is low.
The recovered depth maps with a small motion,
i.e. σ
2
r
= 6.13 × 10
−6
, using all image pairs are
shown in Fig. 6, in which a 3D representation and
a cross-sectional representation of the center region
are shown as (a) and (b) respectively. The result with
middle motion, i.e. σ
2
r
= 2.32×10
−5
, using all image
pairs are also shown in Fig. 7. For the large motion,
i.e. σ
2
r
= 9.39×10
−5
, depth recovery using all image
pairs has a large recovery error, and hence it is omit-
ted here. By comparing both results in Figs. 6 and
7 indicate that, although too small camera motion is
expected to cause no aliases, the generated depth in-
formation is very poor. However, even if the motion
becomes larger, enough improvement of the accuracy
cannot be achieved as far as we use all image pairs.
Figures 8, 9 and 10 show the recovered depth with
the selective use of appropriate image pairs as a cross-
sectional representation. From these figures, we can
confirm that the accuracy of recovery strongly de-
pends on the usage rate of image pairs. We can also
understand that the appropriate usage rate exists. This
tendency is confirmed also from Fig. 11 indicating
the RMSE (root mean square error) of the recovered
depth. For each motion size, the depth map recovered
comparatively well is shown in Figs. 12, 13 and 14
respectively.
It is confirmed from Fig. 11 that selecting the ap-
propriate image pairs is effective for all values of σ
2
r
,
but still, the suitable camera rotations with respect to
the spatial frequency of the object’s texture are desir-
able as a whole. In the experiments, the motion corre-
sponding to σ
2
r
= 2.32 ×10
−5
, i.e. middle motion is
optimal.
(a)
(b)
Figure 6: Depth recovered without selective use of image
pairs for σ
2
r
= 6.13×10
−6
: (a) 3D map, (b) cross-sectional
representation.
(a)
(b)
Figure 7: Depth recovered without selective use of image
pairs for σ
2
r
= 2.32×10
−5
: (a) 3D map, (b) cross-sectional
representation.
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method
559

(a)
(b)
(c)
(d)
Figure 8: Depth recovered with image pair selection for
σ
2
r
= 6.13×10
−6
with cross-sectional representation:(a) us-
age rate of 83%; (b) 64%; (c) 48%; (d) 32%.
The reason can be expected as follows: From
Fig. 11, the image pairs obtained by the motion ac-
cording to σ
2
r
= 2.32 ×10
−5
includes good image
pairs with approximately 60%. Each of such im-
(a)
(b)
(c)
(d)
Figure 9: Depth recovered with image pair selection for
σ
2
r
= 2.32 ×10
−5
with cross-sectional representation: (a)
usage rate of 83%; (b) 68%; (c) 49%; (d) 31%.
age pairs has the motion size of which is in the spe-
cific range. However, the image pairs generated by
a motion with σ
2
r
= 6.13 ×10
−6
or those with σ
2
r
=
9.39×10
−5
does not include enough quantity of such
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
560

(a)
(b)
(c)
(d)
Figure 10: Depth recovered with image pair selection for
σ
2
r
= 9.39×10
−5
with cross-sectional representation:(a) us-
age rate of 80%; (b) 56%; (c) 37%; (d) 25%.
a suitable motion. In addition, for σ
2
r
= 6.13 ×10
−6
or σ
2
r
= 9.39 ×10
−5
, if we select image pairs hav-
ing such a motion included in the suitable range by
adjusting the threshold values, the number of the se-
lected image pairs decreases and hence, the accuracy
of recovery tends to lower.
Figure 11: RMSE of recovered depth against use rate of
image pairs. Blue pot is σ
2
r
= 6.13×10
−6
, red plot is σ
2
r
=
2.32×10
−5
and green plot is σ
2
r
= 9.39×10
−5
.
Since the suitable size of optical flow is deter-
mined with respect to an wavelength of a dominant
intensity pattern, and the size of optical flow changes
according to the depth from the camera, the camera
motion averagely suitable for whole image depends
on a dominant texture and an averaged depth of a tar-
get object. After using such a camera motion, the
appropriate image pairs have to be selected indepen-
dently in each pixel, since a texture is not unique on
an object and local adjustment of optical flow used for
recovery should be performed by the proposed selec-
tive use technique.
As stated above, in the strategy in which appropri-
ate image pairs are selected from the limited number
of images, random camera motions having a variation
that is suited on the average for the texture and the
depth of a target object has to be determined in ad-
vance. However, it is difficult practically. To avoid
the problem, if the optimal threshold values can be
known as a constant, we should determine whether
each image pair should be used or not as an online
operation for obtaining enough amount of image pairs
while acquiring images continuously.
5 CONCLUSIONS
In this study, we proposed a technique to select the ap-
propriate image pairs, and confirmed its effectiveness
through experiments using the developed camera sys-
tem. The results assert that the gradient equation hav-
ing a large amount of high order components should
be discarded to improve the accuracy.
In the future work, the following tasks should be
solved.
• Optimal thresholding process
As described in Sec. 4.2, we have to examine
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method
561

Figure 12: 3D representation of recovered depth for σ
2
r
=
6.13×10
−6
with usage rate of 48%.
Figure 13: 3D representation of recovered depth for σ
2
r
=
2.32×10
−5
with usage rate of 49%.
Figure 14: 3D representation of recovered depth for σ
2
r
=
9.39×10
−5
with usage rate of 56%.
the method to combine the two steps for image
pairs selection. Since the first step is required
to simply evaluate the SNR using J = |f
(i, j)
s
−
f
(i, j+1)
s
|/|f
(i, j)
s
| which is used in the second step,
we should fix the threshold value in the first step
regardless of the second step. The optimal thresh-
old value in the second step is expected to be
determined by the prior simulations using artifi-
cially generated images having various intensity
patterns. The relation between the SNR of f
t
and
the threshold value should be clarified. On the
other hand, we will evaluate the approximation er-
ror obtained in Eq. 9 with respect to the second
order term in Eq. 8. Additionally, the relation be-
tween J
o
and J, which is a worst value of J
o
, will
be examined in order to confirm the effect using J
instead of J
o
.
• Camera Motion Estimation
We have to examine the influence on the accu-
racy of the estimate of {r
( j)
} due to discarding
observations partially, and ease it if it may be se-
vere. In the MAP-EM algorithm, {r
( j)
} is ex-
pected to be randomly sampled according to the
density of Eq. 2, but after discarding some wrong
image pairs, rs observed and used for depth recov-
ery may have a bias. Even if {r
( j)
} is a random
variable set according to the Gaussian distribu-
tion, those selected and used for recovery may be
modeled appropriately by the other distribution.
In addition, we should examine the approxima-
tion error of the density of {r
( j)
}. In this study,
the correlation between r
( j)
and r
( j−1)
is ignored.
• Depth Modeling
We have to modify the 2D Laplacian matrix used
in the prior of {d
(i)
} in Eq. 7 so as to take into ac-
count the discontinuity of an object. If we detect
a object edge in advance, the 2D Laplacian matrix
can be easily revised using such a edge informa-
tion. Alternatively, a line process or a region vari-
able can be additionally introduced, though the
computation is complicated.
REFERENCES
Azevedo, T. (2006). Development of a computer platform
for object 3d reconstruction using computer vision
techniques. In proc. Conf. Comput. Vision, Theory and
Applications, pages 383–388.
Brox, T. and Malik, J. (2011). Large displacement optical
flow: descriptor matching in variational motion esti-
mation. IEEE Trans. Pattern Anal. Machine Intell.,
33(3):500–513.
Bruhn, A. and Weickert, J. (2005). Lucas/kanade meets
horn/schunk: combining local and global optic flow
methods. Int. J. Comput. Vision, 61(3):211–231.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data. J. Roy.
Statist. Soc. B, 39:1–38.
Lazaros, N., Sirakoulis, G. C., and Gasteratos, A. (2008).
Review of stereo vision algorithm: from software to
hardware. Int. J. Optomechatronics, 5(4):435–462.
Ochs, P. and Brox, T. (2012). Higher order motion models
and spectral clustering. In proc. CVPR2012, pages
614–621.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
562

Samaras, D., Metaxas, D., Fua, P., and Leclerc, Y. G.
(2000). Variable albedo surface reconstruction from
stereo and shape from shading. In proc. Int. Conf.
CVPR, volume 1, pages 480–487.
Seitz, S. M. and Dyer, C. M. (1997). Photorealistic scene
reconstruction by voxel coloring. In proc. Int. Conf.
CVPR, pages 1067–1073.
Tagawa, N. (2010). Depth perception model based on fix-
ational eye movements using byesian statistical infer-
ence. In proc. Int. Conf. Pattern Recognition, pages
1662–1665.
Tagawa, N. and Koizumi, S. (2015). Selective use of opti-
mal image resolution for depth from multiple motions
based on gradient scheme. In proc. Int. Workshop on
Image Mining. Theory and Applications, pages 92–99.
Zhang, Z. (2000). A flexible new technique for camera cal-
ibration. IEEE Trans. Pattern Anal. Machine Intell.,
22(11):1330–1334.
APPENDIX
We recover the object shape by a binocular stereopsis,
and assume that the 3D point X
1
on the object mea-
sured from the coordinate associated with a reference
camera position shown in Fig. 15 corresponds to the
image position x
1
= [x
1
,y
1
,1
⊤
]. The same 3D point
is represented as X
2
with the coordinate after rotated
around the x-axis with a rotation matrix R,
R =


1 0 0
0 cosθ −sinθ
0 sinθ cosθ


. (14)
By the rotation, the lens center is translated as T,
which can be represented using the reference coor-
dinate as follows:
T = Z
0
z
2
−Z
0
z
1
= Z
0
Rz
1
−Z
0
z
1
= Z
0
(R−I)z
1
≡ Z
0
Sz
1
, (15)
where z
1
= [0,0,1]
⊤
. The relation between X
1
and X
2
is formulated as,
RX
2
= X
2
−T. (16)
By assuming that x
2
corresponds to x
1
and the posi-
tion of them are known in each image, we can use the
following equations.
x
1
=
X
1
Z
1
, x
2
=
X
2
Z
2
, (17)
where Z
2
is unknown. From those formulations, the
next equation is derived.
Z
2
Rx
2
= X
1
−Z
0
Sz
1
. (18)
Figure 15: Geometric illustration for determining Z
0
.
This equation is rewritten with components as fol-
lows:
Z
2


x
2
y
2
cosθ−sinθ
y
2
sinθ + cosθ


=


X
1
Y
1
+ Z
0
sinθ
Z
1
−Z
0
(cosθ −1)


.
(19)
Using the second and the third rows, Z
0
can be solved
as follows:
Z
0
=
Z
1
(y
2
cosθ−sinθ) −Y
1
(y
2
sinθ+ cosθ)
sinθ(y
2
sinθ+ cosθ) + (cosθ −1)(y
2
cosθ−sinθ)
.
(20)
Selective Use of Appropriate Image Pairs for Shape from Multiple Motions based on Gradient Method
563