
VOPT: Robust Visual Odometry by Simultaneous Feature Matching and
Camera Calibration
Rafael F. V. Saracchini
1
, Carlos Catalina
1
, Rodrigo Minetto
2
and Jorge Stolfi
3
1
Dept. of Simulation and Control, Technological Institute of Castilla y Len, Burgos, Spain
2
Dept. of Informatics, Federal University of Technology, Paran
´
a, Curitiba, Brazil
3
Institute of Computing, State University of Campinas, Campinas, Brazil
Keywords:
3D Tracking, Augmented Reality, Camera Calibration, Real-time and GPU Processing.
Abstract:
In this paper we describe VOPT, a robust algorithm for visual odometry. It tracks features of the environ-
ment with known position in space, which can be acquired through monocular or RGBD SLAM mapping
algorithms. The main idea of VOPT is to jointly optimize the matching of feature projections on successive
frames, the camera’s extrinsic matrix, the photometric correction parameters, and the weight of each feature
at the same time, by a multi-scale iterative procedure. VOPT uses GPU acceleration to achieve real-time per-
formance, and includes robust procedures for automatic initialization and recovery, without user intervention.
Our tests show that VOPT outperforms the PTAMM algorithm in challenging videos available publicly.
1 INTRODUCTION
Visual odometry (VO) is the determination of the mo-
tion of a video camera relative to a static environment
by comparing successive video frames (Scaramuzza
and Fraundorfer, 2011). This technique is used in sev-
eral applications in the field of robotics, entertainment
and autonomous navigation of terrestrial and aerial
vehicles (Weiss et al., 2013). Specifically, it is a core
component in most simultaneous tracking and map-
ping (SLAM) algorithms, which acquire a 3D model
of the environment as it is traversed. See figure 1.
The contribution of this paper is a robust and ef-
ficient algorithm for visual odometry, which we call
VOPT, with a GPU-based real-time implementation.
The VOPT algorithm uses a sparse model of the en-
vironment, consisting of an unstructured collection
of salient points in 3-space (optionally with surface
normals) that are associated to salient features of the
video frames. The positions and normals of those
tracked features can be obtained either by multiview
stereo or RGBD cameras. Our proposed method also
uses local photometric adjustments of individual fea-
tures to cope with variations in lighting, and is rela-
tively insensitive to motion blur and image noise.
This paper is organized as follows. The environ-
ment model and the algorithm are described in Sec-
tions 2 and 3. We describe our tests in Section 4 and
conclusions in Section 5.
(a) (b)
Figure 1: Input frame and associated visual odometry refer-
ence maps: (a) dense depth map and (b) sparse patch map.
1.1 Related Work
Most VO algorithms can be divided in three classes:
feature-based, appearance-based and patch-based.
Feature-based algorithms (Concha and Civera,
2014; Castle et al., 2008) identifies a large set of dis-
Saracchini, R., Catalina, C., Minetto, R. and Stolfi, J.
VOPT: Robust Visual Odometry by Simultaneous Feature Matching and Camera Calibration.
DOI: 10.5220/0005781700590066
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 61-68
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
61

tinguished features (such as corners and edges) in a
frame, matching them with a reference set and esti-
mating motion accordingly. By computing the posi-
tions of features with known 3D position its possible
estimate the camera motion position for each captured
frame. The most popular algorithm of this class is
PTAMM (Castle et al., 2008) and its variants (Klein
and Murray, 2009; Weiss et al., 2013). This class
of algorithms is relatively insensitive to lighting vari-
ations and occlusions. However, the feature detection
step is rather costly, since it must allow for affine dis-
tortions of the feature’s image between frames (Lowe,
2004; Bay et al., 2006; Alcantarilla et al., 2013). Such
algorithms are also badly affected by motion blur and
noise.
An appearance-based algorithm requires a 3D ge-
ometric model of the environment, and tries to de-
termine the camera pose for each frame by minimiz-
ing the difference between each observed frame and
a rendering of that model with the tentative camera
position. This approach was used by the DTAM algo-
rithm of Newcombe et al. (Newcombe et al., 2011b)
algorithm, which used a dense depth map representa-
tion. In order to reduce computational costs, Engel et
al. (Engel et al., 2013) and Forster et al. (Forster et al.,
2014) proposed the use of a semi-dense model con-
taining only the parts of the depth map near salient
elements like edges and corners. These methods are
less sensitive to motion blur and noise but are sensi-
tive to lighting variations (although lighting variations
can be alleviated by using dense maps (Maxime et al.,
2011)).
A patch-based algorithm follows an intermediate
approach. It uses a very sparse model of the envi-
ronment, consisting of a set of flat patches of the en-
vironment’s surface, with known 3D positions, ap-
pearance, and normal vectors. For each frame, the
camera position is adjusted until the computed projec-
tions of these surface patches match the correspond-
ing parts of the frame image. Examples of this class
are the Vachetti et al. (Vacchetti et al., 2004), and
the AFFTRACK algorithm of Minetto et al. (Minetto
et al., 2009). These algorithms have lower computa-
tional cost than appearance-based algorithms because
they don’t have to do a full rendering of the environ-
ment model for each tentative camera pose; and also
lower cost than feature-based algorithms because they
can predict the position and deformation of each patch
caused by the camera motion. VOPT can use ei-
ther the feature-based approach or the patch-based ap-
proach, depending on the availability of surface data.
2 DATA REPRESENTATION
Video Frames. A video is assumed to be a sequence
of N images F
0
,F
1
,...,F
N−1
, the frames, all with n
x
columns by n
y
rows of pixels. Each frame F
i
can be
viewed as a function from the rectangle D = [0,n
x
] ×
[0,n
y
] of R
2
to some color space, that is derived from
the pixel values by some interpolation schema.
Camera Model. We denote by ρ the projection func-
tion that maps a 3D point p of C to a 2D point q of
D belong to a frame, where C ⊂ R
3
is the cone of
visibility of the camera. We assume a pinhole cam-
era model, so that the projection is determined by the
3 × 4 homogeneous intrinsic matrix K of the camera
that defines the projection from the camera’s coor-
dinate system to the image sensor plane, and by the
4×4 homogeneous extrinsic matrix T that defines the
current position and pose of the camera relative to the
world’s coordinate system. We assume K known and
radial distortion removed a priori and that the camera
has fixed focal length (zoom), so that the K matrix is
the same for all video frames. We also assume that
the video frames have been corrected and do not have
any radial distortions.
The projection function ρ is defined by
q = ρ
K,T
(p) = KT
−1
p (1)
where p and q are represented as homogeneous co-
ordinate column vectors. Note that the T matrix in-
cludes the 3 coordinates of the camera’s position and
a 3 × 3 orthonormal rotation submatrix. We denote
by ~v(T, p) the unit direction vector in space from the
point p ∈ R
3
to the position of the camera implied
by the extrinsic matrix T and the projection function
ρ
K,T
0
(p) which maps a point p ∈ R
3
into image coor-
dinates.
Tracked Features. The essential information about
the environment is a list S = (s
0
,s
1
,...,s
n−1
) of fea-
tures on its surface. Each feature s
k
has a space po-
sition s
k
.p in R
3
and (optionally) a local surface nor-
mal s
k
.~u ∈ S
2
. (By convention, s
k
.~u is (0, 0, 0) if the
normal is not available.) Each feature s
k
is also asso-
ciated to a sub-image of some reference image s
k
.J ,
called the canonical projection of the feature. We will
assume that all reference images have the same do-
main D
∗
= [0, n
∗
x
] × [0,n
∗
y
] and were imaged with the
same intrinsic camera matrix K
∗
. The canonical pro-
jection of the feature is represented in the algorithm
by a pointer to the reference image s
k
.J , the extrinsic
camera matrix s
k
.T already determined for that refer-
ence image, a bounding rectangle s
k
.R ⊂ D
∗
, and a
mask s
k
.M . The mask is a pixel array with values in
[0,1], spanning that rectangle, that defines the actual
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
62

Figure 2: Projection of features s
0
and s
1
on the image K =
s
0
.J = s
1
.J , showing their bounding rectangles s
0
.R,s
1
.R
(left) and their masks s
0
.M ,s
1
.M (right).
extend and shape of the image feature on the reference
image. See figure 2.
Key Frames an Pose Graph. In order to start the
tracking, and restart it after a tracking failure, the al-
gorithm requires a list K = (K
∗
0
,K
∗
1
,...,K
∗
N
∗
−1
) of
reference images of the environment, the key frames.
Specifically, for each key frame K
∗
r
∈ K , the algo-
rithm requires an extrinsic matrix T
∗
r
and a set S
∗
r
of
features that are visible in it. It also requires a pose
graph G, whose vertices are the key frames, with an
edge between two key frames if their views have suf-
ficient overlap.
This Key Frame Data can be obtained from several
sources: frame squences, depth maps from with de-
vices like laser rangers and RGBD cameras, structure-
from-motion, etc. The feature set and pose graph are
then derived from sparse (Castle et al., 2008; En-
gel et al., 2013) or dense (Newcombe et al., 2011a;
Whelan et al., 2012) maps computed by SLAM algo-
rithms. The masks s
k
.M can be determined by back-
projecting the bounding rectangle s
k
.R into the scene
geometry, discarding regions which are not connected
to its centre and computing a weight proportional with
the difference of the surface normal with s
k
.~u. In case
of sparse maps, the mask is not computed and all its
values are set to 1.
3 TRACKING ALGORITHM
The VOPT algorithm is applied to each frame I = F
i
of a video sequence. Its normal case is described in
figure 3. It takes as inputs the collection of tracked
space features S, and the previous video frame I
0
=
F
i−1
with its extrinsic camera matrix T
0
. For each
feature s
k
in S it also receives the reliability weight
w
0
k
that measures its visibility in frame I
0
and how
well it matched its canonical projection. If success-
ful, the procedure returns the extrinsic matrix T for
frame I , and, for each feature s
k
, an adjusted weight
w
k
. It requires an startup procedure (Straub et al.,
Procedure VOPT(S,I , I
0
,T
0
,w
0
) returns (T,w)
1. (d,w) ← DISPLACEMENTS(S,I
0
,T
0
,w
0
,I )
2. (T,w) ← ESTIMCAMERA(S, T
0
,d,w);
3. (T,w) ← CAMADJUST(S, I , T,w)
Figure 3: The normal case of the VOPT algorithm.
2013; Saracchini and Ortega, 2014) to select the fea-
tures S to be tracked on the first image of the video,
I = F
0
, the extrinsic matrix T
0
. We used the approach
described in (Saracchini and Ortega, 2014) in order
to initialize the system and select the most likely key-
frames and associated features from the pose-graph
map. This procedure will be briefly described in sec-
tion 3.3.
The VOPT algorithm can be summarized as fol-
lows:
The procedure DISPLACEMENTS in step 1 first com-
putes the position c
0
k
of each feature pont s
k
.p with
w
0
k
> 0 on frame I
0
, using the corresponding camera
matrix T
0
. Then it uses the multiscale KLT algorithm
of Kanade et al. (Shi and Tomasi, 1994) to determine
the optical flow Φ : D → D between the frames I
0
and
I . For efficiency, the flow is computed only in a sub-
set of the domain, consisting of the union of 21 × 21
pixel squares centred at the points c
0
k
. The flow Φ is
applied to the center c
0
k
= ρ
K,T
0
(s
k
.p) of each feature
projection in I
0
to obtain its approximate apparent po-
sition c
k
in I . Note that each feature is independently
mapped, without considering the constraints of per-
spective change. The procedure returns the displace-
ment d
k
= c
k
− c
0
k
∈ R
2
between the projected feature
positions on frame I
0
and their apparent positions on
frame I . The weight w
k
of each feature is set to zero
if w
0
k
= 0, or if any of these steps fails (e.g. if c
0
k
falls
outside D).
In step 2, an initial estimate of the camera matrix
T is obtained from the 3D position s
k
.p of each fea-
ture, the camera matrix T
0
of the previous frame, and
its apparent displacement d
k
between the two frames.
We use Klein’s iterative M-Estimator (Klein, 2006),
except that the diagonal weight matrix W is computed
by the formula
W
2k,2k
= W
2k+1,2k+1
= w
0
k
1 +
r
k
2
−1
(2)
where r
k
the residual of the computed and observed
displacement is the Euclidean length of the difference
between the observed displacement d
k
and the dis-
placement computed from the 3D position s
k
.p, the
matrix T
0
, and the current version of the matrix T .
The M-estimator algorithm usually converges in 10
to 20 iterations. At the end, each reliability weight
w
k
is updated from the weight matrix W , by inverting
formula (2).
VOPT: Robust Visual Odometry by Simultaneous Feature Matching and Camera Calibration
63

In step 3, the initial estimate of the extrinsic matrix
T for frame I (wich is often imprecise, due to errors
in the displacements d
k
) is iteratively refined by the
procedure CAMADJUST, simultaneously with the re-
liability weight w
k
for each tracked feature s
k
. This
step is detailed in section 3.1.
3.1 Camera Pose Refinement
The procedure CAMADJUST receives as input the
list S of features that are being tracked, their cur-
rent weights w
k
, the next frame I , and an initial es-
timate T of its extrinsic matrix. It returns the ad-
justed matrix T and an updated reliability weight w
k
for each feature. The procedure is similar to the core
of the AFFTRACK (Minetto et al., 2009). It adjusts
the camera matrix T and the reliability weights w
k
it-
eratively for each level l of a image pyramid, by re-
fining the apparent positions the features on the cur-
rent frame, allowing for differences in illumination
between the canonical projection and the current pro-
jection of each feature. Features that are not visible
eventually get w
k
set to zero, and excluded from the
computation of T . See figure 4.
Procedure CAMADJUST(S, I ,T,w) returns (T,w)
1. Repeat while T does not converge, or until N
ca
iterations:
2. For each feature s
k
in S,
3. Let P
k
← GETLOCALMAP(s
k
,T )
4. d
k
← (0, 0)
5. For each level ` from N
ms
− 1 down to 0, do
6. For each feature s
k
with a valid map P
k
,
do
7. Scale P
k
,d
k
to level `.
8. (d
k
,w
k
) ←
FADJUST(s
k
,P
k
,I
(`)
,d
k
)
9. (T,w) ← ESTIMCAMERA(s, T, d,w)
Figure 4: The iterative camera adjustment procedure.
Each iteration of CAMADJUST first computes a local
2D projective transformation P
k
that describes the es-
timated position and deformation of each feature s
k
from its key frame s
k
.J to the image I , due to cam-
era motion between the two frames, assuming the cur-
rent guess for the matrix T. Then, for each feature s
k
,
the procedure determines a displacement d
k
from that
estimated position to the position that yields the best
match with the contents of frame I .This displacement
is computed by incremental adjustments at multiple
scales of resolution. Finally, the displacements d
k
are
used to correct the matrix T , by Klein’s M-Estimator.
The iteration stops when the adjusted matrix T does
not change significantly, or after N
ca
iterations.
Feature Deformation Map. The projective map P
k
computed in step 3 is obtained by lifting the rectangle
s
k
.R to 3D space and projecting it onto the frame I .
More precisely, let Π
k
be a plane in R
3
that passes
through the point s
k
.p and is perpendicular to the
surface normal s
k
.~u. If the surface normal s
k
.~u is
not known, then Π is assumed to be perpendicular
to ~v(S,s
k
.p). Each corner p of the rectangle s
k
.R is
mapped to a point q of R
2
by
q = ρ
K,T
(ρ
−1
K
∗
,S,Π
k
(p)) (3)
where S = s
k
.T is the extrinsic matrix of the key frame
of that feature, and ρ
−1
K
∗
,S,Π
k
is the function that back-
projects that key frame onto the plane Π
k
. However,if
s
k
.~u ·~v(T, s
k
.p) ≤ 0, or if a corner lies outside D, the
feature is considered invisible (self-occluded) in the
frame I . and the map P
k
is not defined. If the pro-
jected corners fall behind the camera or outside D the
feature is considered invisible, and P
k
invalid.
Multiscale Processing. In order to achieve robust
and efficient discovery of large (multi-pixel) displace-
ments, the feature adjustment step 8 is repeated at
multiple scales of resolution, using an image pyramid
I
(0)
= I , I
(1)
, I
(N
ms
−1)
, each level I
(`)
being scaled
by 1/2
`
in each axis. Note that the weights w
k
are
recomputed from scratch at each level.
Note also that the map P
k
and the accumulated dis-
placement d
k
are initially scaled by 1/2
N
ms
−1
and then
scaled by 2 when going from one level to the next
finer level. At each level, the FADJUST procedure can
only adjust the displacement d
k
by a few pixels. How-
ever, because of the multiscale processing, the total
displacement can be of the order of 2
N
ms
−1
pixels on
the original images.
3.2 Image Feature Position Adjustment
The FADJUST procedure is called for each feature s
k
and scale l, to refine the position of the feature on
the frame I . The procedure receives a 2D projective
map that defines the position and shape of the feature
on I , computed from the current guess of the matrix
T for that frame; and a displacement d
k
found by
image matching at coarser scales. First, the procedure
estimates the changes in the lighting of the feature
between those two frames, then it applies a small
correction to the displacement d
k
with the Lucas-
Kanade local image matching algorithm (Birchfield,
2014). The weight w
k
of each feature is defined based
on the quality of the match. See figure 5.
Photometric Correction. The procedure
PHOTOCORR in step 3 determines the correc-
tion of pixel values under lighting effects, which is
needed to compensate for changes in illumination
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
64

Procedure FADJUST(s
k
,P
k
,I ,d
k
) returns (d
k
,w
k
)
1. Set R
k
to the bounding box of P
k
(s
k
.R) dis-
placed by d
k
.
2. If R
k
is contained in D and has at least 4 rows
and 4 columns,
3. (α
k
,β
k
) ← PHOTOCORR(s
k
,P
k
,d
k
,I )
4. If α
k
≥ α
min
,
5. (d
k
,w
k
) ← LK(s
k
,P
k
,d
k
,I ,α
k
,β
k
)
6. else set w
k
← 0
7. else set w
k
← 0
Figure 5: The local feature position adjustment procedure.
between the two frames, including the effects of shad-
owing, surface orientation, glossy highlights, etc. We
assume that these effects can be well approximated
by an affine function I (P
k
(p) + d
k
) ≈ α
k
K (p) + β
k
,
for any point p within the mask N = s
k
.M ; where
K = s
k
.J . Basically, α
k
is the relative change in
contrast, and β
k
captures the difference of the ‘black
levels’ of the two images around the respective
projections of the feature. The values of α
k
and β
k
are obtained by weighted least squares, using the
squared discrepancy Q defined by
Q(d
k
,α
k
,β
k
) =
∑
p∈s
0
k
.R
N (p)(α
k
K (p)+β
k
−I (P
k
(p)+d
k
))
2
(4)
for the given value of the displacement d
k
. If α
k
is
negative (meaning that darker areas of the canonical
projection became lighter on the current image, and
vice-versa) or zero, the procedure consider the feature
lost and/or obscured by pixel noise, setting the weight
w
k
to zero. On the other hand, β
k
can be positive or
negative.
Local Feature Matching. In step 5, the Lucas-
Kanade (LK) algorithm (Birchfield, 2014) is used to
adjust the displacement d
k
so that the pixel values of
I are most similar to those of K = s
k
.J , after mapped
by P
k
, displaced by d
k
, and color-corrected accord-
ing to α
k
and β
k
. The similarity is evaluated by the
same Q functional (4) used for photometric correc-
tion. If the LK algorithm does not converge after N
lk
iterations, we consider the adjustment failed, and set-
ting w
k
to zero. Otherwise we set w
k
to exp(−z
2
/2),
where z = Q/(α
2
i
σ
2
) and σ is the expected standard
deviation of the pixel noise.
GPU Acceleration. Steps 3 and 5 of FADJUST are
responsible for most of the computational cost of
the VOPT algorithm, requiring computation of sums
over all pixels of a feature projection, mapped by the
deformation map P
k
. We compute those sums on GPU
by parallel reduction (Harris et al., 2007; Micikevi-
cius, 2009), and warping images by bi-cubic inter-
polation (Ruijters et al., 2008) using texture memory,
which is initialized in the startup procedure. The key
frames s
k
.J and the image feature masks s
k
.M are
copied into the GPU’s texture memory, and the tex-
ture warping functions are used to map the pixel po-
sitions in the key frame to the current frame by fast
cubic interpolation (Ruijters et al., 2008). Those two
steps require solving 2 × 2 linear systems, which are
solved in the CPU.
3.3 Initialization and Recovery
The VOPT algorithm requires an auxiliary startup
procedure to select the features to be tracked on the
first image of the video, I = F
0
, and to define the
extrinsic matrix T
0
for that frame. This procedure is
also needed to restart the odometry if the VOPT al-
gorithm fails, e.g. because there are not enough fea-
tures that are visible in the frame (specifically, if the
CAMADJUST procedure ends with fewer than 5 fea-
tures with non-zero weight w
k
). If VOPT fails when
trying to go from some frame I
0
= F
i−1
to the next
frame I = F
i
, we give up on that frame and apply the
startup procedure to frame I = F
i+1
.
The startup procedure looks for the most similar
key-frame K
∗
r
in K to the target image I by feature-
matching, using the vocabulary tree technique of Nis-
ter and Stewenius (Nister and Stewenius, 2006) and
extended in (Saracchini and Ortega, 2014). After-
wards, we build a list S of features to be tracked as
the union of S
∗
r
and of all S
∗
s
such that K
∗
s
is adja-
cent to K
∗
r
in the pose graph G. The startup pro-
cedure then computes an approximate estimate T for
the matrix of frame I using RANSAC. Finally it uses
the CAMADJUST procedure to improve the estimated
camera pose. This procedure, although very robust,
is noticeably slower than the odometry procedure due
the high computational cost of detecting and match-
ing features.
4 EXPERIMENTS
Test Videos. We tested the VOPT algorithm on both
synthetic and real video sequences. See Table 1. In
all tests, we set N
ca
= 2, N
lk
= 10 iterations, N
ms
= 3
pyramid levels, α
min
= 0, and σ = 0.1. All the al-
gorithms were tested in standard PC with an Intel i5
3.2 Ghz, 4GB of RAM, and Geforce 650 GTX graph-
ics card. The operational system was Linux Debian
”wheezy” 64-bit.
The real videos were captured with a hand-held
Logitech C930 camera, recording 840 × 480 frames
at 30 fps, with fixed focal length. The intrinsic cam-
era matrix K was determined by OpenCV calibration.
One set of real videos (group M) was obtained by mov-
ing the C930 camera back and forth over a cluttered
VOPT: Robust Visual Odometry by Simultaneous Feature Matching and Camera Calibration
65

Table 1: Video dataset information. Notes: videos with (o)
feature occlusion, (m) motion, (l) adverse lighting, (b) mo-
tion blur and (*) navigation in unmapped regions.
Video Frames Notes
S0 241 [m]
S1 241 [o,m]
Synthetic
S2 241 [b,m]
S3 241 [o,b,m]
S4 241 [l,m]
S5 241 [l,o,m]
S6 241 [l,b,m]
S7 241 [l,b,o,m]
Real
M0 711 [o,m]
M1 510 [o,b,m]
C0 1207 [o,b,m]
C1 425 [o,b,m]
C2 1015 [o]
C3 709 [o,m]
C4 666 *[o,b,m]
office desk. Another set of videos (group C) was taken
by walking down a laboratory corridor with the cam-
era.
The synthetic videos (group S) were generated by
rendering a 3D model of an abbey with the Blender
ray-tracer (Blender Online Community, 2014).For
each video frame F
i
, we saved the corresponding ex-
trinsic camera matrix T
#
i
used in the rendering. We se-
lectively enabled challenging factors such as motion
blur, localized illumination by spotlights, and occlu-
sion by several objects.
Key Frame Data. For each of the groups S, M, and
C, we used the PTAMM (Castle et al., 2008) to obtain
one set KPT of key frame data, including the set of key
frames K , the pose graph G, and, for each key frame
K
∗
r
, the extrinsic matrix T
∗
r
, and the set of features S
∗
r
using a reference video without adverse effects. The
input to PTAMM was a reference video in plain RGB
format, distinct from the test videos. For the M and
C groups, the reference video was acquired with the
C930 camera. For the S group, the reference video
was rendered with Blender, without the extra chal-
lenging factors. For each key-frame, we discarded
redundant features, accepting at most 60, and a total
limit of 180.
We also tested the algorithm with reference maps
obtained from depth 3D reconstruction. For the the
groups S and C, we produced a set KSO of key frames
containing dense data, constructing the pose-graph
map with a RGBD-SLAM algorithm (Saracchini and
Ortega, 2014) for the C group and by depth-map ren-
dering the 3D model of the abbey at regularly spaced
intervals for the S group. The feature sets S
∗
r
were
extracted by using a corner detector (Shi and Tomasi,
1994), discarding regions without depth, and normals
computed directly from the depth map.
Algorithms and Metrics. For each test video, we
ran the VOPT algorithm with the KPT key frame
data set (S, M, and C groups) and with the KSO data
set (S and C groups). For comparison, we also ran
the visual odometry module of PTAMM (PTAMM-
VO) on each video with its original frame data with
the key frame data KPT obtained by PTAMM, ex-
cept that the feature sets were not trimmed. For
each test run, we recorded the fraction κ of frames
that were successfully calibrated (either by the startup
procedure or by VOPT), the number L of tracking
losses and average processing time per frame t in mil-
liseconds. For the synthetic videos, we also com-
puted the RMS error ¯e between the estimated T
i
and
the ground-truth T
#
i
. The test videos, key frame
data sets, and outputs of all these runs are available
at http://www.liv.ic.unicamp.br/ saracchini/VOPT/.
Results. Our results are summarized in figures 6, 7
and Table 2. It can be seen that VOPT was gener-
ally more accurate (smaller ¯e) and robust (larger κ,
smaller L), outperforming PTAMM using less data
and achieving best results when using dense data
KSO and in both cases it performed much better than
PTAMM-VO. The latter failed more often, and had
more difficulty in recovery, in the presence of light-
ing variations, motion blur, and occlusions. It failed
only with extreme motion blur or in absence of vis-
ible features, which is the case of video C4. VOPT
executed in 9–45 ms, depending on the number of it-
erations needed in steps 2–1 of CAMADJUST and of
the Lucas-Kanade step 5 in FADJUST. Recovery after
failure was much slower (50− −180 ms) due the high
cost of feature matching. In comparison, PTAMM
processed each frame in 8 − −10 ms.
5 CONCLUSIONS
Our tests show that the VOPT algorithm is slight
slower than PTAMM’s visual odometry mode, but is
considerably more accurate and robust, especially in
the presence of motion blur, occlusions, and localized
lighting variations. It owes these qualities mainly to
the simultaneous adjustment of the camera matrix, the
photometric correction parameters, and the reliability
weights of individual features. VOPT was also used
with success in indoor navigation algorithms of an as-
sisted living device with on-site AR capabilities (NA-
CODEAL, 2014).
Besides its robustness, the proposed algorithm
still have limitations which shall be overcome in fu-
ture works. Namely, it depends on an associated
SLAM method to compute the features data needed
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
66
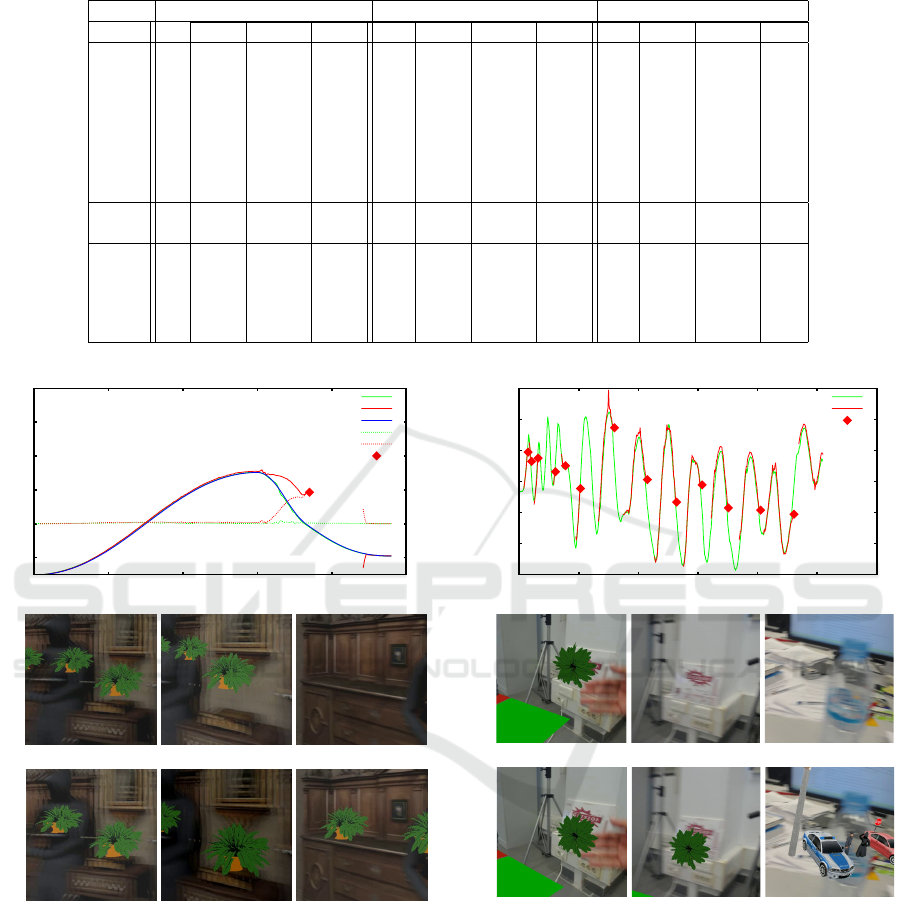
Table 2: Tests with computed values of L (tracking losses), κ (successfully calibration), ¯e (RMS error) and t (time in ms).
Video VOPT (sparse - KPT) VOPT (dense - KSO) PTAMM-VO
L κ ¯e t L κ ¯e t L κ ¯e t
S0 0 1.00 0.048 16.9 0 1.00 0.008 18.8 0 0.98 0.042 3.4
S1 0 1.00 0.049 18.6 0 1.00 0.008 20.9 0 0.98 0.043 3.2
S2 0 1.00 0.062 17.2 0 1.00 0.055 19.5 1 0.85 1.002 2.9
S3 0 1.00 0.061 19.2 0 1.00 0.082 21.6 1 0.84 0.732 2.8
S4 0 1.00 0.042 18.9 0 1.00 0.009 22.1 3 0.79 7.679 1.9
S5 0 1.00 0.037 19.6 0 1.00 0.012 23.1 3 0.48 2.897 3.0
S6 0 1.00 0.060 20.2 0 1.00 0.046 25.1 2 0.11 1.507 1.2
S7 0 1.00 0.064 20.7 0 1.00 0.051 24.8 2 0.14 4.774 1.1
M0 0 1.00 - 27.3 - - - - 6 0.92 - 2.1
M1 0 1.00 - 30.7 - - - - 13 0.67 - 3.1
C0 2 0.99 - 15.2 0 1.00 - 15.5 10 0.52 - 1.8
C1 1 0.97 - 14.9 0 1.00 - 18.8 2 0.88 - 2.0
C2 0 1.00 - 12.3 0 1.00 - 14.6 4 0.79 - 2.1
C3 0 1.00 - 13.5 0 1.00 - 16.4 3 0.81 - 1.7
C4 9 0.83 - 12.8 11 0.87 - 18.7 11 0.71 - 2.3
-2
0
2
4
6
8
0 50 100 150 200 250
frame
VOPT Traj. x
PTAMM Traj. x
Ground-truth Traj. x
VOPT Error. x
PTAMM Error. x
PTAMM L
185
PTAMM
VOPT
(a) S3-165 (b) S3-173 (c) S3-185
Figure 6: Plot of x camera position of sequence S3, and
AR output in the virtual scene with its respective sequence
and frames. Note the increasing drift in the AR output of
PTAMM.
for odometry. It also do not provide an efficient
method to update the list of tracked features from the
map after initialization. In the current implementation
it allows to local tracking only, if the camera moves
outside the region covered by the selected patches a
tracking loss and subsequent reinitialization will fol-
low. Finally the dependency on a GPU makes it less
suitable for devices without a dedicated graphics card.
-1.6
-1.4
-1.2
-1
-0.8
-0.6
-0.4
0 100 200 300 400 500 600
frame
VOPT Traj. x
PTAMM Traj. x
PTAMM L
15
21
32
61
78
103
160
215
264
307
351
405
461
PTAMM
VOPT
(a) C0-794 (b) C3-287 (c) M1-354
Figure 7: Plot of x camera position of sequence M1, and
AR output (plant/car) in occurrence of occlusions(a), mo-
tion blur(b) and both conditions(c) with its respective se-
quence and frames.
Future works will involve the development of
light-weight version of VOPT aimed to mobile de-
vices, as well the incorporation of the VOPT as effec-
tive module of a full SLAM system, overcoming the
aforementioned limitations. We aim also for a more
efficient usage of the GPU capabilities by exploiting
cache and spatial locality.
VOPT: Robust Visual Odometry by Simultaneous Feature Matching and Camera Calibration
67

ACKNOWLEDGEMENTS
This work was funded by the Ambient Assisted Liv-
ing Joint Programme as part of the project Natu-
ral Communication Device for Assisted Living, ref.
AAL-2010-3-116 (NACODEAL, 2014).
REFERENCES
Alcantarilla, P. F., Nuevo, J., and Bartoli, A. (2013). Fast
explicit diffusion for accelerated features in nonlin-
ear scale spaces. In British Machine Vision Conf.
(BMVC).
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In Leonardis, A., Bischof,
H., and Pinz, A., editors, Computer Vision – ECCV
2006, volume 3951 of Lecture Notes in Computer Sci-
ence, pages 404–417. Springer Berlin / Heidelberg.
Birchfield, S. (2014). Derivation of
kanade-lucas-tomasi tracking equation.
https://www.ces.clemson.edu/ stb/klt/birchfield-
klt-derivation.pdf.
Blender Online Community (2014). Blender - a 3D mod-
elling and rendering package. Amsterdam.
Castle, R., Klein, G., and Murray, D. (2008). Video-Rate
Localization in Multiple Maps for Wearable Aug-
mented Reality. In IEEE International Symposium on
Wearable Computers (ISWC), pages 15–22.
Concha, A. and Civera, J. (2014). Using Superpixels in
Monocular SLAM. In IEEE International Conference
on Robotics and Automation (ICRA), pages 365–372.
Engel, J., Sturm, J., and Cremers, D. (2013). Semi-dense
visual odometry for a monocular camera. In IEEE In-
ternational Conference on Computer Vision (ICCV),
pages 1449–1456.
Forster, C., Pizzoli, M., and Scaramuzza, D. (2014). SVO:
Fast Semi-Direct Monocular Visual Odometry. In
IEEE International Conference on Robotics and Au-
tomation (ICRA), pages 15–22.
Harris, M. et al. (2007). Optimizing Parallel Reduction in
CUDA. NVIDIA Developer Technology, 2(4).
Klein, G. (2006). Visual Tracking for Augmented Reality.
PhD thesis, University of Cambridge.
Klein, G. and Murray, D. (2009). Parallel tracking and map-
ping on a camera phone. In IEEE International Sym-
posium on Mixed and Augmented Reality (ISMAR),
pages 83–86.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. Int. J. Comput. Vision, 60(2):91–
110.
Maxime, M., Comport, A., and Rives, P. (2011). Real-Time
Dense Visual Tracking under Large Lighting Varia-
tions. In British Machine Vision Conference (BMVC),
pages 45.1–45.11. BMVA Press.
Micikevicius, P. (2009). 3D Finite Difference Computation
on GPUs using CUDA. In Workshop on General Pur-
pose Processing on Graphics Processing Units, pages
79–84. ACM.
Minetto, R., Leite, N., and Stolfi, J. (2009). AFFTrack: Ro-
bust Tracking of Features in Variable-Zoom Videos.
In IEEE International Conference on Image Process-
ing (ICIP), pages 4285–4288.
NACODEAL (2014). NACODEAL - Natural Communi-
cation Device for Assisted Living. European Union
Project. www.nacodeal.eu. Ambient Assisted Living
Joint Programme ref. AAL-2010-3-116.
Newcombe, R., Izadi, S., Hillige, O., Molyneaux, D., Kim,
D., Davison, A., Kohli, P., Shotton, J., Hodges, S.,
and Fitzgibbon, A. (2011a). KinectFusion: Real-time
Dense Surface Mapping and Tracking. In IEEE Inter-
national Symposium on Mixed and Augmented Reality
(ISMAR), pages 127–136.
Newcombe, R., Lovegrove, S., and Davison, A. (2011b).
DTAM: Dense Tracking and Mapping in Real-Time.
In IEEE International Conference on Computer Vision
(ICCV), pages 2320–2327.
Nister, D. and Stewenius, H. (2006). Scalable recognition
with a vocabulary tree. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion, volume 2, pages 2161–2168.
Ruijters, D., Romeny, B., and Suetens, P. (2008). Efficient
GPU-Based Texture Interpolation using Uniform B-
Splines. Journal of Graphics, GPU, and Game Tools,
13(4):6169.
Saracchini, R. and Ortega, C. (2014). An Easy to Use Mo-
bile Augmented Reality Platform for Assisted Living
using Pico-projectors. In Computer Vision and Graph-
ics, volume 8671 of Lecture Notes in Computer Sci-
ence, pages 552–561. Springer.
Scaramuzza, D. and Fraundorfer, F. (2011). Visual odom-
etry [tutorial]. Robotics & Automation Magazine,
IEEE, 18(4):80–92.
Shi, J. and Tomasi, C. (1994). Good Features to Track.
In IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 593–600.
Straub, J., Hilsenbeck, S., Schroth, G., Huitl, R., Moller,
A., and Steinbach, E. (2013). Fast Relocalization for
Visual Odometry using Binary Features. In IEEE In-
ternational Conference on Image Processing (ICIP),
pages 2548–2552.
Vacchetti, L., Lepetit, V., and Fua, P. (2004). Stable Real-
Time 3D Tracking Using Online and Offline Infor-
mation. IEEE Trans. Pattern Anal. Mach. Intell.,
26(10):1385–1391.
Weiss, S., Achtelik, M., Lynen, S., Achtelik, M., Kneip,
L., Chli, M., and Siegwart, R. (2013). Monocular Vi-
sion for Long-term Micro Aerial Vehicle State Esti-
mation: A Compendium. Journal of Field Robotics,
30(5):803–831.
Whelan, T., Kaess, M., Fallon, M., Johannsson, H.,
Leonard, J., and McDonald, J. (2012). Kintinuous:
Spatially Extended KinectFusion. Technical Report
MIT-CSAIL-TR-2012-020, MIT.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
68
