Low Resolution Sparse Binary Face Patterns

Swathikiran Sudhakaran

and Alex Pappachen James

Fondazione Bruno Kessler, Trento, Italy

Nazarbayev University, Astana, Kazakhstan

Keywords:

Low Resolution, Face Recognition, Thumbnails, Wavelet Transform, Local Binary Pattern, Nearest Neigh-

bour, Sparse Coding.

Abstract:

Automated recognition of low resolution face images from thumbnails represent a challenging image recog-

nition problem. We propose the sequential fusion of wavelet transform computation, local binary pattern

and sparse coding of images to accurately extract facial features from thumbnail images. A minimum dis-

tance classiﬁer with Shepard’s similarity measure is used as the classiﬁer. The proposed method shows robust

recognition performance when tested on face datasets (Yale B, AR and PUT) when compared against bench-

mark techniques for very low resolution (i.e. less than 45x45 pixels) face image recognition. The possible

applications of the proposed thumbnail recognition include contextual search, intelligent image/video sorting

and groups, and face image clustering.

1 INTRODUCTION

The need to have biometric features in electronic de-

vices having personalised contents is seen to grow in

the upcoming years. Among several biometric modal-

ities face images represent an obvious method to re-

veal identity of the individual. This paper focuses on

recognition of faces from thumbnails that has sev-

eral applications in mobile devices such as contex-

tual searching, personalisation of contents, and as a

modality for biometric security, while in surveillance

systems they reﬂect as very low resolution (VLR)

problem (Zou and Yuen, 2010).

The automated recognition of faces in general is

a challenging task for low resolution digital face im-

ages taken under unconstrained recognition environ-

ments (Li et al., 2010; Lai and Jiang, 2012; Marciniak

et al., 2012). The natural variability that complicates

the face recognition methods include changes in face

poses, illumination changes, occlusions, aging, cam-

era sensing errors, and changes in facial expressions.

As a solution to this real world problem, several tech-

niques were proposed by researchers. Most of these

existing solution made use of the technique of super

resolution to generate a high resolution image from

the available low resolution image. Earlier methods

used simple interpolation techniques for generating

the higher resolution images. Because of its unsuit-

ability in producing acceptable results, several super

resolution algorithms involving complex optimization

problems were proposed (Baker and Kanade, 2000),

(Freeman et al., 2000), (Xu et al., 2014). These meth-

ods suffered from the problem of computational com-

plexity thereby making these unusable in real time

conditions.

In this paper, we focus on recognising faces from

very low resolution images under the inﬂuence of dif-

ferent natural variability tested on various standard

face datasets. We use a combination of feature for-

mation techniques that partly mimic the response of

vision systems in human brain and encode the fea-

tures to reduce the impact of natural variability.

2 SPARSE BINARY PATTERNS

The proposed method inspires from the psychovisual

similarity in the functioning of the neurons in the

layer V1 of the visual cortex with that of wavelets

(Field, 1999), sparse features and Shepard’s percep-

tion measure for distance calculations. The proposed

feature extraction technique from thumbnail images

are summarised as a block diagram in Fig. 1 and the

summary of the method is provided in Algorithm 1.

The algorithm primarily consists of wavelet computa-

tion, local binary pattern based image description and

a sparse distributed feature extraction scheme. The

wavelet transform of the facial image allows one to

188

Sudhakaran, S. and James, A.

Low Resolution Sparse Binary Face Patterns.

DOI: 10.5220/0005782601860191

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 188-193

ISBN: 978-989-758-175-5

capture the shape features of the image after neglect-

ing irrelevant noisy edge features. The local binary

pattern enables the efﬁcient description of local facial

features in a pixel level. The sparse distributed feature

extraction method converts the local features present

in the local binary pattern image into a global feature

descriptor.

Figure 1: The block diagram of the proposed feature extrac-

tion technique.

The proposed feature extraction technique divides

the input image into non-overlapping blocks and per-

forms a block-wise computation of wavelet transform.

The two dimensional discrete wavelet transform is

given by Eq 1.

j,n

∞

−∞

− n

)s(x); (1)

where, k = {0,1,2,3}, s(x) is the input image and

is the mother wavelet is deﬁned by: ψ

) =

φ(x

)φ(x

), ψ

) = φ(x

)ψ(x

), ψ

) =

ψ(x

)φ(x

), and ψ

) = ψ(x

)ψ(x

). The two

dimensional wavelet transform results in four sub-

bands consisting of wavelet coefﬁcients. The ﬁrst

sub-band contains the low frequency coarse features

of the image while the other three sub-bands contain

the high pass detail coefﬁcients that give information

about horizontal, vertical and diagonal edges present

in the image. We make use of the low frequency or

approximation coefﬁcients since it contains the shape

features of the image (Zhang et al., 2004) and the de-

tail coefﬁcients are neglected for further processing.

The proposed feature extraction technique begins

by dividing the input image into non-overlapping

blocks followed by the wavelet computation of each

image block. From the wavelet sub-bands of each

block, the approximation image of each block is ex-

tracted and combined to obtain the approximation im-

age of the input image. The block-wise wavelet trans-

form allows to capture more local features compared

to applying the wavelet transform to the whole of

the image. As mentioned above, a careful selection

of wavelet base is required to improve the perfor-

mance of the system. But no study has been previ-

ously conducted regarding the suitability of each fam-

ily of wavelet bases in various image processing ap-

plications. So, we have to experimentally validate the

performance of each wavelet base for the given low

resolution face recognition problem.

Algorithm 1: Feature extraction using sparse distributed

representation for face recognition.

Input: Low resolution facial image(I) of dimension

m×n

Output: Feature vector subset (F

∗

) of length C =

(k×m×n)/(W ×2)

1: Divide the image into blocks of size M×N to

get L number of blocks

2: for l=1 to L do

3: Compute wavelet transform

4: Extract the approximation coefﬁcients

5: end for

6: Combine the approximation image blocks

to get the approximation image(I

) of input

image(I)

7: for Each pixel I

(x,y) in I

8: Extract the 8 immediate neighbours of I

(x,y)

9: Threshold each neighbour using I

(x,y) as

the threshold

10: I

(x − i,y − j) =

(

1, I

(x − i, y − j) ≤ I

(x,y)

0, otherwise

11: i, j ∈ {−1,1}

12: The LBP value of I

(x,y) is obtained as

13: I

LBP

(x,y) = I

(x − 1,y − 1) + 2I

(x − 1,y) +

(x − 1,y + 1) + 8I

(x,y + 1) + 16I

(x +

1,y + 1) + 32I

(x + 1,y) + 64I

(x + 1,y − 1) +

128I

(x,y − 1)

14: end for

15: Convert the image I

LBP

to P bit planes

16: for p=0 to P − 1 do

17: Select p

bit plane

18: for c=1 to C do

19: Choose W number of binary pixels b

∗

from I

LBP

randomly

20: B(c) =

∑

l=1

∗

21: end for

22: Divide the feature vector B

into groups of X

number of B

∗

feature cells

23: B

= [{B

(1),B

(2)..B

(C/X)},...,{B

(C −

C/X ),B

(C − 1)..B

(C)}]

24: for every element in a group in B

25: F

∗

(

1, B

∗

)

0, otherwise

26: end for

27: end for

28: for c=1 to C do

29: F

∗

∑

p=1

p−1

∗

(c)

30: end for

Spatial change detection is the next stage in our al-

gorithm, that makes use of local binary pattern (LBP)

image (Ojala et al., 2002; Ahonen et al., 2006) of

Low Resolution Sparse Binary Face Patterns

189

the resulting wavelet approximation image. LBP fea-

tures introduce illumination invariance that is useful

to improve the feature quality of faces. The LBP

image is computed from the approximation image

of the wavelet decomposition stage by considering

a neighbourhood around each pixel value followed

by thresholding these neighbouring values with the

central pixel as threshold and combining the result-

ing binary vector to obtain a decimal value. Even

though, many types of neighbourhood selections are

possible such as rectangular neighbourhood, and cir-

cular neighbourhood of various sizes, we use the 3×3

square neighbourhood owing to its simplicity. Fur-

ther, the uniform LBP is used for simplicity in imple-

mentation

After computing the LBP image, we have to gen-

erate a feature vector that can represent the facial fea-

tures efﬁciently and robustly. In the traditional lo-

cal binary pattern based face recognition approaches,

the feature vector is represented as a histogram. This

is done by ﬁrst dividing the LBP image into several

overlapping or non-overlapping blocks and then com-

puting the histogram of each block and ﬁnally con-

catenating all the histograms. Instead of the conven-

tional method of using histograms for feature descrip-

tion, we propose to use the feature extraction tech-

nique mentioned in (Sudhakaran and James, 2015).

This method is inspired by the sparse processing ca-

pability of human brain. In this method, the LBP im-

age is ﬁrst converted to bit planes, then the binary

feature vectors are extracted from each bit plane by

performing the random selection, aggregation and bi-

narization operation using winner take all networks

as explained in (Sudhakaran and James, 2015). Here,

we do not make use of the gradient images instead use

the LBP images. After that, the binary feature vectors

are combined together to obtain the ﬁnal facial feature

vector. The selection of various parameters required

for reproducing the result is explained in the Experi-

ments section.

Once the feature descriptors of a face image is

computed, the next step is to apply it to a suitable

classiﬁer. Here, we use the simple yet very effective

nearest neighbour classiﬁer (Cover and Hart, 1967).

In this, the distance between the test image feature

vector and the feature vectors of all the train images

are computed and then the pair with the minimum dis-

tance is found. The test image is then assigned the

Uniform local binary patterns are binary vectors that

contains at most 2 changes in its elements (change from 0

to 1 or vice versa). The reason for selecting the uniform

LBP is from the fact that previous studies have shown that

they tend to occur more in images compared to non uniform

patterns(Pietik

ainen, 2010).

label of the train image obtained. The advantage of

the nearest neighbour classiﬁcation is its simplicity.

We modify the conventional nearest neighbour met-

rics by using the Shepard’s similarity measure (Shep-

ard, 1987) as it has interesting properties related to

perception of similarity; and is a normalising func-

tion to reduce the inter-feature distance outliers. Let

train

(i) be the train feature vector and f

test

(i) be the

test feature vector, each of length N. i = 1, 2, . . . N.

Then, the Shepard’s similarity measure is computed

as:

d =

∑

i=1

−| f

train

(i)− f

test

(i)|

(2)

Since Eq. 2 is a similarity measure, instead of ﬁnding

the pair with the minimum distance, here we will ﬁnd

the pair with the maximum similarity value.

3 EXPERIMENTS AND RESULTS

The performance of the proposed method was evalu-

ated by comparing the recognition accuracy with prin-

cipal component analysis (PCA) (Turk and Pentland,

1991), kernel PCA (KPCA) (Kim et al., 2002), kernel

Fischer analysis (KFA) (Liu et al., 2002), Gabor PCA

(GPCA), Gabor KPCA (GKPCA), and Gabor KFA

(GKFA). Since no standard face databases with low

resolution images are available, the AR face database

(Martinez, 1998), extended Yale face database B (Lee

et al., 2005) and the PUT face database(Kasinski

et al., 2008) were selected for the performance evalu-

ation. All the images in the databases were smoothed

and downsampled to produce the low resolution im-

ages. Previous low resolution face recognition litera-

tures also adapted similar technique for analysing the

results (Li et al., 2010; Patel et al., 2014).

The ﬁrst experiment conducted was to determine

the various parameters that will give the best perfor-

mance. It was done on the AR face database with the

size of the images downscaled to 40 × 30. The pa-

rameters required for the feature extraction stage are

the window size (W), cell size (X) and the degree of

overlap (k). From the different experiments explained

in (Sudhakaran and James, 2015), the value of k can

be ﬁxed as 2 since the accuracy is not much varied

with the value of k. The remaining two parameters,

W and X are selected by analysing the performance

of the proposed method for various values. Here, the

wavelet approximation image selection step is omit-

ted since the selection of a wavelet base is pending.

The local binary pattern of image is computed and

then feature extraction is done by varying the param-

eters and the recognition accuracy for different values

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

190

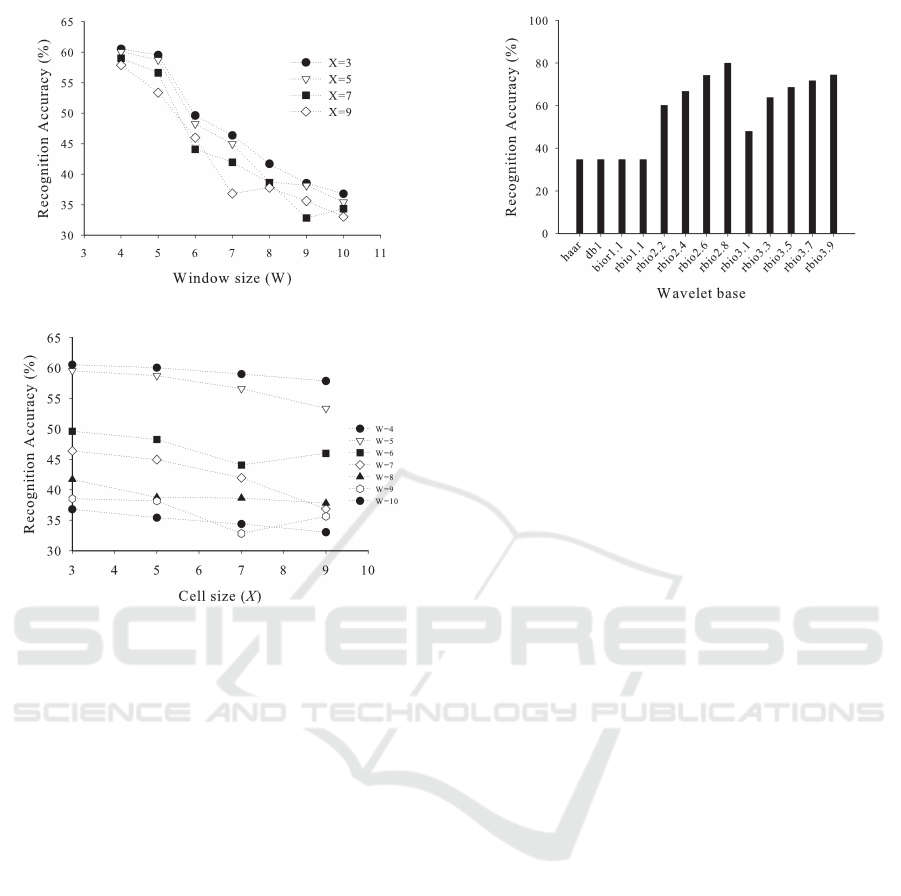
(a)

(b)

Figure 2: The recognition accuracy obtained for different

values of window size (W) and cell size (X). Fig. 2(a) shows

the plot of recognition accuracy versus window size for dif-

ferent values of cell size (X). Fig. 2(b) depicts the graph

of accuracy against cell size for different values of window

size (W).

of W and X are calculated. The result obtained is illus-

trated in Fig. 2. The ﬁgure shows that, the recognition

accuracy decreases as the window size is increasing.

But the accuracy is more or less same for the win-

dow sizes W= 4 and 5. Since the feature vector size

increases with reduction in window size, the window

size is chosen as W=5. The cell size is selected as 3.

The window size for the wavelet operation is selected

as 5 × 5. These values of W and X are then used in all

the experiments mentioned in this paper.

In order to select the suitable wavelet base, the

recognition accuracy of AR face database for differ-

ent wavelet bases were computed. The size of all

images was downsampled to 40 × 30. The following

families of wavelet functions were used in the exper-

iment: Haar, Daubechies (db1), biorthogonal (Mal-

lat, 1999) (bior1.1) and reverse biorthogonal (Gao

and Yan, 2010) (rbio1.1, rbio2.2, rbio2.4, rbio2.6,

rbio2.8, rbio3.1, rbio3.3, rbio3.5, rbio3.7, rbio3.9).

The result obtained is shown in Fig. 3. From the

graph, we can see that the best result was obtained

Figure 3: The recognition accuracy obtained when different

families of wavelet bases were used.

by the reverse biorthogonal wavelet family, especially

the rbio2.8 wavelet. The reverse biorthogonal wavelet

was used for evaluating the performance of the algo-

rithm.

After ﬁnding the optimal parameters, the perfor-

mance of the proposed low resolution face recogni-

tion system is tested on the different face datasets

mentioned above. The results obtained are explained

below. To check the resilience of the proposed

method against illumination changes, the Yale face

database B was used since it contains face images

captured with varying illumination settings. The set

is subdivided into 5 subsets based on the location of

the illumination source. Experiments were conducted

on each of the subset separately. From each image in

the dataset, the face region was cropped and resized

to 45 × 45 for conducting the experiment. The ﬁrst

image in each of the subset was selected as the train-

ing image and the remaining images were selected for

testing. The recognition accuracy was then computed

as a ratio of the number of correctly identiﬁed sam-

ples to the total number of samples tested. The recog-

nition accuracy for the proposed method as well as the

other methods compared is given in Table 1. As seen

from the table, the proposed method outperforms all

the other methods. This indicates the ability of the

proposed method in performing well in the presence

of large illumination variations.

Next, the proposed method was tested on the AR

face dataset which consists of images with varying

conditions such as illumination, expression and oc-

clusions. From the database, images of 50 male and

female persons were selected for the evaluation of

performance. The images were scaled to a size of

40 × 30 and converted to grayscale prior to the exper-

iment. The training dataset was chosen as the ﬁrst im-

age from the two sessions (1

and 14

), thus making

2 training images per person. The remaining images

were used as the test/probe dataset. The performance

Low Resolution Sparse Binary Face Patterns

191

Table 1: The recognition accuracy in % when the experiments were conducted on the Yale B dataset.

Method Subset 1 Subset 2 Subset 3 Subset 4 Subset 5

Proposed 100 100 85.45 78.46 97.06

PCA 100 88.18 58.18 37.69 35.29

KFA 100 87.27 63.64 40 35.29

KPCA 85 65.45 40.91 28.46 32.35

GPCA 100 87.27 67.27 40 34.12

GKFA 100 87.27 68.18 37.69 34.12

GKPCA 100 82.72 65.45 33.85 31.76

(a)

(b)

Figure 4: The cumulative matched curves for the various

methods when tested on the (a) AR face database and (b)

PUT face database.

analysis is given in Fig. 4(a). The higher recogni-

tion accuracy of the proposed method compared to the

other methods indicates its capability to perform even

in the presence of illumination invariance and outliers

due to occlusions.

To test the robustness of the proposed method

against pose variations, the PUT face database was

used. The images were downscaled to 40 × 30

and converted to grayscale for evaluating the perfor-

mance. Because of the presence of variations in pose,

the training set was constructed by selecting two im-

ages and then creating different templates from these

two images by shifting the images horizontally and

Figure 5: A comparison of cumulative matched curves

when using features from wavelet transform, local binary

pattern, sparse features and that of the proposed method.

vertically. The rest of the images in the dataset were

used for testing the performance. The result of the

performance evaluation is shown in Fig. 4(b). Here

also, the proposed method is seen to surpass the per-

formance of the other methods.

Fig. 5 shows the recognition accuracy when face

recognition is performed on the AR face database us-

ing wavelet based template matching, local binary

pattern, sparse distributed features and the proposed

method. The graph clearly indicates the performance

improvement obtained by combining the individual

methods.

4 CONCLUSION

The paper proposes a combination of feature pro-

cessing approaches to arrive at a set of discrimina-

tive sparse features for addressing the problem of low

resolution face recognition. The proposed method

makes use of the principles of wavelet transform, lo-

cal binary pattern and sparse based feature extraction

technique for efﬁciently representing the human facial

features. The features extracted are classiﬁed using a

minimum distance classiﬁer with Shepard’s similarity

measure as the distance measure. The experimental

results demonstrates the proposed method’s capacity

VISAPP 2016 - International Conference on Computer Vision Theory and Applications

192

to perform low resolution face recognition in the pres-

ence of variations such as illumination, occlusions

and pose. The presence of wavelet transform and lo-

cal binary pattern attributes to the proposed method’s

capability in nullifying variations in the face image

caused by illumination effects while the sparse fea-

ture representation and the Shepard’s similarity mea-

sure based nearest neighbour classiﬁcation provided

the efﬁcient elimination of data outliers. The pro-

posed technique can ﬁnd application in image recog-

nising situations demanding the use of low resolution

image, limited storage and low power smart devices.

REFERENCES

Ahonen, T., Hadid, A., and Pietikainen, M. (2006). Face

description with local binary patterns: Application to

face recognition. Pattern Analysis and Machine Intel-

ligence, IEEE Transactions on, 28(12):2037–2041.

Baker, S. and Kanade, T. (2000). Hallucinating faces. In

Automatic Face and Gesture Recognition, 2000. Pro-

ceedings. Fourth IEEE International Conference on,

pages 83–88. IEEE.

Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-

siﬁcation. Information Theory, IEEE Transactions on,

13(1):21–27.

Field, D. J. (1999). Wavelets, vision and the statistics of nat-

ural scenes. Philosophical Transactions of the Royal

Society of London. Series A: Mathematical, Physical

and Engineering Sciences, 357(1760):2527–2542.

Freeman, W. T., Pasztor, E. C., and Carmichael, O. T.

(2000). Learning low-level vision. International jour-

nal of computer vision, 40(1):25–47.

Gao, R. X. and Yan, R. (2010). Wavelets: Theory and appli-

cations for manufacturing. Springer Science & Busi-

ness Media.

Kasinski, A., Florek, A., and Schmidt, A. (2008). The

put face database. Image Processing and Communi-

cations, 13(3-4):59–64.

Kim, K. I., Jung, K., and Kim, H. J. (2002). Face recogni-

tion using kernel principal component analysis. Signal

Processing Letters, IEEE, 9(2):40–42.

Lai, J. and Jiang, X. (2012). Modular weighted global

sparse representation for robust face recognition. Sig-

nal Processing Letters, IEEE, 19(9):571–574.

Lee, K., Ho, J., and Kriegman, D. (2005). Acquiring linear

subspaces for face recognition under variable light-

ing. IEEE Trans. Pattern Anal. Mach. Intelligence,

27(5):684–698.

Li, B., Chang, H., Shan, S., and Chen, X. (2010). Low-

resolution face recognition via coupled locality pre-

serving mappings. Signal Processing Letters, IEEE,

17(1):20–23.

Liu, Q., Huang, R., Lu, H., and Ma, S. (2002). Face recog-

nition using kernel-based ﬁsher discriminant analysis.

In Automatic Face and Gesture Recognition, 2002.

Proceedings. Fifth IEEE International Conference on,

pages 197–201. IEEE.

Mallat, S. (1999). A wavelet tour of signal processing. Aca-

demic press.

Marciniak, T., Dabrowski, A., Chmielewska, A., and Wey-

chan, R. (2012). Face recognition from low resolution

images. In Multimedia Communications, Services and

Security, pages 220–229. Springer.

Martinez, A. M. (1998). The ar face database. CVC Tech-

nical Report, 24.

Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. Pattern Anal-

ysis and Machine Intelligence, IEEE Transactions on,

24(7):971–987.

Patel, V. M., Chen, Y.-C., Chellappa, R., and Phillips, P. J.

(2014). Dictionaries for image and video-based face

recognition. J. Opt. Soc. Am. A, 31(5):1090–1103.

Pietik

ainen, M. (2010). Local binary patterns. Scholarpe-

dia, 5(3):9775.

Shepard, R. N. (1987). Toward a universal law of

generalization for psychological science. Science,

237(4820):1317–1323.

Sudhakaran, S. and James, A. P. (2015). Sparse distributed

localized gradient fused features of objects. Pattern

Recognition, 48(4):1534–1542.

Turk, M. A. and Pentland, A. P. (1991). Face recogni-

tion using eigenfaces. In Computer Vision and Pat-

tern Recognition, 1991. Proceedings CVPR’91., IEEE

Computer Society Conference on, pages 586–591.

IEEE.

Xu, X., Liu, W., and Li, L. (2014). Low resolution face

recognition in surveillance systems. Journal of Com-

puter and Communications, 2(02):70.

Zhang, B.-L., Zhang, H., and Ge, S. S. (2004). Face recog-

nition by applying wavelet subband representation and

kernel associative memory. Neural Networks, IEEE

Transactions on, 15(1):166–177.

Zou, W. and Yuen, P. (2010). Very low resolution face

recognition problem. In Biometrics: Theory Appli-

cations and Systems (BTAS), 2010 Fourth IEEE Inter-

national Conference on, pages 1–6.

Low Resolution Sparse Binary Face Patterns

193