Declassification of Information with Complex Filter Functions
∗
Kurt Stenzel, Kuzman Katkalov, Marian Borek and Wolfgang Reif
Institute for Software and Systems Engineering, University of Augsburg, 86135 Augsburg, Germany
Keywords:
Information Flow Control, Declassification, Information Hiding and Anonymity, Privacy-Enhancing Models
and Techniques, Privacy Metrics and Control.
Abstract:
Many applications that handle private or confidential data release part of this data in a controlled manner
through filter functions. However, it can be difficult to reason formally about exactly what or how much
information is declassified. Often, anonymity is measured by reasoning about the equivalence classes of all
inputs to the filter that map to the same output. An observer or attacker that sees the output of the filter then
only knows that the secret input belongs to one of these classes, but not the exact input. We propose a technique
suitable for complex filter functions together with a proof method, that additionally can provide meaningful
guarantees. We illustrate the technique with a DistanceTracker app in a leaky and a non-leaky version.
1 INTRODUCTION
The more ubiquitous and networked our devices be-
come, the harder it is to secure information they ac-
cess and aggregate. Currently, this is most crucial
for mobile devices such as smartphones, as they con-
stitute for many the main gateway to the Internet.
Since smartphones integrate numerous sensors such
as GPS and microphone, they are capable of collect-
ing a lot of sensible information about their users.
Additionally, users themselves often trust their smart-
phones with their personal information such as pay-
ment data, contacts, and calendar entries. Not only is
this widely abused by ad networks that use this infor-
mation to deliver targeted advertisements (Enck et al.,
2011), developers themselves may inadvertently leak
user’s personal information to other apps or the inter-
net. Given that modern mobile applications can be
quite complex and often consist of several interacting
smartphone apps and web services, such mistakes are
bound to happen.
Mainstream mobile OSes such as iOS and An-
droid implement a permission system that allows the
user to view and in some cases adjust which informa-
tion an app may access. This approach, however, is
not satisfactory in many cases. It is too coarse grained
as it does not allow to set permissions for app-specific
∗
This work is part of the IFlow project and sponsored by
the Priority Programme 1496 “Reliably Secure Software
Systems - RS
3
” of the Deutsche Forschungsgemeinschaft
(DFG).
private information or specify how accessed informa-
tion may be used. For instance, the user may want to
allow the access to the GPS sensor for location data to
be used locally, or to be released to the network only
after it has been sufficiently anonymized.
Information flow control (IFC) is an approach that
goes beyond access control and allows to specify, ver-
ify, and enforce such properties. Both model-based
and language-based flavors of IFC exist:
model-based IFC was pioneered by Goguen and
Meseguer who introduced the notion of noninter-
ference which expresses that confidential data may
not affect public information (Goguen and Meseguer,
1982), while Volpano and Smith first developed a type
system that guarantees noninterference for a program-
ming language (Volpano et al., 1996).
We develop a model-drivenapproach called IFlow
that allows the modeling of a distributed system con-
sisting of mobile apps and web services, as well
as their information flow properties with UML. We
support code and formal model generation, as well
as language-based IFC using JOANA (Hammer and
Snelting, 2009) and formal verification based on
Rushby’s (Rushby, 1992) and van der Meyden’s
(van der Meyden, 2007) theory of intransitive non-
interference.
This paper focuses on modeling and verifying de-
classification routines, a mechanism to allow for lim-
ited release of information that is often necessary in
realistic applications.Since such routines leak infor-
mation about user’s personal private data by design,
490
Stenzel, K., Katkalov, K., Borek, M. and Reif, W.
Declassification of Information with Complex Filter Functions.
DOI: 10.5220/0005782904900497
In Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP 2016), pages 490-497
ISBN: 978-989-758-167-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

we develop an approach to fully specify how infor-
mation is processed, filtered, or anonymized prior to
release, and present a framework for expressing and
verifying their security.
Section 2 outlines work related to declassification,
and section 3 describes our model-driven approach.
Section 4 introduces an example application modeled
with our approach. Section 5 presents security proper-
ties that must hold for declassification routines, while
section 6 shows how such properties can be proven
formally. Section 7 concludes this paper.
2 RELATED WORK
Sabelfeld and Sands (Sabelfeld and Sands, 2009) in-
troduce the “What” dimension of declassification by
stating
Partial, or selective, information flow policies
regulate what information may be released.
[...] Partial release can be specified in terms
of precisely which parts of the secret are re-
leased, or more abstractly as a pure quantity.
While they talk about programs in general the idea
for declassification or filter functions is the same. A
filter function is called with secret (and possibly ad-
ditional public) inputs and computes a public output.
An observer or attacker sees the output and tries to
determine the secret input.
A standard approach is to define equivalence
classes on the inputs (Cohen, 1978): Two inputs be-
long to the same equivalence class if the filter function
returns the same output for them. This means the ob-
server only knows that the input belongs to one of the
equivalence classes. By reasoning about the size of
the classes (the “pure quantity” of the quote) a degree
of anonymity can be determined.
The equivalence classes can be determined with
type theory (e.g. the PER model (Sabelfeld and Sands,
2001) or abstract interpretation (Giacobazzi and Mas-
troeni, 2005)), with deductive techniques (e.g. projec-
tive logic (Cohen, 1978), pre-/post conditions (Joshi
and Leino, 2000) or symbolic execution (Klebanov,
2014)) or bisimulation and model-checking (Backes
et al., 2009).
Quantitative information flow analysis tries to de-
termine the number of bits leaked by the filter func-
tion based on a probability distribution of the in-
puts. This can be based on the size of the equiva-
lence classes (Backes et al., 2009), or by computing
Shannon entropy (Clark et al., 2007) or min-entropy
(Smith, 2011) of the filter function. Usually, a finite
input of a fixed size (e.g. three 32-bit integers) is as-
sumed.
A similar approach is differential privacy (Alvim
et al., 2011; Chatzikokolakis et al., 2013) that is con-
cerned with the probability that an individual can be
identified by, e.g. querying a statistical database that
contains anonymized data.
However, precise computations of entropy mea-
sures or probabilities are very difficult for complex
filter functions that use unbounded loops, complex
data types like sequences or floating point arithmetic
or complex mathematical operations.
We propose a technique that works for such fil-
ter functions by approximating the size of the equiv-
alence classes and adding an additional requirement
that there are enough equivalent inputs with enough
differences. Therefore, our technique complements
others. It will be described in detail in sections
5 and 6.
3 THE IFLOW APPROACH
We present an integrated model-driven approach
called IFlow for developing distributed applications
consisting of mobile apps and web services with se-
cure information flow. This approach is fully tool-
supported and covers every stage of development
from creating an abstract model of the application,
to the generation of a formal model and deployable
code, allowing for checking and verifying informa-
tion flow properties. The approach is described in de-
tail in (Katkalov et al., 2013). More information can
also be found on our website
2
.
The modeling is done using UML extended with a
profile specific to our approach. The static view of the
application is captured using class diagrams. UML
classes represent application components such as mo-
bile apps or web services and are annotated with the
respective stereotypes from our UML profile. The dy-
namic view of the application is represented as UML
sequence diagrams, which specify how the applica-
tion components interact with each other and the user.
Declassification routines such as filter or anonymiza-
tion functions can be expressed using activity dia-
grams and a simple domain specific language.
Furthermore, the modeler can specify a security
policy that defines security domains and their rela-
tionships. Those security domains can then be used
to annotate elements of the application model in or-
der to express allowed information flows. Using an
activity diagram, the modeler may express informa-
tion flow properties by explicitly allowing or forbid-
ding flows between information sinks and sources
2
http://isse.de/iflow
Declassification of Information with Complex Filter Functions
491

(Katkalov et al., 2015). Such properties can then be
shown to the users of the application to explain to
them how their private information is handled.
The abstract model of the application is used
to generate a formal model based on abstract state
machines and algebraic specifications. This formal
model is used as input for the interactive verifier KIV
(Ernst et al., 2014) in order to verify information flow
properties such as “information is declassified prior
to release” (intransitive noninterference properties),
security properties of declassification routines such
as “information is sufficiently anonymized during de-
classification”, as well as trace properties such as
“user is always notified prior to information release”
(Stenzel et al., 2014).
The abstract model of the application is also trans-
formed to Java code which can be checked for infor-
mation flow violations automatically using JOANA
(Hammer and Snelting, 2009) w.r.t. information flow
properties such as “private information may never
leak to a specific information sink” (transitive nonin-
terference properties). The developer may extend this
generated code with a manual implementation, which
is also checked in order to assure information flow
security for the final application. The code can then
be deployed on actual hardware like Android devices
and web servers running Java.
Several model-driven approaches to information
flow security exist, e.g., (Seehusen, 2009), (Heldal
et al., 2004), or (Ben Said et al., 2014). However,
none of those approaches consider information flow
security on the code level, nor do they allow for mod-
eling and verifying declassification routines.
4 EXAMPLE: DistanceTracker
The DistanceTracker is a smart phone app modeled
with our approach.
3
The idea is that the user starts
GPS tracking before jogging or walking, and the
smart phone records periodically the current position.
When the user stops tracking the app computes the
covered distance using the GPS positions and uploads
the result to a server, e.g. for comparison with other
users. The main privacy property of the app is that
the location of the user remains secret, i.e. no GPS
position is uploaded to the server.
In our approach components like an app or a
server and data are modeled with a UML class di-
agram. Figure 1 shows the app
DistanceTracker
and the data involved. A GPS position GPSPos con-
sists of the latitude and longitude in degrees and a
3
The full model can be found on our web page as the “Dis-
tance Tracker with a complex filter function” case study.
-trackerService : String{User,TrackerService}
-name : String
-cutoff : Integer
-interval : Integer
<<Application>>
DistanceTracker
-tracking : boolean
State
-latitude : double
-longitude : double
GPSPos
-distance : Integer
-nickname : String
-appInfo : String
Distance
-nickname : String
Activity
{User}
-gpsPositions
*
{User,TrackerService}
-state
-positions
{ordered}
1..*
{OnlyDistance}
-dist
Figure 1: Class Diagram for the DistanceTracker app.
Distance object containing the distance in meters,
the username, and additional info (like the app ver-
sion) is uploaded to the server. Domains are annotated
with curly brackets (except ordered which denotes a
UML sequence).
<<Application>>
: DistanceTracker
<<Service>>
: TrackerService
<<User>>
: User
[else]
[state.tracking == false]
alt
state.tracking := true6:
dist_decl : Distance := release(dist)16:
{User->User,TrackerService}
Confirm()1:
{User,TrackerService}
ConfirmRelease(dist, trackerService)14:
{OnlyDistance}
Confirm()3:
SendDistance(dist_decl)17:
{User,TrackerService}
dist := d13:
{OnlyDistance}
d : Distance := calcDist(act)12:
{Locations->Distance}
gpsPositions := stopGPSTracking()10:
{User}
startGPSTracking()5:
Confirm()7:
state.tracking := false9:
act : Activity := create Activity(
name, gpsPositions)
11:
Done()18:
{User,TrackerService}
StartTracking()4:
Ok()15:
{OnlyDistance}
WelcomeMsg()2:
StopTracking()8:
Figure 2: Behavior of the DistanceTracker app.
The behavior of the app is modeled with a UML
sequence diagram (see figure 2). The app communi-
cates with the user and the server
TrackerService .
The first part of the alt ernate starts tracking and
the second part shows the behavior when tracking is
stopped. No. 12 contains the call to the filter func-
tion
calcDist that computes the covered distance
and will be described in detail below. Then the user
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
492

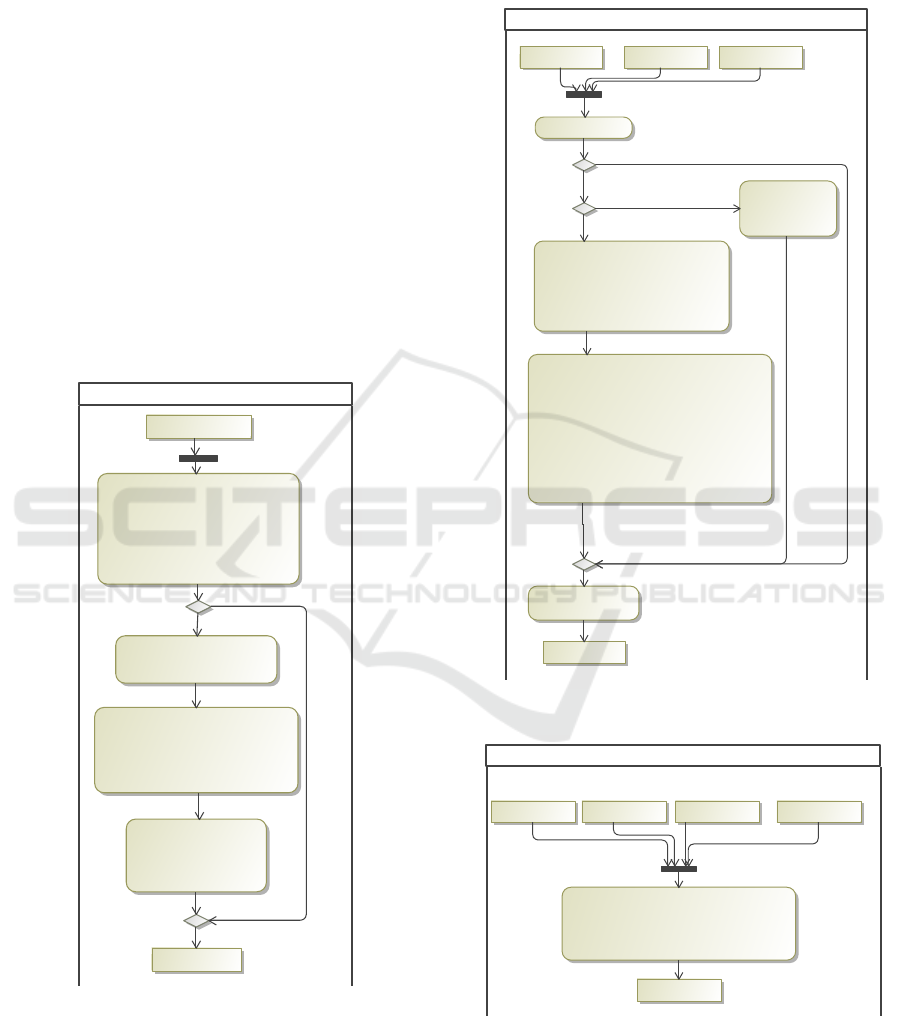
is asked to release the distance (No. 14 and 15), and
finally the result is uploaded to the server (No. 17).
Domains are again annotated in curly brackets.
The {User} domain is the most secret domain
and the GPS positions are annotated with this do-
main (No. 10 in the sequence diagram). The
data uploaded to the server has the most pub-
lic domain {User,TrackerService} (No. 17). Since
there exists an information flow from {User} to
{User,TrackerService} (the covered distance depends
on the GPS positions) the result must be declas-
sified. In the example two declassifications take
place. First, the filter function
calcDist declassi-
fies from {User} to {OnlyDistance} via the declas-
sification domain {Locations->Distance}. Then, af-
ter user confirmation the distance is further declassi-
fied to {User,TrackerService} via the domain {User-
>User,TrackerService} (No. 16 in the sequence di-
agram). Here, no further filtering takes place, i.e.
release is the identity operation.
for(i : int := 1; i < pos.size(); i++) {
next : GPSPos := pos.get(i);
dst := distance(next, cur, max);
len := len + dst;
cur := next;
}
pos : List<GPSPos> :=
act.positions;
nn : String := act.nickname;
max : Integer := 100000;
d := create Distance(0, nn,
"0.0.0.0");
len : double := 0.0;
gp : GPSPos := pos.get(0);
cur : GPSPos := gp;
dst : double := 0.0;
d0 : Distance :=
prepareResult(nn,
len, max, cur);
d := d0;
DistanceTracker::calcDist
act : Activity
d : Distance
[else]
[pos.size() > 0]
Figure 3: Main Filter Function: calcDist.
Figure 3 shows the filter function
calcDist mod-
eled in our domain-specific language MEL. The in-
put is an
Activity object (see figure 1), the output
a
Distance object. The main part is a for -loop that
iterates over the list of GPS positions and sums up
the distance. The actual computation of the distance
between two positions is done by the distance op-
eration (see figure 4). Finally, the resulting object is
created by the
prepareResult operation (figure 5).
latDistance : double := Math.toRadians(lat);
lonDistance : double := Math.toRadians(lon);
a : double := Math.sin(latDistance / 2)
* Math.sin(latDistance / 2)
+ Math.cos(Math.toRadians(lat1))
* Math.cos(Math.toRadians(lat2))
* Math.sin(lonDistance / 2)
* Math.sin(lonDistance / 2);
c : double := 2 * Math.atan2(Math.sqrt(a),
Math.sqrt(1 - a));
z := R * c * 1000; // convert to meters
lat1 : double := p1.latitude;
lat2 : double := p2.latitude;
lon1 : double := p1.longitude;
lon2 : double := p2.longitude;
R : int := 6371; // Radius of the earth
lat : double := lat2 - lat1;
lon : double := lon2 -lon1;
if (z < 0 or z > max)
z := 0.0;
z := Math.abs(
p1.latitude -
p2.latitude) *
111000
z := 0.0;
DistanceTracker::distance
p1 : GPSPos p2 : GPSPos
z : double
max : Integer
[p1.latitude > 90 or p1.latitude < -90 or
p2.latitude > 90 or p2.latitude < -90 or
p1.longitude > 180 or p1.longitude <= -180 or
p2.longitude > 180 or p2.longitude <= -180]
[p1.longitude == p2.longitude]
[else]
[else]
Figure 4: Auxiliary Filter Function: distance.
DistanceTracker
j : Integer := Math.round(x);
if (j >= i) j := 0;
s : String := Math.toString(p.latitude) + "."
+ Math.toString(p.longitude);
d := create Distance(j, nn, s);
nn : String x : double p : GPSPos
d : Distance
i : Integer
Figure 5: Auxiliary Filter Function: prepareResult.
The
distance operation (figure 4) to compute the
distance between two points on earth givenby degrees
uses the so called Haversine formula since we are on
the surface of a sphere. Note that it is not possible to
Declassification of Information with Complex Filter Functions
493

assume a flat surface without further ado because the
distance between longitudes depends on the the lati-
tude. (E.g. about 111 km at the equator, 78 km at 45
degrees north, and 0 at the north pole. The Haversine
formula still is an approximation because the earth is
not a perfect sphere.) Additionally, the
distance op-
eration includes a check that the coordinates are valid,
a shortcut if the longitudes of the two points are equal
and a cutoff if the distance is too large (assuming that
something must be wrong).
PrepareResult rounds the double value to inte-
ger and creates the Distance object. For demon-
stration purposes it also contains a severe infor-
mation leak: The last GPS position is encoded
as a string
Math.toString(p.latitude) + "." +
Math.toString(p.longitute) and stored in the
appInfo field of the Distance object. This means
the user’s last position is uploaded to the server which
violates the privacy requirement mentioned at the be-
ginning.
Next we will discuss properties of the filter func-
tion.
5 PROPERTIES OF FILTER
FUNCTIONS
This filter function serves as an example of a complex
operation because it contains an unbounded loop, uses
complex data types (strings and doubles) and complex
mathematical operations like
toRadians , sinus, cos-
inus and square root. Probably quantitative informa-
tion flow analyses will fail for this example.
We want to reason formally about (the sizes of)
the equivalence classes of all inputs that map to the
same output using first-order logic. In the following,
we will use ff(in) = out to denote a filter function ff
with one input (just for simplicity) in that returns the
output out. We define a finite set of input elements
that return the same output as in, i.e. for a given in
with ff(in) = out:
set ⊆ { a | ff(a) = out }
Then we can specify that the size of the set size(set) is
larger than a given constant, e.g. 10.000.000, or larger
than any natural number n. Since set is a subset of
one of the equivalence classes this means in the latter
case that the equivalence class is infinite. Formally,
we obtain
ff(in) = out →
∃ set. size(set) > c ∧
∀ a. a ∈ set → ff(a) = out
c can be a constant or a variable n for the infinite case.
Since the equivalence classes can be of different sizes
we include an assumption about the input and output
that specifies which class is meant:
∀ in, out. ff(in) = out ∧
assumption(in, out) →
∃ set. size(set) > c ∧
∀ a. a ∈ set → ff(a) = out
Proving this property guarantees lowers bounds on
the sizes of the equivalence classes.
However, reasoning about pure quantity is often
not good enough. Especially for complex filter func-
tions the equivalence classes are often infinite. Con-
sider the filter function
calcDist from the previous
section. Given a list of GPS positions [p
1
, p
2
, ..., p
n
]
we can extend the list by adding the last position as
often as we like: [p
1
, p
2
, ..., p
n
, p
n
, p
n
, p
n
, ...]. This
will result in the same distance, i.e. every equivalence
class is infinite.
Note that this holds for
calcDist even though it
leaks the last GPS position! Therefore we propose
a schema for properties that includes two additional
features. First, all elements of the set should have
a property and two different elements should have
enoughDifferences:
1 ∀ in, out. ff(in) = out ∧
2 assumption(in, out) →
3 ∃ set. size(set) > c ∧
4 (∀ a. a ∈ set →
5 ff(a) = out ∧
6 property(a) ∧
7 (∀ a, b. a ∈ set ∧ b ∈ set ∧ a 6= b →
8 enoughDifferences(a, b))
We can instantiate the three predicates for the Dis-
tanceTracker in the following manner:
assumption(in, out) ≡ true (since all equiva-
lence classes are infinite)
property(a) ≡ “all GPS positions in the input
are valid degrees on earth”
enoughDifferences(a, b) ≡ “the GPS posi-
tions of a and b are mutually disjoint”
The second definition means that each latitude is be-
tween -90 and 90 degrees and each longitude between
-180 and 180 degrees. This seems reasonable since
we are talking about points on earth.
The third definition for enoughDifferences in-
tends to capture the original privacy requirement that
the position of the user remains secret. This is the case
if there are many different inputs with different posi-
tions that return the same output. Then an observer
can only learn that the user was at one of many differ-
ent positions. Obviously, this property does not hold
for the leaky
calcDist filter function. Since the last
position is encoded in the result all inputs must have
the identical last position.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
494

For a corrected calcDist function with the leak
is removed we can prove the property if we define the
constant c of the size of the set as 10.000.000. The
next section shows how to prove this property. In the
remainder of this section we will discuss our proposed
scheme.
Location privacy often requires that an ob-
server/attacker can determine the users position only
up to a certain precision, e.g. the attacker can only
learn that the user is in a certain area, but not exactly
where in this area. The previous definition (“mutually
disjoint positions”) makes no statement about this be-
cause the different positions could be very close to
each other. However, we can strenghten enoughDif-
ferences by specifying that the distance between two
inputs must be larger than, e.g., one kilometer. In
this case it is advisable to reduce the required size of
the set because the proof is not a mathematical proof
about geometry on the surface of a sphere, but a for-
mal proof about the actual implementation of the filter
function.
The scheme is also useful for standard examples
of filter functions, e.g. a password checker. The fil-
ter function
checkPW (username, password, database)
is called with a (possibly nonexistent) username and
a (possibly wrong) password and a database of users
and passwords (a key-value store) and returns either
true or false. Here, the input is the triple consisting of
username, password and database. Obviously, both
equivalence classes for the
true and false result are
infinite since there is an infinite number of usernames
and passwords, and the database can contain arbitrary
many different entries. So the sheer size does not
help.
But we can express that an observerlearns nothing
about the password (other than what it is not) if the
result is false:
assumption(in, out) ≡ out = false
property(a) ≡
a.username = in.username ∧
a.password = in.password ∧
a.database.usernames =
in.database.usernames ∧
(∀ uname. uname 6= a.username ∧
uname ∈ database →
lookup(uname, a.database) =
lookup(uname, in.database))
enoughDifferences(a, b) ≡ true
The property states that all elements of the set have
the same provided username and password, and that
the databases differ only in the password of the pro-
vided username. Since there exist infinitely many
strings, there are infinitely many possibly correct
passwords. enoughDifferences is not needed in this
case.
We can also express that an observer learns noth-
ing about the existence or non-existence of other user-
names if the result of
checkPW is true:
assumption(in, out) ≡ out = true
property(a) ≡
a.username = in.username ∧
a.password = in.password
enoughDifferences(a, b) ≡
a.database.usernames ∩
b.database.usernames = {in.username}
enoughDifferences states that all databases in the set
contain completely different usernames except for the
provided username. This is necessary since the output
of
checkPW is true.
6 PROOF TECHNIQUE
A filter function like
calcDist is translated into
an abstract program and algebraic data types suit-
able for the theorem prover KIV (Ernst et al.,
2014). Strings are mapped to algebraically spec-
ified strings,
Integer to unbounded integers, and
double is mapped to finite decimal numbers with ar-
bitrary precision. The decimal numbers are a super-
set of the Java type
double , but a good approxima-
tion because precision or the limitations of
double
are not important for the DistanceTracker . Classes
like Activity or Distance (input and output of
calcDist ) are mapped to corresponding algebraic
data types, and sequences are mapped to lists.
The properties listed in section 5 all follow the
same schema. Therefore the same proof strategy is
applicable. The idea is to inductively construct the set
of inputs in the correct manner. For the main property
we need a set that
1. contains enough elements, and
2. each element has a list of valid GPS positions that
will compute a given distance, and
3. the GPS positions are disjoint.
The idea is to start with an empty set, then add an
element that is tied to 0, then a second element tied
to 1, and so on until an n-th element tied to n-1 is
added with n greater than the required size of the set.
“Tying” an element to a number n must be done by
encoding n into the GPS positions is such a manner
that all elements are different.
Inspection of the filter function shows that the dis-
tance d returned by calcDist will always be between
0 and 100000 meters, and that two GPS positions are
Declassification of Information with Complex Filter Functions
495

enough to cover this distance. Therefore we can con-
struct our first set element by using the following two
GPS positions [50, -10] and [50 + x, -10] (latitude
and longitude in degrees) where x is the correct value
for distance d. This means we have a track that starts
somewhere in Germany and leads straight North. For
the next element we start a little bit to the east: [50, -
10 - 1/y] and [50 + x, -10 - 1/y]. Again this track leads
straight to the North, but is disjoint from the first track
and is tied to the number 1 (by the term 1/y). The
next element then is [50, -10 - 2/y] and [50 + x, -10
- 2/y] and so on. y must be selected so that we ob-
tain enough set elements with valid coordinates. Each
track has the correct distance d, has valid coordinates
and is disjoint from all other tracks. Hence we have
constructed our set and can prove our property. The
actual proof for the set construction uses induction on
the size of the set n. In the induction step a new ele-
ment is added with coordinates [50, -10 - (n+1)/y] and
[50 + x, -10 - (n+1)/y]. We know that the element is
new because we require all elements in the set to have
values ≤ n. Therefore the actual induction hypothesis
is
∀ i, str. n ≤ 10000000 ∧ 0 ≤ i ∧ i < 100000 →
∃ set. size(set) ≥ n ∧ disjoint(set) ∧
(∀ y. y ∈ set → y.nickname = str ∧
validGPSCoordinates(y) ∧
(∃ m. 0 ≤ m ∧ m ≤ n ∧ y.positions =
[[50, -10 - m/y], [50 + x, 10 - m/y]]))
with suitable values for x and y as explained above
(x = d/111000, y = 10
5
). Even though this formula has
a rather complex nesting of quantifiers the proof suc-
ceeds smoothly. For other properties and other filter
functions another construction of the set elements is
needed, but the induction hypothesis follows the same
schema and the proof is similar.
The specification and proofs can be found on our
website
4
.
7 CONCLUSIONS
Information flow control frameworks often support
the controlled release (or declassification) of confi-
dential information. Qualitative and quantitative ap-
proaches exist to reason about what or how much in-
formation is released. We described a technique that
is useable for complex filter functions that are diffi-
cult to analyse. As an example we used a Distance-
Tracker app where the covered distance is computed
from a sequence of confidential GPS positions. This
4
The direct link is: https://swt.informatik.uni-augsburg.de/swt/
projects/iflow/DistanceTrackerComplexFilterSite/index.html
function uses complex data types and trigonometric
operations. We showed that it is not enough to rea-
son about the number of inputs that map to the same
output with an example containing a serious leak. We
described a scheme to obtain meaningful guarantees
together with a generic proof technique. The results
are fully integrated into our framework for informa-
tion flow control.
Future work includes support for a graphical lan-
guage to model this kind of properties.
REFERENCES
Alvim, M. S., Andres, M. E., Chatzikokolakis, K., and
Palamidessi, C. (2011). On the relation between dif-
ferential privacy and quantitative information flow. In
ICALP 2011, Part II, pages 60–76. Springer LNCS
6756.
Backes, M., K¨opf, B., and Rybalchenko, A. (2009). Au-
tomatic discovery and quantification of information
leaks. In Proceedings of the 30th IEEE Symposium
on Security and Privacy (S&P 2009), pages 141–153.
IEEE Computer Society.
Ben Said, N., Abdellatif, T., Bensalem, S., and Bozga, M.
(2014). Model-driven information flow security for
component-based systems. In Bensalem, S., Lakh-
neck, Y., and Legay, A., editors, From Programs to
Systems. The Systems perspective in Computing, vol-
ume 8415 of Lecture Notes in Computer Science,
pages 1–20. Springer Berlin Heidelberg.
Chatzikokolakis, K., Andrs, M. E., Bordenabe, N. E., and
Palamidessi, C. (2013). Broadening the scope of dif-
ferential privacy using metrics. In PETS 2013, pages
82–102. Springer LNCS 7981.
Clark, D., Hunt, S., and Malacaria, P. (2007). A static anal-
ysis for quantifying information flow in a simple im-
perative language. J. Comput. Secur., 15(3):321–371.
Cohen, E. S. (1978). Information transmission in sequential
programs. In DeMillo, R. A., Dobkin, D. P., Jones,
A. K., and Lipton, R. J., editors, Foundations of Se-
cure Computation, pages 301–339. Academic Press.
Enck, W., Octeau, D., McDaniel, P., and Chaudhuri, S.
(2011). A study of android application security. In
Proceedings of the 20th USENIX conference on Se-
curity, SEC’11, pages 21–21, Berkeley, CA, USA.
USENIX Association.
Ernst, G., Pf¨ahler, J., Schellhorn, G., Haneberg, D., and
Reif, W. (2014). KIV: overview and VerifyThis com-
petition. International Journal on Software Tools for
Technology Transfer, pages 1–18.
Giacobazzi, R. and Mastroeni, I. (2005). Adjoining de-
classification and attack models by abstract interpre-
tation. In Proc. European Symp. on Programming,
pages 295–310. Springer LNCS 3444.
Goguen, J. and Meseguer, J. (1982). Security policies and
security models. In IEEE Symposium on Security and
privacy, volume 12.
ICISSP 2016 - 2nd International Conference on Information Systems Security and Privacy
496

Hammer, C. and Snelting, G. (2009). Flow-sensitive,
context-sensitive, and object-sensitive information
flow control based on program dependence graphs.
International Journal of Information Security,
8(6):399–422. Supersedes ISSSE and ISoLA 2006.
Heldal, R., Schlager, S., and Bende, J. (2004). Supporting
confidentiality in UML: A profile for the decentralized
label model. In Proceedings, 3rd International Work-
shop on Critical Systems Development with UML, Lis-
bon, Portugal, pages 56–70, Munich, Germany. TU
Munich Technical Report TUM-I0415.
Joshi, R. and Leino, K. R. M. (2000). A semantic approach
to secure information flow. Science of Computer Pro-
gramming, 37(1-3):113138.
Katkalov, K., Stenzel, K., Borek, M., and Reif, W.
(2013). Model-driven development of information
flow-secure systems with IFlow. ASE Science Jour-
nal, 2(2):65–82.
Katkalov, K., Stenzel, K., Borek, M., and Reif, W. (2015).
Modeling information flow properties with UML. In
2015 7th International Conference on New Technolo-
gies, Mobility and Security (NTMS). IEEE Conference
Publications.
Klebanov, V. (2014). Precise quantitative information flow
analysisa symbolic approach. Theoretical Computer
Science 538, Elsevier, pages 124–139.
Rushby, J. (1992). Noninterference, Transitivity,
and Channel-Control Security Policies. Techni-
cal Report CSL-92-02, SRI International. avail-
able at http://www.csl.sri.com/
˜ rushby/reports/csl-92-
2.dvi.Z.
Sabelfeld, A. and Sands, D. (2001). A PER model of se-
cure information flow in sequential programs. Higher
Order and Symbolic Computation, 14(1):59–91.
Sabelfeld, A. and Sands, D. (2009). Declassification: Di-
mensions and principles. Journal of Computer Secu-
rity, 17(5):517–548.
Seehusen, F. (2009). Model-Driven Security: Exemplified
for Information Flow Properties and Policies. PhD
thesis, Faculty of Mathematics and Natural Sciences,
University of Oslo.
Smith, G. (2011). Quantifying information flow using min-
entropy. In Eighth International Conference on Quan-
titative Evaluation of SysTems. IEEE.
Stenzel, K., Katkalov, K., Borek, M., and Reif, W. (2014).
A model-driven approach to noninterference. Journal
of Wireless Mobile Networks, Ubiquitous Computing,
and Dependable Applications (JoWUA), 5(3):30–43.
van der Meyden, R. (2007). What, indeed, is intran-
sitive noninterference? (extended abstract). In
Proc. European Symposium on Research in Computer
Security, volume 4734, pages 235–250. Springer
LNCS. An extended technical report is available from
http://www.cse.unsw.edu.au/∼meyden.
Volpano, D., Irvine, C., and Smith, G. (1996). A sound type
system for secure flow analysis. J. Comput. Secur.,
4(2-3):167–187.
Declassification of Information with Complex Filter Functions
497