Applicability of True Voltage Unbalance Approximation Formula for

Unbalance Monitoring in LV Networks with Single-phase Distributed

Generation

Ognjen Gagrica

, Tadeusz Uhl

, Phuong H. Nguyen

and J. F. G. Cobben

AGH University of Science and Technology, Krakow, Poland

Eindhoven University of Technology, Eindhoven, The Netherlands

Keywords: Voltage Unbalance, Power Quality, Photovoltaic, Distributed Generation, Smart Grid.

Abstract: In the hierarchy of power transmission and distribution systems, the three-phase LV distribution networks

are most susceptible to voltage unbalance (VU). The main causes are large presence of randomly distributed

single-phase loads and, following the latest trends, the increasing presence of single-phase distributed

generators. Most widely accepted VU calculation is based on percentile ratio of negative and positive

sequence voltage (voltage unbalance factor, VUF). Obtaining sequence voltages is a complex domain

calculation and requires simultaneous sampling of three-phase voltages and angles. This is why the existing

VU monitoring and mitigation solutions are dominantly three-phase. Without an additional three-phase

aggregation device, there is an inherent gap in VU monitoring for single-phase loads and generators. In this

paper, the data concentrators for a growing PV micro-inverter niche are identified as an infrastructure that

could be exploited to somewhat close this gap. Due to potential technical limitations of PV data

concentrators, a non-complex VUF approximation formula is tested as a "light" calculation alternative, by

comparing it against conventional VUF. The comparison results are obtained from Monte Carlo load flow

simulation for an unbalanced LV network.

1 INTRODUCTION

1.1 PV Penetration and Voltage

Unbalance Mitigation Problem

The voltages in a 3-phase distribution network are

considered unbalanced if differences in magnitudes

and/or angles between phases exist beyond specified

limits (Driesen and Craenenbroeck, 2002). At high

(HV) and medium voltage (MV) level loads are

mostly three-phase and balanced, but at low voltage

(LV) level many single-phase loads are encountered

and randomness of load profiles is greater. Despite

the best practices of LV network planning , some

increased unbalance is always experienced

compared to MV and HV level. The trends of

increasing single-phase distributed generation can

further promote the increase of unbalance at LV

levels. In most cases those are single-phase

photovoltaic (PV) systems, therefore studies were

performed on their impact on unbalance (Vegunta et

al. 2013; Shahnia et al. 2011a). The VU can cause a

decrease in the induction motor efficiency, sub-

optimal operation of power electronics and reduced

capacity in transformers, lines and cables, therefore

it is important to have mitigation solutions at

disposal.

Most basic and most limited solution is to

improve the planning practices. Further solutions

that can come from distribution operator side is the

application of specialized transformers and fast-

acting power electronics devices (Driesen and

Craenenbroeck, 2002). In (Shahnia et al. 2011b) VU

mitigation by distribution static compensators and

dynamic voltage restorers was analyzed. There are

also proposals for an active involvement of

distributed generation. In (Chua et al. 2012) a PV

with storage is used to mitigate unbalance. The new

control designs for PV inverters are integrating the

unbalance mitigation (Caldon et al. 2012; Wang et

al. 2008; Weckx et al. 2014).

286

Gagrica, O., Uhl, T., Nguyen, P. and Cobben, J.

Applicability of True Voltage Unbalance Approximation Formula for Unbalance Monitoring in LV Networks with Single-phase Distributed Generation.

In Proceedings of the 5th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2016), pages 286-292

ISBN: 978-989-758-184-7

1.2 Voltage Unbalance Quantification

and Monitoring

Before reviewing the inverter-based solutions, the

calculation and quantification of VU needs to be

understood, because it impacts the technical

implementation of monitoring and control,

especially for single-phase devices. Whether only

magnitudes or both magnitudes and angles are

considered, the VU calculation depends on the

adopted VU definition (Pillay and Manyage, 2001).

Most widely accepted is the true voltage unbalance

definition that takes both magnitudes and angles into

account. Quantitatively it is expressed in percentages

as the voltage unbalance factor (VUF):

















(1)

where V

and V

represent the magnitudes of

negative and positive sequence voltages. By

applying the method of symmetrical components,

positive and negative sequence voltages are

obtained:



















111

1



1





















(2)

These are complex domain calculations where

complex operator a is function of phase angle:

a=e(j2π/3). In order to calculate sequence voltages,

the instantaneous three-phase voltages and angles

must be obtained simultaneously (ed. Zobaa, 2013).

Technical implementation of monitoring therefore

requires a device directly connected to a 3-phase

supply. This is an inherently insurmountable

problem for single-phase devices unless an external

device acting as their coordinator is used.

1.3. Lack of Solutions for Single-phase

Inverters

In (Caldon et al. 2012) an external controller at

substation level coordinates single-phase and three-

phase inverters in order to mitigate unbalance.

Three-phase inverter control designs are proposed in

(Wang et al. 2008) and (Weckx et al. 2014). In

(Tangsunantham and Pirak, 2013) a three-phase

smart meter is used to monitor VU with high

accuracy and low cost. What is common for all

these referenced solutions is that they all use VUF

to assess VU. This is why these solutions are

dominantly three-phase. It is evident that without an

additional three-phase device, there is an inherent

gap in VUF monitoring and control for single-phase

inverters. Additional device also incurs additional

cost to the PV system, therefore it would be

worthwhile looking into single-phase devices whose

existing ICT infrastructure could be software-

retrofitted for purpose of enabling VUF monitoring

and control in LV networks.

In this paper, data concentrators used in PV

micro-inverters are addressed for their retrofit

potential in VU monitoring application. Due to

potential hardware limitations, a non-complex

approximation formula for VUF calculation (AVUF)

is tested as a light alternative to conventional VUF.

Modelling of VUF and AVUF is carried out in

Matlab/Simulink and presented in Section 2. To

account for randomness of PV generation a Monte

Carlo load flow is performed for an unbalanced 3-

phase 4-wire network model. Both Monte Carlo

scenario setup and network modelling are described

in Section 3. Comparison between VUF and AVUF

on the basis of Monte Carlo simulation results is

given in Section 4. The implication of results are

discussed in Section 5.

2 PROPOSED SOLUTION

2.1 Data Concentrators in LV

Networks

Data concentrators are the key components for

Advanced Metering Infrastructure (AMI). They

aggregate instantaneous data from numerous smart

meters and transmit it to the utility server. Without

their use as a mediator, the direct meter-to-server

communication would face many technical

difficulties. Other than application in AMI, the data

aggregation technology for PV generation is also

increasing its presence. It has become standard part

of the package for PV plants based on micro-inverter

and DC optimizer technology. The implementation

of power electronic converters at module-level

expanded the opportunity for monitoring operational

parameters from a single point to each

module/micro-inverter in the PV plant. This

generates a lot of data. In high PV penetration areas

there can be hundreds of panels and their data needs

to be aggregated and presented to the application or

the end-user in a meaningful way. Most of the

micro-inverters available on the market today are

sold in package with data concentrator devices, more

often called "gateways". They communicate to

micro-inverters via mesh radio or power line

communication while remote communication with

an application is done via internet (Enphase, 2015;

Applicability of True Voltage Unbalance Approximation Formula for Unbalance Monitoring in LV Networks with Single-phase Distributed

Generation

287

Figure 1: Simulink models of VUF (top) and AVUF (bottom).

ABB, 2014). One gateway can cover from several

tens to several hundreds of micro-inverters. PV

owners use them for monitoring and easy

troubleshooting, manufacturers for more

complicated troubleshooting and firmware updates.

In (Gagrica et al. 2015a; Gagrica et al. 2015b) it

was discussed how a gateway infrastructure could

be exploited by DSO for wide area feed-in

management of PV generation, only by software

retrofit without addition of external hardware.

However, trying software retrofit for the purpose of

obtaining VUF would likely face implementation

difficulties on the gateway hardware side. The

symmetrical components sequence analyzer requires

phase detection circuits and complex digital filtering

(ed. Zobaa, 2013). Such features are found in power

quality analyzers which are considerably more

expensive devices. The proposed alternative is to try

approximating the VUF with a less computationally

and technically demanding method.

2.2 VUF Approximation Formula and

Its Application

In (Pillay and Manyage, 2001) an overview of three

VU definitions and their respective calculations was

given: NEMA, IEEE, true definition (VUF). More

importantly a new formula was proposed. This is a

non-complex calculation formula that doesn't use

phase angles but nevertheless approximates VUF by

using only voltage magnitudes:



























(3)

where V

, V

and V

are differences between

phase (a, b, c) voltages and the average phase

voltage. In (Pillay and Manyage, 2001) it was

provided in its final form without derivation steps.

The authors claimed that it can approximate to VUF

better than other definitions even under highly

unbalanced conditions, so it was selected as is for

this study. The modelling is performed in Simulink

for both VUF and AVUF. Models are presented in

Figure 1. For modelling VUF the default Simulink

three-phase sequence analyzer blocks are used, one

for positive and one for negative voltage sequence at

50Hz. Unlike VUF that uses instantaneous voltage at

input the voltages for AVUF had to be averaged to

RMS at fundamental frequency otherwise the output

will be sinusoidal and unsuitable for comparison

with VUF.

2.3 Application Limitations

The technical application would be to aggregate

micro-inverter output RMS voltages and execute

AVUF calculation by the existing gateway

microprocessor. Two limitations are currently

foreseen. The data concentrators often use wireless

communication (mesh radio) to aggregate data.

Compared to micro-inverters their sampling rate is

limited. For example in (ABB, 2014) the sampling

rate is limited to 1 minute. Providing AVUF in 1

min interval might be sufficient for a LV monitoring

application, but protection/control applications (like

fault clearing or dynamic unbalance control) would

be more demanding.

Secondly, the AVUF is only applicable in

scenarios where all three single-phase PV plants

connect to the same 3-phase supply point like in

Figure 2 (left). In reality PV plants will more likely

be scattered (Figure 2, right) due to randomness of

process of consumers becoming prosumers. If the

supply point where only Va is available is the AVUF

acquisition point, the other two phase voltages are

missing. The only available voltages are from the

neighbouring systems on different phases and supply

points (Vb' and Vc'').

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

288

Figure 2: The limitations of aggregating voltages from a

single supply point due to scattered single-phase PV.

In this case AVUF would have to be assisted with

some kind of state estimation method, which is out

of scope of this paper. Also the technical complexity

of acquiring voltages Vb' and Vc'' would increase as

they might be out of range of the data concentrator.

3 DISTRIBUTION NETWORK

MODELING AND SIMULATION

3.1 Distribution Network Model

A 3-phase 4-wire residential feeder is built in

Simulink (Figure 3). The feeder has 14 supply buses

extending radially from a 400kVA delta-star

transformer (400/230V, X/R ratio=3.2). The

transformer tap is set to 1.05pu to compensate for

voltage drop along the feeder. Each bus provides a

three-phase supply where each phase connects one

household. Total feeder length is 490m. There is a

common neutral going through each bus with star

grounding at transformer. The grounding, neutral

and lines are modelled as RL branches. One PV and

three load profiles with hourly resolution were

created based on profiles in (Shahnia et al. 2011a).

Peak values of three loads are 1, 1.8 and 4.6kW.

They are randomly distributed along the feeder. The

PV is modelled as a single-phase AC current with a

phase-locked loop.

The PV rating is in the 1-4kW range and varies in

accordance with Monte Carlo setup. Together, load

and generation form the net power flow subsystems

as shown in Figure 3 (Net flow 1, 2,...,14).

3.2 Monte Carlo Simulation

Monte Carlo is a convenient method for simulating

stochastic nature of PV generation. In particular it

was used in the unbalanced network analysis

(Shahnia et al. 2011a). Similarly, in this study

Monte Carlo is used to vary the PV ratings on all

three phases. The limitation of having PV present on

all three-phases simultaneously is taken into

account. The PV in 1-4kW range is varied following

a (0,1) uniform distribution. In Monte Carlo

applications in power system studies the coefficient

of variance is often used as a convergence criterion

or a stopping rule (Wenyuan, 2005). In this study

coefficient of variance 









is used:



















/



(4)

where Var(VUF)stands for variance. Simulink load

flow is carried out for each iteration until 









)

reaches an acceptable convergence.

4 SIMULATION RESULTS

The AVUF and VUF results are retrieved for the

entire Monte Carlo set (1000 trials). Figure 4 shows

the outcome of applying two different calculation

methods. It can be seen that AVUF results are much

more dispersed with a higher density of extreme

values compared to VUF.

This is attributed to AVUF relying on voltage

magnitudes only. Also it can be observed that AVUF

almost always resolves in the same fashion being the

Figure 3: Simulink model of three-phase four-wire distribution network.

Applicability of True Voltage Unbalance Approximation Formula for Unbalance Monitoring in LV Networks with Single-phase Distributed

Generation

289

Figure 4: AVUF and VUF calculated in 1000 Monte Carlo trials.

highest at bus 14 and lowest at bus 1. Given how

the load and generation is distributed this should not

always be the case. The VUF at bus 7 will often

have a slightly higher unbalance than bus 14

especially during the more extreme unbalance cases

(over 2.5%), but around 2% the bus 14 will have a

higher VUF. Therefore in addition to inflated

magnitudes the AVUF will tend to give a voltage

magnitude-biased result when the whole feeder is

analyzed.

Three extreme VUF peaks and their

corresponding AVUF peaks are circled in Figure 4

at different simulation times (I,II,III). To better

understand when AVUF makes a good

approximation and when it diverges into extreme

peaks, the peaks are zoomed into and compared

against three-phase voltage snapshot at the

corresponding time (Figure 5). Daily three-phase

voltage profiles are taken from bus 1 for each of the

selected trials. It can be seen that the high AVUF

peaks correspond to situations when the load flow

resolves into simultaneous two-phase overvoltage.

VUF will also experience peaks at this time, but

AVUF, relying only on voltage magnitudes, is much

more sensitive to overvoltage than VUF.

In Figure 6 are presented the mean absolute

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

290

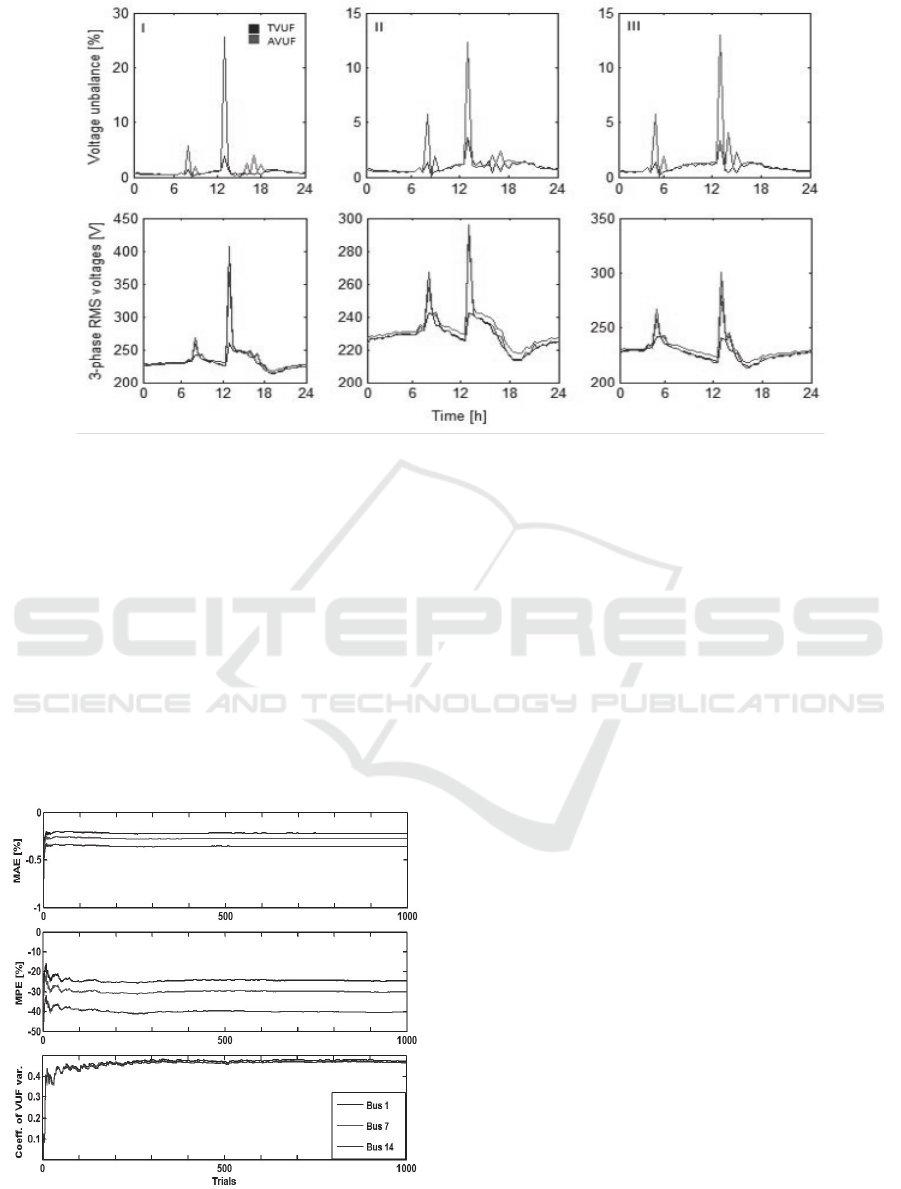
Figure 5: Zoomed-in extreme VU cases I, II, III with voltage profiles.

error (MAE) and mean percentage error (MPE) for

buses 1-7-14 throughout the whole simulation. Also

the converging process of Monte Carlo is presented

in the bottom plot. While mean absolute error

(MAE) does not exceed 0.4% the mean percentage

error is much more sensitive to large peaks being

included in the error averaging process. From the

aspect of entire feeder both MAE and MPE increase

with impedance. The 









converges between

0.46-0.48. after 500 trials. So 500 trials could have

been considered sufficient, although simulation was

run for 1000 trials.

Figure 6: MAE, MPE and η(VUF) at buses 1, 7 and 14.

5 DISCUSSION AND

CONCLUSION

The daily overvoltage occurrences due to excess PV

generation under unbalanced conditions have caused

at least two out of 24-hourly AVUF samples to give

false readings compared to VUF. That makes about

8.3% of recorded AVUF profile. In a power quality

analysis it would be possible to filter-out the false

AVUF peaks by using their corresponding

overvoltage events like it was presented in Figure 5,

however it is likely that such large peaks would not

have the chance to manifest in the first place. The

tips of the analyzed voltage peaks reach almost

400V. If it is a steady-state voltage change (the

subject of this study), its rise would be interrupted

much sooner due to inverter overvoltage protection

(at 253V) or even at a lower level if the inverter has

voltage control capability (curtailment, reactive

power). The AVUF preceding the trip or the

curtailment event would then be smaller.

Overvoltage could also occur in as a fast transient

due to a fault (i.e. floating neutral might cause phase

voltage to approach line voltage value), but again the

inverter protection would act. It was shown that

MAE and MPE increase with feeder impedance.

This suggests that, if AVUF is to be applied, a

calibration constant dependant on impedance would

have to be determined and the calibration itself

would have to be performed independently at each

point of connection by using a suitable standard

Applicability of True Voltage Unbalance Approximation Formula for Unbalance Monitoring in LV Networks with Single-phase Distributed

Generation

291

instrument (i.e. power analyzer).

Based on this study alone it is difficult to say

with certainty that AVUF formula can reliably

approximate VUF. But given the limitations that

distribution operators face at LV level: lack of

power quality monitoring capability, higher potential

for VU and big presence of single-phase loads, it

might be a worthwhile, intermediary monitoring

solution that can add more value to the already

deployed distributed generation. The proposed

concept does not have to be contained only within

the distributed generation context. Also home energy

management systems consisting of data

concentrators and smart single-phase

appliances/meters could be considered for the same

application.

ACKNOWLEDGEMENTS

This research is funded through Erasmus Mundus

Joint Doctoral Programme SELECT+, the support of

which is gratefully acknowledged.

REFERENCES

Driesen, J., Craenenbroeck, V. T., 2002. Voltage

disturbances, Copper Development Association.

Vegunta, S. C., Twomey, P., Randles, D., 2013. Impact of

PV and load penetration on LV network voltages and

unbalance and potential solutions. In CIRED2013,

22nd International Conference on Electricity

Distribution. CIRED.

Shahnia, F., Majumder, R., Ghosh, A., Ledwich, G., Zare,

F., 2011a.'Voltage imbalance analysis in residential

low voltage distribution networks with rooftop PVs'.

Electric Power Systems Research, vol. 81, pp. 1805-

1814.

Shahnia, F., Ghosh, A., Ledwich, G., Zare, F., 2011b.

Voltage correction in low voltage distribution

networks with rooftop PVs using custom power

devices. In IECON 2011, 37th Annual Conference on

IEEE Industrial Electronics Society. IEEE.

Chua, K.H., Lim, Y.S., Wong, J., Taylor, P., Morris, E.,

Morris, S., 2012. 'Voltage unbalance mitigation in low

voltage distribution networks with photovoltaic

systems'. Journal of Electronic Science and

Technology, vol. 10, pp. 1-5.

Caldon, R. Coppo, M., Turri, R., 2012. A network voltage

control strategy for LV inverter interfaced users. In

MEDPOWER2012, 8th Mediterranean Conference on

Power Generation, Transmission, Distribution and

Energy Conversion. IET.

Wang, F., Duarte, J. L., Hendrix, M. A. M., 2008. Control

of Grid-interfacing Inverters with Integrated Voltage

Unbalance Correction. In PESC2008, 39th Power

Electronics Specialist Conference. IEEE.

Weckx, S., Gonzalez, C., Driesen, J., 2014. Reducing Grid

Losses and Voltage Unbalance with PV inverters. In

PES-GM2014, Power & Energy Society General

Meeting. IEEE.

Pillay P., Manyage M., 2001. 'Definitions of Voltage

Unbalance.' IEEE Power Engineering Review, pp. 50-

51.

Zobaa, A. (ed.), 2013. Power Quality Issues. InTech.

Tangsunantham, N., Pirak, C., 2013. Voltage Unbalance

Measurement in Three-Phase Smart Meter Applied to

AMI systems. In ECTICON2013, 10th International

Conference on Electrical Engineering/Electronics,

Computer, Telecommunications and Information

Technology. IEEE.

Enphase 2015. Envoy Communications Gateway.

Available from: <http://enphase.com/global/files/

Envoy_DS_EN_60Hz.pdf>. (3 November 2015).

ABB 2014. Product manual CDD (concentrator data

device). Available from: <http://www05.abb.com/

global/scot/scot232.nsf/veritydisplay/4777de35bd05a2

2b85257cd30002f0fb/$file/CDD%20Product%20man

ual.pdf>.(3 November 2015).

Gagrica, O., Nguyen, P.H., Kling, W.L., Uhl, T., 2015a.

'Micro-inverter curtailment strategy for increasing

photovoltaic penetration in low voltage networks'.

IEEE Transactions on Sustainable Energy, vol. 6, pp.

369-379.

Gagrica, O., Uhl, T., Nguyen, P.H., Kling, W.L., 2015b.

Sustainable transition to high PV penetration:

Curtailment retrofit for the already deployed micro-

inverters. In ECOS2015, 28th International

Conference on Efficiency, Costs, Optimization and

Simulation of Energy Systems.

Wenyuan L., 2005. Risk Assessment of Power Systems:

Models, Methods, and Applications. IEEE.

SMARTGREENS 2016 - 5th International Conference on Smart Cities and Green ICT Systems

292