
Model-Driven Product Line Engineering for Mapping Parallel
Algorithms to Parallel Computing Platforms
Ethem Arkin
1
and Bedir Tekinerdogan
2
1
Aselsan A.Ş., Ankara, Turkey
2
Wageningen University, Information Technology, Wageningen, The Netherlands
Keywords: Model Driven Software Development, Product Line Engineering, Parallel Computing, Tool Support.
Abstract: Mapping parallel algorithms to parallel computing platforms requires several activities such as the analysis
of the parallel algorithm, the definition of the logical configuration of the platform, the mapping of the
algorithm to the logical configuration platform and the implementation of the source code. Applying this
process from scratch for each parallel algorithm is usually time consuming and cumbersome. Moreover, for
large platforms this overall process becomes intractable for the human engineer. To support systematic reuse
we propose to adopt a model-driven product line engineering approach for mapping parallel algorithms to
parallel computing platforms. Using model-driven transformation patterns we support the generation of
logical configurations of the computing platform and the generation of the parallel source code that runs on
the parallel computing platform nodes. The overall approach is illustrated for mapping an example parallel
algorithm to parallel computing platforms.
1 INTRODUCTION
Although Moore’s law (Moore, 1998) is still in effect,
currently it is recognized that increasing the
processing power of a single processor has reached
the physical limitations (Frank, 2002). Hence, to
increase the performance the current trend is towards
applying parallel computing on multiple nodes. Here,
unlike serial computing in which instructions are
executed serially, multiple processing elements are
used to execute the program instructions
simultaneously. To benefit from the parallel
computing power usually parallel algorithms are
defined that can be executed simultaneously on
multiple nodes. As such, increasing the number of
processing nodes will increase the performance of the
parallel programs (Gustafson, 1988). An important
challenge in this context is the mapping of parallel
algorithms on a computing platform that consists of
multiple parallel processing nodes. The mapping
process requires several activities such as the analysis
of the parallel algorithm, the definition of the logical
configuration of the platform, the mapping of the
algorithm to the logical configuration platform and
the implementation of the source code.
Usually the mapping process is done from scratch
for each parallel algorithm and the given parallel
computing platform. Hereby, practically no reuse is
applied. However, the current parallel algorithms, the
computing platform and the overall mapping process
seem to have lots of commonality. Exploiting this
commonality will support systematic reuse and
likewise decrease the time to map the parallel
algorithm to the parallel computing platform and
increase the overall quality.
Further, the overall process is usually applied not
only from scratch but also largely manual whereby
practically no automation is applied. This is not a
huge problem in case we are dealing with a limited
number of processing nodes. However, the current
trend shows the dramatic increase of the number of
processing nodes for parallel computing platforms
with now about hundreds of thousands of nodes
providing petascale to exascale level processing
power. As a consequence the manual mapping of the
parallel algorithm to computing platforms has
become intractable for the human parallel computing
engineer.
To support the mapping of the parallel algorithm
to parallel computing platforms, we adopt a
systematic product line engineering approach. The
approach aims to reduce the development time by
reusing the features of the algorithms and platforms,
and the code templates. Using model-driven
Arkin, E. and Tekinerdogan, B.
Model-Driven Product Line Engineering for Mapping Parallel Algorithms to Parallel Computing Platforms.
DOI: 10.5220/0005783303470354
In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 347-354
ISBN: 978-989-758-168-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
347

transformation patterns we support the automatic
generation of logical configurations of the computing
platform and the generation of the parallel source
code that runs on the parallel computing platform
nodes. The overall approach is illustrated for mapping
an example parallel algorithm to parallel computing
platforms
The remainder of the paper is organized as
follows. In section 2, we describe the problem
statement with a running example. Section 3 presents
the overall approach. Section 4 presents the toolset
that implements the model-driven automation
process. Section 5 presents the related work and
finally section 6 presents the conclusions.
2 PROBLEM STATEMENT
To illustrate the problem statement in more detail we
will shortly discuss the mapping of the parallel matrix
transpose algorithm to a parallel computing platform.
The pseudo code of the algorithm is shown in Figure
1. We aim to map the algorithm to a parallel
computing platform that consists of pxq processing
nodes.
1. Procedure Matrix-Transpose(A, p, q):
2. For j = 0 to p-1
3. Do
4. For i = 0 to q-1
5. Do
6. Copy all blocks of A[p+i, q-j] //gather
7. Swap A[p+i, q-j] A[p-i, q+j] // exchange
8. Restore all blocks of A[p-i, q+j]
9. Done
10. Done
Figure 1: Matrix Transpose Algorithm.
The matrix transpose algorithm swaps the column and
row values with each other. The algorithm consists in
essence of three parallel sections that are executed
iteratively for all nodes. In the first section (line 6),
the data blocks that will be swapped are copied to
dominating nodes (Tsai and McKinley, 1994). A
dominating node is a node that coordinates the
interaction with a group of nodes. In the second
section (line 7), these copied data blocks are swapped
between nodes. Finally in the third section (line 8),
the data blocks are restored to destination nodes. In
essence the three sections can be characterized as
gather, exchange and scatter operations, respectively
(İmre et al., 2011).
Given the physical parallel computing platform
consisting of pxq nodes, we need to define the
mapping of the different sections to these nodes. In
this context, the logical configuration is a view of the
physical configuration that defines the logical
communication structure among the physical nodes.
Typically, for the same physical configuration we can
have many different logical configurations (Arkin et
al., 2013). Hereby, some nodes are selected as
dominating nodes that collect data, exchange data
with each other and distribute the data to the other
nodes. For example for the physical configuration
consisting of 3x3 nodes (p=3, q=3) three different
example logical configurations are provided in
Figure
2.
Figure 2: Physical configuration of a topology (left figure)
with example logical configurations (right three figures).
In general, many different logical configurations can
be defined for the same physical configuration.
Hereby, each logical configuration will perform
differently with respect to different quality concerns
such as speedup and efficiency. Once the logical
configuration is defined the corresponding code that
needs to be deployed on the nodes must be
implemented.
It appears that the above process for mapping a
parallel algorithm to parallel computing platform is
similar for other parallel algorithms. The process
includes the same steps, that is, first the parallel
algorithm needs to be analyzed, the logical
configuration needs to be selected and the parallel
code needs to be written and mapped on the
corresponding nodes. Currently this process is done
from scratch and reuse is primarily implicit or ad hoc.
Table 1: Operation Descriptions for Parallel Algorithms.
Operation Description
Gather
Each dominating node gets data from its
dominated nodes in a pattern.
Scatter
Each dominating node sends data to its
dominated nodes in a pattern.
Collect
A dominating node gets data from other
dominating nodes.
Distribute
A dominating node sends data to other
dominating nodes.
Exchange
All dominating nodes exchange data with each
other dominating nodes.
Broadcast
A dominating node sends data to all other
nodes. In general, the broadcast operation
consists of distribute and scatter operations.
Serial Serial code block that runs on a single node.
An analysis of the parallel algorithms in the
literature shows that these use abstract well-known
operations (İmre et al., 2011).
Table 1 shows, for
example, six operations that form part of different
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
348

parallel algorithms.
Table 2 shows an example set of parallel
algorithms with the implemented operations of Table
1. For example, the parallel algorithm Matrix
Transpose can be defined as a combination of Gather,
Exchange and Scatter operations. The Matrix
Multiply algorithm consists of the operation
Distribute, Serial, Collect and Serial. Similar to these
algorithms other parallel algorithms can be in essence
defined as consisting of these predefined operations.
Table 2: Operations for Parallel Algorithms.
Algorithm Operations
Matrix
Transpose
Gather; Exchange; Scatter
Matrix Multiply
Distribute; Serial (multiply);Collect;
Serial (sum)
Array Increment Distribute; Collect; Serial (increment)
Complete
Exchange
Scatter; Exchange; Gather
Map Reduce Scatter; Serial (custom); Gather
Besides of lack of reuse, the mapping process is
currently largely manual. Due to the small size of the
computing platform the required code can be
implemented manually. For larger platform sizes the
required code will be largely similar. However, one
can easily imagine that manual implementation of the
code for larger configurations such as for petascale
and exascale computing platforms becomes more
time consuming, tedious and error prone. For this
automated support of the overall mapping process is
required.
3 APPROACH
In this section we provide a model-driven approach
for supporting systematic reuse of the mapping of
parallel algorithms to parallel computing platforms.
For this, we apply a software product line engineering
(SPLE) approach targeted to the development of
parallel algorithms and deployment code. The key
motivation for adopting a product line engineering
process is to develop products more efficiently, get
them to the market faster to stay competitive and
produce with higher quality. In alignment with these
goals different software product line engineering
approaches have been proposed. These approaches
seem to share the same concepts of domain
engineering, in which a reusable platform and product
line architecture is developed, and application
engineering, in which the results of the domain
engineering process are used to develop the product
members (Clements and Northrop, 2002).
The mapping process of parallel algorithms to
parallel computing platforms has been defined by
several authors. Usually the following four steps are
defined in the overall process (Foster, 1995):
Partitioning: Partitioning is related to the
decomposition of the parallel algorithm to the
multiple sections. Hereby, a section can be either
serial or parallel. Further, partitioning is also
related to the decomposition of the parallel
computing platform, i.e. the physical
configuration.
Communication: After partitioning,
communication is defined between the nodes.
Nodes can communicate with neighbours using a
certain geometric or functional pattern. In
essence, the communication patterns define the
logical configuration of the system.
Agglomeration: Different logical configurations
can be selected and each configuration alternative
will perform differently with respect to the
speedup and efficiency metrics.
Mapping: In the final step the parallel algorithm
needs to be implemented according to the selected
feasible logical configuration.
Based on the SPLE process and the general steps for
mapping parallel algorithms to parallel computing
platforms we present the approach for model-driven
product line engineering as shown in Figure 3.
Similar to the traditional SPLE process the presented
process also includes two separate life cycle
processes including domain engineering and
application engineering. The domain engineering
process includes domain requirements engineering,
domain design and domain implementation. In the
domain requirements engineering activity the domain
model for the addressed parallel algorithms and
computing platforms are defined using feature
models. In the domain design the reference
architecture for the logical configuration together
with the parallel communication patterns (tiles) are
developed. In the domain implementation the code
fragments for the communication patterns of the
logical configurations are implemented. The results
of the domain engineering activity are stored in the
asset base and later reused during the application
engineering process. In the application requirements
engineering process a particular parallel algorithm
and parallel computing platform is provided as an
input. By reusing the domain model of the domain
requirements engineering the algorithm
decomposition and physical configuration are
defined. In the application design the logical
configuration is generated based on the reference
architecture and the corresponding predefined
Model-Driven Product Line Engineering for Mapping Parallel Algorithms to Parallel Computing Platforms
349
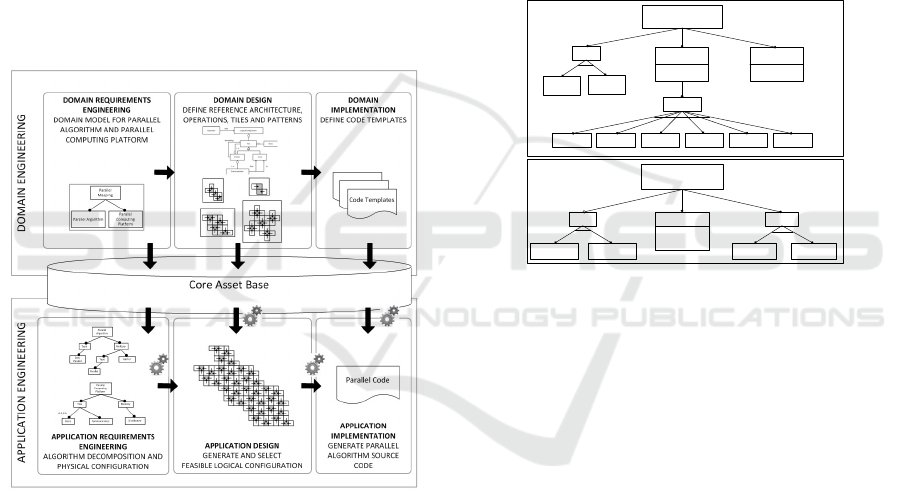
patterns and tiles that define the common
communication structures. Further, a feasible logical
configuration alternative is selected. Finally, in the
application implementation activity the parallel
source code is again generated by reusing the
predefined code templates and the selected logical
configuration.
In the overall process the transformation between
the application activities are automated using model-
driven development techniques. The automation is
shown using the corresponding automation symbol
(gears). The generation of the logical configuration is
realized using model-to-model transformations,
while the generation of the final parallel code is
realized using model-to-text transformations (Arkin
and Tekinerdogan, 2015). In the following
subsections, we will elaborate on each activity and
discuss the approach in more detail using a running
example.
Figure 3: Approach for model-driven software product line
approach for mapping parallel algorithms to parallel
computing platforms.
3.1 Domain Engineering
In this section we describe the domain engineering in
detail, which describes the development of the
reusable core assets for the mapping of parallel
algorithms to parallel computing platforms.
3.1.1 Domain Requirements Engineering
The domain requirements engineering process aims
to define the common and variant parts of both
parallel algorithms and parallel computing platforms.
The corresponding feature model represented using
cardinality based feature modeling (Czarnecki and
Helsen, 2005) is shown in Figure 4. Parallel
Algorithm consists of feature Type that can be either
Data Parallel or Task Parallel, or both. In data
parallelism, the same calculation is performed on
different sets of data. In task parallelism different
calculations can be performed on either the same or
different sets of data (Navarro et al., 2014). A parallel
algorithm consists of zero or more Parallel Sections
and zero or more Serial Sections. Each parallel
section can be considered as an Operation which is
either Gather, Scatter, Collect, Distribute or
Exchange. These operations have been derived from
an analysis to parallel programming language
abstractions such as defined in MPI.
Figure 4: Domain Model for Parallel Algorithm Mapping.
Parallel Computing Platform has a Type, Core
size, and Memory. The type defines whether the
platform is homogenous or heterogeneous. In
homogeneous platforms each core is identical,
whereas in heterogeneous platforms the cores can
change with respect to processing power. Further,
Memory can be either distributed or shared. In
distributed memory model each core has its own
memory, whereas in shared memory model each core
uses the same memory. The Core Size gives the
number of cores in the parallel computing platform
which the algorithm will be mapped to.
3.1.2 Domain Design
The domain requirements define the characteristics of
the parallel algorithm and the parallel computing
platform. Based on the domain model the feasible
logical configuration needs to be defined. As stated
before, the logical configuration is a view on the
physical configuration based on the selected
operation. The logical configuration defines both the
structure of the nodes imposed by the operation as
well as the communication pattern among the nodes.
Parallel Algorithm
Type
Data
Parallel
Parallel Computing
Platform
Type
Heteregenous
Memory
Distributed
ParallelSection
name: String
Operation
Distribute
CoreSize
colSize: Integer
rowSize: Integer
Task
Parallel
[0..*]
SerialSection
name: St ring
[0..*]
Gather Scatter Collect Exchange Broadcast
Homog ene ous Shared
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
350
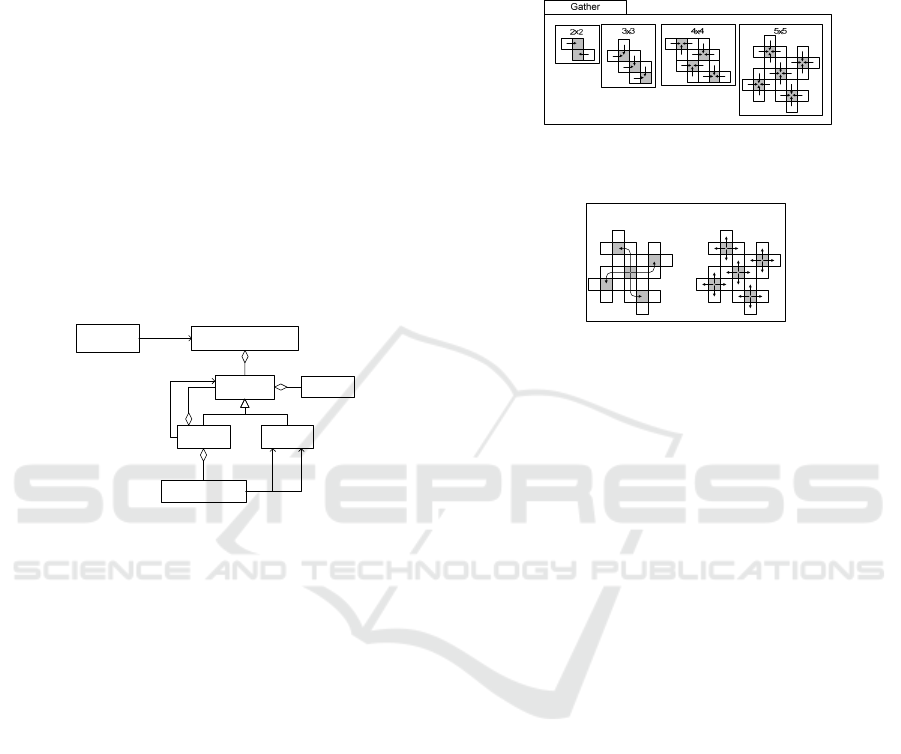
The metamodel for the reference architecture of the
logical configuration is shown in Figure 5. In essence
each logical configuration defined in the application
engineering process will conform to this metamodel.
Each logical configuration consists of a set of tiles.
Tiles as such can be considered as the basic building
blocks of the logical configuration. A tile is used for
addressing group of processing elements that form a
neighbourhood region on which processes and
communication links are mapped. The smallest part
of a tile is a core. The dynamic behaviour of the tile
is the communication between the inner cores of the
tile and the communication with other tiles. Hence,
after defining the primitive tiles, we need to define the
dynamic behaviour among the cores as the
communication pattern. A communication pattern
includes communication paths that consist of a source
node, a target node and a route between the source
and target nodes.
Figure 5: Metamodel for the reference architecture.
The logical configuration is defined by the
semantics of the operation. Each parallel operation
will typically require different logical configurations.
The structure of the logical configuration is further
defined by the total number of physical cores. Figure
6 shows the logical configurations for selected set of
operations and size of nodes. For example, for the
operation Gather we have shown 4 different
examples of logical configurations (2x2, 3x3, 4x4,
and 5x5). Other logical configurations could be
defined as well.
Each operation will in the end run on the tiles of
the logical configuration. To compose the logical
configuration using the primitive tiles, the tiles must
be scaled to larger dimensions. When the tiles are
scaled to a larger size, the operations, in other words
the communication patterns assigned to operations,
must also be scaled to larger logical configuration.
Hereby, the scaling strategy of the operation affects
the order of communication patterns when scaling the
operations. Scaling strategy is the order of
communication pattern generation for operation as
bottom up or top down.
Each of these primitive communication patterns
can be also used to define more complex
communication patterns by composing multiple
different operations. For example, the Broadcast
operation as shown in Figure 7 is a composition of the
operation Distribute and Scatter.
Figure 6: Predefined primitive Communication Patterns per
Tile for Operation.
Figure 7: Example composite communication pattern,
Broadcast, consisting of sequence of Distribute and Scatter
operations.
The logical configurations of all primitive
operations together with the important composite
operations are stored in the asset base for supporting
the application engineering process later on. In
addition to the logical configuration also the
generators for defining application logical
configurations are stored in the asset base. This is
necessary for generating large scale logical
configurations that cannot be defined manually. The
generator is defined as a model-to-model
transformation (Bézivin, 2005) in which the source
model is the application feature model and the output
is the generated logical configuration. The
transformation code is written in the Epsilon
Transformation Language (ETL) (Epsilon, 2015).
3.1.3 Domain Implementation
The previous steps have focused on providing
reusable primitive operations and the definition of
transformation definition that can be used to generate
logical configurations. In the domain implementation
we provide a reusable code template that implements
the common code and provides means to generate the
variant code. The generated code is provided for a
particular computing platform. In practice there are
several computing platforms to implement the
mapping such as, MPI, OpenMP, MPL, and CILK
(Talia, 2001). For different purposes different
platforms might need to be selected. For example, if
LogicalConfiguration
Tile
Core
Pattern
Communication
from to
Data
1..n
1..n
dominating
Operation
defines
Distribute Scatter
Model-Driven Product Line Engineering for Mapping Parallel Algorithms to Parallel Computing Platforms
351
the parallel computing platform is built using
distributed memory architecture then the MPI
implementation platform needs to be chosen. In case
shared memory architecture is used then OpenMP
will be typically preferred. Other considerations for
choosing the implementation platform can be driven
by performance of these platforms. As such, in the
domain implementation we provide multiple code
templates that can be used for various different
platforms.
3.2 Application Engineering
In this section we describe the application
engineering in detail, which describes the
development of the mapping of parallel algorithms to
parallel computing platforms by reusing the core
assets.
3.2.1 Application Requirements Engineering
In the application requirements engineering process,
the algorithm feature model including common and
variant parts is defined based on the domain feature
model. The design and implementation for the
mapping of the parallel algorithm to parallel
computing platform is done based on the selected
features.
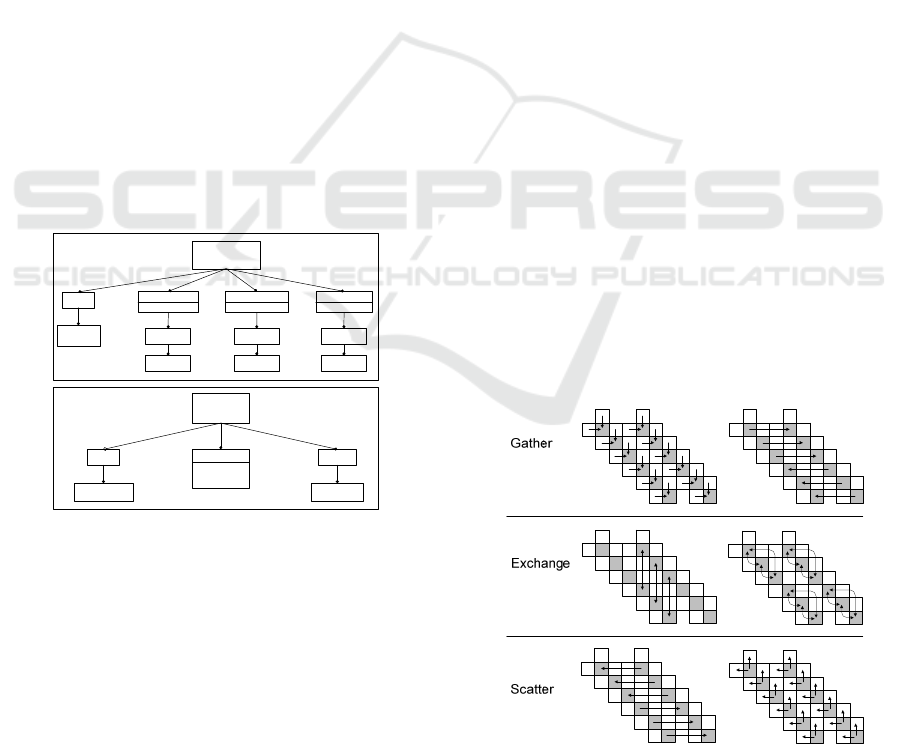
Figure 8: Matrix Transpose algorithm feature model.
Figure 8 depicts the feature model for the earlier
given matrix transpose algorithm. At the top of the
figure, the features of the matrix transpose algorithm
are defined. An analysis of the algorithm reveals that
the type of the algorithm is data parallel. Further the
algorithm consists of three parallel sections as
described in the problem statement. Based on the
analysis of the algorithm, the parallel section
CopyBlocks implements the Gather operation, Swap
implements Exchange, and RestoreBlocks
implements Scatter.
The lower part of the figure defines the features
of the parallel computing platform. Here, based on the
analysis of the platform the computing platform type
is selected to be homogeneous. Further the platform
is constructed by 6x6 cores and uses distributed
memory.
3.2.2 Application Design
In the application design process, the logical
configuration is generated using a predefined
LogicalConfigurationGenerator. The input that is
needed for the transformation, the application feature
model, is defined in the application requirements
engineering. The matrix transpose algorithm
consisted of the operations Gather, Exchange and
Scatter.
Figure 9 shows the logical configurations for
these operations after executing
LogicalConfigurationGenerator. Because the core
size of the parallel computing platform is 6x6, based
on prime factorization the tiles 2x2 and 3x3 are used
to construct the logical configuration.
3.2.3 Application Implementation
The application implementation process aims to
implement the final parallel source code. The source
code is generated automatically from the logical
configurations using the required parallel
programming language code templates by executing
the model-to-text transformation. After the
generation the resulting code is deployed on the
parallel computing platform. This process can be
done manually or in case of large platforms various
tools can be used to automate the deployment as well.
This is however beyond the scope of this paper.
Figure 9: Logical Configurations for Matrix Transpose
Algorithm steps.
Matrix Transpose
Algorithm
Type
Data
Parallel
ParallelSection
CopyBlocks
Operation
Parallel
Computing
Platform
Type
Homogeneous
Memory
Distributed
Gather
ParallelSection
Swap
Operation
Exchange
ParallelSection
RestoreBlocks
Operation
Scatter
CoreSize
colSize: 6
rowSize: 6
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
352

4 RELATED WORK
In this paper we have applied a model-driven
software product line engineering approach for
mapping parallel algorithms to parallel computing
platforms. Since the approach as such integrates the
paradigms of software product line engineering,
model-driven development and parallel computing,
we consider the related work on model driven
development for parallel computing, model driven
software product lines and product line approaches
for parallel computing.
In the domain of model-driven software
development for parallel computing, Palyart et al.,
(2011) propose an approach for using model-driven
engineering in high performance computing. They
focus on automated support for the design of a high
performance computing application based on abstract
platform independent model. The approach includes
the steps for successive model transformations that
enrich progressively the model with platform
information. The approach is supported by a tool
called Archi-MDE. Gamatié et al., (2011) represent
the Graphical Array Specification for Parallel and
Distributed Computing (GASPARD) framework for
massively parallel embedded systems to support the
optimization of the usage of hardware resources.
GASPARD uses MARTE (Object Management
Group, 2009) standard profile for modeling
embedded systems at a high abstraction level.
MARTE models are then refined and used to
automatically generate code. Taillard et.al (2008)
propose a graphical framework for integrating new
metamodels to the GASPARD framework. They used
model-driven development techniques to generate
OpenMP, Fortran or C code. Travinin et al., (2005)
introduce pMapper tool which generates mappings
for numerical arrays. It supports user to generate an
optimal mapping solution by using heuristics. The
heuristics are supplied by an expert parallel
computing engineer and minimize the mapping
search space. The tool generates the source code and
run on parallel system. In our earlier study (Arkin et
al., 2013), we proposed a model driven development
approach for mapping parallel algorithms to parallel
computing platforms based on tiles and
communication patterns to support selecting from
feasible mapping alternatives.
For scientific computation algorithms, the SPLE
process is used for library-centric application design.
The Generative Matrix Computation Library
(Czarnecki and Eisenecker, 1999) is a framework
based on expression templates, idioms and template
meta-programming facilities. The Template
Numerical Toolkit (Pozo, 1997) is a collection of
interfaces and reference implementations of
numerical objects such as multidimensional arrays
and sparse matrices, which are commonly used in
numerical applications.
Software product line engineering for parallel
programming, has been carried out for grid
computing. Silva de Olivera and Rosa (2010) applied
the product line architecture for grid computing
middleware systems. The authors adopted to evaluate
family architecture evaluation method for grid
systems.
In our earlier study (Arkin et al., 2013), we have
proposed an approach for automating the generation
of parallel algorithm that are deployed on parallel
computing platforms. Hereby, we did not consider the
systematic software reuse based on software product
line engineering. Also we focused on the design of
feasible deployment alternatives based on metrics.
The current approach considers the problem from a
product line scope perspective and integrates both
product line engineering and model-driven
engineering approaches to support the reuse as well
as the automation of the generation of logical
configurations and parallel algorithm source code.
In our another study (Tekinerdogan and Arkin,
2013) we have proposed an architecture framework
for modeling various views that are related to the
mapping of parallel algorithms to parallel computing
platforms. An architectural framework organizes and
structures the proposed architectural viewpoints. We
have proposed five coherent set of viewpoints for
supporting the mapping of parallel algorithms to
parallel computing platforms.
5 CONCLUSIONS
In this paper we have provided a model-driven
product line engineering approach for mapping
parallel algorithms to parallel computing platforms.
With the approach we have aimed to solve the tedious
and error prone mapping process. By adopting a
software product line engineering process the
mapping does not need to be developed from scratch
but can be largely based on reusing predefined assets.
Further, by providing model-driven development
approaches we have supported the automation of the
generation of the logical configuration and the
parallel source code. The approach as such integrates
the paradigms of software product line engineering,
model-driven development and parallel computing, to
solve an important and practical problem. To the best
of our knowledge the approach is novel in this sense.
Model-Driven Product Line Engineering for Mapping Parallel Algorithms to Parallel Computing Platforms
353

The approach has also been implemented using the
corresponding toolset. In the toolset we have
implement several parallel algorithms, the required
primitive operations, the generators for the logical
configurations, and the code generators for different
platforms. So far we have focused on mapping
parallel algorithms to homogenous platforms,
therefore in our future work we will also consider the
heterogeneous platform.
REFERENCES
Arkin, E., Tekinerdogan, B., and Imre, K. 2013. Model-
Driven Approach for Supporting the Mapping of
Parallel Algorithms to Parallel Computing Platforms.
Proc. of the ACM/IEEE 16th Int. Conf. on Model
Driven Engineering Languages and Systems.
Arkin, E., Tekinerdogan, B. 2015. Parallel Application
Development using Architecture View Driven Model
Transformations", Springer CCIS, Vol. 580, 1865-
0929.
Bézivin, J. 2005. On the Unification Power of Models.
Software and System Modeling (SoSym) 4(2):171-188.
Clements, P., and Northrop, L. 2002. Software Product
Lines: Practices and Patterns. Boston, MA:Addison-
Wesley.
Czarnecki, K., and Eisenecker,U. W. 1999. Components
and Generative Programming.in ESEC/FSE-7: Proc.
7th ESEC. London, UK: Springer, 1999, pp. 2-19.
Czarnecki, K., Helsen, S., and Eisenecker, U.W. 2005.
Formalizing cardinality-based feature models and their
specialization. Software Process: Improvement and
Practice, 10(1):7–29.
Czarnecki, K.,Antkiewicz, M., Kim, C., Lau, S., and
Pietroszek. K., 2005. Model-driven software product
lines. In Companion to the 20th annual ACM
SIGPLAN Conf. on Object-oriented programming,
systems, languages, and applications (OOPSLA '05).
Epsilon, http://www.eclipse.org/epsilon.
Frank, M. P., 2002. The physical limits of computing.
Computing in Science &Engineering, vol.4, no.3,
pp.16,26.
Foster, I. 1995. Designing and Building Parallel Programs:
Concepts and Tools for Parallel Software Engineering.
Addison-Wesley Longman Publishing Co., Inc.,
Boston, MA, USA.
Gamatié, A., Le Beux, S., Piel, É., Ben Atitallah, R., Etien,
A., Marquet, P., Dekeyser, J.-L. 2011. A Model-Driven
Design Framework for Massively Parallel Embedded
Systems. ACM Transactions on Embedded Computing
Systems, 10(4), 1–36.
Gustafson, J. L., 1988. Reevaluating Amdahl's law,
Communications of the ACM, v 31, n 5, p 532-533.
İmre, K. M., Baransel, C., and Artuner, H. 2011. Efficient
and Scalable Routing Algorithms for Collective
Communication Operations on 2D All–Port Torus
Networks. Int. Journal of Parallel Programming,
Springer Netherlands, ISSN: 0885-7458, pp. 746-782,
Volume: 39, Issue: 6.
Moore, G. E., 1998. Cramming More Components Onto
Integrated Circuits. Proceedings of the IEEE , vol.86,
no.1, pp.82,85.
MPI: A Message-Passing Interface Standart, version 1.1,
http://www.mpi-forum.org/docs/mpi-11-html/mpi-
report.html.
Navarro, C. A., Hitschfeld-Kahler, N., and Mateu, L. 2014.
A Survey on Parallel Computing and its Applications in
Data-Parallel Problems Using GPU Architectures,
Commun. Comput. Phys, Vol. 15, No. 2, pp. 285-329.
Object Management Group. 2009. A UML profile for
MARTE. http://www.omgmarte.org.
Palyart, M., Lugato, D., Ober, I., and Bruel, J. 2011.
MDE4HPC: an approach for using model-driven
engineering in high-performance computing. In
Proceedings of the 15th international conference on
Integrating System and Software Modeling (SDL'11),
Iulian Ober and Ileana Ober (Eds.). Springer-Verlag,
Berlin, Heidelberg, 247-261.
Pozo, R. 1997. Template Numerical Toolkit for Linear
Algebra: High Performance Programming with C++
and the Standard Template Library. Intl. J. of High
Performance Computing Applications, vol. 11, no. 3,
pp. 251-263.
Silva de Oliveira, D. J., and Rosa, N. 2010. Evaluating
Product Line Architecture for Grid Computing
Middleware Systems: Ubá Experience. Advanced
Information Networking and Applications Workshops
(WAINA), 2010 IEEE 24th International Conference
on , vol., no., pp.257,262, 20-23.
Talia, D. 2001. Models and Trends in Parallel
Programming. Parallel Algorithms and Applications
16, no. 2: 145-180.
Taillard, J., Guyomarc'h, F. and Dekeyser, J. 2008. A
Graphical Framework for High Performance
Computing Using An MDE Approach. In Proc. of the
16th Euromicro Conf on Parallel, Distributed and
Network-Based Processing (PDP '08),. Washington,
DC, USA, 165-173.
Tekinerdogan, B., Arkin, E. Architecture Framework for
Mapping Parallel Algorithms to Parallel Computing
Platforms, Proc. of the 2nd Int. Workshop on Model-
Driven Engineering for High Performance and CLoud
computing, MODELS Conf., Miami (2013).
Travinin, N., Hoffmann, H., Bond, R., Chan, H., Kepner, J.,
and Wong, E. 2005. pMapper: Automatic Mapping of
Parallel Matlab Programs. Users Group Conference,
2005 , vol., no., pp.254,261.
Tsai, Y. J., and McKinley, P. K. 1994. An extended
dominating node approach to collective communication
in all-port wormhole-routed 2D meshes, Proceedings of
the Scalable High-Performance Computing
Conference, pp.199-206.
MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development
354
