
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs
Fei He
1
, Akiyoshi Hanai
1
, Hiroshi Nagamochi
1
and Tatsuya Akutsu
2
1
Discrete mathematics, Department of Applied Mathematics and Physics, Graduate School of Informatics,
Kyoto University, Kyoto 606-8501, Japan
2
Institute for Chemical Research, Kyoto University, Gokasho, Uji, Kyoto, 611-0011, Japan
Keywords:
Isomers Enumeration, Naphthalene, Chemical Graph.
Abstract:
In this paper, we consider the problem of enumerating naphthalene isomers, where enumeration of isomers is
important for drug design. A chemical graph G with no other cycles than naphthalene rings is called tree-like,
and becomes a tree T possibly with multiple edges if we contract each naphthalene ring into a single virtual
atom of valence 8. We call tree T the tree representation of G. There may be more than one tree-like chemical
graphs whose tree representations equal to T, which are called naphthalene isomers of T. We present an
efficient algorithm that enumerates all naphthalene isomers of a given tree representation. Our algorithm first
counts the number of all the naphthalene isomers using dynamic programming, and then for each k, generates
the k-th isomer by backtracking the counting computation. In computational experiment, we compare our
method with MolGen, a state-of-the-art enumeration tool, and it is observed that our program enumerates
the same number of naphthalene isomers within extremely shorter time, which proves that our algorithm is
effectively built.
1 INTRODUCTION
Enumeration of chemical structures has been widely
applied in drug discovery (Blum and Reymond,
2009), structure elucidation (Meringer and Schyman-
ski, 2013), exploration of chemical universe (Fink
and Reymond, 2007). It is to be noted that these
are important not only in chemo-informatics but also
in bioinformatics because one of the major targets
of bioinformatics is development of novel drugs.
Since DENDRAL was developed as an enumeration
tool for structure elucidation using data from mass
spectrometry (Buchanan and Djerassi, 1976), sev-
eral enumeration tools have been developed to solve
the Computer-Assisted Structure Elucidation (CASE)
problem. MolGen, whose development was initiated
in 1985, is one of the best enumeration tools so far,
since it can not only enumerate all possible chemical
compounds (Benecke and Wieland, 1995) (Benecke
and Wieland, 1997) (Kerber and Meringer, 1998), but
also allow users to add some restrictions to the input
of the enumeration such as the number of multiple
bonds. Recently, OMG (Open Molecule Generator)
has been newly developed as the first open source
enumeration tool (Peironcely, 2012) based on the
canonical augmentation path strategy which grows in-
termediate chemical structures by adding bonds with
checking the uniqueness, with allowing the use of
prescribed substructures to enumerate more chemi-
cally adequate structures. Although OMG is a useful
tool, it is reported that OMG is not faster than Mol-
Gen (Peironcely, 2012), especially when dealing with
large-sized chemical graphs.
Another important enumeration tool is Enumol
(Fujiwara and Akutsu, 2008) (Shimizu and Akutsu,
2011). This tool enumerates chemical structures with
tree-like graphs efficiently. Akutsu and Nagamochi
initiated the development of Enumol after studying
computational complexity of inference of a chemical
graph from its feature vector given as a labeled path
frequency vector (Akutsu and Nagamochi, 2011).
Then, Fujiwara et al. (Fujiwara and Akutsu, 2008)
proposed a branch-and-boundalgorithm to enumerate
tree-like chemical graphs from a given path frequency
vector. Shimizu et al. (Shimizu and Akutsu, 2011)
gave an algorithm for enumerating structures with a
set of feature vectors. These algorithms can only enu-
merate tree-like chemical graphs.
A benzene is a chemical compound with the
molecular formula C
6
H
6
and the six carbon atoms in
a benzene form into a hexagon. A naphthalene is
a compound with the molecular formula C
10
H
8
, and
its molecule is composed of two benzene rings with
258
He, F., Hanai, A., Nagamochi, H. and Akutsu, T.
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs.
DOI: 10.5220/0005783902580265
In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 3: BIOINFORMATICS, pages 258-265
ISBN: 978-989-758-170-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

one common edge. Among all ten carbon atoms in a
naphthalene ring, only eight of them are attached with
hydrogen atoms. A substitution of a proton by other
atoms (or atom groups) is one of the most common
reactions of naphthalene. In these substitution reac-
tions, such as sulfonation, chlorination and nitration,
the hydrogen atoms of a naphthalene ring is substi-
tuted by other atoms (or atom groups). Thereby a
naphthalene ring may have bonds with other atoms
(or atom groups) (Hardinger, 2005). The difference
of substitutions in the relative positions of the sub-
stituted hydrogen atoms results in non-isomorphic
structures, which are called the naphthalene isomers.
Given a tree-like chemical graph, Li (Li and Akutsu,
2013) proposed a different method with a guaranteed
time complexity to enumerate the benzene isomers by
the two following steps: (1) count the number f of
all the benzene isomers of the input tree representa-
tion using dynamic programming; and (2) for each
k = 1,2,.. ., f, generate the k-th benzene isomer by
backtracking the previous computation using the dy-
namic programming. In this paper, we generalize the
algorithm by Li (Li and Akutsu, 2013) into one for
enumerating the naphthalene isomers from a tree-like
chemical graphs. The major difference is that the
combinatorial complexity of arrangements of atom
groups around a naphthalene ring is much higher than
that around a benzene ring. Yet, we managed to gen-
erate all isomers in a running time per isomer similar
with the result by Li (Li and Akutsu, 2013) by gener-
ating all distinct arrangements of atom groups around
a naphthalene ring in advance and storing them in a
table. As discussed later, it is an important step to-
wards extension of enumeration of benzene isomers
to general chemical structures. Our experimental re-
sult shows that our algorithm runs much faster than
MolGen for enumeration of naphthalene isomers of
tree-like chemical compounds.
In this paper, we consider chemical graphs with
naphthalene rings. A chemical graph G possibly with
naphthalene rings is called tree-like if (i) no two naph-
thalene rings share any atoms; (ii) no multiple edges
exist between a naphthalene ring and an atom (or a
naphthalene ring); and (iii) the graph can be viewed as
a multi-tree (a tree with multiple edges) if we contract
each naphthalene ring into a single vertex of an atom
of a virtual element na of valence 8. We call the tree
in the above (iii) the tree representation of G. Note
that for a given tree representation T, there may be
more than one tree-like chemical graphs whose tree
representations are given by T. All tree-like chemi-
cal graphs whose tree representations equal to T are
called the naphthalene isomers of T. Distinct naph-
thalene isomers of T are caused by different arrange-
ments of the atom groups around a naphthalene ring
when we replace each virtual atom in T with a naph-
thalene ring to obtain a naphthalene isomer.
Given a set of atoms of each kind (including the
virtual atom na ) possibly with constraints on the num-
bers of specified paths, all possible tree-like chemi-
cal graphs can be enumerated by efficient algorithms
created by Fujiwara et al. (Fujiwara and Akutsu,
2008) and Shimizu et al. (Shimizu and Akutsu, 2011).
When we replace each virtual atom in a tree repre-
sentation with a naphthalene ring, different chemical
structures may be generated due to different relative
positions of the substituents (atom groups) around
each of the restored naphthalene rings. Let G(T) de-
note the set of all naphthalene isomers of a tree repre-
sentation T. In this paper, we consider the following
problem of enumerating naphthalene isomers.
Input: A tree representation T of a tree-like chemical
graph.
Output: All naphthalene isomers G ∈ G(T) of T.
In this paper, we design an efficient algorithm that
enumerates all the naphthalene isomers G ∈ G(T) of
a given tree representation T. We use dynamic pro-
gramming to first count the number |G(T)| of all the
naphthalene isomers of T, and then generate all naph-
thalene isomers by tracing back the computation pro-
cess done for counting the total number |G(T)| of
naphthalene isomers. Thus our enumeration algo-
rithm consists of the following two phases.
Phase 1: Count the number |G(T)| of the naphtha-
lene isomers of a tree representation T(v
0
) by a dy-
namic programming.
Phase 2: For each k = 1,2,. ..,|G(T)|, generate the
k-th isomer G
k
∈ G(T) by a procedure of backtrack-
ing the computation in Phase 1.
The paper is organized as follows. Section 2 de-
fines isomorphism of rooted graphs. Section 3 de-
signs a dynamic programming algorithm for counting
the number of isomers of rooted subtrees and that of
T. Section 4 presents an algorithm for generating the
k-th isomer among all isomers of T. Section 5 reports
on experiments to an implementation of our algorithm
for counting and generating isomers. Section 6 makes
some concluding remarks.
2 PRELIMINARIES
We introduce isomorphism in tree-like graphs.
A chemical graph is given by a connected undi-
rected graph G = (V,E) with a set V of vertices and
a set E of edges possibly with multiple edges, where
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs
259

col(v) denotes the atom assigned to each vertex v ∈ V.
For a subgraph H of G, letV(H) and E(H) denote the
sets of vertices and edges in H. For a vertex subset X
or a subgraph X of G, let N
G
(X) denote the set of
neighbors of X (the vertices in V − X or V −V(X) ad-
jacent to some vertex in X). A vertex v with col(v) = ℓ
is called an ℓ-vertex. Let E
G
(u,v) denote the set
of edges between vertices u and v in G. The set
E
G
(u,v) is called a bridge if the graph becomes dis-
connected by removingedges in E
G
(u,v). Two graphs
G = (V, E) and G
′
= (V
′
,E
′
) are isomorphic if there
is an isomorphism between them, i.e., a bijection ψ :
V → V
′
such that col(v) = col(ψ(v)) holds for each
vertex v ∈ V and |E
G
′
(ψ(u),ψ(v))| = |E
G
(u,v)| for
all vertex pairs u,v ∈ V. When two graphs G = (V,E)
and G
′
= (V
′
,E
′
) have designated vertices r ∈ V and
r
′
∈ V
′
called the roots, we say that G = (V, E) and
G
′
= (V
′
,E
′
) are rooted-isomorphic if there is an iso-
morphism ψ : V → V
′
such that r
′
= ψ(r).
Let G be a tree-like chemical graph. A naphtha-
lene ring H is a cycle of ten C-vertices eight of which
has a neighbor in N
G
(H) joined by a single edge. For
an ordered pair (v,w) such that E
G
(v,w) is bridge,
we denote G[v,w] the subgraph induced from G by
the vertex subset {v} ∪ X
w
such that X
w
is the set of
vertices reachable from vertex w by a path that does
not pass through vertex v. We regard v as the root of
G[v,w].
For each vertex v not on a naphthalene ring in
G, we define a coterie of the set {G[v,w] | w ∈
N
G
(v)} of subgraphs to be a maximal subset of
{G[v,w] | w ∈ N
G
(v)} such that any two in the sub-
set are rooted-isomorphic. Hence the set {G[v,w] |
w ∈ N
G
(v)} of subgraphs is partitioned into several
sets of coteries, which is called the coterie-family
of G at vertex v. Fig. 1 shows the coterie-family
{G[v,w
1
],G[v,w
2
]},{G[v,w
3
]} and {G[v,w
4
]} for the
subgraphs of root v of graph G, where G[v,w
i
] denotes
the subgraph composed of root v and its adjacent ver-
tices w
i
for each i = 1,2,3, 4 respectively.
Figure 1: An example of coterie-family with three coteries.
For a naphthalene ring H with C-vertices
v
1
,v
2
,. .. ,v
8
in G and N
G
(H) = {w
1
,w
2
,. .. ,w
8
}
where w
i
∈ N
G
(v
i
), each C-vertex v
i
∈ V(H) is con-
tained in the subgraph G[v
i
,w
i
]. We define a coterie
of the set {G[v
i
,w
i
] | v
i
∈ V(H)} of subgraphs to be
a maximal subset of {G[v
i
,w
i
] | v
i
∈ V(H)} such that
any two in the subset are rooted-isomorphic. Hence
the set {G[v
i
,w
i
] | v
i
∈ V(H)} of subgraphs is parti-
tioned into several sets of coteries, which is called the
coterie-family of G at naphthalene ring H.
The size of a coterie is defined to be the number of
subgraphs that belong to the coterie. Among coteries
with the same size, we introduce some total order, and
we always denote by R
j
i
the subgraph that belong to
the j-th coterie of size i. Fig. 2 illustrates an example
of coterie-family at a vertex v with a coterie with size
1, a coterie with size 3 and a coterie with size 4.
Figure 2: An example for a coterie-family at vertex
v in a tree T where the cf-type at vertex v is c =
(1,0,1,1,0, 0,0,0).
A coterie-family-type (cf-type) of G at a vertex
v or a naphthalene ring H is defined to be the set
of the number of coteries of each size, and is de-
noted by the occurrence vector c whose i-th entry in-
dicates the number of coteries of size i. In Fig. 2,
c = (1,0,1, 1,0,0, 0,0).
Figure 3: The two layout-types in L(c) of cf-type c =
(1,0,0,0,0, 0,1,0).
For a fixed cf-type c of G at a naphthalene ring
H, there may be different ways of placing the sub-
graphs in {G[v
i
,w
i
] | v
i
∈ V(H)} such that the result-
ing graphs are not isomorphic. The set L(c) of layout-
types consists of such different ways of placing the
subgraphs in {G[v
i
,w
i
] | v
i
∈ V(H)}. For example, cf-
type c = (1,0,0, 0,0,0, 1,0) has two layout-types in
L(c), which is illustrated in Fig. 3. Let λ(c) = |L(c)|.
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
260

Table 1 shows the number λ(c) of layout types for
each possible cf-type c of a naphthalene ring. Among
the layout-types in L(c) for each cf-type c, we intro-
duce some total order, and denote by L
i
(c) the i-th
layout-type in L(c). In this paper, we assume that a
complete list of all layout types of each cf-type for
a naphthalene ring is available, where the total num-
ber of layout types is 23,911. An efficient method
for generating all layout types of a geometrical ob-
ject with two axial symmetries including naphthalene
ring has been discussed by He and Nagamochi (He
and Nagamochi, 2015).
Table 1: The number λ(c) of layout types for each possible
cf-type c of a naphthalene ring.
c λ(c) c λ(c)
(0,0,0,0,0,0,0,1) 1 (1,0,0,0,0,0,1,0) 2
(0,1,0,0,0,1,0,0) 10 (2,0,0,0,0,1,0,0) 14
(0,0,1,0,1,0,0,0) 14 (1,1,0,0,1,0,0,0) 42
(3,0,0,0,1,0,0,0) 84 (0,0,0,2,0,0,0,0) 22
(1,0,1,1,0,0,0,0) 70 (0,2,0,1,0,0,0,0) 114
(2,1,0,1,0,0,0,0) 210 (4,0,0,1,0,0,0,0) 420
(0,1,2,0,0,0,0,0) 140 (2,0,2,0,0,0,0,0) 280
(1,2,1,0,0,0,0,0) 420 (3,1,1,0,0,0,0,0) 840
(5,0,1,0,0,0,0,0) 1680 (0,4,0,0,0,0,0,0) 648
(2,3,0,0,0,0,0,0) 1260 (4,2,0,0,0,0,0,0) 2520
(6,1,0,0,0,0,0,0) 5040 (8,0,0,0,0,0,0,0) 10080
In the rest of this section, we discuss the structure
of isomorphism in tree representations.
Let T be a tree representation with virtual na
atoms of valence 8, which we restore naphthalene
rings to obtain a naphthalene isomer of T. Note that
E
T
(v,w) is a bridge of T for each pair of adjacent ver-
tices v,w ∈ V(T), and T[v, w] is the induced subtree
of T rooted at v such that V(T[v,w]) consists of v and
the vertices reachable from w without visiting v. Ev-
ery vertex v in T is shared by |N
T
(v)| subtrees T[v,w]
with w ∈ N
T
(v). For a subtree T
′
= T[v,w] for ver-
tices v ∈ V and w ∈ N(v) in T, restoration of T
′
is an
operation of expanding the na-vertices z (6= v) in T
′
into naphthalene rings H
z
to obtain a chemical graph
G
v
rooted at v, where v may be a na-vertex. Let G(T
′
)
be the set of tree-like graphs G
v
obtained by restoring
a subtree T
′
of T.
Our aim is to generate all isomers in G(T) from
a given tree representation T, supposing that we
know the cf-type c
v
of the coterie-family for the set
{G[v
i
,w
i
] | v
i
∈ V(H
v
), w
i
∈ N
G
(v
i
)} of subgraphs
around the naphthalene ring H
v
restored from each
na-vertex v in T. Since distinct isomers are caused by
different layout-types around naphthalene rings after
restoration of T, an isomer G ∈ G(T) can be specified
by a layout-type L[v] ∈ L(c
v
) of each na-vertex v in
T. Throughout the paper, we assume that non-rooted-
isomorphic subgraphs in {G[v
i
,w
i
] | v
i
∈ V(H
v
), w
i
∈
N
G
(v
i
)} can be arranged in some total order based
on their topological structure, and we assign indices
R
1
i
,R
2
i
,. .. to the coteries with the same size i accord-
ing to the order so that choosing a layout-type in
L(c
v
) uniquely determines the relative positions of all
the subgraphs in {G[v
i
,w
i
] | v
i
∈ V(H
v
), w
i
∈ N
G
(v
i
)}
around the naphthalene ring H
v
. However, when we
change a layout-type L[v] ∈ L(c
v
) for some na-vertex
v in T, the cf-type c
u
of some other na-vertex u may
change. To avoid such inconvenience in generating
all isomers in G(T), we designate a vertex in T as the
root and systematically compute the number of iso-
mers of some subtrees of T by a dynamic program-
ming, where all isomers of T will be generated by
backtracking the computation.
Let G(T[v,w]) denote the set of isomers obtained
from the tree T[v,w] by restoring all na-vertices z (6=
v) in T[v,w] into naphthalene rings H
z
. Clearly if
T[v,w] and T[v,w
′
] are rooted-isomorphic for w,w
′
∈
N
T
(v), then G(T[v,w]) = G(T[v,w
′
]). Conversely
T[v,w] and T[v,w
′
] are not rooted-isomorphic for
w,w
′
∈ N
T
(v), then G(T[v,w]) ∩ G(T[v,w
′
]) =
/
0.
Let us treat a given tree representation T as a tree
rooted at a vertex v
0
, where the root is chosen as a
topologically unique vertex in T such as “center” or
“centroid.” It is known that every tree has either a
vertex or an edge removal of which leaves no com-
ponent with more than ⌊n/2⌋ vertices. The former
vertex is called unicentroid and the latter bicentroid.
We choose the unicentroid of T as the root v
0
of T,
where if T has the bicentroid (v
′
,v
′′
), then we remove
the edge connecting v and v
′
and insert a virtual vertex
v with the two neighbors v
′
and v
′′
as the unicentroid
in the resulting tree. For each vertex v in a rooted
tree representation T = (V,E), let Ch(v) ⊆ N
T
(v) de-
note the set of children of v, where Ch(v) =
/
0 if v is
a leaf vertex of T. When v is not the root of T, let
p(v) ∈ N
T
(v) denote the parent of v. By the topolog-
ical uniqueness of the root v
0
, we see that for each
non-root vertex v, tree T[v,w] with w ∈ Ch(v) is not
rooted-isomorphic to tree T[v,p(v)].
The set Ch(v) of children of a vertex v in T
is decomposed into sets Ch
1
(v),Ch
2
(v),... ,Ch
t
(v)
such that the subtrees T[v,u] and T[v,u
′
] are rooted-
isomorphic if and only if u, u
′
∈ Ch
i
(v) for some i.
Fig. 4 illustrates the rooted-isomorphic decomposi-
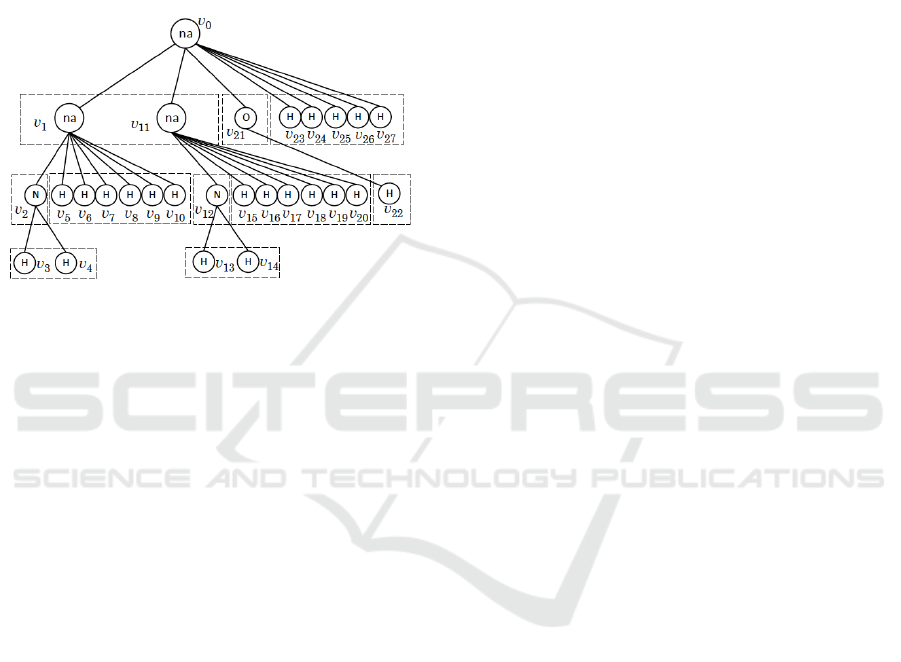
tions of child sets of a tree presentation T. Note that
for a given tree presentation T rooted at a vertex v
0
,
we can compute the rooted-isomorphic decomposi-
tion {Ch
i
(v) | i = 1,2, .. .,t
v
} for all vertices v ∈ V in
polynomialtime in the size of T by expressing all sub-
trees T[v,u], u ∈ Ch(v) for each v ∈ V(T) as canoni-
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs
261
cal forms such as left-heavy trees (Nakano and Uno,
2005).
In what follows, we assume that an input of the
problem is the set
(T,v
0
,{{Ch
i
(v) | i = 1,2, .. .,t
v
},v ∈ V})
of a tree representation T rooted at the unicentroid
v
0
and the rooted-isomorphicdecompositions of child
sets of T.
Figure 4: The rooted-isomorphic decompositions of child
sets of tree representation T, where the dotted rectangles
show the rooted-isomorphic decompositions for all non-leaf
vertices in T.
3 COUNTING THE NUMBER OF
ISOMERS
Let nis(v
0
) = |G(T)| for the root v
0
of T, and nis(v) =
|G(T[p(v),v])| for each non-root vertex v in T. We
derive recursive formulas over {nis(v) | v ∈ V(T)}
such that nis(v) can be computed from {nis(w) | w ∈
Ch(v)}.
Example 1. Before we present details, we show how
the numbers nis(v), v ∈ V(T) of the example T in
Fig. 4 will be computed.
1. Clearly for the leaf vertices v ∈ V(T) −
{v
0
,v
1
,v
2
,v
11
,v
12
,v
21
} in the example T, we have
that nis(v) = 1.
2. For the non-na-vertex v
2
, the rooted-isomorphic
decomposition of the child set Ch(v
2
) is Ch
1
(v
2
) =
{v
3
,v
4
} since T[v
2
,v
3
] and T[v
2
,v
4
] are rooted-
isomorphic, where nis(v
3
) = nis(v
4
) = 1, and we
know that G(T[p(v
2
),v
2
]) contains only one isomer,
implying that nis(v
2
) = 1.
3. We next consider the na-vertex v
1
in the example
T. The rooted-isomorphic decomposition of the child
set Ch(v
1
) is given by Ch
1
(v
1
) = {v
2
} and Ch
2
(v
1
) =
{v
5
,v
6
,v
7
,v
8
,v
9
,v
10
} where we know that nis(v
2
) = 1
and nis(w) = 1, w ∈ Ch
2
(v
1
). For any vertex w ∈
Ch(v
1
), there is only one isomer in G(T[p(w),w]).
The corresponding cf-type c
v
1
=(2,0,0,0,0,1,0,0) has
λ(c
v
1
) = 14 layout-types (see Table 1). Therefore we
have nis(v
1
) = 14.
4. We now consider the root na-vertex v
0
, where
the rooted-isomorphic decomposition of Ch(v
0
) is
Ch
1
(v
0
) = {v
1
,v
11
}Ch
2
(v
1
) = {v
21
} and Ch
3
(v
1
) =
{v
23
,v
24
,v
25
,v
26
,v
27
} and we see that nis(w) = 14,
w ∈ Ch
1
(v
0
), nis(w) = 1, w ∈ Ch
2
(v
0
) and nis(w) =
1, w ∈ Ch
3
(v
0
), respectively. For nis(w) = 14,w ∈
Ch
1
(v
0
) and |Ch
1
(v
0
)| = 2, there are two different
coterie-families at v
0
: i) one when G
′
∈ G(T[v
0
,v
1
])
and G
′′
∈ G(T[v
0
,v
11
]) are rooted-isomorphic; and ii)
the other when they are not isomorphic.
i) The former cf-type is c
v
0
= (1, 1,0,0, 1,0,0, 0),
where R
1
1
∈ G(T[v
0
,v
1
]), R
1
2
∈ G(T[v
0
,v
21
]) and R
1
3
∈
G(T[v
0
,v
23
]). Note that there are nis(v
1
)×nis(v
21
)×
nis(v
23
) = 14 × 1 × 1 = 14 combinations of iso-
mers in G(T[v
0
,w]) with w ∈ Ch(v
0
) that give cf-
type c
v
0
= (1,1,0,0, 1,0,0, 0) at v
0
. Since there
are λ(c
v
0
) = 42 layout-types (see Table 1), we have
14× 42 = 588 isomers in G(T) whose cf-type at v
0
is
(1,1,0, 0,1,0, 0,0).
ii) For the latter cf-type is c
v
0
=
(3,0,0, 0,1,0, 0,0), where R
1
1
∈ G(T[v
0
,v
1
])R
2
1
∈
G(T[v
0
,v
11
])R
1
2
∈ G(T[v
0
,v
21
]) and R
1
3
∈
G(T[v
0
,v
23
]). Note that there are
nis(v
1
)
2
×
nis(v
21
) × nis(v
23
) = 91 × 1 × 1 = 91 combinations
of isomers in G(T[v
0
,w]) with w ∈ Ch(v
0
) for
cf-type c
v
0
= (3,0, 0,0,1, 0,0,0) at v
0
. Since there
are λ(c
v
0
) = 84 layout-types (see Table 1), we have
84× 91 = 7644 isomers in G(T) whose cf-type at v
0
is (3,0,0, 0,1,0, 0,0).
In total, the number nis(v
0
) of isomers in G(T) is
588+ 7644 = 8232.
In what follows, we generalize the above idea
into recursive formulas from which we can system-
atically compute the number nis(v) from nis(w),w ∈
Ch(v). The point is how each subset Ch
i
(v) in the
rooted-isomorphic decomposition of Ch(v) can be
further partitioned into coteries. Different partitions
of subset Ch
i
(v), i = 1,2, .. .,t give rise to distinct
cf-types. Let n
i
= |Ch
i
(v)| and f
i
denote the num-
ber nis(w) = |G(T[v,w])| of isomers of the subtree
T[v,w] rooted at a vertex w ∈ Ch
i
(v). Denote the num-
ber of coteries partitioned from Ch
i
(v) by h
i
. Then
1 ≤ h
i
≤ min{n
i
, f
i
} for each i ∈ {1,2, .. .,t}. Let H
v
be the set of all possible vectors, the i-th entrance of
which is the number of coteries in Ch
i
(v), then H
v
=
{(h
1
,h
2
,. .. ,h
t
) | 1 ≤ h
i
≤ min{n
i
, f
i
}, i = 1,2,...,t},
where |H
v
| =
∏
1≤i≤t
min{n
i
, f
i
}.
For a subtree T
′
⊆ T rooted at v and the rooted-
isomorphic decomposition {Ch
1
,. .. ,Ch
t
v
}, we de-
fine a subset G
h
(T
′
) of G(T
′
), h ∈ H
v
to be the
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
262

set of restored graphs of T
′
whose number of coter-
ies in Ch
i
(v) equals to h
i
for each i ∈ {1,2,...,t
v
}.
Let g(h) = |G
h
(T
′
)|. For any two different vectors
h
1
,h
2
∈ H
v
, restored subgraphs G
h
1
(T
′
) ⊆ G
h
1
(T
′
)
and G
h
2
(T
′
) ⊆ G
h
2
(T
′
) are always non-isomorphic.
Then we have the equation as follows.
nis(v) =
∑
h∈H
v
g(h). (1)
A specific form of function g(h) of h ∈ H
v
can
be derived in a similar manner with the method by Li
et al. (Li and Akutsu, 2013). Due to a space limita-
tion, we here omit deriving the form of function g(h),
which takes a different form in each of the following
three cases:
1. Vertex v is a non-na vertex.
2. Vertex v is a non-root na-vertex.
3. Vertex v is a root na-vertex.
We analyze the time complexity of our algo-
rithm. Since the valence of any atom is constant
and |N(H)| = 8 for a naphthalene ring, the degree
|N
T
(v)| of any vertex v in T is O(1). Hence |H
v
| is
also O(1), and computing {g(h) | h ∈ H
v
} and deter-
mining nis(v) can be executed in O(1) time (Li and
Akutsu, 2013). Therefore the total running time of
our algorithm is O(n) for the input size n = |T(V)|.
4 CONSTRUCTION OF
NAPHTHALENE ISOMERS
In the first phase of our algorithm, given a tree repre-
sentation T, we compute nis(v) and {g(h) | h ∈ H
v
}
for all vertices v ∈ V(T). In the second phase of our
algorithm, we generate isomers in G(T) one by one.
For this, we fix a total order σ
v
0
: G(T) →
[1,nis(v
0
)] over all isomers in G(T) such that
σ
v
0
(G) = k means that G is the k-th isomers in G(T)
in the total order. Similarly for each non-root ver-
tex v in T, we fix a total order σ
v
: G(T[p(v),v]) →
[1,nis(v)] over all isomers in G(T[p(v),v]) such that
σ
v
(G) = j means that G is the j-th isomers in
G(T[p(v),v]). Since the way of fixing total orders
σ
v
is same during the second phase, it holds σ
u
= σ
v
for any two vertices u,v ∈ V(T) such that T[p(u),u]
and T[p(v),v] are rooted-isomorphic. Hence the k-
th isomer G
u
∈ G(T[p(u),u]) and the k
′
-th isomer
G
v
∈ G(T[p(v),v]) will be rooted-isomorphic if and
only if k = k
′
.
Supposing such fixed total orders {σ
v
| v ∈
V(T)}, we generate the k-isomer G ∈ G(T) of T
(i.e., the isomer G such that σ
v
0
(G) = k) for a
specified integer k ∈ [1, nis(v
0
)], where we call k
the search index of vertex v. For the child set
Ch(v) = {w
1
,w
2
,. .. ,w
q
}, the isomer G ∈ G(T) con-
sists of q subgraphs G
w
1
,G
w
2
,..., G
w
q
such that G
w
i
∈
G(T[v,w
i
]). We let k[w
i
] = σ
w
i
(G
w
i
), i.e., G
w
i
is the
k[w
i
]-th isomer in G(T[v,w
i
]). Hence we see that
the isomer G ∈ G(T) consists of k[w
i
]-th isomer in
G(T[v,w
i
]) for each child w
i
∈ Ch(v), where we call
k[w
i
] the search index of vertex w
i
. When v is a na-
vertex, we also identify the layout-type L[v] around
the naphthalene ring H
v
.
In the rest of this section, we show how to com-
pute search indices.
An isomer G ∈ G(T) can be determined by
choices of cf-types c
z
and layout-types L[z] ∈ L(c
z
)
for all naphthalene rings H
z
stored from the na-
vertices z in T. In fact, we see that only the set
{L[z] | na-vertices z in T} determines a cf-type c
z
of
each naphthalene ring H
z
. Each leaf vertex v in T
has a unique cf-type c
v
. Recursively when an isomer
G
w
∈ G(T[v,w]) of each child w ∈ Ch(v) of a ver-
tex v has been determined, the cf-type c
v
of vertex
v can be uniquely determined, and the isomer G
v
∈
G(T[p(v),v]) (or G
v
∈ G(T)) consisting of these sub-
graphs G
w
∈ G(T[v, w]), w ∈ Ch(v) can be uniquely
determined with a specified layout-type when v is a
na-vertex (or G
v
can be uniquely determined only by
G
w
, w ∈ Ch(v) when v is not a na-vertex). Our task
is to output a set {L[z] | na-vertices z in T} of layout-
types as an isomer G ∈ G(T).
Example 2. We show how search indices and layout-
types will be computed in the example T in Fig. 4
1. After counting phase, we have computed {g(h) |
H
v
} for all non-leaf vertices v. In the example, H
v
0
=
{h
1
= (1,1,1),h
2
= (2, 1,1)} with g(h
1
) = 588 and
g(h
2
) = 7644 and |H
v
| = 1 for all the other non-leaf
vertices v in T.
2. Suppose that we generate the k-th isomer in G(T)
of the example. Recall that nis(v
0
) = g(h
1
)+ g(h
2
) =
588 + 7644 = 8232, where we can regard the first
588 isomers in G(T) are constructed based on the
first vector h
1
∈ H
v
0
and the remaining 7644 isomers
in G(T) are based on the second vector h
2
∈ H
v
0
.
Hence when k ≤ 588, we generate an isomer G ∈
G(T) based on h
1
∈ H
v
0
and the corresponding cf-
type c
v
0
= (1,1,0, 0,1,0, 0,0); and when k > 588, we
generate an isomer G ∈ G(T) based on h
2
∈ H
v
0
and
the corresponding cf-type c
v
0
= (3,0,0, 0,1,0, 0,0).
3. Assume k = 600, and consider how to deter-
mine the search indices k[w] of the children w of v
0
.
Since k = 600 > 588, we construct the k-th isomer
G ∈ G(T) based on h
2
= (2,1,1) ∈ H
v
0
and cf-type
c
v
0
= (3, 0,0,0, 1,0,0, 0); i.e., for k
′
:= k− 588 = 12,
we construct the k
′
-th isomer among such g(h
2
) =
7644 isomers based on c
v
0
= (3,0,0, 0,1,0, 0,0). Re-
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs
263
call that
g(h
2
) = 7644 = 91 × 84
=
nis(v
1
)
2
× λ((3,0, 0,0,1, 0,0,0)).
(2)
By h
2
= (2,1, 1), the subset Ch
1
(v
0
) = {v
1
,v
11
} is
partitioned into two sequences (v
1
) and (v
11
), indi-
cating that we select an isomer G
′
∈ G(T[v
0
,v
1
]) and
an isomer G
′′
∈ G(T[v
0
,v
11
]) which are not rooted-
isomorphic. There are
nis(v
1
)
2
=
14
2
= 91 such
pairs of isomers G
′
and G
′′
, and each pair correspond
with root v
0
’s 84 layout-types. By k
′
= 12, we have
0× 84 < 12 ≤ 1 × 84. Then this means that in 600-th
isomer, vertex v
0
has the first layout-type in occur-
rence vector c
v
0
= (3,0,0, 0,1,0, 0,0), which means
that the layout-type L[v
0
] = 1 at na-vertex v
0
in the
example T in Fig. 4.
4. Then we decide the search indices for the two na-
vertices v
1
an v
11
in Ch
1
(v
0
). The 91 pairs of non–
isomorphic graphs G
′
and G
′′
rooted at v
1
and v
11
have search indices of the two vertices listed from
the smallest to the largest: (1,2), (1,3), . .., (1,14),
(2,3), ..., (13,14), and we choose the 12th one, where
(k[v
1
],k[v
11
])=(1,12). Then G
′
has the k[v
1
] = 1-st
isomer in G(T[v
0
,v
1
]) and G
′′
has the k[v
11
] = 12-
th isomer in G(T[v
0
,v
1
]). Since v
1
and v
11
do not
have any descendants that are na-vertex, this directly
means that vertex v
1
has the 1-st layout-type, and v
11
has the 12-th layout-type.
We designed an algorithm that determines the
search indices k[w] of children w of a vertex v with
a search index k, and it runs in O(log|G(T)|) time for
each non-na-vertex v in T. Due to space limitation,
we omit the algorithms and explanation of time com-
plexities.
If we calculate the layout-types for all na-vertices
v in tree T for a search index k, k ∈ [1,nis(v)], then
we get our k-th isomer. The algorithms for determin-
ing the search indices and the layout-type for one ver-
tex run in O(log|G(T)|), and we can see that gen-
erating the k-th isomer runs in time O(nlog|G(T)|).
Hence, all the isomers in G(T) can be generated
in O(n|G(T)| log|G(T)|) time. It should be noted
that the required space for executing our algorithm is
O(n), since we do not need to store any isomers gen-
erated before for a possible comparison with newly
generated isomers to check duplication.
5 EXPERIMENTAL RESULTS
In this section, we attempt to show the correctness and
efficiency of our algorithm. For this, we conducted
two experiments over problem instances constructed
based on some chemical compounds and databases.
We implemented our algorithm in C language and ex-
ecuted it on a PC with Intel(R) Core(TM)i7 CPU 1.7
GHz and 8 GB memory. In this paper, we assume that
a complete list of all layout types of each cf-type for
a naphthalene ring is available as a table. In our pro-
gram, we calculate the total number of isomers and
generate each of them for a specific input using the
table. The experimental results of computing time do
not include the process of preparing this table.
In the first experiment, we solve small problem in-
stances by our algorithm so that we can see whether
all isomers of the instances are correctly and effi-
ciently enumerated. For this, we used five rela-
tively small instances, whose formulas are na
1
O
2
H
8
,
na
1
C
2
O
2
H
10
, na
1
C
3
O
2
H
12
, na
1
C
4
O
2
H
12
, na
1
C
5
O
2
H
12
, to
compare the results with those by MolGen. Here,
chemical formula defines a set of chemical trees, from
which isomers of the same formula are generated by
our algorithm. For example, the first set consists of
two tree representations all of which have the same
formula na
1
O
2
H
8
. We used the algorithm due to
Shimizu et al. (Shimizu and Akutsu, 2011) to gen-
erate all such trees.
Table 2: Comparison of our algorithms with MolGen.
Instance # rep. # iso. Time (s) Mol-Time
na
1
O
2
H
8
2 12 0.0001 0.222 s
na
1
C
2
O
2
H
10
26 294 0.0010 108.025 s
na
1
C
3
O
2
H
12
140 2458 0.0114 1064.696 s
na
1
C
4
O
2
H
12
623 13442 0.0594 > 6 hours
na
1
C
5
O
2
H
12
2046 46354 0.2436 > 4 days
Table 2 summarizes the results, where each row
shows the chemical formula of each instance, the
number of tree representationsgenerated from the for-
mula (abbreviatedas # rep.), the total numberof naph-
thalene isomers generated from these tree represen-
tations by our algorithm (abbreviated as # iso.), the
CPU time of our algorithm (abbreviated as Time),
and that of MolGen (abbreviated as Mol-Time). Note
that MolGen runs on a workstation with Intel(R)
Xenon(R) CPU 3.00 GHz and 32 GB memory. It was
observed that the numbers of isomers generated by
our algorithm completely match with those generated
by MolGen, and that our algorithm runs much faster,
even on a slower CPU, which shows the correctness
and efficiency of our algorithm.
In the second experiment, we measured the com-
puting time by our algorithms for additional eight sets
of relativelylarge instances with multiple naphthalene
rings in the same manner. Table 3 shows the results
on these instances, with each row shows the chemical
formula of each instance, the number of tree represen-
tations generated from the formula (abbreviated as #
rep.), the total number of naphthalene isomers gener-
BIOINFORMATICS 2016 - 7th International Conference on Bioinformatics Models, Methods and Algorithms
264

ated from these tree representations by our algorithm
(abbreviated as # iso.), and the CPU time of our al-
gorithm (abbreviated as Time), from which we can
observe that our algorithm runs fast even for millions
of isomers.
As we can see in Table 3, as the number of na-
vertices in formulas increases, the number of the cor-
responding isomers goes up drastically. On the other
hand, the average computing time per isomer remains
the same level of 10
−6
second, regardless of the large
size of the input instance.
Table 3: Large Instances with Multiple Naphthalene Rings.
Instance # rep. # iso. Time (s)
na
2
COH
16
8 483 0.0017
na
2
C
2
O
2
H
18
141 38,752 0.1261
na
3
COH
22
22 14,276 0.0352
na
3
CO
2
H
22
95 172,516 0.6417
na
3
C
2
O
2
H
24
582 2,219,180 8.9126
na
3
C
2
O
3
H
24
2383 19,679,568 138.7940
na
4
COH
28
60 441,050 1.8361
na
5
COH
34
166 14,019,964 66.3542
6 CONCLUSION
In this paper, we have described our algorithm by
a dynamic programming in a rather general way in
the sense that not only benzene and naphthalene rings
but also some other local chemical structure such as
polycyclic aromatic hydrocarbons can be handled in
a similar way. Thus we can design an algorithm
that, given a tree representation where several local
structures are contracted into virtual atoms, counts
the number of isomers of the tree and generates all
isomers one by one. Such an extended algorithm
will be made available via the EnuMol web server
(http://sunflower.kuicr.kyoto-u.ac.jp/tools/enumol/).
REFERENCES
Akutsu, T. and Nagamochi, H. (2011). Kernel methods for
chemical compounds, from classification to design. In
IEICE Transactions on Information and Systems, Vol.
E94-D, No. 10, pp. 1846-1853.
Benecke, C., G. R.-H. R. K. A. L. R. and Wieland, T.,
M. (1995). A generator of connectivity isomers and
stereoisomers for molecular structure elucidation. In
Analytica Chimica Acta, Vol. 314.
Benecke, C., G. T.-K. A. L. R. and Wieland, T. (1997).
Molecular structures generation with molgen, new
features and future developments. In Fresenius’ Jour-
nal of Analytical Chemistry, Vol. 359, No. 1, pp. 23-
32.
Blum, L. C. and Reymond, J. L. (2009). 970 million drug-
like small molecules for virtual screening in the chem-
ical universe database gdb-13. In J. Am. Chem. Soc.,
Vol. 131, No. 25, pp. 8732-8733.
Buchanan, B. G., S.-D. H. W. W. G. R. F. E. L. J. and
Djerassi, C. (1976). Applications of artificial intel-
ligence for chemical inference. 22, automatic rule for-
mation in mass spectrometry by means of the meta-
dendral program. In J. Am. Chem. Soc., Vol. 98, No.
20, pp. 6168-6178.
Fink, T. and Reymond, J. L. (2007). Virtual explo-
ration of the chemical universe up to 11 atoms of
C,N,O,F, assembly of 26.4 million structures (110.9
million stereoisomers) and analysis for new ring sys-
tems, stereochemistry, physicochemical and proper-
ties, compound classes, and drug discovery. In Jour-
nal of Chemical Information and Modeling, Vol. 47,
No. 2, pp. 342-353.
Fujiwara, H., W. J.-Z. L. N. H. and Akutsu, T. (2008). Enu-
merating tree-like chemical graphs with given path
frequency. In Journal of Chemical Information and
Modeling, Vol. 48, pp. 1345-1357.
Hardinger, S. (2005). Chemistry 14D thinkbook. Hayden
McNeil.
He, F. and Nagamochi, H. (2015). A method for generating
colorings over graph automorphism. In ISORA 2015,
Luoyang, China, pp. 70-81.
Kerber, A., L. R.-G. T. and Meringer, M. (1998). Molgen
4.0, match commun. math. comput. chem. In Vol. 37,
pp. 205-208.
Li, J., N. H. and Akutsu, T. (2013). Enumerating benzene
isomers of tree-like chemical graphs. In Manuscript
submitted to a journal.
Meringer, M. and Schymanski, E. L. (2013). Small
molecule identification with molgen and mass spec-
trometry. In Metabolites, Vol. 3, pp. 440-462.
Nakano, S. and Uno, T. (2005). Generating colored trees.
In Lect. Notes Comput. Sci., Vol. 3787, pp. 249-260.
Peironcely, J. E., R.-C. M. F. D. R. T. C. L. F. J.-L. H. T.
(2012). Omg: open molecule generator. In Journal of
Cheminformatics, Vol. 4, Ariticle 21.
Shimizu, M., N. H. and Akutsu, T. (2011). Enumerating
tree-like chemical graphs with given upper and lower
bounds on path frequencies. In BMC Bioinformatics,
Vol. 12, Suppl 14, S3.
Enumerating Naphthalene Isomers of Tree-like Chemical Graphs
265
