Human Recognition in RGBD Combining Object Detectors and
Conditional Random Fields
Konstantinos Amplianitis
1
, Ronny H
¨
ansch
2
and Ralf Reulke
1
1
Computer Vision Group, Humboldt Universit
¨
at zu Berlin, Rudower Chaussee 25, 12489 Berlin, Germany
2
Computer Vision and Remote Sensing Group, Technische Universit
¨
at Berlin, Marchstr. 23, 10587 Berlin, Germany
Keywords:
Deformable Part Models, RGBD Data, Conditional Random Fields, Graph Cuts, Human Recognition.
Abstract:
This paper addresses the problem of detecting and segmenting human instances in a point cloud. Both fields
have been well studied during the last decades showing impressive results, not only in accuracy but also in
computational performance. With the rapid use of depth sensors, a resurgent need for improving existing
state-of-the-art algorithms, integrating depth information as an additional constraint became more ostensible.
Current challenges involve combining RGB and depth information for reasoning about location and spatial
extent of the object of interest. We make use of an improved deformable part model algorithm, allowing to
deform the individual parts across multiple scales, approximating the location of the person in the scene and
a conditional random field energy function for specifying the object’s spatial extent. Our proposed energy
function models up to pairwise relations defined in the RGBD domain, enforcing label consistency for regions
sharing similar unary and pairwise measurements. Experimental results show that our proposed energy func-
tion provides a fairly precise segmentation even when the resulting detection box is imprecise. Reasoning
about the detection algorithm could potentially enhance the quality of the detection box allowing capturing
the object of interest as a whole.
1 INTRODUCTION
Existing work on RGB and RGBD space has concen-
trated more on semantic segmentation and scene un-
derstanding, i.e. which pixel/voxel should be assigned
to which object label. In spite of the fact that even
though this is an interesting field of research, many
applications require additional knowledge of the dy-
namic, moving objects in the scene. This procedure
requires information about an approximate location
and spatial extent of these objects in the scene. For
the human vision, perception has a physical mean-
ing, as it involves a natural process performed in the
cerebral cortex of the brain. For computer vision, this
natural process was scientifically treated as two sep-
arate and independent tasks. As was mentioned by
(Hariharan et al., 2014), neither the detection box nor
object regions can produce a compelling output rep-
resentation but rather they should be able to comple-
ment each other.
The availability of commodity depth sensors such
as the Kinect, paved the way for researchers to im-
prove the state-of-the-art detection and segmentation
algorithms and increase the richness of available in-
formation. In this paper, we try to bring together de-
tection and segmentation as a recognition task, to in-
fer about the location and spatial extent of an object
in RGBD space. Localization is performed using an
accelerated version of the deformable part algorithm
model proposed by (Dubout and Fleuret, 2013) which
allows deformation of the individual detection parts in
a multi scale fashion. Furthermore, we propose a con-
ditional random field energy function modelling up to
a pairwise 4-neighborhood relation in RGBD space.
The unary potentials are defined by a probabilistic
framework using a simple shape prior which biases
the segmentation towards human shapes and a deci-
sion tree ensemble trained on RGB features. Like-
wise, the edge potentials are modelled using any of
the following RGBD feature functions: Canny edges,
RGB color distance, 3D Euclidean distance and sur-
face normals. Energy function is submodular and can
efficiently be solved in polynomial time using graph
cuts.
We have developed a fully automatic approach for
detecting and segmenting human instances in a point
cloud without requiring any hard biases such as prior
knowledge for the graph cut. We also show that using
Amplianitis, K., Hänsch, R. and Reulke, R.
Human Recognition in RGBD Combining Object Detectors and Conditional Random Fields.
DOI: 10.5220/0005786006550663
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 4: VISAPP, pages 655-663
ISBN: 978-989-758-175-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
655

any of the aforementioned edge potentials in the en-
ergy function, does not influence as much the quality
of the segmentation but mostly depends on the results
of the unary potentials.
One of the main drawbacks of our approach is the
fact that depending on the distance of the camera to
the object but also the quality of the classifier, a de-
tection box may or may not capture the complete body
and hence can lead to an incomplete segmentation. At
this point, we have to stress that potential failure to an
imperfect detection box does not render the segmen-
tation method less accurate. This is clear from the
qualitative results in the experimental section.
2 RELATED WORK
Our proposed method is inspired by the work of
(Ladicky et al., 2010), (Vibhav Vineet and Torr,
2011), (Teichman et al., 2013) and (Lai et al., 2012).
(Ladicky et al., 2010) are the first who combined ob-
ject detectors with CRFs for jointly estimating the
class category, location and spatial extent of ob-
jects/regions in a scene. This work was later on used
by (Vibhav Vineet and Torr, 2011) for approaching
the problem of human instance segmentation. Specif-
ically, they proposed a CRF energy function for inte-
grating instant level information such as shape prior
and exemplar histograms, biasing the segmentation
towards human shape. Incorporating higher level im-
age representations, (Shu et al., 2013) introduced a
method for improving generic detectors and subse-
quently extracting object regions, using a superpixel-
based Bag-of-Words model.
As Convolutional Neural Networks (CNNs) are
becoming more famous in the computer vision com-
munity, literature in this area of research is still lim-
ited but noteworthy. To the best of our knowledge, the
work of (Hariharan et al., 2014) was the first attempt
towards simultaneously detecting and segmenting ob-
jects in an image. Their algorithm is based on classi-
fying region proposals, using features extracted from
both the bounding box of the region and the region
foreground integrated in a jointly trained CNN.
In the RGBD domain, (Lai et al., 2012) proposed
a view-based approach for segmenting objects in a
point cloud generated by a depth sensor. A sliding
window detector trained from different object views is
used for assigning class probabilities to every image
pixel. Then, they performed an MRF inference over
the projected probabilities in voxel space, combining
cues from different views for labeling the scene. To
the best of our knowledge, this work is conceptually
closer to ours. Moreover, (Teichman et al., 2013) pro-
posed a semi-automatic approach for segmenting de-
formable objects in RGBD space, providing an ini-
tial seed as a prior hard constraint for inferring the
segmentation. His approach makes use of a rich set
of features defined in RGBD space. To the best of
our knowledge, recent work in the field is the one of
(Gupta et al., 2014) who studied the problem of ob-
ject detection and segmentation in RGBD by combin-
ing an RGB feature-based CNN with a depth feature-
based CNN in an SVM classifier.
3 OUR APPROACH
3.1 Energy Function
We begin by representing every pixel in the image
as a random variable. Each of these random vari-
ables is assigned a label from the binary label set
Y = {0, 1} where 0 corresponds to the background
and 1 to the foreground. Let X = {x
1
, x
2
, . . . , x
N
} be
a discrete random field defined over a set of pixels
V = {1, 2, . . . , N}. Every x
i
∈ X associated with a
pixel i ∈ V , is assigned a value y
i
from the label set
Y .
A Conditional Random Field is a discriminative
undirected probabilistic graphical model, used to pre-
dict the values of the latent (unobserved) variables
given a set of observed variables. Mathematically,
this is expressed by the a posteriori probability P(y|x)
where y ∈ Y
n
is the segmentation for an image of n
pixels and x represents a set of features computed (in
our case) from an RGBD frame. According to the
Hammersley-Clifford theorem (Lafferty et al., 2001),
a Conditional Random Field can be expressed in the
form of a Gibbs distribution in the following way:
P(y|x) =
1
Z(x)
exp(−E(y, x)) (1)
where Z is known as the normalized or partition func-
tion. The energy function E(y, x), corresponds to a
Gibbs submodular energy function and contains all
the factors for the unary and pairwise potentials which
we will extensively go through in the upcoming sec-
tions. Our proposed energy function takes the form:
E(y, x) = w
N
∑
j∈V
ψ
j
(y, x) + w
E
∑
( j,k)∈N
j
ψ
jk
(y, x) (2)
where ψ
j
(y, x) is a node potential function defined
in our framework by the product of two condition-
ally independent events introduced in Section 3.4.1,
ψ
jk
(y, x) is an edge potential function capturing dif-
ferent pairwise relations in RGBD space as discussed
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
656

in Section 3.4.2 and w
N
,w
E
are the node and edge
potential weights respectively. Our proposed energy
function uses a 4-neighbourhood relation.
Given a set of features x, Eq. 1 can efficiently be
solved by finding a labeling y ∈ Y
n
that maximizes the
Maximum A Posteriori (MAP) inference, satisfying
the following statement:
maximize
y∈L
P(y|x) = minimize
y∈L
E(y, x) (3)
As we will analyze in Section 3.3, equation 1 can-
not be solved exactly due to the existence of the par-
tition function in the gradient. A solution to this, is
to solve the energy function exactly using graph cuts.
According to (Boykov and Kolmogorov, 2004), if an
energy function is submodular, then it can be solved
exactly and in polynomial time using graph cuts.
3.2 Object Detection
We employ an accelerated version of the deformable
part-based detector (Felzenszwalb et al., 2010) intro-
duced by (Dubout and Fleuret, 2013) with the ex-
act same performance but with convolutions of an
order of magnitude faster than the original version.
Due to the non rigidness of the human figure, train-
ing over different parts can generate better prediction
outputs for the position and size of the object. Let
D = {d
1
, . . . , d
n
} represent the amount of detections
found in an image and S = {s
1
, . . . , s
n
} the corre-
sponding detection scores. In order to ensure that the
detector will find all true positives, a lower detection
threshold t
d
is required. This will produce a large
amount of false positives but will guarantee all true
positive solutions. For eliminating all false positives
and preserving only the correct detection outputs, we
convert the detection scores into conditional probabil-
ities. Platt scaling (Platt, 1999) (also known as Platt
calibration) is used to relate the detection scores with
the conditional probabilities according to the follow-
ing regression formulation:
P(c|s
i
) =
1
1 + exp(A ∗ s
i
+ B)
∀s
i
∈ S, c ∈ C (4)
where A, B are the parameters of the sigmoid and can
be found by minimising the negative log likelihood of
the training or validation set and C = {c
B
, c
F
} corre-
spond to the foreground/background classes.
In order to obtain a background probability for
every detection rectangle, the following formulation
should hold:
P(c
B
|s) + P(c
F
|s) = 1, ∀s ∈ S (5)
Detection rectangles with probabilities smaller
than a predefined probability threshold are classified
as background.
3.3 Learning
Learning process involves finding a set of weights w
returning the lowest energy E(y, x) for the current
graph. If x = {x
1
, x
2
, . . . , x
n
} corresponds to a set of
RGBD features computed as shown by Algorithm 1
and D = {(y
1
, d
1
), (y
2
, d
2
), . . . , (y
n
, d
n
)} corresponds
to a set of training images, where y
n
represents the
ground truth image and d
n
an RGBD frame, the goal
is to learn the parameters that maximize the likeli-
hood:
max
w
∏
n
P(y
n
|x
n
) (6)
As already stated in Section 3.1, it is not feasi-
ble to solve the objective condition 6 exactly, due to
the existence of the partition function in the gradient.
The partition function Z(x) =
∑
y
exp(E(y, x)) has an
exponential number of constraints, as it sums up all
possible 2
n
solutions, where n the number of pixels in
the image, making this problem intractable and com-
putationally very expensive.
Algorithm 1: Generate RGBD features.
Require: S = {(y
1
, d
1
), (y
2
, d
2
), . . . , (y
n
, d
n
)}
1: D =
/
0
2: for (y
m
, d
m
) ∈ S do
3: Compute all features x
m
D := D ∪ {(y
m
, x
m
)}
4: end for
5: return D
Tsochantaridis in (Tsochantaridis et al., 2005)
proposed an approach known as the structured sup-
port vector machine (SSVM) which tries to solve the
objective condition 6 using margin maximization op-
timization techniques. This method was later on used
by (Szummer et al., 2008) for the purpose of image
segmentation.
In this paper, we employ the one-slack margin
rescaling SSVM introduced by (Joachims et al.,
2009) which efficiently solves the minimization prob-
lem. The learning process is presented by Algorithm
2. Here, C and ε are constant values, w = {w
N
, w
E
}
are the weights that have to be optimized for a given
training set D , ξ is a slack variable and ∆ represents
a loss function (in our case, a Hamming loss). Within
this learning process, we enforce that the ground truth
Human Recognition in RGBD Combining Object Detectors and Conditional Random Fields
657

Algorithm 2: Structured SVM.
Require: A set of training examples D, constant values C, ε
W ←
/
0
repeat
Update the parameters w to maximize the margin
minimize
w, ξ
1
2
kwk
2
+C ξ
subject to w ≥ 0, ξ ≥ 0
1
M
M
∑
m=1
E(
ˆ
y
m
, x
m
) − E(y
m
, x
m
) ≥
1
M
M
∑
m=1
∆(y
m
,
ˆ
y
m
) − ξ
∀ (
ˆ
y
1
, . . . ,
ˆ
y
M
) ∈ W
(7)
for (y
m
, x
m
) ∈ D do
ˆ
y
m
← argmin
y
E(y, x
m
)
end for
W ← W ∪ {
ˆ
y
1
, . . . ,
ˆ
y
M
}
until
1
M
∑
M
m=1
∆(y
m
,
ˆ
y
m
) − E(
ˆ
y
m
, x
m
) + E(y
m
, x
m
) ≤ ξ + ε
energy will have the lowest value from all other label-
ings. If this constraint is not satisfied, or if the mar-
gin is not achieved, this label solution will be added
in the constraint set. This process continues until
the values of the weights have converged. Accord-
ing to (Joachims et al., 2009), the objective function
is quadratic to w and linear to the constraints, also
known as a quadratic programming problem. Main
advantage is that it is a convex quadratic problem and
can guarantee a global minimum. We implement the
Nesterov non linear quadratic optimization algorithm,
which is part of a family of algorithms known as inte-
rior point solvers, for minimizing the objective func-
tion 7.
3.4 Potentials
3.4.1 Node Potentials
Every pixel in the image should be classified as fore-
ground or background label, based on a cost defined
in the unary term of energy function 2. In this frame-
work, the cost is expressed by the product of two con-
ditionally independent probability events, formulated
as follows:
ψ
j
(y, x) =
(
p
1
(x
j
)p
2
(x
j
), if y
j
= 1
0 otherwise,
where p
1
(x
j
) is the probability of pixel x
j
to be as-
sign a foreground label according to a learned prior
shape probability map (see Algorithm 3) and p
2
(x
j
)
refers to the probability of pixel x
j
to belong to the
foreground, based on the probability outcome of a de-
cision tree classifier, trained on RGB features.
Algorithm 3: Generate shape prior map.
Require: A sequence of label images y
m
and corre-
sponding RGB images I
m
of a person in the scene:
S = {(y
1
, I
1
), (y
2
, I
2
), . . . , (y
n
, I
n
)}
1: R =
/
0
2: for (y
m
, I
m
) ∈ S do
3: Get detection rectangle from image I
4: Extract the corresponding rectangle from la-
bel image y
m
5: Resize rectangle to a 128× 64 sized image r
m
6:
R := R ∪ {r
m
}
7: end for
8: return The probability map of R
Shape Prior - The probability p
1
(x
j
) of pixel x
j
to be assigned to the foreground class is based on a
learned prior shape probability map. Every detection
rectangle contains regions of pixels which do not cor-
respond to the object of interest (e.g. corners of the
rectangle). Using a shape prior, we penalize these re-
gions by assigning them a low probability. The shape
prior map is learned according to Algorithm 3 and ex-
ample is illustrated in Figure 2(a). It basically corre-
sponds to the expectation of each pixel to belong to
the foreground, based on the available training data.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
658

(a) (b) (c) (d)
Figure 1: Different edge potentials: Canny edges (a), color distance (b), 3D Euclidean distance. (c), surface normals (d).
(Best viewed in colour).
(a) (b)
Figure 2: Unary potentials: Shape prior map (a), decision
tree output(b).
Decision Trees Ensemble - As prior probability,
p
1
(x
j
) is completely independent of the measured
RGBD data of a specific image. A data-dependent
initial estimate is represented by p
2
(x
j
), which cor-
responds to the probabilistic output of a pixel-wise
classification based on the Projection-Based Random
Forest (ProB-RF) framework introduced in (H
¨
ansch,
2014). The ProB-RF classifier is used to assign
each pixel a posterior probability to belong to either
foreground or background based on many simple bi-
nary features extracted implicitly by the decision trees
themselves. Figure 2(b) shows the estimated classifi-
cation map of an exemplary scene. Since this estima-
tion is only based on local, appearance-based infor-
mation it cannot provide highly accurate and reliable
results. However, this first pixel-wise probability es-
timate serves as an additional cue to the shape prior
and is now used in the global optimization framework
of CRFs.
3.4.2 Edge Potentials
Edge potentials capture the similarity between pixels
lying within a local neighbourhood (also known as
Markov blanket). Taking into consideration the rich-
ness of RGBD information, two points sharing the
same label should be assigned a cost greater than zero.
Specifically,
ψ
jk
(y, x) =
(
α
jk
if y
j
= y
k
0 otherwise,
Different pairwise relations were evaluated within
the RGBD domain:
Canny Edges - Canny edge extractor is a very
known operator for extracting strong edges in an im-
age. Within this framework, Canny edges are used for
finding the boundaries between areas and objects, as-
signing a value of 1 for neighbourhood pixels that do
not lie on a Canny edge and 0 otherwise.
Color Distance - Points which are part of the same
neighbourhood should have similar colors. Specifi-
cally,
α
jk
= exp

−
kc
j
− c
k
k
σ
c

(8)
where c
j
, c
k
correspond to the RGB values of points
j and k respectively and σ
c
is a bandwidth parameter
whose value is set through cross validation.
3D Euclidean Distance - 3D points which are
very close to each other are more likely to share the
same label. This relationship is expressed by:
α
jk
= exp

−
|(p
j
− p
k
)
T
n
k
|
σ
n
−
kp
j
− p
k
k
2
σ
d

(9)
where p
j
, p
k
correspond to the 3D values of points
j and k respectively, n
k
is the surface normal at point
p
k
and σ
n
, σ
d
are bandwidth parameters whose values
are defined by cross validation.
Surface Normals - 3D points lying on the same
part of the body should have similar normal orienta-
tions. Concretely,
α
jk
= exp

−
θ
σ
θ

(10)
where θ is the angle between two neighbourhood nor-
mals and σ
θ
is a bandwidth parameter whose value is
specified by cross validation.
Human Recognition in RGBD Combining Object Detectors and Conditional Random Fields
659

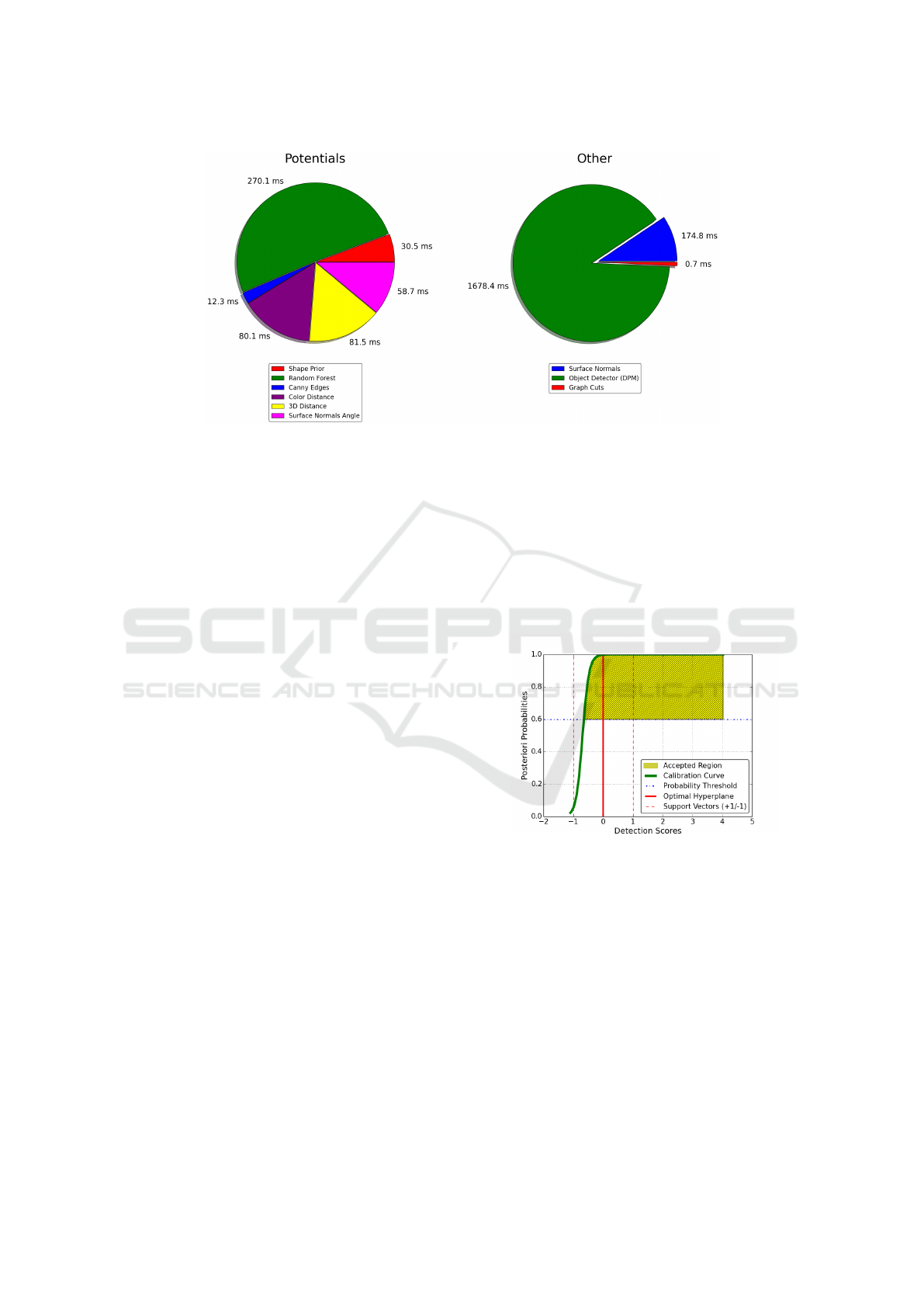
Figure 3: Average computation time for every node potential, edge potential, surface normals, object detector and graph cuts.
(Best viewed in colour).
4 EXPERIMENTAL RESULTS
4.1 Quantitative Analysis
We evaluate our method in an indoor environment,
formed for the purpose of carrying out detection, seg-
mentation and generally recognition tasks within the
internal part of a simulated train wagon. A Kinect
sensor is mounted on an aluminium construction,
looking into the complete FOV of the scene. We cre-
ate a dynamic environment, capable of generating dif-
ferent quality point clouds, depending on the amount
of reflected areas/lightning conditions present in the
scene. Current state of our work performs validation
only on human instances but we plan to extend the
evaluation also on different deformable objects which
could potentially appear in an indoor environment.
Edge potentials defined on depth measurements
require high precision between points lying in the lo-
cal neighbourhood. Although Kinect sensor uses low
distortion lenses with faintly apparent displacement
errors around the corners/edges of the images, we per-
form a calibration of the infrared and RGB cameras
for improving the quality/accuracy of the 3D points
placed on these regions.
A total of 25 sequences were generated, every se-
quence containing 200 frames. From all 5000 images,
3000 images over 15 sequences were used for training
and the rest for testing. The same training set is used
for learning the weights of the structured SVM, shape
prior and decision tree ensemble.
To the best of our knowledge, there is no pub-
licly available RGBD dataset providing label images
with ground truth detection boxes for the task of hu-
man instance detection and segmentation. Generating
ground truth label images is a very time consuming
process as it requires a lot of manual work by the user.
For eliminating the effort, reference images were gen-
erated using the approach of (Shotton et al., 2013), a
well known human pose estimation algorithm which
was also commercialised for Kinect games.
Figure 4: Learned calibration curve from the PASCAL
VOC dataset. (Best viewed in colour).
We learn the calibration curve for converting de-
tector scores into conditional probabilities from the
publicly available PASCAL VOC dataset (Evering-
ham et al., 2015). The resulting curve is shown in
Figure 4. As it is expected, the calibration curve takes
the form of a sigmoid function, capable of switching
between scores and probabilities. For a detection rect-
angle to be assigned to the background class, a prob-
ability threshold of 0.6 was given.
The average computational times recorded for a
complete scene are presented in Figure 3. It is ob-
served that node and edge potentials require minimal
effort within the pipeline while most time is needed
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
660

Figure 5: These figures outline the improvement in quality of our segmentation approach using the ground truth box rather
than the detection box provided by (Dubout and Fleuret, 2013). From top to bottom: segmentation result using the detection
box computed by (Dubout and Fleuret, 2013); segmentation result using the bounding box extracted by the ground truth label
images; ground truth label images. (Best viewed in colour).
Table 1: Results in a tabular form; Every row represents a different metric evaluator; Every column corresponds to a different
edge potential; Top table presents segmentation results produced by the ground truth detection box; Bottom table presents
segmentation results from (Dubout and Fleuret, 2013).
GROUND TRUTH BOUNDING BOX
Metric
Edge Pot.
Canny Edges Color Distance 3D Euclidean Distance Surface Normals
Hamming Loss
5508.970 5566.37 5464.600 5504.360
± 1626.130 ± 1667.510 ± 1590.560 ± 1896.560
Norm. Hamming Loss 0.758 ± 0.063 0.755 ± 0.069 0.760 ± 0.064 0.758 ± 0.079
PASCAL Seg. Acc. 0.799 ± 0.050 0.797 ± 0.056 0.801 ± 0.052 0.798 ± 0.071
DETECTION RECTANGLE (Dubout and Fleuret, 2013)
Hamming Loss
8012.790 7907.000 7911.910 7936.520
± 2578.160 ± 2308.790 ± 2205.740 ± 2178.710
Norm. Hamming Loss 0.646 ± 0.113 0.651 ± 0.104 0.651 ± 0.102 0.650 ± 0.098
PASCAL Seg. Acc. 0.705 ± 0.093 0.712 ± 0.076 0.710 ± 0.075 0.710 ± 0.074
by the object detector. For a VGA image resolution,
our implementation takes ≈ 1.5s per frame. Graph
cuts require the least effort (0.7ms) as they can be
solved in polynomial time. Experiments were per-
formed on a DELL M4800 Workstation, i7-4800MQ
CPU at 2.70GHz processor and 16GB RAM. The
complete pipeline is designed in a multithreaded fash-
ion, parallelising all computations.
4.2 Qualitative Analysis
Segmentation approach was assessed using three dif-
ferent metrics: Hamming loss, normalized Hamming
loss (Teichman et al., 2013) and the intersection over
union loss proposed in (Everingham et al., 2015).
Similarly, the detector was evaluated using a formu-
lation introduced by (Everingham et al., 2015). The
normalized Hamming loss is considered a hard penal-
ization metric compare to the other evaluators, as it
Human Recognition in RGBD Combining Object Detectors and Conditional Random Fields
661

Figure 6: Results of human instance segmentations in RGBD space. (Best viewed in colour).
gives a zero loss if the number of incorrectly labeled
pixels is equal or exceeds the number of pixels corre-
sponding to foreground in the label image.
We provide a comparison evaluation between the
different metrics (see Table 1) computed over 2000
test images. Is it evident that all metrics computed
by the ground truth bounding box show an overall
improvement in the segmentation accuracy, outper-
forming the results produced by the detection box of
(Dubout and Fleuret, 2013). Furthermore, comparing
the metrics computed by the different edge potentials,
it is easy to perceive the insignificance between the
values. This can be explained as follows: as we are
not using any hard constrains such as a manual seed
frame (Teichman et al., 2013) to force the s-t min cut
towards a desired shape, we use the edge potentials
which have a node potential larger than a predefined
probability threshold. Thus, only the edge potential
values which lie at the borders of the object should
effect the cut.
We produce several human instance segmenta-
tions over 10 sequences, presenting only a fraction of
them in Figure 5. All edge potentials discussed in
Section 3.4.2 generated similar segmentation results
making it hard to notice any visual differences. The
main differences between the edge potentials are nu-
merically given in Table 1. As a result, we are in-
terested in showing how the quality of our approach
is effected by different detection boxes. Looking at
columns 1-3, it is clear that using the ground truth
bounding box, a more precise segmentation is pro-
duced. However, columns 4 and 5 show cases were
the segmentation delivers poorer results. This is a
consequence of assigning high weights to the source
node in the graph cut algorithm combined with strong
edge potentials in that region. Furthermore, we be-
lieve that extreme poses may effect the quality of the
segmentation but this is currently under investigation.
The accuracy of the detection box was checked
against the ground truth bounding box over 10 se-
quences using the quality metric introduced by (Ev-
eringham et al., 2015), achieving an overlapping ac-
curacy of 72.3%.
Finally, all bandwidth parameter values related to
the edge potentials were set to: σ
c
= 0.3, σ
n
= 0.5,
σ
d
= 0.5, σ
θ
= 0.2.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
662

5 CONCLUSIONS AND FUTURE
WORK
In this paper, we propose an approach for detecting
and segmenting human instances in a point cloud,
based on an accelerated version of the deformable part
model algorithm and a pairwise CRF energy function
defined over different RGBD features. Experiments
showed that the quality of the segmentation depends
highly on the detection box provided from the detec-
tion algorithm. Also, metric results between the dif-
ferent edge potentials did not provide a significant dif-
ference between them.
Current work in progress is in the direction of
improving the unary potentials, incorporating depth
based features for the decision tree ensemble but also
generating a score map taking into account the scores
returned by the detector.
In the future, we are planning to investigate the
extension of the proposed energy function for incor-
porating higher order potentials (defined over a set of
pixels) using appearance or depth information. We
believe that adding shape constraints will deliver bet-
ter segmentation results compared to the ones mod-
elling only up to pairwise relations. Furthermore, we
are also interested in looking into additional solutions
for improving the quality of the detection boxes. Last
but not least, our proposed algorithm will be tested
and evaluated on different objects for verifying its ro-
bustness, using pairwise but also higher order poten-
tials in the energy function.
REFERENCES
Boykov, Y. and Kolmogorov, V. (2004). An experimental
comparison of min-cut/max-flow algorithms for en-
ergy minimization in vision. IEEE Trans. Pattern
Anal. Mach. Intell., 26(38):1124–1137.
Dubout, C. and Fleuret, F. (2013). Deformable part mod-
els with individual part scaling. In Proceedings of the
British Machine Vision Conference (BMVC), pages
28.1–28.10.
Everingham, M., Eslami, S. M. A., Van Gool, L., Williams,
C. K. I., Winn, J., and Zisserman, A. (2015). The
pascal visual object classes challenge: A retrospec-
tive. International Journal of Computer Vision,
111(38):98–136.
Felzenszwalb, P. F., Girshick, R. B., McAllester, D., and
Ramanan, D. (2010). Object detection with discrimi-
natively trained part-based models. IEEE Trans. Pat-
tern Anal. Mach. Intell., 32(9):1627–1645.
Gupta, S., Girshick, R., Arbel
´
aez, P., and Malik, J. (2014).
Learning rich features from RGB-D images for object
detection and segmentation. In Proceedings of the Eu-
ropean Conference on Computer Vision (ECCV).
H
¨
ansch, R. (2014). Generic object categorization in Pol-
SAR images - and beyond. PhD thesis, Technische
Universit
¨
at Berlin, Germany.
Hariharan, B., Arbel
´
aez, P., Girshick, R., and Malik, J.
(2014). Simultaneous detection and segmentation.
In Proceedings of the European Conference on Com-
puter Vision (ECCV).
Joachims, T., Finley, T., and Yu, C.-N. J. (2009). Cutting-
plane training of structural svms. Mach. Learn.,
77(1):27–59.
Ladicky, L., Sturgess, P., Alahari, K., Russell, C., and Torr,
P. H. S. (2010). What, where and how many? combin-
ing object detectors and crfs. In Daniilidis, K., Mara-
gos, P., and Paragios, N., editors, ECCV, volume 6314
of Lecture Notes in Computer Science, pages 424–
437. Springer.
Lafferty, J. D., McCallum, A., and Pereira, F. C. N. (2001).
Conditional random fields: Probabilistic models for
segmenting and labeling sequence data. In Proceed-
ings of the Eighteenth International Conference on
Machine Learning, ICML ’01, pages 282–289, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
Lai, K., Bo, L., Ren, X., and Fox, D. (2012). Detection-
based object labeling in 3d scenes. In IEEE Interna-
tional Conference on on Robotics and Automation.
Platt, J. C. (1999). Probabilistic outputs for support vector
machines and comparisons to regularized likelihood
methods. In Advances in Large Margin Classifiers,
pages 61–74. MIT Press.
Shotton, J., Girshick, R. B., Fitzgibbon, A. W., Sharp, T.,
Cook, M., Finocchio, M., Moore, R., Kohli, P., Crim-
inisi, A., Kipman, A., and Blake, A. (2013). Efficient
human pose estimation from single depth images.
IEEE Trans. Pattern Anal. Mach. Intell., 35(12):2821–
2840.
Shu, G., Dehghan, A., and Shah, M. (2013). Improving
an object detector and extracting regions using super-
pixels. In Proceedings of the 2013 IEEE Conference
on Computer Vision and Pattern Recognition, CVPR
’13, pages 3721–3727, Washington, DC, USA. IEEE
Computer Society.
Szummer, M., Kohli, P., and Hoiem, D. (2008). Learn-
ing crfs using graph cuts. In European Conference
on Computer Vision.
Teichman, A., Lussier, J. T., and Thrun, S. (2013). Learning
to segment and track in rgbd. IEEE T. Automation
Science and Engineering, pages 841–852.
Tsochantaridis, I., Joachims, T., Hofmann, T., and Altun,
Y. (2005). Large margin methods for structured and
interdependent output variables. J. Mach. Learn. Res.,
6:1453–1484.
Vibhav Vineet, Jonathan Warrell, L. L. and Torr, P.
(2011). Human instance segmentation from video us-
ing detector-based conditional random fields. In Pro-
ceedings of the British Machine Vision Conference,
pages 80.1–80.11. BMVA Press.
Human Recognition in RGBD Combining Object Detectors and Conditional Random Fields
663